《材料力学》中剪力图和弯矩图的快易绘图法
3材料力学 静定悬臂梁受集中力和均布力的剪力图和弯矩图 解题过程

求下图的剪力方程和弯矩方程,作剪力图和弯矩图,并求最大弯矩。
1.问题分析:属于受集中力、均布力的悬臂梁,静定。
2.将B点的固定约束去掉,以F BX,F BY,M代替支座反力,如下图所示。
利用静力平衡方程求解如下:
∑F x=0,得出:F BX=0(1)∑F Y=0,得出:F+ql−F BY=0(2)∑M B=0,得出:ql×l+ql×(0.5l)−M=0(3)由方程(1)、(2)、(3)解得:F BX=40,F BY=2ql, M=1.5ql2
3.剪力方程和剪力图
求解出未知的支座反力后,梁的受力如下图所示。
剪力的正负按照“左上右下,剪力为正”来判断。
剪力方程如下:
F s=−ql−qx
当x=0时,F S=−ql
当x=l时,F S=−2ql
剪力图如下图所示。
4.弯矩方程和弯矩图
弯矩的正负按照“左顺右逆,弯矩为正”来判断。
弯矩方程如下:
M=−qlx−qx×(0.5x)=−0.5qx2−qlx 当x=0时,M=0
当x=l时,M=−1.5ql2
弯矩图如下图所示。
弯矩的最大值M max=−1.5ql2。
剪力图和弯矩图(最全面)-剪刀图弯矩图特征 PPT

P q
Pa 2
qa2 2
A
BM
x x
+ P
=
=+
A
B M1
Pa 2
+
+
q
qa 2
A
B M2
2 +
x
三、对称性与反对称性的应用: 对称结构在对称载荷作用下,Q图反对称,M图对称;对称
结构在反对称载荷作用下,Q图对称,M图反对称。
[例8] 作下列图示梁的内力图。
P
PL
Q
x
0L 0.5P L 0.5P L
q AB
RA qa Q qa/2
+ – qa/2
qa2 CD
RD
– qa/2
M
qa2/2
+
–
3qa2/8 qa2/2
qa2/2
解:求支反力 RAq2a; RDq2a
左端点A:
Q qa; M 0 2
x
B点左: Qqa;M1qa2
2
2
B点右: Q qa;M1qa2
2
2
C点左: Qqa;M1qa2
M
– N图
P1a
M图 P1a+ P2 l
二、曲杆:轴线为曲线的杆件。 内力情况及绘制方法与平面刚架相同。
[例11] 已知:如图所示,P及R 。试绘制Q、M、N 图。
解:建立极坐标,O为极点,OB
R
P
极轴,q表示截面m–m的位置。
A
q
B
O
x
q q qq M ( ) P P ( R x R c ) o P ( 1 c s R ) ( o 0 s )
q q q Q () P 1 P si( n 0)
绘制工程力学剪力图和弯矩图的简易方法-力学论文-物理论文

绘制工程力学剪力图和弯矩图的简易方法-力学论文-物理论文——文章均为WORD文档,下载后可直接编辑使用亦可打印——0引言工程力学中,直梁的弯曲变形是杆件受力变形的基本形式之一,在对梁进行强度和刚度计算时,通常要画出剪力图和弯矩图,以便清楚地看出梁的各个截面上剪力和弯矩的大小、正负以及最大值所在截面的位置[1].但不少学生在学习剪力图和弯矩图绘制知识点时,直呼太难,根本不知从何下手。
因此,总结出一套行之有效的简易绘制剪力图和弯矩图的方法,显得越来越重要。
下面就结合作者实际教学经验,提出解决此类问题的简易方法。
1绘制剪力图和弯矩图的简易方法绘制剪力图和弯矩图时,应严格遵循下列基本步骤:①画梁的受力图,求约束力求出梁上所有约束部位的约束力是至关重要的第一步,这一步如果出现问题,后续步骤基本进行不了,关于求约束力的方法,在画好受力分析图后列平衡方程式即可求得。
②画剪力图。
画剪力图时,应牢记下面几句话:集中力作用处,剪力图有突变,突变幅值等于集中力的大小,突变的方向与力的方向同向;集中力偶作用处,剪力图无变化;均布载荷作用的梁段上,剪力图为一条斜直线;无外力作用的梁段上,剪力图为水平的直线。
对于剪力图为斜直线,只需确定直线的两个端点所对应的剪力值即可确定该直线,要求两个端点所对应的剪力值,采用某截面上的剪力值等于截面左边梁上所有外力的代数和,外力向上,则剪力为正,反之为负的方法。
③画弯矩图画弯矩图时,也须牢记以下几句话:集中力作用处,弯矩图有折点;集中力偶作用处,弯矩图有突变,突变幅值等于力偶矩的大小,力偶方向若为顺时针,则弯矩向上突变,反之向下突变;均布载荷作用的梁段,弯矩图为二次曲线,曲线开口方向与均布载荷同向,在剪力为零的截面,弯矩有极值;无外力作用的梁段,弯矩为直线。
对于弯矩为二次曲线的,只需取曲线上三个特殊的点,求出该点所对应截面的弯矩值即可确定该曲线,而求某截面上弯矩值,采用某截面上的弯矩值等于截面左边梁上所有外力矩的代数和,外力矩为顺时针的,弯矩为正,反之为负的方法。
快速绘制剪力图和弯矩图(25)
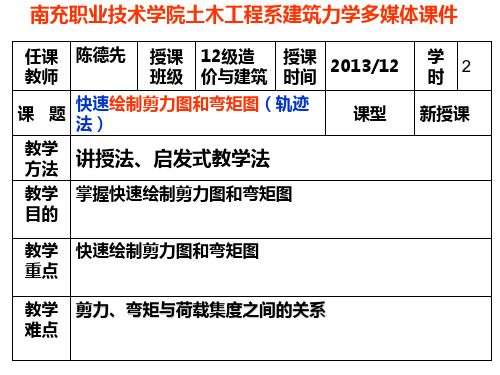
二、荷载图、剪力图、弯矩图的规律 1、无荷载作用的梁段: A、微分关系 剪力图为水平线,弯矩图为斜直 线,斜率的大小等于对应梁段上剪力的 大小。V>0时弯矩图下斜(\),V<0时弯矩 图上斜(/),V=0时弯矩图为水平线(-)。 B、积分关系 斜直线弯矩图上升或下降的铅直 高度等于该段剪力图面积。
南充职业技术学院土木工程系建筑力学多媒体课件
任课 教师 课 题 教学 方法 教学 目的 陈德先 授课 班级 12级造价 授课 2013/12 与建筑 时间 学 时 2
快速绘制剪力图和弯矩图(轨迹 法)
课型
新授课
讲授法、启发式教学法
掌握快速绘制剪力图和弯矩图
教学 重点
教学 难点
快速绘制剪力图和弯矩图
剪力、弯矩与荷载集度之间的关系
D、若梁段上剪力图为位于基线下方的斜直 线,则画一条上升曲线,曲线的凸向与荷载 集度指向一致,曲线上升的铅直高度等于该 梁段剪力图面积; E、若遇集中力偶作用截面,力偶顺时针转 时,则向下画铅直线,力偶逆时针转时,则 向上画铅直线,铅直线的长度等于该集中力 偶的力偶矩; F、若遇铰链,弯矩图必过铰链中心。 注:由以上方法画得的轮廓线与基线所围图 形加上正负号,即得梁的弯矩图(弯矩图可 不标正负号)。
四、快速绘制剪力图和弯矩图举例
4kN m
6kN
2kN m
4.5kN
4.5
1m
1m
2m
5.5kN
+
1.5
_
5.5
FQ(kN)
4
8.5 7
M(kN
D E
40kN m
B
40 kN
F
C
310 kN 2m
120
运用简捷方法绘制剪力图和弯矩图2Mx

教学目标
1、掌握梁在不同外荷载作用下的内力变化规律; 2、能够根据梁的内力规律用简捷法快速绘制梁的内力图。
目录
6.3.1 M(x)、FQ(x)与q(x)之间的关系
6.3.2 M(x)、FQ(x)与q(x)之间的关系在绘制内力图时的应用
6.3 弯矩、剪力与分布荷载集度之间的关系
dFQ ( x ) dx q( x)
dM ( x ) FQ ( x ) dx
d 2 M ( x ) dFQ ( x ) q( x) 2 dx dx
dFQ ( x ) dx
q( x)
dM ( x ) FQ ( x ) dx
d 2 M ( x ) dFQ ( x ) q( x) 2 dx dx
说明: (1)此即适用于平面载荷作用情形 的平衡微分方程。 (2)根据上述微分方程,由 载荷变 化规律,即可推知内力FQ 、M 的变 化规律。
(3)要明确各式的物理意义。
物理意义:
1)FQ图上各点的斜率等于梁上对应位置处的分布载荷集度。 2)M图上各点的斜率等于梁上对应截面上的剪力值。当剪力 FQ =0时,弯矩图在对应截面处产生极值。 3)由q的正负判断M图的凹凸性。
D R A =58kN
1m 1m
G
1m
20 4 18 26 32.4 6 18
12
10
M图(单位kN·m)
MC 0 M A 20 M D 18 M E 26 M F 18 M G左 6 M G右 4
M B左 16
课 后 作 业
P181 (6)(d)
法求出这些控制截面的内力值,按比例绘出相应的内力竖标
,便定出了内力图的各控制点。
梁的内力图剪力图和弯矩图ppt正式完整版

VA<D0段时3:向q右<0上,方V倾图斜为,x向V=下=30.斜时1m直为线水,平线。
3.8
3
2.2
(kN·m)
1.41 3.8
AD段:q<0, V 图为向下斜直线, M图为下凸抛物线。
谢谢观看
vv vv
vv v v
v
利用上述规律:
1、可以检查剪力图和弯矩图是否正确。 2、可以快速的绘制剪力图和弯矩图,步骤如下: (1)将梁正确分段 (2)根据各段梁上的荷载情况,判断剪力图和弯矩图的 形状
(3)寻找控制面,算出各控制面的V和M (4)逐段绘制出V和M图即梁的V和M图
快速绘制剪力图和弯矩图 q
画剪力图和弯矩图时,一定要将梁正确分段, 分段建立方程,依方程而作图
例题1 简支梁受均布荷载作用,如图示, 作此梁的剪力图和弯矩图。
解:1.求约束反力 由对称关系,可得:
2、建立内力方程
Vx
RAq
x1q 2
l q
x
(0<x<l)
3、依方程作剪力图和弯矩图
Vmax=
1 ql 2
Mmax 1 ql 2 8
例2 简支梁受集中荷载作用,如图示, 作此梁的剪力图和弯矩图。
1.求约束反 力 2、分段建立方程 AC段: V
CB段: V
3、依方程而作图
例题3 简支梁受集中力偶作用,如图示,试画梁的剪 力图和弯矩图。 解:1.求约束反力
2.列剪应力方程和弯矩方程 AC段: V
CB段:V
3、依方程而作图
荷载图、剪力图、弯矩图的规律
A
C
D
B
FA
ac
l
FA
b
FB
FB
工程力学之剪力图与弯矩图(PPT46页)
Fy=0, FP-FQC=0
M C=0,
M
+
C
M
-
A
FP
l=0
FQC= FP
M
=
C
FP
l
结果均为正值表明所假设 的C截面上的剪力和弯矩的 正方向是正确的。
MA=0 MO=2FPl
F
P
DB
3、应用截面法确定D截面 上的内力分量
F左P 部A本分l例梁C中,所如选果l 择以的C、研究D剪截对力面象假和以都设弯右是截矩部C开均、分横为梁D截正截作面方面为上向以平的。
根据2-2截面右侧的外力计算Q2 、 M2 Q2 =+(q·1.5)-RB =12·1.5-29 =-11kN
M2 =-(q·1.5)·1.5/2+RB·1.5 =-(12·1.5)·1.5/2+29·1.5 = 30 kN·m
Q3 M3
Q2 RA
RA qa 2a qa
a
qa 4 3qa
2
2
A
通的过外上力述相计平算衡可,以因看而出可,以截直Q面接4上通的过q内一a 力侧 与杆RB该段截上面的3一外q4侧力a 杆直上接
RA
求得截面Q上3 的内力.
M4
5qa2 4
★ 可以直接通过截面一侧杆段上的横向力的代数和直 接求得截面上的剪力,通过一侧杆段上横向力对截面 的力矩以及力偶之代数和求得截面上的弯矩
梁横截面推上导应弯力曲非应均力匀和分变布形,公式强;度失效最先从 应力最大点处建发立生弯。曲其强强度度和计刚算度不设计仅方要法考。虑内力最 大的“危险截面”,而且要考虑应力最大的“危险 点”
绝大多数细长梁的失效,主要与正应力有关, 剪应力的影响是次要的。
材料力学-5-弯矩图与剪力图
FQ
q=0
x
x M
FQ x
q=0
x
M
FQ
q>0
x
x
M
FQ
q>0
x
x
M
FQ
q>0
x
x
M
FQ
q<0
x
x M
FQ
q<0
x
x
M
FQ
q<0
x
x M
剪力图与弯矩图
表示剪力和弯矩沿梁轴线方向变化的图形, 分别称为剪力图(diagram of shearing forces)和 弯矩图(diagram of bending moment)。
FQC=FP MC=FPl
MA=0 MO=2FPl
A
C
FP
l
MA=0 MO=2FPl
A
FP
l
3. 应用截面法确定D截面上的内力:
FP
DB
用假想截面将梁D截面处截 开,以左边部分为平衡对象。
l
D l
MA=0 MO=2FPl
A
C
FP
l
FP
D B
l
MA=0 MO=2FPl
A
FP
l
FQD
D
l
MD
假设截开横截面上的剪力和弯 矩均为正方向。根据截开的局部平 衡建立平衡方程:
在外力作用下,梁的横截面上将产生剪力和弯矩两种内力。
在很多情形下,剪力和弯矩沿梁长度方向的分布不是均匀的。
对梁进行强度计算,需要知道哪些横截面可能最先发生失 效,这些横截面称为危险面。弯矩和剪力最大的横截面就是首 先需要考虑的危险面。
材料力学利用微分关系画剪力弯矩图
2
8
8
dFS (x) q dx
dM (x) 5ql dx 8 qx FS
d
2M (x) dx2
dFS (x) dx
q
BUAA
MECHANICS OF MATERIALS
基于截面平衡法:
MD
FBy xD
q 2
xD2
9ql 2 128
B U A A由微分关系得到的ME积CH分AN关ICS系OF MATERIALS
横截面之间的弯矩平衡约束关系
FS FSa
A
FSb B
a b SaABb
x
M
Mb M a SaABb
Ma
Mb x
BUAA
MECHANICS OF MATERIALS
M D M B SBDE
DE
1 2
xD
3ql 8
9ql 2 128
微分法巧妙地结合上积分法,会使得计算 大为简化而快捷!
BUAA
截面的下边缘或位于截面中间得到了相同的结果;
Page37
BUAA
MECHANICS OF MATERIALS
1700年左右雅各布.伯努利认为自己首先发现梁弯曲时一 边受拉、另一边受压,但无法确定中性轴的位置。最后 提出“中性轴位置无关紧要”的结论。
1713年法国学者帕伦假定中性轴不通过截面型心,横截面 上拉力和压力呈不同的三角形分布。但他认识到了截面上 的内力必须与载荷平衡。
FS
(x)
d 2M (x) dx2 q
平衡微分方程的含义: (1) 数学含义 (2) 力学含义 (3) 几何含义
BUAA
MECHANICS OF MATERIALS
Page7
剪力图与弯矩图的画法38页PPT
•
6、黄金时代是在我们的前面,而不在 我们的 后面。
•
7、心急吃不了热汤圆。
•
8、你可以很有个性,但某些时候请收 敛。口 (蹩脚 的工人 总是说 工具不 好)。
•
10、只要下定决心克服恐惧,便几乎 能克服 任何恐 惧。因 为,请 记住, 除了在 脑海中 ,恐惧 无处藏 身。-- 戴尔. 卡耐基 。
31、只有永远躺在泥坑里的人,才不会再掉进坑里。——黑格尔 32、希望的灯一旦熄灭,生活刹那间变成了一片黑暗。——普列姆昌德 33、希望是人生的乳母。——科策布 34、形成天才的决定因素应该是勤奋。——郭沫若 35、学到很多东西的诀窍,就是一下子不要学很多。——洛克
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《材料力学》中剪力图和弯矩图的快易绘图法
[摘 要]在《材料力学》中,绘制平面弯曲梁的剪力图和弯矩图是“直梁的弯
曲”一章中的重点和难点,传统的规律绘图法用到的一次函数、 二次函数和导数
等相关知识,对于数学基础不很扎实的中专生来说是很难理解的。本文中作者利
用几何图形的面积来绘制剪力图和弯矩图,其方法更为简便快捷。
[关键词]剪力图 弯矩图 面积
在《材料力学》中,直梁的弯曲变形是杆件受力变形的基本形式之一,在对
梁进行强度和刚度计算时,通常要画出剪力图和弯矩图(即把剪力方程和弯矩方
程用函数图象表示出来)以便清楚地看出梁的各个截面上剪力和弯矩的大小、正
负以及最大值所在截面的位置。目前绘制剪力图和弯矩图最常用的规律绘图法中
用到一次函数、 二次函数和导数等相关知识,这对于数学基础不很扎实的中专
生来说是很难理解的。通过教学,作者在原有绘图方法的基础上,利用几何图形
的面积代替一次函数、 二次函数和导数来绘制剪力图和弯矩图的规律,谨供广
大同仁参考。具体方法为:从上至下依次画出直梁的受力分析图——剪力图(直
角坐标系)——弯矩图(直角坐标系),其图象遵循“平行线——斜直线——抛物
线”的顺序,其剪力和弯矩的变化值等于对应的上一个几何图形的面积,其它事
宜与原方法同。
例:一外伸梁受力如图a)所示,已知P=6kN, q=2kN/m,a=1m,绘出梁的
剪力图和弯矩图。
解:(1)求支座反力NA和MA
选整个梁为研究对象,由平衡方程求得NA= 10kN,MA= 18kN.m。
(2)绘制剪力图
A点作用有向上的集中载荷NA和逆时针转向的集中力偶MA,因集中力偶
对剪力图没有影响,故剪力图只在集中力NA的作用下从零值向上突变10 kN;
A、B点之间的剪力图为平行于x轴的直线;B点作用有向下的集中力P,剪力
图向下突变P=6kN,变为4 kN;B、C之间的剪力图为平行于x轴的直线;CD
段作用有向下的均布载荷q=2kN/m,所以剪力图为从4 kN开始向下倾斜的直线,
因此D点剪力值为4 kN -4 kN=0,如图b)所示。
(3)绘制弯矩图
A点作用有逆时针转向的集中力偶MA= 18kN.m,故从A点零开始,向下
突变18 kN.m,AB段剪力图为位于x轴上方且平行于x轴的直线,因此其弯矩
图为向上倾斜的直线,AB段弯矩的变化值为对应的剪力图围成的矩形的面积,
即10kN×1 m =-10 kN.m,因此B点弯矩值为-18kN .m +10 kN.m =-8 kN.m;BC
段剪力图为位于x轴上方且平行于x轴的直线,因此其弯矩图为向上倾斜的斜直
线,BC段弯矩的变化值为对应剪力图所围成的矩形的面积,即4kN×1 m =-4
kN.m,因此C点弯矩值为-8kN .m +4kN.m =--4 kN.m;CD段剪力图为向下倾斜
的直线,因此其弯矩图为开口向下的抛物线,CD段弯矩的变化值为对应剪力图
所围成的三角形的面积,即4kN×2 m/2 =-4 kN.m,因此D点弯矩值为-4kN .m
+4kN.m =0kN.m,如图c)所示。
(4)检验
剪力图和弯矩图均从零开始,最终回到零点,可认为是正确的。
参考文献
[1]王亚双.工程力学[M].北京:中国计量出版社,2006.
[2]张二红,张华龙.小议《工程力学》中剪力图和弯矩图的规律绘图法[J].河
北机电教育,2003(1).
