质点动力学习题课
高二物理竞赛质点动力学习题课件

燕雀安知鸿鹄之志哉。
自信是成功的第一秘诀
有志始知蓬莱近,无为总觉咫尺远。
有志者自有千方百计,无志者只感千难万难。
大丈夫处世,不能立功建业,几与草木同腐乎?
2-6. A、B、C三个物体,质量分别是 mAmB0.1kg, mC 0.8kg,当如图(a)放置时,物体系正好作匀速运
球,使小球从悬挂着的位置以水平初速度 v 0 开始运动,
求小球沿逆时针转过 角度时的角速度和绳子张力。
解:法向方程
Tmcgosm2l
mv022g(lcos1) l
l
m
v0
Tmvl022g3gcos
2-9. 质量均为M的三条小船以相同的速率 v沿一直线同 向航行,从中间的小船向前后两船同时以相同速率 u (相对于该船)抛出质量同为 m的小包。从小包被抛出
2 2mg 5
2-8. 长为l的轻绳,一端固定,另一端系一质量为m的小
球,使小球从悬挂着的位置以水平初速度 v 0 开始运动,
求小球沿逆时针转过 角度时的角速度和绳子张力。
解:在任一时刻,牛顿第二定律的切向方程
m sg i n m d vm sg id n s m dd vs
dt
dt
l
解:在任一时刻,牛顿第二定律的切向方程
绳与滑轮的质量和所有摩擦不计。
1 1 5 比较(1)(2)式解得:
2
W k(3L) k(2L) kL 一质量为m的滑块,沿图示轨道以初速度
2
2
无摩擦地滑动,求滑块由A运动到B的过程中所受的冲量。
2 2 98kg,弹簧的弹性系数为k=100N/m,子弹以初速度
第2章 质点动力学 习题答案
2该-1质. 点质以量为v0.225jkm g的s质1点的,速受度力通过F坐标ti原的点作,用则,该t=质0 点时
大学物理第2章 质点动力学习题(含解答)

第2章质点动力学习题解答2-1如图所示,电梯作加速度大小为a 运动。
物体质量为m ,弹簧的弹性系数为k ,•求图示三种情况下物体所受的电梯支持力(图a 、b )及电梯所受的弹簧对其拉力(图c )。
解:(a )ma mg N =-)(a g m N +=(b )ma N mg =-)(a g m N -=(c )ma mg F =-)(a g m F +=2-2如图所示,质量为10kg 物体,•所受拉力为变力2132+=t F (SI ),0=t 时物体静止。
该物体与地面的静摩擦系数为20.0=s μ,滑动摩擦系数为10.0=μ,取10=g m/s 2,求1=t s 时,物体的速度和加速度。
解:最大静摩擦力)(20max N mg f s ==μmax f F >,0=t 时物体开始运动。
ma mg F =-μ,1.13.02+=-=t mmgF a μ 1=t s 时,)/(4.12s m a =dtdv a =,adt dv =,⎰⎰+=t v dt t dv 0201.13.0t t v 1.11.03+=1=t s 时,)/(2.1s m v =2-3一质点质量为2.0kg ,在O x y 平面内运动,•其所受合力j t i t F 232+=(SI ),0=t 时,速度j v 20=(SI ),位矢i r20=。
求:(1)1=t s 时,质点加速度的大小及方向;(2)1=t s时质点的速度和位矢。
解:j t i t m Fa+==223 223t a x =,00=x v ,20=x ⎰⎰=t v x dt t dv x 0223,23t v x =⎰⎰⎰==txtx dt t dt v dx 03202,284+=t xt a y =,20=y v ,00=y⎰⎰=tv y tdt dv y02,222+=t v y⎰⎰⎰+==tyty dt t dt v dy 020)22(,t t y 263+=(1)1=t s 时,)/(232s m j i a +=(2)j t i t v )22(223++=,1=t s 时,j i v2521+= j t t i t r )26()28(34+++=,1=t s 时,j i r613817+=2-4质量为m 的子弹以速度0v 水平射入沙土中,设子弹所受阻力与速度反向,大小与速度成正比,比例系数为k ,忽略子弹的重力,求:(1)子弹射入沙土后,速度随时间变化的关系;(2)子弹射入沙土的最大深度。
习题课-质点力学

d 2s v2 dv v2 v ˆ ˆ ˆ a = 2 τˆ + n = τˆ + n = aττˆ + an n dt R dt R
角加速度
dω β= dt v v
aτ = β R an = ω R
2
3. 运动学两类问题的求解 已知质点的运动方程,求质点的状态 微分 已知质点的运动方程,求质点的状态—微分 已知质点的状态,求质点的运动方程 积分 已知质点的状态,求质点的运动方程—积分 三 注意区分
t1
v v 1 dA = F ⋅ dr = dEk Ek = mv 2
Aab = ∫
rb ra
力的空间积累效应
2 v v F ⋅ dr = Ekb − Eka
uu d L v M= u v dtv v L=r×p
第三定律
v v v v v v Fij + Fji = 0, ri × Fij + rj × Fji = 0
dx 2 v= = 9t − 6t dt
d2x a = 2 = 9 − 12t dt
从上式可见质点开始时沿x 正向运动, 从上式可见质点开始时沿 正向运动,而加 速度在0.75s后反向,所以运动有折返。正确的解 后反向, 速度在 后反向 所以运动有折返。 法是找到运动折返的时刻。 法是找到运动折返的时刻。 dx v=0 即 =0 由 dt x1.5 = xmax t = 1.5s 得 x1 所以 x2 X1.5
dω = 2dt
∫θ
t
θ + 75
dθ = ∫
t +5
t
2tdt
∫
ω
0
d ω = ∫ 2dt
0
75 = (t + 5)2 − t 2
质点动力学习题
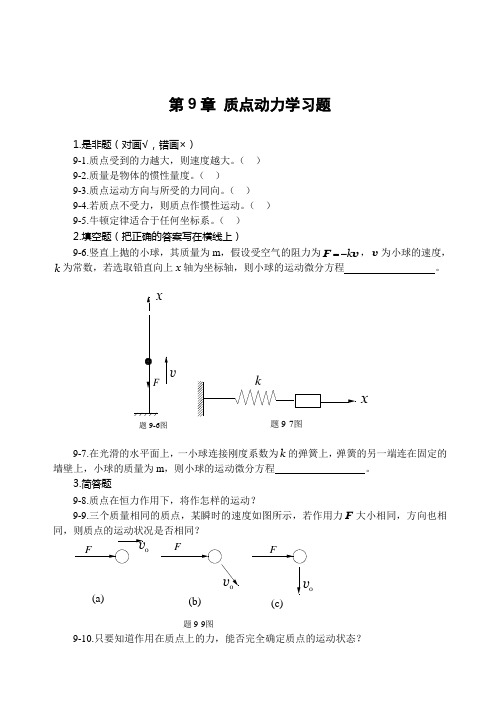
第9章 质点动力学习题1.是非题(对画√,错画×)9-1.质点受到的力越大,则速度越大。
( ) 9-2.质量是物体的惯性量度。
( ) 9-3.质点运动方向与所受的力同向。
( ) 9-4.若质点不受力,则质点作惯性运动。
( ) 9-5.牛顿定律适合于任何坐标系。
( ) 2.填空题(把正确的答案写在横线上)9-6.竖直上抛的小球,其质量为m ,假设受空气的阻力为v F k -=,v 为小球的速度,k 为常数,若选取铅直向上x 轴为坐标轴,则小球的运动微分方程 。
xv题 9-6图x题 9-7图9-7.在光滑的水平面上,一小球连接刚度系数为k 的弹簧上,弹簧的另一端连在固定的墙壁上,小球的质量为m ,则小球的运动微分方程。
3.简答题9-8.质点在恒力作用下,将作怎样的运动?9-9.三个质量相同的质点,某瞬时的速度如图所示,若作用力F 大小相同,方向也相同,则质点的运动状况是否相同?v v 0(a)(b)(c)题 9-9图9-10.只要知道作用在质点上的力,能否完全确定质点的运动状态?4.计算题9-11.质量m =2kg 的重物M 挂在长为l =1m 的绳子下端,已知重物受到水平冲击力而获得的速度为v =5m/s ,如图所示,试求该瞬时绳子的拉力。
9-12.小球重为P ,用两个细绳吊起,如图所示,已知细绳与铅垂线的夹角为 ,现突然剪断其中一根绳子,试求此时另一根绳子的拉力。
题 9-11图B题 9-12图9-13.如图所示,A 、B 两物体的质量分别为1m 、2m ,两者用一根绳子连接,此绳跨过一滑轮,滑轮的半径为r ,若初始时,两物体的高度差为h ,且1m >2m ,不计滑轮的质量,试求两个物体到达相同的高度时所需要的时间。
9-14.半径为R 的偏心凸轮,绕轴O 以匀角速度ω转动,推动导板沿铅直轨道运动,如图所示。
导板顶部放一质量为m 的物块A ,设偏心距为OC=e ,初始时,OC 沿水平线,试求物块对导板的最大压力以及使物块不离开导板时的角速度ω的最大值。
质点和刚体力学习题课.ppt [修复的]
![质点和刚体力学习题课.ppt [修复的]](https://img.taocdn.com/s3/m/c2fcbdfd172ded630b1cb654.png)
平动动能: 力的功:
转动动能: 力矩的功: 动能定理: 注意:
b A a F dr
动能定理: A外 Ek 功能原理:
A外 Ek
能量 关系
A外 A非保内 E E0
机械能守恒:
1. 对于刚体,做功的还应有外力矩的功
2. 机械能应为势能+平动动能+转动动能
A外 A非保内 0 E 0
x x( t )
(2) 分量式
y y( t )
(2) 瞬时速度 (简称速度)
Δr dr v lim v lim Δ t 0 Δt 0 Δt dt
(1-7)
vA
A
B2 B 1
B
速度 = 位置矢量对时间的一阶导数。
★ 直角坐标系中:
v AB
(1-9)
a
方向:
tan a y a x
★ 注意:
位矢
、位移 、速度 Δr r v
、加速度 a
1. 矢量性: 四个量都是矢量,有大小和方向,
加减运算遵循平行四边形法则。
2. 瞬时性:
r, v, a
瞬时量(不同时刻不同) 过程量
Δr
3. 相对性:不同参照系中,同一质点运动描述不同;
1 2 J l ml 3
定轴转动刚体的转动惯量具有可加性。
复习 1. 质点和刚体(mass point, particle and rigid body)
⑴ 物体不形变,不作转动(此时物体上各点的速度及加速度 都相同,其任一点的运动可以代表物体所有点的运动)。 ⑵ 物体本身的线度和它活动的范围相比小得很多(此时物体 的形变及转动显得并不重要)。
质点运动学习题课

1 dv=a; 2 dr =v;
dt
dt
3 ds=v; 4
dt
dv dt
=at.
下述判断正确的是( D )
A 只有1、4是对的 (B) 只有2、4是对的
C 只有2是对的 D 只有3是对的
1-4 一个质点在做圆周运动,则有( B ) (A)切向加速度一定改变,法向加速度也改变 (B)切向加速度可能不变,法向加速度一定改变 (C)切向加速度可能不变,法向加速度不变 (D)切向加速度一定改变,法向加速度不变
法向加速度 an t1s a2 at2 en 1.79 en (m / s2 )
解法2:t 1s时速度和加速度分别为 v 2i 4 j (m / s), a 4 j (m / s2 )
将加速度a分解到平行于速度方向及垂直于速度方向
at
an
4 t=1.0s质点的速度大小为 v
解:(1)
由参数方程
x
y
2t 19
2t 2
消去t
轨迹方程
y
19
x2 2
(2) t 1s 位矢为r1 2i 17 j(m); t 2s 位矢为r2 4i 11 j(m)
平均速度 v r r2 r1 2i 6 j (m / s) t t2 t1
同一平面内且与水平面的夹角分别为1 和2,则任意时刻两
质点的相对速度是一常量。 √
分析:在任意 t 时刻,两质点的速度分别为
v1 v10 gt, v2 v20 gt
此时,两质点间的相对速度为
v2 v1 v20 v10
故相对速度为一常量,正确。
2 质点动力学习题
题图一1a习题二一、选择题1.如图一1a 所示,A 、B 两物体由弹簧连接,竖直悬挂,开始静止。
绳子刚被剪断时,A 、B 两物体的加速度分别为,.;0,2.;2,.;,.========B A B A B A B A a g a D a g a C g a g a B g a g a A 答案:2. 一轻绳跨过一定滑轮,两端各系一重物,它们的质量分别为1m 和2m ,且12m m > (滑轮质量及一切摩擦均不计),此时系统的加速度大小为a ,今用一竖直向下的恒力1F m g =代替1m ,系统的加速度大小为a ',则有 [ ](A )a a ='; (B )a a >'; (C )a a <'; (D )条件不足,无法确定。
答案: 。
3.如图所示,系统置于以g /2加速度上升的升降机内,A 、B 两物块质量均为m ,A 所处桌面是水平的,绳子和定滑轮质量忽略不计。
(1)若忽略一切摩擦,则绳中张力为 [ ] (A )mg ;(B )mg /2;(C )2mg ;(D )3mg /4。
(2)若A 与桌面间的摩擦系数为μ (系统仍加速滑动),则绳中张力为 [ ] (A )mg μ;(B )3/4mg μ;(C )3(1)/4mg μ+; (C )3(1)/4mg μ-。
答案:(1) ; (2) 二、填空题1.m R a H ω=沿半球型碗的光滑内面,质量为的小球以角速度在一水平面内作匀速圆周运动,碗的半径为,如图二1所示。
则该小球作圆周运动的水平面离碗底的高度。
2.质量为m 的质点在变力F=F 0 (1-kt )(F 0、k 为常量)作用下沿ox 轴作直线运动。
若t =0时,质点在坐标原点,速度为v 0,则质点运动微分方程为 ;2ga =x R题图二1aa aa 1m 121速度随时间变化规律为v = ;质点运动学方程x = 。
三、计算题1在光滑的水平桌面上有一根质量均匀分布的细绳,质量为m 、长度为L ,其一端系一质量为M 的物体,另一端施加一水平拉力F ,如图三1a 所示。
质点力学习题课
质点力学习题课
【例3】已知质点运动方程 r 2ti (4 t 2 ) j ①质点的初速度和初加速度; ②质点从 t =1s 到 t =2s 的平均速度; ③t=1s时的切向加速度和法向加速度。
(3)、因为任一时刻的速度大小为
2 2 v vx vy 2 1 t2
解:设子弹穿过后两物体的速度分别为vA、 vB, 子弹穿过物体A时有: A B
F t1 ( m A m B )v A F t 1 vA m A mB
子弹继续穿过物体B时有
F t 2 m B v B m B v A F t 2 vB v A mB
例2、一陨石从距地面高为h处由静止开始落向地 面,忽略空气阻力,求陨石下落过程中,万有引 力的功是多少? a 解:取地心为原点,引力与矢径方向相反 h R b A F d r Rh R R Mm G dr 2 o Rh r
u
(1)在地面上的人认为刚抛出 瞬时小球的动能
1 1 2 2 对不对? Ek mu mv 2 2 1 1 1 2 2 2 Ek mu地 mu mv mu v 2 2 2
(2)当车上的人沿车前进的方向抛出小球,车上和地上的 人看抛出小球过程所作的功是否一样?
v
GMm
R Rh
GMmh R (R h)
dr 1 1 GMm 2 r R h R
【例3】已知质点运动方程 r 2ti (4 t 2 ) j (SI),求: ①质点的初速度和加速度; ②质点从 t =1s 到 t =2s 的平均速度; ③t=1s时的切向加速度和法向加速度。 dr 解:(1)、 v 2 i 2 tj , a 2 j dt -1 故v 0 2i (m s ), a 0 2 j (m s - 2 ) (2)、r1 2i 3 j r2 4i r r2 r1 2i 3 j (m) r v 2i 3 j (m s -1 ) t
第02章 质点动力学习题
dt v0 = 3(m / s ), v 4 = 19(m / s)
1 1 2 2 根据动能定律,有: A = mv 4 − mv 0 = 176( J ) 2 2 dv = 6t − 8 或: a =
A=∫
( 2)
4
(1)
0
dt ( 2) Fdx = ∫ madx
(1)
= ∫ (6t − 8) d (3t − 4t 2 + t 3 ) = 176 ( J )
dv 解:(1) f = − kv = m , dt vm
2
∴ 得: v =
v 1 k ∫0 m dt = ∫v0 v 2 dv t
0
(2)∵ dx = vdt ∴
m + kv0t
∫
x
k dv dv dv 2 ∴− dx = = mv = − Kv , (3) f = m m v dt dx k − x v0 k 积分可得: x = ln , v = v0 e m m v
m kv0 得x = ln( dt 0 m + kv t 0
t
11
7
3.已知氢原子中电子的质量为 已知氢原子中电子的质量为9.11×10-31 kg,它绕原子核 已知氢原子中电子的质量为 × 它绕原子核 运动的平均半径为5.29×10-11 m,角速度为 ,角速度为4.13×1016 × 运动的平均半径为 × × rad/s,则它绕原子核运动的角动量为 1.05×10-34 kg·m2/s 。 , 分析:
dv dv dx 2 1) F = ma = m =m ⋅ = mkv = mk x dt dx dt
dx dx dx , dt = = 2)根据 v = dt v kx t2 x1 dx 1 x1 两边积分得:∆t = dt = ∫ = ln ∫t1 x0 kx k x0
质点力学习题课
牛顿运动定律的应用
第四页,编辑于星期五:五点 四十六分。
•冲量
I=
t2
Fdt
t1
•动量定理
I Fdt= P
•质点系的动量定理
I=P-P0
•动量守恒定律
n
P=
mivi
恒矢量
i 1
•功与功率
dW F dS
P= dW dt
•质点的动能定理
W
1 2
mv
2 2
1 2
mv
2 1
第五页,编辑于星期五:五点 四十六分。
•万有引力、重力、弹性力
作功的特点
•质点系的功能原理
重力势能 E p mgy
Mm
引力势能 E p G r
弹性势能
Ep
1 2
mx 2
•质点系的动能定理
n
n
n
Wi Eki Eki0
i 1
i 1
i 1
W外力+W非保守外力=E-E0
•机械能守恒定律
n
n
n
n
Eki
E
=
pi
Eki0
E pi 0
解:(1)取物体为研究对象,则物体受重力、水平面的支持力和绳对 物体的拉力,如图所示,在竖直方向上,物体无运动,因而有
Mg-N=0
在水平方向上,根据牛顿第二定律,
可得绳拉物体的力为
T=Ma
第十六页,编辑于星期五:五点 四十六分。
(2)以绳为研究对象,绳受到物体的作用力和手的作用力,假 设绳的质量为m,则
计算结果为:
mg sin cos a1 M m sin2
(M m sin )sin a2 M m sin2 g
a2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章教学基本要求:
⒈理解牛顿运动定律的基本内容,掌握牛顿运动定律的适用条件。
⒉掌握常见力的性质和计算方法,能熟练地分析物体受力。
⒊熟练掌握运用牛顿定律和运动学知识解题的思路和步骤,并能科学地表
述。能用微积分方法求解一维变力作用下的质点动力学问题。
内容提要:
牛顿定律
第一定律: 任何物体如果不受其它物体的力的作用,就会保持静止或匀速
直线运动的状态。
第二定律:
当质量m 为常量时,
在直角坐标系中,
在自然坐标系中,
第三定律:
力学问题中的几个常见力
万有引力 G
重力 mg
弹簧力 f = -kx
正压力与支持力 N= -N′
滑动摩擦力 fμ??= μN
静摩擦力 fμ??≤μN
习题1:
一半径为
的环形竖直壁固定在光滑的水平面上,如题图所示,一质量为
的物块紧靠着壁的内侧在水平面上运动。已知物块与环形壁之间的摩擦系数为
,
时物块的速率为
,求物块的速率
随时间t的变化关系。
解: 研究对象:
受力:
自然坐标系
方程:
法向:
(1)
切向:
(2)
(3)
求解:由 上 述 各 式 可 得
分离变量法
得:
习题2:
一细绳跨过光滑的定滑轮,一端挂一m重物,另一端被人用双手拉着,人悬空,
质量
m/2,若人以相对于绳的加速度
向上爬,且不打滑,求:人相对于地的加速度。
解:如图建坐标,
分别选人和重物
为对象,
受力分析,
设m对地加速度为a:
对
:
对人:
解得:
人相对于地的加速度为
习题3:
一根弯成如图所示形状的金属丝,其上套一小环,设环与金属丝间的摩擦可
略去不计.当金属丝以匀角速度ω绕竖直对称轴转动时,小环在金属丝上任何地方
都能平衡,即与金属丝无相对运动,问这根金属丝要弯成什么形状?
?
mg
解 : 小环受力如图所示, 当小环位置坐标为
时其动力学方程为 :
而
,
所以
积分得
由
,
定出
.
此即金属丝形状所满足的方程,应为顶点即坐标原点,口向上的抛物线。
习题4:
如图,升降机内有两个物体,质量分别为m1=100g和m2=200g,用细绳连接
后跨过滑轮;绳子的长度不变,绳和滑轮的质量、滑轮轴上的摩擦及桌面的摩擦均
可略去不计.当升降机以匀加速度a=4.9 m·s 2上升时,
(1)在机内的观察者看来,m1和m2的加速度各是多少?
(2)在机外地面上的观察者看来,它们的加速度又各是多少?
解 :
的受力如图。
设
相对升降机的加速度大小为
,方向为
水平向右,
竖直向下。因此对
分别用牛顿第二定律列方程如下 :
m2g
m1g
m1
m2
解得
m/s2
(1)
机内观察者看 :
地面上观察者看 :
作业:P135,2.15(用牛顿定律求解)
