动力学例题
3.牛顿定律-典型例题-详解

牛顿定律第2课时牛顿第二定律动力学问题题型探究题型1 区分绳与弹簧的特点【例1】如图所示,A、B两球质量相等,光滑斜面的倾角为θ,图甲中,A、B两球用轻弹簧相连,图乙中A、B两球用轻质杆相连,系统静止时,挡板C 与斜面垂直,轻弹簧、轻杆均与斜面平行,则在突然撤去挡板的瞬间有( )A.两图中两球加速度均为gsin θB.两图中A球的加速度均为0C.图乙中轻杆的作用力一定不为0D.图甲中B球的加速度是图乙中B球的加速度的2倍题型2 弹簧的动态分析【例2】如图所示,自由下落的小球下落一段时间后与弹簧接触,从它接触弹簧开始,到弹簧压缩到最短的过程中,小球的速度、加速度的变化情况如何?题型3 与弹簧相连的连接体问题【例3】两个质量均为m的相同的物块叠放在一个轻弹簧上面,处于静止状态.弹簧的下端固定于地面上,弹簧的劲度系数为k.t=0时刻,给A物块一个竖直向上的作用力F,使得两物块以0.5g的加速度匀加速上升,下列说法正确的是()A.A、B分离前合外力大小与时间的平方2t成线性关系B.分离时弹簧处于原长状态C.在t 时刻A、B分离D.分离时B题型4 斜面上的自由滑动问题【例4】一间新房即将建成时要封顶,考虑到下雨时落至房顶的雨滴能尽快地流淌离开房顶,要设计好房顶的坡度(房顶的底边长度相同).设雨滴沿房顶下流时做无初速度无摩檫的运动,那么,下图所示的情况中符合要求的是()A. B.C. D.【例5】如图所示,在光滑水平面AB上,水平恒力F 推动质量为m=1kg的物体从A点由静止开始做匀加速直线运动,物体到达B点时撤去F,接着又冲上光滑斜面(设经过B点前后速度大小不变,最高能到达C.用速度传感器测量物体的瞬时速度,表中记录了部分测量数据),(1)恒力F的大小.(2)斜面的倾角α.(3)t="2.1" s时物体的速度.题型5 等时圆问题【例6】如图所示,AD是固定斜面体底边BC的高,F、G分别是光滑斜面AB、AC的中点DE垂直于AB,DH 垂直于AC,甲、乙两个小球(均视为质点)从斜面的顶点A分别沿斜面AB、AC同时由静止下滑,下列说法正确的是()A.当甲球运动到E点时,乙球可能运动到AG间某点B.当甲球运动到E点时,乙球一定运动到H点C.当甲球运动到F点时,乙球一定运动到G点D.当甲球运动到F点时,乙球一定运动到H点题型6 滑环与杆问题【例7】.如图所示,一端固定在地面上的杆与水平方向的夹角为θ,将一质量为m1的滑块套在杆上,滑块通过轻绳悬挂一质量为m2的小球,杆与滑块之间的动摩擦因数为μ.先给滑块一个沿杆方向的初速度,稳定后,滑块和小球一起以共同的加速度沿杆运动,此时绳子与竖直方向的夹角为β,且β>0,不计空气阻力,则滑块的运动情况是( )A.沿着杆减速上滑B.沿着杆减速下滑C.沿着杆加速下滑D.沿着杆加速上滑【例8】有一质量m=2kg的小球套在长L=1m的固定轻杆顶部,杆与水平方向成θ=37o角.静止释放小球,1s后小球到达杆底端.取重力加速度大小g= 10 m/s2,sin37o=0.6,cos37o=0.8.(1)求小球到达杆底端时速度为多大?(2)求小球与杆之间的动摩擦因数为多大?(3)若在竖直平面内给小球施加一个垂直于杆方向的恒力,静止释放小球后保持它的加速度大小为1m/s2,且沿杆向下云动,则这样的恒力为多大?题型7轻绳连接问题【例9】如图所示,材料相同的物体m l、m2由轻绳连接,在恒定拉力F的作用下沿斜面向上加速运动。
微生物动力学计算例题

12 85 23.58 0.60( g . g 1 ) 180 72 180
例题
【例题4】荧光假单胞菌(Psenudomonas fluorescens)好氧培 养,已知:YX/S=180g/mol,YX/O=30.4g/mol,每消耗1mol葡萄糖 可生成2molATP,氧化磷酸化的P:O比为1,求YATP?
100C 6 H12O6 12NH 3 57Cw H xOy Nz 43C3 H5 (O H) 3 154CO 2 130C 2 H 5O H 3.6H 2O
3-1-3 微生物反应过程的计量学
各元素平衡式为
C : 600 57w 43 3 154 130 2 w 1 H : 1200 12 3 57x 43 8 130 6 3.6 2 x 1.84 O : 600 57 y 43 3 154 2 130 3.6 y 0.52 N : 12 57z z 0.21
3-1-3 微生物反应过程的计量学
【例题3】葡萄糖为碳源,NH3为氮源进行酵 母厌氧培养。培养中分析结果表明,消耗100 mol葡萄糖和12 mol NH3生成了57 mol 细胞、 43 mol甘油、130 mol乙醇、154 mol CO2和 3.6 mol H2O,求酵母的经验分子式。 【解】由题意写出相应的反应方程式为
(1) (2) (3) (4)
3-1-3 微生物反应过程的计量学
已知 RQ = 0.6,即 d = 0.6a,5个式联立求解
a 2.394 b 0.085 c 0.564 d 1.436 e 2.634
所以,反应式为
( 5) ( 6) ( H 2.394O2 0.085NH3 0.564(CH1.75N0.15O0.5 ) 1.436CO2 2.634H 2O
大学物理WJA动力学2

在直角坐标系中
A= ∫
b
a
b v v F ⋅ dr = ∫ (Fxdx + Fydy + Fz dz) a
几个力同时作用在质点上,合力所作的功 几个力同时作用在质点上,
r r r W = ∫ F ⋅ dr = ∫ (Fx + Fy + Fz + ⋅ ⋅ ⋅) ⋅ dr
由矢量标积的分配律,上式为 由矢量标积的分配律, r r r r r r W = ∫ F ⋅ dr + ∫ F ⋅ dr + ∫ F ⋅ dr + ⋅ ⋅ ⋅ 1 2 3
v10
m 1
v20
m2 m m2 1
碰撞
v1
m 1
碰撞后
v2
m2
碰撞前
恢复系数: 恢复系数:碰撞后两球的分离速度与碰撞前两球 的接近速度的比值 e = v2 − v1
v − v20 10
系统动量守恒 m v10 + m2v20 = m v1 + m2v2 1 1 v2 = v + (v − v20 )e 而 1 10 可得
x
作用力和反作用力的元功之和 v v v dW = dW + dW = f21 ⋅ (dr2 − dr ) 1 1 2
v v = f21 ⋅ d r 21
成对力的总功只与相互作用力 相对位移有关 成对力的总功只与相互作用力及相对位移有关 相互作用力及
注意:1 “功”的特殊定义 2 功是过程量 3 摩擦力也可以作正功 4 功是标量,有正负之分
2、质点的动能定理 质点的动能定理
v v r QF ⋅ dr = F cosθ dr v = F dr r
v = mat dr dv v =m dr dt
易错点06 牛顿三定律 两类动力学问题(解析版)

易错点06牛顿三定律 两类动力学问题例题1. (2022·浙江·高考真题)物流公司通过滑轨把货物直接装运到卡车中。
如图所示,倾斜滑轨与水平面成24°角,长度14m l =,水平滑轨长度可调,两滑轨间平滑连接。
若货物从倾斜滑轨顶端由静止开始下滑,其与滑轨间的动摩擦因数均为29,货物可视为质点(取cos240.9︒=,sin 240.4︒=,重力加速度210m /s g =)。
(1)求货物在倾斜滑轨上滑行时加速度1a 的大小; (2)求货物在倾斜滑轨末端时速度v 的大小;(3)若货物滑离水平滑轨末端时的速度不超过2m/s ,求水平滑轨的最短长度2l 。
【答案】(1)22m/s ;(2)4m/s ;(3)2.7m 【解析】(1)根据牛顿第二定律可得1sin 24cos 24mg mg ma μ︒-︒=代入数据解得212m/s a =(2)根据运动学公式2112a l v =解得4m/s v =(3)根据牛顿第二定律2mg ma μ=根据运动学公式2222max 2a l v v -=-代入数据联立解得2 2.7m l =【易错警示】误选A 的原因:错误认为货物在倾斜滑轨上滑行时摩擦力为mg μ,导致货物在倾斜滑轨上滑行时加速度1a 的大小算错,后边两问跟着错。
理解好计算滑动摩擦力的公式f N F F F μμ==压例题2. (多选)(2022·黑龙江·哈尔滨三中模拟预测)如图所示,一足够长的传送带倾斜放置,倾角θ= 37°,以恒定速率v =4m/s 顺时针转动。
一煤块以初速度v 0=12m/s 从A 端冲上传送带,煤块与传送带之间动摩擦因数μ=0.25,取g =10m/s 2,sin37°= 0.6、cos37°= 0.8。
则下列说法正确的是( )A .煤块冲上传送带后经1s 与传送带速度相同B .煤块向上滑行的最大位移为10mC .煤块从冲上传送带到返回A 端所用的时间为5sD .煤块在传送带上留下的痕迹长为(5m 【答案】ABD 【解析】A .对煤块先做匀减速,由牛顿第二定律可得1sin cos mg mg ma θμθ+=解得218m /s a =设经t 时间与传送带共速,由01v a t v -=解得1s t =故A 正确;B .共速后,摩擦力方向向上,由牛顿第二定律2sin cos mg mg ma θμθ-=解得224m /s a =煤块先以12m/s 的初速度,8m/s 2的加速度减速至4m/s ,后又以4m/s 2的加速度减速至0,再反向加速至回到A 点,v -t 图像如图所示由图像煤块上升到最高点的位移大小等于速度时间图线与时间轴所包围的面积的大小11(124)1m 41m 10m 22x =⨯+⨯+⨯⨯= 故B 正确;C .物块上升到最高点后反向向下做初速度为零,加速度为224m /s a =的匀加速直线运动,设返回到A 点所需的时间为t 1,下滑的位移22112x a t = 解得15s t结合图像知,物块从冲上传送带到返回A 端所用时间为(25)s t =总故C 错误;D .在0到1s 内传送带比物块速度慢,则滑块在传送带上的划痕为11(124)1m 41m 4m 2L =⨯+⨯-⨯=此时划痕在物块的下方,在1s 到2s 内,传送带速度比物块速度大,则2141m 41m 2m 2L =⨯-⨯⨯=因为L 2<L 1,所以在上升阶段产生的划痕为4m ,此时煤块在产生的划痕的中点,在2s 到(25)s 时间内,煤块向下滑了10m ,传送带向上滑了45m ,则煤块在传送带上的划痕为3(10452)m (1245)m L =+=+故D 正确。
偏微分方程与机械系统的动力学例题

偏微分方程与机械系统的动力学例题以下是一个关于偏微分方程在机械系统动力学中的应用的例题:假设有一个长度为L的杆件,其横截面为圆形,半径为r。
该杆件由弹簧支撑,并且在其一端有一个质量为m的物体。
当物体以加速度a下落时,求出该杆件的振动频率。
为了解决这个问题,我们需要使用偏微分方程来描述杆件的运动。
假设杆件的运动是轴对称的,即横截面的形状保持不变。
首先,我们可以将问题转化为求解偏微分方程。
对于轴对称的杆件,可以使用以下偏微分方程来描述其振动:mL^2(ddif/dt)^2 + T(r) = A(r)其中,mL是杆件的长度,T(r)是作用于杆件上的力,A(r)是杆件在r处的加速度。
为了求解这个偏微分方程,我们需要给出T(r)和A(r)的表达式。
由于杆件是由弹簧支撑的,所以T(r)可以表示为:T(r) = -k(r)(L - L0) - mgh(r)其中,k(r)是依赖于位置r的弹簧劲度系数,L0是弹簧的自然长度,gh(r)是距离基准位置r的高度。
而A(r)可以通过牛顿第二定律得出:A(r) = -mL^2ddif/dt - T(r)/m将上述表达式代入偏微分方程中,得到:mL^2(ddif/dt)^2 + k(r)(L - L0) + gh(r) - mgh(r) = A(r)接下来,我们可以使用数值方法求解这个偏微分方程。
具体的方法包括有限差分法、有限元法等。
这些方法可以将偏微分方程转化为离散的形式,并通过计算机求解。
最后,我们可以将求解得到的频率进行归一化处理,以便于后续的应用。
归一化处理可以将频率与国际单位制下的标准频率进行比较,从而方便对结果进行分析和比较。
典型例题分析(动力学)

典型例题分析(动力学)一、自由度1.判断自由度的数量。
二、单自由度体系的自振频率1. 试列出图1a结构的振动方程,并求出自振频率。
EI=常数。
图1a 图1b M1 图1c M2分析:(1) 质点m 的水平位移y 为由惯性力和动荷载共同作用引起:()()t F ym y p 1211δδ+-= 。
(2) 挠度系数:EIll l l l l l EI 245232222123222211311=⨯⨯⨯⨯+⨯⨯⨯⨯=δEIll l l EI 822122211312=⨯⨯⨯⨯=δ(3) 自振频率:111δωm =2.图2a 简单桁架,在跨中的结点上有集中质量m 。
若不考虑桁架自重,并假定各杆的EA 相同,试求自振频率。
图2a 图2b分析:(1)由于结构对称,质量分布对称,所以质点m 无水平位移,只有竖向位移,此桁架为单自由度体系。
(2) 挠度系数:()211211+==∑EAl l F EAN δ(3) 自振频率:111δωm =3.计算图3a 结构的自振频率,设各杆的质量不计。
图3a 图3b分析:(1)A 、B 两点的竖向位移相同,()B B A A X X 111δδ=∆=-=∆。
(2) 挠度系数:()13113116482EI l EI l A ==δ,()23223216482EI l EI l B ==δ(3) 自振频率:Am δω1=三、单自由度体系的动力特性 1. 简支梁,跨度a ,抗弯刚度EI ,抗弯截面模量W z 。
跨中放置重量为G 转速n 的电动机.离心力竖直分量()tF t F p p θsin =。
若不计梁重,试求动力系数、最大动位移及最大动应力。
分析:(1)动力系数:211⎪⎭⎫ ⎝⎛-=ωθμEIGag n st st48303=∆∆==ωπθ(2) 最大动位移:EI aF y y y y p st st st st d 4831111max max ==∆+=∆+=δδμ(3) 最大动应力: ()a G F MM MM MW MpGstGd z+=+=+==μμσ41maxmaxmaxmax四、两个自由度体系的特性(自振频率、主振型、位移-振型分解法) 1. 求1a 体系的自振频率和主振型,作振型图并求质点的位移。
流体力学例题(动力学部分)
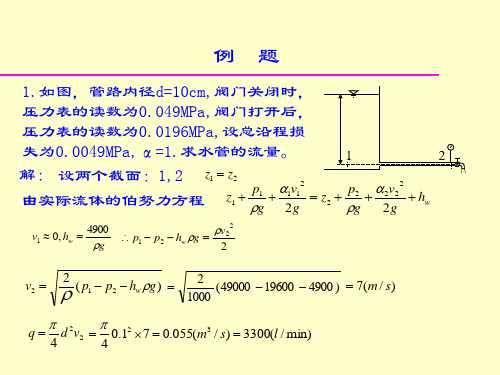
1000
q
49 7 m / s
d 2
4
v2
0 .12
4
7 55 10
3
m /s
3
2
6.一个100N的重物恰被一垂直水射 流所支承,其中d=6cm,出口速度 v=8m/s,不计沿程损失,求Y=? 解:水流接触重物后动量发生了变化
Fiy q ( 2 v y 2 1 v y 1 )
Fiy 100 N q v y2
d 2
4 0
v
0 . 06 2
z1 z 2 z
v2 q2
v1
q1
由伯努利方程: v1 v 2 v
v1 q1
令: 1 由动量方程:
v
A
F i 0 q1v q 2 v qv cos
q1 q 2 q cos v 2 q2 由连续性方程:q1 q 2 q
2 gH v
令: 2 1 1
带入动量方程: F q ( 2 v z 2 1v z1 )
F av ( v a A 2 gH v )
2
水流对水桶的作用为-F
W W 0 F W 0 av ( v a A 2 gH v )
4
8 0 . 0226 m / s
3
令: 2 1 1
则:
v y1
F
q
100 1000 0 . 0226
4 . 42 m / s
由出口和重物底面的伯努利方程:
z1 p
g
v1
拉格朗日动力学方程例题

拉格朗日动力学方程例题拉格朗日动力学方程是描述质点、刚体或连续体运动的重要数学工具。
它是由拉格朗日于18世纪提出的,可以从动能和势能的差异来推导出物体的运动方程。
在此,我们将介绍一个拉格朗日动力学方程的例题,并解答该问题。
例题:一个质量为m的质点在一维势场V(x)中运动。
质点的拉格朗日量L定义为L = T - V,其中T表示质点的动能。
现在假设势场V(x)满足V(x) = kx^2,其中k为常数。
求质点的运动方程。
解答:首先,我们需要计算质点的动能T。
根据动能的定义,T = (1/2)mv^2,其中v表示质点的速度。
由速度与位置的关系可得,v = dx/dt,其中x表示质点的位置,t表示时间。
因此,动能可以写为T = (1/2)m(dx/dt)^2。
接下来,我们将拉格朗日量L表示为动能和势能之差。
由题目中给出的势能表达式可得,V(x) = kx^2。
将动能和势能带入拉格朗日量的定义中可得:L = (1/2)m(dx/dt)^2 - kx^2。
根据拉格朗日动力学方程的定义,我们需要计算质点的广义力F。
广义力F可以通过势能对位置的偏导数来表示,即F = -dV/dx。
将势能表达式V(x)带入可得,F = -d(kx^2)/dx = -2kx。
综上所述,我们得到了质点的运动方程。
根据拉格朗日动力学方程的定义,F = d/dt(dL/d(dx/dt)) - dL/dx = 0。
代入我们计算得到的动能和势能的表达式,可得:d/dt(m(dx/dt)) + kx = 0化简上述方程,我们可以得到:m(d^2x/dt^2) + kx = 0这就是质点在一维势场V(x)中的运动方程。
它表示了质点受到的恢复力和质量的关系。
通过求解这个二阶微分方程,我们可以得到质点的具体运动规律。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
10.连串反应的速率由其中最慢的一步决定,应此速率控制步骤 的级数就是总反应的速率系数。( )
选择题 选择正确答案的编号,填在各题后的括号内:
1.对元反应A+2BC,若将其反应速率方程写为下列形式,
kA、kB、kC间的关系应为:( )
dcA k A cA cB ; dcB k BcA cB ; dt dt
2 已知气相反应 2A + B 2Y的速率方程为
dp A kp A pB 。 dt
将气体A和B按物质的量比2:1引入一抽空的反应器中,反应温 度保持400 K。反应经10min后测得系统压力为84 kPa,经很长时 间反应完了后系统压力为63 kPa。试求: (1)气体A的初始压力pA,0及反应经10 min后A的分压力pA; (2)反应速率系(常)数kA; (3)气体A的半衰期。
1 1 kt pB pB,0
'
2A(g) + B(g) t=0 t=t1 2pB,0 pB,0 2pB pB 0
C(g) + D(s)
pB,0-pB
p(总)=pB,0+2pB pB=p(总)-pB,0/2
t=0时 p(总,0)=3pB,0=3 kPa 则 pB,0=1 kPa t1=50s时 pB,1=p(总,1)-pB,0 / 2=0.5 kPa
A pA 2 B pB 1
dpA pA kA 2 k A pA ( ) pA dt 2 2 2 1 1 min kA ( ) =1.59×103 kPa1· 1 t pA pA , 0
(3)
t1/ 2
1 kA ( ) pA, 0 2
20min
3 反应 2A + B Y由试验测的为二级反应,其反应速率 方程为:
解:根据k的量纲可知该分解反应为一级反应。设反应温 度为T,根据一级反应的速率公式: k(T)=ln(c0/c)/t = – ln0.20/1200=1.34×10-3 s-1 = A exp( – Ea /RT ) Arrhenius公式的对数形式:lnk = lnA – Ea /RT lnk(650K)=lnA – Ea /(R×650)=ln(2.14×10-4)= – 8.450 lnk(T)=lnA – Ea /RT=ln(1.34×10-3) = – 6.615 两式相减解得:T=679K
1 在定温300K的密闭容器中,发生如下气相反应:A(g )+B(g)Y(g)测知其速率方程为
dp A kp A pB dt 假定反应开始只有A(g)和B(g)(初始体积比为1:1
),初始总压力为200 kPa,设反应进行到10 min时,测 得总压力为150 kPa,则该反应在300 K时的反应速率系( 常)数为多少?再过10 min时容器内总压力为多少?
dpA k ( pt pA , 0 ) 2 代入速率微分方程,得 dt 1 1 kt 积分上式,得 pt pA,0 pt ,0 pA,0
1 1 kt 已知pt,0=200kPa,pA,0=100kPa,即 pt 100kPa 100kPa
代入t=10min时,pt=150kPa,得 k=0.001kPa1· 1 min 当 t=20min时,可得 pt =133kPa
今将摩尔比为2∶1的A,B混合气体通入400 K的定温密闭 容器中,系统初始压力为3 kPa,经50s后容器内压力为2 kPa,问经150s后容器中pB为若干?
解:nA,0/ nB,0 = vA/ vB= 2/1;则 nA / nB=pA / pB = 2 -dpB / dt = kpA1.5pB0.5 = k(2pB)1.5pB0.5 = 21.5kpB2 = k’pB2
1 2
6.有两个都是一级的平行反应 下列哪个关系式是错误的? (A) k总=k1+k2 (B) E总=E1+E2 (C)
k1 A k2
Y
Z
t1 / 2 ln 2 。 k1 k 2
k1 cY (D) k 2 cZ
7. 光气热分解的总反应为COCl2 CO + Cl2 ,该反应分为三步 完成: (i)COCl2 (iii)Cl3 总反应速率方程 2Cl+CO 快速可逆 慢 快速可逆 ,则此总反应为( ) (ii)Cl+COCl2 CO + Cl2 Cl2+Cl
dcA 成 dt
3.答:
。
dcA 2 k A cA c B dt
;(ii) ;
4.链反应的一般步骤是(i) (iii) 。 4.答:链的引发 链的传递 链的终止
5.反应AY+Z中,反应物A初始浓度cA,0=1moldm-3,初始速 率A,0=0.01moldm-3s-1,假定该反应为二级,则其速度系数kA 为 ,半衰期t1/2为 。
1 k A k B ,则 2
又
xA t kBcA,0 (1 xA )
0.900 113s 3 1 1 3 0.400dm · mol · 0.200mol dm (1 0.900) s ·
4 反应2A(g)+B(g) Y(g)+Z(s)的速率方程为:
dpB 0 kp 1.5 pB.5 。 A dt
1 1 k 50s 1kPa1 pB,1 pB,0
'
k’ =0.02 kPa1·1 s
B, 2 pB,0
' 1
pB,2=0.25 kPa
5 已知反应2HI
I2 + H2,在508℃下,HI的初
始压力为101325 Pa时,半衰期为135 min;而当HI的初始 压力为101325 Pa时,半衰期为135 min。试证明该反应为 二级,并求出反应速率系(常)数(以dm3· 1·1及以 mol s Pa1·1表示)。 s
dcC kC cA cB dt
;则
(A)kA = kB = kC (B) kA =2 kB = kC (C) kA =1/2 kB = kC
2.某反应,AY,其速率系数kA=6.93min-1,则该反应物A 的浓度从1.0moldm-3变到0.5 moldm-3所需时间是( )
(A)0.2min
5.答:kA=0.01 mol-1dm3s-1
t1/2=100 s
为
6.某反应的速率系数k=4.6210-2min-1,则反应的半衰期 。 6.答:t1/2=15min
7.反应活化能Ea=250kJmol-1,反应温度从300K升高到310K时, 速率系数k增加 倍。 7.答:k(310K)/k(300K)=25.36 8.反应AY+Z中,反应物A初始浓度cA,0=1moldm-3,初 始速率A,0=0.01moldm-3s-1,假定该反应为二级,则其速度常 数kA为 ,半衰期t1/2为 。 8.答:kA=0.01 mol-1dm3s-1 t1/2=100 s
解:
A(g) + B(g ) Y(g)
t=0:
t=t:
pA,0
pA
pB,0
pB
0
pA,0- pA
则时间t时的总压力为 pt = pA+ pB+ pA,0 - pA= pB+ pA,0
因为 pA,0= pB,0 符合化学计量系数比,所以 pA= pB
则
故
pt = pA + pA,0
pA= pB= pt -pA,0
是非题
下列各题的叙述是否正确?正确的在题后括号内画“”, 错误的画“” 1.反应速率系数kA与反应物A的浓度有关。 ( ) 2.反应级数不可能为负值。 ( ) 3.一级反应肯定是单分子反应。( )
4.对二级反应来说,反应物转化同一百分数时,若反应物的 初始浓度愈低,则所需时间愈短。 ( )
5. 质量作用定律仅能用于元反应。(
解:(1)
2A
+
B
2Y
t=0
t=t
pA,0
pA
pA,0/2
0
pA,0- pA
[pA,0/2-(pA,0-pA)/2]
p(总)=pA,0+pA/2
pA=2[p(总)-pA,0]
t=,pA=0, p(总,)= pA,0=63kPa
t=10min
(2)
pA=2×(84-63)kPa=42kPa
pA,0 pB,0
)
6.对同一反应,活化能一定,则反应的起始温度愈低,反应 的速率系数对温度的变化愈敏感。 ( ) 7.Arrhenius活化能的定义是
Ea
def
d lnk () RT dT
2
8.对于元反应,反应速率系数总随温度的升高而增大。( )
9.若反应AY,对A为零级,则A的半衰期 t1 / 2
cA , 0 。( ) 2k A
(B)0.1min
(C)1min。
3. 某反应,AY,如果反应物A的浓度减少一半,它的半衰 期也缩短一半,则该反应的级数为( )
(A)零级
(B)一级
(C)二级
4.元反应:H+Cl2HCl+Cl的反应分子数是( )
(A)单分子反应 (B)双分子反应 (C)四分子反应
k 5.某反应速率系数与各元反应速率系数的关系为 k k 2 1 , 2k 4 则该反应的表观活化能与各元反应活化能的关系是( ) 1 1 (A) Ea E2 E1 - E4 (B) Ea E2 ( E1 - E4 ) 2 2 (C)Ea=E2+(E1-2E4)1/2
dcA 1 1 2 2 k A cA c B k A cA cA k A c A k A cA dt 2 2
分离变量积分,得
或
1 1 1 1 1 1 t k A cA cA ,0 1 k cA cA,0 A 2 xA t 1 kA cA,0 (1 xA ) 2
