小升初数学培优讲义全46讲—第42讲 圆柱与圆锥
小升初奥数圆柱和圆锥体积资料讲解-2023年学习资料

例6.在一个底面直径是40厘米的-圆柱形盛水缸里,有一个直径-是 0厘米的圆推形铸件完全浸-0.5厘米-于水中,取出铸件后,缸里的 水下降0.5厘米,求铸件的高?-d=40厘米
解答-R=40÷2=20厘米,r=10÷2=5厘米-S柱=20× 0×3.14=1256(平方厘米-S锥=5×5×3.14=78. (平方厘米)-V锥=1256×0.5=628(立方厘米)-h锥= 28×3÷78.5=24(厘米-答:铸件的高是24厘米·-牛
第二讲圆柱和圆锥--体积
体积公式ห้องสมุดไป่ตู้导-底面积-高-牛N
圆柱体积公式-长方体的体积=底面积×高-圆柱体的体积=底面积×高 牛
圆锥体积公式-牛小升初奥数圆柱和圆锥体积资料讲解
圆锥体积公式-结论:圆锥的体积等于和它等底等高的圆柱体-积的三分 一-V柱=Sh-V锥=Sh÷3-号尚N
典型例题精讲-例1.一个圆柱体的体积是50.24-立方厘米,底面 径是2厘米-。将它的底面平均分成若干-个扇形后,再截开拼成一个它等底等高的长方体,表-面积增加了多少平方厘米?-等N
课后作业-如图,在一个正方体的前后面和侧面的中心-各打通一个长方 的洞,在上下底面的中心-打通一个圆柱形的洞。已知正方体边长为10 厘米,侧面上的洞口是边长为4厘米的正方-形,上下底面的洞口是直径 4厘米的圆,-求此立体图形的表面积和体积-号
证你学入金迟:-thank-牛尚N
解答-S底=2×2×3.14=12.56(平方厘米-h高=50. 4÷12.56=4(厘米)-S增加=4×2×2=16(平方厘米K根尔一-答:表面积增加了16平方厘米。-牛尚N
例2.在一个圆柱形水桶里放入一-个半径为5厘米的圆柱形钢块·-如 把钢块浸没在水中,桶里-的水面就会上升9厘米;如果沿-竖直方向把 没在水中的钢块-提起8厘米,桶里的水面就会下-降4厘米。求圆柱形 块的体积-牛
【通用版】数学小升初专题复习材料—复杂的圆柱和圆锥问题(附答案)

与几何图形有关的实际问题 重点把握三:复杂的圆柱和圆锥问题 【画龙点睛】
1.半圆柱的表面积=圆柱侧面积的21+1个底面积+切面面积或圆柱的表面积÷2 2.解决复杂的圆柱和圆锥问题,通常用到“转化法”和“图示法”。 【例题把握解读】
【例1】一个酒精瓶,它的瓶身呈圆柱形(不包括瓶颈),如图.已知它的容积为26.4π立方厘米.当瓶子正放时,瓶内的酒精的液面高为6厘米;瓶子倒放时,空余部分的高为2厘米.问:瓶内酒精的体积是多少立方厘米?合多少升?
【解答】(1)液体体积是空余部分体积的几倍: 623 (2)瓶内酒精的体积是多少立方厘米 326.4π62.17231
(平方厘米)
62.172立方厘米62.172毫升0.062172升. 答:瓶内酒精的体积是62.172立方厘米,合0.062172升.
【例2】一只装有水的圆柱形玻璃杯,底面积是80平方厘米,高是15厘米,
水深8厘米.现将一个底面积是16平方厘米,高为12厘米的长方体铁块竖放在水中后.现在水深多少厘米 ? 【解答】 方法一:用水的体积除以水的底面积就是水的高度。 808(8016)6406410(厘米); 方法二:设水面上升了x厘米. 根据上升部分的体积=浸入水中铁块的体积列方程为: 8016(8)xx,
解得:2x,8210(厘米).答:现在水深10厘米.
【同步演练】
液体的体积是不变的,瓶内空余部分的体积也是不变的,因此可知液体体积是空余部分体积的623倍.
根据等积变化原理:用水的体积除以水的底面积就是水的高度。
261.右图是一个零件的直观图.下部是一个棱长为40cm的正方体,上部是圆柱体的一半.求这个零件的表面积和体积.
2.把一个高是8厘米的圆柱体,沿水平方向锯去2厘米后,剩下的圆柱体的表面积比原来的圆柱体表面积减少12.56平方厘米.原来的圆柱体的体积是多少立方厘米?
3.一个酒瓶里面深30cm,底面内直径是10cm,瓶里酒深15cm.把酒瓶塞紧后使其瓶口向下倒立这时酒深25cm.酒瓶的容积是多少?(π取3)
六年级【下】数学-小升初培优:5圆柱圆锥 全国通用 (12张)

•
圆锥的体积=底面积x高x
1 3
,V=
1 3
Sh
解析:因为打一个直径为2 cm、深为1 cm的圆柱形的孔,而几何体是一棱长为4 cm的正方体,所以这个孔没有打穿,而圆柱形的孔是增加了一个侧面积和一个底 面积,但是正方体也损失了一个底面积,就是那个孔,相互抵消,所以只是增加了圆 柱的侧面积。
表面积=正方体表面积+圆柱侧面积×6
4 4 6 3 .1 2 4 1 6 1.6 3(c 8 3 2 ) m
答:这垛草的重量是800.7公斤
如果能得到一个规则的 圆柱就可以算出体积,怎样 可以得到一个规则的圆柱呢? 拼接一个完全一样的立体图
形看看。
r=9.42÷3.14÷2=1.5cm
4
6 V圆柱=S底h=3.14×1.52×(4+6)=70.65(cm3)
V剩=70.65÷2=35.325(cm3)
答:剩下部分体积是32.325cm3
Cl=
2
πdl=
2
×3.14×20×15=471(cm2)
2
S表=S侧+S底=471+3.14×102=785(cm2)
1
1
V= 3S底h= 3×3.1,表面积是785cm2,体积是1256cm3
设底面半径为r,则有: C=2πr=6.28cm2 所以r=6.28÷3.14÷2=1cm
体积=正方体体积-圆柱体积×6
4 4 4 3 .1 1 4 2 1 6 4.1 5 (c 6 3 ) m
答:打孔后表面积是133.68cm2,体积是45.16cm3
表面积增加的部分是两个侧立的三 角形的面积,每个三角形的面积为
24 ÷ 2 =12 平方厘米
小升初数学培优第十讲圆柱和圆锥

例2.如下图,做一个圆柱形纸盒,至少需要多大表面积的纸板?(接口处不计) 解析:求至少需要多大面积的纸板,实际上就是求这个圆柱的表面积,圆柱的侧面积加上两 个底面积就是圆柱的表面积。 即:圆柱的表面积=底面积×2+底面积
底面积: 3.14 10 2 314 (cm 2 )
解: 侧面积: 3.14 10 2 30 1884 (cm 2 )
底面周长
高
S侧 C h
2.圆锥 高 O r 底面 圆锥的体积计算公式: V 3.圆柱与圆锥的关系: h
S表 S侧 2S底
侧面 底面
1 Sh 。 3
(1)一个圆柱的体积是和它等底等高的圆锥体积的 3 倍。 (2)当一个圆柱与一个圆锥的体积和底面积都相等时,圆锥的高是圆柱高的 3 倍。 (3)当一个圆柱与一个圆锥的体积和高都相等时,圆锥的底面积是圆柱底面积的 3 倍。
第十讲
圆柱和圆锥
第十讲
知识导航:
圆柱和圆锥
认识圆柱和圆锥的特征, 掌握圆柱和圆锥的侧面积和表面积的意义, 以及它们侧面的展 开图。圆柱和圆锥表面积的计算方法,了解圆柱和圆锥的关系,合理运用公式解决圆柱和圆 锥的体积,初步建立空间观念,学会用数学的眼光观察生活中物体的形状,并能解决生活中 的一些实际问题。 1.圆柱 O 底面 侧面 高 O 底面 底面 底面
答:它的侧面积是471平方厘米。
关爱成长每一天
我试试:
1、一个圆柱形纸筒(接口处不计),底面周长是72厘米,高是8厘米,它的侧面积是多少平 方厘米?
2、一个圆柱,底面的直径是0.5厘米,高是1.8厘米,求它的侧面积。
3、一个圆柱形的烟囱,底面半径是6厘米,高是50厘米,做这样的一个烟囱至少需要铁皮多 少平方厘米?
小学数学圆柱和圆锥专项讲义(知识点+例题+作业)
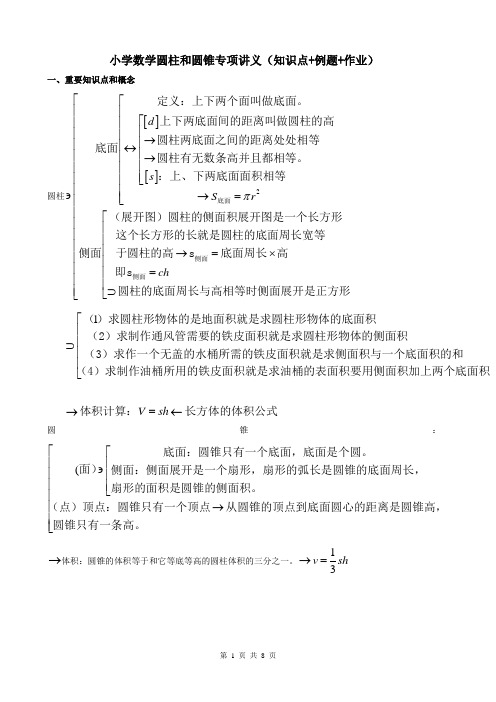
小学数学圆柱和圆锥专项讲义(知识点+例题+作业)一、重要知识点和概念圆柱[][]2d s S r ch π⎡⎢⎡⎢⎢⎢→⎢⎢↔⎢⎢→⎢⎢⎢⎢⎣⎢∍→=⎢⎣⎡⎢⎢⎢→=⨯⎢=⎢⎢⊃⎣底面侧面侧面定义:上下两个面叫做底面。
上下两底面间的距离叫做圆柱的高圆柱两底面之间的距离处处相等底面圆柱有无数条高并且都相等。
:上、下两底面面积相等(展开图)圆柱的侧面积展开图是一个长方形这个长方形的长就是圆柱的底面周长宽等于圆柱的高s 底面周长高侧面即s 圆柱的底面周长与高相等时侧面展开是正方形⎡⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣1⎡⎢⎢⊃⎢⎢⎣()求圆柱形物体的是地面积就是求圆柱形物体的底面积 (2)求制作通风管需要的铁皮面积就是求圆柱形物体的侧面积 (3)求作一个无盖的水桶所需的铁皮面积就是求侧面积与一个底面积的和 (4)求制作油桶所用的铁皮面积就是求油桶的表面积要用侧面积加上两个底面积V s h →=←体积计算:长方体的体积公式 圆锥:(⎡⎡⎢⎢∍⎢⎢⎢⎢⎣⎢→⎢⎢⎢⎣底面:圆锥只有一个底面,底面是个圆。
面)侧面:侧面展开是一个扇形,扇形的弧长是圆锥的底面周长,扇形的面积是圆锥的侧面积。
(点)顶点:圆锥只有一个顶点从圆锥的顶点到底面圆心的距离是圆锥高,圆锥只有一条高。
→体积:圆锥的体积等于和它等底等高的圆柱体积的三分之一。
13v sh →=圆柱和圆锥V ↔()113324⎡⇔⎢⎢⎢⎢⇔⎢⎢⎢⎢→⎢⎢⎢⎢→⎢⎢⎣()圆锥体积等于和它等底等高的圆柱体积的 圆柱体积等于和它等底等高的圆锥体积的倍。
2(2)圆锥体积比和它等底等高的圆柱体积少3 圆柱体积比和它等底等高的圆锥体积大倍。
(3)如果圆柱和圆锥的体积相等底面积也相等 圆锥的高是圆锥的3倍。
()如果圆柱和圆锥的体积相等,高也相等 圆锥的底面积是圆柱的3倍。
二、例题与解析例1, 压路机的滚筒长1.5米,底面半径0.6米,以每分钟滚动15周计算,把25434平方米的地基压完一遍,需要多少小时?分析与解:压路机的滚筒在地面滚动一周,压过的路面面积等于滚筒的侧面积,可以先算出每分钟压过的路面面积,再除总面积,就可以求出所需时间。
小升初数学专题复习——圆柱和圆锥复习

圆柱和圆锥的复习错题回顾1、判断:圆锥的体积等于圆柱体积的31。
( )2、一个直角三角形两条直角边分别是6厘米和10厘米,以6厘米的直角边为轴旋转一周,转出来的立体图形是( )体,它的体积是( )立方厘米。
3、一个圆锥的体积是54平方厘米,它的高是6厘米,底面积是( )平方厘米。
4、在一个底面半径是10cm 的圆柱形水桶中装水,水中放一个底面半径是5cm 的圆锥形铅锤,铅锤全部淹没,取出铅锤后桶面水面下降2cm ,求铅锤的高。
5、将一块棱长为4厘米的正方体铁块浸没在一个圆柱形量杯中,水面升高0.8厘米,求量杯从里面量得的底面积。
相似题巩固一个圆柱形玻璃缸,底面直径20厘米。
把一个底面半径8厘米的圆锥完全放入水中,水面上升了3厘米,求这个圆锥的体积。
6、一个圆柱体的体积增加6立方厘米,那么与它等底、等高的圆锥体的体积就应增加( )7、一个圆锥体的底面半径扩大2倍,高缩小为原来的一半后,它的体积与原来的体积相比( )8、把一个圆柱体海绵削成一个最大的圆锥,所得圆锥的体积是72立方厘米,被削去的海绵有( )9、一个圆锥的体积不变,如果它的高缩小9倍,底面半径应( )10、一个圆柱与一个圆锥底面直径相等,圆锥的高是圆柱的3倍,圆锥的体积是12立方分米,则圆柱的体积是()11、用一个高是30厘米的圆锥形容器盛满水,倒入和它等底等高的圆柱形容器中,水的高度是()12、一个圆柱和一个圆锥的底面积相等,体积也相等,圆柱的高是24厘米,则圆锥的高是()13、一个圆锥的体积是12立方厘米,底面积是4平方厘米,高是()14、把一个圆柱形木材削成一个最大的圆锥,圆锥的质量是0.2千克,削去的木材重()15、一个高是15厘米的圆锥体容器,装满水,倒入和它等底的圆柱形量杯里,水的高度()16、圆锥的高是6cm,底面积是3.14平方厘米,那么体积是()17、等底面积等体积的圆柱和圆锥,圆锥的高为48分米。
圆柱的高为()18、一杯水倒入底面半径为6厘米,高为10厘米的圆锥形容器中刚好装满,这杯水的体积是______ 立方厘米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第42讲 圆柱和圆锥
1、考察范围:①圆柱的表面积和体积公式;②圆锥的表面积和体积公式;③圆柱与圆锥的比;④立体图形的切割。
2、考察重点:能灵活运用圆柱体和圆锥体的表面积与体积公式解决问题。
3、命题趋势:主要以圆柱体和圆锥体的表面积与体积计算为主,并结合比的应用来进行考察。
圆柱与圆锥的特征与基本公式:
名称
图形
特征
字母意义
表面积S 、体积V
圆柱
有三个面,上下两个底面是相等的两个圆,侧面展开是一个长方形或正方形。
这个长方形的长就是底面圆的周长,宽就是圆柱的高。
两个底面之间的距离叫做圆柱的高,高垂直于上下两个底面,圆柱有无数条高。
r —底面半径
h —高
c —底面周长 r c π2=
h r h c S ⋅⋅=⋅=π2侧
2r S ⋅=π底
底侧表S S S 2+=
2
22r rh ππ+=
h r h S V 2π=⋅=底 圆锥
有两个面,底面是圆,侧面展开是
一个扇形。
圆锥只有一个顶点,从圆锥的顶点到底面圆心的距离叫做圆锥的高。
圆锥只有一条高。
r —底面半径
h —高
c —底面周长
h r h S V 231
31π==底
【例1】已知一根圆柱体木料长4米,如果把它锯成3段,表面积就会增加12平方分米,
这根木料的体积是 立方分米。
如果锯成3段用了3分钟,那么把它锯成6段要 分钟。
考点解读
知识梳理
典例剖析
【变式练习】
1、把一个底面周长是18.84分米,高4分米的圆柱,沿底面直径切成两个半圆柱后,表面积共增加了平方分米。
2、一根2米长的圆柱体木材,锯成3段小圆柱后,它的表面积总共比原来增加了12.56平方分米,原来这根木材的体积是多少?
【例2】一个正方形木块的棱长是2dm,现在把它削成一个最大的圆柱,该圆柱的侧面积是,圆柱的体积占原来正方体体积的 %.
【变式练习】
1、把棱长2分米的正方体木块,削成一个最大的圆柱,这个圆柱的体积是多少?
2、一个圆柱形水池,从里面量得底面直径是8米,深3.5米。
在这个水池的底面和四周抹上水泥,抹水泥部分的面积是多少平方米?这个水池最大能蓄水多少立方米?
【例3】一个圆锥形沙滩,底面半径是5米,高是2.7米,如果每立方米沙重2000千克,现用一辆载重8000千克的汽车去运,至少要运多少次?(π取3.14)
【变式练习】
1、一个圆锥形沙堆,底面周长是31.4米,高是1.5米,用这堆沙铺在一个长125米,厚0.1米的路面上,可以铺多宽?
2、一个装满粮食的粮囤,上面是圆锥形,下面是圆柱形,量得圆柱底面的周长是62.8米,高2米,圆锥的高是1.2米。
这个粮囤能装稻谷多少立方米?如果每立方米稻谷重500千克,这个粮囤最多能装多少吨?(保留一位销售)
【例4】把一个圆柱形状的木头削成一个最大的圆锥,已知削去的体积是24立方米,则圆锥的体积是立方米。
【变式练习】
1、已知一个圆锥形的容器可以盛满水34立方米,现在将该玻璃容器用圆柱形塑料盒进行包装,则该塑料盒的体积最小是多少立方米?
2、圆柱和圆锥底面积相等,体积也相等,圆柱的高是15厘米,求圆锥的高是多少厘米?
【例5】如图,该圆柱形玻璃容器的底面直径为10厘米,里面装有水,水中浸没着一个底面直径为8厘米,高15厘米的圆锥形铅锤,如果把铅锤取出,那么容器中的水面高度将下降多少厘米?
【变式练习】
1、如图中,瓶底的面积和锥形高脚杯口的面积相等,将瓶子中的液体倒入锥形被子中,能倒满几杯?
2、有两个空的玻璃容器(如图),先在圆锥形容器里注满水,再把这水倒入圆柱形容器中,圆柱形容器里的水深多少厘米?
课后精练
A、温故知新
1、用铁皮做一个底面直径为6分米,高为8分米的圆柱形无盖水桶,至少要用多少平方米的铁皮?(答案用含有π的式子表示)
2、有10根圆柱形木头,要把每根都锯成3段,每锯一段需要3分钟,把10根木头都锯完,需要多少分钟?
3、有一个圆柱形零件,高10厘米,底面直径是6厘米,零件一端有一个圆柱形的圆孔,圆孔的直径是4厘米,孔深5厘米,如果将这个零件接触空气的部分涂上防锈漆,那么一共要涂多少平方厘米?
4、一个圆柱体,如果把它的高截短3厘米,它的表面积减少18.84平方厘米。
这个圆柱体的体积减少多少立方厘米?
5、一个棱长6厘米的正方体,从正方体的底面内挖去一个最大的圆锥体,剩下的体积是多少立方厘米?
6、一段长4分米的圆柱体木料,横截面积是9.42平方分米,利用它加工成一个尽可能大的圆锥体木质零件,这个零件的体积是多少?
7、把一个圆柱体削成一个最大的圆锥后,削去部分的体积比圆锥的体积多30立方厘米,原来圆柱的体积是多少立方厘米?圆锥的体积是多少立方厘米?
8、一根长方体木料,横截面积是边长为10厘米的正方形,从这根木料上截下6厘米长的一段,切削成一个最大的圆锥,圆锥的体积是多少?削去部分的体积是多少?
9、把一个底面周长是9.42分米,高6分米的圆柱,沿底面直径切成两个半圆柱后,表面积共增加了多少平方分米?
10、甲圆柱体容器是空的,乙长方体容器中水深6.28厘米,将乙容器中的水全部倒入甲容器后,这时水深多少厘米?
B、拓展提升
1、如图,一顶礼帽的帽顶部分是圆柱形,用黄色布做,帽檐部分是一个圆环,用红色布做,如果帽顶的直径、高和帽檐的宽都是12厘米,那么哪种颜色的不用得最多?多了多少平方厘米?
2、已知底面半径是10厘米的圆柱形瓶中,水深8厘米,要再瓶中放入长、宽都是8厘米,高15厘米的一块铁块,把铁块竖放在水中,水面上升几厘米?
3、一个圆柱体容器中,放着一个长方体铁块,现在打开一个水龙头往容器里面注水,3分钟时,水恰好没过长方体的顶面,又过了18分钟,水灌满容器。
已知容器的高度是50厘米,长方体的高度是20厘米,那么长方体底面积与容器底面积之比是多少?
4、如图,将100毫升水倒入一个圆锥形容器中,此时水的深度是圆锥容器高度的一半。
如果要将整个圆锥形容器装满,还要倒入多少毫升的水?。
