连续刚构桥刚度变化对自振频率的影响
钢结构桥梁的自振特性与控制

钢结构桥梁的自振特性与控制钢结构桥梁是现代交通基础设施中常见的一种桥梁型式,具有承载能力强、稳定性好等特点。
然而,钢结构桥梁的自振特性可能导致其在受到外力激励时发生共振现象,进而引发结构破坏和灾害事故。
为了保证桥梁的安全运行,研究钢结构桥梁的自振特性并采取控制措施变得尤为重要。
一、钢结构桥梁的自振特性钢结构桥梁的自振特性主要受到以下几个因素的影响:1. 材料特性:钢结构桥梁采用的钢材具有一定的弹性模量和密度,这些材料特性会直接影响桥梁的固有频率和自振特性。
2. 结构形式:钢结构桥梁的结构形式多种多样,包括悬索桥、梁桥等。
不同结构形式下的桥梁会有不同的固有频率和自振特性。
3. 外力激励:车辆行驶和风力等外力的作用会引起桥梁的振动。
如果外力的频率接近桥梁的固有频率,就会导致桥梁产生共振现象,从而增加桥梁的振动幅度,甚至引发桥梁的破坏。
二、钢结构桥梁的自振控制技术为了减小钢结构桥梁的自振幅度,提高桥梁的稳定性和安全性,需要采取一系列的自振控制技术。
1. 调整刚度:通过增加或减小构件的刚度,可改变桥梁的固有频率,使其远离外力频率,减小共振风险。
例如,通过加装加劲筋、加固节点等方式,增加整个桥梁的刚度,使其固有频率向低频移动。
2. 吸振器:在桥梁结构中安装吸振器可以吸收并分散桥梁振动的能量,从而减小振幅。
常见的吸振器包括液体阻尼器、摩擦阻尼器等。
3. 主动控制系统:通过在桥梁结构中设置传感器和执行器,实现实时的振动调节和控制。
主动振动控制系统可以根据外界振动信号实时调整构件的刚度和阻尼,从而达到减小自振振幅的目的。
三、案例分析以某钢结构桥梁为例,采用了主动控制技术进行自振控制。
在桥梁结构中安装了传感器,实时监测桥梁的振动状态。
当外界振动频率接近桥梁的固有频率时,控制系统会自动调节构件的刚度和阻尼,抑制共振现象的发生。
通过实验和模拟计算,证明了主动控制技术对钢结构桥梁的自振控制具有良好的效果。
在外界激励下,桥梁振幅显著减小,振动能量得到有效吸收和分散,保证了桥梁的安全运行。
钢结构人行天桥自振频率影响因素研究

钢结构人行天桥自振频率影响因素研究摘要城市化进程的不断加快对行人出行安全带来新的问题和挑战,城市道路交叉口往往都会修建人行天桥以保障行人的安全通行。
钢结构人行天桥以其自重轻、强度高的特点被广泛采用,根据规范中频率设计法要求,其自振基频不能超过3Hz,这对人行天桥的设计提出了更高的要求。
本文以某一结构人行天桥为例,采用有限元结构分析方法,分别分析主梁参数、约束条件两项变量对人行天桥自振频率的影响,从而改善桥梁结构的合理性,提高结构的安全性和舒适度。
关键词钢结构人行天桥自振频率主梁参数约束条件0 引言钢结构在恒载和活载作用下,变形及内力易满足设计要求,因此在设计时一般重点考虑其动力特性[1-2]。
如何优化钢结构人行天桥的设计,满足频率设计要求,对于保障桥梁结构和行人的安全具有重要的工程意义。
我国CJJ69—95《城市人行天桥与人行地道技术规范》提出的频率设计法规定[3]:人行天桥的竖向自振频率应不小于3Hz,因此文章以频率分析为主线,利用软件仿真分析,选取了梁高、跨径和约束条件几个参数,对钢人行天桥设计合理性展开研究,以期为同类桥梁设计提供借鉴意义。
1 频率设计法人行天桥主要活载为人群荷载,人群荷载一般取5kN/m2,在组合条件,对结构产生的挠度和应力值也远小于允许值,具有较大的安全储备。
根据桥梁的实际使用工况,正常行人的走步频率介于1.6~2.4Hz之间,为避免共振,提高行人的安全感,我国规范要求自振频率应不小于3Hz。
综上,频率设计法是人行天桥的典型计算方法。
对于钢结构人行天桥,在满足应力、挠度限制的基础上,通过调整钢结构梁体参数和边界约束条件,使梁体自振频率满足规范要求。
2 有限元建模以某一字型简支钢箱梁人行天桥为例建模,天桥跨径为23.8m,钢箱梁净宽4.5m,两侧栏杆各0.15m,全宽4.8m。
钢箱梁材料均采用Q355,梁高为100cm。
桥面铺装为40mm厚CF40钢纤维混凝土。
采用Midas Civil 2019有限元分析软件对全桥进行建模分析,定义自重荷载、二期恒载和人群荷载,将荷载转化为质量以便进行自振频率计算分析。
典型高墩大跨连续刚构桥抗震性能分析
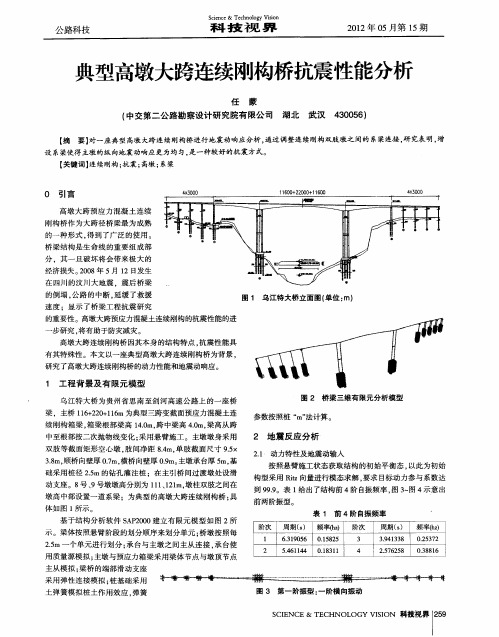
图 4 第二 阶振 型 : 阶纵 向振 动 一
-
厂
O 5 0 0 ●
#0 5 0
.
O o 0
£ 恤
Ⅲ 5
n nm
蝴
,
∞,
-
根据 《 中国地震 动参数 区划 图}G 13 6 20 )桥址区 (B 80 — 0 1,
抗 震设 防烈 度属 6度 区, 设计基本地震加速度值 a 0 5 , = . g 设 0
S in e& Te h oo y Vio ce c c n lg s n i
公路科技
科 技 视 界
21 年 0 月第 1期 02 5 5
典型高墩大跨连续刚构桥抗震性能分析
任 蒙
( 中交第二公 路 勘察设 计研 究院 有 限公 司 湖北
武汉
405 ) 3 0 6
t4 要】 g 对一座典型高墩大跨 连续刚构桥进行 地震 动响应 分析 , 通过调整连续刚构双肢墩之 间的 系梁连接 , 究表 明 , 研 增
图 1 乌江特 大桥立面图 ( 单位 : m)
的重要性。高墩大跨预应力混凝土连续 刚构 的抗震性能的进
一
步研究 , 将有助于防灾减灾 。 高墩大跨连续刚构桥 因其本身 的结构特 点 , 抗震性 能具
有其特殊性 。本文 以一座典型高墩大跨连续 刚构 桥为背景 ,
研究 了高墩大跨连续 刚构桥 的动力性 能和地震动响应。
阶次
3 4
周期() s
39 3 8 .41 3 25 6 5 .7 2 8
频率( ) h z
0.53 2 2 7 03 8 6 .8 1
图 3 第 一 阶 振 型 : 阶 横 向振 动 一
山区大跨连续刚构桥自振特性分析

立 该 桥 的空 间有 限元 模 型 , 对 其 自振 特 性 进 行 计 算 分 析 , 获 得 了该 桥 的 自振 频 率 和振 型 。 关键 词 大 跨 连 续 刚构 桥 有 限 元 自振 特 性
山 区高等 级公 路 连 续 刚构 桥 梁 , 通 常 以跨越 深谷 沟 壑 , 受 力合 理 , 施 工便 利 , 跨 度 大 为其 特 点 而被 广泛 应用 u ] 。又 因桥 墩 固结 的特 点 , 省 去 了 大跨 连续 梁 的支座 , 同时桥墩 厚度 大大减 小 , 减 少
邓 果 陈 昊 吴 俊
( 贵 州 省 交 通 规 划 勘 察 设 计 研 究 院 股 份 有 限公 司 贵 阳 5 5 0 0 0 1 )
摘
要 以 山 区大 跨 连 续 刚 构 桥 —— 鱼 洞 大 桥 为 研 究 对 象 , 运 用 大 型 通 用 有 限 元 软 件 MI DA S建
阵; 五 , U分别 对 应 于系统 加 速度 列 阵 和 位移 列 阵 。 假 定 多 自由度 体 系 的 自 由振 动 是 简 谐 振 动 , 则 位
移 可 写 成
( £ ) 一 s i n( + ) ( 2 )
b ) 第 2阶 振 型 ( 主梁一阶横弯)
物 线变 化 。主墩 的设 计 形 式 为 双 薄 壁式 实 心 墩 , 实 心墩横 桥 向 6 . 5 m, 顺桥向 2 . 2 i n , 两 片墩 问净
图 2 全 桥 有 限元 模 型
收 稿 日期 : 2 0 1 2 - 1 2 2 4
2 0 1 3年 第 2 期
邓
横坡 为单 向 2 . 0 ( 左 右 幅相 反 ) 。上 部箱 梁 为 变 截 面单箱 单 室 断 面 , 箱 顶宽 1 1 . 2 5 m, 底宽 6 . 5
大跨度连续刚构桥抗震性能分析

大跨度连续刚构桥抗震性能分析谢群华【摘要】双肢薄壁墩和单柱式墩是连续刚构桥的常用桥墩结构形式,为研究桥墩形式对桥梁的影响,以某连续刚构桥为基础,建立空间有限元模型,对比分析双肢薄壁墩和单柱式墩对连续刚构桥动力特性与地震相应的影响,研究预应力对桥梁地震响应和抗震性能验算的影响.结果表明,相同截面情况下,双肢薄壁墩比单柱式墩受力更为合理,预应力对刚构桥地震响应影响不大,但抗震性能验算时必须考虑预应力作用,且双肢墩的内外两肢受力要协调,避免正常使用状况下内外两肢内力相差过大.【期刊名称】《现代交通技术》【年(卷),期】2016(013)004【总页数】4页(P32-35)【关键词】双肢薄壁墩;单柱式墩;刚构桥;预应力;抗震性能【作者】谢群华【作者单位】东南大学建筑设计研究院有限公司,江苏南京210096【正文语种】中文【中图分类】U442.5+5连续刚构桥具有造型优美、跨越能力强、施工方便、造价低等优点,近年来在我国山高谷深的西南、西北地区大量采用。
2008年在汶川地震中庙子坪大桥是近年国内第一座大跨度连续刚构桥震害实例,主要震害是桥墩开裂和倾斜[1],并且5号墩水下部分出现横向贯通裂缝,裂缝宽度达0.8 mm。
刚构桥的易损部位位于墩顶和墩底[2-3],由于刚构桥一般跨越峡谷或河流,震后维修较为不便,因此开展大跨度连续刚构桥的抗震性能评价尤为重要。
汶川地震后国内学者对连续刚构桥进行了较多研究,夏修身、陈兴冲等[4]对铁路刚构桥进行了研究,提出对其进行弹性抗震设计是不经济的,尚维波等[5]对高墩刚构桥体系梁进行了抗震研究,李子春[6]针对不同的桥墩形式对刚构桥的动力特性进行了研究,但是对双肢薄壁刚构桥的协同受力没有研究。
本文针对在公路桥梁上采用双肢薄壁墩或单柱式墩,进行了动力性能比较,并对地震荷载作用下的内力进行了相应对比,分析了预应力钢束对桥墩抗震性能的影响。
某3跨大跨径连续刚构桥跨径组成为(97+176+ 97)m,全长370 m,桥梁总体布置图见图1。
四柱式与其它高墩形式连续刚构桥地震反应分析比较
更 莲 村
22 0生 1
四 柱式与其它高墩形式连续冈构桥地震反应分析比 9 较
张 磊 , 胜 荣 苟
( 兰州交通大学 土木 工程 学院, -兰州 7 07 ) 甘a 30 0 摘 要 运用有限元软件 MI A D S对纵 目沟特大桥 采用的四柱式空心墩, 独柱式矩形 空心墩 、 独柱式圆形 空
波作用与结构,直接对结构运动方程进行数值积分而求得结
构地 震反 应的时间历程, 能考虑结构 的弹性和弹塑性状态, 能
反应谱理 论也 称动力法 , 目前世界各 国应用最 为广 泛 是
的抗震分 析方 法 , 其优点是考 虑了地震时地面的运动特性 与 结构物 自身的动力特性 , 只需 要取少数的低阶振型就可 以求 得较 为满意 的结果 , 且计算 量少 , 而加 速度反应谱 值是加 速 度反应 的最大值 , 用它来进行设计 一般 来说是安全的 。该桥 所处场地类型 为 Ⅱ类 , 反应谱采用 Ⅱ类 场地的标准谱作 为谱
二十阶振型, 振型总参与质量为 9. %, 7 4 满足规范要求, 1 6 表 列出 了该桥三种桥墩形式下前 1 0阶振型的频率周期及振型特征。
表 1 结构的 自振频率及振型特征
从表 1中三类墩柱 的全桥频率 和周期分 析得出 : 采用 四
柱式空心桥 墩 、 独柱式矩 形空心 墩 、 独柱式 圆形 空心墩 的 自
墩 ,这种新型桥墩将 有可能取代传统 圆端形或矩形 空心高
墩 。因此 对不 同高墩 的抗震性能进行研究 , 出其性能上 的 指
差异 , 显得 更 为 必 要 。
1 工 程概况
纵 目沟特大桥主桥 :0 2×16 8 m连续刚构桥 。该桥 8+ 3+0 位处地质情况一般 , 表层为 Q 黄土 , 力层 为完整基岩 。主 3 持 墩 采用新 型柱板式空心桥墩 ,柱间设置联系横梁及薄壁板 , 在正常使用阶段桥墩 可提供较 大刚度 ,一旦遭遇强烈地震。
连续刚构桥健康监测自振频率测试和评估研究

连续刚构桥健康监测自振频率测试和评估研究
连续刚构桥健康监测自振频率测试和评估研究
在对桥梁进行健康监测时,准确地测量桥梁的自振频率是非常重要的.以某连续刚构桥为例,简要地介绍了加速度传感器在测量桥梁自振频率中的应用,并提出了桥梁自振频率的评估模式,为后期健康监测桥梁结构技术状态的判定提供了依据.
作者:石鹏程陈宇 SHI Peng-cheng CHEN Yu 作者单位:重庆交通大学土木建筑学院刊名:黑龙江交通科技英文刊名:COMMUNICATIONS SCIENCE AND TECHNOLOGY HEILONGJIANG 年,卷(期):2009 32(2) 分类号:U446.3 关键词:连续刚构桥健康监测自振频率评估。
钢结构自振频率分析与优化设计

钢结构自振频率分析与优化设计自振频率是指结构在自身没有外部激励的情况下产生的固有振动频率。
钢结构自振频率的分析与优化设计是工程领域重要的研究课题之一,对于保证结构的安全性和稳定性具有关键作用。
首先,进行钢结构自振频率分析时,需要考虑结构的动力特性、材料特性以及结构的几何形态。
其中,结构的刚度是影响自振频率的重要因素之一。
刚度较大的结构往往具有较高的自振频率,反之亦然。
因此,优化设计时可以通过调整结构的截面尺寸、材料性质以及梁柱等构件的布置方式来改变结构的刚度,从而达到调节自振频率的目的。
在分析钢结构的自振频率时,还需要考虑结构的振型。
振型是指结构在振动时不同部位的位移分布情况。
结构的振型与其自振频率密切相关,不同的频率对应着不同的振型。
例如,自振频率较低的模态往往具有较大的位移响应,而较高的自振频率则对应着较小的位移响应。
因此,通过对结构进行自振频率分析,可以了解到结构的振型特点,从而为结构的设计提供重要的参考依据。
钢结构自振频率分析与优化设计不仅可以用于评估结构的振动性能,还可以用于探测结构的缺陷和隐患。
由于振动会引起结构内部的应力变化和疲劳破坏,因此通过自振频率分析可以对结构的健康状况进行监测。
通过对结构振动响应的采集和分析,可以及时发现结构的变形、裂缝等缺陷,并采取相应的修复和加固措施。
这不仅可以提高结构的使用寿命,还能够保证结构的安全性和可靠性。
然而,钢结构的自振频率分析与优化设计并非一件简单的任务。
首先,钢结构的模型构建需要考虑多个因素,包括结构的材料、几何形态、运载条件等。
其次,自振频率的计算需要进行大量复杂的数值计算和仿真分析,这对计算资源和算法的要求较高。
此外,在操作过程中还需要考虑结构的实际使用条件和约束,使得优化设计结果能够满足实际需求。
最后,钢结构自振频率分析与优化设计是钢结构工程设计中不可或缺的一环。
通过对结构的自振频率进行分析,可以了解结构的动态特性和振动行为,为结构的设计提供依据和指导。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
连续刚构桥刚度变化对自振频率的影响
摘要:桥梁结构的自振特性对正确进行桥梁的抗震设计、健康检测和维护具有十分重要的意义,因此分析刚构桥各个部位刚度对其自振频率的影响在桥梁设计以及将来桥梁在运营中激振频率对桥体安全性的影响都有很重要的意义。
本文以某连续钢构桥为例建立了有限元计算模型,分别分析了在改变桥梁的梁体、墩和钢筋刚度的情况下,所得出的相应的自振频率的变化,并对计算结果进行了初步分析比较,得出了具有一定指导意义的结论。
关键词:连续刚构桥;有限元;自振频率;ANSYS
一、概述
刚构桥特别是大跨度连续刚构桥已经在桥梁工程领域得到了广泛的应用,其结构特点主要是:其墩、梁、基础三者固结为一个整体而共同受力;墩身的形式、高度等对桥体结构受力都有影响。
随着刚构桥体系的发展,跨度在不断增大,墩部也在不断加高,因此出现了许多有关此类桥梁结构模态和稳定性等动力特性方面的问题,研究此类桥梁结构的动力特性有着非常重要的意义。
随着振动理论及其相关学科的发展,人们早已改变了仅仅依靠强度理论进行结构设计的观念。
桥梁,特别是大跨度桥梁,必须考虑桥梁上车辆荷载振动的影响,过去和现在都发生过由于共振引起的桥梁毁塌事故。
对桥梁的激振频率应尽量避开其各阶自振频率。
由模态分析的结果,即模态频率等参数,对被测结构进行直接动态性能评估。
对一般结构,要求各阶频率远离激振频率,或激振频率不落在某阶模态的半功率带宽内,已成为工程界的基本方法。
二、算例分析
(一)算例介绍
该连续钢构桥全长410.65m,最高桥墩56m,主跨为168m。
主跨为预应力混凝土连续刚构桥,主桥按(96+168+96)m布置。
梁体为单箱单室变高度变截面箱形梁,支墩处高11.0 m,中跨跨中及边跨梁端处梁高5.5 m,梁体下缘除中中跨跨中部10 m梁段,河边跨部17.8 m梁段为等高直线外,其余按二次抛物线变化。
箱梁顶板宽11.0 m,箱宽7.8 m。
除梁段附近区段外,顶板厚60 cm,底板厚50~110 cm,腹板厚50~100 cm。
梁段附近顶板厚100 cm,底板厚100 cm,腹板厚100 cm,边跨梁端腹板外侧进行局部加厚。
全桥共设7道横隔板,为减小梁体内外温差的影响,梁体两侧腹板上留有通风孔。
梁体按三向预应力布筋。
主墩为钢筋混凝土圆形空心墩,2号主墩高56 m,基础嵌固;3号主墩高52 m,钻孔桩基础。
边墩采用圆端形实体墩和T形桥台。
(二)建立有限元模型
在模型建立中主梁采用壳单元(shell63)建立,墩均采用梁单元(beam188),预应力钢筋采用杆单元(link10)。
在模型简化中,将主梁中的一些附属设施,比如铆接块,铆栓,附属钢筋等,等效计入主梁中;墩在简化中将钢筋等结构等效计入混凝土中。
在生成梁体混凝土单元(sheall63)时,采用四点连接生成单元的方法,依次生成顶板、腹板和底板,同时赋予相应厚度。
对于横隔板处应同法四点相连,共计生成单元数目14211个,其中梁体单元4176个,钢筋单元9988个,墩体单元47个。
在生成钢筋单元(link10)时,首先计算出所有纵向钢筋和横向竖向钢筋的截面积和每根钢筋相应的预应力作用下的弹性应变,然后简化到各个截面的相应节点上。
纵向预应力筋为59根(不考虑备用钢筋),由于单根钢筋应变不同,采用单根逐点连接单元;横向和竖向钢筋由于单根钢筋面积和弹性模量相同,故采用程序一次性逐面加出。
生成钢筋单元数量较多,以尽量接近工程实际。
(三)刚度变化对自振特性的影响分析
通过上ANSYS软件可以计算得出该桥的自振频率和主振型。
该连续钢构桥前十阶自振频率及主梁振型以及在当改变桥梁体系各个部位刚度时对桥体自振频率的影响,具体见表1。
表1 改变钢筋刚度时某连续钢构桥前十阶自振频率
阶数频率(Hz)
正常情况改变钢筋刚度时改变梁刚度时改变墩刚度时
刚度减少一半刚度增加一倍刚度减少一半刚度增加一倍刚度减少一半刚度增加一倍
1 0.770 0.769 0.77
2 0.658 0.862 0.610 0.926
2 0.816 0.816 0.816 0.781 0.887 0.628 1.103
3 1.038 1.036 1.043 0.838 1.198 0.849 1.164
4 1.148 1.13
5 1.170 0.913 1.589 1.13
6 1.287
5 1.507 1.499 1.522 1.140 2.048 1.45
6 1.599
6 2.021 2.000 2.061 1.469 2.80
7 2.006 2.038
7 2.252 2.223 2.306 1.644 3.096 2.217 2.270
8 2.389 2.375 2.416 1.734 3.293 2.341 2.424
9 2.883 2.866 2.915 2.170 3.840 2.730 3.033
10 3.025 2.980 3.104 2.230 4.085 2.926 3.071
对正常刚度情况下的自振频率而言,计算所得第一阶频率为0.770Hz,满足铁路桥梁检测规范刚度大于的条件,另外实测值为0.811 Hz,对比分析易知,该桥的实际刚度优于计算所得刚度,满足桥梁的刚度条件且原模型简化是合理的。
对比分析可知,在改变刚构桥桥体各个部位的刚度,即将其刚度分别减少一半和增加一倍时,对其自振频率的影响分析具体如下:在改变钢筋刚度时,对桥体的低阶和高阶自振频率的影响均不大;在改变梁刚度时,对桥体的第二阶自振频率影响不大,对其他自振频率影响均相对较大,尤其是对高阶自振频率影响最大;在改变墩刚度时,对低阶自振频率影响较大,而对高阶自振频率影响不大(第九阶除外)。
因此在设计此类桥梁时,可以结合此变化规律,合理调整各个部位刚度值,从而避开危险频率带,减少对桥梁体系结构的破坏性。
参考文献
[1]周军生.大跨径预应力混凝土连续刚构桥的现状和发展趋势.北京: 中国公路学报,2000.
[2]马保林.高墩大跨度连续刚构桥.北京: 人民交通出版社,2001.
[3]曹叔德,张文德,萧龙翔.振动结构模态分析: 理论、实验与应用.天津: 天津大学出版社,2001.
[4]曾庆元.列车桥梁时变系统振动分析理论与应用.北京: 中国铁道出版社,1999.
[5]曲爱平.三维梁-墩-柱的动力特性研究/硕士论文.成都: 西南交通大学,2001.
[6]铁路桥梁检定规范.北京:中国铁道出版社,2004.
[7]张立明.Algor\Ansys在桥梁工程中的应用方法与实例.北京:人民交通出版社,2003.
注:文章内所有公式及图表请以PDF形式查看。
