一元二次不等式及其解法
简单的一元二次不等式及其解法

一元二次不等式及其解法
第1课时 简单的一元二次不等式及其解法
学习目标
1.理解一元二次方程、一元二次不等式与二次函数的关系.
2.掌握图象法解一元二次不等式.
3.能从实际问题中抽象出一元二次不等式并解决.
内容索引
问题导学
题型探究
达标检测
问题导学
知识点一
思考
一元二次不等式的概念
我们知道,方程x2=1的一个解是x=1,解集是{1,-1},解集中
称为 一元二次 不等式.
(2)能使不等式成立的未知数x的一个值称为不等式的一个解. (3)不等式所有解的 集合 称为解集.
知识点二
“三个二次”的关系
一元二次不等式与相应的一元二次方程、二次函数的联系,如下表.
Δ=b2-4ac
Δ>0
Δ=0
Δ<0
y=ax2+bx+c (a>0)的图象
ax2+bx+Leabharlann =0√ 1 D.xx<-2或x>1
解析 ∵2x2-x-1=(2x+1)(x-1),
1 ∴由 2x -x-1>0,得(2x+1)(x-1)>0,解得 x>1 或 x<-2,
2
1 ∴不等式的解集为xx<-2或x>1 .
1
2
3
4
解析
答案
2.若不等式ax2+8ax+21<0的解集是{x|-7<x<-1},那么a的值是 A.1 B.2 C.3 √ D.4
由于x>0,从而得x甲>30 km/h,x乙>40 km/h.
经比较知乙车超过限速,应负主要责任.
解答
类型二 “三个二次”间对应关系的应用
一元二次不等式及其解法

例1.解不等式:
(1)x2-2x+3>0;(2)x2-2x+3<0. 解: ∵△=(-2)2-4×1×3<0 ∴(1)x2-2x+3>0的解集 为实数集R ; (2)x2-2x+3<0无解, 即它的解集为空集.
-1 O -1 y 3 2 1 1 2 3 x
例2.解下列不等式: (1)x2+4x+4 >0. (2)x2+4x+4 <0. 解: ∵△=42-4×4=0
是
输出区间 (, x1 ) ( x2 ,)
输出区间 ( ,)
输出区间 b b (, ) ( ,) 2a 2a
结束
∴ x2+4x+4=(x+2)2 ∴(1)x2+4x+4>0的解集 为实数集{x∈R|x≠ - 2}; -2 (2)x2+4x+4<0的解集 为空集.
-1 O
y 3 2 1 x
1
-1
小组讨论:解一元二次不等式的一般步骤。
(1)将原不等式化成一般形式 ax2+bx+c>0或ax2+bx+c<0(a>0); (2)计算Δ=b2-4ac; (3)若Δ≥0,求方程ax2+bx+c=0(a>0) 的根;若Δ<0,方程ax2+bx+c=0(a>0) 没有实数根; (4)根据图象写出一元二次不等式的解集。
数的最高次数为2的整式不等式,叫做一 元二次不等式。
一元二次不等式的一般表达式为 ax2+bx+c>0 (a≠0),或ax2+bx+c<0 (a≠0) 其中a,b,c均为常数。 也可以是 ≥ 2 设 f(x)=ax +bx+c (a≠0), 或≤ 一元二次不等式 f(x)>0或f(x)<0 (a≠0) 的解集与二次函数f(x)之间有什么样的关系? f(x)>0 (a≠0)的解集:是使二次函数f(x)的函 数值为正值时的自变量x的取值的集合。 f(x)<0 (a≠0)的解集:是使二次函数f(x)的函 数值为负值时的自变量x的取值的集合。 f(x)=0 (a≠0) 的解集:是使二次函数f(x)的函 数值为零时的自变量x的取值的集合。
一元二次不等式及其解法
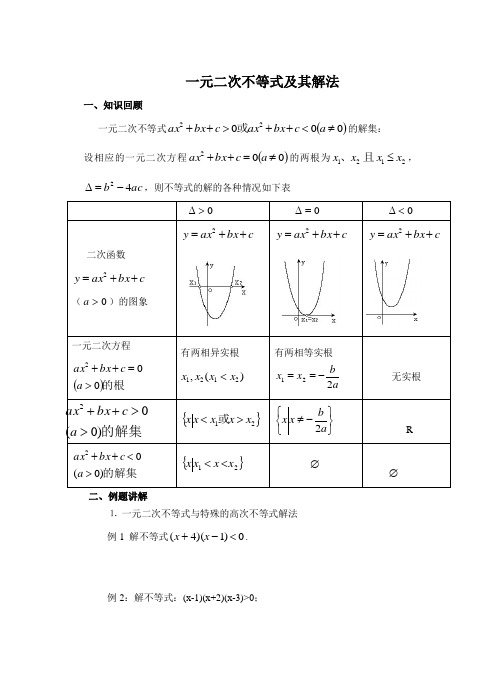
一元二次不等式及其解法一、知识回顾一元二次不等式()00022≠<++>++a c bx ax c bx ax 或的解集: 设相应的一元二次方程()002≠=++a c bx ax 的两根为2121x x x x ≤且、,ac b 42-=∆,则不等式的解的各种情况如下表0>∆0=∆0<∆二次函数c bx ax y ++=2(0>a )的图象c bx ax y ++=2c bx ax y ++=2c bx ax y ++=2一元二次方程()的根002>=++a c bx ax有两相异实根)(,2121x x x x < 有两相等实根ab x x 221-==无实根 的解集)0(02>>++a c bx ax{}21x x x x x ><或⎭⎬⎫⎩⎨⎧-≠a b x x 2R 的解集)0(02><++a c bx ax{}21x x x x <<∅∅二、例题讲解⒈ 一元二次不等式与特殊的高次不等式解法 例1 解不等式0)1)(4(<-+x x .例2:解不等式:(x-1)(x+2)(x-3)>0;例3 解不等式:(x-2)2(x-3)3(x+1)<0.2.分式不等式的解法 例4 解不等式:073<+-x x .例5 解不等式:0322322≤--+-x x x x .例6. 解关于x 的不等式:(x-x 2+12)(x+a)<0. 三、练习【1】设关于x 的不等式x >ax+23的解集为{x 4<x<m},求实数a 和m 的值。
【2】已知关于x 的不等式ax 2+bx+c<0的解集是{x x<-2或x>21-},求ax 2-bx+c>0的解集。
【3】若对x ∈R 恒有n x x x x >++++122322,(n ∈N *),试求n 的值。
一元二次不等式及解法

一元二次不等式及其解法知识点一:一元二次不等式的定义只含有一个未知数,并且未知数的最高次数是2的不等式,称为一元二次不等式。
比如:.任意的一元二次不等式,总可以化为一般形式:或.知识点二:一般的一元二次不等式的解法一元二次不等式或的解集可以联系二次函数的图象,图象在轴上方部分对应的横坐标值的集合为不等式的解集,图象在轴下方部分对应的横坐标值的集合为不等式的解集.设一元二次方程的两根为且,,则相应的不等式的解集的各种情况如下表:(1)一元二次方程的两根是相应的不等式的解集的端点的取值,是抛物线与轴的交点的横坐标;(2)表中不等式的二次系数均为正,如果不等式的二次项系数为负,应先利用不等式的性质转化为二次项系数为正的形式,然后讨论解决;二次函数()的图象有两相异实根有两相等实根(3)解集分三种情况,得到一元二次不等式与的解集。
知识点三:解一元二次不等式的步骤(1)先看二次项系数是否为正,若为负,则将二次项系数化为正数;(2)写出相应的方程,计算判别式:①时,求出两根,且(注意灵活运用因式分解和配方法);②时,求根;③时,方程无解(3)根据不等式,写出解集.知识点四:用程序框图表示求解一元二次不等式ax2+bx+c>0(a>0)的过程类型一:解一元二次不等式1. 初学二次不等式的解法应尽量结合二次函数图象来解决,培养并提高数形结合的分析能力;2. 当时,用配方法,结合符号法则解答比较简洁;当且是一个完全平方数时,利用因式分解和符号法则比较快捷.3. 当二次项的系数小于0时,一般都转化为大于0后,再解答.例题1.解下列一元二次不等式(1);(2);(3)举一反三:【变式1】解下列不等式(1) (2)【变式2】解不等式:类型二:已知一元二次不等式的解集求待定系数二次方程的根是二次函数的零点,也是相应的不等式的解集的端点.根据不等式的解集的端点恰为相应的方程的根,我们可以利用韦达定理,找到不等式的解集与其系数之间的关系,这一点是解此类题的关键。
一元二次不等式及其解法

一元二次不等式及其解法

∵ 32 4 2 2 7 0
∴方程 2x 2 3x 2 0 无实数根 ∴原不等式的解集为 R.
习题 1: 解下列不等式: (1) x 2 5x 6 0 ;
(2) x 2 7x 6 ;
x 2 6x 10 0
(3) 2 xx 3 0 ;
;
当 a 1 ,即 a 1或0 a 1 时,原不等式的解集为 x a x 1 .
原不等式可化为 x 22 0 或 x 22 0 ,所以原不等式的解集为 x x 2或 x x 2;
当 0 ,即 4 a 4 时 方程 x 2 ax 4 0 无实数根,所以原不等式的解集为 R.
例 7. 解不等式 m2 1x 2 4x 1≥0 m R.
第1页
(2)一元二次不等式 ax 2 bx c 0 (≤0)的解集就是二次函数 y ax 2 bx c 0a 0
的图象位于 x 轴下方(包括 x 轴)的部分所对应的自变量的取值范围.
表(1)一元二次方程、二次函数以及一元二次不等式的关系:
判别式 b 2 4ac
解:∵ m 2 ≥0 ∴m2 1 0
42 4m2 1 12 4m2
当 0 ,即
一元二次不等式及其解法
一元二次不等式及其解法【知识归纳】1.一元二次不等式的解法(1)将不等式的右边化为零,左边化为二次项系数大于零的不等式ax 2+bx +c >0 (a >0)或ax 2+bx +c <0 (a >0).(2)求出相应的一元二次方程的根.(3)利用二次函数的图像与x 轴的交点确定一元二次不等式的解集. 2.一元二次不等式与相应的二次函数及一元二次方程的关系如下表:判别式Δ=b 2-4acΔ>0 Δ=0 Δ<0 二次函数y =ax 2+bx +c(a >0)的图像一元二次方程ax 2+bx +c =0 (a >0)的根 有两相异实根x 1,x 2(x 1<x 2) 有两相等实根x 1=x 2=-b 2a没有实数根 ax 2+bx +c >0(a >0)的解集{x |x <x 1或x >x 2} {x |x ≠x 1} {x |x ∈R } ax 2+bx +c <0(a >0)的解集{x |x 1< x <x 2} ∅ ∅【难点提升】1.一元二次不等式的解集及解集的确定 一元二次不等式ax 2+bx +c <0 (a ≠0)的解集的确定受a 的符号、b 2-4ac 的符号的影响,且与相应的二次函数、一元二次方程有密切联系,可结合相应的函数y =ax 2+bx +c (a≠0)的图像,数形结合求得不等式的解集.若一元二次不等式经过不等式的同解变形后,化为ax 2+bx +c >0(或<0)(其中a >0)的形式,其对应的方程ax 2+bx +c =0有两个不等实根x 1,x 2(x 1<x 2) (此时Δ=b 2-4ac >0),则可根据“大于取两边,小于夹中间”求解集.2.解含参数的一元二次不等式,可先考虑因式分解,再对根的大小进行分类讨论;若不能因式分解,则可对判别式进行分类讨论,分类要不重不漏.【学前强化】1.不等式x 2<1的解集为________.2.函数y =x 2+x -12的定义域是____________.3.已知不等式x 2-2x +k 2-1>0对一切实数x 恒成立,则实数k 的取值范围为_____________.4.不等式x -12x +1≤0的解集为 ( ) A.⎝⎛⎦⎤-12,1 B.⎣⎡⎦⎤-12,1 C.⎝⎛⎭⎫-∞,-12∪[1,+∞) D.⎝⎛⎦⎤-∞,-12∪[1,+∞)5.若不等式ax 2+bx -2<0的解集为{x |-2<x <14},则ab 等于( ) A .-28 B .-26 C .28 D .266.设函数f (x )=⎩⎪⎨⎪⎧x 2-4x +6,x ≥0,x +6, x <0, 则不等式f (x )>f (1)的解集是________.7.已知f (x )=ax 2-x -c >0的解集为(-3,2),则a =________,c =________.8.当x ∈(1,2)时,不等式x 2+mx +4<0恒成立,则m 的取值范围为________________.题型一 一元二次不等式的解法【例1】解下列不等式:思维启迪: 解一元二次不等式的一般步骤:(1)对不等式变形,使一端为0且二次项系数大于0,即ax 2+bx +c >0(a >0),ax 2+bx +c <0(a >0);(2)计算相应的判别式;(3)当Δ≥0时,求出相应的一元二次方程的根;(4)根据对应二次函数的图象,写出不等式的解集.(1)-x 2+2x -23>0; (2)9x 2-6x +1≥0. (3)x 2+2x -3≤0;(4)x -x 2+6<0; (5)4x 2+4x +1<0; (6)x 2-6x +9≤0;【变式】 解下列不等式:(1)2x 2+4x +3<0; (2)-3x 2-2x +8≤0; (3)8x -1≥16x 2.题型二 含参数的一元二次不等式的解法【例2】已知不等式ax 2-3x +6>4的解集为{x |x <1或x >b },求a ,b 的值;思维启迪:先化简不等式为标准形式,再依据解集确定a 的符号,然后利用根与系数的关系列出a ,b 的方程组,求a ,b 的值.【变式】解关于x的不等式ax2-(a+1)x+1<0.题型三一元二次不等式恒成立问题【例3】已知f(x)=x2-2ax+2 (a∈R),当x∈[-1,+∞)时,f(x)≥a恒成立,求a的取值范围.思维启迪注意等价转化思想运用,二次不等式在区间上恒成立的问题可转化为二次函数区间最值问题.【变式1】已知不等式ax 2+4x +a >1-2x 2对一切实数x 恒成立,求实数a 的取值范围.思维启迪:化为标准形式ax 2+bx +c >0后分a =0与a ≠0讨论.当a ≠0时,有⎩⎪⎨⎪⎧a >0,Δ=b 2-4ac <0.【变式2】当x ∈(1,2)时,不等式x 2+mx +4<0恒成立,求m 的取值范围。
3.2一元二次不等式及其解法
想一想,当x取何值时,y 的值大 于零?(或小于零?) y O m x y n O x
复习
当x m时y 0 当x m时y 0
当 x n时 y 0 当 x n时 y 0
考察:对一次函数y=2x-7,当x为何值 时,y=0;当x为何值时,y<0;当x为何值 时,y>0?
-2 O
3
x
结论:
解一元二次不等式
ax2+bx+c>0
(a>0,△=0 )的步骤: ① 将二次不等式化成一般式;
② 求出方程ax2+bx+c=0的两根; ③ 画出y=ax2+bx+c的图象;
④ 根据图象写出不等式的解集.
求解一元 二次不等式 ax2+bx+c>0 (a>0)的程序框 图:
△≥0
x
结合函数图 象进行思考
Hale Waihona Puke -2 O3x思考:对二次函数 y=x2-x-6,当x为何值 时,y=0?当x为何值时,y<0?当x为何值时, y>0 ?
y
当 x=-2 或 x=3 时, y=0 即 x2x6=0 当2<x<3 时, y<0 即 x2x6<0 当 x<2 或 x>3 时, y>0 即 x2x6>0
b 2a
x< x1或x> x2
举例
例1 解不等式x2-6x-7>0 y
解:方程x2-6x-7=0的解是
x1 1, x 2 7
作函数图象的草图 所以,不等式的解集是
-1 o
7 x
{x | x<-1 或 x > 7 }
一元二次不等式及其解法
2021年新高考数学总复习第七章《不等式》一元二次不等式及其解法一元二次不等式的解集判别式Δ=b2-4ac Δ>0Δ=0Δ<0二次函数y=ax2+bx+c(a>0)的图象方程ax2+bx+c=0 (a>0)的根有两相异实根x1,x2(x1<x2)有两相等实根x1=x2=-b2a没有实数根ax2+bx+c>0(a>0)的解集{x|x<x1或x>x2}⎩⎨⎧⎭⎬⎫x⎪⎪x≠-b2a{x|x∈R} ax2+bx+c<0(a>0)的解集{x|x1< x<x2} ∅∅概念方法微思考1.一元二次不等式ax2+bx+c>0(a>0)的解集与其对应的函数y=ax2+bx+c的图象有什么关系?提示ax2+bx+c>0(a>0)的解集就是其对应函数y=ax2+bx+c的图象在x轴上方的部分所对应的x的取值范围.2.一元二次不等式ax2+bx+c>0(<0)恒成立的条件是什么?提示显然a≠0.ax2+bx+c>0恒成立的条件是⎩⎪⎨⎪⎧a>0,Δ<0;ax2+bx+c<0恒成立的条件是⎩⎪⎨⎪⎧a<0,Δ<0.题组一思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)若不等式ax 2+bx +c <0的解集为(x 1,x 2),则必有a >0.( √ )(2)若不等式ax 2+bx +c >0的解集是(-∞,x 1)∪(x 2,+∞),则方程ax 2+bx +c =0的两个根是x 1和x 2.( √ )(3)若方程ax 2+bx +c =0(a ≠0)没有实数根,则不等式ax 2+bx +c >0的解集为R .( × ) (4)不等式ax 2+bx +c ≤0在R 上恒成立的条件是a <0且Δ=b 2-4ac ≤0.( × )(5)若二次函数y =ax 2+bx +c 的图象开口向下,则不等式ax 2+bx +c <0的解集一定不是空集.( √ )题组二 教材改编2.已知集合A ={x |x 2-x -6>0},则∁R A 等于( )A .{x |-2<x <3}B .{x |-2≤x ≤3}C .{x |x <-2}∪{x |x >3}D .{x |x ≤-2}∪{x |x ≥3}答案 B解析 ∵x 2-x -6>0,∴(x +2)(x -3)>0,∴x >3或x <-2,即A ={x |x >3或x <-2}.在数轴上表示出集合A ,如图所示.由图可得∁R A ={x |-2≤x ≤3}.故选B.3. y =log 2(3x 2-2x -2)的定义域是________________.答案 ⎝ ⎛⎭⎪⎫-∞,1-73∪⎝ ⎛⎭⎪⎫1+73,+∞ 解析 由题意,得3x 2-2x -2>0,令3x 2-2x -2=0,得x 1=1-73,x 2=1+73, ∴3x 2-2x -2>0的解集为⎝ ⎛⎭⎪⎫-∞,1-73∪⎝ ⎛⎭⎪⎫1+73,+∞. 题组三 易错自纠4.不等式-x 2-3x +4>0的解集为________.(用区间表示)答案 (-4,1)。
一元二次不等式及其解法(精)全
一元二次不等式5x2 10x 4.8 0的解集就是 二次函数y 5x2 10x 4.8的图象(抛物线) 位于x轴下方的点所对应的x的集合.
因此, 求解一元二次不等式可以先解相应的一元二次方程, 确定抛物线与x轴交点的横坐标, 再根据图象写出不等式的解集. 第一步:解方程5x2 10x 4.8 0,得:x1 0.8, x2 1.2;
问题: 怎样解不等式5x2 10x 4.8 0?
思考(:1)当x是什么实数时,函数y 5x2 10x 4.8的值是:
(1)0 (2)正数 (3)负数
(2)能否画出二次函数 y 5x2 10x 4.8 的图象。 y
(3)能否找出抛物线上纵坐标 y 0 的点?其横坐标应取哪些值?
0 0.8
y 5x2 10x 4.8
有两相异实根 x1, x2 (x1<x2)
有两相等实根 x1=x2= b 2a
ax2+bx+c>0 (a>0)的解集 {x|x<x1,或 x>x2}
{x|x≠
b
}
2a
ax2+bx+c<0
(a>0)的解集 {x|x1< x <x2 }
Φ
△<0 y
x O 没有实根
R Φ
例1:解下列不等式:
(1)x2 7x 12 0; (2) x2 2x 3 0; (3)x2 2x 1 0; (4)x2 2x 2 0.
从这题可得出求一元二次不等式的解集的 基本步骤是怎样的?
解一元二次不等式的基本步骤:
(1)化不等式为标准形式:ax2 bx c 0(a 0) 或ax2 bx c (0 a 0)
(2)确定方程ax2 bx c 0 a 0 的根;
