华东师大版数学八年级上册全册知识点汇编(整理版,思维导图)
华东师大版八年级数学上册知识点总结
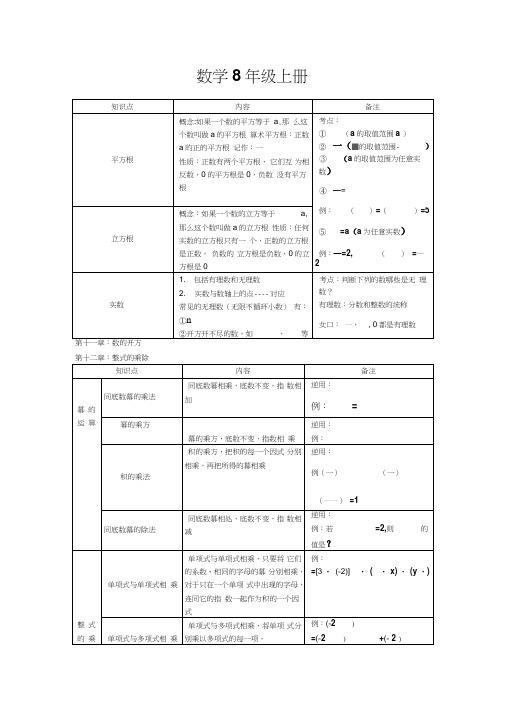
数学8年级上册第十二章:整式的乘除线段的垂直平分线角平分线互逆命题与互逆定理尺规作图等边三角形5.(斜边、直角边)H.L.:如果两个直角三角形中一条斜边和一条直角边都对应相等,那么①等腰三角形的两腰相等②等腰三角形的两底角相等③等腰三角形“三线合一”(顶角的平分线,底边上的中线,底边上的高重合)④等腰三角形是轴对称图形,只有一条对称轴⑤等腰三角形的两底角的平分线相等(两条腰上的中线相等,两条腰上的高相等)①定义法:在同一三角形中,有两条边相等的三角形是等腰三角形。
②判定定理:在同一三角形中,有两个角相等的三角形是等腰三角形(简称:等角对等边)。
这两个三角形全等。
考点:①若是等腰三角形②等腰三角形“三线合一”2.自己补充完整1.若AD 贝U BD=BC,/ BAD玄CAD则说明点的距离相等E若直线EF是线已知:若EF ,垂足为点C,AC=BC点D是直D段AB的垂直平线EF上任意一点I D\分线,结论:DA=DB\则:性质定理的逆定理:到线段两端点距离相等的/A① DA=DB点在线段的垂直平分线上 A C r B②是等已知:DA=DB F腰三角形,因此结论:点D在线段AB的垂直平分线上具有等腰三角形的一切性质性质定理:线段垂直平分线上的点到线段两端考点:性质定理:角平分线上的点到角两边的距离相等已知:OP平分/ AOB且PD , PE , 结论:PE=PD性质定理的逆定理:角的内部到角两边距离相等的点在角的平分线上已知:PD , PE 且PE=PD结论:OP平分/ AOB第一个命题的结论是第二个命题的条件,那么这两个命题叫做互逆命题五个基本的作图方法:①作一条线段等于已知线段②作一个角等于已知角③作已知角的平分线④过一点作已知线段的垂线⑤作已知线段的垂直平分线性质:①是特殊的等腰三角形,因此具有等腰三角形的一切性质。
(等腰三角形包括等边三角形,等腰大于等边)②等边三角形的三条边相等③等边三角形的三个角相等,都为60o。
八年级上册知识点思维导图

八年级上册知识点思维导图八年级上册知识点是中学数学的重要基础,学生要掌握这些知识点才能在未来的学习中更好地理解和应用数学知识。
在学习这些知识点时,使用思维导图可以帮助学生更好地理解和记忆知识点。
本文将为大家介绍八年级上册数学知识点的思维导图。
1.二次根式二次根式是初中数学中一个非常重要的知识点。
在学习二次根式时,学生需要掌握以下几个方面的知识:(1)如何化简二次根式(2)二次根式的乘、除、加、减运算2.二次函数二次函数是初中数学中一个非常重要的知识点,二次函数与二次方程是息息相关的。
在学习二次函数时,学生需要掌握以下几个方面的知识:(1)二次函数的定义和一般式(2)二次函数的图像及其性质(3)解二次函数的最值问题3.三角函数三角函数是中学数学中一个非常重要的知识点,它是应用最广泛的数学工具之一。
在学习三角函数时,学生需要掌握以下几个方面的知识:(1)正弦、余弦、正切函数的定义和图像(2)三角函数的性质(3)应用三角函数解决问题4.向量向量也是中学数学中一个非常重要的知识点。
在学习向量时,学生需要掌握以下几个方面的知识:(1)向量的概念及其表示(2)向量的加、减和数乘(3)向量的点乘和叉乘(4)应用向量解决几何问题5.立体几何立体几何是中学数学中一个非常重要的知识点。
在学习立体几何时,学生需要掌握以下几个方面的知识:(1)四面体、正六面体等常见立体图形(2)体积和表面积的计算公式6.平面向量与解析几何平面向量与解析几何是中学数学中一个重要的知识点,在学习平面向量与解析几何时,学生需要掌握以下几个方面的知识:(1)平面向量的坐标表示(2)平面向量的加、减和数乘(3)平面向量内积的概念和性质(4)直线和平面的解析方程(5)应用向量解决几何问题以上便是八年级上册数学知识点的思维导图,学生可以通过使用思维导图来更好地记忆和理解这些知识点。
同时,老师也可以在教学时使用思维导图帮助学生更好地掌握这些知识点。
通过不断地学习和练习,学生可以更好地理解和应用数学知识,为未来的学习打下坚实的基础。
八年级各章知识点思维导图

八年级各章知识点思维导图厚积薄发,学习的过程离不开知识点的积累。
在学习新知识的同时,我们也需要对已经学过的知识点进行整理和回顾。
在这里,为大家提供八年级各章知识点思维导图,旨在帮助同学们回顾所学知识,加深记忆,提高成绩。
一、数学第一章有理数- 有理数的概念- 有理数的比较大小- 有理数的加减法- 有理数的乘法- 有理数的除法第二章整式与分式- 整式的概念- 分式的概念- 分式的化简与运算- 多项式的运算第三章一次函数及其图象- 一次函数的概念- 一次函数的表示方法及其性质- 一次函数的图象及其特征- 一次函数的应用第四章等比数列- 等比数列的概念- 等比数列的通项公式- 等比数列的前n项和- 等比数列的应用二、英语第一章数字和时间- 数字的读法及运用- 时间的读法及运用第二章班级活动和照片介绍- 班级活动的常用表达- 照片的描述方法- 班级活动和照片的介绍第三章询问地址和指路- 询问地址的表达方式- 指路的表达方式- 询问地址和指路的实际运用第四章常见交通工具及其介绍- 常见交通工具的表达方式- 交通工具的介绍方法- 交通工具的选择与使用三、语文第一章古诗词鉴赏- 古诗词的基本概念- 古诗词的分类- 古诗词的鉴赏方法第二章作文- 作文的基本要素- 作文的分类- 作文的写作技巧第三章阅读理解- 阅读理解的基本技能- 阅读理解的常用题型- 阅读理解的解题技巧第四章修辞手法- 修辞手法的基本概念- 修辞手法的分类- 修辞手法的应用及效果思维导图是一种有效的学习工具,其能够帮助我们整理、归纳知识,帮助我们记忆和应用所学知识。
希望同学们能够运用这些思维导图进行学习,取得更好的成绩。
让我们一起加油!。
最新华东师大版八年级数学上册知识点总结
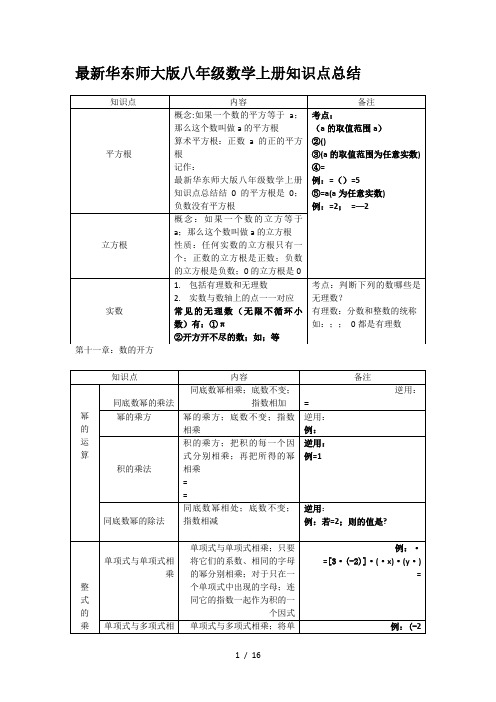
例:
的平方和减去它们的积的 2
逆用
倍
定义:把一个多项式化为几
常考点:
个整式的积的形式;叫做多 ①两种因式分解法一起运用
项式的因式分解 (先提公因式;然后再运用公
因式分解的方法:
式法)
因式分解
①提公因式法
例:
②运用乘法公式法
=
=(a+b)(a-b)
②“1”常Байду номын сангаас要变成“”
例:
第十三章:全等三角形
知识点
2 / 16
常运用于股市与气温的统计
15 / 16
综合考查
①扇形统计图与条形统计图一起考;条形统计图的具体数据为 频数;扇形统计图的百分比为频率;从而可以根据公式计算出
总次数 ②根据统计表;会制作条形统计图(单位值;间隔值要相等)
③根据统计表;会制作扇形统计图(计算百分比和百分数) ④扇形圆心角的度数=百分比
幂
幂的乘方
幂的乘方;底数不变;指数 逆用:
的
相乘
例:
运
积的乘方;把积的每一个因 逆用:
算
式分别相乘;再把所得的幂 例=1
积的乘法
相乘
=
=
同底数幂相处;底数不变; 逆用:
同底数幂的除法 指数相减
例:若=2;则的值是?
单项式与单项式相乘;只要
单项式与单项式相 将它们的系数、相同的字母
乘 的幂分别相乘;对于只在一
⑤扇形的面积之比=各部分所占百分数之比=各部分圆心角之比
16 / 16
整
个单项式中出现的字母;连
式
同它的指数一起作为积的一
的
个因式
乘 单项式与多项式相 单项式与多项式相乘;将单
八年级数学上册《实数》知识点整理华东师大版

八年级数学上册《实数》知识点整理华东师大版八年级数学上册《实数》知识点整理华东师大版知识点1、实数的分类:有理数和无理数2、数轴:规定了原点、正方向和单位长度的直线叫数轴.实数和数轴上点一一对应.3、相反数:符号不同的两个数,叫做互为相反数.a的相反数是-a,0的相反数是0. (若a与b护卫相反数,则a+b=0)4、绝对值:在数轴上表示数a的点到原点的距离叫数a的绝对值,记作∣a∣,正数的绝对值是它本身;负数的绝对值是它的相反数;0的绝对值是0.5、倒数:乘积为1的两个数6、乘方:求相同因数的积的运算叫乘方,乘方运算的结果叫幂.(平方和立方)7、平方根:一般地,如果一个数x的平方等于a,即x2=a 那么这个数x就叫做a的平方根(也叫做二次方根).一个正数有两个平方根,它们互为相反数;0只有一个平方根,它是0本身;负数没有平方根.(算术平方根:一般地,如果一个正数x的平方等于a,即x2=a,那么这个正数x就叫做a的算术平方根,0的算术平方根是0.)实数,是有理数和无理数的总称。
数学上,实数定义为与数轴上的点相对应的数。
实数可以直观地看作有限小数与无限小数,它们能把数轴“填满”。
但仅仅以列举的方式不能描述实数的整体。
实数和虚数共同构成复数。
实数可以用来测量连续的量。
理论上,任何实数都可以用无限小数的方式表示,小数点的右边是一个无穷的数列(可以是循环的,也可以是非循环的)。
在实际运用中,实数经常被近似成一个有限小数(保留小数点后 n 位,n 为正整数,包括整数)。
在计算机领域,由于计算机只能存储有限的小数位数,实数经常用浮点数来表示。
1)相反数(只有符号不同的两个数,它们的和为零,我们就说其中一个是另一个的相反数,叫做互为相反数) 实数a的相反数是-a,a和-a在数轴上到原点0的距离相等。
2)绝对值(在数轴上一个数a与原点0的距离) 实数a的绝对值是:|a|①a为正数时,|a|=a(不变),a是它本身;②a为0时, |a|=0,a也是它本身;③a为负数时,|a|= -a(为a的绝对值),-a是a的相反数。
华东师大版八年级上册数学知识总结.docx

八年级上第11 章数的开方1.平方根( 1)如果一个数的平方等于a,那么这个数就叫做 a 的平方根。
即:如果 x2 a ,那么 x 叫做 a 的平方根( 2)一个正数有两个平方根,它们互为相反数。
其中:正数 a 的正的平方根,叫做 a 的算术平方根,记作a,读作“根号a”,另一个平方根是它的相反数,即 a 。
因此,正数 a 的平方根可以记作 a 。
a称为被开方数。
0 的平方根只有一个,就是0,记作00 。
负数没有平方根。
a 0(a0 )( 3)求一个非负数的平方根的运算,叫做开平方。
2.立方根( 1)如果一个数的立方等于a,那么这个数叫做 a 的立方根。
即:如果x3a,那么x叫做a 的立方根数 a 的立方根,记作3a,读作“三次根号a”,其中 a 称为被开方数, 3 称为根指数。
(2)求一个数的立方根的运算,叫做开立方。
(3)任何数(正数、负数、 0)都有立方根,并且只有一个。
正数有一个正的立方根。
负数有一个负的立方根。
0的立方根是 0。
3.无理数无限不循环小数叫做无理数。
实数有理数和无理数统称为实数。
实数与数轴上的点一一对应。
第 12 章整式的乘除1.幂的运算( 1)同底数幂相乘,底数不变,指数相加。
a m a n a m n(m、n为正整数)(2)幂的乘方幂的乘方,底数不变,指数相乘。
a mnamn( m、n 为正整数)(3)积的乘方积的乘方,等于把积中每一个因式分别乘方,再把所得的幂相乘。
ab n a n b n(n为正整数)(4)同底数幂的除法同底数幂相除,底数不变,指数相减。
(m、 n 为正整数, m>n, a0 )2.整式的乘法( 1)单项式与单项式相乘将它们的系数、相同字母的幂分别相乘,对于只在一个单项式中出现的字母,则连同它的指数一起作为积的一个因式。
( 2)单项式与多项式相乘将单项式分别乘以多项式的每一项,再将所得的积相加。
(3)多项式与多项式相乘先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加。
华师大版八年级数学上册知识点归纳总结

华师大版八年级数学上册知识点归纳总结证明·:AB //FC ,: 噜乙A =LA.C F.在!::i.AD E和l:J.CFE中.贮竺�D E =邓,:.� 山WE 兰A C FE .全等三角形的性质全等三角形的性质是中考必考内容`常用上明两条线段相等或两个角相等�(无乒中名l 已知: A 如闵M -3-9.AB/! CD , E. 是店的中点,CE =D E .求证:(l)LA EC=乙B ED ;(2)AD =B C . 关已词平行线的性质、全等三角形的判定和性证明(l )':.AB f/CD 喊...乙邸c=L5-CD ,LAED立即C ·:cE=DE, 付...乙ED C=L E C D .:. LABD =乙BEC ,:. 乙AEC=LB1ID .i'1)':E 是B 的中点'.赢.AE =B E .在凶E D 和应E C中.·-1�:� 瓦.£.B EC E D =E C, ·互�E D 竺NJEC(S.A .S .}.: . AD =BC. 尺规作图一种作图方式是不足尺规作图关处是它所使用的工具是不是没有刻度的直尺和吩枝如作图工具是没有刻度的立尺和囡规忒是尺规作图,否则不是近年来有关尺规作图问题时常在考试中出戊,气为选择还和块空见但也时含出现几何综合超. ,'i l ,'l i ','l I l B 如图M -3,-11所示,已知如6.4.B C 中.乙er=,90•, 利用尺规按下列要求作图(保陌作图拫迹):(1炸L.ACB的平分线CD ,交AB于点D;.(2)延,长AC到点E,使C�CB,连接BE .在你作出的图形}中,试判断C D 与B双内位悝关系,井证明你的结论厂M -3r-一II 关诅词尺规作图l 邓)作C D //B E. • .., 明:·:e n 早分LAC B 且乙从邓=90•.,.飞Ltf CD .;;;L JJ,C D=45仑·叉·:CE=CB , :. LEBC'= L B E c=4S "'. ·: 乙B CD=乙E B C =4s •,CJ 4如图M -J -]O 所示.在fiAB C中,L C =殉,:乙B =30句,以A 为阅心.任意长为半径面弧分别:关罚词分,虳过程可知AD 是乙B .4C 的平分线,故OO正确.因为乙C =90•,乙B =:3,o •停ch 、、B 所以乙B A C ""'60户,所以图M -3一lO 乙BAD =LC ,A D =L B =3o •所以AD=DB,故@正确.因为AD 司DB,由线段垂直平分线的判定定理可得点D 在AB 的中垂线上故@正确.答案C / 亡勹. 图M -3一1.21.M -3-12. ;. CD//BE.命题与定理这种题型在每年中考中都会高频出现逌常以某些概念、性质.定理及易混淆知识点为及材,以选择处、判断题的形式勺\。
最新华东师大版八年级数学上册知识点总结

最新华东师大版八年级数学上册知识点总结最新华东师大版八年级数学上册知识点总结新版华师版八年级上册知识点总结第十一章:数的开方知识点平方根内容概念:如果一个数的平方等同于a,那么这个数叫做a的平方根微积分平方根:正数a的正的平方根记作:a性质:正数有两个平方根,它们互为相反数,0的平方根是0,负数没有平方根概念:如果一个数的立方等于a,那么这个数叫做a的立方根性质:任何实数的立方根只有一个,正数的圣索弗勒维孔特是正数,负数的立方根是负数,0的立方根是0考点:①(a的取值范围a≥)②(的取值范围≥)③(a的取值范围为任意实数)(≥)④==(多项式与多项式多项式与多项式相乘,用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加例:(X+2)(X3)=+=例:24÷=(24÷)(÷)(÷)=8整式的除法单项式相除,把系数、同底数幂分别相除作为商的因式,对单项式除于单项式于只在被除式中出现的字母,则连同它的指数一起作为商的一个因数列式多项式除于单项式,先用这个多项式除于单项式多项式的每一项除于这个单项式,再把所得的商相加例:(9+)÷(3x)=9÷÷+÷=3+例:(a+b)(a-b)=逆用:=(a+b)(a-b)例:(+)=++逆用++=(+)例:()=+逆用+=()常考点:①两种因式分解法一起运用(先提公因式,然后再运用公式法)例:++=++=(+)乘法公式平方差公式两数和与这两数差的积,等于这两数的平方差两数和的平方公式两数和的平方,等于这两数的平方和加上它们的积的2倍两数差的平方表达式两数差的平方,等于这两数的平方和减去它们的积的2倍定义:把一个有理数化为几个整式的积的形式,叫做自然数的因式分解因式分解的方法:因式分解①提公因式法②运用乘法公式法=(a+b)(a-b)++=(+)+=()②“1”常常要变成“12”例:=()=+()第十三章:全等课文三角形知识点全等三角形内容性质:全等三角形的对应边和对应角相等三角形全等的判定:1.(边边边)S.S.S.:如果两个三角形的三条边都对应地,那么这两个三角形正方形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1/12八年级上册知识点第11章数的平方
11.1平方根与立方根一、平方根的概念如果一个数的平方等于a,那么这个数叫做a的平方根。二、平方根的性质
1.一个正数有两个平方根,它们互为相反数。2.0
有一个平方根,就是它本身。
3.负数没有平方根。三、算术平方根
正数a的正的平方根,叫做a的算术平方根,记作a,读作“根号a”;另一个平方根是它的相反数,即-a。因
此,正数a的平方根可以记作±a,其中a称为被开方数。0的算术平方根是0,负数没有算术平方根。四、平方根与算术平方根的区别与联系
1.概念不同;2.表示方法不同;2/12
3.个数及取值不同。五、开平方求一个非负数的平方根的运算,叫做开平方。六、立方根
1.概念:如果一个数的立方等于a,那么这个数叫做a的立方根。2.性质:任何数(正数、负数和0)的立方根只有一个。
3.表示:数a的立方根,记作3a,读作“三次根号a”。其中a称为被开方数,3是根指数。
4.一个正数只有一个正的立方根,一个负数只有一个负的立方根,0的立方根是0。七、开立方求一个数的立方根的运算,叫做开立方。11.2实数
一、无理数1.无限不循环小数叫做无理数。2.无理数与有理数的区别(1)有理数是有限小数或无限循环小数,而无理数是无限不循环小数。(2)所有的有理数都能写成分数的形式(整数可以看成分母是1的分数),而无理数不能写成分数的形式。二、实数及其分类1.实数的概念
有理数和无理数统称为实数,即实数包括有理数和无理数。2.实数的分类
(1)按概念分类正整数整数0有理数负整数正分数分数实数负分数
正无理数无理数负无理数3/12
(2)按正负分类正整数正有理数正实数正分数正无理数
实数0负整数负有理数负实数负分数负无理数
三、实数与数轴上点的关系实数与数轴上的点意义对应。四、实数的有关概念
1.一个正实数的绝对值是它本身,一个负实数的绝对值是它的相反数,0的绝对值是0。
0,0,00,a
aaa
aa
2.一个数的绝对值是非负数,即a≥0,因此,在实数范围内,绝对值最小的数是零.两个相反数的绝对值相等.4/12
第12章整式的乘除12.1幂的运算12.1.1同底数幂的乘法一、同底数幂的意义及同底数幂的乘法法则1.同底数幂的意义同底数幂是指底数相同的幂。(其中底数可以是数、单独的字母或其他单项式,也可以是多项式)。
2.同底数幂的乘法法则
nmnmaaa
(m、n为正整数),即同底数幂相乘,底数不变,指数相加。
二、逆用同底数幂的乘法法则
同底数幂的乘法法则nmnmaaa
(m、n为正整数)可以逆用,即am+n=am·an(m、n为正整数)。
12.1.2幂的乘方,12.1.3积的乘方一、幂的乘方的意义及运算法则1.幂的乘方的意义幂的乘方是指几个相同的幂相乘。如(a³)²是两个a³相乘。
2.幂的乘方的运算法则
mnnmaa
(m、n为正整数),即幂的乘方,底数不变,指数相乘。
二、幂的乘方运算法则的逆向运用5/12
幂的乘方运算法则可以逆向运用,即amn=(am)n=(an)m(m、n为正整数)。三、积的乘方的意义及运算法则
1.积的乘方的意义积的乘方指底数是乘积形式的乘方。2.积的乘方的运算法则
nnn
baab(n为正整数),即积的乘方,把积的每一个因式分别乘方,再把所得的幂相乘。
四、积的乘方运算法则的的逆向运用积的乘方的运算法则可以逆用,即anbn=(ab)n(n为正整数)。注意:运用积的乘方运算法则进行运算,要注意系数也要乘方;底数是科学计数法的形式时,乘方后的结果往往也需要写成科学计数法的形式。
12.1.4同底数幂的除法
一、同底数幂的除法法则一般地,设m,n为正整数,m﹥n,a≠0,有am÷an=a
m-n
这就是说,同底数幂相除,底数不变,指数相减。注意:只有“同底数”的幂才可应用同底数幂的除法法则,底数互为相反数时可以先化为同底数的幂再进行运算。()二、逆用同底数幂的除法法则
同底数幂的除法法则可以逆用,即am-n=am÷a
n(m,n都是正整数,且m﹥n,a≠0)
12.2整式的乘法
12.2.1单项式与单项式相乘12.2.2单项式与多项式相乘一、单项式与单项式相乘单项式与单项式相乘,只要将它们的系数、相同字母的幂分别相乘,对于只在一个单项式中出现的字母,则连同它的指数一起作为积的一个因式。二、单项式与多项式相乘
单项式与多项式相乘,将单项式分别乘以多项式的每一项,再将所得的积相加。12.2.3多项式与多项式相乘
一、多项式与多项式相乘多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加,即(m+n)(a+b)=ma+mb+na+nb
12.3乘法公式
12.3.1两数和乘以这两数的差6/12
一、两数和与这两数差的乘法公式(平方差公式)两数和与这两数差的乘法公式:22bababa
即两数和与这两数差的积,等于这两数的平方差。此公式也简称为平方差公式。12.3.2两数和(差)的平方
一、两数和(差)的平方公式及其几何意义
两数和(差)的平方公式:2222bababa222
2bababa
语言描述:两数和(差)的平方,等于这两数的平方和加上(减去)它们的积的2倍。(注:此公式简称完全平方公式)。
12.4整式的除法
一、单项式除以单项式单项式相除,把系数、同底数幂分别相除作为商的因式,对于只在被除式中出现的字母,则连同它的指数一起作为商的一个因式。二、多项式除以单项式
多项式除以单项式,先用这个多项式的每一项除以这个单项式,再把所得的商相加。12.5因式分解
一、因式分解的概念把一个多项式化为几个整式的积的形式,叫做多项式的因式分解。注意:多项式因式分解的结果必须是乘积的形式。二、提公因式法
多项式的每项中都含有相同的因式叫做公因式。如ab+ac+ad中,公因式是a.如果一个多项式的各项有公因式,可以把这个公因式提到括号外面,将多项式写成因式乘积的形式,这种因式分解的方法叫做提公因式法。如ma+mb+mc=m(a+b+c).三、公式法
把乘法公式反过来运用,可以把符合公式特点的多项式因式分解,这种因式分解的方法称为公式法。公式法1:平方差公式的逆用:a²-b²=(a+b)(a-b)公式法2:两数和(差)的平方公式的逆用:a²+2ab+b²=(a+b)²,a²-2ab+b²=(a-b)²
四、十字相乘法:abxbax)(2=))((bxax(a、b是常数)
公式特点:1)右边相乘的两个因式都只含有一个相同的字母,都是一次二项式,并且一次项的系数为一。2)左边
是二次三项式,二次项的系数是1,一次项系数是两常数项之和,积的常数项等于两个因式中常数项之积。
五、因式分解的一般步骤在进行因式分解是应遵循“首先提取公因式,然后考虑用公式”的原则。7/12
第13章全等三角形13.1命题、定理与证明一、命题表示判断的语句叫做命题。命题的两层含义:(1)命题必须是一个完整的句子,通常是一个陈述句,包括肯定句和否定句;(2)命题必须是对某件事情作出肯定或否定的判断。二、命题的组成
命题是由条件和结论两部分组成。条件是已知事项;结论是由已知事项推出的事项。这样的命题通常可写成“如果.....
那么.....”的形式。三、命题的分类
命题分为真命题和假命题两类:真命题:有些命题,如果条件成立,那么结论一定成立,像这样的命题,称为真命题。假命题:有些命题,条件成立时,不能保证结论总是正确,也就是说结论不成立或不一定成立,像这样的命题,称为假命题。四、定理
基本事实:人们在长期实践中总结出来的,并作为判断其他命题真假依据的真命题。数学中,有些命题可以从基本事实或其他真命题出发,用逻辑推理的方法判断它们是正确的,并且可以作为进一步判断其他命题真假的依据,这样的真命题叫做定理。五、证明及证明的一般步骤
证明:根据条件、定义以及基本事实、定理等,经过演绎推理,来判断一个命题是否正确,这样的推理过程叫做证
