割集分析法
安全系统工程课件:事故树分析(三)——事故树简化及最小割集的求法

第14页
单二击、此最处小编割辑集母和版最标小题径样集式
(2)径集和最小径集 径集:指的是事故树中某些基本事件的集合
,当这些基本事件都不同时发生时,顶上事 件必然不发生。所以系统的径集也代表了系 统的正常模式,即系统成功的一种可能性。
2024年11月9日星期六12时27分59秒
第15页
单二击、此最处小编割辑集母和版最标小题径样集式
2024年11月9日星期六12时27分55秒
第6页
单击此一处、编事辑故母树版的标简题化样式
解:根据事故树的逻辑关系,可写出其 布尔代数表达式如下:
T=A1A2=(x1+x2)x1x3 按独立事件概率和与积的计算公式,顶 上事件的发生概率为: QT=[1-(1-q1)(1-q2)]q1q3 =[1-(1-0.1)(1-0.1)]×0.1×0.1 =0.0019
化简的方法就是反复运用布尔代数运算 法则,其化简的程序是:
(1)根据事故树列出布尔代数式; (2)代数式若有括号应先去括号将函数 式展开; (3)用布尔代数的基本性质进行简化; (4)作简化后的等效事故树。
2024年11月9日星期六12时27分54秒
第5页
单击此一处、编事辑故母树版的标简题化样式
【例2-17】 如图2-26所示的事故树示意 图,设顶上事件为T,中间事件为Ai,基本事 件为x1、x2、x3,若其基本事件的发生概率均 为0.1,即q1=q2=q3=0.1,求顶上事件的发 生概率。
合取标准形式为:
n
f B1 • B2 • Bn Bi i 1
2024年11月9日星期六12时28分0秒
第18页
三单、击用此布处尔编代辑数母法版求标最题小样割式集
因此,根据前述例子,归纳起来,用布 尔代数法求最小割集,通常分三个步骤:
最小割集计算

最小割集计算:T=A1+A2+A3=B1B2+X6X7+X8X9=(X1+X2+X3)(X4+X5)+X6X7+X8X9= X1X4+X1X5+X2X4+X2X5+X3X4+X3X5+X6X7+X8X9则最小割集有8个,即K1={X1,X4};K2={X1,X5};K3={X2,X4};K4={X2,X5};K5={X3,X4};K6={X3,X5};K7={X6,X7};K8={X8,X9}。
最小径集计算:T′=A1′·A2′·A3′=(B1′+B2′)(X6′+X7′)(X8′+X9′)=(X1′X2′X3′+X4′X5′)(X6′+X7′)(X8′+X9′)=(X1′X2′X3′X6′+X1′X2′X3′X7′+X4′X5′X6′+X4′X5′X7′)(X8′+X9′)= X1′X2′X3′X6′X8′+ X1′X2′X3′X6′X9′+ X1′X2′X3′X7′X8′+ X1′X2′X3′X7′X9′+ X4′X5′X6′X8′+ X4′X5′X6′X9′+ X4′X5′X7′X8′+ X4′X5′X7′X9′则故障树的最小径集为8个,即P1={X1,X2,X3,X6,X8};P2={X1,X2,X3,X6,X9};P3={X1,X2,X3,X7,X8};P4={X1,X2,X3,X7,X9};P5={X4,X5,X6,X8};P6={X4,X5,X6,X9};P7={X4,X5,X7,X8};P8={X4,X5,X7,X9};起重钢丝绳断裂事故发生概率计算:根据最小割集计算顶上事件的概率即g=1-(1-qk1)(1-qk2)(1-qk3)(1-qk4)(1-qk5)(1-qk6)(1-qk7)(1-qk8)=1-(1-q1q4)(1-q1q5)(1-q2q4)(1-q2q5)(1-q3q4)(1-q3q5)(1-q6q7)(1-q8q9)由于q1=q2=q3=q4=q5=q6=q7=q8=q9=0.1则g=1-(1-0.1×0.1)(1-0.1×0.1)(1-0.1×0.1)(1-0.1×0.1)(1-0.1×0.1)(1-0.1×0.1)(1-0.1×0.1)(1-0.1×0.1)=1-(1-0.1×0.1)8=1-0.998=0.07726山东科技大学2005年招收硕士学位研究生入学考试安全系统工程试卷(共2页)一、问答题(共25分)1、说明事故法则的概念,它对安全工作的启示是什么?分析其在安全工作中的应用。
割集分析法工科
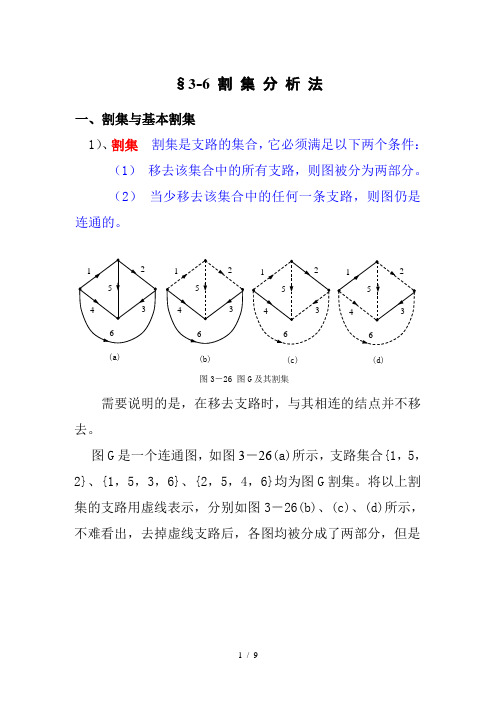
§3-6 割 集 分 析 法一、割集与基本割集1)、割集 割集是支路的集合,它必须满足以下两个条件: (1) 移去该集合中的所有支路,则图被分为两部分。
(2) 当少移去该集合中的任何一条支路,则图仍是连通的。
需要说明的是,在移去支路时,与其相连的结点并不移去。
图G 是一个连通图,如图3-26(a)所示,支路集合{1,5,2}、{1,5,3,6}、{2,5,4,6}均为图G 割集。
将以上割集的支路用虚线表示,分别如图3-26(b)、(c)、(d)所示,不难看出,去掉虚线支路后,各图均被分成了两部分,但是图3-26 图G 及其割集(a)(b)(c)(d)只要少去掉其中的一条虚线支路,图仍然是连通的,故满足割集所要求的条件。
而支路集合{1,5,4,6}、{1,2,3,4,5}不是图G 的割集。
将集合中的支路用虚线表示后如图3-27(a)和(b)所示。
对于图3-27(a)来说,移去支路1、5、4、6后,图虽说被分为两部分(结点①为其中的一部分),但如不移去支路5,图仍被分为两部分;而对于图3-27(b)来说,将支路1、2、3、4、5移去后,图则被分成了三部分,故以上两种支路集合不是割集。
2)、作高斯面确定割集在图G 上作一个高斯面(闭合面),使其包围G 的某些节点,而每条支路只能被闭合面切割一次,去掉与闭合面相切割的支路,图G 将被分为两部分,那么这组支路集合即为图G 的一个割集。
在图G 上画高斯面(闭合面)C 1、C 2、(a)(b)图3-27 非割集说明①②①②C 3如图3-28所示,对应割集C 1、C 2、C 3的支路集合为{1,5,2}、{1,5,3,6}、{2,5,4,6}。
3)、基本割集基本割集又称单树支割集,即割集中只含一条树支,其余均为连支。
如选支路1、5、3为树支,如图3-29所示,则割集C 1,C 2,C 3为基本割集,基本割集的方向与树支的参考方向一致。
当树选定后,对应的基本割集是唯一确定的。
故障树割集下行法

故障树割集下行法摘要:1.故障树割集下行法的定义与概述2.故障树割集下行法的基本原理3.故障树割集下行法的应用实例4.故障树割集下行法的优缺点分析5.故障树割集下行法在我国的发展现状与前景正文:故障树割集下行法是一种基于故障树理论的安全评估方法,主要用于分析和计算系统故障概率,以及确定系统的安全关键部件。
该方法通过构建故障树,分析树中各节点的割集,从而找出可能导致系统故障的最小割集,进而为系统安全管理提供依据。
下面将从五个方面对故障树割集下行法进行详细介绍。
首先,故障树割集下行法的定义与概述。
故障树是一种特殊的决策树,用以表示系统中各部件的故障模式及其对系统整体功能的影响。
故障树割集下行法通过分析故障树中各节点的割集,找出导致系统故障的最小割集,从而计算出系统的故障概率。
其次,故障树割集下行法的基本原理。
该方法的基本原理是利用故障树的结构特征,分析树中各节点的割集,从而找出可能导致系统故障的最小割集。
在此基础上,可以计算出系统的故障概率,并据此评估系统的安全性能。
再次,故障树割集下行法的应用实例。
故障树割集下行法广泛应用于航空航天、核能、化工、电力等高安全风险领域。
例如,在航空航天领域,可以通过该方法分析飞机各部件的故障概率,从而确定哪些部件是安全关键部件,为飞机的设计和维修提供依据。
接着,故障树割集下行法的优缺点分析。
该方法的优点在于可以直观地表示系统的故障模式,便于分析和理解;计算简便,速度快;能够准确找出安全关键部件,为系统安全管理提供依据。
缺点在于,对于复杂的系统,构建故障树需要花费较多时间和精力;此外,该方法对于不确定性因素的处理能力较弱。
最后,故障树割集下行法在我国的发展现状与前景。
故障树割集下行法在我国已经得到广泛应用,并在相关领域的研究中取得了显著成果。
割集分析法

i4
2V I
i4 = i1 + i2 = – 0.25 + 0.85 = 0.6A
II
i5 = 3A(已知), i7 = i1 = – 0.25A
以上各式中,u1、u2、u3分别为支路 1、支路 2 和支路 3 的 电压。
电路分析基础——第一部分:2-5
例2-16 电路如图2-37(a),试求ux。
致,则互电导为正,否则为负;
电流输送:is11、is22、is33 。该基本割集上电流源输 送电流的代数和,电流源电流方向与割
集方向相反者为正,否则为负。
ut1、…、uti、…、ut(n-1):在确定基本割集顺序后, 每个基本割集上的树支电压;
电路分析基础——第一部分:2-5
17/23
注意:在用割集分析时,往往把感兴趣的支路选为树支,使其 电压成为直接求解对象。电路中的电压源支路都应尽量选为树 支,因为电压源是已知的,可以减少未知独立变量的个数。
例如:在图(b)中,切割用虚线表
1
2
示,例如切割II使节点1、3与节点2、 I
3
4分为两个分离部分,所切割的支路 G3、G4、G1和电流源支路的集合就 是割集II。
割集的多样性:一个连通图可以有许
II
4
III
1
2
3
多不同的割集,图(b)中就表明了
三种不同的割集。
4
电路分析基础——第一部分:2-5
7/23
电路分析基础——第一部分:2-5
21/23
i2 =
u2 0.5
=
– ut6 – ut5 – ut4 0.5
= – 2(2–2.75+ 0.326) = 0.85A
2-3-割集电压分析法

b
C2 c
1
2
3
45
d C3
6
IqQ fIsQ fY bU s
I s
6
I s
6
U
R
U s 5
s5 5
R 5
割集电压方程的矩阵形式为:
1 R3
1 R6
1
jL1
1 R6
1
R3
1 R6
11 1
R5 R6 jL2
1 R5
1 R3
R 15R R1153 jC4U U Uqqq132
3
例2-2 写出如图所示电路割集电压方程的矩阵形式。
(1)电感L1、L2 之间无耦合。 (2)电感L1、L2 之间有耦合。
I6
R6
Is 6
I1
I3
L1
R3
M
I4
I2 L 2
C4
I5 R5
+ - U s 5
4
解 (1)电感L1、L2 之间无耦合
画出网络的有向图,对节点和支路进行编号,选支路1、
2、4为树支,如图所示。
§2-3 割集电压分析法
北京邮电大学
电子工程学院 俎云霄
1
割集分析法是以割集电压亦即树支电压为变量列写方程进行 求解的一种方法。
U QTf Ut I Y bU I sY bU s IY bQ T fU tIsY bU s Qf I 0 Q fY b Q T fU t Q fI s Q fY b U s ——割集电压方程的矩阵形式
I s 6
I
s
6
U
R
U s 5
s5 5
R 5
7
(2)电感L1、L2 之间有耦合
大学物理电路分析精品课程 第三章 电路的一般分析方法

I S I4 I1 0
I
1
I3
I2
0
I
4
I3
I5
0
U 4 U S1 U 3 U1 0 U1 U 2 U 0 U 3 U S1 U 5 U S 2 U 2 0
I1R1 U1
I I
2 3
R2 R3
U2 U3
I
4
R4
U4
I 5 R5 U 5
支路电流法(1B法)
1) U 2
2
添加以下方程:
2U 23 2(U 2 U 3 ) 4U 43 4(U 4 U 3 ) U1 U 4
例题3——割集分析法
5 + 19V - 2
I1 +
30V _
4A 1.5I1
4
+ 25V
_
选树如图所示,则只需要对2、4支路 (树支)所决定的基本割集列写方程即可
(5 2 4) I1 (2 4) 4 4 1.5I1 30 25 19
I S
U4 R4
U1 R1
0
UR11
U3 R3
U2 R2
0
U
4
U3
U5
0
R4 R3 R5
3-3 节点法与割集法
一、节点法
1 .方法
任选电路中某一节点为参考节点, 其他节点与此参考节点间的电压称为 “节点电压”。节点法是以节点电压作 为独立变量,对各个独立节点列写KCL 电流方程,得到含(n-1)个变量的(n-1)个 独立电流方程,从而求解电路中待求量。
第三章 电路的一般分析方法
❖重点 1、支路法 2、节点法 3、网孔法
❖难点 1、改 拓扑术语
支路 节点 回路 网孔 基本回路 割集 基本割集
2-3 割集电压分析法

-
解 (1)电感L1、L2 之间无耦合 画出网络的有向图,对节点和支路进行编号,选支路1 画出网络的有向图,对节点和支路进行编号,选支路1、2、 为树支,如图所示。 4为树支,如图所示。
& I6
& I s6
a
R6
C1 6 b C2 c 2 4 3 5
& I1
& I3
M L1 & I4 C4 & I 2 L2 & I5 R5
∆ = jω ( L1 L2 − M 2 )
割集电压方程的矩阵形式为: 割集电压方程的矩阵形式为:
1 1 L2 + + R 3 R6 ∆ 1 −M R6 ∆ 1 R3 1 M − R6 ∆ 1 1 L1 + + R5 R6 ∆ 1 − R5
1 & I s6 R3 & U q1 & 1 & = I − U s5 & U s6 − R5 q2 R5 & U q 3 U & 1 1 s5 + + j ωC 4 R R3 R5 5
割集电压方程的矩阵形式为: 割集电压方程的矩阵形式为:
1 1 1 + + R3 R6 jωL1 1 − R6 1 − R3 1 − R6 1 1 1 + + R5 R6 jωL2 1 − R5
1 − & R3 & I s6 U q1 & 1 U = I − U s 5 & & − q 2 s6 R R5 & U q 3 & 5 1 1 U s5 + + j ωC 4 R3 R5 R 5
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§3-6 割 集 分 析 法
一、割集与基本割集
1)、割集 割集是支路的集合,它必须满足以下两个条件: (1) 移去该集合中的所有支路,则图被分为两部分。
(2) 当少移去该集合中的任何一条支路,则图仍是连通的。
需要说明的是,在移去支路时,与其相连的结点并不移去。
图G 是一个连通图,如图3-26(a)所示,支路集合{1,5,2}、{1,5,3,6}、{2,5,4,6}均为图G 割集。
将以上割集的支路用虚线表示,分别如图3-26(b)、(c)、(d)所示,不难看出,去掉虚线支路后,各图均被分成了两部分,但是
图3-26 图G 及其割集
(a)
(b)
(c)
(d)
只要少去掉其中的一条虚线支路,图仍然是连通的,故满足割集所要求的条件。
而支路集合{1,5,4,6}、{1,2,3,4,5}不是图G 的割集。
将集合中的支路用虚线表示后如图3-27(a)和(b)所示。
对于图3-27(a)来说,移去支路1、5、4、6后,图虽说被分为两部分(结点①为其中的一部分),但如不移去支路5,图仍被分为两部分;而对于图3-27(b)来说,将支路1、2、3、4、5移去后,图则被分成了三部分,故以上两种支路集合不是割集。
2)、作高斯面确定割集
在图G 上作一个高斯面(闭合面),使其包围G 的某些节点,而每条支路只能被闭合面切割一次,去掉与闭合面相切割的支路,图G 将被分为两部分,那么这组支路集合即为图G 的一个割集。
在图G 上画高斯面(闭合面)C 1、C 2、
(a)
(b)
图3-27 非割集说明
①
②
③
①
②
C 3如图3-28所示,对应割集C 1、C 2、C 3的支路集合为{1,5,2}、{1,5,3,6}、{2,5,4,6}。
3)、基本割集
基本割集又称单树支割集,即割集中只含一条树支,其余均为连支。
如选支路1、5、3为树支,如图3-29所示,则割集C 1,C 2,C 3为基本割集,基本割集的方向与树支的参考方向一致。
当树选定后,对应的基本割集是唯一确定的。
当然选的树不同,相应的基本割集也就不同。
如选支路1、5、6为树支以及选支路1、5、2为树支的基本割集分别如图3-30 (a)和(b)所示。
当图G 有n 个结点、b 条支路时,基本割集的数目等于树支数,为(n -1)。
图3-28 作高斯面确定割集
C 1
2
C 3
图3-29 基本割集
二、割集分析法
割集分析法与回路分析法一样,是建立在“树”的基础上的一种分析方法。
割集分析法是将树支电压作为一组独立的求解变量,根据基本割集建立KCL 方程,因此割集分析法也可以称为割集电压分析法。
割集分析法的选树原则与回路分析法相同,即尽可能将电压源及电压控制量选为树支,电流源及电流控制量选为连支。
设网络的图有n 个结点,b 条支路,则割集分析法中基本割集的数目与树支数相等,为(n -1)个,树支电压变量也为(n -1)个。
因此当电路中电压源支路较多时,采用割集分析法最为有效。
下面通过例题说明割集分析法的求解过程。
图3-30 基本割集示例 C 1
(b)
(a)
C 3
C 2
例3-16 用割集分析法求图3-34(a )所示电路。
解:割集分析法的求解步骤如下:
(1) 画出电路的拓扑图,选一个“合适”的树,并给各
支路定向。
本电路的拓扑图如图3-34(b )所示。
其中粗线为树,树支电压为u 1、u 2、u 3,参考方向如箭头方向所示。
(2) 画出基本割集及其参考方向。
基本割集C 1、C 2、C 3如图3-34(b )所示,其参考方向与树支电压方向相同。
(3) 写基本割集的KCL 方程。
图3-34 例3-16图
5s (a )
(b )
C 12
C 3
为写方程方便起见,将基本割集C 1、C 2、C 3画在原电路上,如图3-34(c )所示。
每一条支路的电流都可以用树支电压以及激励源表示。
对应基本割集的KCL 方程分别为
03
2
15
11
1
23=++
-+
---R u u R u u R u u u s
(1)
01
1
233
2
142
=---
++
+-R u u u R u u R u i s
(2)
023
1
1
23=++
--s i R u R u u u (3)
(4) 联立求解,得树支电压u 1、u 2、u 3。
(5) 利用树支电压求得电路的其它物理量。
(c )
s C 3
C
C C 2
C 3
(d )
图3-34 例3-16图
如所选树如图3-34(d )所示,则所得基本割集方程正好是结点电压方程,所以结点电压法是割集分析法的特例。
例3-17 重做例3-7所示电路。
求结点①与结点②之间的
电压12
u 。
解:选树支电压如图,分别为u 1、u 2和u 3 。
u 3等于22V ,可以不建立关于u 3的基本割集方程。
另外两个基本割集的KCL 方程分别为 C 1
8)1(3)22(411=+++-u u
C 2 025)22(51822=-++⨯+u u 两式联立求解得
V u 111=,V u 5.152-= 所以 V u u 11112==
4S
2
图3-35 例3-17图
例3-18 电路如图3-36(a )所示。
已知:
S
G 11=,S G 2 2=,S G 3 3=,S G 5 5=,V u s 1 1=, V u s 3 3=,
A i s 3 3=, 4 4V u s =,V
u s 6 6
=。
试用割集分析法求电流i 1以
及电压源u s1发出的功率p 。
解:选树如图粗线所示,树支电压如图3-36(b )所示,为u 1、u 4和u 6。
因为V u u s 4 44==,V u u s 6 66== ,所以可以不建立关于u 4和u 6的基本割集方程,故只需要列关于u 1的基本割集方程。
基本割集C 1如图3-36(a )所画,其方程为
)()()(36145612111=+++-+++-s s s s s i u u u G u u G u u G
图3-36 例3-18图
u s4(a )
(b )
即 024 81=+u 得 V u 3 1-=
所以 A u u G i s 4)13()(1111-=--=-= W i u p s 411=-=。
