DFT近似计算信号频谱专题研讨 数字信号处理
DFT在信号频谱分析中的应用

DFT在信号频谱分析中的应用目录Ⅰ.设计题目 (1)Ⅱ.设计目的 (1)Ⅲ.设计原理 (1)Ⅳ.实现方法 (1)Ⅴ.设计内容及结果 (5)Ⅵ.改进及建议 (11)Ⅶ.思考题及解答 (14)Ⅷ.设计体会及心得 (15)Ⅸ.参考文献 (16)Ⅰ.设计题目DFT 在信号频谱分析中的应用Ⅱ.设计目的掌握离散傅里叶变换的有关性质,利用Matlab 实现DFT 变换。
了解DFT 应用,用DFT 对序列进行频谱分析,了解DFT 算法存在的问题及改进方法。
学习并掌握FFT 的应用。
Ⅲ.设计原理所谓信号的频谱分析就是计算信号的傅里叶变换。
连续信号与系统的傅里叶分析显然不便于直接用计算机进行计算,使其应用受到限制,而DFT 是一种时域和频域均离散化的变换,适合数值运算,成为分析离散信号和系统的有力工具。
工程实际中,经常遇到的连续信号Xa(t),其频谱函数Xa(jW)也是连续函数。
数字计算机难于处理,因而我们采用DFT 来对连续时间信号的傅里叶变换进行逼近,进而分析连续时间信号的频谱。
Ⅳ.实现方法离散傅里叶变换是有限长序列的傅里叶变换,它相当于把信号的傅里叶变换进行等频率间隔采样,并且有限长序列的离散傅里叶变换和周期序列的离散傅里叶级数本质是一样的。
快速傅里叶变换(FFT )并不是一种新的变换,它是离散傅里叶变换的一种快速算法,并且主要是基于这样的思路而发展起来的:(1)把长度为N 的序列的DFT 逐次分解成长度较短的序列的DFT 来计算。
(2)利用WN(nk)的周期性和对称性,在DFT 运算中适当的分类,以提高运算速度。
(对称性nkNnk NW W N-=+2,12-=NN W ;周期性nkN nk N nrN N k rN n NW W W W ---==)(,r 为任意整数,1=nrNN W )离散傅里叶变换的推导:离散傅里叶级数定义为nk j N k p p ek x Nn x N21)(1)(π∑-==(1-1) 将上式两端乘以nm j Neπ2-并对n在0~N-1求和可得⎥⎦⎤⎢⎣⎡==∑∑∑∑∑-=---=-=-=---=-10)(110101)(1N2N2N2)()(1)(N n m k n j N N k p N n N k m k n j pN n nm j pe k X ek XNen xπππ 因为{m k 1mk 0)(N )(1)(N 2N2N2-1-1N 11=≠---=-==∑m k j m k j N n m k n je eeNπππ所以∑∑-=-=--=110)()()(N2N k p N n nm j p m k k X en x δπ 这样∑-=-=10N2)()(N n nm j p p en x m X π用k 代替m 得∑-=-=1N2)()(N n nk j p P en x k X π(1-2)令N2πj N eW -=则(1-2)成为DFS []∑-===10)()()(N n nkN p p p W n x k X n x (1-3)(1-1)成为IDFS []∑-=-==1)(1)()(N n nkN pp p W k XNn x k X (1-4)式(1-3)、(1-4)式构成周期序列傅里叶级数变换关系。
用DFT(FFT)对连续信号进行频谱分析

电子信息工程系实验报告课程名称:数字信号处理Array实验项目名称:用DFT(FFT)对连续信号进行频谱分析实验时间:班级:通信姓名: xxp 学号:一、实验目的:1.掌握用DFT(FFT)对模拟信号进行谱分析的方法,理解可能出现的分析误差及其原因,以便在实际中正确应用FFT。
2.熟悉应用FFT实现两个序列的线性卷积的方法。
二、实验原理:1.用DFT(FFT)对连续信号进行频谱分析用DFT(FFT)对模拟信号做谱分析是一种近似的谱分析。
首先一般的模拟信号(周期信号除外)的频谱是连续谱,而用FFT做谱分析得到的是数字谱,因此应该取FFT的点数多一些,用它的包络作为模拟信号的近似谱。
另外,如果模拟信号不是严格的带限信号,会因为频谱混叠现象引起谱分析的误差,这种情况下可以预先将模拟信号进行预滤,或者尽量将采样频率取高一些。
最后要注意一般的模拟信号是无限长的,分析时要截断,截断的长度与对模拟信号进行频谱分析的分辨率有关。
如果要进行谱分析的模拟信号是周期信号,最好选择观测时间是信号周期的整数倍,如果不知道信号的周期,要尽量选择观测时间长一些,以减少截断效应的影响。
在运用DFT(FFT)对模拟信号进行谱分析的过程中主要可能产生以下三种误差:(1) 混叠现象对模拟信号进行谱分析时首先要对其采样,当采样速率不满足Nyquist定理时,就会发生频谱混叠,使得采样后的信号序列频谱不能真实的反映原模拟信号的频谱。
避免混叠现象的唯一方法是保证采样速率足够高,使频谱混叠现象不致出现,即在确定采样频率之前,必须对频谱的性质有所了解,在一般情况下,为了保证高于折叠频率的分量不会出现,在采样前,先用低通模拟滤波器对信号进行滤波。
(2) 截断效应实际中我们往往用截短的序列来近似很长的甚至是无限长的序列,这样可以使用较短的DFT来对信号进行频谱分析,这种截短等价于给原信号序列乘以一个矩形窗函数,也相当于在频域将信号的频谱和矩形窗函数的频谱卷积,所得的频谱是原序列频谱的扩展。
数字信号实验-用DFT分析自己语音频谱实验
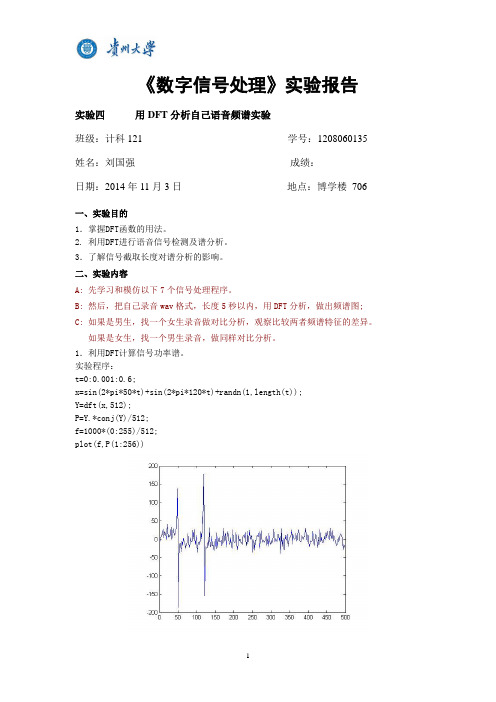
《数字信号处理》实验报告实验四用DFT分析自己语音频谱实验班级:计科121 学号:1208060135 姓名:刘国强成绩:日期:2014年11月3日地点:博学楼706一、实验目的1.掌握DFT函数的用法。
2. 利用DFT进行语音信号检测及谱分析。
3.了解信号截取长度对谱分析的影响。
二、实验内容A: 先学习和模仿以下7个信号处理程序。
B: 然后,把自己录音wav格式,长度5秒以内,用DFT分析,做出频谱图; C: 如果是男生,找一个女生录音做对比分析,观察比较两者频谱特征的差异。
如果是女生,找一个男生录音,做同样对比分析。
1.利用DFT计算信号功率谱。
实验程序:t=0:0.001:0.6;x=sin(2*pi*50*t)+sin(2*pi*120*t)+randn(1,length(t));Y=dft(x,512);P=Y.*conj(Y)/512;f=1000*(0:255)/512;plot(f,P(1:256))2. 进行信号检测。
分析信号频谱所对应频率轴的数字频率和频率之间的关系。
模拟信号)8cos(5)4sin(*2)(t t t x ππ+=,以n t 01.0= 10-≤≤N n 进行取样,求N 点DFT 的幅值谱。
实验程序: subplot(2,2,1)N=45;n=0:N-1;t=0.01*n; q=n*2*pi/N;x=2*sin(4*pi*t)+5*cos(8*pi*t); y=dft(x,N);plot(q,abs(y));title('DFT N=45') subplot(2,2,2)N=50;n=0:N-1;t=0.01*n; q=n*2*pi/N; x=2*sin(4*pi*t)+5*cos(8*pi*t); y=dft(x,N);plot(q,abs(y));title('DFT N=50') subplot(2,2,3)N=55;n=0:N-1;t=0.01*n; q=n*2*pi/N;x=2*sin(4*pi*t)+5*cos(8*pi*t); y=dft(x,N);plot(q,abs(y));title('DFT N=55') subplot(2,2,4)N=60;n=0:N-1;t=0.01*n; q=n*2*pi/N;x=2*sin(4*pi*t)+5*cos(8*pi*t); y=dft(x,N);plot(q,abs(y));title('DFT N=60')3. 对2,进一步增加截取长度和DFT 点数,如N 加大到256,观察信号频谱的变化,分析产生这一变化的原因。
实验一 利用DFT分析信号频谱

实验一 利用DFT 分析信号频谱一、实验目的1.加深对DFT 原理的理解。
2.应用DFT 分析信号的频谱。
3.深刻理解利用DFT 分析信号频谱的原理,分析实现过程中出现的现象及解决方法。
二、实验设备与环境计算机、MATLAB 软件环境。
三、实验基础理论 1.DFT 与DTFT 的关系DFT 实际上是DTFT 在单位圆上以k Njezπ2=的抽样,数学公式表示为:∑-=-===102)(|)()(2N n k Njez en x z X k X k Njππ ,1,..1,0-=N k(2—1) 2、利用DFT 求DTFT方法一:利用下列公式:)2()()(1∑-==-=N k k j Nkk X e X πωφω(2—2)其中21)2/sin()2/sin()(--=N j eN N ωωωωφ为内插函数方法二:实际在MATLAB 计算中,上述插值运算不见得是最好的办法。
由于DFT 是DTFT 的取样值,其相邻两个频率样本点的间距为Nπ2,所以如果我们增加数据的长度N ,使得到的 DFT 谱线就更加精细,其包络就越接近DTFT 的结果,这样就可以利用DFT 计算DTFT 。
如果没有更多的数据,可以通过补零来增加数据长度。
3、利用DFT 分析连续时间函数利用DFT 分析连续时间函数是,主要有两个处理:①抽样,②截断 对连续时间信号)(t x a 一时间T 进行抽样,截取长度为M ,则 nT j M n a tj a a e nT x T dt et x j X Ω--=+∞∞-Ω-∑⎰==Ω)()()(10 (2—3)再进行频域抽样可得 )()(|)(122k TX enT x T j X M M n n Nk ja NTk a ==Ω∑-=-=Ωππ (2—4)因此,利用DFT 分析连续时间信号的步骤如下: (1)、确定时间间隔,抽样得到离散时间序列)(n x .(2)、选择合适的窗函数和合适长度M ,得到M 点离散序列)()()(n w n x n x M =. (3)、确定频域采样点数N ,要求N ≥M 。
数字信号处理DFT

DFT[x(n)]
1 N
X1(k)
X 2 (k )
3.3 频率域采样
1、对于有限长(N点)序列x(n)
Z[x(n)]=X (Z)
取单位圆上的Z变换
X (e j ) FT[x(n)]
会引起x(n)周期延拓
频域一周内等间隔N点采样
~
~
X (k) DFS[x(n)]
X (k) DFT[x(n)]
00
tt
T TpTp / N
XXXaa(a((jjfjff)))
fs 2 fc
T (2 fc )1
N 1
X ( jf ) T xa (nT )e j2 fnT n0
令f kF
00
F fs2/fNsc
N 1
j 2 kn
X ( jkF) T xa (nT )e N
n0
N 1
j 2 kn
时域信号 频域信号
连续的 非周期的
周期的 离散的
三 离散时间、连续频率的序列傅里叶变换
x(nT) T
X e j 或 X (e jT )
---
-T 0 T 2T t
0
时域信号 频域信号
离散的 周期的 非周期的 连续的
---
s
2 T
四 离散时间、离散频率的离散傅里叶变换
x(nT)=x(n)
Tp
1 F
1
W k4 4
1 W4k
4 0
k 0 k 1, 2,3
x(n)的8点DFT为
X (k)
7
x(n)WNkn
3
j 2 kn
e8
n0
n0
x(n)的幅频特性特性曲线及其4点、8点、16点DFT.
用DFT进行频谱分析及其误差问题研究.

目录1. 引言 (1)2. 利用 DFT 对有限长序列进行谱分析 (1)2.1谱分析原理 (1)2.2 实验结果及分析 (2)3. 利用 DFT 对周期序列进行谱分析 (2)3.1 谱分析原理 (2)3.2 实验结果及分析 (3)4. 利用 DFT 对连续时间非周期信号进行谱分析 (4)4.1 谱分析原理 (4)4.2 实验结果及分析 (5)5. 利用 DFS 对连续时间周期信号进行谱分析 (5)5.1 谱分析原理 (5)5.2实验结果及分析 (6)6. 利用DFT进行谱分析的误差问题及其参数选择 (7)6.1谱分析的误差分析 (7)6.2谱分析的近似性问题 (7)6.3谱分析的参数选择 (8)7. 利用DFT进行谱分析的误差仿真 (9)7.1混叠效应仿真 (9)7.2栅栏效应仿真 (9)7.3频谱泄露效应仿真 (10)8. 结束语 (14)参考文献 (15)致谢 (16)1 引言随着信息时代和数字世界的到来,数字信号处理己成为当今一门极其重要的学科和技术领域,数字信号处理在通信、语音、图像、自动控制、医疗和家用电器等众多领域得到了广泛的应用。
任意一个信号都具有时域与频域特性,信号的频谱完全代表了信号,因而研究信号的频谱就等于研究信号本身。
通常从频域角度对信号进行分析与处理,容易对信号的特性获得深入的了解。
因此,信号的频谱分析是数字信号处理技术中的一种较为重要的工具。
[1]众所周知,傅里叶变换和Z变换是信号处理中常用的重要数学变换。
对于有限长序列,还有一种更加重要的数学变换即离散傅里叶变换(Discrete Fourier Transform,DFT)。
DFT[2]之所以重要,是因为其实质是有限长序列傅里叶变换的有限点离散采样,从而实现了频域离散化,使得数字处理可以在频域采用数值运算的方法进行,这样就大大加大了数字信号处理的灵活性。
信号的频谱分析的实质,就是通过信号的傅立叶变换(FT)来分析信号的频谱结构,信号的FT 可以借助于DFT用计算机仿真方法实现。
数字信号处理,第六讲DFT应用
3.4 利用DFT分析连续信号的频谱
例4. 利用DFT近似分析连续信号x(t) etu(t)的 幅度频谱并与理论值比较。
解:X ( j) x(t)e jtdt 1
1 j
| X ( j) | 1 1 2
| X ( j) |
准确的频谱如图所示:
0 50
现以fs 20Hz对其抽样,抽样点数 N =20或N=100,分别进行200的DFT。
精确x(t)的幅度谱,画出DFT的幅度谱。 (2)T 0.005s, N 40或N 50,画出DFT的
幅度谱。
3.4 利用DFT分析连续信号的频谱
解:(1)由信号的构成可见,频率分辨率F=2Hz 当T=0.01s时,fs=100Hz
此时DFT的点数应满足 2, 0, 0, 0, 0; n 0,1, 2,3, 4,5, 6, 7}
(1)计算X (e j ), X (k)并比较两者的关系。
(2)计算Y (e j )与Y (k),有何结论?
3
解:(1)X (e j )
x(n)e jn
e
j
3 2
[4
cos(
3 2
)
6
cos(
1 2
)]
n03
X (k)
x(n)e
j
2 4
nk
{10, 1
j, 0, 1
j}
n0
X
(k)
X
(e
j
)
2
k
4
7
(2)Y (e j )
y(n)e jn
e
j
3 2
[4
cos(
3 2
)
6
cos(
1 2
)]
实验四 利用DFT分析离散信号频谱
数字信号处理及实验实验报告实验题目利用DFT分析离散信号频谱姓名组别班级光电14 学号144320200206 【实验目的】应用离散傅里叶变换(DFT),分析离散信号的频谱。
深刻理解DFT分析离散信号频谱信号频谱的原理,掌握改善分析过程中产生的误差的方法。
【实验原理】根据信号傅里叶变化建立的时域与频域之间的对应关系,可以得到有限序列的离散傅里叶变换(DFT)与4种确定信号傅里叶变换之间的关系,实现由DFT分析其频谱。
【实验结果与数据处理】1、利用FFT分析信号x[k] = cos(3πk/8),k = 0,1,2……,31的频谱:(1)确定DFT计算的参数。
(2)进行理论值与计算值比较,讨论信号频谱分析过程中产生误差的原因及改善方法。
分析:信号的周期T = 16,角频率w=2π/N=π/8。
clc,clear,close allN = 16; k = 0 : N-1;x = cos(3*pi*k/8);X = fft(x,N);subplot(2,1,1);stem(k - N/2,abs(fftshift(X)));ylabel('幅度','fontsize',15);xlabel('频率(rad)','fontsize',15);subplot(2,1,2);stem(k - N/2,angle(fftshift(X)));ylabel('相位','fontsize',15);xlabel('频率(rad)','fontsize',15);2、有限长脉冲序列x[k]= [2,3,3,1,0,5;k = 0,1,2,3,4,5],利用FFT分析其频谱,并绘出其幅度谱与相位谱。
clc,clear,close allN = 6; k = 0 : N-1; w = k-3;x=[2,3,3,1,0,5];X=fft(x,N);subplot(2,1,1);stem(w,abs(fftshift(X)));ylabel('幅度','fontsize',15);xlabel('频率(rad)','fontsize',15);subplot(2,1,2);stem(w,angle(fftshift(X)));ylabel('相位','fontsize',15);xlabel('频率(rad)','fontsize',15);3、某周期序列由3个频率组成:x[k] = cos(7πk/16) + cos(9πk/16) + cos(πk/2),利用FFT分析其频谱。
数字信号处理第三章8 用DFT对模拟信号作频谱分析
信号最高频率f h的确定
t0 Th / 2
1 1 fh Th 2t0
2013-8-8
数字信号处理
例:有一频谱分析用的FFT处理器,其抽样点数 必须是2的整数幂,假设没有采用任何的数据处理 措施,已给条件为:
1)频率分辨率 10 Hz 2)信号最高频率 4kHz
x(n)为周期序列,周期N 14
抽样点数至少为14点
或者因为频率分量分别为500、 、 600 700Hz
得 F0 100Hz
N f s / F0 1400/100 14
最小记录点数N 14
2013-8-8 数字信号处理
2013-8-8
数字信号处理
T 2 f / f s 2 k / N
2013-8-8
X ( j) T x (nT )e jnT
n 0
数字信号处理
3)频域抽样:一个周期分N段,采样间隔 F0 ,时域周期延拓,
周期为 T0 1/ F0
N-1 n 0 N 1
n 0
0 2 F0
X ( jk 0 ) T x (nT )e jk0nT
试确定以下参量: 1)最小记录长度T0 3)在一个记录中最少点数N
2)抽样点间的最大时间间隔T(即最小抽样频率)
2013-8-8
数字信号处理
解: 1)最小记录长度:
1 1 T0 0.1s F0 10
2)最大抽样间隔 (f s 2 f h
f s 1/ T)
1 1 T 0. ms 125 3 2 f h 2 4 10
2013-8-8 数字信号处理
f fs * k / N
数字信号处理实验DFT
数字信号处理实验(第七章DFT)一、实验内容利用DFT对信号(如由多个正弦信号组成的信号)进行频谱分析,并研究不同数据长度,补零,加窗等对频率分辨率的影响。
二、实验工具MATLAB2012b软件三、实验涉及知识1.加窗:通常情况下,信号都是无限长的。
而在运用计算机进行模拟时,这是无法操作的。
所以实际情况下,要把观测的信号限制在一定长的时间之内。
为了从无限长的信号中得到有限长的数据,在时域乘一个窗函数,将信号截短,叫做加窗。
2.补零:为了增加频域抽样点数N,在不改变时域数据的情况下,在时域数据末端加一些零值点,叫做补零。
3.频率分辨率:指对两个最近的频谱峰值能够分辨的能力。
四、实验设计思路实验要求是利用DFT进行频谱分析,并研究不同数据长度,补零,加窗等对频率分辨率的影响。
我们利用DFT计算频谱的目的在于,针对计算机只能计算有限个离散的点的取值这一特点,实现计算机对连续时间信号的频谱的模拟。
所以我们比较关心的是模拟频谱和原信号频谱的拟合程度,我们希望拟合程度越高越好。
这就需要增加频率分辨率,因为频率分辨率越高,根据公式,说明相同采样频率下,采样的长度就越长,也就是频谱采样的点数就越多,我们可以看到的模拟频谱图像就越清晰,这样与原信号的拟合程度就越好。
根据实验要求,我将实验定为五部分,用4个m文件分别研究不同数据长度,补零,加窗,采样频率对频率分辨率的影响。
在程序设计中,出现的一个问题是,如何计算DFT后的频域函数的值。
课堂用的参考书上曾经给出一个将DFT转换为矩阵运算的方法,查阅相关参考书后,我发现在MATLAB信号处理工具箱中自带了一个dftmtx的函数,这个函数的功能是可以计算出旋转因子,计算出旋转因子后再将时域函数也转换成矩阵的形式进行DFT就可以了。
这里说明一下,由于dftmtx这个函数默认取值间隔为1,所以在没有特意设定采样频率的值得情况下,我们将采样频率默认为 1 。
实验设计中,为了更好的理解频率分辨率的概念,我不仅采用了绘图的形式,还直接计算了频率的分辨率,从而更直观的得到频率分辨率的具体数值。
