种群增长逻辑斯蒂方程
种群的逻辑斯蒂增长模型

华南师范大学实验报告学生姓名 学 号 专 业 年级、班级 课程名称生态学实验 实验项目 种群的逻辑斯蒂增长模型 实验类型 验证 □设计□综合 实验时间 年 月 日 实验指导老师 实验评分种群的逻辑斯蒂增长模型1 实验目的1.1 了解种群在有限环境中的增长方式,理解环境对种群增长的限制作用;1.2 学习种群密度的检测,种群增长模型的建立,参数的估计以及种群增长曲线的拟合等实验技术; 1.3 加深对逻辑斯蒂增长模型的特征及其模型中两个参数r 、k 的理解。
2 材料与方法2.1 材料与试剂草履虫、干稻草、鲁哥氏固定液2.2 实验仪器六孔培养皿、量筒、解剖镜、锥形瓶、烧杯、锥形瓶2.3 实验方法2.3.1 配制人工海水 按表1配制30‰人工海水的人工海水,再将30‰人工海水加矿泉水稀释为20‰的人工海水。
表1 30‰人工海水配方(1升水) 药品 含量 NaCL 28.000g KCL 0.800g MgCl 2·6H 2O 25.000g CaCl 2·H 2O1.200g2.3.2 接种红色伪角毛虫 在六孔平板中的两个孔滴加5ml20‰人工海水,两个孔滴加5ml30‰人工海水→做好标记→每孔分别放两粒米粒→分别在解剖镜中吸取50只红色伪角毛虫→常温下培养→实验开始的7天内,每天定时对培养液中的草履虫密度进行检测。
(每次计数至少重复3次)2.3.3 Logistic 增长模型的拟合 种群在有限环境中的连续增长表现为Logistic 增长,其增长曲线呈S 型。
Logistic 增长数学模型为:)(K N K N N -r dt d =或)(KNN N -1r dt d = 式中:dtd N为种群的增长;N 为种群大小;t 为时间;r 为种群的瞬时增长率;K 为环境容纳量; )(KN-1为“剩余空间”。
因此,Logistic 模型的积分公式为:rt-a e 1+=KN式中:a 与初始数量0N 有关的常数;e 为自然对数的底。
第4章种群增长

种群数量周期波动
种群波动:种群数量随着时间变化而围绕平衡密度 种群波动 (Logistic增长曲线的渐近线)上下波动,波动幅度有大 有小,波动有规则的,也有不规则的。 种群波动大多是不规则的 大多是不规则的;但有些是规则的波动, 大多是不规则的 即种群数量的周期波动 周期波动,一般在两个波峰之间相隔的时间 周期波动 基本相等,如旅鼠的3-4年周期波动 、猞猁和雪兔的9-10 年周期波动 。周期波动现象主要发生在北方针叶林、北 极苔原地带等比较单调的生境中,而在生物多样性丰富区 域,则周期波动不太明显。 • 种群周期波动的学说: 种群周期波动的学说 归为两大学派:一派主张种群数量的周期波动是由 自然环境中的某些因素或种群自身的一些因素引起的,如 Pitelka提出的营养恢复学说 营养恢复学说;另一学派,以Cole等为代表, 营养恢复学说 认为种群的周期波动和随机波动在统计学上是难以区分的, 种群因受多种环境因素的影响而表现出随机波动,而环境 环境 条件的随机波动可能引起种群的周期波动。 条件的随机波动
逻辑斯谛方程生物学含义
(1)当种群数量N趋向于O时,那么(1-N/K)项就逼近于1,这表 示几乎全部K空间没有被利用;种群接近指数增长 . (2)当N趋向于K时,那么1-N/K趋向于为零,这表示几乎 全部K空间已被利用; (3)当种群数量N由O增加到K时,(1-N/K) 项由1下降为O, 3 N O K (1-N/K) 1 O 这表示种群增长的”剩余空间”在减小。 • 因此,Logistic系数对种群数量的变化有一制约作用,使 种群数量总是趋向于环境容纳量K值,形成一种S形的增 长曲线。K值就是种群在该环境中的稳定平衡密度 (stable equilibrium density)。 • 种群的瞬时增长率(dN/dt值)随种群数量(N)的变化 而变化 ,当N=0和N=K时最小;当N=(1/2)K时最大, 此时种 群密度正处种群增长曲线的拐点上。 •
草履虫种群在有限环境中的逻辑斯谛增长测定

草履虫种群在有限环境中的逻辑斯谛增长测定一、实验课题名称:草履虫种群在有限环境中的逻辑斯谛增长测定二、文献综述教科书常用“s”曲线表示逻辑斯谛增长模型导致的种群动态。
[1].逻辑斯蒂曲线又称“s” 曲线,是种群在一个有线的环境中增长时,种群的密度变化曲线。
因为环境条件是有限的,大多数种群的指数增长都是暂时的,一般仅发生在早起阶段,种群密度很低,资源丰富的情况下,随着种群密度增大,资源匮乏,代谢产物积累等,增长曲线也渐渐由"J"型变成“s”型[2]。
草履虫(Paramccium caodatum)取材培养方便,繁殖迅速,体型大,易于观察,是常用的实验动物。
在动物学与生态学教学中,“种群在有限环境中的逻辑斯蒂增长实验”普遍选取草履虫作为实验材料,一般采用锥形瓶培养法。
[3][1]赵苹贾林柏逻辑斯蒂曲线中的1/2K J《高考(理化生)》2007年04期G634.91 [2]周玉田春华等逻辑斯蒂增长导致的复杂种群动态及其实验验证 J 生物学通报2010年07期Q145[3]仲倩用微量培养法改进尾草履虫种群逻辑斯蒂增长实验 J 《潍坊学院学报》 2010年02期 Q-4三、实验目的和要求1.了解种群在有限环境中的增长方式,理解环境对种群增长的限制作用。
2.学习种群大小的检验、种群增长模型的建立、参数的估计以及种群增长曲线的拟合等实验技术。
四、实验条件1.实验材料:纯培养的草履虫(Paramecium caudatum).2.波氏固定液:75ml饱和苦味酸清液,25ml福尔马林,3ml冰乙酸。
3.恒温培养箱,体视显微镜,计数器,250ml烧杯,5ml移液管,培养皿等。
五、实验原理与方法世代重叠种群在无限环境中呈现J,型增长。
但在现实生态环境中,种群不可能长期而连续地按指数增长,往往受到有限的环境资源和其它必要生活条件的限制。
随着密度的上升,种内竞争加剧,必然会影响种群的出生率和死亡率,使种群每员瞬时增长率随着密度上升而下降,一直到种群停止增长,甚至使种群数量下降,增长曲线呈现S,型。
逻辑斯蒂增长模型
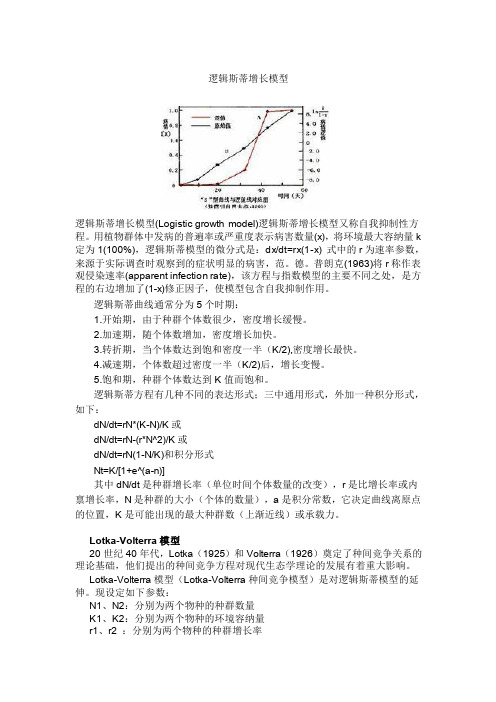
逻辑斯蒂增长模型逻辑斯蒂增长模型(Logistic growth model)逻辑斯蒂增长模型又称自我抑制性方程。
用植物群体中发病的普遍率或严重度表示病害数量(x),将环境最大容纳量k 定为1(100%),逻辑斯蒂模型的微分式是:dx/dt=rx(1-x) 式中的r为速率参数,来源于实际调查时观察到的症状明显的病害,范。
德。
普朗克(1963)将r称作表观侵染速率(apparent infection rate),该方程与指数模型的主要不同之处,是方程的右边增加了(1-x)修正因子,使模型包含自我抑制作用。
逻辑斯蒂曲线通常分为5个时期:1.开始期,由于种群个体数很少,密度增长缓慢。
2.加速期,随个体数增加,密度增长加快。
3.转折期,当个体数达到饱和密度一半(K/2),密度增长最快。
4.减速期,个体数超过密度一半(K/2)后,增长变慢。
5.饱和期,种群个体数达到K值而饱和。
逻辑斯蒂方程有几种不同的表达形式;三中通用形式,外加一种积分形式,如下:dN/dt=rN*(K-N)/K或dN/dt=rN-(r*N^2)/K或dN/dt=rN(1-N/K)和积分形式Nt=K/[1+e^(a-n)]其中dN/dt是种群增长率(单位时间个体数量的改变),r是比增长率或内禀增长率,N是种群的大小(个体的数量),a是积分常数,它决定曲线离原点的位置,K是可能出现的最大种群数(上渐近线)或承载力。
Lotka-Volterra模型20世纪40年代,Lotka(1925)和Volterra(1926)奠定了种间竞争关系的理论基础,他们提出的种间竞争方程对现代生态学理论的发展有着重大影响。
Lotka-Volterra模型(Lotka-Volterra种间竞争模型)是对逻辑斯蒂模型的延伸。
现设定如下参数:N1、N2:分别为两个物种的种群数量K1、K2:分别为两个物种的环境容纳量r1、r2 :分别为两个物种的种群增长率依逻辑斯蒂模型有如下关系:dN1 / dt = r1 N1(1 - N1 / K1)其中:N/K可以理解为已经利用的空间(称为“已利用空间项”),则(1-N/K)可以理解为尚未利用的空间(称为“未利用空间项”)当两个物种竞争或者利用同一空间时,“已利用空间项”还应该加上N2种群对空间的占用。
生态学种群生态学23节

• 有一个环境容纳量(K,Nt=K零增长)
• 增长率随密度上升按比例变化
4、逻辑斯谛增长
dN / dt=N (r - cN) N→K, dN / dt=0, r - cN=0 , c=
r/ K dN/dt = rN (1- N/K) = rN (K-N) /
K (k - N) / k: 逻辑斯谛系数
第二节 种群增长
第二节 种群增长
• 简单的模型 • 几何增长 • 指数增长 • 逻辑斯谛增长★ • 种群的数量自然调节
1、简单的模型
• Nt+1 – Nt = B + I – D – E
B: birth, B=bNt I: immigrant D: death, D=dNt E: emigrant
λ=er
与密度有关的种群连续增长模型
• 环境容量有限、没有迁入迁出、世代重叠、具年
龄结构
• 与密度有关的单种群连续增长模型
• Logistic增长 • dN/dt=rN·(1-N/K)= rN·[(K-N)/K] • Nt=K/(1+eα-rt) • 环境容量K • 相邻压力:N/K • 剩余空间: 1-N/K
大米草 (Spartina anglica)
薇甘菊(Mikania micrantha)
红瓜(Coccinia cordifolia)
猫爪藤 (Macfadyena unguis-cati)
银胶菊 (Parthenium hysterophorus
五爪金龙 (Ipomoea cairica)
当没有竞争情况下, α12或N2等于0, α21或 N1等于0;即呈S曲线.
有的内在增长能力)
dN / dt = r N → dN / N = r dt
简述种群增长的逻辑斯谛模型及其主要参数的生物学意义

简述种群增长的逻辑斯谛模型及其主要参数的生物学意义在一定条件下,生物种群增长并不是按几何级数无限增长的。
即开始增长速度快,随后速度慢直至停止增长(只是就某一值产生波动),这种增长曲线大致呈“S”型,这就是统称的逻辑斯谛(Logistic)增长模型。
意义当一个物种迁入到一个新生态系统中后,其数量会发生变化.假设该物种的起始数量小于环境的最大容纳量,则数量会增长.增长方式有以下两种:(1) J型增长若该物种在此生态系统中无天敌,且食物空间等资源充足(理想环境),则增长函数为N(t)=n(p^t).其中,N(t)为第t年的种群数量,t为时间,p为每年的增长率(大于1).图象形似J形。
(2) S型增长若该物种在此生态系统中有天敌,食物空间等资源也不充足(非理想环境),则增长函数满足逻辑斯谛方程。
图象形似S形.逻辑斯谛增长模型的生物学意义和局限性逻辑斯谛增长模型考虑了环境阻力,但在种群数量较小时未考虑随机事件的影响。
比较种群指数增长模型和逻辑斯谛增长模型指数型就是通常所说的J型增长,是指在理想条件下,一个物种种群数目所呈现的趋势模型,但其要求食物充足,空间丰富,无中间斗争的情况,通常是在自然界中不存在的,当然,科学家为了模拟生物的J型增长,会在实验室中模拟理想环境,不过仅限于较为简单的种群(如细菌等)逻辑斯谛型是指通常所说的S型曲线,其增长通常分为五个时期1.开始期,由于种群个体数很少,密度增长缓慢。
2.加速期,随个体数增加,密度增长加快。
3.转折期,当个体数达到饱和密度一半(K/2),密度增长最快。
4.减速期,个体数超过密度一半(K/2)后,增长变慢。
5.饱和期,种群个体数达到K值而饱和自然界中大部分种群符合这个规律,刚开始,由于种群密度小,增长会较为缓慢,而后由于种群数量增多而环境适宜,会呈现J型的趋势,但随着熟练进一步增多,聚会出现种类斗争种间竞争的现象,死亡率会加大,出生率会逐渐与死亡率趋于相等,种群增长率会趋于0,此时达到环境最大限度,即K值,会以此形式达到动态平衡而持续下去。
生态学基础模拟练习题(附答案)

生态学基础模拟练习题(附答案)一、单选题(共84题,每题1分,共84分)1.下列有关阳性植物的叙述中,正确的是( )A、荫蔽处生长良好B、强光下生长不好C、强光下生长良好D、弱光下生长良好正确答案:C2.下列概念中,由英国植物学家坦斯利首次提出的是( )A、生物种群B、生物群落C、生态系统D、生物多样性正确答案:C3.狼和羊的种间关系是( )A、捕食B、互利共生C、编利共生D、竞争正确答案:A4.通过对水生生态系统的研究,提出著名“十分之一”定律的生态学家是( )A、谢尔福德B、林德曼C、奥德姆D、克列门茨正确答案:B5.生活在同一地段、生态要求相近的两个物种,发生竞争的原因是( )。
A、年龄相同B、资源不足C、生态型不同D、生活型不同正确答案:B6.阴性植物的特点是( )A、光补偿点较低,生长在阴湿条件下B、光补偿点较低,生长在全光照条件下C、光补偿点较高,生长在全光照条件下D、光补偿点较高,生长在阴湿条件下正确答案:A7.甲乙两个群落都由5种植物构成,其中甲群落每种植物的个体数几乎相同,而乙群落90%的植物个体属于同一种,则甲乙两群落的植物物种多样性相比()A、甲高B、相等C、不确定D、乙高正确答案:A8.下列中间关系中属于正相互作用的是( )。
A、竞争B、寄生C、捕食D、互利共生正确答案:D9.植物的病原真菌与该种植物的种间关系是( )A、互利共生B、寄生C、竞争D、偏利共生正确答案:B10.物种在自然界存在的基本单位和繁殖单位是( )A、群落B、种类C、个体D、种群正确答案:D11.下列属于生态系统大型消费者的是( )A、肉食动物B、细菌C、植物D、真菌正确答案:A12.有效积温计算公式K=N(T—C)中,C表示( )A、生物学零度B、摄氏零度C、月平均温度D、年平均温度正确答案:A13.当光合作用强度因光照不足而下降时,增加二氧化碳可在一定程度上减小其下降幅度,这表明生态因子的作用具有( )A、不可替代性B、阶段性C、补偿性D、限制性正确答案:C14.20世纪30年代首次提出“生态系统”概念的科学家是( )A、马世骏B、海克尔C、坦斯利D、竺可桢正确答案:C15.下列生态因子中,属于间接因子的是( )A、光照B、海拔C、温度D、水分正确答案:B16.下面关于群从的说法,正确的是( )。
逻辑斯蒂增长

种群在资源有限环境中的逻辑斯谛增长姓名:学号:系别:生命科学学院生物科学专业班号:2实验日期:4月5日同组同学:实验目的1)认识到任何种群数量的动态变化都受到环境条件的制约(2)领会logistic model 生物学特性参数r与环境因子参数K的重要作用(3)学会通过实验估算这两个参数和进行曲线拟合实验原理•离散种群增长和连续种群增长•种群在有限资源环境下的连续增长的一种最简单的形式就是逻辑斯谛增长逻辑斯谛增长模型是建立在以下两个假设基础上的:①有一个环境容纳量(carrying capacity)(通常以K表示),当Nt=K时,种群为零增长,即dN/dt=0;②增长率随密度上升而降低的变化是按比例的。
最简单的是每增加一个个体,就产生1/K的抑制影响。
例如K=100,每增加一个体,产生0.01影响,或者说,每一个体利用了1/K的“空间”,N个体利用了N/K的“空间”,而可供种群继续增长的“剩余空间”只有(1-N /K)。
逻辑斯蒂增长的数学模型dN/dT=rN[(K-N)/K]dN/dT=rN(1-N/K)dN/dT···························种群在单位时间内的增长率N·······························种群大小t································时间r································种群的瞬时增长率K·······························环境容纳量1-N/K····························剩余空间逻辑斯蒂增长的数学模型的积分式:N=K/[1+EXP(a-rt)]S”型曲线有两个特点:①曲线渐近于K值,即平衡密度;②曲线上升是平滑的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
种群增长逻辑斯蒂方程
种群增长逻辑斯蒂方程是一种数学模型,用于描述生物种群的增长规律。
它是由比利时数学家皮埃尔·弗朗索瓦·韦洛德·罗吉斯提(Pierre François Verhulst)在19世纪提出的。
逻辑斯蒂方程的形式为:
dN/dt = rN[(K-N)/K]
其中,N表示种群数量,t表示时间,r表示种群增长率,K表示环境容纳量。
这个方程的含义是,种群数量的变化率是种群数量和环境容纳量的函数,当种群数量接近环境容纳量时,增长率会逐渐减小,最终趋于稳定。
逻辑斯蒂方程的应用范围非常广泛,可以用于研究各种生物种群的增长规律,包括人口、动物、植物等。
例如,人口学家可以用逻辑斯蒂方程来预测人口增长趋势和稳定水平,生态学家可以用它来研究物种数量的动态变化。
逻辑斯蒂方程的优点是比较简单易懂,可以用来预测种群数量的未来趋势。
但它也有一些缺点,比如忽略了环境变化对种群数量的影响,以及种群内部个体之间的相互作用等。
为了弥补逻辑斯蒂方程的不足,生态学家还发展了其他种群增长模型,比如洛特卡-沃尔特拉方程、罗森韦格方程等。
这些模型在考虑
更多因素的基础上,对于复杂的生态系统具有更好的适用性。
种群增长逻辑斯蒂方程是描述生物种群增长规律的一种数学模型,虽然它有一些局限性,但是在一定的范围内仍然有广泛的应用价值。
随着科技的不断进步,未来还会有更加精细、全面的种群增长模型被提出,进一步推动生态学的发展。
