河北省冀州中学10—11学年高三数学上学期期末考试 理【会员独享】
河北省冀州中学高三数学上学期期末考试(理)a卷

试卷类型:A 卷 河北冀州中学2008—2009学年度上学期期末考试高三年级 数学试题(理)考试时间 120分钟 试题满分 150分一、选择题 共12个小题,每个小题5分,满分60分。
在每个小题的四个选项中只有一个是正确的,请将正确答案的代号涂在答题卡上。
1.已知全集{1,2,3,4,5,6}U =,集合{1,2,5}A =,U {4,5,6}B =ð,则集合AB =A .}2,1{B . {}5C .}3,2,1{D .{3,4,6}2.已知直线m ,n 和平面α,则m ∥n 的一个必要非充分条件是 A .m ∥α、n ∥α B .m ⊥α、n ⊥α C .m ∥α、n ⊂α D .m , n 与α成角相等3. 椭圆的焦点为(-2,0)和(2,0),且椭圆过点53(,)22-,则椭圆方程是A. 221610x y +=B. 221106x y +=C. 22148x y +=D. 22184x y +=4. 已知等差数列{}n a 的公差0d ≠,它的第1、5、17项顺次成等比数列,则这个等比数列的公比是 A .4 B .3 C. 2 D .125.若m 、n 为两条不同的直线,α、β为两个不同的平面,则以下命题 正确的是A .若m ∥α,n ⊂α,则m ∥nB .若m ∥α,m ⊂β,α∩β=n ,则m ∥nC .若m ∥α,n∥α,则m ∥nD .若α∩β =m ,m ⊥n ,则n ⊥α6.若x ∈[0,2π],当y=2cos(cos )6x x x π++取最大值时,x 所取得值是....64812A B C D ππππ7.将一根铁丝切割成三段做一个面积为24.5m 、形状为直角三角形的框架,在下列四种长度的铁丝中,选用最合理(够用且浪费最少)的是A .9.5mB .10 mC .10.5mD .11m8.数列{n a }满足:113a =,且对于任意的正整数m,n 都有m n m n a a a +=⋅,则12lim()n n a a a →∞+++= A.12 B.23 C.32 D.2 9. 已知三棱柱111ABC A B C -的侧棱与底面边长都相等,1A 在底面ABC 内的射影为ABC △的中心,则1AB 与底面ABC 所成角的正弦值等于A .13B .3C D .2310.设双曲线22221(00)x y a b a b-=>>,且它的一条准线与抛物线24y x =的准线重合,则此双曲线的方程为A .2211224x y -= B .2214896x y -= C .221312x y -= D .22136x y -= 11.已知P 是椭圆x 24+y 23=1上一点,F 1、F 2是该椭圆的两个焦点,若△PF 1F 2的内切圆半径为12,则PF 1→·PF 2→的值为 A 、32B 、94C 、-94D 、012.已知函数21()()log 3x f x x =-,0a b c <<<,()()()0f a f b f c <,实数d 是函数()f x 的一个零点(即使()0f x =的x 值).给出下列四个判断:①a d <; ②b d >;③c d <;④c d >.其中可能成立的个数为 A .1 B .2 C .3 D .4二、填空题 每小题5分,满分20分。
2023-2024学年河北省衡水市冀州中学高三(上)期中数学试卷【答案版】
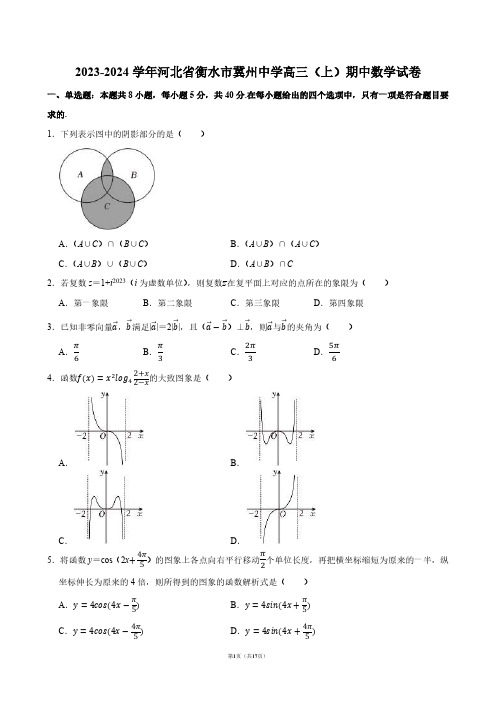
2023-2024学年河北省衡水市冀州中学高三(上)期中数学试卷一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列表示图中的阴影部分的是( )A .(A ∪C )∩(B ∪C ) B .(A ∪B )∩(A ∪C ) C .(A ∪B )∪(B ∪C )D .(A ∪B )∩C2.若复数z =1+i 2023(i 为虚数单位),则复数z 在复平面上对应的点所在的象限为( ) A .第一象限B .第二象限C .第三象限D .第四象限3.已知非零向量a →,b →满足|a →|=2|b →|,且(a →−b →)⊥b →,则a →与b →的夹角为( ) A .π6B .π3C .2π3D .5π64.函数f(x)=x 2log 42+x2−x的大致图象是( )A .B .C .D .5.将函数y =cos (2x +4π5)的图象上各点向右平行移动π2个单位长度,再把横坐标缩短为原来的一半,纵坐标伸长为原来的4倍,则所得到的图象的函数解析式是( ) A .y =4cos(4x −π5)B .y =4sin(4x +π5)C .y =4cos(4x −4π5) D .y =4sin(4x +4π5)6.已知数列{a n }的首项为1,D 是△ABC 边BC 所在直线上一点,且AC →=3(a n +1)AD →−(a n+1−2)AB →,则数列{a n }的通项公式为( ) A .3n ﹣2 B .3n +1﹣2 C .5×(−3)n−1−14D .5×(−3)n −147.已知正方形ABCD 的边长为2,将△ACD 沿AC 翻折到△ACD ′的位置,得到四面体D ′﹣ABC ,在翻折过程中,点D ′始终位于△ABC 所在平面的同一侧,且BD ′的最小值为√2,则点D 的运动轨迹的长度为( ) A .πB .2πC .2√2π3D .4√2π38.已知三角形ABC 中,BC =3,角A 的平分线交BC 于点D ,若BDDC =12,则三角形ABC 面积的最大值为( ) A .1B .2C .3D .4二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分. 9.下列命题中正确的是( )A .若a >0,b >0,a +b =1,则a 2+b 2≥12B .命题:“∀x ≥0,x 2≥0”的否定是“∃x <0,x 2<0”C .已知函数f (2x +1)的定义域为[﹣1,1],则函数f (x )的定义域为[﹣1,3]D .若函数f(√x −1)=x −3√x ,则f (x )=x 2﹣x ﹣2(x ≥﹣1)10.已知A ,B 是函数f(x)=tan(3x +π6)的图象与直线y =3的两个交点,则下列结论正确的是( )A .|AB|min =π3B .f (x )的定义域为{x ∈R|x ≠3kπ+3π2,k ∈Z} C .f (x )在区间(0,π6)单调递增D .f (x )的图象的对称中心为点(kπ6−π18,0),k ∈Z 11.已知数列{a n }的前n 项的和为S n ,S 1=4,S 2=8,4S n =S n +1+4S n ﹣1(n ≥2),则下列说法正确的是( ) A .S 4=32B .{a n +1﹣2a n }是等比数列C .a n ={4,n =12n+1−4,n ≥2D .a n ={4,n =12n,n ≥212.设函数f (x )的定义域为R ,且满足f (x )=f (2﹣x ),f (x )=﹣f (x +2),当x ∈(0,1]时,f (x )=e x ﹣2x ﹣1,则( ) A .f (x )是奇函数 B .f (2023)=e ﹣3C .f (x )的值域是[1﹣2ln 2,2ln 2﹣1]D .方程f (x )=3﹣e 在区间[0,2024]内恰有1518个实数解 三、填空题:本题共4小题,每小题5分,共20分.13.已知等差数列{a n }满足a 1=4,a 3+a 5=a 42+1,则a 7= .14.已知函数f (x )的定义域为(﹣∞,+∞),y =f (x )+e x 为偶函数,y =f (x )﹣2e x 为奇函数,则f (x )的最小值为 .15.在三棱锥A ﹣BCD 中,∠ABD =∠ABC =60°,BC =BD =2,AB =4,则三棱锥A ﹣BCD 外接球的表面积为 .16.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,已知c =4,C =60°,BD →=DC →2+DA →,则DA →⋅DB→的最大值为 .四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(10分)已知数列{a n }为等比数列,在数列{b n }中,b 1=2,b 2=4,且a n +1=a n (b n +1﹣b n ). (1)求数列{b n }的通项公式;(2)若a 1=1,c n =a n +b n ,求数列{c n }的前n 项和S n . 18.(12分)已知α∈(0,π),sinα+cosα=√62,且cos α<sin α.(1)求角α的大小;(2)已知函数f (x )=sin2x +2sin 2(x +α),若f (x )在区间(0,m )上有极大值,无极小值,求m 的取值范围.19.(12分)已知函数f(x)=−2a 2lnx +12x 2+ax(a ∈R).(1)当a =1时,求曲线y =f (x )在(1,f (1))处的切线方程; (2)讨论函数f (x )的单调性.20.(12分)已知数列{a n }的前n 项和为S n ,a 1=√2,a n >0,a n +1•(S n +1+S n )=2. (1)求S n ;(2)求1S 1+S 2+1S 2+S 3+⋯+1S n +S n+1.21.(12分)如图,有一景区的平面图是一个半圆形,其中O 为圆心,直径AB 的长为2km ,C ,D 两点在半圆弧上,且BC =CD ,设∠COB =θ. (1)当θ=π6时,求四边形ABCD 的面积;(2)若要在景区内铺设一条由线段AB ,BC ,CD 和DA 组成的观光道路,则当θ为何值时,观光道路的总长l 最长,并求出l 的最大值.22.(12分)已知函数f (x )=sin 3x cos x ,f ′(x )为f (x )的导函数. (1)求f (x )在(0,2π)上的极值;(2)设n ∈N *,求证:sin 2x •sin 22x •sin 24x …sin 22nx ≤3n4n .2023-2024学年河北省衡水市冀州中学高三(上)期中数学试卷参考答案与试题解析一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列表示图中的阴影部分的是( )A .(A ∪C )∩(B ∪C ) B .(A ∪B )∩(A ∪C ) C .(A ∪B )∪(B ∪C )D .(A ∪B )∩C解:图中阴影部分表示元素满足:是C 中的元素,或者是A 与B 的公共元素, 故可以表示为C ∪(A ∩B ), 也可以表示为:(A ∪C )∩(B ∪C ), 结合选项可知应为:(A ∪C )∩(B ∪C ). 故选:A .2.若复数z =1+i 2023(i 为虚数单位),则复数z 在复平面上对应的点所在的象限为( ) A .第一象限B .第二象限C .第三象限D .第四象限解:因为z =1+i 2023=1﹣i ,所以z =1+i 在复平面上对应的点为(1,1),该点在第一象限. 故选:A .3.已知非零向量a →,b →满足|a →|=2|b →|,且(a →−b →)⊥b →,则a →与b →的夹角为( ) A .π6B .π3C .2π3D .5π6解:∵(a →−b →)⊥b →,∴(a →−b →)⋅b →=a →⋅b →−b →2=|a|→|b|→cos <a →,b →>−b →2=0, ∴cos <a →,b →>=|b|→2|a|→|b|→=|b|→22|b|→2=12,∵<a →,b →>∈[0,π],∴<a →,b →>=π3.故选:B . 4.函数f(x)=x 2log 42+x2−x的大致图象是( )A .B .C .D . 解:方法一:因为2+x2−x >0,即(x +2)•(x ﹣2)<0,所以﹣2<x <2,所以函数f(x)=x 2log 42+x2−x的定义域为(﹣2,2),关于原点对称, 又f(−x)=(−x)2log 42−x2+x=−f(x),所以函数f (x )是奇函数,其图象关于原点对称, 故排除B ,C ; 当x ∈(0,2)时,2+x 2−x>1,即log 42+x2−x >0,因此f (x )>0,故排除A .故选:D .方法二:由方法一,知函数f (x )是奇函数,其图象关于原点对称,故排除B ,C ; 又f(1)=12log 23>0,所以排除A .故选:D . 5.将函数y =cos (2x +4π5)的图象上各点向右平行移动π2个单位长度,再把横坐标缩短为原来的一半,纵坐标伸长为原来的4倍,则所得到的图象的函数解析式是( ) A .y =4cos(4x −π5)B .y =4sin(4x +π5)C .y =4cos(4x −4π5) D .y =4sin(4x +4π5) 解:由题意函数y =cos(2x +4π5)的图象上各点向右平移π2个单位长度,得到y =cos(2x −π+4π5)=cos(2x −π5),再把横坐标缩短为原来的一半,得到y =cos(4x −π5),再把纵坐标伸长为原来的4倍,得到y =4cos(4x −π5),考察四个选项知,A 是正确的 故选:A .6.已知数列{a n }的首项为1,D 是△ABC 边BC 所在直线上一点,且AC →=3(a n +1)AD →−(a n+1−2)AB →,则数列{a n }的通项公式为( ) A .3n ﹣2 B .3n +1﹣2 C .5×(−3)n−1−14D .5×(−3)n −14解:依题意,由B ,C ,D 三点共线,可得3(a n +1)﹣(a n +1﹣2)=1,化简整理,可得a n +1=3a n +4, 两边同时加2,可得a n +1+2=3a n +4+2=3(a n +2), ∵a 1+2=3,∴数列{a n +2}是以3为首项,3为公比的等比数列, ∴a n +2=3×3n−1=3n , ∴a n =3n −2,n ∈N *. 故选:A .7.已知正方形ABCD 的边长为2,将△ACD 沿AC 翻折到△ACD ′的位置,得到四面体D ′﹣ABC ,在翻折过程中,点D ′始终位于△ABC 所在平面的同一侧,且BD ′的最小值为√2,则点D 的运动轨迹的长度为( ) A .πB .2πC .2√2π3D .4√2π3解:设方形ABCD 对角线AC 与BD 交于O ,由题意,翻折后BD ′=√2时,△OD ′B 为边长为√2的等边三角形,此时∠D ′OB =π3,若继续翻折BD ′<√2,如下图示BD ′=√2,所以点D 的运动轨迹是以O 为圆心,√2为半径的圆心角为2π3的圆弧,所以点D的运动轨迹的长度为2π3×√2=2√2π3.故选:C.8.已知三角形ABC中,BC=3,角A的平分线交BC于点D,若BDDC=12,则三角形ABC面积的最大值为()A.1B.2C.3D.4解:因为角A的平分线交BC于点D,若BDDC=12,由角平分线的性质可得ABAC=BDDC=12,设AB=x,则AC=2x,BC=3,由余弦定理可得cos A=AB2+AC2−BC22AB⋅AC=5x2−94x2,所以sin A=√(4x2)2−(5x2−9)24x2=√−9x4+90x2−814x2=3√−x4+10x2−94x2,所以S△ABC=12AB•AC•sin A=12•2x2•3√−x4+10x2−94x2=34•√−x4+10x2−9=34•√−(x2−5)2+16≤34•√16=3,当x2=5时,即x=√5时取等号.所以三角形ABC面积的最大值为3.故选:C.二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.下列命题中正确的是()A.若a>0,b>0,a+b=1,则a2+b2≥12B.命题:“∀x≥0,x2≥0”的否定是“∃x<0,x2<0”C.已知函数f(2x+1)的定义域为[﹣1,1],则函数f(x)的定义域为[﹣1,3]D.若函数f(√x−1)=x−3√x,则f(x)=x2﹣x﹣2(x≥﹣1)解:对于A,由a>0,b>0,a+b=1,得b=1﹣a,且0<a<1,则a2+b2=a2+(1−a)2=2a2−2a+1=2(a−12)2+12,0<a<1,所以当a=12时,a2+b2取到最小值12,所以a2+b2≥12,故A正确;对于B,“∀x≥0,x2≥0”的否定是“∃x≥0,x2<0”,故B错误;对于C,f(2x+1)的定义域为[﹣1,1],设t=2x+1,当x∈[﹣1,1]时,t∈[﹣1,3],故f(x)的定义域为[﹣1,3],C正确;对于D ,令t =√x −1,则√x =t +1,t ≥﹣1,由f(√x −1)=x −3√x ,得f (t )=(t +1)2﹣3(t +1)=t 2﹣t ﹣2,t ≥﹣1, 所以函数f (x )的表达式为f (x )=x 2﹣x ﹣2,x ≥﹣1,D 正确. 故选:ACD .10.已知A ,B 是函数f(x)=tan(3x +π6)的图象与直线y =3的两个交点,则下列结论正确的是( )A .|AB|min =π3B .f (x )的定义域为{x ∈R|x ≠3kπ+3π2,k ∈Z} C .f (x )在区间(0,π6)单调递增D .f (x )的图象的对称中心为点(kπ6−π18,0),k ∈Z 解:因为A ,B 是函数f(x)=tan(3x +π6)的图象与直线y =3的交点,所以|AB |的最小值为函数f (x )的最小正周期,T =π3,所以|AB|min =π3,故A 正确;令3x +π6≠π2+kπ,k ∈Z ,解得x ≠π9+kπ3,k ∈Z ,所以f (x )的定义域为{x ∈R|x ≠π9+kπ3,k ∈Z},故B 错;因为x ∈(0,π6),所以3x +π6∈(π6,2π3),因为函数y =tan x 在(π6,2π3)上不单调,所以函数f (x )在(0,π6)上不单调,故C 错;令3x +π6=kπ2,k ∈Z ,解得x =−π18+kπ6,k ∈Z ,所以f (x )的对称中心为点(−π18+kπ6,0),k ∈Z ,故D 正确. 故选:AD .11.已知数列{a n }的前n 项的和为S n ,S 1=4,S 2=8,4S n =S n +1+4S n ﹣1(n ≥2),则下列说法正确的是( ) A .S 4=32B .{a n +1﹣2a n }是等比数列C .a n ={4,n =12n+1−4,n ≥2D .a n ={4,n =12n ,n ≥2解:由题意可知S 3=4S 2﹣4S 1=16,所以S 4=4S 3﹣4S 2=32,故A 正确; 因为a 3﹣2a 2=S 3﹣S 2﹣2(S 2﹣S 1)=S 3﹣3S 2+2S 1=0, 所以{a n +1﹣2a n }不能是等比数列,故B 错误;因为4S n =S n +1+4S n ﹣1(n ≥2),即S n +1=4S n ﹣4S n ﹣1(n ≥2),所以S n+1−2S n =21(S n −2S n−1)=22(S n−1−2S n−2)=⋯=2n (S 2﹣2S 1)=0, 所以S n +1﹣2S n =0,即S n+1S n=2,又因为S 2S 1=84=2,所以{S n }是以2为首项,4为公比的等比数列,所以S n =4×2n−1=2n+1,所以a 1=S 1=4,a n =S n −S n−1=2n+1−2n =2n (n ≥2), 即a n ={4,n =12n ,n ≥2,故选项C 错误;D 正确.故选:AD .12.设函数f (x )的定义域为R ,且满足f (x )=f (2﹣x ),f (x )=﹣f (x +2),当x ∈(0,1]时,f (x )=e x ﹣2x ﹣1,则( ) A .f (x )是奇函数 B .f (2023)=e ﹣3C .f (x )的值域是[1﹣2ln 2,2ln 2﹣1]D .方程f (x )=3﹣e 在区间[0,2024]内恰有1518个实数解解:函数f (x )的定义域为R ,关于原点对称,因为f (x )=f (2﹣x ),所以f (﹣x )=f (x +2), 又因为f (x +2)=﹣f (x ),所以f (﹣x )=﹣f (x ),所以f (x )是奇函数,A 正确; 由f (x )=﹣f (x +2),得f (x +4)=﹣f (x +2)=f (x ),所以f (x )以4为周期,因为f (2023)=f (4×506﹣1)=f (﹣1)=﹣f (1)=3﹣e ,所以f (2023)=3﹣e ,故B 错误; 因为当x ∈(0,1]时,f (x )=e x ﹣2x ﹣1,所以f ′(x )=e x ﹣2, 当0<x <ln 2时,f ′(x )<0,当ln 2<x ≤1时,f ′(x )>0, 所以f (x )在(0,ln 2)上单调递减,在(ln 2,1)上单调递增,所以f (x )min =f (ln 2)=1﹣2ln 2,又f (1)=e ﹣3<0,所以f (x )∈[1﹣2ln 2,0). 因为f (x )为奇函数,所以当x ∈[﹣1,0]时,f (x )∈[0,2ln 2﹣1],因为f (x )的图象关于直线x =1对称,所以当x ∈[﹣1,3]时,f (x )∈[1﹣2ln 2,2ln 2﹣1], 因为f (x )的周期为4,所以当x ∈R 时,f (x )∈[1﹣2ln 2,2ln 2﹣1],故C 正确; 方程f (x )=3﹣e 的解的个数,即y =f (x )的图象与y =3﹣e 的图象交点个数. 因为y =f (x )的周期为4,且当x ∈[0,4]时,y =f (x )与y =3﹣e 有3个交点, 所以当x ∈[0,2024]时,y =f (x )与y =3﹣e 有20244×3=1518个交点,故D 正确.故选:ACD.三、填空题:本题共4小题,每小题5分,共20分.13.已知等差数列{a n}满足a1=4,a3+a5=a42+1,则a7=﹣2.解:在等差数列{a n}中,∵等差数列{a n}满足a1=4,a3+a5=a42+1,又a3+a5=2a4,∴a42−2a4+1=0,解得a4=1,又a1=4,而a1+a7=2a4,解得a7=﹣2.故答案为:﹣2.14.已知函数f(x)的定义域为(﹣∞,+∞),y=f(x)+e x为偶函数,y=f(x)﹣2e x为奇函数,则f(x)的最小值为√3.解:y=f(x)+e x是偶函数,所以f(﹣x)+e﹣x=f(x)+e x,y=f(x)﹣2e x是奇函数,所以f(﹣x)﹣2e﹣x=﹣f(x)+2e x,两式联立解得f(x)=12e x+32e−x,由基本不等式得f(x)=12e x+32e−x≥12×2√e x⋅3e−x=√3,当且仅当e x=3e﹣x,即x=ln√3时,等号成立,因此f(x)的最小值是√3.故答案为:√3.15.在三棱锥A﹣BCD中,∠ABD=∠ABC=60°,BC=BD=2,AB=4,则三棱锥A﹣BCD外接球的表面积为16 π.解:由∠ABD=∠ABC=60°,BC=BD=2,AB=4,根据余弦定理可得 AC =AD =2√3, 则 AC ⊥BC ,AD ⊥BD ,取AB 中点O ,则OA =OB =OC =OD , 则三棱锥A ﹣BCD 外接球的直径为AB =4, 故三棱锥A ﹣BCD 外接球的表面积为4π⋅(AB 2)2=16π. 故答案为:16π.16.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,已知c =4,C =60°,BD →=DC→2+DA →,则DA →⋅DB→的最大值为 −8825. 解:由题意,BD →=DC →2+DA →=32DC →+CA →=−32CD →+CA →,BD →=BC →+CD →,消去BD →得:CD →=25(CA →+CB →),因为DA →⋅DB →=(DC →+CA →)⋅(DC →+CB →)=(35CA →−25CB →)⋅(35CB →−25CA →)=−625(a 2+b 2)+1325abcos60°,由cos60°=a 2+b 2−162ab,得a 2+b 2=ab +16≥2ab ,当且仅当a =b 时等号成立,所以0<ab ≤16, 所以原式=−625(16+ab)+1350ab =150ab −9625≤−8825. 故答案为:−8825.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(10分)已知数列{a n }为等比数列,在数列{b n }中,b 1=2,b 2=4,且a n +1=a n (b n +1﹣b n ). (1)求数列{b n }的通项公式;(2)若a 1=1,c n =a n +b n ,求数列{c n }的前n 项和S n . 解:(1)设数列{a n }的公比为q , 由a n +1=a n (b n +1﹣b n ),知b n +1﹣b n =a n+1a n=q ,为常数,所以数列{b n }是等差数列,设其公差为d , 由b 1=2,b 2=4,知d =2,所以b n =2+(n ﹣1)×2=2n ,且q =2, 故数列{b n }的通项公式为b n =2n . (2)由(1)知a n+1a n=2,若a 1=1,则a n =2•2n ﹣1=2n , 所以c n =a n +b n =2n +2n ,所以S n =(21+2)+(22+4)+(23+6)+…+(2n+2n )=(21+22+23+ (2))+(2+4+6+…+2n )=2−2n⋅21−2+n(2+2n)2=2n +1﹣2+n 2+n . 18.(12分)已知α∈(0,π),sinα+cosα=√62,且cos α<sin α.(1)求角α的大小;(2)已知函数f (x )=sin2x +2sin 2(x +α),若f (x )在区间(0,m )上有极大值,无极小值,求m 的取值范围.解:(1)因为sinα+cosα=√62,所以(sinα+cosα)2=1+sin2α=32,则sin2α=12,因为α∈(0,π), 所以2α∈(0,2π), 则2α=π6或2α=5π6,解得α=π12或α=5π12, 因为cos α<sin α, 所以α=5π12; (2)由(1)知f(x)=sin2x +2sin 2(x +5π12)=sin2x +1−cos(2x +5π6) =32sin2x +√32cos2x +1=√3sin(2x +π6)+1, 当x ∈(0,m )时,2x +π6∈(π6,2m +π6),因为f(x)在区间(0,m)上有极大(最大)值,无极小(最小)值,所以π2<2m+π6≤3π2,解得π6<m≤2π3,则m的取值范围为(π6,2π3].19.(12分)已知函数f(x)=−2a2lnx+12x2+ax(a∈R).(1)当a=1时,求曲线y=f(x)在(1,f(1))处的切线方程;(2)讨论函数f(x)的单调性.解:(1)当a=1时,f(x)=−2lnx+12x2+x,f′(x)=−2x+x+1,f′(1)=−2+1+1=0,f(1)=32,所以曲线y=f(x)在(1,f(1))处的切线方程为y=3 2.(2)f′(x)=x2+ax−2a2x=(x+2a)(x−a)x,①当a=0时,f′(x)=x>0,所以函数在(0,+∞)上单调递增;②当a>0时,令f′(x)=0,则x1=﹣2a(舍)或x2=a,f′(x)<0,0<x<a,当x∈(0,a)时,函数f(x)单调递减;f′(x)>0,x>a,当x∈(a,+∞)时,函数f(x)单调递增.③当a<0时,令f′(x)=0,则x1=﹣2a或x2=a(舍),f′(x)<0,0<x<﹣2a,当x∈(0,﹣2a)时,函数f(x)单调递减;f′(x)>0,x>﹣2a,当x∈(﹣2a,+∞)时,函数f(x)单调递增.综上所述:当a=0时,函数在(0,+∞)上单调递增;当a>0时,函数f(x)在(0,a)上单调递减,函数f(x)在(a,+∞)上单调递增;当a<0时,函数f(x)在(0,﹣2a)上单调递减,函数f(x)在(﹣2a,+∞)上单调递增.20.(12分)已知数列{a n}的前n项和为S n,a1=√2,a n>0,a n+1•(S n+1+S n)=2.(1)求S n;(2)求1S1+S2+1S2+S3+⋯+1S n+S n+1.解:(1)a1=√2,a n>0,a n+1•(S n+1+S n)=2,可得(S n+1﹣S n)(S n+1+S n)=2,可得S n+12﹣S n2=2,即数列{S n2}为首项为2,公差为2的等差数列,可得S n2=2+2(n﹣1)=2n,由a n>0,可得S n=√2n;(2)1S n+S n+1=√2n+√2(n+1)=√22(√n+√n+1)=√22(√n+1−√n),即有1S1+S2+1S2+S3+⋯+1S n+S n+1=√22(√2−1+√3−√2+2−√3+⋯+√n+1−√n)=√22(√n+1−1).21.(12分)如图,有一景区的平面图是一个半圆形,其中O为圆心,直径AB的长为2km,C,D两点在半圆弧上,且BC=CD,设∠COB=θ.(1)当θ=π6时,求四边形ABCD的面积;(2)若要在景区内铺设一条由线段AB,BC,CD和DA组成的观光道路,则当θ为何值时,观光道路的总长l最长,并求出l的最大值.解:(1)连结OD,则∠COD=π6,∠AOD=2π3,所以四边形ABCD的面积为S四边形ABCD=S四边形OBCD+S△AOB=2×12×1×1×sinπ6+12×1×1×sin2π3=2+√34(km2);(2)由题意,在△BOC中,∠OBC=π−θ2,由正弦定理得BCsinθ=OBsinπ−θ2=1cosθ2,所以BC=CD=sinθcosθ2=2sinθ2,同理在△AOD中,∠OAD=θ,∠DOA=π﹣2θ,由正弦定理得DAsin(π−2θ)=ODsinθ,所以DA=sin2θsinθ=2cosθ,所以l=2+4sin θ2+2cosθ=2+4sinθ2+2(1−2sin2θ2),0<θ<π2;令t =sin θ2(0<t <√22),所以l =2+4t +2(1−2t 2)=4+4t −4t 2=−4(t −12)2+5,当t =12时,即θ=π3,l 的最大值为5.22.(12分)已知函数f (x )=sin 3x cos x ,f ′(x )为f (x )的导函数. (1)求f (x )在(0,2π)上的极值;(2)设n ∈N *,求证:sin 2x •sin 22x •sin 24x …sin 22nx ≤3n4n .解:(1)已知函数f (x )=sin 3x cos x ,因为f (x +π)=sin 3(x +π)cos (x +π)=sin 3x cos x =f (x ) 所以π是函数f (x )的周期,可得f ′(x )=3sin 2x cos 2x ﹣sin 4x =sin 2x (4cos 2x ﹣1), 当0<x <π3时,f ′(x )>0,f (x )单调递增;当π3<x <2π3时,f ′(x )<0,f (x )单调递减;当2π3<x <π时,f ′(x )>0,f (x )单调递增,所以f (x )在(0,π)上的极小值为−3√316,极大值为3√316, 由周期性可知函数f (x )在(π,2π)上的极小值为−3√316,极大值为3√316, 且函数f (x )在(2π3,π)上单调递增,(π,4π3)上单调递增, 因为f (x )是基本初等函数,一定连续, 所以x =π不是f (x )的极值点, 故f (x )在(0,2π)上的极小值为−3√316,极大值为3√316; (2)证明:易知f (0)=0,由(1)知f(x)=sin 3xcosx =12sin 2xsin2x ∈[−3√316,3√316],所以0≤|sin 2xsin2x|≤3√38,则|sin2x⋅sin22x⋅sin24x⋯sin22n x|=|(sin3x⋅sin32x⋅sin34x⋯sin32n x)2 3|=[|sinx||sin2xsin2x|⋯|sin22n x|]23≤(|sinx|×3√38×⋯×|sin22n x|)23≤[(3√38)n]23=(34)n=3n4n,故sin2x⋅sin22x⋅sin24x⋯⋯sin22n x≤3n4n成立.。
2021年河北省衡水市冀州镇中学高三数学理上学期期末试卷含解析

2021年河北省衡水市冀州镇中学高三数学理上学期期末试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 已知实系数一元二次方程x2+(1+a)x+a+b+1=0的两个实根为x1、x2,并且0<x1<2,x2>2,则的取值范围是()A.(﹣1,﹣)B .(﹣3,﹣1)C .(﹣3,﹣)D .(﹣3,)C略2. 定义域是一切实数的函数,其图像是连续不断的,且存在常数()使得对任意实数都成立,则称是一个“—伴随函数”.有下列关于“—伴随函数”的结论:①是常数函数中唯一一个“—伴随函数”;②“—伴随函数”至少有一个零点.;③是一个“—伴随函数”;其中正确结论的个数是()A.1个;B.2个;C.3个;D.0个;参考答案:A①设是一个“—伴随函数”,则,当时,可以取遍实数集,因此不是唯一一个常值“—伴随函数”,故①不正确;②令,得,所以,若,显然有实数根;若,.又因为的函数图象是连续不断,所以在上必有实数根.因此任意的“—伴随函数”必有根,即任意“—伴随函数”至少有一个零点,故②正确。
③用反证法,假设是一个“—伴随函数”,则(x+λ)2+λx2=0,即(1+λ)x2+2λx+λ2=0对任意实数x成立,所以λ+1=2λ=λ2=0,而此式无解,所以f(x)=x2不是一个“—伴随函数”,故③不正确;所以正确的为1个,选A.3. 已知a为正实数,若函数的极小值为0,则a的值为A. B. 1 C. D. 2参考答案:A【分析】由于,而,可求得在处取得极小值,即,从而可求得的值.【详解】解:由已知,又,所以由得或,即函数在和上单调递增,由得,函数在上单调递减,所以在处取得极小值0,即,又,解得,故选:A.【点睛】本题考查了函数的极值与导数关系的应用,考查运算求解的能力,属于中档题.4. 若为不等式组表示的平面区域,则当的值从连续变化到时,动直线扫过的中的那部分区域的面积为 .参考答案:略5. 已知S n是等差数列{a n}的前n项和,若a1+a3+a5=3,则S5=( )A.B.5 C.7 D.9参考答案:B【考点】等差数列的前n项和.【专题】转化思想;数学模型法;等差数列与等比数列.【分析】由等差数列{a n}的性质,a1+a3+a5=3=3a3,解得a3.再利用等差数列的前n项和公式即可得出.【解答】解:由等差数列{a n}的性质,a1+a3+a5=3=3a3,解得a3=1.则S5==5a3=5.故选:B.【点评】本题考查了等差数列的通项公式及其性质、前n项和公式,考查了推理能力与计算能力,属于中档题.6. 已知椭圆的焦点在x轴上,若椭圆的短轴长为4,则n的取值范围是( )A. (12,+∞)B. (4,12)C. (4,6)D. (6,+∞)参考答案:A【分析】由题意可知:且,这样可以求出的取值范围.【详解】依题意得,且,故选A.【点睛】本题考查了根据椭圆焦点的位置求参问题,考查了解不等式的能力.7. 已知某简单几何体的三视图如图所示,若主视图的面积为1,则该几何体最长的棱的长度为()A.B.C.D.参考答案:C8. 下列命题正确的是()A.函数在区间内单调递增B.函数的最小正周期为C.函数的图像是关于点成中心对称的图形D.函数的图像是关于直线成轴对称的图形参考答案:C9. 2002年8月在北京召开了国际数学家大会, 会标如图示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形, 若直角三角形中较小的锐角为θ,大正方形面积是1, 小正方形面积是, 则的值是( )A. 1B.C.D.参考答案:D10. 已知集合A={x|y=lnx},集合B={﹣2,﹣1,1,2},则A∩B=( )A.(1,2)B.{1,2} C.{﹣1,﹣2} D.(0,+∞)参考答案:B考点:交集及其运算.专题:计算题.分析:集合A表示的是对数函数的定义域,令真数大于0求出A,利用交集的定义求出A∩B.解答:解:∵A={x|y=lnx}={x|x>0}又∵B={﹣2,﹣1,1,2},∴A∩B={1,2}故选B点评:本题考查求对数函数的定义域、考查利用交集的定义求集合的交集.二、填空题:本大题共7小题,每小题4分,共28分11. 正三棱柱ABC—A1B1C1的高为2,AB1与平面ABC所成的角为45°,则点C到平面ABC1的距离是;参考答案:答案:12. 设一球的半径为,则该球的表面积、体积分别为______、_________参考答案:,13. 一个三棱锥的正视图和侧视图及其尺寸如图所示,则该三棱锥俯视图的面积为.参考答案:1考点:由三视图求面积、体积.专题:计算题;空间位置关系与距离.分析:由于三视图中,正视图与侧视图一样高,正视图与俯视图一样长,俯视图与侧视图一样宽.又由图知,所以俯视图为两直角边长为2,1的三角形,即可求面积.解答:解:由于侧视图是宽为1,高为3的直角三角形,正视图是长为2,高为3的直角三角形,故三棱锥的底面为直角三角形,且两直角边分别为1,2.故该三棱锥的俯视图的面积为1.故答案为1点评:本题主要考查有三视图求面积,体积.要注意三视图中的等价关系:正视图与侧视图一样高,正视图与俯视图一样长,俯视图与侧视图一样宽.14. 一个几何体的三视图如图所示,则该几何体的体积为_________。
河北省冀州中学2006—2007学年度上学期期末考试高三数学(理)试题

河北省冀州中学2006—2007学年度上学期期末考试高三数学(理)试题一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号涂在答题卡上(每小题5分,共60分) 1.不等式032≥--xx 的解集是A .]2,(-∞B .(3,+∞)C .(2,3)D .)3,2[2.设),2(,53sin ππαα∈=,则αtan 的值为A .43B .-43C .34D .-343.设条件A :几何体的各个面都是三角形,条件B :几何体是三棱锥,则条件A 是条件B 的A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件 4.设),1(32)1(2≤+-=-x x x x f ,则函数)(1x f-的图象为5.设集合M ={a ,b ,c},N ={0,1},映射f :M →N 满足)()()(c f b f a f =+,则映射f :M →N 的个数为A .1B .2C .3D .46.设二项式1)nx的展开式的各项系数的和为P ,所有二项式系数的和为S.若有P +S =272,则n等于 A .4B .5C .6D .87.圆心在抛物线21(0)2y x x =<上,且与抛物线的准线及y 轴都相切的圆的方程为 A .221204x y x y +--+= B .22210x y x y ++-+=C .221204x y x y ++-+= D .22210x y x y +-++=8.设()()(),,[,]2F x f x f x x R ππ=+-∈--是函数F(x )的单调递增区间,将F(x )的图象按(,0)a π=平移得到新的函数G(x )的图象,则G(x )的单调递减区间必定是 A .]0,2[π-B .],2[ππC .]23,[ππD .]2,23[ππ9.已知函数()y f x =的反函数是212sec 2007()log (tan ),(0,)2f x x θπθθ-+∈=,则方程()f x =2007的解集为 A .{-1} B .{-1,1} C .{1} D .φ10.若m.n 均为非负整数,在做m +n 的加法时各位均不进位(例如,134+3802=3936),则称(m,n )为“简单的”有序对,而m+n 称为有序数对(m,n)的值,那么值为1942的“简单的”有序对的个数是 A 、20 B 、16 C 、150 D 、300 11.设三棱锥的三个侧面两两互相垂直,侧棱长均为32,则其外接球的表面积为A .48πB .36πC .32πD .12π12.如图:已知点O 为ABC ∆的外心,且2||4AC AB ==,则()AO AB AC ⋅-等于:A .2B .4C .6D .8二、填空题:本大题共4小题,每小题4分,共16分,把答案填在答题纸相应题 号的横线上 13、设()00,P x y 是函数tan y x y x ==-与图象的交点,则200(1)(1cos 2)x x ++= .14.按ABO 血型系统学说,每个人的血型为A ,B ,O ,AB 四种之一,依血型遗传学,当且仅当父母中至少有一人的血型是AB 型时,子女一定不是O 型,若某人的血型为O 型,则父母血型所有可能情况有种.15.若双曲线22214x y a -=过点(2)-,则该双曲线的焦距为 . 16、如图是各棱长均相等的正四棱锥表面展开图, T 为QS 的中点,则在四棱锥中PQ 与RT 所成角的余弦值为____________三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤把答案写在答题纸相应题号的矩形框内。
河北冀州中学10—11学年高三上学期期末考试文科数学试题及答案

河北冀州中学10—11学年高三上学期期末考试文科数学试题
及答案
2012年05月23日亲,很高兴访问《河北冀州中学10—11学年高三上学期期末考试文科数学试题及答案》一文,也欢迎您访问店铺()的高考频道,为您精心准备了2011高考数学日常练习的相关模拟考试试题内容!同时,我们正在加紧建设高考频道,我们全体编辑的努力全是为了您,希望您能在本次高考中能获得好的名次,以及考上满意的大学,也希望我们准备的《河北冀州中学10—11学年高三上学期期末考试文科数学试题及答案》内容能帮助到您。
在即将到来的高考上助您一臂之力!加油,童鞋!
【店铺提供正确答案】。
冀州中学高三数学试卷

一、选择题(每题5分,共50分)1. 若函数f(x) = 2x + 3,则f(2)的值为()A. 7B. 8C. 9D. 102. 下列命题中正确的是()A. 对于任意实数x,都有x^2 ≥ 0B. 对于任意实数x,都有x^3 ≥ xC. 对于任意实数x,都有x^2 = xD. 对于任意实数x,都有x^3 = x3. 已知函数f(x) = x^2 - 2x + 1,则f(1)的值为()A. 0B. 1C. 2D. 34. 下列函数中,定义域为全体实数的是()A. y = √(x^2 - 1)B. y = x/(x - 1)C. y = √xD. y = x^25. 已知数列{an}满足an = 2an-1 + 1,且a1 = 1,则数列{an}的通项公式为()A. an = 2^n - 1B. an = 2^n + 1C. an = 2^n - 2D. an = 2^n + 26. 已知函数f(x) = x^3 - 3x + 2,若f(x)的零点个数为3,则f(x)的图像在x轴上的交点个数为()A. 1B. 2C. 3D. 47. 已知数列{an}满足an = 3an-1 - 2an-2,且a1 = 1,a2 = 2,则数列{an}的前n项和为()A. Sn = 2^n - 1B. Sn = 2^n + 1C. Sn = 2^n - 2D. Sn = 2^n + 28. 下列命题中正确的是()A. 对于任意实数x,都有x^2 ≥ 0B. 对于任意实数x,都有x^3 ≥ xC. 对于任意实数x,都有x^2 = xD. 对于任意实数x,都有x^3 = x9. 已知函数f(x) = x^2 - 2x + 1,则f(1)的值为()A. 0B. 1C. 2D. 310. 下列函数中,定义域为全体实数的是()A. y = √(x^2 - 1)B. y = x/(x - 1)C. y = √xD. y = x^2二、填空题(每题5分,共50分)11. 若函数f(x) = 2x - 3,则f(-1)的值为______。
河北省冀州中学高三上学期期中考试(数学理A).pdf
试卷类型:A卷 冀州市中学 2011—2012学年度上学期期中 高三年级应届数学试题(理) 一、选择题:(本大题共12小题,每小题5分,共60分). 1.复数=( ) A.-3-4i B.-3+4iC.3-4i D.3+4i.某程序框图如图所示,该程序运行后输出的值是 ()A.8B.6C.4D.3 的图像, 只需把函数 的图像( )A.向左平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向右平移个单位长度 4、如图是某几何体的三视图,其中正视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则该几何体的体积是 ( ) A.... O5下列命题错误的是( ) A对于命题,使得,则为:,均有 B命题“若,则”的逆否命题为“若, 则” C若为假命题,则均为假命题 D “”是“”的充分不必要条件 .若函数在其定义域内的一个子区间(k-1,k+1)内不是单调函数,则实数k的取值范围是( ) A.[1,+∞) B.[1,)C.[1,2) D.[,2).等差数列{}的前n项和为,若=2,=10,则等于( ) A.12 B.18C.24 D.42 如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=2,BC=,D、E分别是AC1和BB1的中点,则直线DE与平面BB1C1C所成的角为 ( ) A. B. C. D. 9.对实数和,定义运算“”:设函, .若函数的图象与轴恰有两个公共点,则的取值范围是. . . . 在内有极小值,则实数的取值范围是 A. B. C. D. 11.已知函数,则( ) A.函数最小值是-1,最大值是0B.函数最小值是-4,无最大值 C.函数无最小值,最大值是0D.函数最小值是-4,最大值是0 的定义域为,且,为的导函数,函数的图象如右图所示.若正数,满足,则的取值范围是 A. B. C. D. 二、填空题:本大题共4小题,每小题5分,共20分。
将正确答案写在答题纸上。
河北省冀州中学2010-2011学年高二上学期期末考试(数学理A)
试卷类型:A 卷 河北冀州中学2010—2011学年度上学期期末高二年级数学试题(理)考试时间 120分钟 试题分数 150一:选择题:本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的.选项填涂在答题卡上。
1.下列选项中表示最小整数的是( )A. 321(4)B.58C.111000(2)D.73(8)2.设A 、B 两点的坐标分别为(-1,0)、 (1,0),条件甲:点C 满足0>⋅;条件乙:点C 的坐标是方程 x 24 + y 23=1 (y ≠0)的解. 则甲是乙的( )A、充分不必要条件 B、必要不充分条件C、充要条件 D、既不是充分条件也不是必要条件3. 12名同学合影,站成前排4人后排8人,现摄影师要从后排8人中抽2人调整到前排 若其他人的相对顺序不变,则不同调整方法的总数是( )A.2283C AB. 2686C AC. 2286C AD. 2285C A4.如图,在正方体ABCD -A 1B 1C 1D 1中,P 是侧面BB 1C 1C 内一动点,若P 到 直线BC 与直线C 1D 1的距离相等,则动点P 的轨迹所在的曲线是( )A .直线B .双曲线C .抛物线D .圆5.口袋里放有大小相等的两个红球和一个白球,有放回地每次摸取一个球,定义数列}{n a :1n 1n n a ⎧=⎨-⎩第次取得白球第次取得球当当红,如果n S 为数列}{n a 的前n 项和,那么2703S S ≥=且的概率为( ) A .402187 B . 802187 C . 562187 D . 2421876. 若2011220110122011(14)()x a a x a x a x x R -=+++⋅⋅+∈,则201112022011222a a a a +++⋅⋅+= ( )A.1-B.0C.1D.20107. 如图,已知正三棱柱111ABC A B C -的各条棱长都相等,M 是侧棱1CC 的中点,则异面直线1AB BM 和所成的角的大小是 ()A .60°B .90°C .105°D .75°8.则y 与x 的线性回归方程为ˆˆy bx a =+必过定点 ( ) A .(2,2) B .(1,2) C .(1.5,4) D .(1.5,0)9.设随机变量ξ~1(9,)3B 且21ξη+=,则D (η)的值等于 ( )A.1B.2C.21D.410.为调查深圳中学生平均每人每天参加体育锻炼时间X (单位:分钟),按锻炼时间分下列四种情况统计(1)0—10 分钟(2)11—20 分钟(3)21—30 分钟(4)30 分钟以上。
河北省冀州中学10—11学年度高三一轮检测二(数学理)
河北冀州中学2010—2011学年高三年级一轮复习质量检测(二)理科数学试题第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的.1、复数2(1)1i z i+=-的共轭复数是A 、1i --B 、1i -+C 、1122i + D 、1122i -2、设nS 为等差数列}{na 的前n 项和,且12010a =-,20102008220102008S S -=,则2a =( )A 、2008B 、2008-C 、2012D 、2012-3、已知函数23,0(),0x x f x ax -≠⎧=⎨=⎩在0x =处连续,则2221n an lim a n n →∞+=+ A 、0 B 、1 C 、13D 、13-4、已知向量,m n 的夹角为6π,且||3m =,||2n =,在∆ABC 中,,3AB m n AC m n =+=-,D为BC 边的中点,则||AD =A 、1B 、2C 、3D 、45、已知函数()log (01)af x x a a =>≠且满足23()()f f a a >,则1(1)0f x->的解是A 、01x <<B 、1x <C 、0x >D 、1x >6、若22ln 6ln (2),ln 2ln 3,44a b c π==⋅=,则a ,b ,c 的大小关系是A 、b a c <<B 、a b c <<C 、c b a <<D 、c a b <<7、函数()sin()(0,||)2f x A x A πωϕϕ=+><其中的图象如图所示,为了得到()sin3g x x=的图象,则只要将()f x 的图象A 、向右平移4π个单位长度B 、向右平移12π个单位长度C 、向左平移4π个单位长度D 、向左平移12π个单位长度8、1F 、2F 分别是双曲线12222=-by a x 的左、右焦点,A 是其右顶点,过2F 作x 轴的垂线与双曲线的一个交点为P ,G 是0,2121=⋅∆F F GA F PF 若的重心,则双曲线的离心率是A 、2 B 、3 C 、2 D 、39、如右图所示,△ADP 为正三角形,四边形ABCD 为正方形,平面PAD⊥平面ABCD .点M 为平面ABCD 内的一个动点,且满足MP=MC .则点M 在正方形ABCD 内的轨迹为10、已知函数()lg ,010,16,02x x f x x x ⎧≤⎪=⎨-+⎪⎩<>1若,,a b c 互不相等,且()()()f a f b f c ==,则a b c ⋅⋅的取值范围是A 、()1,10B 、()5,6C 、()10,12D 、()20,24[来11、形如45132这样的数称为“波浪数”,即十位数字,千位数字均比它们各自相邻的数字大,则由1、2、3、4、5可构成的数字不重复的五位“波浪数”的个数为A 、12B 、24C 、16D 、2012、已知函数)(x f y =的定义域为R ,当0x <时,()1f x >,且对任意的实数x 、y ,等式()()f x f y =()f x y +恒成立,若数列{}na 满足1(0)a f =,且11()(2)n n f a f a +=--*()n N ∈,则2011a 的值为A 、4017B 、4018C 、4019D 、4021第Ⅱ卷(非选择题,共90分)二、填空题:本大题共4小题,每小题5分,共20分。
冀州中学高三数学期末试卷
一、选择题(本大题共10小题,每小题5分,共50分)1. 已知函数$f(x)=\frac{x^2-4x+3}{x-1}$,则函数的定义域为()A. $x\neq 1$B. $x\neq 0$C. $x\neq 3$D. $x\neq -1$2. 若向量$\vec{a}=(1,2)$,$\vec{b}=(3,-1)$,则$\vec{a}\cdot\vec{b}$的值为()A. 5B. -5C. 1D. -13. 已知等差数列$\{a_n\}$的前$n$项和为$S_n$,若$a_1=2$,$S_5=20$,则$a_6$的值为()A. 6B. 7C. 8D. 94. 若复数$z=a+bi$(其中$a,b$为实数)满足$|z+1|=|z-1|$,则$a$的值为()A. 0B. 1C. -1D. 无法确定5. 已知函数$f(x)=x^3-3x^2+4x$,若$f(x)=0$有三个不同的实数根,则$f'(x)=0$的解的个数为()A. 1B. 2C. 3D. 46. 在直角坐标系中,点A(2,1)关于直线$x+y=1$的对称点为B,则点B的坐标为()A. (1,-1)B. (1,2)C. (-1,1)D. (-1,-1)7. 已知函数$f(x)=\ln(x+1)-\sqrt{x}$,则$f(x)$在定义域内的极值点个数为()A. 1B. 2C. 3D. 48. 若等比数列$\{a_n\}$的公比为$q$,且$a_1=3$,$a_5=24$,则$q$的值为()A. 2B. $\frac{1}{2}$C. 3D. $\frac{1}{3}$9. 已知数列$\{a_n\}$满足$a_1=1$,$a_{n+1}=a_n+2^n$,则数列$\{a_n\}$的通项公式为()A. $a_n=2^n-1$B. $a_n=2^n+1$C. $a_n=2^n-2$D. $a_n=2^n+2$10. 在平面直角坐标系中,点P(2,3)到直线$x+y-5=0$的距离为()A. $\frac{1}{\sqrt{2}}$B. $\sqrt{2}$C. $\frac{3}{\sqrt{2}}$D. $\frac{5}{\sqrt{2}}$二、填空题(本大题共5小题,每小题5分,共25分)11. 已知函数$f(x)=\frac{1}{x^2-1}$,则$f(-1)$的值为______。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河北冀州中学2010—2011学年度上学期期末考试高三年级理科数学试题考试时间120分钟 试题分数150分第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1、已知}2{},{222=+===y x y N x y y M ,则M N =A 、{(1,1),(-1,1)}B 、{1}C 、[0,1]D 、]2,0[ 2、设i 为虚数单位,则=+++++10321i i i iA 、iB 、i -C 、i 2D 、i 2-3、已知关于x 的二项式n xa x )(3+展开式的二项式系数之和为32,常数项为80,则a 的值为A 、1B 、1±C 、2D 、2±4、已知实数d c b a ,,,成等比数列,且对函数x x y -+=)2ln(,当b x =时取到极大值c ,则ad 等于 A 、1- B 、0 C 、1 D 、25、已知直线α平面⊥l ,直线β平面⊂m ,给出下列命题:①α∥m l ⊥=β;②l ⇒⊥βα∥m ;③l ∥βα⊥⇒m ;④α⇒⊥m l ∥β。
其中正确命题的序号是A 、①②③ B、②③④ C、①③ D、②④6、设,a b 都是非零向量,那么命题“a 与b共线”是命题“a b a b +=+ ”的A 、充分不必要条件B 、必要不充分条件C 、充要条件D 、非充分非必要条件7、设函数,))((为奇函数R x x f ∈=+=+=)5(),2()()2(,21)1(f f x f x f f 则A 、0B 、1C 、25 D 、58、函数f (x )=⎩⎨⎧ax 2+1,x ≥0(a 2-1)e ax,x <0在(-∞,+∞)上单调,则a 的取值范围是A 、(-∞,-2]∪(1,2]B 、[-2,-1)∪[2,+∞)C 、(1,2]D 、[2,+∞)9、正方体ABCD -A 1B 1C 1D 1的棱长为4,点P 、Q 在棱CC 1上,PQ =1,则三棱锥P -QBD 的体积是A 、83B 、43C 、8D 、与P 点位置有关10、某人5次上班途中所花的时间(单位:分钟)分别为x 、y 、10、11、9。
已知这组数据的平均数为10,方差为2,则||x y -的值为A 、1B 、2C 、3D 、411、如右图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第n 行有n个数且两端的数均为1n(n≥2),每个数是它下一行左右相邻两数的和,如11=12+12,12=13+16,13=14+112,…,则第10行第4个数(从左往右数)为A 、11260B 、1840C 、1504D 、136012、过抛物线)0(22>=p px y 的焦点F 的直线l 与抛物线在第一象限的交点为A ,与抛物线的准线的交点为B ,点A 在抛物线的准线上的射影为C ,若48,=⋅=,则抛物线的方程为 ( ) A 、x y 82=B 、x y 42=C 、x y 162=D 、x y 242=第Ⅱ卷(非选择题,共90分)二、填空题:本大题共4小题,每小题5分,共20分。
把答案直接答在答题纸上。
13、若直线032=++a y ax 与直线a y a x +-=-+7)1(3平行,则实数a 的值为 。
14、已知向量1(sin ,),(cos ,1),(2,)4a b c m θθ===满足a b ⊥ 且()a b + ∥c ,则实数m= 。
15、从集合{}1,2,3,0,1,2,3,4---中,随机选出4个数组成子集,使得这4个数中的任何两个数之和不等于...1,则取出这样的子集的概率为____ __。
16、有以下四个命题:①ABC ∆中,“B A >”是“B A sin sin >”的充要条件; ②若数列{}n a 为等比数列,且6,9,4684±===a a a 则;③不等式051≤+-x x 的解集为{}5|-<x x ; ④若P 是双曲线221916x y -=上一点,21、F F 分别是双曲线的左、右焦点,且1||7PF =,则2||13PF =。
其中真命题的序号为_____________.(把正确的序号都填上)三、解答题:本大题共6小题,共70分。
解答时应写出文字说明、证明过程或演算步骤。
17、(本小题满分10分)已知向量m→=(sinB,1-cosB)与向量n→=(2,0)的夹角为3π,其中A、B、C是∆ABC的内角。
(Ⅰ)求角B的大小;(Ⅱ)求sin sinA C+的取值范围。
18、(本小题满分12分)甲、乙、丙、丁4名同学被随机地分到A、B、C三个社区参加社会实践,要求每个社区至少有一名同学。
(Ⅰ)求甲、乙两人都被分到A社区的概率;(Ⅱ)求甲、乙两人不在同一个社区的概率;(Ⅲ)设随机变量ξ为四名同学中到A社区的人数,求ξ的分布列和ξE的值。
19、(本小题满分12分)如图,△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC ,AB=2,已知AE与平面ABC所成的角为θ,且tanθ=32。
(Ⅰ)证明:平面ACD⊥平面ADE;(Ⅱ)记AC=x,V(x)表示三棱锥A-CBE的体积,求V(x)的表达式;(Ⅲ)当V(x)取得最大值时,求二面角D-AB-C20、(本小题满分12分)设各项均为正数的数列{}n a的前n项和为n S,已知3122aaa+=,数列{}n S是公差为d的等差数列。
(Ⅰ)求数列{}n a的通项公式(用dn,表示);(Ⅱ)设c为实数,对满足nmknm≠=+且3的任意正整数knm,,,A BE不等式k n m cS S S >+都成立。
求c 的最大值。
21、(本小题满分12分)已知圆O :822=+y x 交x 轴于B A ,两点,曲线C 是以AB 为长轴,直线l :4-=x 为准线的椭圆.(Ⅰ)求椭圆的标准方程;(Ⅱ)若M 是直线l 上的任意一点,以OM 为直径的圆K 与圆O 相交于Q P ,两点,求证:直线PQ必过定点E ,并求出点E 的坐标; (Ⅲ)如图所示,若直线PQ 与椭圆C 交于H G ,两点,且3=,试求此时弦PQ 的长。
22、(本小题满分12分)已知函数32()(63),.x f x x x x t e t R =-++∈(Ⅰ)若函数(),,()y f x x a x b x c a b c ====<<依次在处取极值,求t 的取值范围;(Ⅱ)若存在实数[0,2]t ∈,使对任意的[1,],()x m f x x ∈≤不等式恒成立,求正整数m 的最大值。
2010-2011学年上学期期末考试 高三年级理科数学参考答案一、选择题:A 卷:DACACB CAABBD B 卷:CBDAAB CCBDCA二、填空题:13、3; 14、2± 15、835; 16、①④。
17、解:(Ⅰ)∵2sin m n B ⋅=…………………………………………1分122m n ⋅=⨯= 2分∴2sin B = 化简得:22cos cos 10B B --=∴cos 1B =(舍去)或1cos 2B =- ………………………4分又∵(0,)B π∈ ∴23B π= ………………………5分②11sin sin sin sin()sin sin sin 3222A C A A A A A A π+=+-=+-=+sin()23A A π=+…………………………………………………8分 ∵03A π<< ∴2333A πππ<+<sin()13A π<+≤∴sin sin A C +∈ …………………………………………10分18、解:(Ⅰ)记甲、乙两人同时到A 社区为事件A E ,那么2223431()18A A P E C A ==,即甲、乙两人同时到A 社区的概率是118. …………………4分(Ⅱ)记甲、乙两人在同一社区为事件E ,那么3323431()6A P E C A ==,所以,甲、乙两人不在同一社区的概率是5()1()6P E P E =-=. (8)分(Ⅲ)随机变量ξ可能取的值为1,2.事件“(1,2)i i ξ==”是指有i 个同学到A社区,则224223431(2)3C A P C A ξ===.所以2(1)1(2)3P P ξξ==-==, ξ的分布列是34312321=⨯+⨯=ξE . …………………12分19、(Ⅰ)证明:∵四边形DCBE 为平行四边形 ∴CD∥BE,BC∥DE∵ DC⊥平面ABC ,BC ⊂平面ABC ∴DC⊥BC.∵AB 是圆O 的直径 ∴BC⊥AC 且DC∩AC=C ∴BC⊥平面ADC . ∵DE//BC ∴DE⊥平面ADC又∵DE ⊂平面ADE ∴平面ACD⊥平面ADE ………………3分(Ⅱ)∵ DC ⊥平面ABC ∴BE ⊥平面ABC∴EAB ∠为AE 与平面ABC 所成的角,即EAB ∠=θ在R t△ABE 中,由tan 2BE AB θ==2AB =得BE =在Rt△ABC 中∵AC ==02x <<)∴1122ABC S AC BC ∆=⋅=∴1()3C ABE E ABC ABC V x V V S BE --∆===⋅6=02x <<)---7分(Ⅲ)由(Ⅱ)知02x <<要()V x取得最大值,当且仅当=取得最大值,∵222224(4)()42x x x x +--≤=当且仅当224x x =-,即x =时,“=”成立,∴当()V x 取得最大值时AC =,这时△ACB 为等腰直角三角形--9分连结CO ,DO ∵AC=BC,DC=DC∴Rt DCA ∆≌Rt DCB ∆ ∴AD=DB又∵O 为AB 的中点 ∴,CO AB DO AB ⊥⊥∴DOC ∠为二面角D -AB -C 的平面角在Rt DCO ∆中 ∵112CO AB ==,DC BE =∴tan DCDOC CO∠==, ∴DOC ∠=60 即当()V x 取得最大值时,二面角D -AB -C 为60°.------12分 20、(Ⅰ)由题意知:0d >,(1)(1)n d n d =-=-21323213233()a a a a S S S S =+⇒=⇒-=,2221)]2),d a d -= 化简,得:2211,a d d d a d -+===22(1),n d n d nd S n d =+-==,当2n ≥时,222221(1)(21)n n n a S S n d n d n d -=-=--=-,适合1n =情形。
