06【数学】高考数学基础知识总结:第六章 不等式
高考数学一轮复习 第六章 不等式、推理与证明 6.6 数学归纳法(理)

【特别提醒】 1.数学归纳法证题时,误把第一个值n0认为是1,如证明 多边形内角和定理(n-2)π时,初始值n0=3.
2.数学归纳法证题的关键是第二步,证题时应注意: (1)必须利用归纳假设作基础. (2)证明中可利用综合法、分析法、反证法等方法. (3)解题时要搞清从n=k到n=k+1增加了哪些项或减少了 哪些项.
(n∈N*).
2 3 4 2n1 2n
11
1
【n解题1导n引2】根据2n数学归纳法证明等式的步骤进行证
明.
【规范解答】(1)当n=1时,左边= 1 1 1 ,
右边=
1
1
左边=右边.
,
22
11 2
(2)假设n=k时等式成立,
即 1111 1 1 2 3 4 2k1 2k
则k当1n1=kk+11时2,21k,
求证:f(1)+f(2)+…+f(n-1)=n[f(n)-1](n≥2,n∈N*).
【证明】(1)当n=2时,左边=f(1)=1,
右边= 左边=右2(1边,12等1式) 成1,立.
(2)假设n=k(k≥2,k∈N*)时,结论成立, 即f(1)+f(2)+…+f(k-1)=k[f(k)-1], 那么,当n=k+1时, f(1)+f(2)+…+f(k-1)+f(k) =k[f(k)-1]+f(k)=(k+1)f(k)-k
【解析】用数学归纳法证明不等式
1 1 1 1 9(n∈N*且n>1)时,
第n 一1步n : 不2等n 式3 的左边3 是n10
高考数学 考前最后一轮基础知识巩固之第六章 不等式汇总
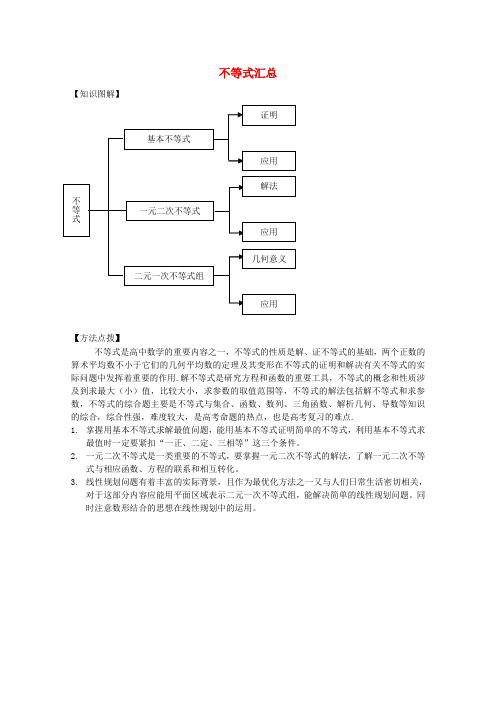
不等式汇总
【知识图解】
【方法点拨】
不等式是高中数学的重要内容之一,不等式的性质是解、证不等式的基础,两个正数的算术平均数不小于它们的几何平均数的定理及其变形在不等式的证明和解决有关不等式的实际问题中发挥着重要的作用.解不等式是研究方程和函数的重要工具,不等式的概念和性质涉及到求最大(小)值,比较大小,求参数的取值范围等,不等式的解法包括解不等式和求参数,不等式的综合题主要是不等式与集合、函数、数列、三角函数、解析几何、导数等知识的综合,综合性强,难度较大,是高考命题的热点,也是高考复习的难点.
1.掌握用基本不等式求解最值问题,能用基本不等式证明简单的不等式,利用基本不等式求
最值时一定要紧扣“一正、二定、三相等”这三个条件。
2.一元二次不等式是一类重要的不等式,要掌握一元二次不等式的解法,了解一元二次不等
式与相应函数、方程的联系和相互转化。
3.线性规划问题有着丰富的实际背景,且作为最优化方法之一又与人们日常生活密切相关,
对于这部分内容应能用平面区域表示二元一次不等式组,能解决简单的线性规划问题。
同时注意数形结合的思想在线性规划中的运用。
高考数学一轮总复习第六章不等式第1讲不等式的概念与性质课件文

bz+cx)=a(z-y)+b(y-z)=(a-b)(z-y)<0,故 az+by+cx<ay
+bz+cx.故最低费用为 az+by+cx.故选 B. 第二十二页,共34页。
考点 3 利用(lìyòng)作商比较大小
例 3:已知在正项数列{an}中,a1=6,点 An(an, an+1)在 抛物线 y2=x+1 上;在数列{bn}中,点 Bn(n,bn)在过点(0,1),
A.1 个
B.2 个
其中能成立的个数是(
C.3 个
)
D.4 个
第十六页,共34页。
解析:∵a>0>b>-a,c<d<0,∴ad<0,bc>0.∴ad< bc.∴①错误.∵a>0>b>-a,∴a>-b>0.∵c<d<0,∴-c >-d>0.∴a(-c)>(-b)(-d).∴ac+bd<0.∴ad+bc=ac+cdbd< 0.∴②正确.∵c<d,∴-c>-d.∵a>b,∴a+(-c)>b+(-d), 即 a-c>b-d,∴③正确.∵a>b,d-c>0,∴a(d-c)>b(d- c).∴④正确.故选 C.
一个命题为假命题时,可以(kěyǐ)用特殊值法,但不能用特殊值法肯 定一个命题,此时只能用所学知识严密证明.
第十五页,共34页。
【互动(hù dònɡ)探究】
1.若 a>0>b>-a,c<d<0,则下列命题(mìng tí): ①ad>bc;②ad+bc<0;③a-c>b-d;④a(d-c)>b(d-c).
性质
性质内容
对称性 传递性 可加性
a>b⇔b<a a>b,b>c⇒__a_>__c___
a>b⇔a+c>b+c
可乘性
ac>>0b⇒ac>bc ac<>0b⇒_a_c_<__b_c__
1高考数学理基础知识总复习精讲课件:第6章 第8节 不等式的证明

高考总复习•数学(理科)
点评:用比较法证不等式,一般要经历作差(或商)、 变形、判断三个步骤.变形的主要手段是通分、因式分 解,利用各因式的符号进行判断,或进行配方,利用非 负数的性质进行判断,有时在变形过程中,还可利用基 本不等式进行放缩.
高考总复习•数学(理科) 变式探究
1.已知a, b, m都是正数,并且a<b,求证:ab++mm>ba.
高考总复习•数学(理科)
证明:假设|f(1)|,|f(2)|,|f(3)|都小于 1 ,则|f(1)|+2|f(2)|+
2
|f(3)|<2,而 |f(1)|+2|f(2)|+|f(3)|≥|f(1)+f(3)-2f(2)|=|(1+p+q)+ (9+3p+q)-(8+4p+2q)|=2,相互矛盾,假设不成立.
自主解答:
高考总复习•数学(理科) 证明:∵a,b,c∈R+,且a+b+c=1, ∴要证原不等式成立, 即 证 [(a + b + c) + a]·[(a + b + c) + b][(a + b + c) +
c]≥8[(a+b+c)-a]·[(a+b+c)-b]·[(a+b+c)-c]. 也就是证[(a+b)+(c+a)][(a+b)+(b+c)]·[(c+a)+
高考总复习•数学(理科) 变式探究
3.当n>2时,求证:logn(n-1)logn(n+1)<1.
证明:∵n>2,∴logn(n-1)>0,logn(n+1)>0. ∴logn(n-1)logn(n+1)<lognn-1+2 lognn+12= lognn22-12<log2nn22=1. ∴当n>2时,logn(n-1)logn(n+1)<1.
高考总复习•数学(理科)
高考数学一轮总复习 第六章 不等式、推理与证明 第二节 一元二次不等式及其解法课件(理)

答案:A
(2)已知函数 f(x)=x2+2xx+a,若对任意 x∈[1,+∞),f(x)>0
恒成立,则实数 a 的取值范围是________.
解析:因为
x∈[1,+∞)时,f(x)=
x2+2x+a x >0
恒成立,即
x2
+2x+a>0 恒成立.即当 x≥1 时,a>-(x2+2x)恒成立.设 g(x)=-
(1)若不等式 ax2+bx+2>0 的解为-12<x<13,则不等式 2x2+bx +a<0 的解集是________.
(2)不等式2xx-+11≤0 的解集是________. 解析:(1)由题意,知-12和13是一元二次方程 ax2+bx+2=0 的两 根且 a<0,
所以--1212×+3311==2a-,ba,解得ab==--122. ,
(x2+2x),而 g(x)=-(x2+2x)=-(x+1)2+1 在[1,+∞)上单调递减,
所以 g(x)max=g(1)=-3,故 a>-3.
所以,实数 a 的取值范围是{a|a>-3}.
答案:{a|a>-3}
某汽车厂上年度生产汽车的投入成本为 10 万元/辆,出 厂价为 12 万元/辆,年销售量为 10 000 辆.本年度为适应市场需求, 计划提高产品质量,适度增加投入成本.若每辆车投入成本增加的比 例为 x(0<x<1),则出厂价相应地提高比例为 0.75x,同时预计年销售 量增加的比例为 0.6x,已知年利润=(出厂价-投入成本)×年销售量.
(2)要保证本年度的年利润比上年度有所增加,必须有
y-(12-10)×10 0<x<1,
000>0,即0-<6x<010,0x2+2
高考数学一轮复习第六章不等式推理与证明6.6数学归纳法课件理

【规范解答】(1)当n=1时,因为a2是方程a22+a2-1=0的
正根,所以a2= 5 ,即1 a1<a2成立. 2
(2)假设当n=k(k∈N*,k≥1)时,0≤ak<ak+1, 所以ak+12-ak2=(ak+12+ak+2-1)-(ak+12+ak+1-1) =(ak+2-ak+1)(ak+2+ak+1+1)>0, 又ak+1>ak≥0,所以ak+2+ak+1+1>0, 所以ak+1<ak+2,即当n=k+1时,an<an+1也成立. 综上,可知an<an+1对任何n∈N*都成立.
)
A.1项
B.k项
C.2k-1项 D.2k项
【解析】选D.
112132k111(112132k11) 共增21k加了2k121k项.2k111,
4.(2016·武汉模拟)用数学归纳法证明不等式 1 1 1 1 9(n∈N*且n>1)时,第一步:
1133152k112k12k112k3
2kk12k112k3
k2k31 2k12k3
22kk2132kk13
2kk132kk111,
所以当n=k+1时,等式也成立, 由(1)(2)可知,对一切n∈N*等式都成立.
( 1 1 1 )( 1 1 ) k1 k2 2k 2k1 2k2
1 1 1 1 . k2 k3 2k1 2k2
即当n=k+1时,等式也成立.
综合(1)(2)可知,对一切n∈N*,等式成立.
高考数学复习第六章第三节不等式的证明课件
首页
上一页
下一页
末页
首页
上一页
下一页
末页
首页
上一页
下一页
末页
首页
上一页
下一页
末页
首页
上一页
下一页
末页
首页
上一页
下一页
末页
首页
上一页
下一页
末页
首页
上一页
下一页
末页
首页
上一页
下一页
末页
首页
上一页
下一页
末页
首页
上一页
下一页
末页
首页
上一页
下一页
末页
首页
上一页
下一页
末页
首页
上一页
下一页
下一页
末页
首页
上一页
下一页
末页
首页
上一页
下一页
末页
首页
上一页
下一页
末页
天每
开个
放孩
;子
有的
的花
孩期
子不
是一
菊样
花,
,有
选的
择孩
在子
秋是
天牡
开丹
放花
;,
而选
有择
的在
孩春
➢ He who falls today may rise tomorrow.
子天
是开
梅放
花;
,有
选的
择孩
在子
冬是
天荷
开花
放,
首页
上一页
下一页
末页
首页
上一页
下一页
末页
首页
上一页
下一页
高二数学 第六章 不等式重要知识和重要题型回顾
word 1 / 8 第六章 不等式重要知识和重要题型回顾
一、基础知识 6.1 不等式的性质 1.熟练掌握实数比较大小的依据: 2.作差比较法:作差→变形→判断→结论 3.重要性质 (1)对称性:a>bb(2)传递性:a>b,b>ca>c (3)可加性:a>ba+c>b+c 推论1:bcacba; 推论2:a>b,c>da+c>b+d;a>b,cb-d (4)可积性:a>b,c>0ac>bc;a>b,c<0ac
推论1:0dc0baac>bd 推论2:a>b>0an>bn(n∈N,n>1)
推论3:dbcadc00ba,特例:a>b,ab>0b1a1 (5)开方性:a>b>0nnba(n>1,n∈N) 4.重要方法:特值法 二、典型例题: 例1:(1)已知x≠0,比较(x2+1)2与x4+x2+1的大小;(2)已知a>b,比较a3与b3的大小;
(3)已知2,比较1+cosα与sinα的大小。
例2: 若a>b>0,c例3:已知α,β∈),2(,求α+β,α-β,的取值X围。 例4:设f(x)=ax2+bx(a≠0),若1≤f(-1)≤2,2≤f(1)≤4,求f(2)取值X围。 三、巩固练习 (一)选择题 1.若a
A.a1ba1 B.b1a1 C.|a|>|b| D.a2>b2 2.下列推导中,错误的是
A.c-ab B.ba0cbcac
C.cbda0dc0baD.ba)2n,Nn(bann 3.若a>b,x>y,则下列不等式中正确的是 word 2 / 8 A.a-x>b-y B.axy-a 4.若a、b是任意实数,a>b,则下列不等式正确的是 A.A2>b2 B.1ab C.lg(a-b)>0 D.ba)21()21( 5.若a、b∈R,则下列命题为真命题的是 A.若|a|>b,则a2>b2B.若aa2
高考数学第六章 不等式
1.(2015·福建)若直线a +b=1(a >0,b >0)过点(1,1),则a+b 的最小值等于( )A .2B .3C .4D .52.(2015·湖南)若实数a ,b 满足1a +2b=ab ,则ab 的最小值为( )A.2B .2 C .22D .43.(2015·山东)若函数f (x )=2x +12x -a 是奇函数,则使f (x )>3成立的x 的取值范围为( )A .(-∞,-1)B .(-1,0)C .(0,1)D .(1,+∞)4.(2015·北京)设{a n }是等差数列,下列结论中正确的是( ) A .若a 1+a 2>0,则a 2+a 3>0 B .若a 1+a 3<0,则a 1+a 2<0 C .若0<a 1<a 2,则a 2>a 1a 3 D .若a 1<0,则(a 2-a 1)(a 2-a 3)>05.(2015·福建)已知AB →⊥AC →,|AB →|=1t,|AC →|=t ,若点P 是△ABC 所在平面内的一点,且AP →=AB→|AB →|+4AC→|AC →|,则PB →·PC →的最大值等于( )A .13B .15C .19D .216.(2015·陕西)设f (x )=ln x ,0<a <b ,若p =f (ab ),q =f ⎝ ⎛⎭⎪⎫a +b 2,r =12(f (a )+f (b )),则下列关系式中正确的是( ) A .q =r <p B .q =r >p C .p =r <q D .p =r >q7.(2015·浙江)有三个房间需要粉刷,粉刷方案要求:每个房间只用一种颜色,且三个房间颜色各不相同.已知三个房间的粉刷面积(单位:m 2)分别为x ,y ,z ,且x <y <z ,三种颜色涂料的粉刷费用(单位:元/m 2)分别为a ,b ,c ,且a <b <c .在不同的方案中,最低的总费用(单位:元)是( )A .ax +by +czB .az +by +cxC .ay +bz +cxD .ay +bx +cz8.(2014·重庆)若log 4(3a +4b )=log 2ab ,则a +b 的最小值是( )A .6+23B .7+2 3C .6+43D .7+4 39.(2014·福建)要制作一个容积为4m 3,高为1m 的无盖长方体容器.已知该容器的底面造价是每平方米20元,侧面造价是每平方米10元,则该容器的最低总造价是( )A .80元B .120元C .160元D .240元10.(2015·天津)已知a >0,b >0,ab =8,则当a 的值为________时,log 2a ·log 2(2b )取得最大值.11.(2015·浙江)已知函数f (x )=⎩⎪⎨⎪⎧x 2,x ≤1,x +6x-6,x >1,则f (f (-2))=________,f (x )的最小值是________.12.(2015·山东)定义运算“⊗”:x ⊗y =x 2-y 2xy(x ,y ∈R ,xy ≠0),当x >0,y >0时,x ⊗y +(2y )⊗x 的最小值为________.13.(2015·重庆)设a ,b >0,a +b =5,则a +1+b +3的最大值为________.14.(2015·天津)在等腰梯形ABCD 中,已知AB ∥DC ,AB =2,BC =1,∠ABC =60°,动点E 和F 分别在线段BC 和DC 上,且BE →=λBC →,DF →=19λDC →,则|AE →|·|AF →|的最小值为________.1.(2015·临沂一模)y>1的一个充分不必要条件是( ) A .x >y B .x >y >0 C .x <y D .y <x <02.(2015·山东青岛质检)设a <b <0,则下列不等式中不成立的是( )A.1a >1bB.1a -b >1aC .|a |>-b D.-a >-b3.(2015·武汉模拟)若a >b >0,则下列不等式中一定成立的是( )A .a +1b >b +1a B.b a >b +1a +1C .a -1b >b -1a D.2a +b a +2b >a b4.(2015·山西重点中学模拟)不等式x -2x 2-1<0的解集为( )A .{x |1<x <2}B .{x |x <2且x ≠1}C .{x |-1<x <2且x ≠1}D .{x |x <-1或1<x <2}5.(2015·沈阳四校联考)若全集U ={x ∈R |x 2≤4},则集合A ={x ∈R ||x +1|≤1}的补集∁U A 为( )A .{x ∈R |0<x <2}B .{x ∈R |0≤x <2}C .{x ∈R |0<x ≤2}D .{x ∈R |0≤x ≤2}6.(2015·山西省质检二)对于函数f (x )定义域内的任意一个x 都有f (x )≤M 恒成立的所有常数M 中,我们把M 的最小值叫做函数f (x )的上确界,则函数g (x )=-12x -21-x (x ∈(0,1))的上确界是( )A.14B .-4C.92D .-927.(2015·河南洛阳质检)若不等式x 2-2ax +a >0对一切实数x ∈R 恒成立,则关于t 的不等式at 2+2t -3<1的解集为( )A .(-3,1)B .(-∞,-3)∪(1,+∞)C .∅D .(0,1)8.(2015·山东泰安一模)若a ,b ∈R ,且ab >0,则下列不等式中,恒成立的是( )A .a +b ≥2ab B.1a +1b>2abC.b a +ab≥2D .a 2+b 2>2ab 9.(2015·皖南八校联考)函数f (x )=a x -1+3(a >0,且a ≠1)的图象过一个定点P ,且点P 在直线mx +ny -1=0(m >0,n >0)上,则1m +4n的最小值是( )A .12B .13C .24D .2510.(2015·湖南株洲调研)若正数x ,y 满足4x 2+9y 2+3xy =30,则xy 的最大值是( )A.43B.53C .2D.5411.(2015·郑州市预测)已知a ,b 是两个零点的单位向量且c ·a=c ·b =1,则对任意的正实数t ,⎪⎪⎪⎪⎪⎪c +t a +1t b 的最小值是( )A .2B .22C .4D .4 212.(2015·河南八市质量监测)已知f (x )=⎩⎪⎨⎪⎧ax 2+x ,x ≥0,-ax 2+x ,x <0,当x ∈⎣⎢⎡⎦⎥⎤-14,14时恒有f (x +a )<f (x ),则实数a 的取值范围是( ) A.⎝ ⎛⎭⎪⎪⎫1-174,0B .[-2,0) C .(-∞,-2)D .[-2,-2)13.(2015·山西省三诊)不等式1x<a 的解集是{x |a <x <0},则a =________.14.(2015·江西省质检三)若不存在整数x 满足不等式(kx -k 2-2)(x -2)<0,则实数k 的取值范围是________.15.(2015·邯郸市质检)已知x ,y ∈(0,+∞),2x -3=⎝ ⎛⎭⎪⎫12y ,则1x +4y的最小值为________.16.(2015·吉林市高三摸底)已知正项等比数列{a n }的公比q =2,若存在两项a m ,a n ,使得a m a n =4a 1,则1m +4n的最小值为________.1.(2015·天津)设变量x ,y 满足约束条件⎩⎪⎨⎪⎧x -2y ≤0,x +2y -8≤0,则目标函数z =3x +y 的最大值为( )A .7B .8C .9D .142.(2015·湖南)若变量x ,y 满足约束条件⎩⎪⎨⎪⎧x +y ≥1,y -x ≤1,x ≤1,则z =2x-y 的最小值为( )A .-1B .0C .1D .23.(2015·安徽)已知x ,y 满足约束条件⎩⎪⎨⎪⎧x -y ≥0,x +y -4≤0,y ≥1,则z =-2x +y 的最大值是( )A .-1B .-2C .-5D .14.(2015·陕西)某企业生产甲、乙两种产品均需用A ,B 两种原料,已知生产1吨每种产品所需原料及每天原料的可用限额如表所示,如果生产1吨甲、乙产品可获利润分别为3万元、4万元,则该企业每天可获得最大利润为( )A.12万元BC .17万元D .18万元5.(2015·四川)设实数x ,y 满足⎩⎪⎨⎪⎧2x +y ≤10,x +2y ≤14,x +y ≥6,则xy 的最大值为( )A.252B.492C .12D .14 6.(2015·重庆)若不等式组⎩⎪⎨⎪⎧x +y -2≤0,x +2y -2≥0,x -y +2m ≥0表示的平面区域为三角形,且其面积等于43,则m 的值为( )A .-3B .1C.43D .37.(2015·福建)变量x ,y 满足约束条件⎩⎪⎨⎪⎧x +y ≥0,x -2y +2≥0,mx -y ≤0.若z =2x -y 的最大值为2,则实数m 等于( )A .-2B .-1C .1D .28.(2014·福建)已知圆C :(x -a )2+(y -b )2=1,平面区域Ω:⎩⎪⎨⎪⎧x +y -7≤0,x -y +3≥0,y ≥0.若圆心C ∈Ω,且圆C 与x 轴相切,则a 2+b 2的最大值为( )A .5B .29C .37D .499.(2014·四川)执行如图所示的程序框图,如果输入的x ,y ∈R ,那么输出的S 的最大值为( )A .0B .1C .2D .310.(2015·新课标全国Ⅰ)若x ,y 满足约束条件⎩⎪⎨⎪⎧x +y -2≤0,x -2y +1≤0,2x -y +2≥0,则z =3x +y 的最大值为________.11.(2015·新课标全国Ⅱ)若x ,y 满足约束条件⎩⎪⎨⎪⎧x +y -5≤0,2x -y -1≥0,x -2y +1≤0,则z =2x +y 的最大值为________.12.(2015·北京)如图,△ABC 及其内部的点组成的集合记为D ,P (x ,y )为D 中任意一点,则z =2x +3y 的最大值为________.13.(2015·浙江)已知实数x ,y 满足x 2+y 2≤1,则|2x +y -4|+|6-x -3y |的最大值是________.考点20 二元一次不等式(组)与简单的线性规划一年模拟试题精练⎩⎪⎨⎪⎧1≤x +y ≤3,-1≤x -y ≤1表示图形的面积等于( ) A .1B .2C .3D .42.(2015·武汉调研试题)设A ={(x ,y )|x ,y ,1-x -y 是三角形的三边长},则A 所表示的平面区域(不含边界的阴影部分)是( )3.(2015·汕头模拟)已知约束条件⎩⎪⎨⎪⎧x ≥1,x +y -4≤0,kx -y ≤0表示面积为1的直角三角形区域,则实数k 的值为( )A .1B .-1C .0D .-24.(2015·山西省三诊)已知x ,y 满足⎩⎪⎨⎪⎧y ≤x ,x +y ≤1,y ≥-1,则z =2x +y的最大值为( )A .-3B .-1C.32D .35.(2015·昆明一中检测)设x ,y 满足约束条件⎩⎪⎨⎪⎧x -y +1≥0,x +y -1≥0,x ≤3,则z =2x -3y 的最小值是( )A .-7B .-6C .-5D .-36.(2015·贵州七校一联)一个平行四边形的三个顶点的坐标为(-1,2),(3,4),(4,-2),点(x ,y )在这个平行四边形的内部或边上,则z =2x -5y 的最大值是( )A .16B .18C .20D .367.(2015·云南师大附中适应性考试)设x ,y 满足约束条件⎩⎪⎨⎪⎧3x -y -2≤0,x -y ≥0,x ≥0,y ≥0,若目标函数z =ax +by (a >0,b >0)的最大值为4,则a +b 的值为( )A.14B .2C .4D .0 8.(2015·郑州市预测)已知点P (x ,y )的坐标满足条件⎩⎪⎨⎪⎧x ≥1,y ≥x ,x -2y +3≥0,则x 2+y 2的最大值为( )A .17B .18C .20D .219.(2015·西安八校联考)已知变量x ,y 满足约束条件⎩⎪⎨⎪⎧x +2y ≥1,x -y ≤1,y -1≤0,若z =x -2y 的最大值与最小值分别为a ,b ,那么函数y =bx 2+ax 在区间[b ,a ]上的值域为( )A .[-30,-2]B.⎣⎢⎡⎦⎥⎤-30,112C.⎣⎢⎡⎦⎥⎤-2,112D .[-3,1]10.(2015·枣庄模拟)已知实数x ,y 满足约束条件⎩⎪⎨⎪⎧x ≥0,4x +3y ≤4,y ≥0,则w =y +1x的最小值是( ) A .-2B .2C .-1D .111.(2015·北京朝阳区高三期末)在平面直角坐标系中,若关于x ,y 的不等式组⎩⎪⎨⎪⎧y ≥0,y ≤x ,y ≤k (x -1)表示一个三角形区域,则实数k 的取值范围是________.12.(2015·宝鸡市质检)若目标函数z =kx +y 在约束条件⎩⎪⎨⎪⎧2x -y ≤1,x +y ≥2,y -x ≤2表示的可行域内,不仅在点(1,1)处取得最小值,则实数k 的取值范围是________.13.(2015·三明模拟)若x ,y 满足约束条件⎩⎪⎨⎪⎧x +y -1≥0,y ≥2x -2,y ≤2,且z=kx +y 取得最小值时的点有无数个,则k =________.14.(2015·厦门市质检)点P (x ,y )在直线y =kx +2上,记T =|x |+|y |,若使T 取得最小值的点P 有无数个,则实数k 的取值是________.15.(2015·赤峰市测试)已知O (x ,y )为区域⎩⎪⎨⎪⎧y 2-x 2≤0,0≤x ≤a 内的任意一点,当该区域面积为4时,z =2x -y 的最大值为________.参考答案第六章 不等式考点19 不等式的性质、解法与基本不等式【两年高考真题演练】1.C [由题意1a +1b=1,∴a +b =(a +b )⎝ ⎛⎭⎪⎫1a +1b =2+b a +a b≥4,当且仅当a =b =2时,取等号.故选C.2.C [由1a +2b =ab ,知a >0,b >0,由于1a +2b ≥22ab,∴ab ≥22ab,∴ab ≥2 2.故选C.]3.C [∵f (x )为奇函数,∴f (-x )=-f (x ), 即2-x +12-x -a =-2x +12x -a,整理得(1-a )(2x +1)=0, ∴a =1,∴f (x )>3即为2x +12x -1>3,化简得(2x -2)(2x -1)<0,∴1<2x <2,∴0<x <1.]4.C [A ,B 选项易举反例,C 中若0<a 1<a 2, ∴a 3>a 2>a 1>0,∵a 1+a 3>2a 1a 3,又2a 2=a 1+a 3,∴2a 2>2a 1a 3,即a 2>a 1a 3成立.] 5.A [建立如图所示坐标系,则B ⎝ ⎛⎭⎪⎫1t ,0,C (0,t ),AB →=⎝ ⎛⎭⎪⎫1t,0,AC →=(0,t ),AP →=AB→|AB →|+4AC →|AC →|=t ⎝ ⎛⎭⎪⎫1t ,0+4t(0,t ) =(1,4),∴P (1,4),PB →·PC→ =⎝ ⎛⎭⎪⎫1t -1,-4·(-1,t -4) =17-⎝ ⎛⎭⎪⎫1t +4t ≤17-21t·4t =13,故选A.] 6.C [∵0<a <b ,∴a +b2>ab ,又∵f (x )=ln x 在(0,+∞)上为增函数,故f ⎝ ⎛⎭⎪⎫a +b 2>f (ab ),即q >p .又r =12(f (a )+f (b ))=12(ln a +ln b )=12ln a +12ln b =ln(ab )12 =f (ab )=p . 故p =r <q .选C.]7.B [作差比较,∵x <y <z ,a <b <c ,则(az +by +cx )-(ax +by +cz )=a (z -x )+c (x -z )=(a -c )(z -x )<0,∴az +by +cx <ax +by +cz ;(az +by +cx )-(ay +bz +cx )=a (z -y )+b (y -z )=(a -b )(z -y )<0,∴az +by +cx <ay +bz +cx ;(ay +bz +cx )-(ay +bx +cz )=b (z -x )+c (x -z )=(b -c )(z -x )<0,∴ay +bz +cx <ay +bx +cz ,∴az +by +cx 最小.故选B.]8.D [因为log 4(3a +4b )=log 2ab ,所以log 4(3a +4b )=log 4(ab ),即3a +4b =ab ,且⎩⎪⎨⎪⎧3a +4b >0,ab >0,即a >0,b >0,所以4a +3b =1(a >0,b >0),a +b =(a +b )⎝ ⎛⎭⎪⎫4a +3b =7+4b a +3ab ≥7+24b a ·3ab=7+43,当且仅当4b a =3ab时取等号,选择D.]9.C [设该容器的总造价为y 元,长方体的底面矩形的长为x m ,因为无盖长方体的容积为4m 3,高为1m ,所以长方体的底面矩形的宽为4xm ,依题意,得y =20×4+10⎝⎛⎭⎪⎫2x +2×4x =80+20⎝⎛⎭⎪⎫x +4x ≥80+20×2x ·4x =160(当且仅当x =4x,即x =2时取等号).所以该容器的最低总造价为160元.故选C.]10.4 [log 2a ·log 2(2b )=log 2a ·(1+log 2b )≤⎝⎛⎭⎪⎫log 2a +1+log 2b 22=⎝⎛⎭⎪⎫log 2ab +122=⎝ ⎛⎭⎪⎫log 28+122=4,当且仅当log 2a =1+log 2b ,即a =2b 时,等号成立,此时a =4,b =2.]11.-12 26-6 [因为f (x )=⎩⎪⎨⎪⎧x 2,x ≤1x +6x-6,x >1,∴f (-2)=(-2)2=4,∴f [f (-2)]=f (4)=-12.当x ≤1时,f (x )min =f (0)=0.当x >1时,f (x )=x +6x-6≥26-6,当且仅当x=6时“=”成立.∵26-6<0,∴f (x )的最小值为26-6.]12. 2 [由题意,得x ⊗y +(2y )⊗x =x 2-y 2xy +(2y )2-x 22yx =x 2+2y 22xy ≥2x 2·2y 22xy=2,当且仅当x =2y 时取等号.] 13.3 2 [∵a ,b >0,a +b =5,∴(a +1+b +3)2=a +b +4+2a +1b +3≤a +b +4+(a +1)2+(b +3)2=a +b +4+a +b +4=18,当且仅当a =72,b =32时,等号成立,则a +1+b +3≤32,即a +1+b +3最大值为3 2.]14.2918 [在梯形ABCD 中,AB =2,BC =1,∠ABC =60°,可得DC =1,AE →=AB →+λBC →,AF →=AD →+19λDC →,∴AE →·AF →=(AB →+λBC →)·(AD →+19λDC →)=AB →·AD →+AB →·19λDC →+λBC →·AD →+λBC →·19λDC →=2×1×cos60°+2×19λ+λ×1×cos60°+λ·19λ×cos120°=29λ+λ2+1718≥229λ·λ2+1718=2918,当且仅当29λ=λ2,即λ=23时,取得最小值为2918.] 【一年模拟试题精练】1.B [当x >y >0时,xy >1成立;而当x y>1时,可得x >y >0或x <y <0,故选B.]2.B [由题设得a <a -b <0,所以有1a -b <1a 成立,即1a -b >1a 不成立.]3.A [检验法:取a =2,b =1,排除B 和D ;另外,函数f (x )=x -1x是(0,+∞)上的增函数,但函数g (x )=x +1x在(0,1]上递减,在[1,+∞)上递增.所以,当a >b >0时,f (a )>f (b )必定成立.但g (a )>g (b )未必成立,这样,a -1a >b -1b⇔a +1b >b +1a,故选A.]4.D [x -2x 2-1<0⇔(x -1)(x +1)(x -2)<0⇔x <-1或1<x <2,故选D.]5.C [∵全集U ={x ∈R |-2≤x ≤2},A ={x ∈R |-2≤x ≤0}, ∴∁U A ={x ∈R |0<x ≤2},故选C.]6.D [g (x )=-12x -21-x =-⎝ ⎛⎭⎪⎫12x +21-x ·[x +(1-x )]=-⎝ ⎛⎭⎪⎫52+1-x 2x +2x 1-x ≤-92,所以M ≥-92,上确界为-92.] 7.B [不等式x 2-2ax +a >0对一切实数x ∈R 恒成立,则Δ=(-2a )2-4a <0,即a 2-a <0,解得0<a <1,所以不等式at 2+2t -3<1转化为t 2+2t -3>0, 解得t <-3或t >1,故选B.]8.C [因为ab >0,所以b a >0,a b >0,即b a +ab≥2b a ·ab=2(当且仅当a =b 时等号成立),所以选C.]9.D [函数f (x )=a x -1+3恒过点P (1,4), ∴m +4n -1=0,m +4n =1.∴1m +4n =⎝ ⎛⎭⎪⎫1m +4n (m +4n )=1+4n m +4mn+16≥25.]10.C [由x >0,y >0知4x 2+9y 2+3xy ≥2×(2x )×(3y )+3xy (当且仅当2x =3y 时等号成立),∴12xy +3xy ≤30,即xy ≤2,故选C.]11.B [设a =(1,0),b =(0,1),则c =(1,1), 代入c +t a +1tb =⎝⎛⎭⎪⎫1+t ,1+1t ,∴⎪⎪⎪⎪⎪⎪c +t a +1t b =(1+t )2+⎝⎛⎭⎪⎫1+1t 2=t 2+1t 2+2t +2t+2≥2 2.]12.A [由题意知在⎣⎢⎡⎦⎥⎤-14,14上y =f (x +a )的图象应在函数y =f (x )图象的下方,当a =0时,显然不合题意,当a >0时,作出y =f (x+a )和y =f (x )图象,由图象知不合题意,当a <0时作出y =f (x +a )和y =f (x )图象如图所示,由图象可知,要使f (x +a )<f (x )在⎣⎢⎡⎦⎥⎤-14,14上恒成立,只需f ⎝ ⎛⎭⎪⎫-14+a <f ⎝ ⎛⎭⎪⎫-14即可,则有-a ⎝ ⎛⎭⎪⎫-14+a 2-14+a <-a ⎝ ⎛⎭⎪⎫-142-14,整理得a 2-12a -1<0,即1-174<a <0.]13.-1 [1x<a 化为x (-ax +1)<0,它的解集是{x |a <x <0},知a <0,则由x (-ax +1)<0得1a <x <0,则a =1a,解得a =-1.]14.[1,2] [可判断k =0或k <0均不符合题意,故k >0.于是原不等式即为k ⎝ ⎛⎭⎪⎫x -k 2+2k (x -2)<0⇒⎝ ⎛⎭⎪⎫x -k 2+2k (x -2)<0,依题意应有1≤k 2+2k≤3且k >0,∴1≤k ≤2.]15.3 [∵2x -3=⎝ ⎛⎭⎪⎫12y=2-y ,∴x +y =3, 因此,1x +4y =13⎝ ⎛⎭⎪⎫1x +4y (x +y )=13⎣⎢⎡⎦⎥⎤1+y x +4x y +4≥13⎣⎢⎢⎡⎦⎥⎥⎤5+2y x ·4x y =3.]16.32 [正项等比数列{a n }的公比q =2, ∵存在两项a m ,a n ,使得a m a n =4a 1, ∴a 1·2m -1×a 1·2n -1=4a 1, ∵a 1≠0,∴2m +n -2=24,∴m +n =6.则1m +4n =16(m +n )⎝ ⎛⎭⎪⎫1m +4n =16⎝⎛⎭⎪⎫5+n m +4m n ≥16⎝⎛⎭⎪⎪⎫5+2n m ·4m n =32,当且仅当n =2m =4时取等号. ∴1m +4n 的最小值为32.]考点20 二元一次不等式(组)与简单的线性规划【两年高考真题演练】 1.C [作出约束条件对应的可行域,如图中阴影部分,作直线l :3x +y =0,平移直线l 可知,经过点A 时,z =3x +y 取得最大值,由⎩⎪⎨⎪⎧x -2=0,x +2y -8=0,得A (2,3), 故z max =3×2+3=9.选C.] 2.A [作出⎩⎪⎨⎪⎧x +y ≥1,y -x ≤1,x ≤1表示的平面区域如图:平移直线y =2x -z 知,过点M (0,1)时,z 最小=-1.故选A.]3.A [(x ,y )在线性约束条件下的可行域如图,∴z max =-2×1+1=-1.故选A.]4.D [设甲、乙的产量分别为x 吨,y 吨,由已知可得⎩⎪⎨⎪⎧3x +2y ≤12,x +2y ≤8,x ≥0,y ≥0,目标函数z =3x +4y ,线性约束条件表示的可行域如图阴影部分所示:可得目标函数在点A 处取到最大值.由⎩⎪⎨⎪⎧x +2y =8,3x +2y =12,得A (2,3).则z max =3×2+4×3=18(万元).] 5.A [xy =12×2xy ≤12⎝ ⎛⎭⎪⎫2x +y 22≤12⎝ ⎛⎭⎪⎫1022=252,当且仅当x =52,y =5时,等号成立,把x =52,y =5代入约束条件,满足.故xy 的最大值为252.] 6.B [不等式组表示的区域如图,则图中A 点纵坐标y A =1+m ,B 点纵坐标y B =2m +23, C 点横坐标x C =-2m ,∴S =S △ACD -S △BCD =12×(2+2m )×(1+m )-12×(2+2m )×2m +23=(m +1)23=43, ∴m +1=2或-2(舍),∴m =1.]7.C [由图形知A ⎝ ⎛⎭⎪⎫-23,23, B ⎝ ⎛⎭⎪⎫22m -1,2m 2m -1,O (0,0).只有在B 点处取最大值2, ∴2=42m -1-2m 2m -1.∴m =1.] 8.C [平面区域Ω为如图所示的阴影部分的△ABD ,因圆心C (a ,b )∈Ω,且圆C 与x 轴相切,所以圆心C 在如图所示的线段MN 上,线段MN 的方程为y =1(-2≤x ≤6),由图形得,当圆心C 在点N (6,1)处时,a 2+b 2取得最大值62+12=37,故选C.]9.C [在约束条件⎩⎪⎨⎪⎧x ≥0,y ≥0,x +y ≤1下,S =2x +y 的最大值应在点(1,0)处取得,即S max =2×1+0=2,显然2>1,故选C.]10.4 [x ,y 满足条件的可行域如图所示的阴影部分,当z =3x +y 过A (1,1)时有最大值,z =4.]11.8[画出约束条件⎩⎪⎨⎪⎧x +y -5≤0,2x -y -1≥0,x -2y +1≤0表示的可行域,为如图所示的阴影三角形ABC .作直线l 0:2x +y =0,平移l 0到过点A 的直线l 时,可使直线z =x+y 在y 轴上的截距最大,即z 最大,解⎩⎪⎨⎪⎧x +y -5=0,x -2y +1=0得⎩⎪⎨⎪⎧x =3,y =2即A (3,2), 故z 最大=2×3+2=8.] 12.7 [z =2x +3y ,化为y =-23x +13z ,当直线y =-23x +z 3在点A (2,1)处时,z 取最大值,z =2×2+3=7.]13.15 [因为实数x ,y 满足x 2+y 2≤1,则2x +y -4<0,6-x -3y >0,所以|2x +y -4|+|6-x -3y |=4-2x -y +6-x -3y =-3x -4y +10.令z =-3x -4y +10,则3x +4y -10+z =0.当直线3x+4y -10+z =0与圆x 2+y 2=1相切时,z 取最值,故|z -10|5=1,∴z =5或z =15,∴|2x +y -4|+|6-x -3y |的最大值为15.]【一年模拟试题精练】1.B [该线性约束条件所表示平面区域如下图所示,该区域为边长为2的正方形,故其面积为(2)2=2.]2.A [由已知得⎩⎪⎨⎪⎧x +y >1-x -y ,x +(1-x -y )>y ,y +(1-x -y )>x ,即⎩⎪⎨⎪⎧x +y>12,y <12,x <12.]3.A [该约束条件表示的平面区域如图所示,故12·(3-k )·⎝ ⎛⎭⎪⎫4k +1-1=1,得k =1,k =7(舍去).] 4.D [作出可行域如图,由z =2x +y ,得y =-2x +z ,平移直线y =-2x +z ,由图象可知,当直线y =-2x +z 经过点E 时,直线的截距最大,此时z 最大.由⎩⎪⎨⎪⎧x +y =1,y =-1得⎩⎪⎨⎪⎧x =2,y =-1,即E (2,-1),代入得z =2×2-1=3.]5.B [由z =2x -3y 得y =23x -z 3, 作出不等式组对应的平面区域如图(阴影部分包括边界);平移直线y =23x -z 3,由图象可知当直线y =23x -z 3,过点C 时,直线y =23x -z 3截距最大,此时z 最小, 由⎩⎪⎨⎪⎧x =3,x -y +1=0,解得⎩⎪⎨⎪⎧x =3,y =4,即C (3,4). 代入目标函数z =2x -3y ,得z =2×3-3×4=6-12=-6.∴目标函数z =2x -3y 的最小值是-6.故选B.]6.C [平行四边形的对角线互相平分,如图,当以AC 为对角线时,由中点坐标公式得AC 的中点为⎝ ⎛⎭⎪⎫32,0,也是BD 的中点,可知顶点D 1的坐标为(0,-4).同理,当以BC 为对角线时,得D 2的坐标为(8,0),当以AB 为对角线时,得D 3的坐标为(-2,8),由此作出(x ,y )所在的平面区域,如图阴影部分所示,由图可知当目标函数z =2x -5y 经过点D 1(0,-4)时,取得最大值,最大值为2×0-5×(-4)=20.]7.C [作出不等式组表示的区域如图阴影部分所示,由图可知,z =ax +by (a >0,b >0)过点A (1,1)时取最大值,所以a +b =4.]8.B [依题意,在坐标平面内画出题中的不等式组表示的平面区域.注意到x 2+y 2可视为该平面区域内的点(x ,y )与原点间的距离的平方,结合图形可知,在该平面区域内所有的点中,与原点间的距离最远的点是(3,3),因此x 2+y 2的最大值等于32+32=18.]9.B [根据可行域的图形可知目标函数z =x -2y 在点(1,0)处取得最大值1,即a =1,在点(-1,1)处取得最小值-3,即b =-3,则y =-3x 2+x =-3⎝ ⎛⎭⎪⎫x -162+112,x ∈[-3,1],∴y min =-30,y max =112,故选B.]10.D [该线性约束条件表示平面区域如图所示,w =y +1x表示(x ,y )和(0,-1)两点的斜率,故w min =k AB =0-(-1)1-0=1.]11.(-∞,0) [该约束条件所表示平面区域如图所示,要使该区域为三角形,需k <0.]12.(-2,1) [该约束条件表示平面区域如图所示:由题意可得:k CD <-k <k AB ,即-1<-k <2,得k ∈(-2,1).]13.-2或1 [该线性约束条件表示平面区域如图所示,由题意可得-k =k AB =2或-k =k AC =-1,即k =-2或1.] 14.±1 [y =kx +2恒过(0,2),T =|x |+|y |表示由A (0,-T ),B (T ,0),C (0,T ),D (-T ,0)构成的图形,k CD =1,k BC =-1,由题意可得T =2,k =±1.]15.6 [由⎩⎪⎨⎪⎧y 2-x 2≤0,0≤x ≤a 作出可行域,如图,由图可得A(a,-a),B(a,a),由S△OAB=12×2a×a=4得a=2,∴A(2,-2),化目标函数为y=2x-z,∴当y=2x-z过A点时,z最大,z max=2×2-(-2)=6.]。
高考数学一轮复习 第6章 不等式、推理与证明 第2节 基本不等式课件 文
时取等号,即当 f(x)取得最小值时,即 a=3,选 C.
12/11/2021
(2)由 x>0,得x2+3xx+1=x+11x+3≤2 x1·1x+3=15,当且仅当
x=1 时,等号成立.则 a≥15,故选 A.
(3)∵正实数 x,y 满足 2x+y=2,
则2x+1y=12(2x+y)2x+1y=125+2xy+2yx≥125+2× 当且仅当 x=y=23时取等号.
)
(3)x>0,y>0 是xy+xy≥2 的充要条件.
()
(4)若 a>0,则 a3+a12的最小值为 2 a.
()
[答案] (1)× (2)× (3)× (4)×
12/11/2021
答案
2.(教材改编)设 x>0,y>0,且 x+y=18,则 xy 的最大值为( )
A.80
B.77
C.81
D.82
[常用结论] 重要不等式链
若 a≥b>0,则 a≥
a2+2 b2≥a+2 b≥ ab≥a2+abb≥b.
12/11/2021
[基础自测]
1.(思考辨析)判断下列结论的正误.(正确的打“√”,错误的
打“×”)
(1)函数 y=x+1x的最小值是 2.
()
(2)函数 f(x)=cos x+co4s x,x∈0,π2的最小值等于 4. (
12/11/2021
解析答案
5.若实数 x,y 满足 xy=1,则 x2+2y2 的最小值为________.
2 2 [由 xy=1 得 x2+2y2≥2 2x2y2=2 2. 当且仅当 x2=2y2 时等号成立.]
12/11/2021
解析答案
课堂 题型全突破
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学第六章-不等式考试内容:不等式.不等式的基本性质.不等式的证明.不等式的解法.含绝对值的不等式. 考试要求:(1)理解不等式的性质及其证明.(2)掌握两个(不扩展到三个)正数的算术平均数不小于它们的几何平均数的定理,并会简单的应用.(3)掌握分析法、综合法、比较法证明简单的不等式. (4)掌握简单不等式的解法.(5)理解不等式│a │-│b │≤│a+b │≤│a │+│b │§06. 不 等 式 知识要点1. 不等式的基本概念(1) 不等(等)号的定义:.0;0;0b a b a b a b a b a b a <⇔<-=⇔=->⇔>- (2) 不等式的分类:绝对不等式;条件不等式;矛盾不等式. (3) 同向不等式与异向不等式. (4) 同解不等式与不等式的同解变形. 2.不等式的基本性质 (1)a b b a <⇔>(对称性) (2)c a c b b a >⇒>>,(传递性) (3)c b c a b a +>+⇒>(加法单调性)(4)d b c a d c b a +>+⇒>>,(同向不等式相加) (5)d b c a d c b a ->-⇒<>,(异向不等式相减) (6)bc ac c b a >⇒>>0,.(7)bc ac c b a <⇒<>0,(乘法单调性)(8)bd ac d c b a >⇒>>>>0,0(同向不等式相乘)(9)0,0a b a b c d c d>><<⇒>(异向不等式相除) 11(10),0a b ab a b>>⇒<(倒数关系) (11))1,(0>∈>⇒>>n Z n b a b a n n 且(平方法则)(12))1,(0>∈>⇒>>n Z n b a b a n n 且(开方法则) 3.几个重要不等式 (1)0,0||,2≥≥∈a a R a 则若(2))2||2(2,2222ab ab b a ab b a R b a ≥≥+≥+∈+或则、若(当仅当a=b 时取等号) (3)如果a ,b 都是正数,那么.2a b ab +≤(当仅当a=b 时取等号)极值定理:若,,,,x y R x y S xy P +∈+==则: ○1如果P 是定值, 那么当x=y 时,S 的值最小; ○2如果S 是定值, 那么当x =y 时,P 的值最大. 利用极值定理求最值的必要条件: 一正、二定、三相等.3,3a b c a b c R abc +++∈≥(4)若、、则(当仅当a=b=c 时取等号) 0,2b aab a b>+≥(5)若则(当仅当a=b 时取等号)2222(6)0||;||a x a x a x a x a x a x a a x a >>⇔>⇔<-><⇔<⇔-<<时,或(7)||||||||||||,b a b a b a R b a +≤±≤-∈则、若 4.几个著名不等式(1)平均不等式: 如果a ,b 都是正数,那么222.1122a ba b ab a b ++≤≤≤+(当仅当a=b 时取等号)即:平方平均≥算术平均≥几何平均≥调和平均(a 、b 为正数):特别地,222()22a b a b ab ++≤≤(当a = b 时,222()22a b a b ab ++==)),,,(332222时取等c b a R c b a c b a c b a ==∈⎪⎭⎫ ⎝⎛+++≥++ ⇒幂平均不等式:22122221)...(1...n n a a a na a a +++≥+++ 注:例如:22222()()()ac bd a b c d +≤++.常用不等式的放缩法:①21111111(2)1(1)(1)1n n n n n n n n n n-==-≥++--②11111(1)121n n n n n n n nn n +-==--≥+++-(2)柯西不等式: 时取等号当且仅当(则若nn n n n n n n b a b a b ab a b b b b a a a a b a b a b a b a R b b b b R a a a a ====+++++++≤++++∈∈ 332211223222122322212332211321321))(();,,,,,,,,(3)琴生不等式(特例)与凸函数、凹函数若定义在某区间上的函数f(x),对于定义域中任意两点1212,(),x x x x ≠有12121212()()()()()().2222x x f x f x x x f x f x f f ++++≤≥或则称f(x)为凸(或凹)函数. 5.不等式证明的几种常用方法比较法、综合法、分析法、换元法、反证法、放缩法、构造法.6.不等式的解法(1)整式不等式的解法(根轴法).步骤:正化,求根,标轴,穿线(偶重根打结),定解. 特例① 一元一次不等式ax >b 解的讨论;②一元二次不等式ax 2+bx +c >0(a ≠0)解的讨论.(2)分式不等式的解法:先移项通分标准化,则()()0()()0()()0;0()0()()f x g x f x f x f x g x g x g x g x ≥⎧>⇔>≥⇔⎨≠⎩(3)无理不等式:转化为有理不等式求解 ○1()0()()()0()()f x f x g x g x f x g x ⎧≥⎫⇒⎪⎬>⇔≥⎨⎭⎪>⎩定义域○2⎩⎨⎧<≥⎪⎩⎪⎨⎧>≥≥⇔>0)(0)()]([)(0)(0)()()(2x g x f x g x f x g x f x g x f 或 ○3⎪⎩⎪⎨⎧<≥≥⇔<2)]([)(0)(0)()()(x g x f x g x f x g x f (4).指数不等式:转化为代数不等式()()()()()(1)()();(01)()()(0,0)()lg lg f x g x f x g x f x a a a f x g x a a a f x g x a b a b f x a b>>⇔>><<⇔<>>>⇔⋅>(5)对数不等式:转化为代数不等式()0()0log ()log ()(1)()0;log ()log ()(01)()0()()()()a a a a f x f x f x g x a g x f x g x a g x f x g x f x g x >>⎧⎧⎪⎪>>⇔>><<⇔>⎨⎨⎪⎪><⎩⎩(6)含绝对值不等式○1应用分类讨论思想去绝对值; ○2应用数形思想; ○3应用化归思想等价转化⎩⎨⎧>-<>≤⇔>⎩⎨⎧<<->⇔<)()()()(0)()0)(),((0)()(|)(|)()()(0)()(|)(|x g x f x g x f x g x g x f x g x g x f x g x f x g x g x g x f 或或不同时为注:常用不等式的解法举例(x 为正数): ①231124(1)2(1)(1)()22327x x x x x -=⋅--≤=②2222232(1)(1)12423(1)()223279x x x y x x y y --=-⇒=≤=⇒≤类似于22sin cos sin (1sin )y x x x x ==-,③111||||||()2x x x x x x+=+≥与同号,故取等基础训练一、选择题:只有一项是符合题目要求的. 1.不等式(1+x )(1-|x |)>0的解集是 A .{x |0≤x <1} B .{x |x <0且x ≠-1} C .{x |-1<x <1}D .{x |x <1且x ≠-1}2.给出下列三个命题 ①若1->≥b a ,则bba a +≥+11 ②若正整数m 和n 满足n m ≤,则2)(n m n m ≤- ③其中假命题的个数为 A .0B .1C .2D .33.如果x ,y 是实数,那么“xy <0”是“|x -y |=|x |+|y |”的 A .充分条件但不是必要条件 B .必要条件但不是充分条件 C .充要条件D .非充分条件非必要条件4.若a =ln22,b =ln33,c =ln55,则 A .a <b <cB .c <b <aC .c <a <bD .b <a <c5.设10<<a ,函数)22(log )(2--=x xa a a x f ,则使0)(<x f 的x 的取值范围是A .(-∞,0)B .(0,+∞)C .(-∞,log a 3)D .(log a 3,+∞)6.二、填空题:.把答案填在横线上.7.对于-1<a <1,使不等式(12)2x ax +<(12)2x +a -1成立的x 的取值范围是_______ . 8. 9. 10三、解答题:解答应写出文字说明,证明过程或演算步骤. 1112.已知函数2()2sin sin 2,[0,2].f x x x x π=+∈求使()f x 为正值的x 的集合.13.⑴已知,a b 是正常数,a b ≠,,(0,)x y ∈+∞,求证:222()a b a b x y x y++≥+,指出等号成立的条件;⑵利用⑴的结论求函数29()12f x x x =+-(1(0,)2x ∈)的最小值,指出取最小值时x 的值.14.设函数f (x )=|x -m |-mx ,其中m 为常数且m <0.⑴解关于x 的不等式f (x )<0;⑵试探求f (x )存在最小值的充要条件,并求出相应的最小值.15.已知a >0,函数f (x )=ax -bx 2.⑴当b >0时,若对任意x ∈R 都有f (x )≤1,证明a ≤2b ;⑵当b >1时,证明对任意x ∈[0,1],都有|f (x )|≤1的充要条件是b -1≤a ≤2b ; ⑶当0<b ≤1时,讨论:对任意x ∈[0,1],都有|f (x )|≤1的充要条件.16。
