九年级数学北师大版PPT课件
合集下载
4.1.1成比例线段 课件(共16张PPT) 北师大版数学九年级上册
教师讲评
知识点2：成比例线段
四条线段a，b，c，d中，如果a与b的比等于c与d
的比，即
=
，那么这四条
线段a，b，c，d叫做成比例线段，简称比例线段.
四条线段a，b，c，d成比例，有顺序关系，即a，b，c，d是成比例线段，则比
例式为a:b=c:d;a,b,d,c是成比例线段,则比例式为a:b=d:c.
分别叫做这个线段比的前项和后项.如果把 表示成比值k，那么
（1）在 比或a:b中，a是比的前项，b是比的后项；
（2）两条线段的长度单位要统一；
（3）在同一单位下线段的比与选用的长度单位无关；
（4）线段的比是一个没有单位的正数.
= ，其中，线段AB，CD
=k，AB=k∙CD.
+
例 2: 若 − = ,则 : =. ________,
= __________.
例 3: 若
=
= = ,且 + + = ,则 + + 的值为
( B )
A.10
B.4
C.一4
D.一5
【题型三】解决实际问题
例4：已知同一时刻物高与影长成比例，现在有一棵很高的古树，
③成比例线段的基本性质是什么？
Fra bibliotek
（如果 = ，那么bc=ad；如果bc=ad（a，b，c，d都不为0），那么 = ）
1.教材习题：完成课本79页随堂 练习
2.作业本作业：完成对应练习
《相似三角形的性质》PPT课件 北师大版九年级数学
图1 （1） △ACD与△A′C′D′ 相似吗？为什么？如果相似，指出它们的相似比. （2） 如果CD =1.5 cm，那么模型房的房梁立柱有多高？
探究新知
图1
解：（1）△ACD与△A′C′D′ 相似. 理由是 A A，ADC ADC 90.
相似比是 1 : 2.
（2）由CD : C′D′ =1:2，得C′D′ = 2CD=3 cm，即模型房的房梁立柱高3 cm.
第四章 图形的相似
4.7 相似三角形的性质（第1课时）
回顾复习
还记得相似三角形的定义吗？还记得相似多边形的对应边、 对应角有什么关系吗？
相似三角形的对应边成比例、对应角相等.
在两个相似三角形中是否只有对应角相等、对应边成比例 这个性质呢？本节课我们将研究相似三角形的其他性质.
探究新知
如图1，小王依据图纸上的△ABC，以 1：2 的比例建造了模型房 的房梁△A′B′C′，CD 和 C′D′ 分别是它们的立柱.
C
比吗？
C'
A
B A'
B'
图1
由已知，得
C
∴ AB BC AC AB k.
AB BC AC AB
分别过点C与C′作△ABC和△A′B′C′的高CD，
C' A'
C′D′，如图2.
AD
B
D'
B'
∵定△理ABC∽△A′B′C′，
图2
∴相CC似DD 三 AA角BB 形（k周相长似三的角比形等对应于高相的似比等比于，相面似比积）比. 等于相似比的平方.
点 S 在 AB 边上，BC = 60 cm，AD = 40 cm，四边形 PQRS 是正方形.
（1）△ASR 与△ABC 相似吗？为什么？
探究新知
图1
解：（1）△ACD与△A′C′D′ 相似. 理由是 A A，ADC ADC 90.
相似比是 1 : 2.
（2）由CD : C′D′ =1:2，得C′D′ = 2CD=3 cm，即模型房的房梁立柱高3 cm.
第四章 图形的相似
4.7 相似三角形的性质（第1课时）
回顾复习
还记得相似三角形的定义吗？还记得相似多边形的对应边、 对应角有什么关系吗？
相似三角形的对应边成比例、对应角相等.
在两个相似三角形中是否只有对应角相等、对应边成比例 这个性质呢？本节课我们将研究相似三角形的其他性质.
探究新知
如图1，小王依据图纸上的△ABC，以 1：2 的比例建造了模型房 的房梁△A′B′C′，CD 和 C′D′ 分别是它们的立柱.
C
比吗？
C'
A
B A'
B'
图1
由已知，得
C
∴ AB BC AC AB k.
AB BC AC AB
分别过点C与C′作△ABC和△A′B′C′的高CD，
C' A'
C′D′，如图2.
AD
B
D'
B'
∵定△理ABC∽△A′B′C′，
图2
∴相CC似DD 三 AA角BB 形（k周相长似三的角比形等对应于高相的似比等比于，相面似比积）比. 等于相似比的平方.
点 S 在 AB 边上，BC = 60 cm，AD = 40 cm，四边形 PQRS 是正方形.
（1）△ASR 与△ABC 相似吗？为什么？
北师大版九年级数学下册《二次函数——二次函数的图象与性质》教学PPT课件(4篇)
5
这两种呢?有没有其他形式的二次
3
函数？
4Байду номын сангаас
2
1
–4
–3
–2
–1
O
–1
–2
–3
–4
–5
–6
–7
–8
–9
–10
1
2
3
4
x
y =－x2
新知讲解
在画有y
=x2直角坐标系中，画出
=
，y
=2x2的图象.
①列表； ②描点； ③连线.
10
y
y=2x2
9
x
··· －2 －1
y =x2
8
0
1
2
···
7
6
D．抛物线y＝－3x2向上平移1个单位得到
新知讲解
在同一坐标系中，画出二次函数 = − ,y=− + ，
y=−
− 的图象，并分别指出它们的开口方向，对称轴和顶
点坐标，指明抛物线y=− + 通过怎样的平移可得到抛物线
=
−
-4
− .
如图所示
关于y轴对称，对称轴方程是直线x＝0
顶点坐标是原点（0，0）
当x=0时，y最小值=0
当x=0时，y最大值=0
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
典例精析
已知二次函数y=x2.求：
（1）当x=5时，y的值；
（2）当y=4时，x的值；
（3）当x为何值时，y随x的增大而增大？
新北师大版九年级数学下册《三角函数的计算》优质ppt教学课件
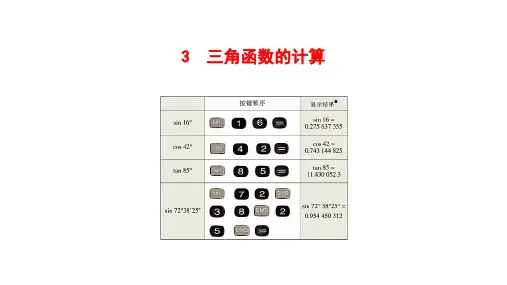
上表的显示结果是以“度”为单位的，再按 ˚ ′ ″ 键即可显示 以“度、分、秒”为单位的结果.
根据上述方法你能求出问题1中∠A的大小吗？
sin A = 1 = 0.25. 按键顺序和显示结果为
4
SHIFT sin 0 · 2 5 = 14.477 512 19°
再按 ° ′ ″ 键可显示14˚28′39″，所以∠A=14˚28′39″.
正弦值随着角度的增大（或减小）而增大（或减小）； 余弦值随着角度的增大（或减小）而减小（或增大）； 正切值随着角度的增大（或减小）而增大（或减小）.
知识点1 利用计算器求锐角三角函数值
1.如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器 求边AC的长,则下列按键顺序正确的是( D )
D 39°
E
45°
C
A
【解析】（1）由题意，AC＝AB＝610 米.
（2）DE＝AC＝610米，
在Rt△BDE中，tan∠BDE＝ BE ，
DE
故BE＝DEtan39°． 因为CD＝AE，
所以CD＝AB－DE·tan 39°
＝610－610×tan 39°≈116（米）. 答：大楼的高度CD约为116 米．
B．sin65°54′-sin35°54′=sin30°
C．2sin15°30′=sin31°
D．sin72°18′-sin12°18′=sin47°42′
•2. 已知sin α＝1 ，求α，若用科学计算器计算且结果以“度、分、秒
2
”为单位，最后按键(D )
•A．AC/ON
B. SHIFT
C．MODE
(4)sin18°＋cos55°－tan59°≈－0.7817.
7 切线长定理 课件 初中数学北师大版九年级下册
.
5.如图所示,四边形ABCD的各边都与圆相切,它的周长为18,若AB=6,
则CD的长为 3 .
6.如图所示,PA,PB分别与☉O相切于点A,B,AC为弦,BC为☉O的直径,
若∠P=60°,PB=2 cm.
(1)求证:△PAB是等边三角形;
(1)证明:∵PA,PB分别与☉O相切于点A,B,
∴PA=PB.
∴CD=CF= (AC+BC-AB)= ×(12+9-15)=3(cm).
∴OD=CD=3 cm.
∴☉O 的半径为 3 cm.
+-
++
(1)设直角三角形内切圆的半径为 R,则 R=
为直角边长,c 为斜边长);
(2)圆外切四边形的两组对边的和相等.
或 R=
(其中 a,b
新知应用
1.如图所示,△ABC的内切圆☉O分别与AB,AC,BC相切于点D,E,F.若
∠C=90°,AC=6,BC=8,则☉O的半径为 2
.
2.如图所示,在菱形ABCD中,∠B=60°,AB=4,☉O内切于菱形ABCD,则
☉O的半径为 .
1.如图所示,P为☉O外一点,PA,PB分别切☉O于点A,B,CD切☉O于点E,
(cm).
则BD的长是(
A.4
B.3
C
C.2
)
D.1
2.如图所示,P 是☉O 外一点,PA,PB 分别和☉O 相切于 A,B 两点,C 是
上任意一点,过点 C 作☉O 的切线分别交 PA,PB 于点 D,E.连接
CA,CB.
(1)若△PDE 的周长为 10,则 PA 的长为
(2)若∠P=50°,则∠BCA 的度数为
5.如图所示,四边形ABCD的各边都与圆相切,它的周长为18,若AB=6,
则CD的长为 3 .
6.如图所示,PA,PB分别与☉O相切于点A,B,AC为弦,BC为☉O的直径,
若∠P=60°,PB=2 cm.
(1)求证:△PAB是等边三角形;
(1)证明:∵PA,PB分别与☉O相切于点A,B,
∴PA=PB.
∴CD=CF= (AC+BC-AB)= ×(12+9-15)=3(cm).
∴OD=CD=3 cm.
∴☉O 的半径为 3 cm.
+-
++
(1)设直角三角形内切圆的半径为 R,则 R=
为直角边长,c 为斜边长);
(2)圆外切四边形的两组对边的和相等.
或 R=
(其中 a,b
新知应用
1.如图所示,△ABC的内切圆☉O分别与AB,AC,BC相切于点D,E,F.若
∠C=90°,AC=6,BC=8,则☉O的半径为 2
.
2.如图所示,在菱形ABCD中,∠B=60°,AB=4,☉O内切于菱形ABCD,则
☉O的半径为 .
1.如图所示,P为☉O外一点,PA,PB分别切☉O于点A,B,CD切☉O于点E,
(cm).
则BD的长是(
A.4
B.3
C
C.2
)
D.1
2.如图所示,P 是☉O 外一点,PA,PB 分别和☉O 相切于 A,B 两点,C 是
上任意一点,过点 C 作☉O 的切线分别交 PA,PB 于点 D,E.连接
CA,CB.
(1)若△PDE 的周长为 10,则 PA 的长为
(2)若∠P=50°,则∠BCA 的度数为
北师大版九年级数学下册《二次函数——确定二次函数的表达式》教学PPT课件(4篇)
y=ax2+bx+c,把（－3，0），（－1，0），
1.设：
（表达式）
（0，－3）代入y=ax2+bx+c得
2.代：
a=－1，
9a
－
3b+c=0，
（坐标代入）
a－b+c=0， 解得 b=－4，
3.解：
c=－3，
c=－3.
方程（组）
4.还原：
∴所求的二次函数的表达式是
（写表达式）
y=－x2－4x－3.
第二章 二次函数
3 确定二次函数的表达式
CONTENTS
目
录
1
学习目标
2
新课导入
3
新课讲解
4
课堂小结
5
当堂小练
6
拓展与延伸
学习目标
1.用一般式(三点式)确定二次函数表达式
2.用顶点式确定二次函数表达式
3.用交点式确定二次函数表达式（重点、难点）
新课导入
1. 一次函数的表达式是什么?如何求出它的表达式?
2
(2)△ABC的面积是6.
O
B
A
C
x
随堂即练
6.已知一条抛物线经过E（0，10），F（2，2），G
（4，2），H（3，1）四点，选择其中两点用待定系
a b c 6
9a 3b c 0
c 3
解这个方程组，得a= 0.5，b= – 2.5，c=3
∴所求得的函数解析式为y=0.5x²– 2.5x+3
当堂小练
已知：二次函数的图像的对称轴为直线x= –3，并且函数有最
大值为5，图像经过点(–1,–3)，求这个函数的解析式。
1.设：
（表达式）
（0，－3）代入y=ax2+bx+c得
2.代：
a=－1，
9a
－
3b+c=0，
（坐标代入）
a－b+c=0， 解得 b=－4，
3.解：
c=－3，
c=－3.
方程（组）
4.还原：
∴所求的二次函数的表达式是
（写表达式）
y=－x2－4x－3.
第二章 二次函数
3 确定二次函数的表达式
CONTENTS
目
录
1
学习目标
2
新课导入
3
新课讲解
4
课堂小结
5
当堂小练
6
拓展与延伸
学习目标
1.用一般式(三点式)确定二次函数表达式
2.用顶点式确定二次函数表达式
3.用交点式确定二次函数表达式（重点、难点）
新课导入
1. 一次函数的表达式是什么?如何求出它的表达式?
2
(2)△ABC的面积是6.
O
B
A
C
x
随堂即练
6.已知一条抛物线经过E（0，10），F（2，2），G
（4，2），H（3，1）四点，选择其中两点用待定系
a b c 6
9a 3b c 0
c 3
解这个方程组，得a= 0.5，b= – 2.5，c=3
∴所求得的函数解析式为y=0.5x²– 2.5x+3
当堂小练
已知：二次函数的图像的对称轴为直线x= –3，并且函数有最
大值为5，图像经过点(–1,–3)，求这个函数的解析式。
北师大版初中九年级数学上册-《三角形的垂心》课件
请你说明CD为什么是AB的垂直平分线, 并与同伴进行交流.
老师提示:
因为直线CD与线段AB的交点就是AB的中 点,所以我们也用这种方法作线段的中点.
驶向胜利 的彼岸
回顾 思考
线段的垂直平分
线的性质
定理 线段垂直平分线上的点到这条线段两个端点
距离相等. 如图,
M P
∵AC=BC,MN⊥AB,P是MN上任
驶向胜利 的彼岸
做一做 1
几何的三种语言
定理:三角形三条边的垂直平分线相交于一点,并且 这一点到三个顶点的距离相等.
如图,在△ABC中, ∵c,a,b分别是AB,BC,AC的垂直 c
aA b
平分线(已知),
∴c,a,b相交于一点P,且
B
PA=PB=PC(三角形三条边的垂直
P C
平分线相交于一点,并且这一点
九年级数学（上册）第一章 证明(二)
3.线段的垂直平分线（2） 三角形的垂心
回顾 思考
线段的垂直平分线
用尺规作线段的垂直平分线.
的作法 C
已知:线段AB,如图.
求作:线段AB的垂直平分线.
作法:
A
B
1.分别以点A和B为圆心,以大于 AB/2长为半径作弧,两弧交于点C和D.
2. 作直线CD.
D
则直线CD就是线段AB的垂直平分线.
第三条直线上即可.这时可以考虑前面刚刚学到的A逆定理.
如图,在△ABC中,设AB,BC的垂直平
分线相交于点P,连接AP,BP,CP.
∵点P在线段AB的垂直平分线上,
∴PA=PB (或AB的中点,). 同理,PB=PC.
B
∴PA=PC.
P C
∴点P在线段AB的垂直平分线上, ∴AB,BC,AC的垂直平分线相交于一点. 想一想:若作出∠P的角平分线,结论是否也 可以得征?
北师大版九年级数学下册《圆——圆周角和圆心角的关系》教学PPT课件(6篇)
D
O2
O1
E
B
F
新知探究
【跟踪训练】
1.圆内接四边形ABCD中，∠A, ∠B, ∠C的度数之比是
135°
1：2：3，则这个四边形最大角的度数是_________.
D
A
2.四边形ABCD内接于圆，AD∥BC，AB+CD=AD+BC ,
25
若AD=4，BC=6，则四边形ABCD的面积为_______.
A
A
O
O
BB
C
C
课堂小测
3. 如图，点B，C在⊙O上，且BO=BC，则圆周角∠BAC等于（ D ）
A
A.60°
B.50°
C.40°
D.30°
O
B
C
课堂小测
4 . 如图，已知BD是⊙O的直径，⊙O的弦AC⊥BD于点E.若
∠AOD=60°，则∠DBC的度数为（ A）
A.30°
B.40°
C.50°
B
D.60°
D
C
OC垂直平分AD
(1)OC与AD的位置关系是__________________;
A
平行
(2)OC与BD的位置关系是___________;
4
(3)若OC=2cm,则BD=______cm.
O1
O
B
新知探究
4.如图,△ABC的顶点均在⊙O上, AB=4, ∠C=30°,求⊙O的直径.
解：连接AO并延长交⊙O于点E，
3 . 当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC与圆
心角∠AOC的大小关系会怎样?
提示:能否也转化为1的情况?
A
C
过点B作直径BD.由1可得: