与矩形波导类似
微波技术第3章1矩形波导

可见前五个导模是 TE10、TE20、TE01、 TE11、TM11。
35
则TE10模 TE20模 TE01模 TE11和TM11模 TE21和TM21模 TE12和TM12模
• 当f0 = 10GHz时,λc=3cm
fcTE10=6.562GHz fcTE20=13.123GHz fcTE01=14.764GHz fcTE11=16.156GHz fcTE21=19.753GHz fcTE12=30.248GHz
传播。
编辑ppt
13
TE20模场结构
TE10 TE20
编辑ppt
14
(2)TE01模与TE0n模
其场分量为
Ex
j n
b H mn sin n b y e
jz
Hy
j n
b
ny
H mn sin b e
jz
Hz
ny H mn cos b e
jz
Ey Ez H x 0
TE01模只有Ex、Hy和Hz三个场分量,它们与x无关,故 沿a边场无变化;
波分布或TM11模场;如 图。
注:TE11与TM11是简并模,这种简并称为模式简并; 同理,TEmn与TMmn (m>0, n>0) 是简并模。
编辑ppt
19
3.管壁电流 Js nˆHtan
主模:TE10模工作下
波导底面 y = 0 ; nˆ yˆ
JSy 0 y ˆ [x ˆHx zˆHz] x ˆHz zˆHx
ZTM
Eu Hv
2
1
k
c
编辑ppt
31
(5)TE10模矩形波导的传输功 率
P Re 1 E H * ds 2S
圆波导与矩形波导比较
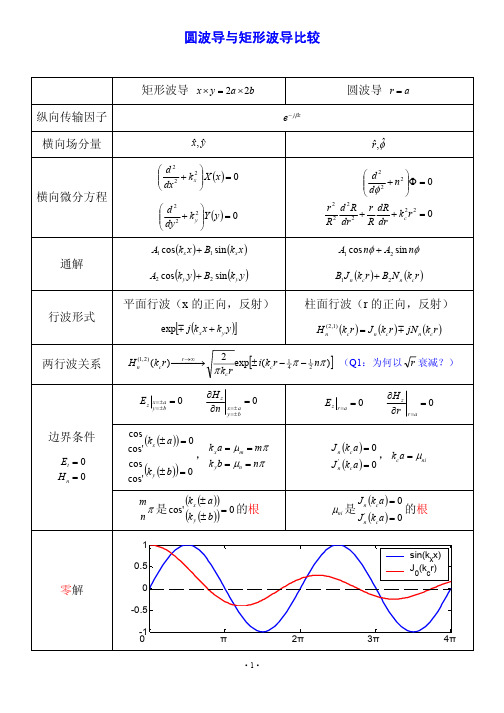
B1 J n (kc r ) + B2 N n (kc r )
平面行波(x 的正向,反射) 行波形式
exp m j (k x x + k y y )
→∞ (1, 2 ) Hn (kc r ) r →
柱面行波(r 的正向,反射)
( 2 ,1) (kc r ) = J n (kc r ) m jN n (kc r ) Hn
驻波波节数: 从中心到边界 的半驻波数
0 0 π 2π 3π 0.5
|sin(kxx)| |J0(kcr)|
4π
相邻波节反相,柱面波周向周期变化 各自周期相等 边界处的函数值取其中一零解上,不同的零点,包含波节数不同 驻波异同 零解从 = 0 开始 等幅驻波 两驻波关系 坐标系/驻波函数的不同仅方便满足边界条件时,函数形式简单 *柱面波的求解方法 3 级数、积分、插值,高阶递推
[
]
两行波关系
2 1 ] (Q1:为何以 r 衰减?) exp[± i(kc r − 1 4 π − 2 nπ ) π kc r
Ez
x=± a y =±b
=0
∂H z ∂n
x=± a y =±b
=0
Ez
r =a
=0
∂H z ∂r
=0
r =a
边界条件
Et = 0 Hn = 0
cos (k x (± a )) = 0 k a = µ m = mπ cos' , x k y b = µ n = nπ cos ( k y (± b )) = 0 cos'
0 -0.5 -1 0 π
·1·
2π
3π
4π
满足边界条件 后的驻波解
cos mπ A cos' a
微波技术基础试题三

一.简答:(50分)1.什么是色散波和非色散波?(5分)答:有的波型如TE波和TM波,当波导的形状、尺寸和所填充的介质给定时,对于传输某一波形的电磁波而言,其相速v p和群速v g都随频率而变化的,把具有这种特性的波型称为色散波。
而TEM波的相速v p和群速v g 与频率无关,把具有这种特性的波型称为非色散波。
2.矩形波导、圆波导和同轴线分别传输的是什么类型的波?(5分)答:(1)矩形波导为单导体的金属管,根据边界条件波导中不可能传输TEM 波,只能传输TE波和TM波。
(2)圆波导是横截面为圆形的空心金属管,其电磁波传输特性类似于矩形波导不可能传输TEM波,只能传输TE波和TM波。
(3)同轴线是一种双导体传输线。
它既可传输TEM波,也可传输TE 波和TM波。
3.什么是TE波、TM波和TEM波?(5分)答:根据导波系统中电磁波按纵向场分量的有无,可分为三种波型: (1)横磁波(TM 波),又称电波(E 波):0=H Z ,0≠E Z ; (2)横电波(TE 波),又称磁波(H 波):0=E Z ,0≠H Z ;(3)横电磁波(TEM ):0=E Z ,0=H Z 。
4.导波系统中的相速和相波长的含义是什么?(5分)答:相速v p 是指导波系统中传输电磁波的等相位面沿轴向移动的速度。
相波长λp 是指等相位面在一个周期T 移动的距离。
5.为什么多节阶梯阻抗变换器比单节阻抗变换器的工作频带要宽?(5分) 答:以两节阶梯阻抗变换器为例,设每节4λ阻抗变换器长度为θ,三个阶梯突变的电压反射系数分别为ΓΓΓ21,,则点反射系数为eeUU j j ir θθ42210--ΓΓΓ++==Γ,式中说明,当采用单节变换器时只有两个阶梯突变面,反射系数Γ的表达式中只有前两项,若取ΓΓ=10,在中心频率处,2/πθ=这两项的和为零,即两突变面处的反射波在输入端相互抵消,从而获得匹配;但偏离中心频率时,因2/πθ≠,则两个反射波不能完全抵消。
波导中微波的模式

波导中微波的模式波导是一种用来传输微波信号的导波结构,由金属壁面构成,中间空腔内充满介质。
在波导中,微波信号通过内部的反射而传播,产生各种模式。
不同模式具有不同的传播特性和分布特点,对于波导设计和应用都非常重要。
本文将介绍波导中常见的几种微波模式。
1.矩形波导模式:矩形波导是最常见的一种波导类型,由金属矩形管道组成。
在矩形波导中,有许多不同的模式,包括正交模式(TE模式)和纵向模式(TM模式)。
(1)TE模式:TE模式是横向电场模式,在矩形波导中,电场垂直于波导的横截面方向。
TE模式的特点是不含有磁场分量,只有电场分量。
TE模式分为TE10,TE20,TE01等不同的阶次。
(2)TM模式:TM模式是纵向磁场模式,在矩形波导中,磁场沿波导的横截面方向。
TM模式的特点是不含有电场分量,只有磁场分量。
TM模式也分为TM10,TM20,TM01等不同的阶次。
矩形波导模式的分布特点是波束在波导内壁上反射,形成驻波模式。
TE和TM模式可以共存,交替出现。
2.圆形波导模式:圆形波导是由金属圆管构成的波导结构。
圆形波导模式与矩形波导模式类似,也有TE模式和TM模式,但其阶次的确定方式略有不同。
(1)TE模式:TE模式是横向电场模式,电场沿着圆柱壁面方向。
TE 模式中的波动电场与壁面垂直,并且没有磁场分量。
(2)TM模式:TM模式是纵向磁场模式,磁场沿着圆柱壁面方向。
TM 模式中的波动磁场与壁面垂直,并且没有电场分量。
与矩形波导不同的是,圆形波导模式的阶次由径向模式数目(m)和角向模式数目(n)两个参数共同确定。
例如,TE11模式表示径向和角向模式都为13.表面波模式:除了矩形和圆形波导模式外,波导中还存在一种特殊的模式,称为表面波模式。
表面波模式是指波在波导壁面上沿着壁面传播的模式,不进一步传播到波导的深处。
表面波模式包括射线波、栅波和电磁波导模式。
射线波模式是指波束沿着表面传播,而不发散或收敛;栅波模式是指波束被壁面上的栅格结构所限制;电磁波导模式是指在电磁波导中,电磁波束是由电和磁场的耦合形成的。
声学波导管

声学波导管食不厌精 脍不厌细1、恒定截面波导内的声传播1.1、矩形波导管1.2 、圆柱形波导管设有一半径为a 的圆柱形管,一端延伸到无限远。
圆柱形管的声波方程应以柱坐标系来描述。
设管的径向坐标为r ,极角为θ,管轴用z 来表示。
直角坐标与柱坐标之间有如下关系⎪⎩⎪⎨⎧===z z r y r x θθsin cos 而柱坐标系的拉普拉斯算符可表示为2222221)(1zr r r r r ∂∂+∂∂+∂∂∂∂=∇θ (1-2-1) 于是三维声波动方程就可变换为:2222222211)(1t p c z p p r r p r r r ∂∂=∂∂+∂∂+∂∂∂∂θ (1-2-2) 根据分离变量法,令解,)()()(),,,(t j e z Z r R t z r p ωθθΘ=将其代入(1-2-2)式可得如下三个常微分方程⎪⎪⎪⎩⎪⎪⎪⎨⎧=-++=Θ+Θ=+0)(10022222222222R r m k dr dR r drR d m d d Z k dz Zd r z θ (1-2-3) 其中.22222r z k k ck +==ω (1-2-4)由于圆柱管道向无限远处延伸,对于Z 的方程可取行波解:;)(z jk z z e A z Z -= (1-2-5)对于Θ的方程可取解为),cos()(m m A ϕθθθ+=Θ (1-2-6) 因为)2()(πθθ+Θ=Θ的关系应该满足,所以式中m 一定要为正整数。
对于R 的方程我们作一适当变换,令x r k r =,则方程就化为0)1(12222=-++R xm dx dR x dx R d . (1-2-7) 这是一个标准的m 解贝塞尔方程,其一般解可表示为),()()(r k N B r k J A r k R r m r r m r r += (1-2-8) 这里)(r k J r m 与)(r k N r m 分别代表宗量为)(r k r 的m 阶柱贝塞尔函数与柱诺伊曼函数。
矩形波导的模式(3篇)

第1篇一、矩形波导的模式分类矩形波导中的电磁波模式主要分为TE(横电磁波)模式和TM(纵电磁波)模式。
1. TE模式TE模式是指电场只在波导的横向(垂直于传播方向)分量存在,而磁场则在纵向(沿传播方向)分量存在。
根据电场和磁场在波导横截面上的分布,TE模式又可以分为TE10、TE20、TE01等模式。
(1)TE10模式:TE10模式是矩形波导中最基本、最常用的模式。
其电场分布呈矩形,磁场分布呈椭圆。
TE10模式的截止频率最高,适用于高频传输。
(2)TE20模式:TE20模式的电场分布呈矩形,磁场分布呈圆形。
其截止频率低于TE10模式,适用于中频传输。
(3)TE01模式:TE01模式的电场分布呈矩形,磁场分布呈椭圆。
其截止频率最低,适用于低频传输。
2. TM模式TM模式是指磁场只在波导的横向分量存在,而电场则在纵向分量存在。
根据电场和磁场在波导横截面上的分布,TM模式又可以分为TM01、TM11、TM21等模式。
(1)TM01模式:TM01模式的电场分布呈矩形,磁场分布呈圆形。
其截止频率最高,适用于高频传输。
(2)TM11模式:TM11模式的电场分布呈矩形,磁场分布呈椭圆。
其截止频率低于TM01模式,适用于中频传输。
(3)TM21模式:TM21模式的电场分布呈矩形,磁场分布呈圆形。
其截止频率最低,适用于低频传输。
二、矩形波导的模式特性1. 截止频率截止频率是矩形波导中一个重要的参数,它决定了电磁波在波导中能否有效传输。
不同模式的截止频率不同,其中TE10模式的截止频率最高,适用于高频传输。
2. 相速度相速度是指电磁波在波导中传播的速度。
不同模式的相速度不同,TE模式的相速度比TM模式快。
3. 模式损耗模式损耗是指电磁波在波导中传播时,由于波导壁的吸收和辐射等原因,能量逐渐衰减的现象。
不同模式的损耗不同,TE模式的损耗比TM模式小。
4. 传输特性矩形波导中不同模式的传输特性不同,如TE模式的传输特性较好,适用于高频传输;TM模式的传输特性较差,适用于低频传输。
题库-微波技术与天线
微波技术与天线题库一、填空题1. 驻波比的取值范围为;当传输线上全反射时,反射系数为,此时驻波比ρ等于。
2. γ=α+jβ称为,其中α称为,它表示传输线上的波,β称为,它表示传输线上的波。
3. 特性阻抗50欧的均匀传输线终端接负载Z1为20j欧、50欧和20欧时,传输线上分别形10cm,如图所示:Z in=;Z in=;在z=5cm处的输入阻抗Z in=;2.5cm<z<5cm处,Z in呈性。
ρ=。
5. 无耗传输线的终端短路和开路时,阻抗分布曲线的主要区别是终端开路时在终端处等效为谐振电路,终端短路时在终端处等效为谐振电路。
6. 一段长度为l(0<l<λ/4)短路线和开路线的输入阻抗分别呈纯和纯。
7. 阻抗匹配分为阻抗匹配、阻抗匹配和阻抗匹配,它们反映Z0,根据各点在下图所示的阻抗圆( );( );⑤R<Z0,X=0 ( ); ⑥R=Z0,X=0 ( );⑦Г=0 ( ); ⑧SWR=1 ( );⑨=1Γ( ); ⑩ SWR=∞( ).9. 在导行波中, 截止波长λc最长的电磁波模称为该导波系统的主模。
矩形波导的主模为模, 因为该模式具有场结构简单、稳定、频带宽和损耗小等特点, 所以实用时几乎毫无例外地工作在该模式。
10. 与矩形波导一样,圆波导中也只能传输TE波和TM波;模是圆波导的主模,模是圆波导第一个高次模,而模的损耗最低,这三种模式是常用的模式。
11. 在直角坐标系中,TEM波的分量E z和H z为零;TE波的分量为零;TM波的分量为零。
12. 低频电路是参数电路,采用分析方法,微波电路是参数电路,采用分析方法。
13. 简并模式的特点就是具有相同的和不同的。
14. 微带线的弯区段、宽度上的阶变或接头的不连续性可能会导致电路性能的恶化,主要是因为这种不连续性会引入。
15. 写出下列微波元件的名称。
(a) (b) (c) (d)16. 下图(a)为微带威尔金森功分器,特性阻抗等于,其电长度L等于。
圆波导
cTE
mn
2a
mn
cTM
mn
2a
mn
在所有的模式中,TE11模截止波长最长,其次为 TM01模,三种典型模式的截止波长分别为
cTE 3.4126a
11
cTM 2.6127 a
01
cTE 1.6398a
01
微波工程基础
5
第二章 规则金属波导之圆波导
圆波导中各模式截止波长的分布图
11
第二章 规则金属波导之圆波导
磁场有径向 和轴向分量
(3)低损耗的TE01模
波导内壁电流:
TE01模的场分布
圆波导三种模式的导体衰减曲线
J s n H a a z H z a H z
TE01 模是圆波导的高次模式,比它低的模式有 TE11 、TM01 、 TE21 ,它与TM11是简并模。它也是圆对称模故无极化简并。
方圆波导变换器
TE11模的截止波长最长,是圆波导中的最低次模,也是主模。圆 波导中模的场分布与矩形波导的模的场分布很相似,因此工程上容 易通过矩形波导的横截面逐渐过渡变为圆波导,从而构成方圆波导 变换器。 但由于圆波导中极化简并模的存在,所以很难实现单模传输,因 此圆波导不太适合于远距离传输场合。 微波工程基础
微波工程基础
7
第二章 规则金属波导之圆波导
极化简并
旋转
利用极化兼并现象制成极化衰减器、极化变换器等
微波工程基础
8
第二章 规则金属波导之圆波导
(c)传输功率 TEmn和TMmn模的传输功率分别为:
PTE mn
2 πa m 2 2 Z H ( 1 ) J TE mn m (kc a) 2 2 2 m kc k a 2
chap2 9矩形波导 圆波导
三TE波、TM波的特性分析
求解出特解H0z或E0z。 有 H z (u, v, z, t ) Hoz (u, v)e j (t z ) TE模 Ez (u, v, z, t ) Eoz (u, v)e j (t z ) TM模 或 (2)由横-纵关系,求解出其余四个横切面的 场分量Eu、Ev、Hu和Hv。
复习
1.同轴线Eτ、Hφ场分布特点? 2.画出同轴线TEM的场结构图? 3.同轴线特性阻抗、波阻抗的定义、表达式 与哪些因素有关? 4.同轴线的主模?
2.2 矩形波导与圆波导
一. 矩形波导
(一)场分量
(二)模式分布与简并 (三)场结构和管壁电流分布
一. 矩形波导 作为空心金属柱面波导的典型例子是矩形波导和圆波 导。由第一章分析知道,它们不能传播TEM波,但可单 独传播TE或TM波。它们主要用于厘米波段,也用于毫米 波段。
(一)场分量
n,m成为波形型号,不同一组(n,m)代表不同导波波型。
n,m可以取零或正实数,但是不能同时为零。
TE波有三种类型:TEn0、TE0n、TEnm
(一)场分量
2. TM波的场分量 ez≠0 , hz=0
t2ez xy kc2ez xy 0
由方程(1.58)和边界条件 ez
hz 再由 x
(2.36)
n n 0,1, 2, 0 有 sin k x a 0 可得 k x a xa (2.37a) m hz m 0,1, 2, 0 有 sin k y b 0 可得 k y 再由 b y (2.37b)
y b
注意:n、m不能同时为零,因为n、m同时为零时,hz 的 解为常数,其它场分量为零,此解无意义。
1 d2X k x2 X dx 2
圆波导、同轴线、带状线、微带线简介
1、3 带状线简介
带状线的结构 带状线的结构如下图所示,由一个宽度为W, 厚度为t的中心导带和相距为d的上、下两块接地 板构成,接地板之间填充 r 的均匀介质。 带状线支持TEM波传输,这也是带状线的主 模式。同时带状线可认为是由同轴线演变而来, 故存在高次波形TE或TM模。一般可通过选择带 状线的横向尺寸来抑制高次模的出现,当取 min min b W 时可保证TEM波主模单模工 2 r 2 r 作。
2.7 10 Rs r Z 0 A 30 (b t ) c 0.16 Rs B Z 0b
r Z0 120
r Z0 120
带状线简介
Rs f / 为导体表面电阻,且 式中,
2W 1 b t 2b t A 1 ln bt bt t
同轴线简介
同轴线结构图
同轴线简介
同轴线的场方程 求解同轴线中的TEM波各场量,就是在柱坐标系 下求解横向分布函数φ所满足的拉普拉斯方程。 求得的同轴线中TEM波的横向场分量为:
E0 j z Et ar e r E0 j z HБайду номын сангаасt a e r
其中,E0是振幅常数,η =120π/ 是TEM波的 波阻抗。
圆波导
圆波导TM01场结构分布图
圆波导 线(ρ=0)附近最强。根据上述特点,它可以有 效地和轴向流动的电子流交换能量, 由此将其应 用于微波电子管中的谐振腔及直线电子加速器中 的工作模式。
1、2 同轴线简介 同轴线的概念 同轴线是一种典型的双导体传输系统, 它由内、 外同轴的两导体柱构成, 中间为支撑介质。其中, 内、 外半径分别为a和b, 填充介质的磁导率和介电常数 分别为μ 和ε。 同轴线是微波技术中最常见的TEM模传输线,它 既能支持TEM波传输,也能支持TE、TM波传播。 同时,同轴线是一种宽频带微波传输线,因此它得 到广泛的应用。其结构如下图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2E x 2
2E y 2
2E z 2
k2E
0
2
H
x 2
2H y 2
2H z 2
k2H
0
上式包含了 Ex , Ey , Ez 及 H x , H y , H z 6个直角坐标 分量,分别满足齐次标量亥姆霍兹方程。
可以证明, x 和 y 分量与 z 分量的关系为
k
2 x
Y Y
k
2 y
式中,k x 和 k y 称为分离常数。
显然
kc2
kx2
k
2 y
两个常微分方程的通解分别为
X C1 cos kx x C2 sin kx x Y C3 cos k y y C4 sin k y y
式中,常数C1 ,C2 , C3 , C4 取决于导波系统 的边界条件。
2Ez y 2
kc2 Ez
0
kc2
k2
k
2 z
考虑到 Ez Ez0 (x, y)e jkzz,其振幅 Ez0 也应满足 上述方程, 即
2Ez0 x 2
2Ez0 y 2
kc2 Ez0
0
2Ez0 x 2
2Ez0 y 2
kc2 Ez0
0
采用分离变量法求解上述方程。
0 0
已知 f fc , c ,求得真空波导中vp c 。
波导中的相速不能代表能速。
波导中的相速与频率有关。因此,电磁波在 波导中传播时会出现色散现象。
波导尺寸及模式不同,其相速也不同。
矩形波导中电磁波的波长 g 为
g
2π kz
1
fc f
2
式中
kc2
k2
k
2 z
只要求出 z 分 量,其余分量即可 求出。
z 分量为纵向 分量,因此这种方 法又称为纵向场法。
对于圆波导,选择圆柱坐标系,r 和 横向
分量可用 z 纵向分量表示为
Er
1 kc2
jkz
Ez r
j
r
H z
E
1 kc2
y e jkz z
式中 m, n 0,1, 2,,但两者不能同时为零。
与TM波一样,TE波也具有多模特性,但是
m 及 n 不能同时为零。因此,TE波的最低模式
为TE01波或TE10波。
截止传播常数和截止频率
已知
k
2 c
k2
k
2 z
,即
k
2 z
k2
kc2
。
若 k kc ,则 kz 0 ,意味波的传播被截止,因此,
j kz r
Ez
j
H z r
Hr
1 kc2
j
r
Ez
jkz
H z r
H
1 kc2
j
Ez r
j kz r
H z
2. 矩形波导传播特性 矩形波导如图所示,宽壁的内尺寸为 a ,窄 壁的内尺寸为 b 。
n
2
a b
截止频率和截止波长均与波导尺寸 a, b 及模式
m, n 有关。
模次越高,截止频率越高,截止波长越短。
TE01 TE20
TM11
0
a
TE10 2a
波导尺寸为 a 2b 时,
各种模式的截止波长分布
如图所示。
c
TE01 TE20
TM11
0
a
当 2a 时,全部模
fc f
2 1
表明电磁场没有传播,而是沿正 z 方向不断衰减
的凋落场。
对于一定的模式和波导尺寸来说,f c 是能够传输 该模式的最低频率,波导相当于一个高通滤波器。
截止波长
由 k 2π
,求得对应于截止传播常数 kc 的截止
波长 c 为
c
2π kc
2
m
2
mπ a
cos
mπ a
x sin
nπ b
y e jkz z
Ey
j kz E0 kc2
nπ b
sin
mπ a
x cos
nπ b
y e jkz z
Hx
j
E0
kc2
nπ b
sin
TE10 截
式被截止。
止
当a 2a 时,只有
区 2a
c
TE10 波存在,其他模式 被截止。
当 a时,才有其他模式出现。 若工作波长满足 a 2a,即可实现单模传输, 单模传输的惟一模式就是TE10波。
TE10波为矩形波导中的常用模式或称为主模。
通常取 a 2b,以便在 a 2a 波段内实现TE10波 单模传输。
1
fc f
2
k
1 jk
fc f
2
,
2
fc f
1,
f fc
f fc
当
f
f
c
时,
k
为实数,因子
z
e
jk
z
z
代表向正
z
方向
传播的波。 当f fc 时,k z为虚数,因子
e e jkz z
kz
mπ a
x cos
nπ b
y e jkz z
Hy
j
E0
kc2
mπ cos a
mπ a
x sin
nπ b
y e jkz z
上应上mT由在M半述为及于3z124个T非,15,方,1n表波m,M,驻零当的z向由示及。波大相等波的每上m于为的mn位于整的一或为均非m=m仅常数数种行1不均n及及与,数。目组为波n为匀n变的。n合=m零,零的为模量平1构为时在,平多的式面宽成z,故面值x场称为有壁一及上矩波,结为波关上种述形y。因构高面,的模方各波此,次。而半式向个导场具模但振个,上分中结有,振幅驻以形量T构这小辐与MT波成均均种的M与波的驻为x具场m,称的数x波n零y有,表结为最y目。有,多示构低有低,关因种。的次关模。此n模波模,例式为因式m称。因如是窄此及。为此壁,n TM11波。
已知
Ezபைடு நூலகம்
0
,求出
x0,a; y0,b
kx
mπ , a
m 1,2,3,
ky
nπ , b
n 1,2,3,
那么矩形波导中TM 波的各个分量为
Ez
E0
sin
mπ a
x
sin
nπ b
ye jkz z
Ex
j
kz E0 kc2
mπ a
cos
c
Z
ZTM Z
2
1
fc f
Z
1
c
2
同理可得,TE波的波阻抗为
ZTE
Z
1
fc f
2
Z
1
c
2
可见,当 f fc , c 时,ZTM 及 Z TE均为虚数,表明
第九章 导行电磁波
主要内容 几种常用的导波系统、矩形波导传播特性、 圆波导传播特性、谐振腔、同轴线
1. TEM波、TE波及TM波 2. 矩形波导传播特性 3. 矩形波导中TE10波 4. 电磁波的群速
5. 圆波导传播特性 6. 波导传输功率和损耗 7. 谐振腔 8. 同轴线
沿一定的路径传播的电磁波称为导行电磁波, 传输导行波的系统称为导波系统。
Ex
1 kc2
jkz
Ez x
j
H z y
Ey
1 kc2
jkz
Ez y
j
H z x
Hx
1 kc2
j
Ez y
jkz
H z x
Hy
1 kc2
j
Ez x
jkz
H z y
1
c
2
式中, 为工作波长;g称为波导波长。
已知 f fc ,c ,故 g 。
波导中的横向电场与磁场之比称为波导波阻抗。
对于TM波,其波阻抗为
Z TM
Ex Hy
Ey Hx
求得
ZTM Z
1
fc f
2
Z
2
1
常用的导波系统有双导线、同轴线、带状线、 微带、金属波导等。
本章仅介绍同轴线和金属波导。尤其是矩形 金属波导的传播特性。
几种常用导波系统的示意图
双导线
同轴线
矩形波导
圆波导
带状线
微带
介质波导 光纤
1. TEM 波、TE 波及TM 波
