江苏省高邮市阳光双语初中2018-2019年苏科版八年级数学期中复习第1章 全等三角形 同步练习(无答案)
苏科版数学八年级知识点整理

苏科版数学八年级知识点整理苏科版数学八年级知识点整理第一章三角形全等 1 全等三角形的对应边、对应角相等2边角边公理(SAS) 有两边和它们的夹角对应相等的两个三角形全等 3 角边角公理( ASA)有两角和它们的夹边对应相等的两个三角形全等 4 推论(AAS) 有两角和其中一角的对边对应相等的两个三角形全等 5 边边边公理(SSS) 有三边对应相等的两个三角形全等 6 斜边、直角边公理(HL) 有斜边和一条直角边对应相等的两个直角三角形全等定义:能够完全重合的两个三角形叫做全等三角形。
理解:①全等三角形形状与大小完全相等,与位置无关;②一个三角形经过平移、翻折、旋转可以得到它的全等形;③三角形全等不因位置发生变化而改变。
性质:(1)全等三角形的对应边相等、对应角相等。
理解:①长边对长边,短边对短边;最大角对最大角,最小角对最小角;②对应角的对边为对应边,对应边对的角为对应角。
(2)全等三角形的周长相等、面积相等。
(3)全等三角形的对应边上的对应中线、角平分线、高线1/ 25分别相等。
判定:边边边:三边对应相等的两个三角形全等(可简写成“SSS”) 边角边:两边和它们的夹角对应相等两个三角形全等(可简写成“SAS”) 角边角:两角和它们的夹边对应相等的两个三角形全等(可简写成“ASA”) 角角边:两角和其中一角的对边对应相等的两个三角形全等(可简写成“AAS”) 斜边.直角边:斜边和一条直角边对应相等的两个直角三角形全等(可简写成“HL”) 证明两个三角形全等的基本思路:(1)、已知两边:①找第三边(SSS);②找夹角(SAS);③找是否有直角(HL). 、已知一边一角:①找夹角(AAS);②找夹角(SAS);③找是否有直角(HL). 、已知两边:①找第三边(SSS);②找夹角(SAS);③找是否有直角(HL). 第二章轴对称把一个图形沿着某一条直线折叠,如果它能够与另一个图形完全重合,那么这两个图形关于这条直线对称,也称这两个图形成轴对称,这条直线叫对称轴,两个图形中对应点叫做对称点轴对称图形把一个图形沿某条直线折叠,如果直线两旁的部分能够完全重合,那么成这个图形是轴对称图形,这条直线式对称轴垂直平分线垂2/ 25直并且平分一条线段的直线,叫做这条线段的垂直平分线轴对称性质:1、成轴对称的两个图形全等2、如果两个图形成轴对称,那么对称轴是对应点连线的垂直平分线3、成轴对称的两个图形的任何对应部分成轴对称4、成轴对称的两条线段平行或所在直线的交点在对称轴上线段的对称性:1、线段是轴对称图形,线段的垂直平分线是对称轴2、线段的垂直平分线上的点到线段两端距离相等3、到线段两端距离相等的点在垂直平分线上角的对称性:1、角是轴对称图形,角平分线所在的直线是对称轴2、角平分线上的点到角的两边距离相等3、到角的两边距离相等的点在角平分线上等腰三角形的性质:1、等腰三角形是轴对称图形,顶角平分线所在直线是对称轴2、等边对等角3、三线合一等腰三角形判定:1、两边相等的三角形是等边三角形2、等边对等角直角三角形的推论:直角三角形斜边上中线等于斜边一半30°角所对的边是斜边的一半等边三角形判定及性质:1、三条边相等的三角形是等边三角形2、等边三角形是轴对称图形,有3条对称轴3、等边三角形每个角都等于60°判定:三条边都相等、三个角都是60°、有一个角是60°的等腰3/ 25三角形是等边三角形等腰梯形:两腰相等的梯形是等腰梯形等腰梯形性质:1、等腰梯形是轴对称图形,过两底中点的直线是对称轴2、等腰梯形在同一底上的两个角相等3、等腰梯形对角线相等等腰梯形判定:1.、两腰相等的梯形是等腰梯形2、在同一底上两个角相等的梯形是等腰梯形第三章勾股定理直角三角形两直角边的平方和等于斜边的平方a²+b²=c² 勾股定理逆定理:如果一个三角形三边a、b、c满足a²+b²=c²,那么这个三角形是直角三角形勾股数:满足a²+b²=c²的三个正整数a、b、c称为勾股数第四章实数平方根:如果一个数的平方等于a,那么这个数叫做a 的平方根,也称二次方根如果x²=a,那么x叫做a的平方根平方根的性质:1、一个正数有两个平方根,它们互为相反数2、0只有一个平方根,是03、负数没有平方根算术平方根:正数a的正的平方根叫a的算术平方根0的算术平方根是0 开平方:求一个数a的平方根的运算,叫做开平方立方根:如果一个数的立方等于a,那么这个数叫做a的立方根,也称三次方根如果x³=a,那么a是x的立方根立方根的性质:1、正数的立方根是正数2、负数的立方根是负数3、04/ 25的立方根是0 开立方:求一个数的立方根的运算,叫做开立方有效数字:对于一个近似数,从左边第一个不是0的数字起,到末尾数字止,所有的数字都称为这个近似数的有效数字补充:平方根和立方根1、算术平方根:一般地,如果一个正数x的平方等于a,即x2=a,那么这个正数x就叫做a的算术平方根。
2019年秋江苏省八年级上册数学期中考试《全等三角形》试题分类——填空题
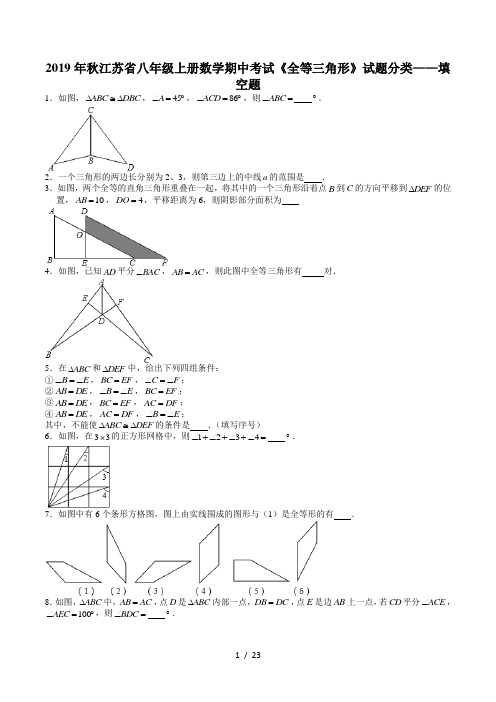
2019年秋江苏省八年级上册数学期中考试《全等三角形》试题分类——填空题1.如图,ABC DBC ∆≅∆,45A ∠=︒,86ACD ∠=︒,则ABC ∠= ︒.2.一个三角形的两边长分别为2、3,则第三边上的中线a 的范围是 .3.如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B 到C 的方向平移到DEF ∆的位置,10AB =,4DO =,平移距离为6,则阴影部分面积为4.如图,已知AD 平分BAC ∠,AB AC =,则此图中全等三角形有 对.5.在ABC ∆和DEF ∆中,给出下列四组条件:①B E ∠=∠,BC EF =,C F ∠=∠;②AB DE =,B E ∠=∠,BC EF =;③AB DE =,BC EF =,AC DF =;④AB DE =,AC DF =,B E ∠=∠;其中,不能使ABC DEF ∆≅∆的条件是 .(填写序号)6.如图,在33⨯的正方形网格中,则1234∠+∠+∠+∠= ︒.7.如图中有6个条形方格图,图上由实线围成的图形与(1)是全等形的有 .8.如图,ABC ∆中,AB AC =,点D 是ABC ∆内部一点,DB DC =,点E 是边AB 上一点,若CD 平分ACE ∠,100AEC ∠=︒,则BDC ∠= ︒.9.如图,90ABC ∠=︒,//AD BC ,以B 为圆心,BC 长为半径画弧,与射线AD 相交于点E ,连接BE ,过点C 作CF BE ⊥,垂足为F .若6AB =,10BC =,则EF 的长为 .10.如图,BA AC ⊥,//CD AB .BC DE =,且BC DE ⊥,若2AB =,6CD =,则AE = .11.如图所示,已知AF DC =,//BC EF ,若要用“ASA ”去证ABC DEF ∆≅∆,则需添加的条件是 .12.如图ABC ∆中,点D 为BC 的中点,5AB =,3AC =,2AD =,则ABC ∆的面积是 .13.下列4个图形中,属于全等的2个图形是 .(填序号)14.已知(ABC DEF A ∆≅∆、B 分别与D 、E 对应),2AC =,1BC =,则EF 的长为 .15.如图,已知ABC DEF ∆≅∆,若20A ∠=︒,则D ∠的度数是 .16.如图,若ABE ACF ∆≅∆,且9AB =,4AE =,则EC 的长为 . 17.如图,点E 、F 在AC 上,若ADF CBE ∆≅∆,则AD 与BC 的位置关系是 .18.如图,ABC EDC ∆≅∆,BC CD ⊥,点A ,D ,E 在同一条直线上,20ACB ∠=︒,则ADC ∠的度数是 . 19.如图,在ABC ∆中,45ABC ∠=︒,9AC cm =,F 是高AD 和BE 的交点,则BF 的长是 .20.已知ABC ∆≅△A B C ''',△A B C '''的周长为32cm ,9A B cm ''=,12B C cm ''=,则AC = .21.已知ABC DEF ∆≅∆,且80A ∠=︒,60F ∠=︒,则B ∠= ︒.22.已知ABC DEF ∆≅∆,2AB =,4AC =,DEF ∆的周长为10,则BC 的值为 .23.如图,若ABE ACD ∆≅∆,且65A ∠=︒,20C ∠=︒,则AEB ∠= ︒.24.如图,已知ABC DCB ∠=∠,增加下列条件:①AB CD =;②AC DB =;③A D ∠=∠;④BO CO =.能判定ABC DCB ∆≅∆的是 .(填正确答案的序号)25.如图,12∠=∠,B C ∠=∠,则ABD ∆与ACD ∆ (填“全等”、“不一定全等” ).26.如图,ABC ADE ∆≅∆,若130BAE ∠=︒,32DAC ∠=︒,则EAC ∠的度数为 ︒.27.如图,ABC ADE ∆≅∆,若45B ∠=︒,30C ∠=︒,则DAE ∠的度数为 ︒. 28.如图,若Rt ABC Rt ADE ∆≅∆,且60B ∠=︒,则E ∠= ︒.29.如图,ABC ADE ∆≅∆,BC 的延长线经过点E ,交AD 于F ,105AED ∠=︒,10CAD ∠=︒,50B ∠=︒,则EAB ∠= ︒.30.如图,A 、E 、C 三点在一条直线上,ABE CED ∆≅∆,90A C ∠=∠=︒,3AB cm =,7CD cm =,则AC =cm .31.如图,ABC DEC ∆≅∆,CA 和CD ,CB 和CE 是对应边,28ACD ∠=︒,则BCE ∠= ︒.32.已知ABC DEF ∆≅∆,30A ∠=︒,80B ∠=︒,则F ∠= . 33.根据下列已知条件,能够画出唯一ABC ∆的是 (填写正确的序号).①5AB =,4BC =,60A ∠=︒;②5AB =,6BC =,7AC =;③5AB =,50A ∠=︒,60B ∠=︒;④40A ∠=︒,50B ∠=︒,90C ∠=︒.34.如图,在ABC ∆中,E 为边AC 的中点,//CN AB ,过点E 作直线交AB 于点M ,交CN 于点N .若6BM cm =,5CN cm =,则AB = cm .35.如图,ABC ADE ∆≅∆,若80B ∠=︒,30C ∠=︒,34DAC ∠=︒,则EAC ∠的度数为 .36.如图,ABC DEF ∆≅∆.若5BC cm =,7BF cm =,则EC 的长是 .37.如图,ABE ACD ∆≅∆,58A ∠=︒,24B ∠=︒,则DOE ∠的度数为 ︒.38.如图,6AB cm =,4AC BD cm ==.60CAB DBA ∠=∠=︒,点P 在线段AB 上以1/cm s 的速度由点A 向点B 运动,同时,点Q 在线段BD 上由点B 向点D 运动.它们运动的时间为()t s ,则点Q 的运动速度为 /cm s ,使得A 、C 、P 三点构成的三角形与B 、P 、Q 三点构成的三角形全等.39.如图所示,ABC ADE ∆≅∆,且55DAE ∠=︒,25B ∠=︒,则ACG ∠= .40.如图,ABE ACD ∆≅∆,60A ∠=︒,25B ∠=︒,则DOE ∠的度数为 .41.如图所示,AD AE =,AB AC =,BAC DAE ∠=∠,B 、D 、E 在同一直线上,122∠=︒,230∠=︒,则3∠= .42.如图,ABC DEF ∆≅∆,3BE =,2AE =,则DE 的长是 .43.如图所示,点A 、B 、C 、D 在同一条直线上,ACF DBE ∆≅∆,10AD cm =,6BC cm =,则AB 的长为 cm .44.等腰三角形ABC 中,AB AC =,D 、E 分别是AC 、AB 上两点,连结BD 、CE ,BD CE =,且BC BD >,48A ∠=︒,36BCE ∠=︒,则ADB ∠的度数等于 .45.如图,点D 是BC 上的一点,若ABC ADE ∆≅∆,且65B ∠=︒,则EAC ∠= ︒.46.如图,在Rt ABC ∆中,90ACB ∠=︒,EF AB ⊥于点D ,交BC 的延长线于点E .若AB EF =且16BE =,6CF =,则AC = .47.若ABC DEF ∆≅∆,5AB DE cm ==,若ABC ∆的面积为210cm ,则DEF ∆的边DE 上的高为 cm .48.三个全等三角形按如图的形式摆放, 若188∠=︒,则23∠+∠= ︒.49.如图,ABC ADE ∆≅∆,若35C ∠=︒,75D ∠=︒,25DAC ∠=︒,则BAD ∠= ︒.50.如图,12∠=∠,要利用“AAS ”得到ABD ACD ∆≅∆,需要增加的一个条件是 .2019年秋江苏省八年级上册数学期中考试《全等三角形》试题分类——填空题1.如图,ABC DBC ∆≅∆,45A ∠=︒,86ACD ∠=︒,则ABC ∠= 92︒.【解答】解:ABC DBC ∆≅∆,ACB DCB ∴∠=∠,86ACD ∠=︒,43ACB ∴∠=︒,45A ∠=︒,18092ABC A ACB ∴∠=︒-∠-∠=︒,故答案为:92.2.一个三角形的两边长分别为2、3,则第三边上的中线a 的范围是 0.5 2.5x << .【解答】解:如图,延长中线AD 到E ,使DE AD =,AD 是三角形的中线,BD CD ∴=,在ACD ∆和EBD ∆中,BD CD ADC BDE DE AD =⎧⎪∠=∠⎨⎪=⎩,()ACD EBD SAS ∴∆≅∆,AC BE ∴=,三角形两边长为2,3,第三边上的中线为x ,32232x ∴-<<+,即125x <<,0.5 2.5x ∴<<.故答案为:0.5 2.5x <<3.如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B 到C 的方向平移到DEF ∆的位置,10AB =,4DO =,平移距离为6,则阴影部分面积为 48【解答】解:由平移的性质知,6BE =,10DE AB ==,1046OE DE DO ∴=-=-=,()()1110664822ODFC ABEO S S AB OE BE ∴==+⋅=+⨯=四边形梯形. 故答案为48.4.如图,已知AD 平分BAC ∠,AB AC =,则此图中全等三角形有 4 对.【解答】解:全等三角形有:ABD ACD ∆≅∆,BDE CDF ∆≅∆,AED AFD ∆≅∆,AFB AEC ∆≅∆,共4对,故答案为:4.5.在ABC ∆和DEF ∆中,给出下列四组条件:①B E ∠=∠,BC EF =,C F ∠=∠;②AB DE =,B E ∠=∠,BC EF =;③AB DE =,BC EF =,AC DF =;④AB DE =,AC DF =,B E ∠=∠;其中,不能使ABC DEF ∆≅∆的条件是 ④ .(填写序号)【解答】解:①B E ∠=∠,BC EF =,C F ∠=∠,可根据ASA 判定ABC DEF ∆≅∆;②AB DE =,B E ∠=∠,BC EF =,可根据SAS 判定ABC DEF ∆≅∆;③AB DE =,BC EF =,AC DF =,可根据SSS 判定ABC DEF ∆≅∆;④AB DE =,AC DF =,B E ∠=∠,不能判定ABC DEF ∆≅∆;故答案为:④.6.如图,在33⨯的正方形网格中,则1234∠+∠+∠+∠= 180 ︒.【解答】解:1∠和4∠所在的三角形全等,1490∴∠+∠=︒,2∠和3∠所在的三角形全等,2390∴∠+∠=︒,123∴∠+∠+∠十4180∠=︒.故答案为:180.7.如图中有6个条形方格图,图上由实线围成的图形与(1)是全等形的有 (2),(3),(6) .【解答】解:由图可知,图上由实线围成的图形与(1)是全等形的有(2),(3),(6),故答案为:(2),(3),(6),8.如图,ABC ∆中,AB AC =,点D 是ABC ∆内部一点,DB DC =,点E 是边AB 上一点,若CD 平分ACE ∠,100AEC ∠=︒,则BDC ∠= 80 ︒.【解答】解:设ACD DCE x ∠=∠=,ECB y ∠=.AB AC =,DB DC =,2ABC ACB x y ∴∠=∠=+,DCB DBC x y ∠=∠=+,AEC ECB EBC ∠=∠+∠,22100x y ∴+=︒,1802280BDC x y ∴∠=︒--=︒故答案为809.如图,90ABC ∠=︒,//AD BC ,以B 为圆心,BC 长为半径画弧,与射线AD 相交于点E ,连接BE ,过点C 作CF BE ⊥,垂足为F .若6AB =,10BC =,则EF 的长为 2 .【解答】解:90ABC ∠=︒,//AD BC ,18090A ABC ∴∠=︒-∠=︒,AEB FBC ∴∠=∠,10BE BC ==,22221068AE BE AB ∴=-=-=,CF BE ⊥,90A BFC ∴∠=∠=︒,在AEB ∆和FBC ∆中,A BFC AEB FBC BE BC ∠=∠⎧⎪∠=∠⎨⎪=⎩,()AEB FBC AAS ∴∆≅∆,8BF AE ∴==,1082EF BE BF ∴=-=-=;故答案为:2.10.如图,BA AC ⊥,//CD AB .BC DE =,且BC DE ⊥,若2AB =,6CD =,则AE = 4 .【解答】解:BA AC ⊥,90A ∴∠=︒,//CD AB ,90DCE ∴∠=︒,BC DE ⊥,90DCB D ∴∠+∠=︒,90DCB BCA ∠+∠=︒,BCA D ∴∠=∠,在ABC ∆和CED ∆中A DCE BCA D BC ED ∠=∠⎧⎪∠=∠⎨⎪=⎩,()ABC CED AAS ∴∆≅∆,2AB CE ∴==,6AC CD ==,624AE AC CE ∴=-=-=.故答案为4.11.如图所示,已知AF DC =,//BC EF ,若要用“ASA ”去证ABC DEF ∆≅∆,则需添加的条件是 A D ∠=∠ .【解答】解:A D ∠=∠,理由是:AF CD =,AF FC CD FC ∴+=+,AC DF ∴=,//BC EF ,BCA EFD ∴∠=∠,在ABC ∆和DEF ∆中,A D AC DFBCA EFD ∠=∠⎧⎪=⎨⎪∠=∠⎩, ()ABC DEF ASA ∴∆≅∆.故答案为:A D ∠=∠.12.如图ABC ∆中,点D 为BC 的中点,5AB =,3AC =,2AD =,则ABC ∆的面积是 6 .【解答】解:延长AD 至E ,使AD DE =,连接BE ,在ADC ∆和BDE ∆中,AD DE ADC EDB BD CD =⎧⎪∠=∠⎨⎪=⎩,()ADC BDE SAS ∴∆≅∆,3BE AC ∴==,4AE =,5AB =,222345+=,ABE ∴∆为Rt △,AE BE ⊥,ABC ∴∆的面积等于ABE ∆的面积为:1134622AE BE =⨯⨯=. 故答案为:6.13.下列4个图形中,属于全等的2个图形是 ①③ .(填序号)【解答】解:根据全等三角形的判定()SAS 可知属于全等的2个图形是①③,故答案为:①③.14.已知(ABC DEF A ∆≅∆、B 分别与D 、E 对应),2AC =,1BC =,则EF 的长为 1 .【解答】解:(ABC DEF A ∆≅∆、B 分别与D 、E 对应),1BC =,1EF BC ∴==,故答案为:1.15.如图,已知ABC DEF ∆≅∆,若20A ∠=︒,则D ∠的度数是 20︒ . 【解答】解:ABC DEF ∆≅∆,20A ∠=︒,20D A ∴∠=∠=︒,故答案为:20︒.16.如图,若ABE ACF ∆≅∆,且9AB =,4AE =,则EC 的长为 5 .【解答】解:ABE ACF ∆≅∆,9AC AB ∴==,5EC AC AE ∴=-=,故答案为:5.17.如图,点E 、F 在AC 上,若ADF CBE ∆≅∆,则AD 与BC 的位置关系是 平行 .【解答】解:ADF CBE ∆≅∆,A C ∴∠=∠,//AD BC ∴,则AD 与BC 的位置关系是:平行.故答案为:平行.18.如图,ABC EDC ∆≅∆,BC CD ⊥,点A ,D ,E 在同一条直线上,20ACB ∠=︒,则ADC ∠的度数是 65︒ .【解答】解:ABC EDC ∆≅∆,20DCE ACB ∴∠=∠=︒,90BCD ACE ∠=∠=︒,AC CE =,902070ACD ∴∠=︒-︒=︒,点A ,D ,E 在同一条直线上,180ADC EDC ∴∠+∠=︒,180EDC E DCE ∠+∠+∠=︒,20ADC E ∴∠=∠+︒,90ACE ∠=︒,AC CE =90DAC E ∴∠+∠=︒,45E DAC ∠=∠=︒在ADC ∆中,180ADC DAC DCA ∠+∠+∠=︒,即4570180ADC ︒+︒+∠=︒,解得:65ADC ∠=︒,故答案为:65︒.19.如图,在ABC ∆中,45ABC ∠=︒,9AC cm =,F 是高AD 和BE 的交点,则BF 的长是 9cm .【解答】解:AD BC ⊥,BE AC ⊥,90ADC ADB ∴∠=∠=︒,90BEA ∠=︒,又180FBD BDF BFD ∠+∠+∠=︒,180FAE FEA AFE ∠+∠+∠=︒,且BFD AFE ∠=∠,FBD FAE ∴∠=∠,又45ABC ∠=︒,90ABD BAD ∠+∠=︒,45BAD ∴∠=︒,BD AD ∴=,且90ADC BDF ∠=∠=︒,FBD FAE ∠=∠,()ADC BDF ASA ∴∆≅∆9BF AC cm∴==, 故答案为:9cm .20.已知ABC ∆≅△A B C ''',△A B C '''的周长为32cm ,9A B cm ''=,12B C cm ''=,则AC = 11cm.【解答】解:△A B C '''的周长为32cm ,32A B B C A C ''''''∴++=,3291211A C ''∴=--=,ABC ∆≅△A B C ''',11()AC A C cm ''∴==,故答案为:11cm .21.已知ABC DEF ∆≅∆,且80A ∠=︒,60F ∠=︒,则B ∠= 40 ︒.【解答】解:ABC DEF ∆≅∆,且80A ∠=︒,60F ∠=︒,60C F ∴∠=∠=︒,则180806040B ∠=︒-︒-︒=︒.故答案为:40.22.已知ABC DEF ∆≅∆,2AB =,4AC =,DEF ∆的周长为10,则BC 的值为 4 .【解答】解:ABC DEF ∆≅∆,2AB =,4AC =,DEF ∆的周长为10,ABC ∴∆的周长为:10,故BC 的值为:10424--=.故答案为:4.23.如图,若ABE ACD ∆≅∆,且65A ∠=︒,20C ∠=︒,则AEB ∠= 95 ︒.【解答】解:ABE ACD ∆≅∆,20C ∠=︒,20B C ∴∠=∠=︒,65A ∠=︒,180180652095AEB A B ∴∠=︒-∠-∠=︒-︒-︒=︒,故答案为:95.24.如图,已知ABC DCB ∠=∠,增加下列条件:①AB CD =;②AC DB =;③A D ∠=∠;④BO CO =.能判定ABC DCB ∆≅∆的是 ①③④ .(填正确答案的序号)【解答】解:能判定ABC DCB ∆≅∆的是①③④,理由是:①在ABC ∆和DCB ∆中AB DC ABC DCB BC BC =⎧⎪∠=∠⎨⎪=⎩()ABC DCB SAS ∴∆≅∆;③在ABC ∆和DCB ∆中ABC DCBA D BC CB∠=∠⎧⎪∠=∠⎨⎪=⎩()ABC DCB AAS ∴∆≅∆;④OB OC =,DBC ACB ∴∠=∠,在ABC ∆和DCB ∆中ACB DBCBC CB ABC DCB∠=∠⎧⎪=⎨⎪∠=∠⎩()ABC DCB ASA ∴∆≅∆,故答案为:①③④.25.如图,12∠=∠,B C ∠=∠,则ABD ∆与ACD ∆ 全等 (填“全等”、“不一定全等”). 【解答】解:ABD ∆与ACD ∆全等,理由是:1C CAD ∠=∠+∠,2B BAD ∠=∠+∠,又12∠=∠,B C ∠=∠,CAD BAD ∴∠=∠,在ABD ∆和ACD ∆中CAD BADC B AD AD∠=∠⎧⎪∠=∠⎨⎪=⎩()ABD ACD AAS ∴∆≅∆,故答案为:全等.26.如图,ABC ADE ∆≅∆,若130BAE ∠=︒,32DAC ∠=︒,则EAC ∠的度数为 49 ︒.【解答】解:ABC ADE ∆≅∆, BAC EAD ∴∠=∠,130BAE ∠=︒,32DAC ∠=︒,13032492BAD EAC ︒-︒∴∠=∠==︒.故答案为:49.27.如图,ABC ADE ∆≅∆,若45B ∠=︒,30C ∠=︒,则DAE ∠的度数为 105 ︒.【解答】解:ABC ADE ∆≅∆,45B D ∴∠=∠=︒,30C E ∠=∠=︒,1804530105DAE ∴∠=︒-︒-︒=︒.故答案为:105.28.如图,若Rt ABC Rt ADE ∆≅∆,且60B ∠=︒,则E ∠= 30 ︒.【解答】解:60B ∠=︒,90BAC ∠=︒,18030C B BAC ∴∠=︒-∠-∠=︒,Rt ABC Rt ADE ∆≅∆,30E C ∴∠=∠=︒,故答案为:30.29.如图,ABC ADE ∆≅∆,BC 的延长线经过点E ,交AD 于F ,105AED ∠=︒,10CAD ∠=︒,50B ∠=︒,则EAB ∠= 60 ︒.【解答】解:ABC ADE ∆≅∆,50B ∠=︒,50D B ∴∠=∠=︒,EAD CAB ∠=∠,105AED ∠=︒,18025EAD D AED ∴∠=︒-∠-∠=︒,25CAB ∴∠=︒,10CAD ∠=︒,25102560EAB EAD DAC CAB ∴∠=∠+∠+∠=︒+︒+︒=︒30.如图,A 、E 、C 三点在一条直线上,ABE CED ∆≅∆,90A C ∠=∠=︒,3AB cm =,7CD cm =,则AC = 10 cm .【解答】解:ABE CED ∆≅∆,3AB cm =,7CD cm =,3EC AB cm ∴==,7AE CD cm ==,7310AC AE CE cm cm cm ∴=+=+=,故答案为:10.31.如图,ABC DEC ∆≅∆,CA 和CD ,CB 和CE 是对应边,28ACD ∠=︒,则BCE ∠= 28 ︒.【解答】证明:ABC DEC ∆≅∆,ACB DCE ∴∠=∠,ACB ACE DCE ACE ∴∠-∠=∠-∠,即28ACD BCE ∠=∠=︒.故答案是:28.32.已知ABC DEF ∆≅∆,30A ∠=︒,80B ∠=︒,则F ∠= 70︒ .【解答】解:ABC DEF ∆≅∆,30A D ∴∠=∠=︒,80B E ∠=∠=︒,C F ∠=∠,180D E F ∠+∠+∠=︒,70F ∴∠=︒.故答案是:70︒.33.根据下列已知条件,能够画出唯一ABC ∆的是 ②③ (填写正确的序号).①5AB =,4BC =,60A ∠=︒;②5AB =,6BC =,7AC =;③5AB =,50A ∠=︒,60B ∠=︒;④40A ∠=︒,50B ∠=︒,90C ∠=︒.【解答】解:①当两边及其中一边的对角确定时,此时是ASS ,可知这个三角形是不确定的; ②当三角形的三边确定时,由SSS 可知这个三角形是确定的;③此时可知三角形的两角及其夹边确定,由ASA 可知这个三角形是确定的;④根据40A ∠=︒,50B ∠=︒,90C ∠=︒不能画出唯一三角形;故答案为:②③.34.如图,在ABC ∆中,E 为边AC 的中点,//CN AB ,过点E 作直线交AB 于点M ,交CN 于点N .若6BM cm =,5CN cm =,则AB = 11 cm .【解答】解://CN AB ,NCE MAE ∴∠=∠,又E 是AC 中点,AE CE ∴=,而AEM CEN ∠=∠,在CNE ∆和AME ∆中,NCE MAE AE CEAEM CEN ∠=∠⎧⎪=⎨⎪∠=∠⎩, ()CNE AME ASA ∴∆≅∆,AM CN ∴=,5611AB AM BM CN BM ∴=+=+=+=,故答案为:1135.如图,ABC ADE ∆≅∆,若80B ∠=︒,30C ∠=︒,34DAC ∠=︒,则EAC ∠的度数为 36︒ .【解答】解:80B ∠=︒,30C ∠=︒,180803070BAC ∴∠=︒-︒-︒=︒,ABC ADE ∆≅∆,70DAE BAC ∴∠=∠=︒,703436EAC DAE DAC ∴∠=∠-∠=︒-︒=︒.故答案是:36︒.36.如图,ABC DEF ∆≅∆.若5BC cm =,7BF cm =,则EC 的长是 3cm .【解答】解:ABC DEF ∆≅∆,5BC cm =,7BF cm =,5BC EF cm ∴==,2FC BE BF BC cm ∴==-=,523()EC BC BE cm ∴=-=-=.故答案为:3cm .37.如图,ABE ACD ∆≅∆,58A ∠=︒,24B ∠=︒,则DOE ∠的度数为 106 ︒.【解答】解:ABE ACD ∆≅∆,58A ∠=︒,24B ∠=︒,582472BEC BDC A B ∴∠=∠=∠+∠=︒+︒=︒,7224106DOE B BDC ∴∠=∠+∠=︒+︒=︒.故答案为:106.38.如图,6AB cm =,4AC BD cm ==.60CAB DBA ∠=∠=︒,点P 在线段AB 上以1/cm s 的速度由点A 向点B 运动,同时,点Q 在线段BD 上由点B 向点D 运动.它们运动的时间为()t s ,则点Q 的运动速度为 1或43/cm s ,使得A 、C 、P 三点构成的三角形与B 、P 、Q 三点构成的三角形全等. 【解答】解:设点Q 的运动速度是/xcm s ,60CAB DBA ∠=∠=︒,A ∴、C 、P 三点构成的三角形与B 、P 、Q 三点构成的三角形全等,有两种情况: ①AP BP =,AC BQ =,则161t t ⨯=-⨯,解得:3t =,则43x =,解得:43x =; ②AP BQ =,AC BP =,则1t tx ⨯=,614t -⨯=,解得:2t =,1x =,故答案为:1或43. 39.如图所示,ABC ADE ∆≅∆,且55DAE ∠=︒,25B ∠=︒,则ACG ∠= 80︒ . 【解答】解:ABC ADE ∆≅∆,55BAC DAE ∴∠=∠=︒,552580ACG BAC B ∴∠=∠+∠=︒+︒=︒,故答案为:80︒.40.如图,ABE ACD ∆≅∆,60A ∠=︒,25B ∠=︒,则DOE ∠的度数为 110︒ .【解答】解:60A ∠=︒,25B ∠=︒,85CEO ∴∠=︒,ABE ACD ∆≅∆,25B C ∴∠=∠=︒,110DOE C CEO ∴∠=∠+∠=︒.故答案为:110︒.41.如图所示,AD AE =,AB AC =,BAC DAE ∠=∠,B 、D 、E 在同一直线上,122∠=︒,230∠=︒,则3∠= 52︒ .【解答】解:BAC DAE ∠=∠,1CAE ∴∠=∠,且AD AE =,AB AC =,()ABD ACE SAS ∴∆≅∆230ABD ∴∠=∠=︒,3252ABD ∴∠=∠+∠=︒,故答案为:52︒42.如图,ABC DEF ∆≅∆,3BE =,2AE =,则DE 的长是 5 .【解答】解:3BE =,2AE =,325AB AE BE ∴=+=+=ABC DEF ∆≅∆,5DE AB ∴==,故答案为:5.43.如图所示,点A 、B 、C 、D 在同一条直线上,ACF DBE ∆≅∆,10AD cm =,6BC cm =,则AB 的长为 2 cm . 【解答】解:ACF DBE ∆≅∆,AC BD ∴=,AB CD ∴=,10AD cm =,6BC cm =,10AB BC CD cm ∴++=,24AB cm ∴=,2AB cm ∴=,故答案为:244.等腰三角形ABC 中,AB AC =,D 、E 分别是AC 、AB 上两点,连结BD 、CE ,BD CE =,且BC BD >,48A ∠=︒,36BCE ∠=︒,则ADB ∠的度数等于 102︒或78︒ .【解答】解:作BG AC ⊥于G ,作CH AB ⊥于H ,如图所示:则90BHC EHC CGB DGB ∠=∠=∠=∠=︒,AB AC =,1(180)662ABC ACB A ∴∠=∠=︒-∠=︒, 在BCH ∆和CBG ∆中,BHC CGB ABC ACB BC CB ∠=∠⎧⎪∠=∠⎨⎪=⎩,()BCH CBG AAS ∴∆≅∆,CH BG ∴=,在Rt BDG ∆和Rt CEH ∆中,BD CE BG CH =⎧⎨=⎩, Rt BDG Rt CEH(HL)∴∆≅∆,BDG CEH ∴∠=∠,ADB AEC ∴∠=∠,6636102AEC ABC BCE ∠=∠+∠=︒+︒=︒,102ADB ∴∠=︒;将BD 沿BG 作轴对称变换得BD BD '=,则18010278AD B BDC '∠=∠=︒-︒=︒;故答案为:102︒或78︒.45.如图,点D 是BC 上的一点,若ABC ADE ∆≅∆,且65B ∠=︒,则EAC ∠=50 ︒.【解答】解:ABC ADE ∆≅∆,AB AD ∴=,EAD CAB ∠=∠,65ADB B ∴∠=∠=︒,EAD CAD CAB CAD ∠-∠=∠-∠, 50EAC BAD ∴∠=∠=︒,故答案为:50.46.如图,在Rt ABC ∆中,90ACB ∠=︒,EF AB ⊥于点D ,交BC 的延长线于点E .若AB EF =且16BE =,6CF =,则AC = 10 .【解答】解:90ACB ∠=︒,EF AB ⊥于点D , 90ECF ACB ADF ∴∠=∠=∠=︒,90A B ∴∠+∠=︒,90E B ∠+∠=︒,A E ∴∠=∠,在ACB ∆和ECF ∆中,A E ACB ECF AB EF ∠=∠⎧⎪∠=∠⎨⎪=⎩,()ACB ECF AAS ∴∆≅∆,AC EC ∴=,6BC CF ==,16BE =,16610AC EC BE BC ∴==-=-=,故答案为10.47.若ABC DEF ∆≅∆,5AB DE cm ==,若ABC ∆的面积为210cm ,则DEF ∆的边DE 上的高为 4 cm .【解答】解:设ABC ∆边AB 上的高为h ,则1102AB h =,即15102h ⨯=, 解得4h =,ABC DEF ∆≅∆,AB 与DE 是对应边,DE ∴边上的高为4cm .故答案为:4.48.三个全等三角形按如图的形式摆放, 若188∠=︒,则23∠+∠= 92 ︒.【解答】解: 由图形可得:145369287540∠+∠+∠+∠+∠+∠+∠+∠+∠=︒, 三个全等三角形,498180∴∠+∠+∠=︒,576180∠+∠+∠=︒,123180180540∴∠+∠+∠+︒+︒=︒,123∴∠+∠+∠的度数是180︒,231808892∴∠+∠=︒-︒=︒.故答案为: 92 .49.如图,ABC ADE ∆≅∆,若35C ∠=︒,75D ∠=︒,25DAC ∠=︒,则BAD ∠= 45 ︒. 【解答】解:ABC ADE ∆≅∆,75D ∠=︒,75D B ∴∠=∠=︒,又35C ∠=︒,70BAC ∴∠=︒,又25DAC ∠=︒,45BAD ∴∠=︒,故答案为:45.50.如图,12∠=∠,要利用“AAS ”得到ABD ACD ∆≅∆,需要增加的一个条件是 B C ∠=∠ .【解答】解:12∠=∠,ADB ADC ∴∠=∠,又AD AD =,∴当B C ∠=∠时,()ABE ACE AAS ∆≅∆;或BD CD =时,()ABE ACE SAS ∆≅∆;或BAE CAE ∠=∠时,()ABE ACE ASA ∆≅∆. 故答案为:B C ∠=∠(答案不唯一).。
苏科版数学八年级知识点整理

苏科版数学八年级知识点整理苏科版数学八年级知识点整理第一章三角形全等 1 全等三角形的对应边、对应角相等 2边角边公理(SAS) 有两边和它们的夹角对应相等的两个三角形全等 3 角边角公理( ASA)有两角和它们的夹边对应相等的两个三角形全等4 推论(AAS) 有两角和其中一角的对边对应相等的两个三角形全等5 边边边公理(SSS) 有三边对应相等的两个三角形全等6 斜边、直角边公理(HL) 有斜边和一条直角边对应相等的两个直角三角形全等定义:能够完全重合的两个三角形叫做全等三角形。
理解:①全等三角形形状与大小完全相等,与位置无关;②一个三角形经过平移、翻折、旋转可以得到它的全等形;③三角形全等不因位置发生变化而改变。
性质:(1)全等三角形的对应边相等、对应角相等。
理解:①长边对长边,短边对短边;最大角对最大角,最小角对最小角;②对应角的对边为对应边,对应边对的角为对应角。
(2)全等三角形的周长相等、面积相等。
(3)全等三角形的对应边上的对应中线、角平分线、高线分别相等。
判定:边边边:三边对应相等的两个三角形全等(可简写成“SSS”) 边角边:两边和它们的夹角对应相等两个三角形全等(可简写成“SAS”) 角边角:两角和它们的夹边对应相等的两个三角形全等(可简写成“ASA”) 角角边:两角和其中一角的对边对应相等的两个三角形全等(可简写成“AAS”) 斜边.直角边:斜边和一条直角边对应相等的两个直角三角形全等(可简写成“HL”) 证明两个三角形全等的基本思路:(1)、已知两边:①找第三边(SSS);②找夹角(SAS);③找是否有直角(HL).、已知一边一角:①找夹角(AAS);②找夹角(SAS);③找是否有直角(HL).、已知两边:①找第三边(SSS);②找夹角(SAS);③找是否有直角(HL).第二章轴对称把一个图形沿着某一条直线折叠,如果它能够与另一个图形完全重合,那么这两个图形关于这条直线对称,也称这两个图形成轴对称,这条直线叫对称轴,两个图形中对应点叫做对称点轴对称图形把一个图形沿某条直线折叠,如果直线两旁的部分能够完全重合,那么成这个图形是轴对称图形,这条直线式对称轴垂直平分线垂直并且平分一条线段的直线,叫做这条线段的垂直平分线轴对称性质:1、成轴对称的两个图形全等2、如果两个图形成轴对称,那么对称轴是对应点连线的垂直平分线3、成轴对称的两个图形的任何对应部分成轴对称4、成轴对称的两条线段平行或所在直线的交点在对称轴上线段的对称性:1、线段是轴对称图形,线段的垂直平分线是对称轴2、线段的垂直平分线上的点到线段两端距离相等3、到线段两端距离相等的点在垂直平分线上角的对称性:1、角是轴对称图形,角平分线所在的直线是对称轴2、角平分线上的点到角的两边距离相等3、到角的两边距离相等的点在角平分线上等腰三角形的性质:1、等腰三角形是轴对称图形,顶角平分线所在直线是对称轴2、等边对等角3、三线合一等腰三角形判定:1、两边相等的三角形是等边三角形2、等边对等角直角三角形的推论:直角三角形斜边上中线等于斜边一半30°角所对的边是斜边的一半等边三角形判定及性质:1、三条边相等的三角形是等边三角形2、等边三角形是轴对称图形,有3条对称轴3、等边三角形每个角都等于60° 判定:三条边都相等、三个角都是60°、有一个角是60°的等腰三角形是等边三角形等腰梯形:两腰相等的梯形是等腰梯形等腰梯形性质:1、等腰梯形是轴对称图形,过两底中点的直线是对称轴2、等腰梯形在同一底上的两个角相等3、等腰梯形对角线相等等腰梯形判定:1.、两腰相等的梯形是等腰梯形 2、在同一底上两个角相等的梯形是等腰梯形第三章勾股定理直角三角形两直角边的平方和等于斜边的平方a²+b²=c² 勾股定理逆定理:如果一个三角形三边a、b、c满足a²+b²=c²,那么这个三角形是直角三角形勾股数:满足a²+b²=c²的三个正整数a、b、c称为勾股数第四章实数平方根:如果一个数的平方等于a,那么这个数叫做a的平方根,也称二次方根如果_²=a,那么_叫做a的平方根平方根的性质:1、一个正数有两个平方根,它们互为相反数2、0只有一个平方根,是03、负数没有平方根算术平方根:正数a的正的平方根叫a的算术平方根 0的算术平方根是0 开平方:求一个数a的平方根的运算,叫做开平方立方根:如果一个数的立方等于a,那么这个数叫做a的立方根,也称三次方根如果_³=a,那么a是_的立方根立方根的性质:1、正数的立方根是正数2、负数的立方根是负数3、 0的立方根是0 开立方:求一个数的立方根的运算,叫做开立方有效数字:对于一个近似数,从左边第一个不是0的数字起,到末尾数字止,所有的数字都称为这个近似数的有效数字补充:平方根和立方根 1、算术平方根:一般地,如果一个正数_的平方等于a,即_2=a,那么这个正数_就叫做a的算术平方根。
数学八年级苏科版(上册)第一章全等三角形电子课件

∠ C= ∠ E. (全等三角形的对应角相等)
应用新知, 体验成功
例 如图, AD平分∠BAC,AB=AC,△ABD与 △ACD全等吗?BD与CD相等吗?∠B与∠C呢?请说
1. 能够完全重合的图形是全等 图形,全等图形的形状和大小 都相同;
2. 只要我们用心去观察,定会 发现数学之美,生活之美.
苏科八年级 上册
1.2 全等三角形
下列各组图形的形状与大小有什么特点?
(1)
(2)
(3)
(4)
能够完全重合的图形叫做全等图形.
能够完全重合的两个三角形叫做全等三角形.
小试身手
换两个角和一条线段,试试看,是否有同样 的结论.
两角和它们的夹边对应相 等两个三角形全等.
简记为 “角边角”或“ASA” .
A
符 在ABC和DEF中
B
号
C
语
B=E(已知)
BC=EF(已知)
D
言
C=F(已知)
ABC ≌ DEF(A.S.A.)
E
F
做一做
如图,画线段AB=2.6cm,再画∠BAP=45°, ∠ABQ=60°,AP与BQ相交与点C.
试一试,摆一摆
用符号来表示两个全等三角形,并指出它们的对应顶点、对 应边、对应角.
C
B
C
B
O A
A
D
O D
全等三角形对应角所对的边是对应边, 对应边所对的角是对应角.
两个全等三角形的 位置变化了,对应边、 对应角的大小有变化吗? 由此你能得到什么结论?
苏科版数学八年级上册重点知识点汇总

苏科版数学八年级上册重点知识点汇总第一章全等三角形知识导图重点知识点要点一、全等三角形的判定与性质要点二、全等三角形的证明思路SAS HL SSS AAS SAS ASA AAS ASA AAS ⎧→⎧⎪⎪→⎨⎪⎪⎪→⎩⎪⎪→→⎧⎪⎪→⎧⎪⎪⎨⎨⎪→⎨⎪⎪⎪⎪⎪→⎩⎩⎪⎪→⎧⎪⎨→⎪⎩⎪⎩找夹角已知两边找直角找另一边边为角的对边找任一角找夹角的另一边已知一边一角边为角的邻边找夹边的另一角找边的对角找夹边已知两角找任一边要点三、角平分线的性质1.角的平分线的性质定理角的平分线上的点到这个角的两边的距离相等.2.角的平分线的判定定理角的内部到角的两边距离相等的点在角的平分线上.3.三角形的角平分线三角形角平分线交于一点,且到三边的距离相等.一般三角形直角三角形判定边角边(SAS)角边角(ASA)角角边(AAS)边边边(SSS)两直角边对应相等一边一锐角对应相等斜边、直角边定理(HL)性质对应边相等,对应角相等(其他对应元素也相等,如对应边上的高相等)备注判定三角形全等必须有一组对应边相等4.与角平分线有关的辅助线在角两边截取相等的线段,构造全等三角形;在角的平分线上取一点向角的两边作垂线段.要点四、全等三角形证明方法全等三角形是平面几何内容的基础,这是因为全等三角形是研究特殊三角形、四边形、相似图形、圆等图形性质的有力工具,是解决与线段、角相关问题的一个出发点.运用全等三角形,可以证明线段相等、线段的和差倍分关系、角相等、两直线位置关系等常见的几何问题.可以适当总结证明方法.1.证明线段相等的方法:(1)证明两条线段所在的两个三角形全等.(2)利用角平分线的性质证明角平分线上的点到角两边的距离相等.(3)等式性质.2.证明角相等的方法:(1)利用平行线的性质进行证明.(2)证明两个角所在的两个三角形全等.(3)利用角平分线的判定进行证明.(4)同角(等角)的余角(补角)相等.(5)对顶角相等.3.证明两条线段的位置关系(平行、垂直)的方法;可通过证明两个三角形全等,得到对应角相等,再利用平行线的判定或垂直定义证明. 4.辅助线的添加:(1)作公共边可构造全等三角形;(2)倍长中线法;(3)作以角平分线为对称轴的翻折变换全等三角形;(4)利用截长(或补短)法作旋转变换的全等三角形.5.证明三角形全等的思维方法:(1)直接利用全等三角形判定和证明两条线段或两个角相等,需要我们敏捷、快速地发现两条线段和两个角所在的两个三角形及它们全等的条件.(2)如果要证明相等的两条线段或两个角所在的三角形全等的条件不充分时,则应根据图形的其它性质或先证明其他的两个三角形全等以补足条件.(3)如果现有图形中的任何两个三角形之间不存在全等关系,此时应添置辅助线,使之出现全等三角形,通过构造出全等三角形来研究平面图形的性质.第二章轴对称图形知识导图重点知识点要点一、轴对称1.轴对称图形和轴对称(1)轴对称图形如果一个图形沿着某一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.轴对称图形的性质:轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线.(2)轴对称定义:把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,这条直线叫做对称轴.成轴对称的两个图形的性质:①关于某条直线对称的两个图形形状相同,大小相等,是全等形;②如果两个图形关于某条直线对称,则对称轴是任何一对对应点所连线段的垂直平分线;③两个图形关于某条直线对称,如果它们的对应线段或延长线相交,那么它们的交点在对称轴上.(3)轴对称图形与轴对称的区别和联系区别:轴对称是指两个图形的位置关系,轴对称图形是指具有特殊形状的一个图形;轴对称涉及两个图形,而轴对称图形是对一个图形来说的.联系:如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形关于这条轴对称;如果把成轴对称的两个图形看成一个整体,那么它就是一个轴对称图形.2.线段的垂直平分线垂直并且平分一条线段的直线,叫做这条线段的垂直平分线,也叫线段的中垂线.3.作轴对称图形(1)几何图形都可以看作由点组成,我们只要分别作出这些点关于对称轴的对应点,再连接这些点,就可以得到原图形的轴对称图形;(2)对于一些由直线、线段或射线组成的图形,只要作出图形中的一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.4.用坐标表示轴对称点(x,y)关于x轴对称的点的坐标为(x,-y);点(x,y)关于y轴对称的点的坐标为(-x,y);点(x,y)关于原点对称的点的坐标为(-x,-y).要点二、线段、角的轴对称性1.线段的轴对称性(1)线段是轴对称图形,线段的垂直平分线是它的对称轴.(2)线段垂直平分线的性质定理:线段垂直平分线上的点到线段两端的距离相等;(3)线段垂直平分线的性质定理的逆定理:到线段两个端距离相等的点在线段的垂直平分线2.角的轴对称性(1)角是轴对称图形,角的平分线所在的直线是它的对称轴.(2)角平分线上的点到角两边的距离相等.(3)角的内部到角两边距离相等的点在角的平分线上.要点三、等腰三角形1.等腰三角形(1)定义:有两边相等的三角形,叫做等腰三角形.(2)等腰三角形性质①等腰三角形的两个底角相等,即“等边对等角”;②等腰三角形顶角的平分线、底边上的中线与底边上的高线互相重合(简称“三线合一”).特别地,等腰直角三角形的每个底角都等于45°.(3)等腰三角形的判定如果一个三角形有两个角相等,那么这两个角所对的边也相等(即“等角对等边”).2.等边三角形(1)定义:三条边都相等的三角形,叫做等边三角形.(2)等边三角形性质:等边三角形的三个角相等,并且每个角都等于60°.(3)等边三角形的判定:①三条边都相等的三角形是等边三角形;②三个角都相等的三角形是等边三角形;③有一个角为60°的等腰三角形是等边三角形.3.直角三角形的性质定理:直角三角形斜边上的中线等于斜边的一半.第三章勾股定理知识导图重点知识点要点一、勾股定理1.勾股定理:直角三角形两直角边a b 、的平方和等于斜边c 的平方.(即:222a b c +=)2.勾股定理的应用勾股定理反映了直角三角形三边之间的关系,是直角三角形的重要性质之一,其主要应用是:(1)已知直角三角形的两边,求第三边;(2)利用勾股定理可以证明有关线段平方关系的问题;(3)解决与勾股定理有关的面积计算;(4)勾股定理在实际生活中的应用.要点二、勾股定理的逆定理1.勾股定理的逆定理如果三角形的三边长a b c 、、,满足222a b c +=,那么这个三角形是直角三角形.要点诠释:应用勾股定理的逆定理判定一个三角形是不是直角三角形的基本步骤:(1)首先确定最大边,不妨设最大边长为c ;(2)验证:22a b +与2c 是否具有相等关系:若222a b c +=,则△ABC 是以∠C 为90°的直角三角形;若222a b c +>时,△ABC 是锐角三角形;若222a b c +<时,△ABC 是钝角三角形.2.勾股数满足不定方程222x y z +=的三个正整数,称为勾股数(又称为高数或毕达哥拉斯数),显然,以x y z 、、为三边长的三角形一定是直角三角形.要点诠释:常见的勾股数:①3、4、5;②5、12、13;③8、15、17;④7、24、25;⑤9、40、41.如果(a b c 、、)是勾股数,当t 为正整数时,以at bt ct 、、为三角形的三边长,此三角形必为直角三角形.观察上面的①、②、④、⑤四组勾股数,它们具有以下特征:1.较小的直角边为连续奇数;2.较长的直角边与对应斜边相差1.3.假设三个数分别为a b c 、、,且a b c <<,那么存在2a b c =+成立.(例如④中存在27=24+25、29=40+41等)要点三、勾股定理与勾股定理逆定理的区别与联系区别:勾股定理是直角三角形的性质定理,而其逆定理是判定定理;联系:勾股定理与其逆定理的题设和结论正好相反,两者互为逆定理,都与直角三角形有关.第四章实数知识导图重点知识点要点一:平方根和立方根类型项目平方根立方根被开方数非负数任意实数符号表示a±3a性质一个正数有两个平方根,且互为相反数;零的平方根为零;负数没有平方根;一个正数有一个正的立方根;一个负数有一个负的立方根;零的立方根是零;重要结论⎩⎨⎧<-≥==≥=)0()0()0()(22a a a a a a a aa 333333)(aa a a aa -=-==要点二:实数有理数和无理数统称为实数.1.实数的分类①按定义分:实数⎧⎨⎩有理数:有限小数或无限循环小数无理数:无限不循环小数②按与0的大小关系分:实数0⎧⎧⎨⎪⎩⎪⎪⎨⎪⎧⎪⎨⎪⎩⎩正有理数正数正无理数负有理数负数负无理数要点诠释:(1)所有的实数分成三类:有限小数,无限循环小数,无限不循环小数.其中有限小数和无限循环小数统称有理数,无限不循环小数叫做无理数.等;②有特殊意义的数,如π;③有特定结构的数,如0.1010010001…(3)凡能写成无限不循环小数的数都是无理数,并且无理数不能写成分数形式.(4)实数和数轴上点是一一对应的.2.实数与数轴上的点一一对应.数轴上的任何一个点都对应一个实数,反之任何一个实数都能在数轴上找到一个点与之对应.3.三类具有非负性的实数在实数范围内,正数和零统称为非负数.我们已经学习过的非负数有如下三种形式:(1)任何一个实数a 的绝对值是非负数,即|a |≥0;(2)任何一个实数a 的平方是非负数,即2a ≥0;0≥(0a ≥).非负数具有以下性质:(1)非负数有最小值——零;(2)有限个非负数之和仍是非负数;(3)几个非负数之和等于0,则每个非负数都等于0.4.实数的运算数a 的相反数是-a ;一个正实数的绝对值是它本身;一个负实数的绝对值是它的相反数;0的绝对值是0.有理数的运算法则和运算律在实数范围内仍然成立.实数混合运算的运算顺序:先乘方、开方、再乘除,最后算加减.同级运算按从左到右顺序进行,有括号先算括号里.5.实数的大小的比较有理数大小的比较法则在实数范围内仍然成立.(1)实数和数轴上的点一一对应,在数轴上表示的两个数,右边的数总比左边的数大;(2)正数大于0,0大于负数,正数大于一切负数,两个负数比较,绝对值大的反而小;(3)两个数比较大小常见的方法有:求差法,求商法,倒数法,估算法,平方法.要点三、近似数及精确度1.近似数接近准确值而不等于准确值的数,叫做这个精确数的近似数或近似值.一般采用四舍五入法取近似数,只要看要保留位数的下一位是舍还是入.2.精确度近似数中,四舍五入到哪一位,就称这个数精确到哪一位,精确到的这一位也叫做这个近似数的精确度.要点诠释:(1)精确度是指近似数与准确数的接近程度.(2)精确度一般用“精确到哪一位”的形式的来表示,一般来说精确到哪一位表示误差绝对值的大小,例如精确到0.1米,说明结果与实际数相差不超过0.05米.第五章平面直角坐标系知识导图重点知识点要点一、有序数对把一对数按某种特定意义,规定了顺序并放在一起就形成了有序数对,人们在生产生活中经常以有序数对为工具表达一个确定的意思,如某人记录某个月不确定周期的零散收入,可用(13,2000),(17,190),(21,330)…,表示,其中前一数表示日期,后一数表示收入,但更多的人们还是用它来进行空间定位,如:(4,5),(20,12),(13,2),…,用来表示电影院的座位,其中前一数表示排数,后一数表示座位号.要点二、平面直角坐标系平面内两条互相垂直的数轴构成平面直角坐标系,简称直角坐标系.水平的数轴称为x 轴或横轴,向右为正方向;铅直方向的数轴称为y 轴或纵轴,向上为正方向,两轴的交点O 是原点.如下图:要点诠释:(1)两条坐标轴将平面分成4个区域:第一象限、第二象限、第三象限、第四象限,x 轴与y 轴上的点(包括原点)不属于任何一个象限.(2)在平面上建立平面直角坐标系后,坐标平面上的点与有序数对(x,y)之间建立了一一对应关系,这样就将‘形’与‘数’联系起来,从而实现了代数问题与几何问题的转化.(3)要熟记坐标系中一些特殊点的坐标及特征:①x 轴上的点纵坐标为零;y 轴上的点横坐标为零.②平行于x 轴直线上的点横坐标不相等,纵坐标相等;平行于y 轴直线上的点横坐标相等,纵坐标不相等.③关于x 轴对称的点横坐标相等,纵坐标互为相反数;关于y 轴对称的点纵坐标相等,横坐标互为相反数;关于原点对称的点横、纵坐标分别互为相反数.④象限角平分线上的点的坐标特征:一、三象限角平分线上的点横、纵坐标相等;二、四象限角平分线上的点横、纵坐标互为相反数.注:反之亦成立.(4)理解坐标系中用坐标表示距离的方法和结论:①坐标平面内点P(x,y)到x 轴的距离为|y|,到y 轴的距离为|x|.②x 轴上两点A(x 1,0)、B(x 2,0)的距离为AB=|x 1-x 2|;y 轴上两点C(0,y 1)、D(0,y 2)的距离为CD=|y 1-y 2|.③平行于x 轴的直线上两点A(x 1,y)、B(x 2,y)的距离为AB=|x 1-x 2|;平行于y 轴的直线上两点C(x,y 1)、D(x,y 2)的距离为CD=|y 1-y 2|.(5)利用坐标系求一些知道关键点坐标的几何图形的面积常用方法:切割、拼补.要点三、坐标方法的简单应用1.用坐标表示地理位置(1)建立坐标系,选择一个适当的参照点为原点,确定x 轴、y 轴的正方向;(2)根据具体问题确定适当的比例尺,在坐标轴上标出单位长度;(3)在坐标平面内画出这些点,写出各点的坐标和各个地点的名称.要点诠释:(1)我们习惯选取向东、向北分别为x 轴、y 轴的正方向,建立坐标系的关键是确定原点的位置.(2)确定比例尺是画平面示意图的重要环节,要结合比例尺来确定坐标轴上的单位长度.2.用坐标表示平移(1)点的平移点的平移引起坐标的变化规律:在平面直角坐标中,将点(x,y)向右(或左)平移a 个单位长度,可以得到对应点(x+a,y)(或(x-a,y));将点(x,y)向上(或下)平移b 个单位长度,可以得到对应点(x,y+b)(或(x,y-b)).要点诠释:上述结论反之亦成立,即点的坐标的上述变化引起的点的平移变换.(2)图形的平移在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减去)一个正数a,相应的新图形就是把原图形向右(或向左)平移a 个单位长度;如果把它各个点的纵坐标都加(或减去)一个正数a,相应的新图形就是把原图形向上(或向下)平移a 个单位长度.要点诠释:平移是图形的整体运动,某一个点的坐标发生变化,其他点的坐标也进行了相应的变化,反过来点的坐标发生了相应的变化,也就意味着点的位置也发生了变化,其变化规律遵循:“右加左减,纵不变;上加下减,横不变”.第六章一次函数知识导图重点知识点变化的世界函数建立数学模型应用概念选择方案概念再认识表示方法图象性质一次函数(正比例函数)一元一次方程一元一次不等式二元一次方程组与数学问题的综合与实际问题的综合列表法解析法图象法要点一、函数的相关概念一般地,在一个变化过程中.如果有两个变量x 与y ,并且对于x 的每一个确定的值,y 都有唯一确定的值与其对应,那么我们就说x 是自变量,y 是x 的函数.y 是x 的函数,如果当x =a 时y =b ,那么b 叫做当自变量为a 时的函数值.函数的表示方法有三种:解析式法,列表法,图象法.要点二、一次函数的相关概念一次函数的一般形式为y kx b =+,其中k 、b 是常数,k ≠0.特别地,当b =0时,一次函数y kx b =+即y kx =(k ≠0),是正比例函数.要点三、一次函数的图象及性质1、函数的图象如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.要点诠释:直线y kx b =+可以看作由直线y kx =平移|b |个单位长度而得到(当b >0时,向上平移;当b <0时,向下平移).说明通过平移,函数y kx b =+与函数y kx =的图象之间可以相互转化.2、一次函数性质及图象特征掌握一次函数的图象及性质(对比正比例函数的图象和性质)要点诠释:理解k 、b 对一次函数y kx b =+的图象和性质的影响:(1)k 决定直线y kx b =+从左向右的趋势(及倾斜角α的大小——倾斜程度),b 决定它与y 轴交点的位置,k 、b 一起决定直线y kx b =+经过的象限.(2)两条直线1l :11y k x b =+和2l :22y k x b =+的位置关系可由其系数确定:12k k ≠⇔1l 与2l 相交;12k k =,且12b b ≠⇔1l 与2l 平行;12k k =,且12b b =⇔1l 与2l 重合;(3)直线与一次函数图象的联系与区别一次函数的图象是一条直线;特殊的直线x a =、直线y b =不是一次函数的图象.要点四、用函数的观点看方程、方程组、不等式方程(组)、不等式问题函数问题从“数”的角度看从“形”的角度看求关于x 、y 的一元一次方程ax b +=0(a ≠0)的解x 为何值时,函数y ax b =+的值为0?确定直线y ax b =+与x 轴(即直线y =0)交点的横坐标求关于x 、y 的二元一次方程组1122=+⎧⎨=+⎩,.y a x b y a x b 的解.x 为何值时,函数11y a x b =+与函数22y a x b =+的值相等?确定直线11y a x b =+与直线22y a x b =+的交点的坐标求关于x 的一元一次不等式ax b +>0(a ≠0)的解集x 为何值时,函数y ax b =+的值大于0?确定直线y ax b =+在x 轴(即直线y =0)上方部分的所有点的横坐标的范围。
苏科版八年级上册数学第一章全等三角形1-2全等三角形( 含答案)

苏科版八年级上册数学第一章全等三角形1.2全等三角形一、选择题1.如图,小强利用全等三角形的知识测量池塘两端M ,N 之间的距离,如果△PQO ≌△NMO ,那么只需测出其长度的线段是()A .POB .PQC .MOD .MQ2.如图,ABC CDA ∆≅∆,则下列结论错误的是()A .AC CA =B .AB AD =C .ACB CAD ∠=∠D .B D ∠=∠3.下列说法:①全等三角形的形状相同,大小相等. ②全等三角形的对应边相等;③全等三角形的对应角相等;④全等三角形的周长,面积分别相等;⑤所有的等边三角形都是全等三角形.其中正确的说法有()A.5个B.4个C.3个D.1个4.已知△ABC≌△A´B´C´,且△ABC 的周长为20,AB=8,BC=5,则A´C´等于()A.5B.6C.7D.85.已知图中的两个三角形全等,则么a 的度数是().6.如图,△ABC ≌△DEF ,则此图中相等的线段有()A .1对B .2对C .3对D .4对7.如图,在Rt △ABC 中,∠ACB =90°,∠A =50°,将其折叠,使点A 落在边CB 上的A'处,折痕为CD ,则∠A'DB 等于().A .40°B .30°C .20°D .10°8.如图,将△AOB 绕点O 按逆时针方向旋转45°后得到△A'OB',若∠AOB =15°,则∠AOB'的度数是().A .25°B .30°C .35°D .40°二、填空题9.已知△AB C ≌△A'B'C',若△A'B'C'的周长为8cm ,则△ABC 的周长为cm .10.如图,若△ABC ≌△EFC,且CF=3cm,∠EFC=64°,则BC=cm,∠B=11.如图,△ABD ≌△CBD ,如果∠A=80°,∠ABC=60°,则∠ADC=°12.如图,ABC ADE ∆≅∆,25EAC ∠=︒,则BAD ∠=︒.13.如图,在矩形ABCD 中,AB =10,BC =5,点E 、F 分别在AB 、CD 上,将矩形ABCD 沿EF 折叠,使点A 、D 分别落在矩形ABCD 外部的点A 1、D 1处,则阴影部分图形的周长为14.已知△ABC ≌△A ′B ′C ′,△ABC 的三边为3、m 、n,△A ′B ′C ′的三边为5、p 、q,若△ABC 的各边都是整数,则m+n+p+q 的最大值为__________.15.如图所示,△ABE 和△ACD 是分别沿着AB ,AC 边翻折180°形成的,若∠BAC =150°,则∠θ的度数是.16.如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B 到C 的方向平移到DEF ∆的位置,10AB =,4DO =,平移距离为6,则阴影部分面积为三、解答题17.如图所示,已知△ABD≌△ACE,∠B=∠C,试指出这两个三角形的对应边和对应角.AB CDEO18.如图,在△ADC 中,∠ADC =90°,△AD C ≌△BDH ,那么BH 与AC 互相垂直吗?请说明理由.19.如图,已知△ABE≌△ADC,∠1=36°,∠DAE=76°,∠B=25°.求∠DAC、∠C的度数.20.如图,已知△EFG≌△NMH,∠F与∠M是对应角.若EF=2.1cm,FH=1.1cm,HM=3.3cm,求MN和HG的长度.21.如图,△ABC≌△ADE,∠BAD=60°.求证:△ACE是等边三角形.22.如图,用同样粗细,同种材料的金属构制两个全等三角形,△ABC和△DEF,已知∠B=∠E,∠C=∠F,AC的质量为25克,EF的质量为30克,求金属丝AB的质量的取值范围.参考答案:1.B2.B3.B4.C5.D6.D7.D8.B9.810.3,64°11.140°12.2513.3014.2215.6016.4817.解:对应边有:AB和AC,AD和AE,BD和CE;对应角有:∠BAD=∠CAE,∠ADB=∠AEC,∠B=∠C.18.∵△ADC≌△BDH,∴∠B=∠A.又∵∠ADC=90°,∴∠A+∠C=90°,∴∠B+∠C=90°,∴∠BEC=90°,∴BH⊥AC19.43°20.2.2cm21.解:∵△ABC≌△ADE,∴∠BAC=∠DAE,AC=AE.∴∠BAD+∠DAC=∠CAE+∠DAC.即∠BAD=∠CAE.∵∠BAD=60°,∴∠CAE=60°.又∵AC=AE,∴△ACE是等边三角形22.∵△ABC≌△DEF,∴BC=EF.故BC的质量应等于EF的质量30克,∴(30-25)克<AB的质量<(30+25)克,即5克<AB的质量<55克.。
苏科版八年级上册数学第一章 全等三角形 含答案
苏科版八年级上册数学第一章全等三角形含答案一、单选题(共15题,共计45分)1、如图,把菱形ABCID向右平移至DCEF的位置,作EG⊥AB,垂足为G,EG与CD相交于点K,GD的延长线交EF于点H,连接DE.则下列结论:①DG=DE;②∠DHE= ∠BAD;③EF+FH=2KC;④∠B=∠EDH.则其中所有成立的结论是()A.①②③④B.①②④C.②③④D.①③2、如图,AC和BD相交于O点,若OA=OD,用“SAS”证明△AOB≌△DOC还需()A.AB=DCB.OB=OCC.∠C=∠DD.∠AOB=∠DOC3、下列各组图案中,不是全等形的是( )A. B.C. D.4、下列判断正确的个数是()①能够完全重合的两个图形全等;②两边和一角对应相等的两个三角形全等;③两角和一边对应相等的两个三角形全等;④全等三角形对应边相等.A.1个B.2个C.3个D.4个5、如图,AD平分,BD平分,于E,交ED的延长线于点F,给出以下三个结论:①;②;③,其中正确的结论共有()A.0个B.3个C.2个D.1个6、如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是()A.BD=CDB.AB=ACC.∠B=∠CD.∠BAD=∠CAD7、已知,如图△ABC≌△ADE,AE=AC,∠CAE=20°,则∠BED的度数为()A.60°B.90°C.80°D.20°8、如图,已知的3条边和3个角,则能判断和全等的是()A.甲和乙B.乙和丙C.只有乙D.只有丙9、如图,,和,和为对应边,若,,则等于()A. B. C. D.10、如图,D,E分别是AB,AC上的点,BE与CD交于点F,给出下列三个条件:①∠DBF=∠ECF;②∠BDF=∠CEF;③BD=CE.两两组合在一起,共有三种组合:(1)①②;(2)①③;(3)②③问能判定AB=AC的组合的是()A.(1)(2)B.(1)(3)C.(2)(3)D.(1)(2)(3)11、用直尺和圆规操作一个角等于已知角的依据是()A.SASB.SSSC.AASD.ASA12、如图,△AOC≌△BOD,∠A和∠B,∠C和∠D是对应角,下列几组边中是对应边的是()A.AC与BDB.AO与ODC.OC与OBD.OC与BD13、在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,且AE=AD.连接DE交对角线AC于H,连接BH.下列结论:△ACD≌△ACE;②△CDE为等边三角形;③=2;④=.其中结论正确的是()A.只有①②B.只有①②④C.只有③④D.①②③④14、如图,AB∥DE,CD=BF,若要证明△ABC≌△EDF,还需补充的条件是()A.AC=EFB.AB=EDC.∠B=∠ED.不用补充15、如图:在△ABC中,AD是∠BAC的平分线,DE⊥AC于E,DF⊥AB于F,且FB=CE,则下列结论:①DE=DF,②AE=AF,③BD=CD,④AD⊥BC.其中正确的个数有()A.1个B.2个C.3个D.4个二、填空题(共10题,共计30分)16、如图所示,AB=AC,再添加一个条件________,就可以使△ABE≌△ACD.17、如图,已知DE∥BC,AB∥CD,E为AB的中点,∠A=∠B.下列结论:①AC=DE;②CD=AE;③AC平分∠BCD;④O点是DE的中点;⑤AC=AB.其中正确的序号有________.18、AD是△ABC的边BC上的中线,AB=5,AD=4,则AC的取值范围是________.19、如图,△ABC的面积为9cm2, BP平分∠ABC,AP⊥BP于P,连接PC,则△PBC的面积为________cm2.20、如图,和中,,在不添加任何辅助线的情况下,请你添加一个条件________,使和全等.21、如图所示,AD=AE,要使△ABE≌△ACD,应添加一个条件,可以是________.22、如图,有一个直角三角形ABC,∠C=90°,AC=10,BC=5,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于 AC的射线AX上运动,当AP=________时,才能使△ABC与△QPA全等.23、如图,已知,点A、D、B、F在一条直线上,要使,还需添加一个条件,这个条件可以是________24、如图,中,,,,,点、分别在边和射线上运动,若与全等,则的长是________.25、如图,△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过C作CF ⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D,则下列结论:①若BD=4,则AC=8;②AB=CD;③∠DBA=∠ABC;④S△ABE =S△ACE;⑤∠D=∠AEC;⑥连接AD,则AD=CD.其中正确的是________.(填写序号)三、解答题(共5题,共计25分)26、如图,已知AB=AD,且AC平分∠BAD,求证:BC=DC27、如图所示,内一点满足于点,且,.找出图中一条与相等的线段,并加以证明.28、已知:AB⊥BC,AD⊥DC,∠1=∠2,求证:29、如图,于于.求证:.30、如图,A、D、F、B在同一直线上,AD=BF,AE=BC,且AE∥BC.求证:△AEF ≌△BCD.参考答案一、单选题(共15题,共计45分)1、A2、B3、D4、C5、B6、B7、D8、B9、A10、C11、B12、A13、B14、B15、D二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、25、三、解答题(共5题,共计25分)26、27、29、30、。
苏科版八年级上册数学第一章 全等三角形 含答案
苏科版八年级上册数学第一章全等三角形含答案一、单选题(共15题,共计45分)1、如图,D在AB上,E在AC上,且∠B=∠C,那么补充下列一个条件后,仍无法判定△ABE≌△ACD的是()A.AD=AEB.∠AEB=∠ADCC.BE=CDD.AB=AC2、下列命题中正确的是()A.周长相等的两个三角形全等B.关于某条直线对称的两个三角形全等 C.顶角相等的两个等腰三角形全等 D.两边和一角对应相等的两个三角形全等3、如图所示,△ACB≌A′CB′,∠BCB′=30°,则∠ACA′的度数为()A.20°B.30°C.35°D.40°4、下列语句正确的是()A.对角线互相垂直的四边形是菱形B.有两边及一角对应相等的两个三角形全等C.矩形的对角线相等D.平行四边形是轴对称图形5、如图,在正方形中,是对角线上一点,且满足.连接并延长交于点,连接,过点作于点,延长交于点.在下列结论中:①;②;③;④,其中正确的结论有()个A.1B.2C.3D.46、如图,线段与交于点,且,则下面的结论中错误的是()A. B. C. D.7、如图,△ABC 和△DEF 中,给出下列四组条件:①AB=DE, BC=EF, AC=DF②AB=DE, ∠B=∠E, BC=EF③∠B=∠E, BC=EF, ∠C=∠F ④∠A=∠D, ∠B=∠E, AB=DF其中能使△ABC≌△DEF 的条件有()A.1 组B.2 组C.3 组D.4 组8、如图,用直尺和圆规作一个角等于已知角,能得出的依据是()A.(SAS)B.(SSS)C.(ASA)D.(AAS)9、下列命题的逆命题正确的是()A.如果两个角都是45°,那么它们相等B.全等三角形的周长相等 C.同位角相等,两直线平行 D.若a=b,则10、下列命题:①两直线平行,内错角相等;②对角线互相平分的四边形是平行四边形;③全等三角形对应角相等;④平行四边形的两组对边分别相等.其逆命题成立的个数有()A.1个B.2个C.3个D.4个11、如图,亮亮书上的三角形被墨迹污染了一部分,他根据所学的知识很快就画了一个与书上完全一样的三角形,那么亮亮画图的依据是( )。
苏科版八年级上册数学第一章 全等三角形含答案(夺冠系列)
苏科版八年级上册数学第一章全等三角形含答案一、单选题(共15题,共计45分)1、如图,和都是等边三角形,点、、在同一条直线上,、分别与、交于点、,和交于点,有如下结论:① 是等边三角形;② ;③ ≌ ;④ ;⑤ 平分;⑥ ;⑦ .其中错误的结论的个数是()A.1B.2C.3D.42、如图,∠CAB=∠DBA,再添加一个条件,不一定能判定△ABC≌△BAD的是()A.AC=BDB.∠1=∠2C.AD=BCD.∠C=∠D3、下列条件能判定△ABC≌△DEF的一组是()A.∠A=∠D,∠C=∠F,AC=EFB.AB=DE,BC=EF,∠A=∠D C.∠A=∠D,∠B=∠E,∠C=∠F D.AB=DE,AC=DF,BC边上的高等于EF边上的高4、如图,AC、BD相交于点O,∠1=∠2,若用“SAS”说明△ACB≌△BDA,则还需要加上条件()A.AD=BCB.BD=ACC.∠D=∠CD.OA=AB5、如图,已知直线AB:y=分别交x轴、y轴于点B、A两点,C(3,0),D、E分别为线段AO和线段AC上一动点,BE交y轴于点H,且AD=CE.当BD+BE的值最小时,则H点的坐标为()A. B.(0,5) C.(0,4) D.6、如图的中,,且为上一点.今打算在上找一点,在上找一点,使得与全等,以下是甲、乙两人的作法:(甲)连接,作的中垂线分别交、于点、点,则、两点即为所求(乙)过作与平行的直线交于点,过作与平行的直线交于点,则、两点即为所求对于甲、乙两人的作法,下列判断何者正确?()A.两人皆正确B.两人皆错误C.甲正确,乙错误D.甲错误,乙正确7、如图是两个全等三角形,图中的字母表示三角形的边长,则∠1等于()A.60°B.54°C.56°D.66°8、下列条件中,能利用“ ”判定△ ≌△A′B′C′的是()A.AB=A′B′,AC=A′C′,∠C=∠C′B.AB=A′B′,∠A=∠A′,BC=B′C′ C.AC=A′C′,∠C=∠C′,BC=B′C′ D.AC=A′C′,∠A=∠A′,BC=B′C′9、如图,在△ABC中,AC=AB,∠BAC=90°,BD平分∠ABC,与AC相交于点F,CD⊥BD,垂足为D,交BA的延长线于点E,AH⊥BC交BD于点M,交BC于点H,下列选项不正确的是()A.∠E=67.5°B.∠AMF=∠AFMC.BF=2CDD.BD=AB+AF10、如图,用直尺和圆规画∠AOB的平分线OE,其理论依据是()A.SASB.ASAC.AASD.SSS11、如图,在中,,直角的顶点是的中点,两边、分别交、于点、,当在内绕点旋转时,下列结论错误的是()A. B. 为等腰直角三角形 C. D.12、如图,已知MB=ND,∠MBA=∠NDC,下列哪个条件不能判定△ABM≌△CDN ()A.AM=CNB.AB=CDC.AM∥CND.∠M=∠N13、如图是作的作图痕迹,则此作图的已知条件是()A.已知两边及夹角B.已知三边C.已知两角及夹边D.已知两边及一边对角14、如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加一个条件是()A.AD∥BCB.DF∥BEC.∠A=∠CD.∠D=∠B15、下列说法中不正确的是( )A.如果两个三角形全等,那么这两个三角形相似B.如果两个三角形相似,且相似比为1,那么这两个三角形必全等C.如果两个三角形都与另一个三角形相似,那么这两个三角形相似D.如果两个三角形相似,那么它们一定能互相重合二、填空题(共10题,共计30分)16、如图,AB=AC , BD=CD ,∠B=20° ,则∠C=________°.17、如图,已知,要使,还需添加一个条件,则可以添加的条件是________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《全等三角形》同步练习姓名
一、选择题
1.(2018•贵州黔西南州)下列各图中A.B.c 为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC 全等的是()
A.甲和乙B.乙和丙C.甲和丙D.只有丙
2.AD=AE , AB=AC , BE、CD交于F , 则图中相等的角共有()
A.5对
B.4对
C.3对
D.2对
3.如图,OA=OB,OC=OD, ∠O=60°, ∠C=25°则∠BED的度数是 ( )
A.70°
B. 85°
C. 65°
D. 以上都不对
4.已知:如图,△ABC≌△DEF,AC∥DF,BC∥EF.则不正确的等式是()
A.AC=DF
B.AD=BE
C.DF=EF
D.BC=EF
第2题第3题第 4题第5题
5.如图 , ∠A=∠D , OA=OD , ∠DOC=50°, 求∠DBC的度数为()
A.50°
B.30°
C.45°
D.25°
6.(2018•河北)已知:如图,点P在线段AB外,且PA=PB,求证:点P在线段AB的垂直平分线上,在证明该结论时,需添加辅助线,则作法不正确的是()
A.作∠APB的平分线PC交AB于点C
B.过点P作PC⊥AB于点C且AC=BC
C.取AB中点C,连接PC
D.过点P作PC⊥AB,垂足为C
7.如图,用直尺和圆规作一个角等于己知角的示意图如图所示,则说明∠A'O'B'=∠AOB的依据是()
A、SSS
B、SAS
C、ASA
D、AAS
8.下列说法:①如果两个三角形可以依据“AAS”来判定全等,那么一定也可以依据“ASA”来判定它们全等;②如果两个三角形都和第三个三角形不全等,
那么这两个三角形也一定不全等;
C
E
D
B
O
A
③要判断两个三角形全等,给出的条件中至少要有一对边对应相等.其中正确的是()A.①和②B.②和③C.①和③D.①②③
9.如图所示是5×5的正方形网格图,以点D,E为两个顶点作位置不同的格点三角形(三个顶点在正方形格点上的三角形),使所作的格点三角形与△ABC全等,这样的格点三角形最多可以画出( )
A.2个B.4个C.6个D.8个
10.(2018•临沂)如图,∠ACB=90°,AC=BC.AD⊥CE,BE⊥CE,垂足分别是点D、E,AD=3,BE=1,则DE的长是()
A.B.2 C.2D.
二、填空题
1.(2018•金华、丽水)如图,△ABC 的两条高AD ,BE相交于点 F ,请添加一个条件,使得△ADC≌△BEC(不添其他字母及辅助线),你添加的条件是.
2.如图,∠1=∠2,由AAS 判定△ABD ≌△ACD ,则需添加的条件是____________.
3.如图,ABC △中,∠B =∠C ,D ,E ,F 分别在AB ,BC ,AC 上,且BD CE ,=DEF B ∠∠
求证:=ED EF .
证明:∵∠DEC =∠B +∠BDE ( ), 又∵∠DEF =∠B (已知),
∴∠______=∠______(等式性质).
在△EBD 与△FCE 中, ∠______=∠______(已证),
______=______(已知),
∠B =∠C (已知), ∴EBD FCE △≌△( ).
∴ED =EF( ).
4.如图,△ACD≌△ECB,A 、C 、B 在一条直线上,且
A 和E 是一对对应顶点,如果∠BCE=1300,那么将△ACD
绕着C 点顺时针旋转 度与△ECB 重合.
5.AD 是△ABC 的边BC 上的中线,AB =12,AC =8,则边BC 的取值范围是 ;中线AD 的取值范围是 .
6.如图,△ABC ≌△ADE ,BC 的延长线经过点E ,交AD 于F ,∠ACB =∠AED =105°,∠CAD =10°,∠B =50°,则∠EAB = °,∠DEF = °.
三、简答题:
1.如图,△ABC ≌△A’B ’C ’,AD 、A’D’分别是△ABC 、△A’B’C’的高.
试用全等识别法说明AD=A’D’.
2.(2018·湖南怀化)已知:如图,点 A .F ,E .C 在同一直线上,AB ∥DC,AB=CD ,
∠B=∠D .
A
D E
C
B F A
B C D 12
(1)求证:△ABE ≌△CDF ;
(2)若点 E ,G 分别为线段 F C ,FD 的中点,连接 E G ,且 E G=5,求 A B 的长.
3.如图,△ABC 的形状大小确定,将AB 边绕点A 顺时针旋转90°至AE 处,
这时AC 就跟着旋转到AD 处,试说明BC ⊥DE .
4.如图,AB//CD ,AB=CD ,过AC 中点O 的直线分别交AD 、BC 于点E 、F ,试说明OF=OE
5.已知:∠AOB (如图) 求作:(1)∠AOB 的平分线OC ;
(2)作射线OD ⊥OC ;(3)在OC 上取一点P ,作出点P 到∠AOB
两边的垂线段,并比较这两条垂线段的大小关系。
(要求保留作图痕迹,不写作法和证明过程) .
E
C
D A O B
6.已知:如图,A F C D ,,,四点在同一直线上,ABC DEF △≌△
求证:(1)AB ∥DE ,(2)AF =DC
7.(2018•江苏苏州)如图,点 A ,F ,C ,D 在一条直线上,AB ∥D E ,AB=DE ,AF=DC .求 证:BC ∥E F .
8.在数学课本中我们研究过这样一道题目:
(1)如图①,∠ACB =90°,AC =BC ,BE ⊥MN ,AD ⊥MN ,垂足分别为E ,D .图中哪条线段与AD 相等?
(2)试问在图①这种情况下线段DE ,AD ,BE 具有怎样的等量关系?请写出来,不需要说明理由;
(3)当直线CE 绕点C 旋转到图②中直线MN 的位置时,试问DE ,AD ,BE 具有怎样的等量关系?请写出这个等量关系,并说明理由.
A D F
C B
E。
