华师大版八年级数学上册13.2 三角形全等的判定(第4课时 A.S.A.)课件
华师大版八年级数学上册《13.2.3三角形全等的判定》课件
结论:
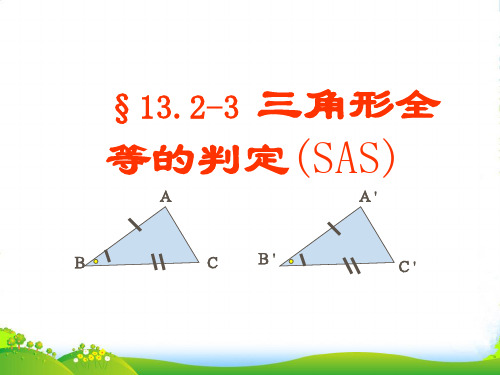
两边及其夹角分别相等 的两个三角形全等(简 记为S.A.S.或边角边)
温馨提示:
两边及其夹角分别相等的两个三角形 全等(简记为S.A.S.或边角边)
用符号语言表达为:
A
AB=DE
在△ABC与△DEF中 ∠B=∠E B BC=EF
C D
∴△ABC≌△DEF(SAS) E
F
分别找出各题中的全等三角形
探究新知
A B
因铺设电线的需要,要 在池塘两侧A、B处各埋 设一根电线杆(如图), 因无法直接量出A、B两 点的距离,现有一足够的 米尺。请你设计一种方案, 粗略测出A、B两杆之间 的距离。。
小明的设计方案:先在池塘 旁取一个能直接到达A和B处的 点C,连结AC并延长至D点, 使AC=DC,连结BC并延长至E 点,使BC=EC,连结CD,用 米尺测出DE的长,这个长度就 等于A,B两点的距离。请你说 明理由。 AC=DC
应该有两种情况:一种是角夹在两条边的 中间,形成两边夹一角;另一情况是角不 夹在两边的中间,形成两边一对角。
思考
如果已知两个三角形有两边一角对应
相等时,应分为几种情形讨论?
A
A
B
C
B
C
A'
A'
B'
C'
边-角-边
第一种
B'
C'
边-边-角
第二种
做一做:画△ABC,使AB=3cm,AC=4cm。
这样画出来的三角形与同桌所画的三角 形进行比较,它们互相重合吗?
A
B
40°
A
B
DC
D
C
(2)
F
△ADC≌△CBA 根据“SAS”
八年级数学上册第十三章全等三角形13.2三角形全等的判定-角边角教案新版华东师大版

13.2 三角形全等的判定-角边角教学目标1.三角形全等的条件:角边角、角角边.2.三角形全等条件小结.3.掌握三角形全等的“角边角”“角角边”条件.4.能运用全等三角形的条件,解决简单的推理证明问题.教学重点已知两角一边的三角形全等探究.教学难点灵活运用三角形全等条件证明.教学过程Ⅰ.提出问题,创设情境1.复习:(1)三角形中已知三个元素,包括哪几种情况?三个角、三个边、两边一角、两角一边.(2)到目前为止,可以作为判别两三角形全等的方法有几种?各是什么?两种:①定义;②S.A.S.2.在三角形中,已知三个元素的四种情况中,我们研究了三种,今天我们接着探究已知两角一边是否可以判断两三角形全等呢?Ⅱ.导入新课问题1:三角形中已知两角一边有几种可能?1.两角和它们的夹边.2.两角和其中一角的对边.问题2:三角形的两个内角分别是60°和40°,它们的夹边为4.5cm,你能画一个三角形同时满足这些条件吗?将你画的三角形剪下,与同伴比较,观察它们是不是全等,你能得出什么规律?将所得三角形重叠在一起,发现完全重合,这说明这些三角形全等.提炼规律:两角和其夹边对应相等的两个三角形全等(可以简写成“角边角”或“A.S.A.”).问题3:如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF,△ABC与△DEF全等吗?能利用角边角条件证明你的结论吗?D C AB FE证明:∵∠A +∠B +∠C =∠D +∠E +∠F =180°∠A =∠D ,∠B =∠E∴∠A +∠B =∠D +∠E∴∠C =∠F在△ABC 和△DEF 中∴△ABC ≌△DEF (A.S.A.).两个角和其中一角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS ”). 小试牛刀:例:如图,∠ABC =∠DCB ,∠ABD =∠DCA ,试说明:AB =DC .解:因为∠ABC =∠DCB ,∠ABD =∠DCA ,所以∠ABC -∠ABD =∠DCB -∠DCA ,即∠DBC =∠ACB ,∵∠ABC =∠DCB ,BC =CB (公共边),∠ACB =∠DBC ,∴△ABC ≌△DCB (A.S.A )∴AB =DC (全等三角形的对应边相等).试一试:如图,D 在AB 上,E 在AC 上,AB =AC ,∠B =∠C .求证:AD =AE .【解析】AD 和AE 分别在△ADC 和△AEB 中,所以要证AD =AE ,只需证明△ADC ≌△AEB 即可.证明:在△ADC 和△AEB 中所以△ADC ≌△AEB (A.S.A.)所以AD =AE .Ⅲ.随堂练习(一)课本练习1.2.(二)补充练习图中的两个三角形全等吗?请说明理由.50︒50︒45︒45︒DC A B (1)29︒29︒DC A B (2)E【答案】图(1)中由“A .S.A.”可证得△ACD ≌△ACB .图(2)由“A .A.S.”可证得△ACE ≌△BDC . Ⅳ.课时小结至此,我们有五种判定三角形全等的方法:1.全等三角形的定义2.判定定理:边角边(S.A.S.)角边角(A.S.A.)角角边(A.A.S.)推证两三角形全等时,要善于观察,寻求对应相等的条件,从而获得解题途径.Ⅴ.作业1.课本习题。
八年级数学上册 13.2 三角形全等的判定(第4课时 A.S.A.)课件 (新版)华东师大版

(角边角 (biān jiǎo))
第三页,共19页。
(角角边)
如图,已知两个(liǎnɡ ɡè)角和一条线段 ,以这两个(liǎnɡ ɡè)角为内角,以这条 线段为这两个(liǎnɡ ɡè)角的夹边,画一 个三角形.
M
N C
600
400
A
4cm
B
步骤(bùzhòu):
图 19。2。7
A
A′口答:BC NhomakorabeaB′
C′
1.两个直角三角形中,斜边和一锐角对应(duìyìng)相等,这两个直角 三角形全等吗?为什么?
答:全等,根据(gēnjù)A.A.S.
2.两个直角三角形中,有一条直角边和一锐角(ruìjiǎo)对应相等,这 两个直角三角形全等吗?为什么?
答:全等,根据A.S.A.
第十页,共19页。
第十六页,共19页。
D
已知,如图,∠1=∠2,∠C=∠D
求证(qiúzhèng):AC=AD。
证明:在△ABD和△ABC中 ∵∠1=∠2 (已知)
1
A2
B
∠D=∠C(已知)
AB=AB(公共(gōnggòng)边)
C
∴△ABD≌△ABC (AAS)
∴AC=AD (全等三角形对应边相等)
第十七页,共19页。
如图:△ABC是等腰三角形,AD、 BE分别(fēnbié)是∠A、∠B的角 平分线,△ABD和△BAE全等吗? 试说明理由.
若改为(:ɡǎAiD、wéBiE)分:别AD(、fēBnEb分ié别) 是两腰上上的的高中,线△,A△BDA和BD△和BAE △全等BA吗E全?等试吗说?明试理说由明. 理由.
结 论 有两角和它们中的一边(yībiān)对应相等的
2022年华东师大版数学八上《三角形全等的判定4》精品课件

以后,如果没 有特别说明, 我们总假设所 给出的式子是 有意义的.本 例中我们约定
a 0.
解: (1)a8a3a83a5
( 2 ) ( a ) 1 0 ( a ) 3 ( a ) 1 0 3 ( a ) 7 a 7 ( 3 ) ( 2 a ) 7 ( 2 a ) 4 ( 2 a ) 7 4 ( 2 a ) 3 8 a 3
(3)根据“A.A.S.〞需添加条件 ∠B=∠C .
D C
B D
C
“S.S.S.”判定三角形全等
假设两个三角形有三个角对应相等,那么这两个三角形是
否全等? 画△ABC,其中∠A=50°,∠B=60°,∠C=70°.
A
A
A 50°
50°
B 60°70°C
B B
60°
70°C
C
三个角对应相等的两个三角形不一定全等.
当堂练习
1.如图,AB=CD,AC=BD,△ABC和△DCB是否全等?请完 成以下解题步骤.
解: △ABC≌△DCB. 理由如下: 在△ABC和△DCB,
AB = DC,
A
=Ⅴ
BDⅤ=C来自AC = DB,BC = CB,
△ABC ≌ △DCB〔 S.S.S.〕
2.如图,D、F是线段BC上的两点,AB=CE,AF=DE,要使
a(4cm)的长为半径画圆弧;两弧交于
点C.
3.连结AC、BC.
把你画的三角形与 其他同学画的三角
△ABC即为所求. 形相比较,它们全
等吗?
B
知识要点
“边边边〞判定方法 文字语言:三边分别相等的两个三角形全等. 〔简写为“边边边〞或“S.S.S.〞〕 A
几何语言:
在△ABC和△ DEF中, AB=DE,
华师版八年级数学上册第13章2 三角形全等的判定

解:∵△ACE≌△BDF,AC=2,∴ BD=AC=2.
又∵AB=8,∴CD=AB-AC-BD=4.
知3-练
3-1. [中考·乐山]如图,AB和CD相交于点O,AC//BD,点O 为AB的中点,求证:AC=BD.
证明:∵AC∥BD,∴∠A=∠B,∠C=∠D. ∵点 O 为 AB 的中点,∴OA=OB.
在△BCE和△ADF中,ቐ∠CBE=∠DAF, BC=AD,
∴△BCE≌△ADF(A.A.S.). ∴ CE=DF.
知5-练
5-1. 如图是乐乐荡秋千的侧面示意图,静止时秋千位于铅 垂线BD上(BD⊥DE),转轴B到地面的距离BD=2.5 m. 乐乐在荡秋千的过程中, 当秋千摆动到最高点A时, 测得点A到BD的距离AC=1.5 m(AC⊥BD于点C),当 他从A处摆动到A′处时,测得点A′到BD的 距离A′F=BC(A′F⊥BD于点F),已知 秋千的绳长固定不变(即 BA=BA′), 求FD的长度.
需寻找的条件
直 角 一锐角(A)
三
角 形 斜边(H)
A.S.A.或 A.A.S.
H.L.或 A.A.S.
可证直角与已知锐角的夹 边对应相等或锐角(或直角) 的对边对应相等
可证一条直角边对应相等 或证一锐角对应相等
续表:
知5-讲
已知对应 可选择的 相等的元素 判定方法
需寻找的条件
直 角 三 角
H.L.或
已知对应 可选择的 相等的元素 判定方法
需寻找的条件
锐角 三角
两边(SS)
S.S.S.或 S.A.S.
形或
钝角 三角
形
一边及其邻 角(SA)
S.A.S.或 A.S.A.或
A.A.S.
2019年八年级数学上册13.2三角形全等的判定第4课时华东师大版

◎第二阶
◎第三阶
)
◆知识导航
◆典例导学
◆反馈演练 (
◎第一阶
◎第二阶
◎第三阶
)
◆知识导航
◆典例导学
◆反馈演练 (
◎第一阶
◎第二阶
◎第三阶
)
◆知识导航
◆典例导学
◆反馈演练 (
◎第一阶
◎第二阶
◎第三阶
)
◆知识导航
◆典例导学
◆反馈演练 (
◎第一阶
◎第二阶
◎第三阶
)
◆知识导航
◆典例导学
◆反馈演练 (
◎第一阶
◎第二阶
◎第三阶
)
◆知识导航
◆典例导学
◆反馈演练 (
◎第一阶
◎第二阶
◎第三阶
)
◆知识导航
◆典例导学
◆反馈演练 (
◎第一阶
◎第二阶
◎第三阶
)
◆知识导航
◆典例导学
◆反馈演练 (
◎第一阶
◎第二阶
◎第三阶
)
◆知识导航
◆典例导学
◆反馈演练 (
◎第一阶
◎第二阶
◎第三阶
)
◆知识导航
◆典例导学
◆反馈演练 (
◎第一阶
◎第二阶
◎第三阶
)
◆知识导航
◆典例导学
◆反馈演练 (
◎第一阶
◎第二阶
◎第三阶
)
◆知识导航
◆典例导学
◆反馈演练 (
◎第一阶
◎第二阶
◎第三阶
)
◆知识导航
◆典例导学
◆反馈演练 (
◎第一阶
◎第二阶
◎第三阶
)
◆知识导航
13.2 三角形全等的判定(第4课时)(课件)八年级数学上册(华东师大版)
= ,
=.
∴△ABC≌△DFE(SSS).
讲授新课
变式2 若将上题中的三角形继续向左平移(如图),若AB=DC,
AC=DB,问:△ABC≌△DCB 吗?
D
A
B
E
C
F
解:全等.
在△ABC和△DCB中,
=,
= ,
=.
∴△ABC≌△DCB(SSS).
讲授新课
(简写为“边边边”或“S.S.S.”)
A
几何语言:
在△ABC和△ DEF中,
AB=DE,
B
C
D
BC=EF,
CA=FD,
∴ △ABC ≌△ DEF(S.S.S.).
E
F
讲授新课
典例精析
【例1】如图,在四边形 ABCD 中,AD = CB,AB = CD.
求证: ∠B = ∠D.
证明:在△ABC 和△CDA 中,
在△ABE和△CDF中,
AE=CF,∠A=∠C,AB=DC.
∴△ABE≌△CDF(SAS).
∴BE=DF.
当堂检测
8. 如图,点 B、E、C、F 在同一条直线上,AB = DE,AC = DF ,
BE = CF.求证:∠A = ∠D.并找出图中相互平行的线段,说明
你的理由.
证明:∵BE=CF,∴BE+CE=FC+EC,
b
3 cm
2.以点A为圆心,以线段b(3cm)的长为半
径画圆弧;以点B为圆心,以线段a(4cm)
的长为半径画圆弧;两弧交于点C.
c
4.5 cm
C
a
b
3.连结AC、BC.
△ABC即为所求.
c
A
B
13.2 三角形全等的判定 第4课时 边边边 【八年级上册数学(华东师大版)】
原创新课堂
原创新课堂
9.(宜昌中考)如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个 点中找出符合条件的点P,则点P有( C ) A.1个 B.2个 C.3个 D.4个
10.如图,CA=CB,AD=BD,M,N分别是CA,CB的中点,若DM=5 cm,则DN=( C ) A.3 cm B.4 cm C.5 cm D.6 cm
6.如图,点A,E,F,D在同一直线上,若AB∥CD,AB=CD,AE=FD,则图中的全等三角形有( C ) A.1对 B.2对 C.3对 D.4对
7.(娄底中考)如图,已知AB=BC,要使△ABD≌△CBD,还需添加一个条件,你添加的条件是 _____∠_A_B_D__=__∠_C_B_D_或__A_D__=__C_D___.(只需写一个,不添加辅助线)
原创新课堂
AB=CD, 解:(1)证明:连结 AD.在△BAD 和△CDA 中,∵ DB=AC,∴△BAD
AD=DA,
≌△CDA(S.S.S.),∴∠B=∠C(全等三角形对应角相等) (2)作辅助
线的意图是构造全等三角形
原创新课堂
4.(2017·福建)如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.求证:∠A=∠D.
AB=DE, 证明:∵BE=CF,∴BC=EF.在△ABC 和△DEF 中,∵ AC=DF,∴
BC=EF, △ABC≌△DEF(S.S.S.),∴∠A=∠D
原创新课堂
5.给出下列四组条件:①AB=DE,BC=EF,AC=DF;②AB=DE,∠B=∠E,BC=EF;③∠B=∠E, BC=EF,∠C=∠F;④AB=DE,AC=DF,∠B=∠E.其中能使△ABC≌△DEF的条件共有( C ) A.1组 B.2组 C.3组 D.4组
2022八年级数学上册第13章全等三角形13.2三角形全等的判定4边边边授课课件新版华东师大版12
知2-讲
全等三角形判定方法教的选你用一:招
(1)若已知两边,可证第三边相等(S.S.S.)或夹角相等 (S.A.S.);
(2)若已知一边一角,可证已知角的另一边相等 (S.A.S.)或
证一角相等(A.S.A.、A.A.S.); (3)若已知两角相等,可证三角形的任一边相等 (A.A.S.、
A.S.A.).
知2-讲
综合法:利用某些已经证明过的结论和性质及
教你一招
条件,推导出所要证明的结论成立的方法叫综合
法.其
思维特点是:由因索果,即从已知条件出发,利用
已知
的数学定理、性质和公式,推出结论.本书的证明
基本
上都是用综合.
本题运用了综合法,根据条件用“S.S.S.”可得到全等
的三角形,从全等三角形出发可找到与结论有关的
知2-练
1 如图,根据相应的条件,能否判定下面分别给出的两个
三角形全等? (1)线段AD与BC相交于 点O, AO=DO, BO=CO . △ ABO与△ DCO. (2)AC = AD, BC = BD.
△ ABC与△ ABD. (3)线段 AC与 BD相交 于点O, ∠A = ∠C, ∠B = ∠D. △ ABO与△ CDO . (4) ∠CAB =∠DBA, ∠1 = ∠ 2.△ABC与△BAD .
知1-讲
知1-讲
本例的导引采用的是分析法.下面就分析法进行解
读.分析法:(逆推证教法你或一执果招索因法)它是从证明的
结论 出发,逐步寻求使它成立的充分条件,直到把要证
明的 结论归结为判定一个明显成立的条件(已知、定理、
定义、 公理等),这种证明方法叫分析法. 注意:(1)分析法一般用来寻找证明或解题思路,而 证明或解题过程一般都采用综合法(下例讲)来完
华师大版八年级数学上册13.2.2三角形全等的判定— 边角边(S.A.S).docx
13.2.2三角形全等的判定—边角边(S.A.S)公开课教案一、背景介绍与教学资料本教材强调直观和操作,在观察中学会分析,在操作中体验变换。
教材的编排淡化概念的识记,强调图形性质的探索。
全等三角形的判定是今后证明线段相等和角相等的重要工具,是学习后续课程的必要基础。
在教学呈现方式上,改变了“结论——例题——练习”的陈述模式,而采用“问题——探索——发现”等多种研究模式。
在直观感知、操作确认的基础上,适当地进行数学说理,将两者有机地结合起来,让学生体验说理的必要性,用自己的语言说明理由,学会初步说理。
二、教学设计教学内容分析本节课的主要内容是探索三角形全等的条件“边角边”以及利用“S.A.S”判定基本事实证明三角形全等。
学生通过自己实验,经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的方法。
由于本节课是学生探索三角形全等的条件的第一课时,所以对学生来讲是一次知识的飞跃,也为下面几节课的探索做铺垫。
教学目标:1、知识与技能:探索、领会“S.A.S”判定两个三角形全等的方法2、过程与方法:经历探索三角形全等的判定方法的过程,能灵活地运用三角形全等的条件,进行有条理的思考和简单推理,并能利用三角形的全等解决实际问题,体会数学与实际生活的联系。
3、情感态度与价值观:培养学生合理的推理能力,感悟三角形全等的应用价值,体会数学与实际生活的联系。
重难点与关键:1、重点:会用“边角边”证明两个三角形全等。
2、会正确运用“S.A.S”判定基本事实,在实践观察中正确选择判定三角形的方法。
同时通过作图,论证S.S.A不能证明两个三角形一定全等。
既是难点也是关键点。
教学方法:采用“问题----操作---结论—运用”的教学方法,让学生有一个直观的感受。
教学过程:一、创设情境。
1、因铺设电线的需要,要在池塘两侧A、B处各埋设一根电线杆(如图),因无法直接量出A、B两点的距离,现有一足够的米尺。
怎样测出A、B两杆之间的距离呢?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
你已经知道的判定三角形全等的方法有几种? 1.根据三角形全等的定义; 2.定理:当两个三角形的两条边及其夹角分 别对应相等时,两个三角形等.(S.A.S.) 注意:当两个三角形的两条边及其中一边的对 角分别对应相等时,两个三角形不一定全等。
(角边角)
(角角边)
如图,已知两个角和一条线段,以这两个角为内角, 以这条线段为这两个角的夹边,画一个三角形.
A 口答:
A′
B
C
B′
C′
1.两个直角三角形中,斜边和一锐角对应相等,这两个直角 三角形全等吗?为什么? 答:全等,根据A.A.S. 2.两个直角三角形中,有一条直角边和一锐角对应相等,这 两个直角三角形全等吗?为什么? 答:全等,根据A.S.A.
练一练
根据题目条件,判别下面的两个三角形 是否全等,并说明理由.
C O D
A
探索继续
如图,AB//DC,AD//BC,BE⊥AC,DF ⊥ AC 垂足为E、F。试说明:BE=DF
D E A F B A
C
D F E B
C
变形,如图,将上题中的条件“BE⊥AC,DF ⊥ AC”变为“BE //DF”,结论还成立吗?请说 明你的理由。
你也试一试:
如图:△ABC是等腰三角形, AD、BE分别是∠A、∠B的角平 分线,△ABD和△BAE全等吗? 试说明理由.
例题讲解:
已知:点D在AB上,点E在AC上,BE和CD相 交于点O,AB=AC,∠B=∠C. 求证: △ABE≌△ACD
证明:在△ABE和△ACD中, ∵ ∠B=∠C , AB=AC, ∠A=∠A,
A D O B E
∴ △ABE≌△ACD(A.S.A.)
C
考考你自己
如图,AB⊥BC, AD⊥DC, ∠1=∠2. 求证:AB=AD .
∠A=∠B (ASA) (2) AC=BD, AC∥BD ,__________. ∠ AEC=∠BFD,∠ C=∠D. (ASA) (3) CE=DF, —————— ———— AC=BD ∠A=∠B (4)∠ C= ∠D,————,————. (ASA) A C
F
E B
D
A
D
思考
B C
如图,∠ABC=∠DCB,试添加一个条件, 使得△ABC≌△DCB,这个条件可以是 ∠ACB=∠DBC _________(A.S.A.) ∠A=∠D 或_______(A.A.S.) AB=DC 或_______(S.A.S.)
M N C 600 A 步骤: 4cm 400 B
图 19。2。把你画的三角形与其他同学画 7 1.画一条线段AB,使它等于4cm; 的三角形进行比较,所有的三角形
2.画∠MAB=600、∠NBA=400,与 MA交 换两个角和一条线段,试试看, 于点C。 是否有同样的结论. ⊿ABC即为所求。
都全等吗?
若改为:AD、BE分别是两腰上 的中线,△ 的高,△ ABD ABD 和△ 和△ BAE BAE 全等吗? 全等吗 试说明理由.
D
已知,如图,∠1=∠2,∠C=∠D
求证:AC=AD。
证明:在△ABD和△ABC中 ∵∠1=∠2 (已知) ∠D=∠C(已知) AB=AB(公共边) ∴△ABD≌△ABC (AAS)
A
1 2
B
C
∴AC=AD (全等三角形对应边相等)
一张教学用的三角形硬纸板不小心被撕坏了, 如图,你能制作一张与原来同样大小的新教具? 能恢复原来三角形的原貌吗?
课堂小结
1、通过本节课的学习,你又知道了 哪些判定三角形全等的方法? 2、我们已经掌握了哪些判定三角 形全等的方法?
A A'
用几何语言叙述为:
在△ABE和△A’CD中, ∵∠B=∠C(已知 ) ∠A=∠A’ (已知 ) AE=A’D(已知 )
∴ △ABE≌△A’CD(ASA)
E
D
B
课 堂 如图,要证明△ACE≌ △BDF,根据给定的条件 练 和指明的依据,将应当添设的条件填在横线上。 习 AC=BD.(SAS) (1)AC∥BD,CE=DF,___
证明:∵
∠A=∠A′,∠B=∠B′, ∠A+∠B+∠C=180° ∠A′+∠B′+∠C′=180° ∴ ∠C=∠C′. 在△ABC和△A′B′C′中, ∵ ∠A=∠A′ AC=A′C′ ∠C=∠C′ ∴ △ABC≌△A′B′C′(A.S.A.)
结 论
有两角和它们中的一边对应相等的两个三 角形全等(简写成“角角边”或“AAS”)。
都全等
A
D
C
F
E
定理:当两个三 角形的两个角及 其夹边分别对应 相等时,两个三 角形全 等.(A.S.A.)
用几何语言叙述为: ∵∠A=∠D,
AB=DF,
∠B=∠E, ∴⊿ABC≌⊿DEF(A.S.A.)
如果两个三角形有两个角及其中一个角的对 边分别对应相等,那么这两个三角形是否一定全等? 已知:∠A=∠A′, ∠B=∠B′, AC=A′C′ 求证: △ABC≌△A′B′C′
证明:∵ AB⊥BC,AD⊥DC, ∴∠B=∠D=900. 在⊿ABC和⊿ADC中, ∵ ∠B=∠D,
∠1=∠2 ,
AC=AC, ∴ ⊿ABC≌⊿ADC(A.A.S.) ∴AB=AD
B
如图,填空: 在△ADC和 △BOD中, ∵∠A=∠B(已知) (已知) ∠C=∠D (已知) ∴△ADC≌△BOD( )
