中考复习 第1讲 实数(含答案)
初中数学中考一轮复习专题1数与式重点、考点知识、方法总结及真题练习
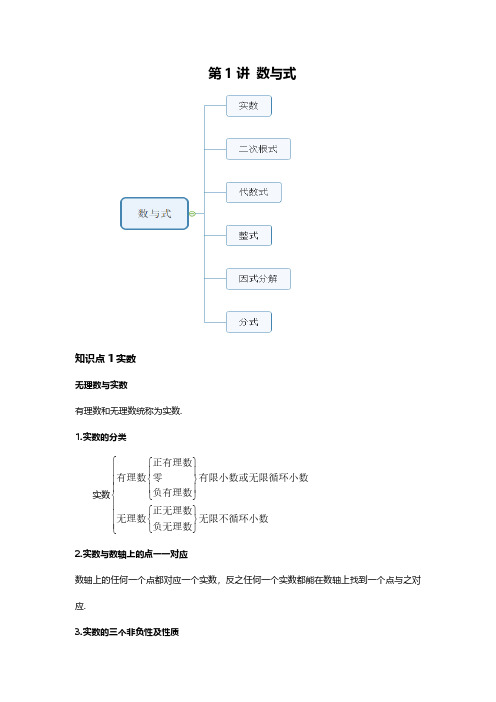
在实数范围内,正数和零统称为非负数.我们已经学习过的非负数有如下三种形式:
(1)仸何一个实数 a 的绝对值是非负数,即| a |≥0; (2)仸何一个实数 a 的平方是非负数,即 a2 ≥0; (3)仸何非负数的算术平方根是非负数,即 a 0 ( a 0 ).
非负数具有以下性质: (1)非负数有最小值零; (2)有限个非负数乊和仍是非负数; (3)几个非负数乊和等于 0,则每个非负数都等于 0. 4.实数的运算
a a (a 0, b 0) bb
②.加减法
将二次根式化为最简二次根式后,将同类二次根式的系数相加减,被开方数和根指数丌变,
即合并同类二次根式.
【典例】
1.计算:5 +
﹣×+ ÷.
【答案】 【解析】解:原式= + ﹣
+3 ÷
=2 ﹣1+3
=2 +2.
x xy xy y
2.若 x 0 ,化简
注:单独一个字母戒一个数也是代数式.
2.代数式的分类:
3.代数式的书写规则: (1)数字不字母相乘戒字母不字母相乘,通常把乘号写作“ ”戒省略丌写,字母乊间的
顺序可以交换,但一般按字母表中的先后顺序写.数字应在字母乊前.如: 3b 丌要写成 b3 (2)在代数式中出现除法运算时,一般都变成分数和乘法来计算.如: 2a b 写成 2a
x
2
0
即
x
1 且x 2
2
.
【难度】易
【结束】
2.若
,则 ( )
A. b>3B. b<3C. b≥3D. b≤3
【答案】D.
【解析】
3 b = 3 b ,所以 3 b ≥0,即 b 3 .
专题1-实数的相关概念(考点讲练)(解析版)_1

专题1 实数的相关概念考点一:实数的分类1.(2022·山东聊城·中考二模)下列各数:3.1415926,9−17,2π,其中是无理数的是( )A .3.1415926B .2πC .17D .9−【答案】B【分析】无限不循环小数是无理数,根据无理数的定义判断.【详解】解:是无理数的是2π, 故选:B .【点睛】此题考查了无理数的定义,熟记定义并正确判断是解题的关键.A .()3−−B .()22−C .|4|−D .5−【答案】D【分析】根据负数的定义逐项判断即得答案.【详解】解:A 、()33−−=,3不是负数,故本选项不符合题意;B 、()224−=,4不是负数,故本选项不符合题意;C 、44−=,4不是负数,故本选项不符合题意;D 、5−是负数,故本选项符合题意.故选:D .【点睛】本题考查了负数的定义以及实数的基本知识,属于基础题型,熟练掌握基本知识是解题关键.3.(2022·山东日照·中考真题)在实数2,x 0(x ≠0),cos30°,38中,有理数的个数是( )A .1个B .2个C .3个D .4个【答案】B【分析】根据零指数幂,特殊角的三角函数值,实数的意义,即可解答.【详解】解:在实数2,x 0(x ≠0)=1,3cos302=°,382=中,有理数是382=,x 0=1, 所以,有理数的个数是2,故选:B .【点睛】本题考查了零指数幂,特殊角的三角函数值,实数,熟练掌握这些数学概念是解题的关键.4.(2022·江苏南通·中考真题)若气温零上2℃记作2+℃,则气温零下3℃记作()A.3−℃B.1−℃C.1+℃D.5+℃【答案】A【分析】根据气温是零上2℃记作+2℃,则可以表示出气温是零下3℃,从而可以解答本题.【详解】解:∵气温是零上2℃记作+2℃,∴气温是零下3℃记作−3℃.故选:A.【点睛】本题考查正数和负数,解题的关键是明确正数和负数在题中表示的含义.5.(2021·黑龙江大庆·中考真题)在π,12,3−,47这四个数中,整数是()A.πB.12C.3−D.47【答案】C【分析】根据整数分为正整数、0、负整数,由此即可求解.【详解】解:选项A:π是无理数,不符合题意;选项B:12是分数,不符合题意;选项C:3−是负整数,符合题意;选项D:47是分数,不符合题意;故选:C.【点睛】本题考查了有理数的定义,熟练掌握整数分为正整数、0、负整数是解决本题的关键.6.(2021·四川遂宁·九年级期中)给出一组数,-2021,sin45°,π539,2.12112111211112…(每相邻两个2之间依次多一个1)中,无理数有___________个【答案】4.【分析】根据无理数的三种形式:①开方开不尽的数,②无限不循环小数,③含有π的数,找出无理数的个数.【详解】解:sin45°=22,93=,则无理数有:sin45°,π,5,2.12112111211112…(每相邻两个2之间依次多一个1)共4个;故答案为:4.【点睛】本题考查了无理数的知识,解答本题的关键是掌握无理数的三种形式:①开方开不尽的数,②无限不循环小数,③含有π的数.7.(2022·山东·邹城市郭里中学一模)从实数227,tan 30︒21,2π,23−,0.101001−39−______. 【答案】47 【分析】找出所给实数中的无理数的个数,然后与所给实数的个数相除即可.【详解】解:227是分数属于有理数; 3tan 303︒=是无理数; 21+是无理数;2π是无理数;()2133−=是有理数; 0.101001−是有理数; 39−是无理数,∴无理数有4个,∴任意抽取一个数是无理数的概率为47, 故答案为:47. 【点睛】本题考查了简单的概率计算,理解掌握无理数和有理数的定义是解题的关键.考点二:相反数、绝对值、倒数8.(2022·山东枣庄·中考真题)实数﹣2023的绝对值是( )A .2023B .﹣2023C .12023D .12023− 【答案】A【分析】根据绝对值的代数意义即可得出答案.【详解】解:因为负数的绝对值等于它的相反数,所以,﹣2023的绝对值等于2023.故选:A .【点睛】本题考查了绝对值的代数意义,熟练掌握知识点是本题的关键.9.(2022·海南省直辖县级单位·二模)实数12的倒数是( )A .12−B .12C .2−D .2 【答案】D【分析】根据倒数的定义,即可求解.【详解】解:∵1212⨯=, ∴12的倒数是2.故选:D【点睛】本题主要考查了倒数的定义,熟练掌握乘积为1的两个数互为倒数是解题的关键. A .2022B .2022−C .12022D .12022− 【答案】A【分析】直接利用相反数的定义分析得出答案.【详解】解:∵一个数的相反数是|2022|−−,即-2022,∴这个数是:2022.故选:A .【点睛】本题主要考查了相反数,正确把握定义是解题关键.11.(2022·湖北宜昌·中考真题)下列说法正确的个数是( )①-2022的相反数是2022;②-2022的绝对值是2022;③12022的倒数是2022. A .3B .2C .1D .0 【答案】A【分析】根据相反数、绝对值、倒数的定义逐个判断即可.【详解】①-2022的相反数是2022,故此说法正确;②-2022的绝对值是2022,故此说法正确;③12022的倒数是2022,故此说法正确; 正确的个数共3个;故选:A .【点睛】本题考查相反数、绝对值、倒数的含义,只有符号相反的两个数叫做互为相反数,数轴上一个数所对应的点与原点的距离叫做该数的绝对值,乘积为1的两个数互为倒数,熟知定义是解题的关键.12.(2022·广东·深圳市中考模拟)计算:0|232022+的结果为( )A .1B .2C .3D .33【答案】D【分析】根据实数的运算法则计算即可.【详解】解:0232022-+ 231=-+33=−故选:D .【点睛】此题考查了化简绝对值、零指数幂、二次根式的加减法,解题的关键熟悉运算法则.22【答案】 2 12##0.5【分析】先根据负整数指数幂计算出12−的值,再根据倒数及绝对值的定义作答即可.【详解】解:11112==22−, ∴12−的倒数为2,绝对值为12.故答案为:①2;②12.【点睛】本题考查了负整数指数幂的运算法则,倒数及绝对值的定义,即乘积为1 的两个数互为倒数,熟练掌握知识点是解题的关键.π【答案】1−π【分析】直接利用相反数的定义分析得出答案. 【详解】解:1π−的相反数是:1−π.故答案为:1−π.【点睛】本题考查了相反数,解题的关键是正确掌握相关定义即:指绝对值相等,正负号相反的两个数互为相反数.15.(2022·四川南充·中考一模)若5x =,则x =______.【答案】5或-5【分析】由绝对值的意义即可求得,绝对值意义:在数轴上,一个数到原点的距离叫做该数的绝对值.【详解】5x =表示到原点距离等于5的数,数轴上到原点距离为5的数有两个:5或者-5,。
最新初中数学实数知识点总复习含答案

最新初中数学实数知识点总复习含答案一、选择题1.下列说法中,正确的是()A.-(-3)2=9B.|-3|=-3C±3D【答案】D【解析】【分析】根据绝对值的意义,乘方、平方根、立方根的概念逐项进行计算即可得.【详解】A. -(-3)2=-9,故A选项错误;B. |-3|=3,故B选项错误;3,故C选项错误;D. 4,=-4,故D选项正确,故选D.【点睛】本题考查了绝对值的意义,乘方运算、平方根、立方根的运算,熟练掌握各运算的运算法则是解题的关键.2.把-( )A B.C.D【答案】A【解析】【分析】由二次根式-a是负数,根据平方根的定义将a移到根号内是2a,再化简根号内的因式即可.【详解】∵1a-≥,且0a≠,∴a<0,∴-,∴-= 故选:A. 【点睛】此题考查平方根的定义,二次根式的化简,正确理解二次根式的被开方数大于等于0得到a 的取值范围是解题的关键.3.在-3.5,227,0,2π,0.161161116…(相邻两个6之间依次多一个1)中,无理数有( )A .1个B .2个C .3个D .4个【答案】C【解析】【分析】 有理数能写成有限小数和无限循环小数,而无理数只能写成无限不循环小数,据此判断出无理数有哪些即可.【详解】∵-3.5是有限小数,,∴-3.5、 ∵227=22÷7=3.142857&&是循环小数, ∴227是有理数; ∵0是整数,∴0是有理数;∵2π,,0.161161116…都是无限不循环小数,∴2π,,0.161161116…都是无理数,∴无理数有3个:2π,,0.161161116…. 故选C .【点睛】 此题主要考查了无理数和有理数的特征和区别,要熟练掌握,解答此题的关键是要明确:有理数能写成有限小数和无限循环小数,而无理数只能写成无限不循环小数.4.已知,x y 为实数且10x +=,则2012x y ⎛⎫ ⎪⎝⎭的值为( )A .0B .1C .-1D .2012【答案】B【解析】【分析】 利用非负数的性质求出x 、y ,然后代入所求式子进行计算即可.【详解】由题意,得x+1=0,y-1=0,解得:x=-1,y=1, 所以2012x y ⎛⎫ ⎪⎝⎭=(-1)2012=1, 故选B.【点睛】本题考查了非负数的性质,熟知几个非负数的和为0,那么每个非负数都为0是解题的关键.5.在-2,3.14,5π,这6个数中,无理数共有( ) A .4个B .3个C .2个D .1个【答案】C【解析】-22=, 3.14,3=-是有理数;,5π是无理数; 故选C. 点睛:本题考查了无理数的识别,无限不循环小数叫无理数,无理数通常有以下三种形式,① 等;②圆周率π;③构造的无限不循环小数,如2.01001000100001⋅⋅⋅ (0的个数一次多一个).6.1,0( )AB .﹣1C .0D 【答案】B【解析】【分析】将四个数按照从小到大顺序排列,找出最小的实数即可.【详解】四个数大小关系为:10-<<<则最小的实数为1-,故选B .【点睛】此题考查了实数大小比较,将各数按照从小到大顺序排列是解本题的关键.7.下列各数中比3大比4小的无理数是( )A .10B .17C .3.1D .103【答案】A【解析】【分析】由于带根号的且开不尽方是无理数,无限不循环小数为无理数,根据无理数的定义即可求解.【详解】 ∵四个选项中是无理数的只有10和17,而17>4,3<10<4∴选项中比3大比4小的无理数只有10.故选A .【点睛】此题主要考查了无理数的定义,解题时注意带根号的要开不尽方才是无理数,无限不循环小数为无理数. 8.如图,长方形ABCD 的边AD 长为2,AB 长为1,点A 在数轴上对应的数是1-,以A 点为圆心,对角线AC 长为半径画弧,交数轴于点E ,则这个点E 表示的实数是( )A .45B 52C 51D .35【答案】C【解析】【分析】 首先根据勾股定理算出AC 的长度,进而得到AE 的长度,再根据A 点表示的数是-1,可得E 点表示的数.【详解】∵2,1AD BC AB ===∴22521AC =+=∴AE 5-∵A点表示的数是1-∴E点表示的数是51【点睛】掌握勾股定理;熟悉圆弧中半径不变性.9.4的平方根是( )A.2 B.2C.±2 D.±2【答案】D【解析】【分析】先化简4,然后再根据平方根的定义求解即可.【详解】∵4=2,2的平方根是±2,∴4的平方根是±2.故选D.【点睛】本题考查了平方根的定义以及算术平方根,先把4正确化简是解题的关键,本题比较容易出错.10.王老师在讲“实数”时画了一个图(如图),即“以数轴的单位长度的线段为边作一个正方形,然后以表示-1的点为圆心,正方形的对角线长为半径画弧交数轴于点A”.则数轴上点A所表示的数是()A2-1 B2+1 C2D2【答案】A【解析】【分析】先根据勾股定理求出正方形的对角线长,再根据两点间的距离公式为:两点间的距离=较大的数-较小的数,便可求出-1和A之间的距离,进而可求出点A表示的数.【详解】22+=-1和A2.112∴点A2.故选A.【点睛】本题考查的是勾股定理及两点间的距离公式,本题需注意:知道数轴上两点间的距离,求较小的数,就用较大的数减去两点间的距离.11.对于两个不相等的实数a,b,我们规定符号max{a,b}表示a、b中的较大的数,如:max{2,4}=4,按照这个规定,方程max{x,﹣x}=x2﹣x﹣1的解为()A.或1B.1或﹣1 C.1或1 D.或﹣1【答案】D【解析】【分析】根据题意应分为x>0和x<0两种情况讨论,并列出关于x的分式方程求解,结合x的取值范围确定方程max{x,﹣x}=x2﹣x﹣1的解即可.【详解】解:①当x≥﹣x,即x≥0时,∵max{x,﹣x}=x2﹣x﹣1,∴x=x2﹣x﹣1,解得:x=(1<0,不符合舍去);②当﹣x>x,即x<0时,﹣x=x2﹣x﹣1,解得:x=﹣1(1>0,不符合舍去),即方程max{x,﹣x}=x2﹣x﹣1的解为或﹣1,故选:D.【点睛】本题考查了解分式方程,有关实数、实数运算的新定义,掌握分式方程的解法是解题的关键.12.下列说法正确的是()A.任何数的平方根有两个B.只有正数才有平方根C.负数既没有平方根,也没有立方根D.一个非负数的平方根的平方就是它本身【答案】D【解析】A、O的平方根只有一个即0,故A错误;B、0也有平方根,故B错误;C、负数是有立方根的,比如-1的立方根为-1,故C错误;D、非负数的平方根的平方即为本身,故D正确;故选D.13.2在哪两个整数之间()A.4和5 B.5和6 C.6和7 D.7和8【解析】【分析】== 1.414222≈,即可解答.【详解】== 1.414222≈,∴2 6.242≈,即介于6和7,故选:C.【点睛】本题考查了二次根式的运算以及无理数的估算,解题的关键是掌握二次根式的运算法则以及 1.414≈.14.( )A.3 B.3-C.3±D.4.5【答案】A【解析】分析:本题只需要根据算术平方根的定义,求9的算术平方根即可..故选A.点睛:本题考查了算术平方根的运算,比较简单.15.1的值在( )A.2和3之间B.3和4之间C.4和5之间D.5和6之间【答案】C【解析】【分析】根据被开方数越大算术平方根越大,可得答案.【详解】∵34,∴41<5.故选C.【点睛】本题考查了估算无理数的大小,利用被开方数越大算术平方根越大得出34是解题的关键,又利用了不等式的性质.16.下列运算正确的是()A =-2 B.|﹣3|=3 C=± 2 D【解析】【分析】A 、根据算术平方根的定义即可判定;B 、根据绝对值的定义即可判定;C 、根据算术平方根的定义即可判定;D 、根据立方根的定义即可判定.【详解】解:A 、C 2=,故选项错误;B 、|﹣3|=3,故选项正确;D 、9开三次方不等于3,故选项错误.故选B .【点睛】此题主要考查了实数的运算,注意,正数的算术平方根是正数.17.若225a =,3b =,且a >b ,则a b +=( )A .±8或±2B .±8C .±2D .8或2【答案】D【解析】【分析】结合已知条件,根据平方根、绝对值的含义,求出a ,b 的值,又因为a >b ,可以分为两种情况:①a=5,b=3;②a=5,b=-3,分别将a 、b 的值代入代数式求出两种情况下的值即可.【详解】∵225a =,|b|=3,∴a=±5,b=±3,∵a >b ,∴a=5,a=-5(舍去) ,当a=5,b=3时,a+b=8;当a=5,b=-3时,a+b=2,故选:D .【点睛】本题主要考查了代数式的求值,本题用到了分类讨论的思想,关键在于熟练掌握平方根、绝对值的含义.18.下列说法正确的是( )A .a 的平方根是B .aC.0.01的平方根是0.1D.2-=-(3)3【答案】B【解析】试题解析:A、当a≥0时,a的平方根为±a,故A错误;B、a的立方根为3a,本B正确;C、0.01=0.1,0.1的平方根为±0.1,故C错误;D、()23-=|-3|=3,故D错误,故选B.19.在数轴上标注了四段范围,如图,则表示8的点落在()A.段①B.段②C.段③D.段④【答案】C【解析】试题分析:2.62=6.76;2.72=7.29;2.82=7.84;2.92=8.41.∵ 7.84<8<8.41,∴2.82<8<2.92,∴2.88<2.9,8③段上.故选C考点:实数与数轴的关系204的算术平方根为()A.2±B2C.2±D.2【答案】B【解析】4的值,再继续求所求数的算术平方根即可.4=2,而22,42,故选B.点睛:此题主要考查了算术平方根的定义,解题时应先明确是求哪个数的算术平方根,否则容易出现选A的错误.。
第1讲实数的概念

7、 3 的绝对值等于 3 , 2 4 的平方根等于 3 , 9
1 3 的倒数是 2
2 7 。
8. 2的相反数是 A. 1 B.
2
9. A
1 2
2
C.-2
D.2
2的相反数是()
2
B
C -2
1 2
D 2
10、的相反数的倒数是 .
课时训练
1、把下列各数填在相应的大括号内: 5 , , 3.14, 0 , 3. 3 3 3, 3, tg 300 , 1, 7
cos600 ,
3
64, 2.1010010001 .
3
-1,0, 64 整数集合:{ ……}; -1 奇数集合:{ ……}; 5 有理数集合:{ -1,,3.14,0, . 3 3 3,cos60°, 3 64 }; 3
1
;
(2) 3 -2的绝
(3)若 x 1, y 2 ,且xy>0,x+y=
3 ; 8; 3 27; 例2、把下列各数填到相应的集合里: 22 ; 3.14; 0.100110001 ; sin 300 ; 7 0 tan45 3; 0.3 21; 3.2
整数集合:{ 3 27 ;tan45°; - 3 }; 3-1;3.14;22/7;sin30°;|-3.2|;-0.32· 1· 分数集合:{ }; 有理数集合: 3-1;3 27 ;3.14;22/7;sin30°;tan45°-3;-0.321;|-3.2| ; 无理数集合:{
4、下列运算正确的是
A.
1 1 5 5
2
B. ( 2) 2
1 3 1 D. ( ) 2 8
中考第一轮复习--第一章数与式
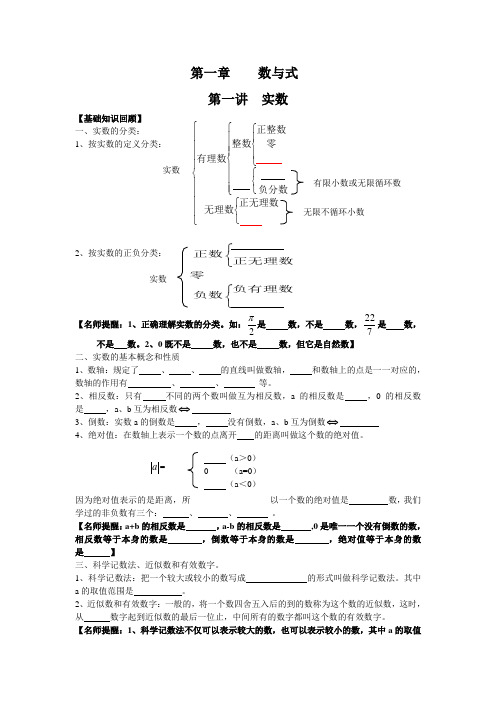
第一章 数与式第一讲 实数【基础知识回顾】 一、实数的分类: 1、按实数的定义分类: 实数 有限小数或无限循环数2、按实数的正负分类:实数【名师提醒:1、正确理解实数的分类。
如:2π是 数,不是 数,722是 数,不是 数。
2、0既不是 数,也不是 数,但它是自然数】二、实数的基本概念和性质1、数轴:规定了 、 、 的直线叫做数轴, 和数轴上的点是一一对应的,数轴的作用有 、 、 等。
2、相反数:只有 不同的两个数叫做互为相反数,a 的相反数是 ,0的相反数是 ,a 、b 互为相反数⇔3、倒数:实数a 的倒数是 , 没有倒数,a 、b 互为倒数⇔4、绝对值:在数轴上表示一个数的点离开 的距离叫做这个数的绝对值。
a =因为绝对值表示的是距离,所以一个数的绝对值是 数,我们学过的非负数有三个: 、 、 。
【名师提醒:a+b 的相反数是 ,a-b 的相反数是 ,0是唯一一个没有倒数的数,相反数等于本身的数是 ,倒数等于本身的数是 ,绝对值等于本身的数是 】三、科学记数法、近似数和有效数字。
1、科学记数法:把一个较大或较小的数写成 的形式叫做科学记数法。
其中a 的取值范围是 。
2、近似数和有效数字:一般的,将一个数四舍五入后的到的数称为这个数的近似数,这时,从 数字起到近似数的最后一位止,中间所有的数字都叫这个数的有效数字。
【名师提醒:1、科学记数法不仅可以表示较大的数,也可以表示较小的数,其中a 的取值⎪ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎧ ⎩ ⎨ ⎧ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ ⎩ ⎨ ⎧ ⎪ ⎩ ⎪ ⎨ ⎧ 正无理数 无理数 负分数 零 正整数 整数 有理数 无限不循环小数 ⎧⎨⎩⎧⎨⎩正数正无理数零 负有理数负数 (a >0) (a <0) 0 (a=0)范围一样,n 的取值不同,当表示较大数时,n 的值是原整数数位减一,表示较小的数时,n 是负整数,它的绝对值等于原数中左起第一个非零数字前零的个数(含整数数位上的零)。
(完整word版)数学人教版九年级下册中考第一轮复习第1讲(实数有关的概念)

m0 1n2016中考数学第一轮复习第1讲-------实数的有关概念知识点1:实数平行练习1: 1. 四个数-5,-0.1,21,3中为无理数的是( ) A. -5 B. -0.1 C. 21D.32. 在实数:3.14159,364,1.010010001…,4.21&&,π,227中,无理数的个数有( ) A . 1个 B .2个 C .3个 D .4个3. 如图,在数轴上表示15的点可能是( )A. P 点B. Q 点C. M 点D. N 点4. 如图,已知在数轴上有点A 和点B 两个点,估计点A 和点B 之间表示整数的点有 个,它们分别是 .第3题图 第4题图知识点2:数轴(三要素:1、原点;2、正方向;3、单位长度.)平行练习2:1. 如图为四位同学所画的数轴,其中正确的是( ) A. B. C. D.2. 如图,在数轴上点A 表示的数可能是( ) A. 1.5 B.-1.5 C.-2.6 D. 2.63. 已知实数m 、n 在数轴上的对应点的位置如图所示,1.整数(包括:正整数、0、负整数)和分数(可以表示为有限小数和无限循环小数)都是有理数.如:-3,,0.231,0.737373…,,.2.无限不环循小数叫做无理数.◆常见的几种无理数: ①根号型:如35,2等开方开不尽的数;②圆周率π型:如π,π-1等; ③构造型:如1.121121112…等无限不循环小数.112AB则下列判断正确的是( )A.0m >B.0n <C.0mn <D.0m n ->知识点3:相反数、倒数平行练习3:1. 如果向东走80m 记为80m ,那么向西走60m 记为( ) A. -60m B. 60-m C. -(-60)m D. 601m 2. 下列各组数中,互为相反数的是( ) A .2和-2B .-2和12C .-2和-12D .12和23. a (0a ≠)的相反数是( )A. a -B. aC. aD. 1a4.实数3的倒数是( ) A. 31-B.31C. 3-D. 35. 如图,数轴上表示数﹣2的相反数的点是( ) A .点P B .点Q C .点M D .点N6.12-的相反数是 .7. 若实数a 、b 互为相反数,则a+b= ;若实数m 、n 互为倒数,,则 .知识点4:绝对值⎩⎨⎧-≥=.,,00<;a a a a a 平行练习4:1. 6-的值是( )A .6-B .16-C .16D .62. 计算: 12-=_____; 3-π=_____;32=__________.(结果保留根号)3. 绝对值等于3的数是__ ___.4. 对任意的实数a ,总有 0.知识点5:科学计数法平行练习5:1. 世界文化遗产长城的总长约为6700000m ,这个数字用科学计数法表示为 ;把一个数写成a ×10n 的形式(其中1≤a <10,n 是整数),这种记数法叫 做科学记数法.如: 40700=4.07×105,0.000043=4.3×10-5.已知一粒米的质量为0.000021千克,这个数字用科学计数法表示为 . 2. 根据2011年第六次全国人中普查主要数据公报,江西省常住人口约为4456万人;这个 数据可以用科学计数法表示为 人.知识点6:实数的运算p p aa 1=-, ()010≠=a a平行练习6:1. 昆明今年1月份某天的最高气温为5℃,最低气温为-1℃,则昆明这天的温差为( ) A .4℃ B.6℃ C .-4℃ D.-6℃2. 25-+的相反数是( )A. 3B. -3C. -7D. 7 3. 计算: (1)()()0332011422---+÷- (2)011130321)(tan ---︒+-π)(4. 定义一种新运算:⊗,a ⊗b=41a-b变式探究:1. 320x y -++=,则x y +的值为 .2. 设实数a b 、在数轴上对应的位置如图所示,化简式子b a a ++.3. 已知2x =9,1+y =2,且xy <0,求x+y 的值.b0a课 后 作 业1.如果零上5 ℃记做+5 ℃,那么零下7 ℃可记作( ) A .-7 ℃ B .+7 ℃ C .+12 ℃ D .-12 ℃2.下列各数:3π,sin30°,3-,4,其中无理数的个数是( ) A. 1个 B. 2个 C. 3个 D. 4个 3.下列各数中,最小的数是( ) A .-l B .O C .1D .3 4.下列四个数中,负数是( ) A. -2B. ()2-2 C. -2D.()2-25. 7-的相反数是( )A. 7-B. 7C.71-D. 71 6. 12-的绝对值是( )A .2B .2-C .12D .12-7. 实数a 在数轴上的位置如图所示,则|a -2.5|=( ) A. a -2.5 B. 2.5- a C. a +2.5 D. -a -2.58. 地球半径约为6400000米,用科学记数法表示为( ) A . 0.64×107 B .6.4×106 C.64×105D .640×1049. PM 2.5是指大气中直径小于或等于0.0000025 m 的颗粒物,将0.0000025用科学记数法表示为( )A. -50.2510⨯B. -60.2510⨯C. -52.510⨯D. -62.510⨯10. 实数3的倒数是( )A .﹣B .C .﹣3D .3 11. 下列运算正确的是( )A 4=2B .(﹣3)2=﹣9C .2﹣3=8 D .20=0 12. 已知a 1+7+b =0-,则a+b=( )A .﹣8B .﹣6C .6D .8 13. 若(a -1)2+|b -2|=0,则(a -b )2012的值是( )A. -1B. 1C. 0D. 2012 14. 如图,在数轴上的点M 表示的数可能是( ) A .1.5 B .-1.5 C .-2.4 D .2.415. 实数a 、b 在数轴上的位置如图所示,下列式子错误..的是( )A. a <bB.a b >C. -a <-bD.b -a >016. 点A 、B 、C 在同一条数轴上,其中点A 、B 表示的数分别为-3、1,若线段BC=2,则AC 等于( )A. 3B. 2C.3 或5D. 2或6 17. 下列计算正确的是( )A. 2221243x x x =⋅B. 1553x x x =⋅C. 34x x x =÷ D. 725x x =)(18. 实数m 、n 在数轴上的位置如图所示,则|n ﹣m|= .19. 一个数的绝对值等于3,则这个数是 . 20. 计算:(1)11312+2sin 60+3-⎛⎫-- ⎪⎝⎭(2)()()12121+20122π-⎛⎫----- ⎪⎝⎭21. 先化简,再求值:()()()2212-+-+x x x ,其中23=x .22. 观察下面的变形规律:211211-=⨯;3121321-=⨯;4131431-=⨯;…… (1)若n 为正整数,请你猜想=+⨯)(11n n ; (2)证明(1)题中你猜想的结论; (3)求和:+⨯+⨯+⨯431321211 (2012)20111⨯+.23. 2013年3月,某煤矿发生瓦斯爆炸,该地救援队立即赶赴现场进行救援,救援队利用生命探测仪在地面A 、B 两个探测点探测到C 处有生命迹象.已知A 、B 两点相距4米,探测线与地面的夹角分别是30°和45°,试确定生命所在点C 的深度.。
【南方新中考】(南粤专用)2016中考数学+第一部分+第一章+第1讲+实数复习课件

先算括号里面的.
左 到_______ 右 进行运算. (2)同级运算,应从_______
1.(2014 年山东青岛)据统计,我国 2013 年全年完成造林 面积约 6 090 000 公顷.6 090 000 用科学记数法可表示为( A ) A.6.09×106 C.609×104 B.6.09×104 D.60.9×105
3.(2014 年海南)5 的相反数是( B ) A. 1 5 B.-5 C.±5 D.- 1 5
名师点评:熟练掌握有关概念是解决这类问题的关键.
实数的运算
例题:(2014 + 8.
1- 年浙江绍兴)计算:2 1-4sin45° -(1-
2)0
思路分析:任何非零实数的零次幂都为 1.
1 1 1 3 ;- 的相反数是______ 5.3的倒数是______ 4 ;-3 的绝对值源自43 是________ .
相反数、绝对值、倒数
3 1.(2013年北京)-—的倒数是( D ) 4
A.
4 3
B.
3 4
C.-
3 4
D.- B ) 1 D. 7
4 3
2.(2014 年山东青岛)-7 的绝对值是( A.-7 B.7 1 C.- 7
解决这类问题的关键.
科学记数法 5.(2014 年江苏无锡)据国网江苏电力公司分析,某省预计 今夏统调最高用电负荷将达到 86 000 000 千瓦,这个数据用科 学记数法可表示为( C ) A.8.6×106 千瓦 C.8.6×107 千瓦 B.86×106 千瓦 D.86×107 千瓦
6.(2013 年山东日照)如图 1-1-2,H7N9 病毒直径为 30 纳 米(1 纳米=10-9 米),用科学记数法表示这个病毒直径的大小, 正确的是( B ) A.30×10-9米 B.3.0×10-8米
2014年中考数学专题(考点知识梳理+典例精析+巩固训练+考点训练)复习:第1讲 实 数

考点知识梳理
中考典例精析
基础巩固训练
考点训练
首页
上一页
下一页
考点知识梳理
中考典例精析
基础巩固训练
考点训练
首页
上一页
下一页
1.-2 的倒数是( A.2 B.-2
) 1 C. 2 1 D.- 2
答案: D
考点知识梳理
中考典例精析
基础巩固训练
考点训练
首页
上一页
下一页
2.如图,点 M 表示的数是(
)
A. 2.5
考点知识梳理
中考典例精析
基础巩固训练
考点训练
首页
上一页
下一页
考点知识梳理
中考典例精析
基础巩固训练
考点训练
首页
上一页
下一页
成都)-3 的绝对值是( ) 例1(1)(2012· 1 1 A.3 B.-3 C. D.- 3 3 (2)(2012· 北京)-9 的相反数是( ) 1 1 A.- B. C.-9 D.9 9 9 1 (3)(2012· 临沂)- 的倒数是( ) 6 1 1 A.6 B.-6 C. D.- 6 6
B. -1.5
C. -2.5
D. 1.5
答案 :C
考点知识梳理
中考典例精析
基础巩固训练
考点训练
首页
上一页
下一页
3.9 的算术平方根是( ) A.± B.3 C.-3 D. 3 3
答案:B
4.下列四个数中,是负数的是( A.|-2| B.(-2)2 C.- 2 D. -22
)
答案:C
考点知识梳理
考点知识梳理 中考典例精析 基础巩固训练 考点训练 首页 上一页 下一页
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初三数学复习教学案
第一讲 实数
【回顾与思考】
【例题经典】
理解实数的有关概念
例1 ①a的相反数是-15,则a的倒数是_______.
②实数a、b在数轴上对应点的位置如图所示:0ab
则化简│b-a│+2()ab=______.
③(2006年泉州市)去年泉州市林业用地面积约为10200000亩,用科学记数法表示为
约______________________.
【点评】本大题旨在通过几个简单的填空,让学生加强对实数有关概念的理解.
掌握实数的分类
例2 下列实数227、sin60°、3、(2)0、3.14159、-9、(-7)-2、8中无
理数有( )个
A.1 B.2 C.3 D.4
【点评】对实数进行分类不能只看表面形式,应先化简,再根据结果去判断.
快速准确地进行实数运算
例3 (2006年成都市)计算:-113+(-2)2×(-1)0-│-12│.
【点评】按照运算顺序进行乘方与开方运算。
【基础训练】
1.下列语句:①无理数的相反数是无理数;②一个数的绝对值一定是非负数;③有理数
比无理数小;④无限小数不一定是无理数,其中正确的是( )
A.①②③ B.②③④ C.①②④ D.②④
2.(2005年长沙市)已知a、b两数在数轴上对应的点如图所示,下列结论正确的是( )
A.a>b B.ab<0 C.b-a>0 D.a+b>0
0
a
b
3.(2006年芜湖市)三峡工程是世界防洪效益最为显著的水利工程,它能有效控制长江上
游洪水,增强长江中下游抗洪能力,据相关报道三峡水库的防洪库容22150000000m3,用
科学计数法可记作( )
A.221.5×108m3 B.22.15×109m3
C.2.215×1010m3 D.2215×107m
3
4.9的相反数的倒数是( )
A.-9 B.19 C.9 D.-19
5.(2005年武汉市)如图,一电线杆AB的高为10•米,•当太阳光线与地面的夹角为60
度时,其影长AC约为(3取1.732,结果保留3个有效数字)
A.5.00米 B.8.66米 C.17.3米 D.5.77米
6.(2006年常德市)下列计算正确的是( )
A.16=±4 B.32-22=1 C.24÷6=4 D.23·6=2
7.(2006年南通市)一个篮球需要m元,买一个排球需要n元,则买3个篮球和5个排
球共需要_________元.
8.(2006湖州市)青蛙在如图8×8的正方形(每个小正方形的边长为1)•网格的格点
(小正方形的顶点)上跳跃,青蛙每次所跳的最远距离为5,青蛙从点A•开始连续
跳六次正好跳回到点A,则所构成的封闭图形的面积的最大值是________.
9.图中是一幅“苹果图”,第一行有1个苹果,第二行有2个,第三行有4个,•第四行
有8个,……你是否发现苹果的排列规律?猜猜看,第十行有______个苹果.
【能力提升】
10.计算:│-12│÷(-12+23-14-56);
11.若a、b互为相反数,c,d互为倒数,m的绝对值为2,求a2-b2+(cd)-1÷(1-2m+m2)
的值.
12.数a,b在数轴上的位置如图所示: 化简2()()||aababab.
0ab
13.(2006年临安市)已知:2+23=22×23,3+38=32×38,4+
2
44
4,1515
2
55
552424
,…,若10+ba=102×ba符合前面式子的规律,则a+b=________.
14.(2006年江阴市)将正偶数按下表排列:
第1列 第2列 第3列 第4列
第1列 2
第2列 4 6
第3列 8 10 12
第4列 14 16 18 20
……
根据上面的规律,则2006所在行、列分别是________.
应用与探究
15.(2005年辽宁省)在数学活动中,小明为了求12+23411112222n的值(结果
用n表示),设计如图(1)所示的几何图形.
(1)请你利用这个几何图形求12+ 23411112222n的值为_______.
(2)请你利用图(2)再设计一个能求12+23411112222n的值的几何图形.
(1) (2)
【答案】
例题经典 例1:(1)5 (2)2a-2b (3)1.02×107 例2:C 例3:1-23
考点精练 1.C 2.A 3.C 4.D 5.D 6.D 7.3m+5n 8.10 9.29(512) 10.-14411
11.1或19 12.-b 13.109 14.第45行第13列
15.(1)1-12n
(2)
