第3章Kirchhoff积分法叠前深度偏移
基于共聚焦的三维最大能量积分法叠前深度偏移

)t
( k, l= 1, 2, &, n) 。为找出携带最大能量
计算地震波传播的数值格林函数。在三维球坐标系 下波动方程的 H elmholt z 形式为 2 U U 1 r + 21 sin ∀ + 2 r ∀ r r sin ∀ ∀ r 2 U = - 2U + 2 12 ( 10) 2 2 r sin ∀ v 式中 : U 为地震波场 ; r 为外推半径; ∀ 为倾角 ; 为 方位角; 为角频率; v 为地震波传播速度。通过推 导[ 4] , 可以得到以下方程组 U 1 + i # = U ( 11a) r r 1+ =
* 山东省东营市胜利油田有限公司物探研究院 , 257022 本文于 2006 年 8 月 8 日收到。
[ 1]
2
方法原理
通过对地震波传播过程的分解, Berkhout 建立
了 WRW 模型, 使用矩阵形式对地震波传播的复杂 物理过程给出一种正确清晰的数学描述。炮道集数 据体的单个频率切片被称作数据矩阵, 其中每一行
1
引言
长期以来, 由于 Kirchhof f 积分法偏移对输入 /
和检波器进行两次独立而连续的时移和聚焦计算, 能够提供地下每个网格点的丰富信息, 这些信息可 以应用到成像速度分析、 消除多次波及岩性分析等 多个地震处理领域。 本文从 WRW 模型理论出发, 提出了基于共聚 焦成像理论的积分成像技术。该方法的实现基于波 动方程 , 在地震波的有效频带范围内计算携带最大 能量的地震波旅行时和振幅 , 相比基于高频近似的 地震波初至旅行时的常规积分方法具有理论上的优 势。该方法成像精度接近波动方程方法 , 同时又具 有常规积分方法适应野外观测系统、 计算效率高的 优点, 因此是一种兼具精度和效率的实用方法。
VTI介质克希霍夫叠前深度偏移及其应用

VTI介质克希霍夫叠前深度偏移及其应用夏常亮;王永明;夏密丽;刘红久;胡浩;王祥春【摘要】针对叠前深度偏移速度反演多解性及层位标定和偏移结果不匹配,以伊拉克某构造复杂区块地震资料为例,详细介绍了垂直对称轴横向各向同性(VTI)介质的克希霍夫(Kirchhoff)叠前深度偏移及其应用和注意事项.提出利用剥层层速度修正方法反演层速度和测井曲线趋势约束联合解决速度反演多解性问题;利用叠前时间偏移均方根速度场通过约束速度反演(CVI)获得初始沿层层速度,从而保证初始层速度场的准确性和有效减少剥层层速度修正方法反演层速度的迭代次数;通过VTI介质的偏移解决偏移结果与层位标定不匹配问题.实际应用表明,前述Kirchhoff叠前深度偏移流程,能够有效提高叠前深度偏移工作效率,获得可靠性更强的深度域层速度模型,有效提高速度反演精度,获得与井上层位一致的地震层位,满足勘探开发的需求.【期刊名称】《新疆石油地质》【年(卷),期】2018(039)006【总页数】5页(P732-736)【关键词】Kirchhoff叠前深度偏移;横向各向同性介质;Thomsen参数;层剥离;层速度【作者】夏常亮;王永明;夏密丽;刘红久;胡浩;王祥春【作者单位】中国地质大学地球物理与信息技术学院,北京100083;中国石油东方地球物理勘探有限责任公司研究院长庆分院,西安710021;中国石油东方地球物理勘探有限责任公司研究院长庆分院,西安710021;中国石油东方地球物理勘探有限责任公司研究院长庆分院,西安710021;中国石油东方地球物理勘探有限责任公司研究院长庆分院,西安710021;中国石油东方地球物理勘探有限责任公司研究院长庆分院,西安710021;中国地质大学地球物理与信息技术学院,北京100083【正文语种】中文【中图分类】P631.4叠前深度偏移是解决复杂地质构造条件下地震波场成像的有效工具,偏移算法及其理论依据是决定偏移效果的关键[1]。
弯曲射线Kirchhoff积分叠前时间偏移及并行实现.

弯曲射线Kirchhoff积分叠前时间偏移及并行实现【中文摘要】复杂条件下地震波传播成像是地震勘探领域一直以来研究的焦点之一,特别是勘探广度和深度都已经大幅度进步的今天。
固然诸如CRS 等新技术不断的涌现,以及大家一致以为叠前深度偏移是复杂条件下最好的成像工具,但由于诸如深度偏移对速度模型精度敏感等因素,应用起来依然存在困难。
而基于Kirchhoff积分的积分法叠前时间偏移由于其方便,有效,速度快,面向目标,适应性强,对速度模型的敏感性不强等特点而成为现在应用最为广泛的偏移成像方法。
人们也从未停止对Kirchhoff积分法偏移精度以及实现方式的研究,本文将就该方法实现过程中的重要环节进行讨论。
Kirchhoff积分法的精度很大程度上取决于走时的计算,而现在很多贸易软件诸如Geodepth等中的走时计算是采用直射线计算走时。
这种夸大等效性的方法可以用基于水平层状地层假设的弯曲射线方法进行替换。
弯曲射线走时计算更贴近实际地质状况使走时计算更正确,从而进步Kirchhoff积分法叠前时间偏移的精度。
除此之外,本文还阐述了旨在增强Kirchhoff偏移聚焦能力的非对称走时计算理论,他是应用现代数学诸如李代数,拟微分算子,从地震波传播的保结构算法中推导出来的。
假频题目一直是各类偏移成像方法需要解决的题目。
本文就Kirchhoff积分偏移中可能出现的假频类型进行了分析,并着重分析解决了算子假频题目。
通过几种反假频方法的对比,采用Lumly三角平滑滤波的方法有效的降低了算子假频的影响,并具体分析解决了应用该方法时出现的题目。
最后的数据实验中对应用效果进行了比对。
除了走时计算和反假频两个重要的环节外,本文还对实现中诸如速度模型的建立以及振幅的影响因素进行了讨论,并在程序中得到了实现。
论文中还具体的先容了并行计算的有关知识以及它在积分法叠前时间偏移中的应用,并根据叠前时间偏移的性质先容了数据域并行和成像域并行两种并行策略。
200609-复杂介质下保真振幅Kirchhoff深度偏移

徐 升,G illes Lambar é.复杂介质下保真振幅K irchhoff 深度偏移.地球物理学报,2006,49(5):1431~1444Xu S ,G illes Lambar é.T rue am plitude K irchhoff prestack depth migration in com plex media.Chinese J .G eophys .(in Chinese ),2006,49(5):1431~1444复杂介质下保真振幅Kirchhoff 深度偏移徐 升1,G illes Lambar é21Veritas DG C Inc.10300T own Park Drive H ouston TX 77072,US A 2Ecole des M ines de Paris ,35Rue saint H onor é77305F ontainebleau ,France摘 要 本文详细讨论地下复杂介质地震成像问题.当速度模型含有强横向变化时,射线场会折叠形成多次走时,在这种情况下,文中证明在保真振幅叠前深度偏移时,应当考虑所有的到时才能得到定量的像.通过实例证明,在多次走时情况下,常规的共炮集、共检波器集都存在强的假像;由此提出共角度偏移的概念.最后,在多次走时下,讨论多次偏移算子(走时、相移、振幅等)的高效重构,给出了三维叠前深度偏移的快速算法.关键词 叠前深度偏移,真振幅,复杂介质文章编号 0001-5733(2006)05-1431-14中图分类号 P631收稿日期2006-01-12,2006-05-23收修定稿作者简介 徐升,男,1967年生.1990年毕业于北京大学地球物理系;1993年于中国科学院地球物理研究所获地磁学硕士学位;2001年在法国巴黎矿业学院获地球物理学博士学位;2003年到美国休斯敦Veritas 公司工作;主要从事深度偏移、速度模型估计和地震资料处理方面的研究.E -mail :sheng -xu @T rue amplitude K irchhoff prestack depth migration in complex mediaX U Sheng 1,G illes Lambar é21Veritas DGC Inc .10300Town Park Drive ,Houston TX 77072,USA 2E cole des Mines de Paris ,35Rue saint Honor é77305Fontainebleau ,FranceAbstract In this paper ,we address the com plex geological structures imaging problem ,when the velocity macro 2m odel is characterized by very strong lateral variations ,and the ray fields may triplicate providing multi 2arrivals ;we dem onstrated that all the multi 2arrivals have to be taken into account for a quantitative migration.Furtherm ore ,we propose a comm on image gather strategy in angle domain to handle the strong artifacts appear in conventional comm on image gathers (offset or shot domain )when multi 2arrivals occurs.In the multi 2arrival case ,we als o propose a high efficient migration alg orithm for 32D prestack multi 2arrival depth migration based on the fast reconstruction alg orithms for the traveltime ,phase rotation and am plitude of the migration operator.K eyw ords Prestack depth migration ,Am plitude ,C om plex media1 引 言 20世纪90年代起,勘探地震学的研究集中到复杂地质情况下三维叠前成像方面.其中三维叠前深度偏移研究获得了一系列重要成果,其应用在墨西哥湾盐丘、中国古潜山等的深度偏移成像都很成功.这些成果在定量油藏描述中起着决定性作用.由于这些新理论和概念的产生和发展,地震资料处理的三个主要环节的关键技术都得到提高:(1)预处理:当地下介质很复杂时,高精度偏移成像变得越来越具有挑战性.例如用反馈模型的三维去多次波法[1],高精度Radon 变换法[2],以及数据规则化法[3~7].这些技术的发展使得预处理的技术含量有了极大的提高,计算量也随着增加,计算成本有时甚至超过波动方程叠前深度偏移.(2)速度模型的建第49卷第5期2006年9月地 球 物 理 学 报CHI NESE JOURNA L OF GE OPHY SICSV ol.49,N o.5Sep.,2006立:长期以来,它是叠前深度成像的关键和难点,由于其问题含有强烈的非线性,而且其解的不惟一性,在复杂条件下,很难获得和地质解释相一致的解.虽然各种不同的反演方法取得了相当大的进步[8~14],但离高精度成像的要求尚有一定的差距.(3)定量偏移成像:是地震资料处理中的关键技术之一,它建立了速度模型和定量油藏描述之间的桥梁.其效果不仅直接影响对地下结构的解释,而且也对建立精确的速度模型至关重要.其中保真振幅偏移可以提供地下反射系数振幅随入射角变化的信息,对地下储层结构解释提供物理信息.图1 Marm ousi 速度模型(a )和光滑速度模型和射线场(b )图1a 中没有画出大于180°角的射线和波前;射线和波前的折叠使得偏移计算的理论和算法难度增加.Fig.1 Marm ousi velocity m odel (a )and sm ooth velocity m odel (b )2 复杂结构成像与射线追踪 随着三维地震勘探技术的发展,叠前深度偏移算法提高了效率,改善了成像精度,更好、更精确地给油藏描述提供了优质地下成像.这些技术发展主要针对复杂地质条件下的定量成像及其应用.复杂地质条件在此可定义为:在勘探工区地震波传播速度模型含有强横向不均匀性.因此地震波传播展现出复杂波传播现象,例如出现焦散场.直到20世纪末,虽然振幅保真并没有真正包含在偏移算法中,但单程波动方程依然是复杂条件下最精确的算法[15].结合三维叠前深度偏移技术的发展,各式各样的传统算法都在新的计算条件下被重新评估,其中,高频近似下的射线法以其快速、精确和适应大批量计算处理等优点而获得工业界的重视,并成为三维地震数据叠前深度处理的常规算法.与此同时,真振幅叠前深度偏移理论研究也在发展,散射理论中的散射算子和逆散射算子的高频近似,也就是我们所称的射线保真振幅偏移算子,能凭其一次迭代而获得物理模型的短波长分量,并利用射线追踪进行波传播正演计算,理论上保证了其快速计算的优势.但是射线法用于深度偏移也存在数值计算的难点.因为三维保真振幅叠前深度偏移要求计算走时、振幅以及各种旁轴参数表.具体计算这些参数并不是轻而易举的.仅仅快速的走时表计算就使人止步不前.首先取得突破的是有限差分程函方程的稳定快速算法[16],它解决了叠前深度偏移中最重要的问题:稳定的走时表的算法.这使得走时叠前深度偏移可以在有限的计算量下得以实现.然而保真振幅偏移及基于偏移的AVO 研究需要计算射线场的振幅和一些旁轴参数表,用来计算保真振幅偏移中的雅可比行列式等,这时,只有动态射线追踪可以快速提供保真振幅偏移所需的各种旁轴变量.在复杂介质情况下,波前重建法以模拟波前向前传播为基础,用三角形来表示复杂的波前面,并动态地插入射线以保证波场计算的精度.这种方法首先由Vinje et al.提出[17],尔后其发展极为快速而有建设性,在诸多研究成果下[18~21],很快地这种方法在学术界及工业界都得到了推广和应用.当然从现在来看,Vinje et al.[17]最先提出波前重建法时,其算法并不完善,在焦散场的情况下,插入的射线不是很充分,走时计算的精度还有待提高.Lambar éet al.[19]和Lucio et al.[22]修改了插入的射线密度判据,他们在相空间中引入计算新的射线密度参数,使得在焦散场情况下,走时和振幅的计算都达到了相当高的精度.在复杂介质下,当速度模型含有强横向变化时,常常出现焦散场,这时射线场是扭结的.例如在二维Marm ousi 模型[23],图1a 为合成Marm ousi 速度深度精确模型,图1b 显示其射线场和波阵面,背景彩色为用以进行射线追踪的Marm ousi 光滑速度模型.其中只显示向下传播的射线和波前面.从图1a 可以看2341地球物理学报(Chinese J.G eophys.)49卷 出,射线场在横向速度变化大的区域被多次折叠,在模型的深部,可以观测到高达5次的走时.这是复杂情况下多次走时的一个普通的例子,它展现了复杂介质下地震波传播的复杂性,也是射线追踪、走时表的计算、叠前深度偏移的难度所在.3 单次走时偏移和多次走时偏移 在地质条件不很复杂的情况下,利用动态射线追踪的叠前深度偏移方法早已成熟[24~27].在这些研究工作中,利用射线计算出的走时被假设成单值的,而且走时表具有连续光滑性,从而可以对偏移算子进行简单的线性插值,偏移算法的效率可由走时表的插值得以大大提高[25,28].图2 单次走时的保真振幅叠前深度偏移在Marm ousi 中的结果(a )偏移所用的走时为最小走时;(b )偏移所用的走时为最大振幅.Fig.2 T rue am plitude migration result with single valued traveltime(a )First arrival ;(b )S trongest arrival. 在复杂地质条件下,由于速度模型含有强的横向变化,地震波的传播现象变得很复杂,不能简单地用单一走时来表达两点之间的地震波传播的格林函数(如图1b 所示).所以,单次走时偏移效果很不理想.虽然如此,研究工作者还是对此进行了大量的研究工作,这些工作主要是对不同的走时进行挑选,希望能挑出某一种单值的走时,用以提高复杂地质结构的偏移成像效果.其中,G eoltrain and Brac[29]研究了最小走时叠前深度偏移,Marm ousi 模型中复杂地质逆断层下的目标区,最小走时叠前深度偏移基本不成像,其主要原因是在复杂速度模型下,最小走时的振幅通常很小,即携带的能量很少,而绝大多数的能量受载于次级以上的走时,最小走时偏移算法并没有考虑这些次级走时[28,30,31](图2a );虽然这些研究工作目的并不在于保真振幅偏移,但也足以证明最小走时偏移不适于复杂情况下深度成像.如果考虑到保真振幅,实验表明在Marm ousi 模型复杂地质逆断层下,模型反射率远远地被低估[28,30]了.另外一些变通的方法期望通过走时的选择来提高成像效果,也取得了一定的成效.例如采用最大能量走时,由于走时携带的能量增加,能提高成像效果.但最大能量走时也并不能代表整个格林函数,有一大部分能量没有考虑到偏移中去,成像效果还远达不到理论要求.Nichols et al.[32]提出采用最短路程走时进行叠前深度偏移,其成像效果可以接近最大能量走时偏移,但从未超越它.走时计算时可以不必考虑射线的振幅,也不需要旁轴射线,算法比较简单.所有的这些研究工作导出一个明确的结论:仅仅考虑一次走时不足以对复杂地下结构成像. 一些研究工作已经间接证明射线法可以对复杂地下结构进行成像,其效果足以和单程波动方程偏移相媲美.Bevc[33]将速度模型分解成几个虚层,在每一层中用一次走时进行成像,每一层顶用射线法向下延拓地震数据.由于他们的虚层比较薄,以层顶为源作射线追踪时,都只存在一次走时.多个虚层相结合,则相当于间接利用了多次走时;虽然每一层都只用到一次走时,但地震数据用射线法向下延拓时,多重传播路径已被自动考虑进去.它等价于多次走时的高频渐近叠前深度成像,其意义相当重要.由于受现有的计算条件和实际地震资料的采集系统所制约,Bevc 的方法很难推广到三维,但只要偏移时考虑了多次走时的影响,射线法依然可以给出相当理想的成像效果.另一方面,由于原始的保真振幅的理论是在没有焦散场的情况下(简单传播介质)建立起来的,自从Beylkin[34]的文章发表以来,理论研究工作者一直3341 5期徐 升等:复杂介质下保真振幅K irchhoff 深度偏移追求把它推广到含有焦散场的复杂介质情况[35,36].得到的结论是:考虑了多次走时的影响情况下,只要多次覆盖地震资料采集时的采集系统满足一些条件,保真振幅偏移可以自然而然地推广到含有焦散场的复杂地质构造成像中去.这些条件中,最重要的是走时一一对应条件.它表明在接收到的地震数据中,任一局部同相轴可以一一对应地映射到深度域中.虽然这个条件在井间地震成像过程中不容易满足,而且会产生强振幅的假像(如何清除这些假像,是令人头疼的实际生产问题[37]).但是在反射地震数据成像中,如果地面接收覆盖比较完备,只在一些极端的情况下才会产生假像,即理论上存在可能性,而实际应用中几乎遇不到.Operto et al.[38]首先把这些偏移理论运用到合成地震数据模型Marm ousi中去,其研究结果显示:只要考虑到多次走时的影响,射线法保真振幅偏移完全可以定量求解出复杂地质结构,其结果可以和波动方程偏移结果[39]或高斯射线束偏移结果[40]相媲美.以上提到的理论研究和实际资料处理都是在二维多次覆盖地震勘探的框架下进行的,将它推广到单次覆盖成像中去有巨大的理论和实用价值,因为常规单次覆盖地震成像,要求对一个最小地震数据集在深度域里成像,从而可以形成共像集,如共偏移距像集.而后者不仅是常规叠前速度模型分析算法最常见的输入数据,也是定量储藏分析有力的佐证.4 深度域中的共角度像集 在常规叠前深度成像处理中,共像集一般有共偏移距像集或共炮像集.这些常规处理要求一个最小地震数据集;一般地,最小地震数据集为多次覆盖地震数据的子集,如共偏移距道集、共炮集、共检波器道集等.其基本假设是,输入的最小地震数据集可以对地下覆盖地区进行单次覆盖成像.这样每一个地震数据子集都可以对同一地下构造成像,也就是说,对于多次覆盖的地震数据,同样的深度点可以有多个地震像.因为地下结构是惟一的,如果成像都正确,所有的这些成像理论上应该等价.由此可推知,在理想情况下,深度域中的共像集的同相轴应该是平的.速度模型是影响深度域中的共像集的同相轴平否的主要因素,而共像集的同相轴平否是检验叠前速度模型的重要标准.如果共像集的同相轴不平,说明叠前速度模型不够准确,就可以利用这些不平同相轴的曲率反过来求取速度模型[41~43].此外,在储藏分析中的振幅随偏移距变化分析(AVO)也是在共偏移距像集中进行的[26,44].所以勘探地震界普遍认为共偏移距像集是常规的共像集[45].在复杂地质条件下,共偏移距像集出现很多假像.Duquet[46]在研究二维Marm ousi时注意到了如下现象:即使用精确速度模型,用波动方程计算格林函数的共偏移距像集中存在很多假像,而且其同像轴并不平!这在叠加地震图中观测不到.初步看来这有违上面所得的常识.这不仅使复杂地质构造下的偏移速度分析变得很困难,也让AVO分析走入绝境.为了走出这种困境,可以引入额外的约束来迫使共像集变平[46],但这在理论上没有说服力,实际操作效果也并不好.这些研究工作是在波动方程的框架下进行的,对问题的理解并不直观.相反,高频渐近分析可以提供理论分析的平台.多次走时的K irchhoff偏移理论工作[36],其初步成果局限于二维理想多次覆盖地震数据.有必要从最小地震数据集的角度进行分析.N olan and Symes[47]证明成像条件在二维情况下应当进行推广,在三维实际接收系统下,一般情况下的子集成像条件只有相对简单的速度模型才成立.而常用的共偏移距道集,共炮集都会因为存有焦散场而出现假象.结果是,强烈的假象会淹没真实的地质结构反射,在共像集的复杂区域,基本上找不到平的同相轴.Xu et al.[48]对这个问题首先进行了研究.他们通过理论证明这些假象的存在性,并利用对一个正则合成数据地计算,在共偏移距像集、共炮像集实验观测到这些假象(图3). 在勘探地球物理学界,对焦散场影响共偏移距像集的问题并没有很深刻的认识,在实际资料处理中,这些假象通常混在复杂速度模型的估计问题中,而且多次走时及其振幅的计算在数值计算中又很艰难繁琐,因此缺乏这方面的研究.Xu et al.[48]提出共衍射角或共反射角成像并首次计算复杂情况下的共衍射角像集.此概念曾在文献[49,50]中提出过,但这些文献没有研究过焦散场的情况,也没有透澈地分析过这方面存在的问题,只是提出在角度域,波场传播的外推数值表示比较自然简单.最近的数学分析表明,即使在共反射角度域里,射线Born偏移还会存在假象,这是因为在无穷高频的情况下,如果存在焦散场,只对单一的参数积分不能完全消除假象[51].无假象的共角度像集可以由双平方根波动方程偏移计算得到.在K irchhoff偏移中,也可以通过引入对不同斜率的同相轴加权,在输入4341地球物理学报(Chinese J.G eophys.)49卷 图3 对地震道子集的保真振幅偏移(a)共炮点像集;(b)共偏移距像集.在复杂情况下,常规共像集的能量分布不均匀(在M arm ousi,x=612km).Fig.3 T rue am plitude migration for single fold dataset(a)C omm on shot gather;(b)C omm on offset gather.In com plex case,the conventionalcomm on image gathers are alternated with strong am plitude artifacts.数据中对地震数据同相轴进行斜叠加,这样可以极大地清除假象.无论如何,当使用共反射角度域偏移时,假象都比共偏移距偏移或共炮点偏移少得多.进入21世纪以来,Audebert et al.[52、53]将共反射角度域K irchhoff偏移推广到三维;S ollid and Ursin[54]将它推广到各向异性介质中的偏移成像,并在实际资料处理中取得应用;在实际资料处理中,对于每一个接收系统,为了得到真振幅的偏移结果,地下照明技术变得很重要,研究者作了大量的工作[55~58].储藏分析方面,当地下结构很复杂时,在深度域进行振幅随偏移距变化分析具有很大的优势,而共反射角度域偏移直接给出振幅随反射角的变化[59,60];在速度分析方面,共反射角度域偏移是复杂情况下惟一合理的共像集,给层析成像带来了新的机遇[11,12,61,62].与此同时,用波动方程输出共反射角度像集也正在展开,例如Prucha et al.[63]提出分两步实现波动方程共反射角度像集偏移:首先输出局部共偏移距道集,然后通过斜叠加将局部共偏移距道集转换成共反射角度像集;Sava and F omel[64]提出另外一种转换方法,利用傅里叶变换提高效率,但他们的算法只在二维是正确可行的;最近Wang et al.[65]利用“小束波”在波动方程偏移中直接输出共反射角度像集,此方法对绕射波也有效;S oubaras[66]提出在进行波动方程向下延拓时,对波场进行球谐分解而实现波动方程共反射角度成像.在这里必须指出的是,以上偏移方法提到的波动方程方法都只是单程波动方程[15],Zhang et al.[67]证明了这个波动方程,阐明了该方程不保证波传播的振幅保真,并提出保真振幅的单程波动方程,他们的方法在三维不均匀介质得到了验证,从而突破了单程波动方程保真振幅的瓶颈.进一步地,Zhang etal.[68]将Claerbout[15]的成果推广到保真振幅共角度像集的波动方程偏移中.5 叠前K irchhoff偏移的效率 虽然波前重构法射线追踪可以提供多次走时的走时表,但最初的保真振幅偏移还是建立在单次走时上[26~28,69].单次走时偏移很容易提高计算效率.因为走时表可以只在粗网格上存储,而在细网格上的成像可以通过双线性插值来获得;而且射线追踪的出射点位置也可以只在粗网格上计算并存储,地震道的真实炮点和检波器点位置的走时表也可以通过线性插值获得.Xu and Lambaré[70,71]对多次走时偏移插值算法进行了系统性的研究,提出了两种插值方案.并在二维合成数据Marm ousi上测试了精度和效率.这两种5341 5期徐 升等:复杂介质下保真振幅K irchhoff深度偏移方案都适用于三维多次走时保真振幅偏移,他们在三维理论合成数据SEG ΠE AGE 盐丘模型[72]运行了其算法,获得良好的效果.本文从理论上重点阐述复杂地质构造情况下,保真振幅叠前深度偏移的概念、理论公式和适用方法.基于文献[36,38,48]的工作,推导二维和三维情况下的共炮集偏移、共偏移距道集偏移、共角度道集偏移的公式;从波场的插值与外推出发,详细讨论保真振幅偏移的应用效率.6 多次走时下的Born 近似 考虑标量波动方程,其参考格林函数G (r ,t ,s )(s 表示源点,r 为接收器位置,t 为时间)是下列方程的解:1c 20(x )929t2-Δ2 G 0(x ,t ,s )=δ(x -s )δ(t ). (1)这里c 0(x )表示地震波在参考模型中传播的速度,一般来说,可以理解为光滑速度模型,或通过速度分析得到的速度模型,主要是指速度模型的低频分量.格林函数满足相互关系G 0(x ,t ,s )=G 0(s ,t ,x ).射线理论提供了格林函数的高频渐近解G 0≈G 0[73,74].在频率域,格林函数可以写成:G (x ,ω;s )=S (ω)∑N (x ,s )n =1A n (x ,s )ei ωT n(x ,s )-iπ2sign (ω)αn(x ,s ),(2)其中n 标记为射线所处的分支,N 为局部的射线分支的总数,A 为射线的振幅,T 为走时,S 为格林函数的源的符号(源的子波),ω为角频率,α一般为整数,是焦散射线场的K MAH 标记[73,74].物理上K MAH 标记指折叠射线场的相移之和,它通常是一个正整数,并在源点被初始化为零,每经过焦散场时增加一个整数[74].通常二维或三维情况下,折叠射线族中的每一个分支都会有相同的K MAH 标记值,但具有相同的K MAH 标记值的射线并不一定属于射线族的同一分支.在二维或三维情况下,几何扩散度J ,渐近振幅A ,源符号S 可由下表给出: 表1中9L 和9S 为射线管中正交与射线方向的线元和面元,9φ和9Ω为初始出射的角元和角面元[28].在焦散点,9L 或9S 为零,其结果是渐近振幅为无穷大,这是众所周知的射线理论的奇性,物理上并不存在这样无穷高振幅的地震波.方程(2)渐近格林函数中的各个参数都可以通过射线追踪以及对沿射线的常微分方程积分得到[75],也就是众所周知的表1 几何扩散度、渐近振幅和源符号值T able 1 T able of geometry spreading ,ray amplitude and source signature2-D73-DJ (x ,s )9L (x )9φ(s )9S (x )9Ω(s )A (x ,s )c (x )8πJ 2D (x ,s )116π2c (x )c (s )J 3D (x ,s )S (ω)1-i ω1旁轴射线理论.为了引入Born 近似,我们考虑模型扰动δm (x ),它代表参考速度模型的平方倒数,即平方慢度深度模型1Πc 2(x )的扰动量,模型扰动会引起格林函数的扰动δG :1c 2(x )=1c 20(x )+δm (x ),G (r ,ω;x )=G 0(r ,ω;x )+δG (r ,ω;x ).(3) Born 近似是对模型扰动量的线性近似,对于参考模型c 0(x )的模型扰动量δm (x ),相对的格林函数扰动量δG 为δG (r ,ω;s )≈B (r ,ω;s )[δm (x )]=ω2∫d xδm (x )G 0(r ,ω;x )G 0(x ,ω;s ),(4)其中B 为一阶正演Born 算子.只要模型扰动量足够小,一阶Born 近似可以精确地模拟反射或散射场.但是线性化的一阶Born 近似不能模拟多次波或直达波,而这些波在偏移成像中并不太重要.把方程(2)表示的高频渐近格林函数代入Born 近似方程(4),给出射线Born 近似关系,它是Born 近似的高频渐近表示,因此扰动格林函数可以写为δG (r ,ω;s )≈B (r ,ω;s )[δm (x )]=K (ω)∫d x δm (x )×∑N (x ,r )n =1∑L (s ,x )l =1A nl (r ,x ,s )ei ωT nl(r ,x ,s ), (5)A nl 和T nl 分别表示扰动格林函数的每一分支的总振幅和总位相,相应于源的射线分支l 和接收器位置射线分支n .它们可由下列方程式给出:A nl (r ,x ,s )=A n (r ,x )A l (x ,s )T nl (r ,x ,s )=T n (r ,x )+T l (x ,s )-π2sign (ω)ω(αn (r ,x )+αl (x ,s )),(6)在215维的情况下,Born 算子的振幅[76]为6341地球物理学报(Chinese J.G eophys.)49卷 A2.5Dnl (r,x,s)=A2D nl(r,x,s)2π(τn(r,x)+τl(x,s)),(7)其中参数τ定义为dτ=c(x)d s,s是射线长度.源符号K为:K2D=-iωK215D=-ωiωK3D=ω2.(8) 在格林函数计算中引入了高频渐进近似,计算出散射场的δG,只有其高频分量才符合真实的散射格林函数的δG.在物理上,它标志着反射场或散射场δG的奇性.Rakesh[35]证明射线Born正演算子是一个加权傅里叶积分,其条件是只要在地表不存在掠射波.,此证明也成立;而在没有焦散场的情况下,理论证明工作是Beylkin[34]在20世纪80年代完成的.射线Born算子B仅表示Born 算子最奇性的部分,由它得到的偏移算法只能对模型的高频部分(如不连续面、衍射点等)成像.7 射线Born真振幅偏移公式 为了简单起见,首先考虑二维多次覆盖地震数据,地震道的坐标可以由独立的炮点坐标和检波器坐标来表示(s,r).方程(5)中的线性关系可在广义反演理论框架下求逆[77].用加权L2范数测量理论计算和实际测量之差别,可以定义一个目标函数:C[δm]=12∫dωκd s d r Q|δG obs-δG cal[δm]|2.(9)式中δGobs为记录到的反射地震数据,Q为权因子,等价于反问题中数据空间中的协变矩阵[77].δG cal为通过对模型扰动δm利用Born算子计算出的理论散射地震波场值.对目标函数(9)式,未知的模型扰动δm解的表达式是δm=(B Q B)-1B QδGobs,(10)其中 表示伴随算子.-B QδG obs是目标函数的梯度,算子B Q B是Hessian二阶梯度矩阵.一般地,地震数据处理应用中,Hessian是一个无比巨大的矩阵,数值求逆几乎不可能;迭代求解又很容易陷入局部极小[44].任何对二阶梯度矩阵的逆的计算效率的提高,都可以极大地加速成像计算.在此项研究中, Jin et al.[78]提出的对Hessian矩阵进行渐近近似分析,是在单次走时假设下进行的,Operto et al.[38]将工作推广多次走时的情况,并运用到二维Marm ousi 合成数据中,其结果表明,即使只有一次迭代,模型的高频分量也收敛到良好的结果.Jin et al.[78]提出:可以通过引入一个特别的权因子Q,而使得Hessian矩阵渐近对角化.Jin et al.的方法得到的结果和Beylkin[34]得到的相似,Beylkin证明一阶Born近似在理想的条件下是一个加权傅里叶变换;而Jin的方法是在统计反演的框架下得到的[77].在这里,我们将Jin et al.[78]的成果推广到含有焦散场的复杂地质结构成像中去.二阶梯度Hessian矩阵:B Q B(x,x0)=∫dωκd s d r∑N,L n,l=1 ∑N′,L′n′,l′=1K2(ω)×Anl(r,x,s)QAn′l′(r,x,s)×e iω(T n′l′(r,x0,s)-T nl(r,x,s))(11)可以分解成奇异的和规范的两部分,因为我们用高频渐近对正演算子进行近似,所以就只考虑奇异的那一部分.在参考文献[36,79]中Hessian矩阵是一族椭圆拟微分算子及低阶傅里叶积分算子.这意味着Hessian矩阵的奇性部分都集中在对角线x=x0上,而且成像射线的分支也必须相同,所以有n′=n和l′=l,这使我们可以进行“微局部分析”.而且ten K roode et al.[36]证明如果射线满足“走时一一映射条件”,除了对角部分外,Hessian矩阵的其他部分不存在奇异性.在这种情况下,只要不在焦散点上, Hessian算子是一个纯的椭圆拟微分算子,由此可见,Beylkin[34]的公式在多次走时的情况下依然成立.“走时一一映射条件”的数学推导要求有很深的数学背景,如拟微分算子及傅里叶积分算子[80].这样的数学推导并不适用于地球物理学界,但我们可以从物理角度来理解它.这个条件相当于地震数据中任意一个局部相干的同相轴,可以由炮点坐标、检波器点坐标、同相轴在两坐标处的局部斜率以及同相轴的局部走时来描述[9],它可以清晰地对应于一对射线[47,48].在运用正确的速度模型前提下,记录到的一个局部相干的地震数据同相轴应成像于惟一的一个深度点.多次走时偏移理论可以建立在广义的接收系统框架下,例如单次覆盖的地震数据集的共炮集、共检波器集等,或三维海洋接收系统(有限的方位角)[47,81].在这些情况下进行地震成像,如果要得到7341 5期徐 升等:复杂介质下保真振幅K irchhoff深度偏移。
叠前深度偏移技术的研究及应用

195随着我国油气资源的进一步消耗,发现新探区成为目前油气勘探的重点,而复杂地表和复杂地质条件地区的资料由于以前处理技术落后成像效果还有一定的提高空间,因此运用新的处理手段对老资料进行重新处理,能在节约成本的前提下最大限度的挖掘这些地区的勘探潜力,而叠前深度偏移技术对横向速度变化剧烈,地震资料较差的数据成像有很大的提升效果是解决复杂构造成像的一种有效手段。
1 方法原理叠前深度偏移技术是建立在构造起伏及横向速度剧烈变化的基础上,是一种真正的全三维成像技术。
叠前深度偏移方法遵守波的反射、绕射和折射定律,符合斯奈尔定律,适应于复杂地质条件的成像问题。
生产中常用的叠前深度偏移方法是克希霍夫积分法。
实现方法是,将地下地质体分成均的面元网格,然后计算地下不同面元网格与地面每一个炮点位置之间的旅行时,产生走时表,使用射线追踪技术计算出的走时表和叠前数据道集,计算出地面炮点和接收点到地下成像点到的几何扩散因子以及相应的走时最后在偏移孔径范围内对时距曲面进行加权叠加,实现最终成像。
克希霍夫叠前深度偏移算式为:作为地震资料处理技术的一个重要发展方向的叠前深度偏移,相对于叠前时间偏移在速度横向变化剧烈及陡倾角等复杂地区地震资料成像上具有明显的优势,它突破了叠后时间偏移和叠前时间偏移等传统处理方法的应用条件限制。
2 深度偏移处理的关键步骤2.1 时间域构造模型建立层位解释原则如下:1)第一层反射的最大偏移距应小于该层的最大深度。
2)层位拾取应选择能量强、连续性好的同相轴追踪,最好一个地质时代界面的反射或者是一大套地层的速度界面。
3)层与层之间的厚度不能太薄。
4)层位解释后得到的间域构造模型是每一层的时间域构造平面图的。
2.2 初始速度模型建立为了使速度能够迅速收敛、逼近地下正确的地质模型需要有一个较准确的初始速度模型,GeoDepth提供了RMS 速度转换的方法:2.3 速度模型优化初始模型往往是不够精确,为了得到一个跟地下地质情况相吻合的速度模型,需要通过多次迭代收敛、优化层速度模型,直至每CRP道集成像结果一致为止。
叠前深度三维偏移成像

野外数据 水平NMO 叠前部分偏移(PSPM) 更好的叠加剖面 零炮检距偏移(叠后偏移)
什么是PSPM?常规叠加剖面存在倾角不一致所出现的问 题------叠后偏移是不正确的。为说明PSPM,必需重新考虑单倾 向反射的NMO方程(Levin, 1971):
t 2 (x)
t 2 (0)
x2
cos 2 v2
野外数据
↓
速度分析
↓
利用水平同相轴的速度作NMO校正
↓
DMO校正
↓
利用第二步中用过的速度作反NMO校正
↓
速度分析
↓
利用第五步中求得的速度作NMO校正
↓
叠加
↓
偏移
图1-42 DMO处理流程
现在来检验倾斜同相轴,图1-43表示一个零炮检距剖面,
它由倾角范围从0 ~ 45 每隔 5递变的一系列倾斜同相轴组成,
图1-32 常速介质中 六个散射点的深度模型 星号表示散射点所在位置
图1-33 图1-32深度模型的非 零炮检距地震合成数据进行 DMO处理的各中间结果
(1) 图1-33(c)表示经拉伸切除后的NMO校正道集,校正所用 的介质速度为3000m/s;这是随后作DMO校正[方程(1.3.2)]的必 要条件,其结果使位于中心点(CMP32)以及附近的同相轴经 NMO校正之后拉平,偏离中心点的同相轴随偏离程度而过校正。
现在见图1-46(a)中的野外数据例子,紧接DMO校正, 在2.35s处拾取速度的二重性消除了,通过速度分析对速度进行 了倾角校正。PSPM处理的叠加剖面示于图1-46(b)。该剖面 的 偏 移 结 果 ( 图 1-47 ( c ) ) 可 以 跟 叠 前 全 偏 移 结 果 ( 图 1-47 ( a ) ) 媲 美 。 利 用 DMO 处 理 后 不 仅 获 得 了 较 好 的 叠 加 剖 面 (比较图1-46(a)和1-46(b)),而且能得到经过倾角校正的 速度,从而取得良好的叠后偏移效果(比较图1-47(b)和图147(c)),它的成象质量相近于叠前全偏移结果(图1-47(a))。
叠前深度偏移速度建模保幅偏移
偏移速度建模
模型试算及分析
偏移速度建模
共反射点CRP道集偏移速度建模
CRP道集偏移速度建模是基于叠前深度偏移、 地震层析成像(ST)、和深度聚集分析 (DFA)。在DFA中,若偏移深度和聚焦深 度之间的误差为零,则偏移速度合理;否则, 依据误差修正偏移速度 。
偏移速度建模
共反射点CRP道集偏移速度建模
r
ms ( x, z ) us ( x, z; )vs ( x, z; )
分析:
(2) (3)
可见成像的核心是波场外推算子,目前基于波动方 程的波场延拓算子不外乎:有限差分波场延拓算子 和付立叶波场延拓算子。
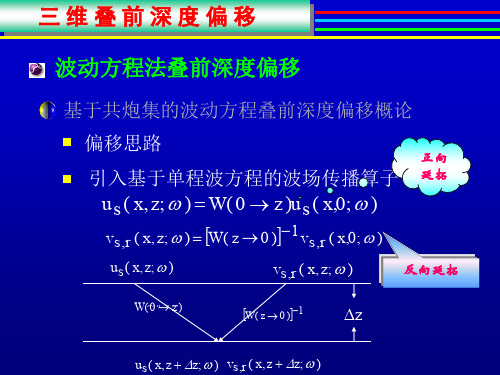
三维叠前深度偏移
频率空间域有限差分(FXFD)法叠前深度偏移
基本理论
波动方程保幅偏移
波动方程法三维叠前深度偏移技术在很大程 度上能够实现保幅处理,特别是付立叶有限 差分(FFD)法,综合了付立叶方法与有限 差分法的优点,对陡倾角地层和强横向变速 介质有很好的适应性,是目前精度最高的叠 前深度偏移方法。下面主要在叠前深度偏移 方法的基础上讨论适用于各向异性介质的保 幅偏移,以及基于粘滞声波、弹性波和粘弹 性波动方程的保幅偏移。
2 u 1 2 u 0 (9)
v 2 t 2
2u 2 u 0
v2
(10)
三维叠前深度偏移
s( x, y, z ) s0 ( z ) s( x, y, z ) (11)
u (x, y, z,) u0(x, y, z,) us (x, y, z,) (12)
反演公式如下:
m(x)
1 2
St
H
(x)
L
L
S
Kirchhoff积分叠前时间偏移全方位角度道集生成方法与实现

取汇聚后的波场值作为成像结果便实现了 K-PSTM。在时间域,(1)式可以表示为:
1 cos U
V
I r, t = 0 2
dA
RV
t
(x, t)
R
U(x, t) R t t0 V
(2)
其中:A 为地表处炮点和检波点的分布范围;θ是从成像点到一个接收点时地震波传播所沿 射线的出射角;V 为地震波传播速度,R 代表反射点到检波点时地震波所走过的距离;
要的全部共中心点地震数据。该地震数据对于
三维大规模工区,数据量级比较大,需要一定
数量的集群节点内存来分散存储,否则可能因
为内存不足而影响计算效率或无法计算。 在成像阶段,由于一次只对一条线进行成
像,即使分选到全方位角、反射角,成像体的
规模仍旧是可控的,也不会需求太大内存而造
成无法计算。在所有进程对某条线成像完成后,
PS
, psx , psy psz
TS x
,
TS y
,
TS z
(4)
PR
prx , pry , prz
TR x
,
TR ,
y
TR z
利用 PS 和 PR 可计算得到入射角γ和散射方位角φ:
2
=a
(5) (6)
=
arccos
入射角γ(散射张角的一半)和散射方位角
图 1 散射点处地震波传播角度示意图
( 即 局部 入 射 与散 射 慢 度 所在 平 面 的方 位 Fig.1 Sketch of seismic wave transmission
角)。入射与散射慢度矢量和 PM 称为照明矢
angle at a scatter point
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章 Kirchhoff 积分法叠前深度偏移大家知道,叠前偏移的概念早在70年代中期就提出来了,但由于叠前记录的信噪比较低,偏移的初始模型又很难选准,加之当时的计算机无法承受叠前偏移较大的计算量,直到90年代叠前偏移才开始尝试应用于油气勘探地震数据的精细处理中。
常见的叠前深度偏移方法可以分为两类:第一类是基于绕射扫描叠加原理的Kirchhoff 积分法,另一类是基于波动方程的偏移方法(如有限差分偏移方法、Fourier 偏移方法等)。
本章重点讨论Kirchhoff 积分法叠前深度偏移。
Kirchhoff 积分法叠前深度偏移被认为是一种高效实用的叠前深度偏移方法,目前主要完善三维采集和叠前深度偏移软件。
积分法具有高偏移角度、无频散、占用资源少和实现效率高的特点,并且积分法能够适应变化的观测系统和起伏的地表,优化的射线追踪法和改进的有限差分法能够在速度场变化的情况下快速准确地计算绕射波和反射波旅行时,从而使积分法能够适应复杂的构造成像。
地震偏移成像问题,经过最近十多年的研究与发展,已经基本解决了和正在解决三维偏移,叠前深度偏移和多分量地震偏移等诸问题。
但是偏移中有诸多问题尚未解决,例如真振幅偏移问题和各向异性介质中的地震偏移问题。
近年来,解决真振幅偏移问题就是偏移地震数据得到真正的振幅和相位信息,从而为岩性解释服务。
由于积分法具有许多优点,因此研究Kirchhoff 型保幅叠前深度偏移具有很高的理论价值和实用价值。
下面就变速射线追踪法计算走时、有限差分法计算走时以及Kirchhoff 型常规叠前深度偏移和保幅叠前深度偏移做详细讨论和分析。
§3.1 变速射线追踪法计算走时Kirchhoff 积分法叠前深度偏移已在实际生产中应用了多年,并解决了不少复杂构造的成像问题(Zhu & Lines, 1998)。
Kirchhoff 积分法的关键是绕射旅行时的计算,目前常用的计算方法是射线追踪法和有限差分法(Schneider, 1992, 1995)。
有限差分绕射旅行时计算是基于费马原理,可在直角坐标系或球坐标系实现,具体方法原理将在本章第二节介绍。
射线追踪法计算绕射旅行时可分为常速法和变速法,常速法很简单,在此不再赘述;下面主要介绍变速法。
考虑到地下介质在纵横向上通常是变速的,为通过射线追踪较精确地生成CMP 道集中各道的反射旅行时,下面我们基于Langan (1985)的思想,推导变速介质条件下的射线追踪方程。
由程函方程可推出如下的射线方程])(1[])(1[r v ds r d r v ds d r ∇= (3-1) 其中,)(r v 是波速,r是空间位置,s 是与路径长度有关的仿射参数。
路径长度l 由(3-2)式给出⎰''=s s d r n l 0)( (3-2)其中, dsr d r n =)( (3-3))(r n 是位置r 处指向射线传播方向的矢量,射线旅行时为s d r v r n s t s'''=⎰0)()()( (3-4) 若)(n v 为正实数且时不变,则有1)(=r n(3-5) 由射线方程,经推导得出 s d s d ])r (v 1[)r (v s d )r (v )r (v n ˆr )s (r s 0s 0r s 0000'''''∇'+''+=⎰⎰⎰''' (3-6) 其中,0r 是炮点(s=0)相对于原点的位置,0nˆ 为s=0处射线方向的单位矢量。
当射线通过恒定速度梯度或恒定慢度梯度介质传播时,可建立方程(3-6)的简单近似解。
如果射线通过恒定速度梯度介质传播,速度场可表示为r v r v ⋅+=λ*)( (3-7)其中,*v 是原点处的速度,λ 为速度梯度)]([r v r ∇。
借助于Taylor 展开()1(*<⋅v r λ),由(3-6)、(3-3)和(3-4)分别求得())(O ]n ˆ[s v 6n ˆv 2s )]n ˆ(v 2s 1[s n ˆr )s (r 32023200020000λ+⋅λ-λ-λ-⋅λ++= (3-8)())(O ]n ˆ[s v 2n ˆv s )]n ˆ(v s 1[n ˆ)s (n 320222000000λ+⋅λ-λ-λ-⋅λ+= (3-9) ())(O }v 2s )n ˆ(]n ˆ[v 6s 1{v s )s (t 3002022020λ+⋅λ-⋅λ+λ+= (3-10) 其中,)1(11*0*0v r v v ⋅-=λ, 0v 是射线入射点处的速度。
方程(3-8)、(3-9)、和(3-10)就是恒定速度梯度介质条件下的射线追踪方程。
§3.2 有限差分法计算走时一.二维有限差分绕射旅行时计算方法在Kirchhoff 叠前深度偏移中,绕射走时的计算精度直接影响了成像精度。
为此,我们利用Eikonal 方程、费马原理和有限差分近似,基于二维介质在规则网格上进行绕射走时的有限差分计算,它无需走时的内插,并且把它扩展到三维是很简单的。
1.方形网格情况下的绕射走时有限差分计算在高频近似下,二维几何路径及二维波前的传播符合射线追踪的程函方程,()2022,z x s z t x t =⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂ (3-11) 方程(3-11)建立了走时梯度与速度模型的基本定量关系。
坐标轴是x 和z ,s 0是慢度(速度的倒数)。
方程(3-11)中的两个微分项能够应用有限差分来近似表示:()312021t t t t xx t --+∆=∂∂ (3-12a ) ()321021t t t t zz t --+∆=∂∂ (3-12b ) 其中t 0、t 1、t 2和t 3的含义如图3-1所示,x ∆和z ∆分别是横向和纵向采样间距,方形网格情况下,h z x =∆=∆。
在平面波近似下,已知t 0、t 1和t 2可以求t 3的值。
即已知 四个点中的任意三个都可以把另一点计算出来。
2122003)()(2t t hs t t --+= (3-13)为获取待求行或列上第一个点处的旅行时,利用有限差分得出如下计算公式 图3-1 方形网格走时计算示意图2122003)(25.0)(t t hs t t --+= (3-14)其中,3210,,,t t t t 分别是内行或内列上旅行时的相对极小值、两侧的旅行时、和待求行或列上的旅行时。
2.矩形网格情况下的绕射走时有限差分计算为提高绕射走时有限差分计算方法的适应性,考虑具有不同纵、横向采样间距的矩形网格。
矩形网格走时计算见图3-2a 。
基于方程(3-11)和(3-12),经推导可以得出:经过(3-15)式,“十”字形的四个顶点值都可以求取出来,这样十字形的各个顶点构成一个环,下面要做的是如何把该环进行外推,求取整个模型上的走时。
我们把距离前一个环上的极小和极大走时点最近的点定义为该环的相对极小和极大走时点。
对于沿z 方向边界上的 图3-2b ‘十’字型中, O 点是震源点的位置, ‘十’字型各点的走时已知, 各顶点的走时可由相邻三个点的走时求出。
O A B C D图3-2a 矩形网格中水平距离为x ∆, 垂直距离为z ∆,慢度s 0为常数, t 0、t 1和t 2的走时已知, 可以求t 3的走时值。
S 0t 3 t 2 x ∆ z ∆t 0、 t 1 (3-15) 22221202212022102)1(3)()(2)()(z x t t s z x z x t t t z t t t x t a ∆+∆--∆+∆∆∆+-+∆+-+∆=t 0、 t 1 z ∆S 0x ∆ t 2 t 3第一个点可由方程(3-11)的非中心有限差分求出,即方程(3-16a ), )4)((222120)1(3z t t s x t t b ∆--∆+= (3-16a ) t 3是待求C 和D 的走时,t 0是图3-2b 中点O 的走时(相对极小值走时),t 1和t 2、分别为A 和B 点的走时。
同理可求得沿x 方向边界上的第一个点的走时为:)4)((2221200)1(3x t t s z t t b ∆--∆+= (3-16b ) 式(3-15)和(3-16)考虑了平面透射波的情况。
当计算下一环走时时,在四条边上依次进行(当震源点在地下时,震源下面的点的走时不必要计算)。
逐个从相对极小走时点出发,沿边界向前、向后逐点扫描计算走时,直到遇到极大走时点或顶点为止。
当所有四个边上的网格点的走时都计算出来后,再计算四个顶点的走时。
在扫描过程中,相对极大值被计算了两次,选其中较小的一个作为该点的走时,这等价于几何射线从两边到达同一个点,我们只考虑了初至射线。
另外,当(3-15)式右边根号下出现负值时有, ⎩⎨⎧∆+∆+=x s s t z s s t t a ),min(),min(202101)2(3 (3-17) 当(3-16)式方程的右边根号下出现负值时,我们选取: l s s t t b ∆+=),min(100)2(3 (3-18)当向z 方向外推时,z l =,当向x 方向外推时x l =。
式(3-17)和(3-18)考虑了首波出现的情况。
若考虑顶点的散射波,则有:0220)3(3s z x t t ∆+∆+= (3-19)式(3-19)考虑了散射波传播的情况。
依据费马原理,在考虑了平面透射波、首波和散射波情况下的最终初至走时为:),,min()3(3)2(3)1(33t t t t = (3-20)具体的实现步骤如下:如图3-3所示,从源点到各边的长度分别为R 1、R 2、R 3和R 4,以R 1<R 2<R 3<R 4为例,按照上面的方法一环一环地逐渐向外扩展。
首先由源点O 进行矩阵扩展直到R 1环,如图3-3虚线所示;然后基于R 1环向左、向上和向右外推直到R 2环,如图2细实线所示;再由R 2环向上和向右外推至R 3环,如图3-3中较粗实线所示;最后由R 3环向上外推至R 4环,如图3-3中最粗实线所示。
扩展矩阵与方阵所不同的是不需要整环外推,而是只对未到达边界的各边进行外推,直至各边都到达边界为止,这样整个模型上的图3-3 扩展矩阵图 R 1、R 2、R 3和R 4分别为源点O 到下边、左边、上边和右边的距离。
先由源点O进行矩阵扩展直到R 1环,如虚线所示;然后基于R 1环向左、向上和向右外推直到R 2环;再由R 2环向上和向右外推至R 3环;最后由R 3环向上外推至R 4环,这样整个模型上的走时就可计算出来。
R 1 R 2 R 3R 4 O最终初至走时(公式(3-20))就都计算出来了。
