第九章 回归与相关
第九章多元回归与多项式回归

学习要求
了解多元回归、偏相关系数、通径分析、多项式回归的概念;理解多 元回归、多项式回归关系的显著性检验及准确度测定的意义;掌握正 规方程组求解求逆紧凑法的步骤及建立最优回归方程、通径分析方法。
重点与难点
重点:涉及本章统计量的含义,建立最优回归方程及通径分析方法 难点:求解求逆紧凑法的应用
(9—4)
(9—5)
3b1 5b2 26 例1. 5b1 2b2 18
3 2 5 3 2 5 当需要解三元或三元以上方程组时,则用以下计算方法。目前最为流行的是求 解求逆紧凑法。 2.消元法 消元法求解的原理是利用乘或除法使方程组中两方程式的同一项具 有相同的系数,然后将此两式相加或相减使该项系数为零,从而消去一元。逐次 消元,最后得一方程及各元之解(略)。
这些方程用矩阵的形式表示为:
10 7 4 7 7 3 4 3 4 b1 4 b 4 2 b3 3
a13 10 7 4 a 23 7 7 3 a 33 4 3 4
式中: l —变换的次数,a(l+1)—变换 l 次后的元素,a(l)—变换 l 次时的元素, k—每次变换的主行列标号,akk—变换行主单元的元素,i—元素a的行标,j—元 素a的列标。9.1式用于变换主行(k)主元素的变换;9.2式用于变换主行除主元 素外其它元素的变换;9.3式用于变换主列(k)除主元素外其它元素的变换; 9.4式用于除变换主行主列元素外其它各元素的变换。
2 2
b1
26 2 5 18
2
b2
3 18 5 26
4
以上两种方法都无求逆过程,而逆矩阵元素是偏回归系数显著性检验所不可缺 少的。故以上两种方法不常用。 3.矩阵法 正规方程组的求解可用矩阵法来进行。
第九章 直线相关与回归
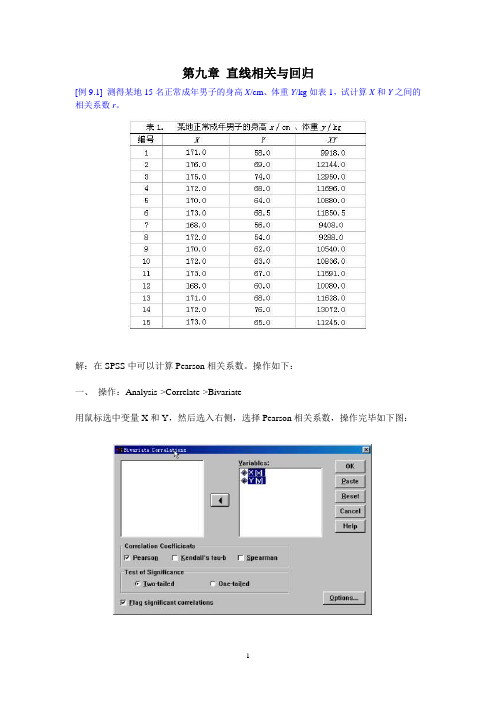
第九章直线相关与回归[例9.1] 测得某地15名正常成年男子的身高X/cm、体重Y/kg如表1,试计算X和Y之间的相关系数r。
解:在SPSS中可以计算Pearson相关系数。
操作如下:一、操作:Analysis->Correlate->Bivariate用鼠标选中变量X和Y,然后选入右侧,选择Pearson相关系数,操作完毕如下图:二、结果见下:SPSS给出相关系数交叉表,可以看出X和Y的相关系数为0.599,p=0.000。
可以认为X和Y线性相关,并且有统计意义。
[例9.2] 为了研究3岁至8岁男孩身高与年龄的规律,在某地区在3岁至8岁男孩中随机抽样,共分6个年龄层抽样:3岁,4岁,…,8岁,每个层抽3名男孩,共抽18名男孩。
资料列于表2。
解:本题需要计算回归方程式,在SPSS中可以直接菜单完成。
操作如下:一、操作:Analysis->Regression->Linear用鼠标选中变量X和Y,分别选入自变量和应变量对话框,操作完毕如下图:二、主要结果见下首先给出方差分析表,由p=0.000,可以认为回归模型有统计意义。
根据回归系数得到回归方程式为:Y=75.363+6.257X。
由p=0.000,可以认为回归系数有统计意义。
[例9.3] 调查了某地区10个乡的钉螺密度与血吸虫感染率/%数据如表3。
试分析该地区螺密度与感染率之间有无相关关系?解:本题选用Spearman秩相关,在SPSS中操作如下:一、操作:Analysis->Correlate->Bivariate用鼠标选中变量X和Y,分别选入右侧对话框,并且选择Spearman相关系数,操作完毕如下图:二、主要结果见下:可见Spearman相关系数为0.817,p=0.004。
可以认为Spearman相关系数有统计意义。
第九章 第四节 相关性、最小二乘估计、回归分析与独立性检验

分析与独立性检验
9/30/2013
9/30/2013
1.相关性 (1)散点图:在考虑两个量的关系时,为了对_____之间的关 变量 系有一个大致的了解,人们通常将___________的点描出来, 变量所对应 这些点就组成了变量之间的一个图,通常称这种图为变量之间 的散点图.
1.利用统计量χ 2来判断“两个变量X,Y有关系”计算公式为:
2
(A)ad-bc越小,说明X与Y关系越弱
(B)ad-bc越大,说明X与Y关系越强 (C)(ad-bc)2越大,说明X与Y关系越强 (D)(ad-bc)2越接近于0,说明X与Y关系越强
a b c d a c b d
1 2
9/30/2013
【拓展提升】线性相关关系与函数关系的区别 (1)函数关系中的两个变量间是一种确定性关系.例如,正 方形面积S与边长x之间的关系S=x2就是函数关系.
(2)相关关系是一种非确定性关系,即相关关系是非随机变
量与随机变量之间的关系.例如,商品的销售额与广告费是相
关关系.两个变量具有相关关系是回归分析的前提.
50 13 20-10 7) ( 4.844, 23 27 20 30
2
因为χ 2≥3.841,所以有
答案:95%
9/30/2013
考向 1
相关关系的判断
【典例1】(1)对变量x,y有观测数据(xi,yi)(i=1,2,„,
10),得散点图(1);对变量u,v有观测数据(ui,vi)(i=1,
9/30/2013
3.独立性检验
(1)2×2列联表
设A,B为两个变量,每一个变量都可以取两个值,变量A:
第九章 相关分析

第九章 相关分析
( y y)2
=
( y yc )2
+
( yc y)2
由此可以推导出:
( y yc ) ( y y) ( yc y)
2 2
2
2
Lyy (a bx a b x) Lyy b ( x x)
2 2
Lyy b Lxx
表明两变量完全不相关。 (4)当计算相关系数的原始数据较多(如50项以 上)时,认为相关系数在0.3以下为无相关, 0.3以上为有相关;0.3-0.5为低度相关;0.5-0.8 为显著相关;0.8以上为高度相关。
9
第九章 相关分析
相关系数计算分析例题
生产费用
序 月产量 号 1 1.2 2 2.0 3 3.1 4 3.8 5 5.0 6 6.1 7 7.2 8 8.0 ∑ 36.4
2 2
x n y y
2
2
0.97
说明产量和生产费用之间存在高度正相关。
第九章 相关分析
第三节
回 归 分 析
一、回 归 分 析 的 意 义 回归分析是对具有相关关系的两个或两个以 上变量之间的数量变化的一般关系进行测定,确 立一个相应的数学表达式,以便从一个已知量来 推测另一个未知量,为估算预测提供一个重要的 方法。 二、回 归 的 种 类 按自变量的个数分 按回归线的形态分 一元回归 多元回归 线性回归 非线性回归
Lxx x b b y Lyy
y br r x
Lyy L21 xx
第九章 相关分析
五 回归分析与相关分析的特点
1、回归分析必须区分自变量和因变量,而相关 分析不必区分。 2、回归分析的两个变量一个是自变量,一个是 因变量,通过给定自变量的值来推算因变量 的可能值;而相关分析的两个变量都是随机 变量。 3、回归分析中对于因果关系不甚明确的两个变量, 可以建立两个回归方程;而相关分析只能计算 出一个相关系数。 4、一种回归方程只能做一种推算,即只能给出自 变量的值来推算因变量的值,不能逆推。
课件第9部分相关与回归

i
i
i
i
取其期望得:
E( ei2 ) E[ (ui u)2 ] E[(1 1)2 xi2 ]
i
i
i
2E[(1 1) xi (ui u)]
等式右边第一项
i
E[
(ui u)2 ] E(
ui2 ) E(
2
u ) 2E(u
ui )
i
i
i
i
D(1)
2
xi2
i
于是等式右边第二项有:
假定3. 对于每个给定的Xi,ui的方差是一个常数,即各个Y总体
具有相同方差,即D(ui|Xi)=D(ui )= 2 假定4. ui与Xi不相关。即Cov(ui,Xi ) E[(ui Eui )(Xi EXi )] 0
▪满足以上4条假设的线性回归模型称为古典或普通线性回归模型, 其参数估计所采用的最小平方法称作普通最小平方法
Y=1
n
i
Yi
1 n
i
(ˆ0 ˆ1Xi ei ) ˆ0 ˆ1X
Yi=ˆ0 ˆ1Xi=(Y ˆ1X)+ˆ1Xi=Y ( ˆ1 Xi -X)
1
n
i
Yi=Y
1 n
ˆ1
(Xi -X)
i
于是:Y Y
性质3.
剩余项ei与解释变量X
不相关
i
ei2
由公式: i
ˆ1
= 2 (Yi ˆ0 ˆ1Xi )Xi 0,可得 eiXi=0,
其内容和步骤: 1.根据理论和对问题的分析判断,区分自变量和因变量。 2.设法找出合适的回归模型来描述变量间的关系。 3.对回归模型进行统计检验。 4.利用回归模型,根据解释变量去估计、预测因变量。
第九章双变量线性回归与相关

1 ( X X )2 SYˆ SY .X n ( X X )2
当X
X时,SYˆ
SY X n
Syˆ 是 Yˆ 的标准误。
例 计算当X0=150时, yˆ 95%可信区间。 yˆ 的95%可信区间为:
(46.52, 51.75)Kg
其含义是:当身高为150cm时,15岁男童的体重
的总体均数为49.135kg(点值估计),95%可信区 间为:(46.52, 51.75)Kg (区间估计)。
男性:身高(cm)-105=标准体重(kg) 女性:身高(cm)-100=标准体重(kg)
北方人理想体重=(身高cm-150)×0.6+50(kg) 南方人理想体重=(身高cm-150)×0.6+48(kg)
回归与相关是研究变量之间相互关系的统计分 析方法,它是一类双变量或多变量统计分析方法 (本章主要介绍双变量分析方法),在实际之中有 着广泛的应用。
如年龄与体重、年龄与血压、身高与体重、体 重与肺活量、体重与体表面积、毒物剂量与动物死 亡率、污染物浓度与污染源距离等都要运用回归与 相关方法对资料进行统计分析。
变量之间的关系: (1)直线关系(线性 关系); (2)曲线关系(非线 性关系)。 在回归与相关分析中, 直线回归与相关是最简单 的一种,是本章主要内容。
变量间的关系 函数关系: 确定的关系。 例如园周长与半径:y=2πr 。
回归关系:不确定的关系(随机的关系)。 例如血压和年龄的关系,称为直线 回归 (linear regression)。
北方人理想体重=(身高cm-150)×0.6+50(kg)
变量间的回归关系 由于生物间存在变异,故两相关变量之间的关 系具有某种不确定性,如同性别、同年龄的人,其 肺活量与体重有关,肺活量随体重的增加而增加, 但体重相同的人其肺活量并不一定相等。因此,散 点呈直线趋势,但并不是所有的散点均在同一条直 线上,肺活量与体重的关系与严格对应的函数关系 不同,它们之间是一种回归关系,称直线回归。这 种关系是用直线回归方程来定量描述。
最新九章相关与回归分析
散点图
(例题分析)
散点图
(不良贷款对其他变量的散点图)
不良贷款
14
12
10
8
6
4
2
0
0
100
200
300
400
贷款余额 不良贷款与贷款余额的散点图
14
12
10
8
6
4
2
0 0
10
20
30
40
贷款项目个数
不良贷款与贷款项目个数的散点图
不良贷款
不良贷款
14
12
10
8
6
4
2
0 0
10
20
30
累计应收贷款
1. 度量变量之间线性关系强度的一个统计量 2. 对两个变量之间线性相关强度的度量称为简单相
关系数 3. 若相关系数是根据总体全部数据计算的,称为总
体相关系数,记为
4. 若相关系数是根据样本数据计算的,则称为样本 相关系数,简称为相关系数,记为 r
– 也称为线性相关系数(linear correlation coefficient) – 或称为Pearson相关系数 (Pearson’s correlation
不良贷款与累计应收贷款的散点图
14 12 10
8 6 4 2 0
0
50
100
150
200
固定资产投资额
不良贷款与固定资产投资额的散点图
不良贷款
散点图
(5个变量的散点图矩阵)
不良贷款 贷款余额
累计应收贷款
贷款项目个数
固定自产投资
相关关系的描述与测度 (相关系数)
相关系数
(correlation coefficient)
统计学基础 第9章相关与回归分析
由表9.1数据可以大致看出,随着居民收入的增长,食品支出在生活 费支出的比例有稳步下降的趋势。
若将收集到的数据以坐标点的形式绘制于坐标系中,形成二维图形 ,就是散点图。散点图也称为相关图,可以比相关表更直观地判断 变量之间是否存在相关关系,以及相关的形态和方向。散点图的绘 制方法在第三章中已有说明,在此不再赘述。如图9.1(第13页)可 以直观地观察两个变量的关系。
完全正线性相关关系;若
,表明x与y之间为完全负线性相关关
系。但需要注意的是,r=0只表示两个变量之间不存在线性相关关系,
并不说明两个变量之间没有相关关系,它们之间可能存在非线性关系。
r=0时我们称为零相关。
统计学 9.1.3相关关系的测度
STATISTICS
• 通常按以下标准划分相关程度:
•
视为无直线相关;
3. 能够利用Excel软件对两个变量间的相关关系进 行分析,并能够拟合两变量的回归方程
统计学
STATISTICS
9.1 相关分析
9.1.1 函数关系与相关关系 9.1.2 相关关系的描述 9.1.3 相关关系的测度
统计学 9.1.1 函数关系与相关关系
STATISTICS
• 在日常生活中我们时常会注意到并利用变量间的关系说明 一些问题。如企业没有完成销售任务,市场占有率下降, 领导为此责怪销售部门,销售负责人申辩说,别的企业都 在大做广告,我们一分钱的广告都不做,销售下降是正常 的。那么,做广告与企业的产品销售有关系吗?在法官的 判决书中也会常常看到某某的行为与某某某的损失没有直 接关系或存在直接关系等等的说法,这些都是指变量间的 关系。
94statisticsstatisticsstatistics913设显著性水平为通常取值为005根据自由度n2查附录3t分布表得到检验统计量的临界值则不能拒绝原假设表明变量间线性关系在统计上是不显著的即不能认为变量x与y之间存在显著相关关则拒绝原假设表明变量间的线性关系在统计上是显著的即样本数据支持变量x与y之间存在显著相关关系的假定
09 第九章 直线相关与回归分析20130204
SS总 Σ(Y Y ) lYY 78.400
2
SS回 blxy 0.2348 226 53.065
SS残 SS总 - SS回 78.400- 53.065 25.335
35
表9-2 20岁男青年身高前臂长直线回归关系方差分析表 变异来源 总变异 回归 残差 自由度 9 1 8 SS 78.400 53.065 25.335 53.065 3.167 16.765 <0.01 MS F P
26
图9-2 20岁男青年身高与前臂长散点图
27
四、回归系数的假设检验
回归系数b为样本回归系数,假设在总体回 归系数β=0的总体中抽样,得出样本的b不
一定为0。
因此需作总体回归系数β是否为0的假设检
验,
常用t检验或方差分析。
28
四、回归系数的假设检验
1、t检验法
|b0| |b| tb Sb Sb
19
四、相关分析应用中应注意的问题
1、进行相关分析前应先绘制散点图。
2、直线相关分析的统计推断要求两个随机变量均服从正 态分布。 3、出现离群点时慎用相关。
4、相关关系不一定是因果关系。
5、分层资料不可盲目合并。
20
21
第二节 直线回归(linear regression)
2
例9-1资料可验证
37
F 16.756 4.09 tb
五、直线回归方程的应用
(一)描述两变量间的依存关系 可用直线回归来描述 。 (二)利用回归方程进行预测 将X代入直线回归方程,可得到应变量Y的估计值。 (三)利用回归方程进行统计控制 通过X取值来控制Y的变化。
38
统计学第九章 相关与回归分析
第九章相关与回归分析Ⅰ. 学习目的和要求本章所要学习的相关与回归分析是经济统计分析中最常重要的统计方法之一。
具体要求:1.掌握有关相关与回归分析的基本概念;2.掌握单相关系数的计算与检验的方法,理解标准的一元线性回归模型,能够对模型进行估计和检验并利用模型进行预测;3.理解标准的多元线性回归模型,掌握估计、检验的基本方法和预测的基本公式,理解复相关系数和偏相关系数及其与单相关系数的区别;4.了解常用的非线性函数的特点,掌握常用的非线性函数线性变换与估计方法,理解相关指数的意义;5.能够应用Excel软件进行相关与回归分析。
Ⅱ. 课程内容要点第一节相关与回归分析的基本概念一、函数关系与相关关系当一个或几个变量取一定的值时,另一个变量有确定值与之相对应,这种关系称为确定性的函数关系。
当一个或几个相互联系的变量取一定数值时,与之相对应的另一变量的值虽然不确定,但仍按某种规律在一定的范围内变化。
这种关系,称为具有不确定性的相关关系。
变量之间的函数关系和相关关系,在一定条件下是可以互相转化的。
116117二、相关关系的种类按相关的程度可分为完全相关、不完全相关和不相关。
按相关的方向可分为正相关和负相关。
按相关的形式可分为线性相关和非线性相关。
按所研究的变量多少可分为单相关、复相关和偏相关。
三、相关分析与回归分析相关分析是用一个指标来表明现象间相互依存关系的密切程度。
回归分析是根据相关关系的具体形态,选择一个合适的数学模型,来近似地表达变量间的平均变化关系。
通过相关与回归分析虽然可以从数量上反映现象之间的联系形式及其密切程度,但是无法准确地判断现象内在联系的有无,也无法单独以此来确定何种现象为因,何种现象为果。
只有以实质性科学理论为指导,并结合实际经验进行分析研究,才能正确判断事物的内在联系和因果关系。
四、相关图相关图又称散点图。
它是以直角坐标系的横轴代表变量X ,纵轴代表变量Y,将两个变量间相对应的变量值用坐标点的形式描绘出来,用来反映两变量之间相关关系的图形。
