等边三角形包括等腰三角形吗
八年级数学 等腰三角形的判定 等边三角形的性质与判定 浙江版

【本讲教育信息】一. 教学内容:1. 等腰三角形的判定2. 等边三角形的性质与判定二. 重点、难点:重点:1. 等腰三角形的判定方法及其运用。
2. 等边三角形的性质与判定。
难点:1. 等腰三角形判定方法证明中添加辅助线的思想方法以及等腰三角形性质与判定的区别。
2. 等边三角形的轴对称变换与旋转变换。
三. 知识要点及学习目标1. 理解等腰三角形的判定方法的证明过程。
判定方法:如果一个三角形有两个角相等,那么这个三角形是等腰三角形。
简单地说:在同一个三角形中,等角对等边。
如图,已知:ΔABC中,∠B =∠C。
那么:AB = AC. 即△ABC是等腰三角形。
说理如下:作△ABC的角平分线AD,则在△ABD与△ACD中,∠B =∠C (已知)∠BAD =∠CAD(角平分线的定义)AD = AD(公共边)所以:△ABD≌△ACD(AAS)所以:AB=AC(全等三角形的对应边相等)所以:△ABC是等腰三角形。
2. 通过定理的证明和应用,初步了解转化思想,并培养学生逻辑思维能力、分析问题和解决问题的能力。
应用判定方法应该有一个正确地表述,通常结合图形按下面的方式表述:如图,在△ABC中∵∠B =∠C ∴AB=AC(在一个三角形中,等角对等边)一般解决判断一个三角形是等腰三角形的问题,通常转化为寻找一个三角形中两个角相等的问题来解决。
当然也可以通过直接寻找两边相等来解决。
3. 理解等边三角形的性质与判定。
首先明确等边三角形定义。
三边相等的三角形叫做等边三角形,也称正三角形。
其次明确等边三角形与等腰三角形的关系。
等边三角形是特殊的等腰三角形,等腰三角形不一定是等边三角形。
等边三角形的性质:(具有等腰三角形的所有性质,结合定义更特殊)1)等边三角形的内角都相等,且为60度2)等边三角形每条边上的中线、高线和所对角的平分线互相重合(三线合一)3)等边三角形是轴对称图形,它有三条对称轴,对称轴是每条边上的中线、高线或所对角的平分线所在直线等边三角形的判定:(首先考虑判断三角形是等腰三角形)(1)三边相等的三角形是等边三角形(定义)(2)三个内角都相等的三角形是等边三角形(3)有一个角是60度的等腰三角形是等边三角形【典型例题】例1. 如下图,∠DAC是△ABC的外角,且∠DAC=80°,∠C=40°,试判断△ABC 是否是等腰三角形。
等腰三角形与等边三角形的特征与相关计算问题的解决

等腰三角形与等边三角形的特征与相关计算问题的解决一、等腰三角形的特征1.等腰三角形的定义:等腰三角形是指有两边相等的三角形。
2.等腰三角形的性质:a.底角相等:等腰三角形的两个底角相等。
b.高线、中线、角平分线重合:等腰三角形的底边上的高线、中线、角平分线三条线段相交于一点,并且这一点是三角形的垂心、中点和角平分线的交点。
c.底边上的中线垂直平分底边:等腰三角形的底边上的中线垂直于底边,并且平分底边。
d.顶角平分线、底边上的高、底边上的中线互相重合:等腰三角形的顶角平分线、底边上的高、底边上的中线三条线段互相重合。
二、等边三角形的特征1.等边三角形的定义:等边三角形是指三边都相等的三角形。
2.等边三角形的性质:a.三个角都相等:等边三角形的三个角都相等,每个角都是60度。
b.三条高线、中线、角平分线重合:等边三角形的每条高线、中线、角平分线三条线段都相交于一点,并且这一点是三角形的垂心、中点和角平分线的交点。
c.每条中线垂直平分对应边:等边三角形的每条中线垂直于对应边,并且平分对应边。
d.每条高线、中线、角平分线互相重合:等边三角形的每条高线、中线、角平分线三条线段互相重合。
三、等腰三角形与等边三角形的计算问题解决1.计算等腰三角形的面积:a.已知底边和高:等腰三角形的面积 = (底边 × 高) / 2。
b.已知底边和底角:等腰三角形的面积 = (底边 × 高) / 2,其中高可以通过底角和顶角的关系求得。
2.计算等边三角形的面积:a.已知边长:等边三角形的面积 = (边长 × 高) / 2,其中高可以通过正三角形的性质求得。
b.已知边长和角度:等边三角形的面积 = (边长 × 高) / 2,其中高可以通过边长和角度的关系求得。
四、等腰三角形与等边三角形的判定1.判定一个三角形是否为等腰三角形:a.如果一个三角形有两边相等,那么这个三角形是等腰三角形。
b.如果一个三角形有两个角相等,那么这个三角形是等腰三角形。
北师大版九年级数学下册 第16讲 等腰、等边即直角三角形 知识点梳理
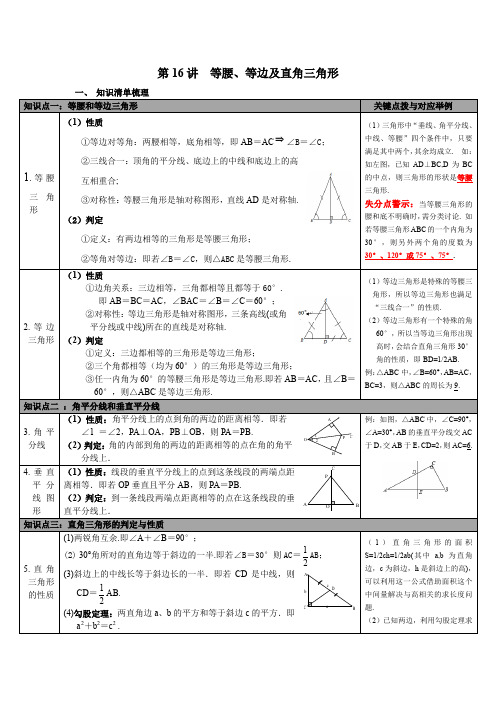
3.角平分线
(1)性质:角平分线上的点到角的两边的距离相等.即若
∠1=∠2,PA⊥OA,PB⊥OB,则PA=PB.
(2)判定:角的内部到角的两边的距离相等的点在角的角平
分线上.
例:如图,△ABC中,∠C=90°,∠A=30°,AB的垂直平分线交AC于D,交AB于E,CD=2,则AC=6.
③任一内角为60°的等腰三角形是等边三角形.即若AB=AC,且∠B=60°,则△ABC是等边三角形.
(1)等边三角形是特殊的等腰三角形,所以等边三角形也满足“三线合一”的性质.
(2)等边三角形有一个特殊的角60°,所以当等边三角形出现高时,会结合直角三角形30°角的性质,即BD=1/2AB.
例:△ABC中,∠B=60°,AB=AC,BC=3,则△ABC的周长为9.
(3)勾股定理的逆定理:若a2+b2=c2,则△ABC是Rt△.
2.等边三角形
(1)性质
①边角关系:三边相等,三角都相等且都等于60°.
即AB=BC=AC,∠BAC=∠B=∠C=60°;
②对称性:等边三角形是轴对称图形,三条高线(或角平分线或中线)所在的直线是对称轴.
(2)判定
①定义:三边都相等的三角形是等边三角形;
②三个角都相等(均为60°)的三角形是等边三角形;
4.垂直平分线图形
(1)性质:线段的垂直平分线上的点到这条线段的两端点距离相等.即若OP垂直且平分AB,则PA=PB.
(2)判定:到一条线段两端点距离相等的点在这条线段的垂直平分线上.
知识点三:直角三角形的判定与性质
5.直角三角形的性质
(1)两锐角互余.即∠A+∠B=90°;
(2)30°角所对的直角边等于斜边的一半.即若∠B=30°则AC= AB;
等边三角形

1 2 3
E
B
D
C
如图, ABC是等边三角形 分别延长CA AB, 是等边三角形. CA, 如图, △ABC是等边三角形.分别延长CA,AB, BC到 BC到A′,B′,C′,使AA′=BB′=CC′. △ CC A′B′C′是等边三角形吗?请说明理由。 是等边三角形吗?请说明理由。
A′ A C C′
1.等边三角形三条对称轴的交点到各边的 1.等边三角形三条对称轴的交点到各边的 距离都相等吗?请说明理由. 距离都相等吗?请说明理由.
A
F O
E
B
D
C
如图,在等边三角形ABC中,AD⊥BC与D.以AD为 如图,在等边三角形ABC中 AD⊥BC与D.以AD为 ABC 一边作等边三角形ADE ADE, DE与AC垂直吗 垂直吗? 一边作等边三角形ADE,则DE与AC垂直吗?请说 明理由。 明理由。
O B C
等边三角形性质探索: 等边三角形性质探索 3.等边三角形是轴对称图形吗?若是, 等边三角形是轴对称图形吗?若是, 有几条对称轴? 有几条对称轴?
结论:等边三角形是轴对称图形, 是轴对称图形, 结论 是轴对称图形 有三条对称轴. 有三条对称轴
等边三角形的性质
1.等边三角形的内角都相等 且等于 ° 等边三角形的内角都相等,且等于 等边三角形的内角都相等 且等于60 2.等边三角形是轴对称图形,有三条对称轴. 等边三角形是轴对称图形,有三条对称轴 等边三角形是轴对称图形 3.等边三角形各边上中线 高和所对角的平分 等边三角形各边上中线,高和所对角的平分 等边三角形各边上中线 线都三线合一. 线都三线合一
A
C
等边三角形的判定方法: 等边三角形的判定方法
1.三边相等的三角形是等边三角形 三边相等的三角形是等边三角形. 三边相等的三角形是等边三角形 2.三个内角都等于 °的三角形是等边 三个内角都等于60 三个内角都等于 三角形. 三角形 3.有两个内角等于 °的三角形是等边 有两个内角等于60 有两个内角等于 三角形. 三角形 4.有一个内角等于 °的等腰三角形是 有一个内角等于60 有一个内角等于 等边三角形. 等边三角形
等腰三角形和等边三角形..

等腰三角形和等边三角形
黄寨镇半坡店小学 王保华
一、学习目标
• 1.通过观察、操作、比较、发现三角形三
条边的特点会给三角形分类,理解并掌握 三角形的特征; • 2.掌握等腰三角形、等边三角形的特点; • 3.培养学生动手操作能力和灵活的思维能 力,激发学生主动参与的意识
二、自学指导一
认真自学课本83-84页例6完成下列问题
四、自学指导二
认真学习课本84—85页例7完成下列问题
1.用刻度尺量出例7中三角形三条边的长度,看是否相等?用 量角器测量出三个内角的度数,你有什么发现? 2.划出“三条边者相等的三角形是等边三角形,也叫正三角 形。”这句话并熟记。 3.在书中找出等边三角形的特点,并熟记。
4.动手操作:认真观察84页最下面剪等边三角形的方法,自 己动手操作,剪出等边三角形,不能完成的同学可与同桌 交流或小合作来完成。 5.把剪下的三角形按照课本85页最上面的方法进行折一折, 你有什么发现?
2.三角形按边分类
三边都不相 等的三角形
等腰三角 形
等边三角形
七、课堂检测,当堂训练
• 课本85页
练一练:1、2、3题。
课后作业
• 课本86页第4题。 • 课本87页第10、13、14题。
谢谢大家!
六、归纳总结
1.等腰三角形与等边三角形的区别与联系 等腰三角形 等边三角形 有三边都相等 三个角都相等,都是 60°且是锐角三角形 是轴对称图形,三条 高分别在它的三条对 称轴上
等腰三角形等边三角形

等腰三角形性质
思路点拨:只要把“等边对等角”这一性质用在三个不同的等腰三角形中,然后用方程思想解题,列方程的依据是三角形的内角和定理。
注:用代数方法解几何计算题常可使我们换翻为简。
【例2】如图所示,
求证:AO⊥BC
思路点拨:要证AO⊥BC,即证
注:对文字题一定要逐字逐句地分析,画好图形,写出已知、求证,按步骤解题。
练习:求证等腰三角形底边上任一点到两腰的距离之差等于一腰上的高。
落在△BDE中,
,所以它们都为直角三角形。
∠F与∠2的余角分别为∠B
思路点拨:由DE∥BC,得∠3=∠2
而问题得证。
点D是AB的中点,∠
思路点拨:由∠BAC=2∠DBC 垂直BC,即可得证。
例题1:如图,⊿ABC是等边三角形,DE∥BC,交AB,AC于D,E.求证:⊿ADE是等边三角形.
类比:。
学习等边、等腰和直角三角形

学习等边、等腰和直角三角形三角形是几何学中最基本的图形之一,在我们的日常生活中也经常能够见到。
本文将介绍三种常见的三角形:等边三角形、等腰三角形和直角三角形。
通过学习它们的定义、特性以及相关性质,我们可以更好地理解和应用它们。
一、等边三角形等边三角形是一种特殊的三角形,指的是三条边的长度都相等的三角形。
它的特点是三个内角均为60度。
在一个等边三角形中,任一边的长度都可以表示为其他两边长度的乘积。
等边三角形的相关性质还包括以下几点:1. 等边三角形的三个高度、三条中线以及三条角平分线都重合于一个点,称为垂心、重心和内心;2. 等边三角形的内切圆和外切圆的半径都相等,且与三边长度相等。
二、等腰三角形等腰三角形是一种具有两边长度相等的三角形。
在等腰三角形中,两个底角(底边对应的两个角)相等,而顶角(顶点对应的角)则与两个底角之和相等。
等腰三角形的性质如下:1. 等腰三角形的高度通过顶点至底边的垂直线构成,且与底边中点相交;2. 等腰三角形的两条边上的角平分线与底边垂直;3. 等腰三角形可以通过图形的对称性得出,即对称轴为底边的中垂线。
三、直角三角形直角三角形是指其中一个角度为90度的三角形。
直角三角形中,直角为其特点,其他两个角度分别为锐角和钝角。
直角三角形的特性及其相关性质包括:1. 直角三角形中,根据勾股定理,直角边的平方等于两直角边平方和。
即a²+ b²= c²,其中a和b分别为直角边的长度,c为斜边的长度;2. 直角三角形中,斜边是两直角边中最长的一边;3. 直角三角形还可以通过三边长度的比较来分类,如3:4:5三角形、5:12:13三角形等。
通过学习等边、等腰和直角三角形的特性,我们可以应用它们解决一些实际问题,如测量边长、计算角度等。
同时,这些三角形也在建筑、工程、地理和几何学等领域中得到广泛应用。
总结:等边、等腰和直角三角形是我们常见的几何学中的基本三角形。
中考一轮复习--第16讲 等腰、等边与直角三角形

又AD⊥BC,∴△AEF是等腰三角形.∴∠E=∠F;
∵AB=BE,∴∠ABC=2∠E;
同理,得∠ACB=2∠F;∴∠ABC=∠ACB,
即AB=AC,△ABC是等腰三角形;
④在△ABC中,AD⊥BC,根据勾股定理,得
AB2-BD2=AC2-CD2,
即(AB+BD)(AB-BD)=(AC+CD)(AC-CD);
. 35°
解析:在Rt△ABC中,∠ABC=90°,D为AC的中点,∴BD是中
线,∴AD=BD=CD,∴∠DBC=∠C=55°,∴∠ABD=90°-55°=35°.
考法1
考法2
等腰(边)三角形的性质与判定
例2(2019·重庆)如图,在△ABC中,AB=AC,AD⊥BC于点D.
(1)若∠C=42°,求∠BAD的度数;
(2)若点E在边AB上,EF∥AC交AD的延长线于点F.求证:AE=FE.
分析:(1)根据等腰三角形的性质得到∠BAD=∠CAD,根据三角形
的内角和即可得到∠BAD=∠CAD=90°-42°=48°;(2)根据等腰三角形
的性质得到∠BAD=∠CAD,根据平行线的性质得到∠F=∠CAD,等量
代换得到∠BAD=∠F,于是得到结论.
∵∠D=90°,∴CD2+DF2=FC2,
∴CD2+12=32,∴CD=2 2 .
方法总结勾股定理是直角三角形中的一个重要性质,可以由角的
关系得到三角形的边的关系,常用的方法是已知直角三角形的两边
求第三边,或者是已知直角三角形三边之间的关系,列方程求出某
些边长.
考法1
考法2
对应练1(2019·安徽萧县期末)如图,在△ABC
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
等边三角形包括等腰三角形吗
不包括,它们之间的关系是:等腰三角形不一定是等边三角形,
等边三角形一定是等腰三角形。等边三角形(又称正三边形),为三
边相等的三角形,其三个内角相等,均为60°,等边腰角形的两腰长相
等。
等边三角形判定方法
(1)三边相等的三角形是等边三角形(定义)。
(2)三个内角都相等的三角形是等边三角形。
(3)有一个内角是60度的等腰三角形是等边三角形。
(4) 两个内角为60度的三角形是等边三角形。
等腰直角三角形的边角之间的关系
(1)三角形三内角和等于180°。
(2)三角形的一个外角等于和它不相邻的两个内角之和。
(3)三角形的一个外角大于任何一个和它不相邻的内角。
(4)三角形两边之和大于第三边,两边之差小于第三边。
(5)在同一个三角形内,等边对等角,等角对等边。
等边三角形性质
(1)等边三角形是锐角三角形,等边三角形的内角都相等,且均
为60°。
(2)等边三角形每条边上的中线、高线和角平分线互相重合。
(三线合一)
(3)等边三角形是轴对称图形,它有三条对称轴,对称轴是每条
边上的中线、高线 或角的平分线所在的直线。
(4)等边三角形重心、内心、外心、垂心重合于一点,称为等边
三角形的中心。(四心合一)
(5)等边三角形内任意一点到三边的距离之和为定值。(等于其
高)
(6)等边三角形拥有等腰三角形的一切性质。(因为等边三角形
是特殊的等腰三角形)
