2019年高考理科数学必考知识点双向细目表.
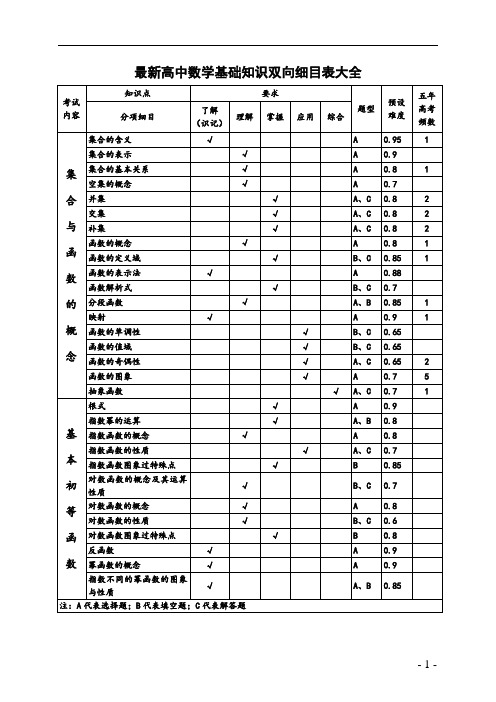
最新推荐高中数学基础知识双向细目表(定稿)
了解
(识记)
理解
掌握
应用
综合
空
间
几
何
体
公理1
√
A
0.95
公理2
√
A
0.9
公理3
√
A
0.85
公理4
√
A
0.85
等角定理
√
A
0.8
线面平行的判定定理
√
A、B、C
0.8
3
面面平行的判定定理
√
A、B、C
0.8
线面平行的性质定理
√
A、B、C
0.8
面面平行的性质定理
√
A、B、C
0.8
1
线面垂直的判定定理
秦九韶算法
√
B
0.8
进位制
√
B
0.65
统
计
简单随机抽样
√
A
0.95
抽签法
√
A
0.95
随机数法
√
A
0.9
系统抽样
√
AC
0.7
1
分层抽样
√
B
0.88
频率分布
√
BC
0.7
总体密度曲线
√
A
0.95
茎叶图
√
BC
0.8
1
众数、中位数、平均数
√
B
0.8
标准差与方差
√
AC
0.75
1
频率分布直方图的应用
√
A
0.8
1
两个变量的线性相关
分项细目
了解
(识记)
理解
掌握
应用
最新推荐高中数学基础知识双向细目表(定稿)

最新推荐高中数学基础知识双向细目表(定稿)最新的高中数学基础知识双向细目表包括集合的含义、表示和基本关系、空集的概念、并集、交集、补集、函数的概念、定义域、表示法、解析式、分段函数、映射、单调性、值域、奇偶性、图象、抽象函数、根式、指数幂的运算等知识点。
要求掌握这些知识点的应用、综合和理解,包括识记、填空和解答题型。
五年的高考考试频数为0.7至1,难度在0.6至0.95之间。
基本初等函数包括指数函数、对数函数和幂函数,要掌握它们的概念、性质、图象以及特殊点等内容。
此外,还要了解函数的零点与方程根的联系、一元二次方程根的存在性及根的个数,以及根据具体函数的突象判断相应方程解的情况。
对于几何学,要了解棱柱、棱锥、棱台、圆柱、圆锥、圆台、球和简单组合体的结构特征。
空间几何体的投影研究空间几何体的投影,包括中心投影和平行投影。
掌握三视图的画法,能够根据给定的图形画出其三视图。
理解主观图的画法,能够根据给定的图形画出其主观图。
了解平面图与直观图面积的关系,能够根据给定的图形计算其面积。
掌握棱柱、棱锥、棱台的表面积和体积的计算方法,能够根据给定的图形计算其表面积和体积。
理解球的表面积和体积的计算方法,能够根据给定的半径计算其表面积和体积。
了解几何体内切球和外接球的问题,能够根据给定的图形计算其内切球和外接球的半径。
空间几何体的投影是几何学中的重要内容,包括中心投影和平行投影。
掌握三视图的画法,可以根据给定的图形画出其三视图。
此外,理解主观图的画法,能够根据给定的图形画出其主观图。
在计算面积方面,需要了解平面图与直观图面积的关系,并能够根据给定的图形计算其面积。
在计算体积和表面积方面,需要掌握棱柱、棱锥、棱台的计算方法,以及球的表面积和体积的计算方法。
此外,需要了解几何体内切球和外接球的问题,能够根据给定的图形计算其内切球和外接球的半径。
本文介绍了数学必修三中的两个知识点:圆的方程和算法概念,以及一个统计学知识点。
什么是双向细目表

什么是双向细目表?双向细目表一、试卷编制的具体步骤1、进行总体构思,确定试卷的目标要求明确考试的目的(为什么考)和性质:是期前预备性(摸底、预测、分组)的,或者是期中形成性(评定)的;根据考试目的确定考试的内容、范围和要求(合格标准)。
2、拟订命题计划,设计多项细目表命题计划包括两项内容:一是编制试题的原则和要求,说明试题类型、编制试题和组配试卷的要求体考试内容中各部分试题的数量分布和所占比例。
根据《课程标准》、《考试大纲》、教材、考试目的、性质与要求,设计好试卷多项细目表,这是3、选择题型,实施编制4、编选和审查试题,组编试卷5、检查、修改、试做、复核、调整、编制标准答案和评分标准二、试卷命题双向细目表(一)为什么在编制试卷时需要制定双向细目表原因之一:命题双向细目表是设计试卷的蓝图。
它使题工作避免盲目性而具有计划性,使命题者明量,提高命题的效率和质量。
原因之二:它对于审查试题的效度也有重要的指导意义。
命题双向细目表包括两个维度(双向)的型与难度之间的关系。
(二)什么是双向细目表所谓“双向细目表”,实际上就是教材内容和学习结果两个维度,其中一维反映教学的内容,另一维水平”这一维,普遍采用布卢姆等人关于认知领域教育目标的分类,即把学习结果或认知水平分为价”六种水平。
教材内容这一维则根据具体学科内容加以确定。
双向细目表是在命题中根据考试的目的和要求制定的测试内容和目标的具体计划,并以图表形式详用以规范、指导编题和制卷。
案例1:高考文综Ⅱ卷政治试题双向细目表案例2:高三月考数学试题双向细目表马鞍山市二十二中学2010届高中教学质量第一次月考数学试卷双向细目表(理科)高三数学第一次月考目的:检查前一阶段复习效果考试范围:第一次月考前已复习完成的内容,必修3和选修2-3中的概率和统计、排列组合、二程。
命题计划:按照2009年安徽省高考理科试卷的试题类型、试卷结构组配试卷;试卷中试题为第一建议:为了把握好试题方向,所命试题要以近两年的高考原题为参考依据,但是,为了考试公平,过四分之一,可以适当改编,或从各地模拟题中选择,还可以从教材中选择或改编题目。
2019年高考数学必考知识点大全(20200102195847)

把 ax b 看 成 一 个 整 体 , 化 成 | x | a , | x | a( a 0) 型不等式来求 解
4
判别式
0 b2 4ac
二次函数
y ax2 bx c(a 0)
的图象
一元二次方程
x1,2
ax2 bx c 0(a 0)
b b2 4ac 2a
的根
(其中 x1 x2 )
ax2 bx c 0(a 0)
的解集
{ x | x x1 或 x x2}
2
ax bx c 0( a 0)
的解集
{ x | x1 x x2}
0
b x1 x2
2a
{x|x
b}
2a
0
O
无实根
R
〖1.2 〗函数及其表示 【1.2.1 】函数的概念 (1 )函数的概念 ①设 A 、 B 是两个非空的数集,如果按照某种对应法则 f ,对于集 合 A 中任何一个数 x,在集合 B 中都有唯一确定的数 f (x) 和它对应, 那么这样的对应(包括集合 A , B 以及 A 到 B 的对应法则 f )叫做 集合 A 到 B 的一个函数,记作 f : A B .
(k Z) .
2
⑥零(负)指数幂的底数不能为零.
⑦若 f ( x) 是由有限个基本初等函数的四则运算而合成的函数时,
6
则其定义域一般是各基本初等函数的定义域的交集. ⑧对于求复合函数定义域问题,一般步骤是:若已知 f ( x) 的定义 域为 [ a,b] ,其复合函数 f [ g( x)] 的定义域应由不等式 a g ( x) b 解出. ⑨对于含字母参数的函数,求其定义域,根据问题具体情况需对 字母参数进行分类讨论.
2019高考数学(理科)知识点总结(精辟)

求反函数的步骤掌握了吗?
的反函数 0
(①反解 x ;②互换 x 、 y ;③注明定义域)
x (x) x x 0 1 x 1 )
如 : 求 函 数 f (x )
( 答:f
1
13.
反函数的性质有哪些?
③ 设y f
1 1
①互为反函数的图象关于直线
A,b b
1
y = x 对称;
f
②保存了原来函数的单调性、
1
5 a
0 a 5 1, 3 9, 25 )
∴ M,
・5 a 5
2
5 a
0
).
5. 可 以 判 断 真 假 的 语 句 叫 做 命 题 , 逻 辑 连 接 词 有 “ 或 ” ( ) , “ 且 ” ( ) 和 “ 非 ” ( 若p 若 q为 真 , 当 且 仅 当 p、 q均 为 真 p 为 真 , 当 且 仅 当 p为 假 若p q 为真,当且仅当 p 、 q 至少有一个为真
注意如下结论: ( 1)在公共定义域内:两个奇函数的乘积是偶函数;两个偶函数的乘积是偶函数;一个偶函数 与奇函数的乘积是奇函数。 ( 2 ) 若 f(x) 是 奇 函 数 且 定 义 域 中 有 原 点 , 则 f(0) 如 : 若 f (x) a・ 2 2
x
0。
a 1
2
x
为奇函数,则实数a a・ 2 2
奇函数性;
f(x) 的 定 义 域 为 A , 值 域 为 C , a f ( a) f (b) a, f f (b ) f ( a)
C , 则 f(a) = b
( b)
a
14.
如何用定义证明函数的单调性?
(取值、作差、判正负)
如何判断复合函数的单调性?
2019理科数学高考考点

离散型随机变量的均值与方差、正态分布
考点61
坐标系及参数方程(参数方程与普通方程的互化)
考点62
绝对值不等式
考点63
不等式的证明
考点39
空间几何体的结构及其三视图
考点40
空间几何体的表面积和体积
考点41
空间点、直线、平面之间的位置关系
考点42
直线、平面平行的判定及其性质
考点43
直线、平面垂直的判定及其性质
考点44
直线的倾斜角与斜率、直线的方程
考点45
直线的交点坐标与距离公式
考点46
圆的方程
考点47
直线与圆、圆与圆的位置关系
考点48
考点28
数列的概念与简单表示法
考点29
等差数列
考点30
等比数列
考点31
数列求和及其综合方法
考点32
数列及其综合应用
考点33
不等关系与不等式
考点34
一元二次不等式及其解法
考点35
二元一次不等式(组)与简单的线性规划问题
考点35
基本不等式
考点37
合情推理与演绎推理
考点38
直接证明与间接证明,综合法及分析法,反证法
考点20
两角和与差的正弦、余弦和正切公式
考点21
简单的三角恒等变换
考点22
正弦定理和余弦定理
考点23
正弦定理和余弦定理的应用
考点24
平面量的概念及其线性运算
考点25
平面向量、空间向量的基本定理及其坐标表示、数量积及坐标运算
考点26
用空间向量求异面直线,直线与平面,二面角的夹角的余弦值
考点27
数系的扩充与复数的引入
2019届高考理科数学考前必记的60个知识点含公式推理推论总结

定义域
R
y= log ax(a>0 且 a≠ 1) (0,+∞ )
值域
(0,+∞ )
Rห้องสมุดไป่ตู้
图象
关系 奇偶性
单调性
指数函数 非奇非偶 0<a<1 时,在 R 上是减函数; 0<a<1 时,在 (0,+∞ ) 上是减 函数;
对数函数 非奇非偶
a>1 时,在 R 上是增函数 a>1 时,在(0 ,+∞ )上是增函 数
1
①如果 p? q,那么 p 是 q 的充分条件,同时 q 是 p 的必要条件. ②如果 p? q,但 q? / p,那么 p 是 q 的充分不必要条件. ③如果 p? q,且 q? p,那么 p 是 q 的充要条件. ④如果 q? p,且 p? / q,那么 p 是 q 的必要不充分条件. ⑤如果 p? / q,且 q? / p,那么 p 是 q 的既不充分也不必要条件.
2
x A( y)
(3)换元法: 无理函数、 三角函数 (用三角代换 ) 等,如求函数 y=2x- 3+ 13- 4x的值域.
(4)数形结合法: 函数和其几何意义相联系的函数类型,如求函数
3- sin y=2- cos
x 的值域.
x
(5)不等式法 :利用几个重要不等式及推论求最值,如
a2+ b2≥ 2ab, a+ b≥ 2 ab(a, b
2 对于集合 A, B, C,如果 A? B 且 B? C,则有 A? C. 3 含有 n 个元素的集合有 2n 个子集,有 2n-1 个真子集,有 2n-2 个非空真子集.
4 集合中元素的三大特性:确定性、互异性、无序性.
常见关键词及其否定形式
关等
一定
2019届高三考生--高中数学基础知识清单(理科)

高中数学基础知识归类祝你们高考成功!!!一.集合与简易逻辑1.注意区分集合中元素的形式.如:{|lg }x y x =—函数的定义域;{|lg }y y x =—函数的值域;{(,)|lg }x y y x =—函数图象上的点集.2.集合的性质: ①任何一个集合A 是它本身的子集,记为A A ⊆. ②空集是任何集合的子集,记为A ∅⊆.③空集是任何非空集合的真子集;注意:条件为A B ⊆,在讨论的时候不要遗忘了A =∅的情况如:}012|{2=--=x ax x A ,如果AR +=∅,求a 的取值.(答:0a ≤)④()U U U C A B C A C B =,()U U U C A B C A C B =;A B C A B C =()();A B C A B C =()(). ⑤A B A A B B =⇔=U U A B C B C A ⇔⊆⇔⊆U A C B ⇔=∅U C A B R ⇔=. ⑥A B 元素的个数:()()card A B cardA cardB card A B =+-.⑦含n 个元素的集合的子集个数为2n ;真子集(非空子集)个数为21n -;非空真子集个数为22n -. 3.补集思想常运用于解决否定型或正面较复杂的有关问题。
如:已知函数12)2(24)(22+----=p p x p x x f 在区间]1,1[-上至少存在一个实数c ,使0)(>c f ,求实数p 的取值范围.(答:32(3,)-)4.原命题: p q ⇒;逆命题: q p ⇒;否命题: p q ⌝⇒⌝;逆否命题: q p ⌝⇒⌝;互为逆否的两个命题是等价的.如:“βαsin sin ≠”是“βα≠”的 条件.(答:充分非必要条件)5.若p q ⇒且q p ≠>,则p 是q 的充分非必要条件(或q 是p 的必要非充分条件).6.注意命题p q ⇒的否定与它的否命题的区别: 命题p q ⇒的否定是p q ⇒⌝;否命题是p q ⌝⇒⌝. 命题“p 或q ”的否定是“p ⌝且q ⌝”;“p 且q ”的否定是“p ⌝或q ⌝”. 如:“若a 和b 都是偶数,则b a +是偶数”的否命题是“若a 和b 不都是偶数,则b a +是奇数”否定是“若a 和b 都是偶数,则b a +是奇数”. 7.常见结论的否定形式二.1.①映射f :A B →是:⑴ “一对一或多对一”的对应;⑵集合A 中的元素必有象且A 中不 同元素在B 中可以有相同的象;集合B 中的元素不一定有原象(即象集B ⊆).②一一映射f :A B →: ⑴“一对一”的对应;⑵A 中不同元素的象必不同,B 中元素都有原象. 2.函数f : A B →是特殊的映射.特殊在定义域A 和值域B 都是非空数集!据此可知函数图像与x 轴的垂线至多有一个公共点,但与y 轴垂线的公共点可能没有,也可能有任意个.3.函数的三要素:定义域,值域,对应法则.研究函数的问题一定要注意定义域优先的原则.4.求定义域:使函数解析式有意义(如:分母0≠;偶次根式被开方数非负;对数真数0>,底数0>且1≠;零指数幂的底数0≠);实际问题有意义;若()f x 定义域为[,]a b ,复合函数[()]f g x 定义域由()a g x b ≤≤解出;若[()]f g x 定义域为[,]a b ,则()f x 定义域相当于[,]x a b ∈时()g x 的值域.5.求值域常用方法: ①配方法(二次函数类);②逆求法(反函数法);③换元法(特别注意新元的范围).④三角有界法:转化为只含正弦、余弦的函数,运用三角函数有界性来求值域;⑤不等式法⑥单调性法;⑦数形结合:根据函数的几何意义,利用数形结合的方法来求值域;⑧判别式法(慎用):⑨导数法(一般适用于高次多项式函数).6.求函数解析式的常用方法:⑴待定系数法(已知所求函数的类型); ⑵代换(配凑)法; ⑶方程的思想----对已知等式进行赋值,从而得到关于()f x 及另外一个函数的方程组。
