实验五 纯弯曲梁正应力实验
纯弯曲梁正应力电测实验

实验二、纯弯曲梁正应力电测实验一、 实验目的1、 电测法测定纯弯曲梁正应力分布规律。
2、验证纯弯曲梁正应力计算公式。
二、 实验装置与仪器1、 纯弯曲梁实验装置。
2、 数字式电阻应变仪。
三、 实验装置与实验原理1、实验装置弯曲梁试验装置如图1所示。
它有弯曲梁1,定位板2,支座3,试验机架4,加载系统5,两端带万向接头的加载杆6,加载压头(包括φ16钢珠)7,加载横梁8,载荷传感器9和测力仪10等组成。
该装置有已粘贴好应变片的钢梁(其弹性模量2210m GNE =)用来完成纯弯曲梁正应变分布规律试验。
纯弯曲梁正应变分布规律试验纯弯曲梁受力状态及有关尺寸见图2。
图 2在梁的纯弯曲段内已粘贴好两组应变片,每组8片,分别为1~8号片和1*~8*号片,各片距中心层的距离在图3中已标出。
当梁受力变形后,可由应变仪测出每片应变片产生的应变,这样就可得到实测的沿梁横截面高度的正应变分布规律。
根据材料力学中纯弯曲梁的平面假设,沿梁横截面高度的正应变分布规律应当是直线。
另外材料力学中还假设梁在纯弯曲段内是单向应力状态,为此,我们在梁的下表面粘贴有与7号片和7*号片垂直的8号片和8*号片,当梁受力变形后,可测得8ε和*8ε,根 据泊松比纵横εεμ=,可由78εε或**78εε计算得到 'μ,若'μ近似等于μ时,则证明梁纯弯曲段内近似于单向应力状态。
2、实验原理梁的纯弯曲段内,每片应变片所处状态是单向应力状态。
根据单向应力状态的虎克定律:σ = E ε可以计算出梁的纯弯曲段内每片应变片所处的应力。
注:该装置只允许加4KN 载荷,超载会损坏传感器。
梁的纯弯曲正应力实验

梁的纯弯曲正应力实验
梁的纯弯曲正应力实验是为了确定梁在弯曲的情况下的受力机制以及测定梁的弯曲刚
度和受力性能的试验。
在这项实验中,主要是测试梁的弯曲刚度性能,这样可以更清楚地
了解梁的特性,并且可以判断梁受到外力时应如何反应。
这项实验是建筑结构设计中的重
要内容,当结构受外力时,梁的刚度将决定结构的中止和模态。
梁的纯弯曲正应力实验,通常需要两个或三个支撑点。
它们可以是球形、凸形或圆形
的轴承。
其中,球形轴承最常用,其支撑的特性是最佳的,最不容易产生不必要的侧向力,影响试验的准确性。
在一个纯弯曲正应力实验中,支撑一端的梁头会受到一个外载荷,即弯矩,使其变形。
强度和刚度试验系统通常由模拟电源、试验控制台、力传感器等设备组成,力导致模拟器
输出同时加载在梁上,并通过力数据计算出受力的曲率系数和强度系数。
该实验的基本步骤是:(1)在梁上安装支持设备,并将梁放在试验台上;(2)给各
支撑点安装传感器,并通过模拟器输出同时加载在梁上;(3)测量梁承受的外载荷以及
梁的变形量;(4)分析测量结果,并计算出梁在弯曲时的曲率系数和受力
总之,梁的纯弯曲正应力实验是非常重要的,它可以查明梁的强度系数,曲率和强度
系数,以及梁受外力时的变形性能和应力变化规律。
实验结果对于确定结构抗震性能等具
有重大意义,在建筑结构分析和设计中扮演着巨大的作用。
纯弯曲梁正应力实验报告-纯弯曲实验报告思考题

纯弯曲梁正应力实验报告材料力学课程实验报告纯弯曲梁正应力实验报告学院系班级实验组别实验人员姓名实验日期年月日一、实验目的二、实验设备静态电阻应变仪型号实验装置名称型号量具名称精度㎜三、实验数据及处理梁试件的弹性模量11101.2EPa 梁试件的横截面尺寸h ㎜b ㎜支座到集中力作用点的距离d ㎜各测点到中性层的位置1y ㎜2y ㎜3y ㎜4y ㎜5y ㎜6y ㎜材料力学课程实验报告载荷N 静态电子应变仪读数106 1点2点3点4点5点6点F F 读数1 增量1 读数2 增量2 读数3 增量3 读数4 增量4 读数5 增量5 读数6 增量6 F 1 2 3 4 5 6 应变片位置1点2点3点4点5点6点实验应力值/MPa 理论应力值/MPa 相对误差/ 泊松比值注表中读数1、2、3、4、5、6为两次实验所得读数的平均值。
F为荷载增量的平均值。
1、2、3、4、5、6为各点应变增量的平均值材料力学课程实验报告四、应力分布图理论和实验的应力分布图画在同一图上五、思考题1.为什么要把温度补偿片贴在与构件相同的材料上2.影响实验结果的主要因素是什么材料力学课程实验报告测定材料E、实验报告学院系班级实验组别实验人员姓名实验日期年月日一、实验目的二、实验设备静态电阻应变仪型号实验装置名称型号量具名称精度㎜三、实验数据及处理板试件尺寸试件截面宽b ㎜高h ㎜截面积oA mm2 NF oAFMPa 纵向应变106 横向应变106 1r 2r 3r 1r 2r 3r 材料力学课程实验报告数据处理方法1平均法均均oAFE 均均计算过程2最小二乘法niiniiiE121 niiniii121 计算过程材料力学课程实验报告四、画出关系图理论和实验的关系图画在同一图上平均法理论和实验的关系图最小二乘法理论和实验的关系图五、思考题1.试件尺寸和形式对测定弹性模量E有无影响2.影响实验结果的因素有那些为何要用等量增载法进行实验材料力学课程实验报告圆管扭转应力试验实验报告学院系班级实验组别实验人员姓名实验日期年月日一、实验目的二、实验设备静态电阻应变仪型号实验装置名称型号量具名称精度㎜三、实验数据及处理薄壁圆管尺寸外径D ㎜内径d ㎜加力臂长度L ㎜切变模量111082.0G Pa 弹性模量11101.2E Pa 泊松比28.0 电阻片号kNPo1.0 kNPn1.1 两次读数平均值两次读数平均值1 2 3 4 5 6 注由于纯扭实验中004545故045采用1、4、3、6的绝对值加以平均表中电阻号1、4相对于45°应变片3、6相对于-45°应变片2、5相对于0°应变片材料力学课程实验报告四、计算B、D点实测时的主应力和主方向五、计算B、D点理论主应力和主方向六、思考题1.求出实测主应力、主方向与理论主应力、主方向的相对误差。
纯弯曲梁上正应力测量实验

纯弯曲梁上正应力测量实验1 实验目的⑴掌握多点静态应变、应力的测量方法;⑵用电测法测量矩形梁在纯弯曲时正应力的分布大小及金属材料泊松比μ; ⑶通过正应力测量的结果分析,验证理论计算正应力公式。
2 设备仪器⑴电子万能试验机一台; ⑵纯弯曲测试梁一根; ⑶静态电阻应变仪一台。
3 实验原理实验装置如图6—1,在矩形梁中间取截面I —I 。
该截面上共有6个测点,其中上表面2个测点:一个纵向、一个横向;下表面一个纵向测点;侧面等分布置3个纵向测点。
各测点上已粘贴电阻应变片。
当电子万能试验机对矩形梁施加压力时,可分别测得6个测点处微应变的大小。
其中5个纵向粘贴电阻应变片测出的应变就是该点弯曲正应力作用产生的,且满足虎克定律。
由此得到该点正应力:E σε=式中E 为材料弹性常数 E=200GPa而上表面的横向粘贴电阻应变片则是为测量泊松比μ准备的。
/μεε=横向纵向4 实验步骤:⑴、按单臂测量组桥方式把6个电阻应变片顺序接入静态电阻应变仪的6个测量电桥中,分别测出6个被测点在载荷作用下的微应变值。
⑵、开启电子万能试验机,按等量加载程序对试验梁加载。
当F=0时,将静态电阻应变仪上所接电桥的输出值调为0。
然后,当F 依次每增加500N 时,分别记录该电桥测出的微应变值,直至加载程序结束。
附:实验数据记录表(表6-1)5 实验结果处理由弯曲理论知纯弯曲梁的横截面上各点的正应力大小 σ=-My/I z 式中M 为弯矩;y 为欲求点到弯曲中性轴的距离;I z 为梁的横截面对中性轴Z 的惯性矩,且有I z =bh 3/12 所以,可理论计算截面I —I 上5个点的纯弯曲正应力大小和方向。
把5个点上F=500N 时的弯曲正应力求得之后可与实验测出的这5个点上弯曲正应力作比较。
实验测出的正应力i i E σε=(i=1、2…5)式中E=200Gpa ;i 是5个纵向粘贴应变片的序列数;εi 是第i 点应变增量的平均值。
F/2F/2I-I图6-1实验装置图计算实验测出的材料泊松比61/μεε=6 思考题:⑴弯曲正应力大小是否受材料弹性常数E 的影响? ⑵弯曲正应力沿梁的高度上是怎样分布?。
纯弯梁弯曲的应力分析实验报告
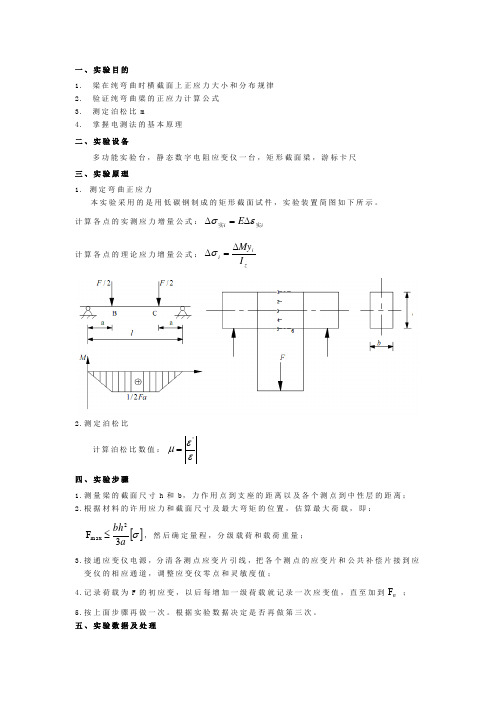
一、实验目的1. 梁在纯弯曲时横截面上正应力大小和分布规律2. 验证纯弯曲梁的正应力计算公式3. 测定泊松比m4. 掌握电测法的基本原理 二、实验设备多功能实验台,静态数字电阻应变仪一台,矩形截面梁,游标卡尺 三、实验原理 1. 测定弯曲正应力本实验采用的是用低碳钢制成的矩形截面试件,实验装置简图如下所示。
计算各点的实测应力增量公式:i i E 实实εσ∆=∆计算各点的理论应力增量公式:zi i I My ∆=∆σ2.测定泊松比计算泊松比数值:εεμ'=四、实验步骤1.测量梁的截面尺寸h 和b ,力作用点到支座的距离以及各个测点到中性层的距离;2.根据材料的许用应力和截面尺寸及最大弯矩的位置,估算最大荷载,即:[]σabh 3F 2max ≤,然后确定量程,分级载荷和载荷重量; 3.接通应变仪电源,分清各测点应变片引线,把各个测点的应变片和公共补偿片接到应变仪的相应通道,调整应变仪零点和灵敏度值;4.记录荷载为F 的初应变,以后每增加一级荷载就记录一次应变值,直至加到n F ;5.按上面步骤再做一次。
根据实验数据决定是否再做第三次。
五、实验数据及处理梁试件的弹性模量11101.2⨯=E Pa梁试件的横截面尺寸h = 40.20 ㎜,b = 20.70 ㎜支座到集中力作用点的距离d = 90 ㎜各测点到中性层的位置:1y = 20.1 ㎜ 2y = 10.05 ㎜3y = 0 ㎜4y = 10.05 ㎜ 5y = 20.1 ㎜六、应力分布图(理论和实验的应力分布图画在同一图上)七、思考题1.为什么要把温度补偿片贴在与构件相同的材料上?答:应变片是比较高精度的传感元件,必须考虑温度的影响,所以需要把温度补偿片贴在与构件相同的材料上,来消除温度带来的应变。
2.影响实验结果的主要因素是什么?答:影响本实验的主要因素:实验材料生锈,实验仪器精度以及操作的过程。
一、实验目的和要求:1) 用电测法测定纯弯曲梁受弯曲时A A -(或B B -)截面各点的正应力值,与理论计算值进行比较。
纯弯曲梁正应力的测定
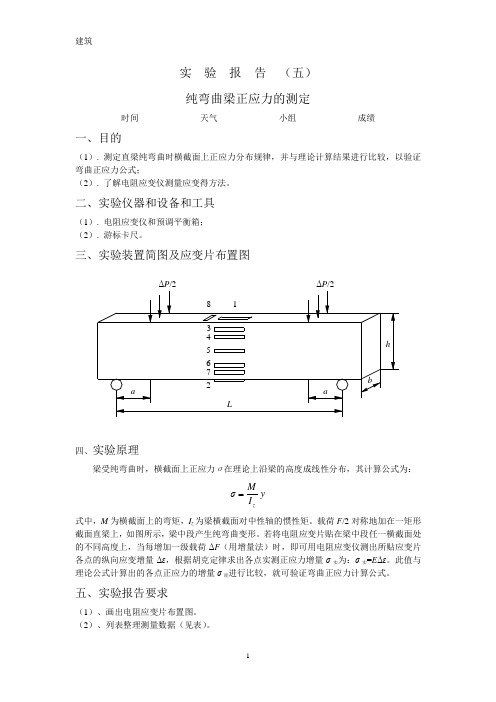
实 验 报 告 (五) 纯弯曲梁正应力的测定时间 天气 小组 成绩一、目的(1). 测定直梁纯弯曲时横截面上正应力分布规律,并与理论计算结果进行比较,以验证弯曲正应力公式;(2). 了解电阻应变仪测量应变得方法。
二、实验仪器和设备和工具(1). 电阻应变仪和预调平衡箱; (2). 游标卡尺。
三、实验装置简图及应变片布置图四、实验原理梁受纯弯曲时,横截面上正应力σ在理论上沿梁的高度成线性分布,其计算公式为:y I M σz式中,M 为横截面上的弯矩,I z 为梁横截面对中性轴的惯性矩。
载荷F /2对称地加在一矩形截面直梁上,如图所示,梁中段产生纯弯曲变形。
若将电阻应变片贴在梁中段任一横截面处的不同高度上,当每增加一级载荷ΔF (用增量法)时,即可用电阻应变仪测出所贴应变片各点的纵向应变增量Δε,根据胡克定律求出各点实测正应力增量σ实为:σ实=E Δε。
此值与理论公式计算出的各点正应力的增量σ理进行比较,就可验证弯曲正应力计算公式。
五、实验报告要求(1)、画出电阻应变片布置图。
(2)、列表整理测量数据(见表)。
(3)、计算各纤维层的应力σ实,画出应力分布图。
(4)、对σ理和σ实进行比较,计算相对误差,并分析误差原因。
附表1 试件相关数据附表2 实验数据六、实验结果处理实验值和理论值的比较测点 理论值σi 理(MPa )实际值σi 实(MPa )相对误差(%)1 -14.06 -14.28 1.56 3 -10.55 -11.13 5.50 4 -7.03 -7.77 10.53 5 0.00 -0.42 ∞ 6 7.03 6.51 7.40 7 10.55 10.08 4.45 8 3.40 3.99 2.10 214.0614.704.55七、结论1、影响实验结果准确性的主要因素是什么?2、弯曲正应力的大小是否受弹性模量E 的影响?3、实验时没有考虑梁的自重,会引起误差吗?为什么?4、梁弯曲的正应力公式并未涉及材料的弹性模量E ,而实测应力值的计算却用上了弹性模量E ,为什么?1、是否进行温度补偿,梁的摆放位置,应变片的位置和方向的精确程度。
梁的弯曲正应力实验
夹层梁上、下层是45号钢板,厚度相同,中层是铝合金板,三层用螺栓联结,锥销定位。在梁指定截面的上、下表面各粘贴两枚应变片,一个侧面上等间距地粘贴五枚应变片。
由于夹层梁和叠梁测点分布在钢和铝合金两种材料上因此温度补偿片应有两片它们分别粘贴在钢和铝合金当梁在载荷作用下发生弯曲变形时工作片的电阻值将随着梁的变形而发生变化通过电阻应变仪可以分别测量出各对应点的实际应变值为梁材料的弹性模量
梁的弯曲正应力实验
梁弯曲变形时,其横截面上会产生弯曲正应力和弯曲切应力,测定梁横截面上弯曲正应力分布规律,了解约束对梁弯曲正应力的影响,对弯曲理论有进一步的了解。
对于叠梁,因上、下梁自由叠放,不难知道,各梁绕自身中性轴弯曲,因此计算公式同上。但应注意,此时M为作用在各梁横截面上的弯矩,Iz为各梁横截面对自身中性轴的惯性矩,y为测点至自身中性轴的距离。
四、实验数据处理
1.据应变读数 ,计算各点每级加载后的应变读数增量 ,进而求出各点每级应变读数增量的平均值 。
2.根据所测各点应变增量平均值 ,计算相应的实验应力增量值 ;再计算各点理论应力增量值。然后将实验应力增量值和理论应力增量值进行比较,计算它们间的相对误差。实验数据记录和处理参考表4.1。
五、实验报告
实验报告应包括:实验目的,实验原理简述,实验装置简图,仪器设备的名称、型号,数据记录和处理,误差分析等。对于组合梁同时应包括理论计算公式的推导过程(只须一种解法)。
叠梁上、下梁可以是同一材料,亦可以是不同材料,可任意组合。图示是由45号钢和LY12CZ铝合金叠合而成的组合梁,截面为正方形。加载方式分别为三点弯曲加载(图4.1c)。在梁的指定截面位置粘贴有十枚应变片,其中:上梁顶面和下梁底面分别布置二枚应变片,上、下梁侧面均等间距地粘贴三枚应变片。
实验五直梁弯曲实验实验报告
实验五直梁弯曲实验实验报告实验五直梁弯曲实验⼀、实验⽬的:1. ⽤电测法测定纯弯时梁横截⾯上的正应变分布规律,并与理论计算结果进⾏⽐较。
2. ⽤电测法测定三点弯梁某⼀横截⾯上的正应变分布与最⼤切应变,并与理论计算结果进⾏⽐较。
3.学习电测法的多点测量。
⼆、实验设备:1. 微机控制电⼦万能试验机;2. 电阻应变仪;三、实验试件:本实验所⽤试件为两种梁:⼀种为实⼼中碳钢矩形截⾯梁,其横截⾯设计尺⼨为h ×b =(50×28)mm 2 ;另⼀种为空⼼中碳钢矩形截⾯梁,其横截⾯设计尺⼨为h ×b =(50×30)mm 2,壁厚t=2mm 。
材料的屈服极限MPa s 360=σ,弹性模量E=210GPa ,泊松⽐µ=0.28。
实验时间:2010年12图⼀实验装置图(纯弯曲)图⼆实验装置图(三点弯)四.实验原理及⽅法:在⽐例极限内,根据平⾯假设和单向受⼒假设,梁横截⾯上的正应变为线性分布,距中性层为 y 处的纵向正应变和横向正应变为:()()Z ZM y y E I M y y E I εεµ='=-? (1)距中性层为 y 处的纵向正应⼒为:()()zM yy E y I ?=?=σε(2)对于三点弯梁,梁横截⾯上还存在弯曲切应⼒:()()S z z F S y I ωτδ=(3)并且,在梁的中性层上存在最⼤弯曲切应⼒,对于实⼼矩形截⾯梁:max 32SF A=τ(4)对于空⼼矩形截⾯梁:22max [((2)(2)]16Sz F bh b t h t I t=---τ(5)由于在梁的中性层处,微体受纯剪切受⼒状态,因此有:maxmax Gτγ=(6)实验时,可根据中性层处045±⽅向的正应变测得最⼤切应变:45454545max 22)(εεεεγ-==-=-- (7)本实验采⽤重复加载法,多次测量在⼀级载荷增量?M 作⽤下,产⽣的应变增量?ε、?ε’和图三纯弯梁受⼒简图(a=90mm )图四三点弯梁受⼒简图(a=90mm )max γ?。
纯弯曲梁的正应力测定的实验报告
贴片位置
b
8
y3
0
h
16
y2(y4)
a
200
y1(y5)
3应变读数记录
读数A
应变片号
载荷
1
2
3
4
A
0
120
567
168
637
92
4500
0
7449
91
4
522
606
4500
7481
8
120
461
184
576
92
4500
0
7510
89
12
399
545
4500
7540
16
120
338
185
514
三.实验原理及方法:
梁受纯弯曲时,根据平面假设和纵向纤维间无挤压的假设,得纯弯曲时正应力公式:
图1
在矩形截面梁纯弯曲部分(见图1,CD段),贴有四个应变片,其中3在中性层上,1,2和4,5分别贴在离中性层为梁高的1/4及上下表面,加载后,梁弯曲变形,由应变仪可测出个测量点的纵向应变 ,可确定横截面上正应力分布规律。
2:学习电测法。
主要实验仪器:1:弯曲试验装置。
2:电阻应变仪和预调平衡箱。
主要实验步骤:
一:取一矩形截面的等截面剪支梁AB,其上作用两个对称的集中力P/2,未加载前,在中间CD段表面画些平行于梁轴线的纵向线和垂直于梁轴线的横向线。加载后在梁的AC和DB两段内,各横截面上有不同的剪力和弯矩M。
二;在矩形截面梁弯曲部分,贴有四个应变片,其中3在中性层上,1,2,4,5分别在离中性层为梁高的1/4及上下表面,加载后,梁弯曲变形,由应变仪可测出各测量点的纵向应变,可确定横截面上的应变分布规律。
纯弯曲梁正应力电测实验报告
纯弯曲梁正应力电测实验报告纯弯曲梁正应力电测实验是一种常用的材料力学实验方法,用于测量梁在弯曲过程中的正应力分布情况。
本实验通过加载施加在金属横截面上的外力,测量由于弯曲产生的电势差,从而得到梁在各个截面上的正应力大小。
下面是一份纯弯曲梁正应力电测实验报告的参考内容。
实验目的:1. 理解材料在弯曲过程中的正应力分布特性;2. 掌握纯弯曲梁正应力电测实验的原理和方法;3. 学习使用实验仪器和数据处理软件。
实验仪器:1. 弯曲实验台;2. 弯曲应变计;3. 电压采集仪;4. 电压放大器;5. 计算机。
实验原理:在纯弯曲梁实验中,通过加载施加在梁上的外力,梁发生弯曲变形。
根据材料力学理论,梁在弯曲过程中会产生正应力。
实验中利用弯曲应变计测量梁在各个截面上的应变大小。
弯曲应变计通过压电效应将应变转化为电荷,产生电势差。
通过电压采集仪和电压放大器将电势差放大并记录下来,就可以得到梁在各个截面上的正应力大小。
实验步骤:1. 将要进行实验的梁固定在弯曲实验台上,调整梁的位置和姿态,使其能够正常受力并产生弯曲变形;2. 将弯曲应变计安装在梁的截面上,保证其能够准确测量应变;3. 连接弯曲应变计和电压采集仪,调整采集仪的参数,使其能够正常采集电势差;4. 将电压采集仪与电压放大器连接,调整放大器的增益,保证能够得到合适范围的电压信号;5. 开始加载外力,在加载过程中,实时记录电压采集仪采集到的电势差数据;6. 加载外力达到一定值后停止,记录下此时的电势差数据。
数据处理:1. 将采集到的电势差数据导入计算机;2. 对电势差数据进行处理,根据电压放大器的增益和弯曲应变计的灵敏度,将电势差数据转换为应变数据;3. 根据应变计的位置和梁的材料参数,计算出各个截面上的应变值;4. 利用梁的几何参数和材料参数,计算出各个截面上的正应力大小。
实验结果:根据数据处理的结果,可以得到梁在各个截面上的正应力大小的分布情况。
通过绘制应力-位置曲线,可以直观地观察梁在弯曲过程中正应力的变化趋势,并分析其特点和规律。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验五 纯弯曲梁正应力实验一、试验目的1、熟悉电测法的基本原理。
2、进一步学会静态电阻应变仪的使用。
3、用电测法测定钢梁纯弯曲时危险截面沿高度分布各点的应力值。
二、试验装置1、材料力学多功能实验装置2、CM-1C 型静态数字应变仪三、试验原理本试验装置采用低碳钢矩形截面梁,为防止生锈将钢梁进行电镀。
矩形截面钢梁架在两支座上,加载荷时,钢梁中段产生纯弯曲变形最大,是此钢梁最危险的截面。
为了解中段危险截面纯弯曲梁应力沿高度方向分布情况,采用电测法测出加载时钢梁表面沿高度方向的应变情况,再由σ实=E ε实得到应力的大小。
试验前在钢梁上粘贴5片应变片见图5—1,各应变片的间距为4h,即把钢梁4等分。
在钢梁最外侧不受力处粘贴一片R 6作为温度补偿片。
图5—1 试验装置示意图对于纯弯曲梁,假设纵向纤维仅受单向拉伸或压缩,因此在起正应力不超过比例极限时,可根据虎克定律进行计算:σ实=E ε实E 为刚梁的弹性模量,ε实是通过电测法用电阻应变仪测得的应变值。
四、电测法基本原理1、电阻应变法工作原理电测法即电阻应变测试方法是根据应变应力关系,确定构件表面应力状态的一种实验应力分析法。
将应变片紧紧粘贴在被测构件上,连接导线接到电桥接线端子上 当构件受力 构件产生应变 应变片电阻值随之变化 应变仪内部的惠斯登电桥将电阻值的变化转变成正比的电压信号电阻应变仪内部的放大、相敏、检波电路转换显示器读出应变量。
2、电阻应变片1)电阻应变片的组成由敏感栅、引线、基底、盖层和粘结剂组成,其构造简图如图5—2所示。
敏感栅能把构件表面的应变转换为电阻相对变化。
由于它非常敏感,故称为敏感栅。
它用厚度为0.002~0.005mm的铜合金或铬合金的金属箔,采用刻图、制版、光刻及腐蚀等工艺过程制成,简称箔式应变。
它粘贴牢固、散热性能好、疲劳寿命长,并能较好的反映构件表面的变形,使测量精度较高。
在各测量领域得到广泛的应用。
图5—2 电阻应变片构造简图2)电阻应变片种类电阻应变片按敏感栅的结构形状可分为:单轴应变片:单轴应变片一般是指具有一个敏感栅的应变片。
应变花(多轴应变片):具有两个或两个以上轴线相交成一定角度的敏感栅制成的应变片称为多轴应变片,也称为应变花。
其敏感栅可由金属丝或金属箔制成。
采用应变花可方便地测定平面应变状态下构件某一点处的应变。
3)应变灵敏系数(K)将应变片贴在单向应力状态的试件表面,且其轴向与应力方向重合。
在单向应力作用下,应变片的电阻相对变化ΔR/P与试件表面沿应变片轴线方向的应变ε之比值,称为应变片的灵敏系数K=(ΔR/P)/ε应变片灵敏系数是使用应变片的重要数据。
它主要取决于敏感栅的材料、型式和几何尺寸。
应变片的灵敏系数受到多种因素的影响,无法由理论求得,是由制造厂经抽样在专门的设备上进行标定,并于包装上注明。
常用的应变片灵敏度系数为2—2.4。
当我们使用应变片时,必须在测量前进行校准。
校准方法:根据应变片的K值,查表5—1,再根据表内K值所对应的标定值,来调节静态应变仪。
K值1.9 1.95 22.05 2.1 2.15 2.2 2.25 2.3 2.35校准值120Ω5263 5182 5000 4878 4762 4651 4545 4444 4347 42553、CM-1C型静态数字应变仪通过应变片可以将试件的应变转换为应变片的电阻变化。
但通常这种电阻变化是很小的。
为了便于测量,需将应变片的电阻变化转换成电压(或电流)信号,再通过电子放大器将信号放大,然后由指示仪或记录器指示出应变数值。
这一任务由静态电阻应变仪来完成。
静态电阻应变仪中电桥的作用是将应变片的电阻变化转换成电压变化。
见图5—3CM-1C型静态数字应变仪前后面板静态数字应变仪内部主要由惠斯顿电桥组成,它可把电阻变化转换成电压(或电流)信号。
电桥结构如图4—3所示。
电桥各桥臂电阻分别为R1、R2、R3、R4,其中的任一个都可以是应变片或电阻。
电桥的A、C为输入端,接直流电源,输入电压为V0;而B、D为输出端,输出电压为V BD。
下面分析当R1、R2、R3、R4变化时,电桥输出电压V BD 的大小。
图5—3 CM-1C型静态数字应变仪前后面板图5—4 惠斯顿电桥由电工原理可知:电流I1 、I2为I1=V0/(R1+R3)I2=V0/(R3 +R4)BD端输出电压为:R1R4V BD=V BA-V DA =I1R1 - I1R4=(──-──)V0R1+R2 R3+R4 R1R3-R2R4= ───────V0( R1+R2)(R3+R4)当R1R3=R2R4时电桥平衡,V BD=0测量时,先使材料不受外力作用,电桥调平衡使V BD=0这样显示器读数为零,当材料受力时,桥臂四片电阻应变片产生微小电阻变化:ΔR1、ΔR2、ΔR3、ΔR4。
于是电压输出不为零。
通过信号放大显示器直接读出数值来。
应变仪上读数就是测量桥所测综合应变值:εd=ε1-ε2+ε3-ε4本次试验选用的CM-1C型静态数字电阻应变仪具体使用,在实验室内讲解。
4、温度补偿粘贴在被测构件测点上的应变片,如果周围环境变化时,应变片栅丝的电阻应变值也将随着温度改变而变化;同时,又因为栅丝材料和被测构件材料的膨胀系数不同,应变片被迫拉长或缩短,使栅丝电阻值也发生变化,这种由于温度改变引起的虚假应变,并不是由于载荷作用而引起的,如果只想测定构件承受在载荷作用下的变形,就应该设法消除它。
消除的办法就是温度补偿。
在常温应变测量中温度补偿的方法是采用桥路补偿法。
这种方法简单、经济、补偿效果好。
这是利用电桥特性来进行温度补偿的。
桥路补偿法可以分为以下两种:1)补偿块补偿法其材料应与被测构件相同,但不受外力,并将它置与构件被测点附近,使补偿片与工作片处于同一温度场中。
2)工作片补偿法这种方法不需要补偿块和补偿片,而是在同一被测试件上粘贴几个工作应变片,将它们接入电桥中。
当试件受力且测点环境温度变化时,每个应变片的应变中都包含外力和温度变化引起的应变,根据电桥基本特性,在应变仪的读数应变中即可消除温度变化所引起的虚假应变,而得到所需测量的应变。
因此工作应变片既参加工作,又起到了温度补偿的作用。
5、应变片在电桥中的接线方法应变片在应变仪的测量电桥中有各种接法。
在实际测量中,常利用电桥基本特性并采用不同的接线方法,来达到以下目的:a、实现温度补偿;b、从复杂的变形中测出所需要的应变分量;c、扩大应变仪的读数,以减少误差,提高测量灵敏度。
测量电桥是用于测量应变的,其各桥臂电阻可以全部是或部分是应变片。
在应变测量中,常采用以下几种接线方法:1)全桥接线法测量电桥的四个桥臂上全部接电阻应变片,称为全桥接线法(或全桥线路)。
对于等臂电桥,此时应变仪的读数应变由公式即可得出:εd=ε1-ε2+ε3-ε4实际测量时,可有以下两种情况:a、全桥测量:电桥的四个桥臂上都接工作应变片。
b、相对两臂测量:电桥相对两臂接工作应变片,另相对两臂接温度补偿应变片。
2)半桥接线法若在测量电桥的桥臂AB和BC上接电阻应变片,而另外两臂AD和CD接电阻应变仪的内部固定电阻R,则称为半桥接线法。
由于桥臂AD和CD接固定电阻,不感受应变,因此对于等臂电桥,按公式可得到应变仪的读数为:εd=ε1-ε2实际测量时,可有以下两种情况:a、半桥双臂测量:电桥的两桥臂AB和BC上均接工作应变片。
b、半桥单臂测量:电桥的两桥臂AB和BC上,任意桥臂接工作应变片,而另一桥臂接温度补偿应变片。
五、试验步骤1、试验前的准备了解钢梁材料:低碳钢弹性模量E=2×105MP a测出钢梁尺寸(单位:mm)L=800 a=300 b=10 h=20 c=5砝码重量P=40N检查钢梁支座位置及加载的位置,保证加力准确。
2、应变仪准备1)接通电源,预热半小时。
2)灵敏度调节:K=2.08 标定48083、进行试验测纯弯曲梁由上至下R1~R5点应变值,了解应力分布情况。
1)试验中用半桥单臂连接。
将R1两根引线接于静态数字应变仪背部第一个电桥的A、B端,R2接到第二个电桥的A、B端,同理将R3 ~ R5接线。
补偿片R6接到变换器旁边的A0 B0上,相当于1~10个电桥BC点都接了补偿片R6,应变仪的测量电桥被接好。
2)用螺丝刀调节1~5个电桥相应旋钮使显示器显示为零,这时应变仪的测量电桥被调节平衡。
在调节仪器灵敏度。
3)本试验加载为“增量法”,每次增加等量载荷ΔP(40N),共加三次砝码记录三组读数,填入表中。
以便观察各点应变的线性程度。
然后利用第n次减第n-1次得到增量,求出增量平均值,即为Δε实。
Δε实单位为με即10-6ε。
最后带入试验值公式计算应力。
4、结束工作试验完毕,卸下砝码关闭仪器电源,从仪器接线柱上拆下接线并将试验装置复原。
六、注意事项1、接完线后不要随便移动仪器,保持其内部稳定,防止接线脱落。
2、接线时一定将导线全部压紧,以免应变值不断变化。
3、加载砝码时要轻轻、平稳地加在砝码盘上,切勿重击。
加卸砝码都要紧慎,防止掉落伤人。
七、数据记录处理1、钢梁材料:低碳钢弹性模量E=2×105MP a2、钢梁尺寸(单位:mm)L=800 a=300 b=10 h=20 3、砝码重量 P=40N 4、试验数据记录 5、计算1)理论值计算在纯弯曲部分,与ΔP 相应的弯矩分别为:ΔM=21P ·a 由公式Δσ理=IyM •∆ 求出各测点应力的理论值。
其中I=121bh 3;y 为各测点到中性轴的距离。
2)分别计算1~5点的试验应力 Δσ实=E ·Δε实相对误差=理实理σσσ∆∆-∆×100%绝对误差=Δσ理-Δσ实。
