2016年数学建模
2016数学建模国赛论文

(5.10) (5.11)
得到
1 V g mg mg )l sin 0 Fxl cos ( Fy Mg 水 桶 2
由此解得第一根钢管的倾斜角度的表达式
1 arctan
1 V g mg mg Fy Mg 水 桶 2
以及上方钢管施加的约束力。钢桶的受力如图 4 所示:
5
0
mg
Mg
1
mg
F1
图 4 钢桶的受力分析示意图
图 5 第一根钢管受力分析示意图
) , F ( F , F ) , 将各力写成直角坐标系下坐标的形式有: GM (0, Mg x y 锚 水V桶g ) .此时, GM G桶 F桶 =(0,-mg 与 F锚 的作用点坐标为: ( l sin , l cos ) , l l 而 G桶 F桶 的作用点为 ( sin , cos ) ,钢桶的倾角为 . 2 2 根据虚功原理: ( F锚 GM ) r ( F G 1 桶 桶) r2 0 1 V g 1 mg )l sin 0 Fxl cos ( Fy Mg 2 水 桶 2 Fx 0 arctan 由此可以解得 1 V g 1 mg Fy Mg 2 水 桶 2
系泊系统的设计
摘要
系泊系统是一种通过机械装置将水面结构与固定点进行连接的系统。它能够 使被系结构物具有抵御一定环境条件的能力, 并在遭遇极端海况时保证结构物和 系泊系统本身的安全。 本文建立了单点系泊系统的数学模型,并针对不同海况对 系泊系统进行结构上的优化设计。 针对问题一,首先,假定浮标吃水深度为 h ,在满足题目要求的情况下,求 解得到锚链对浮标、钢管、钢桶整体的作用力;随后从下至上依次对钢桶以及各 节钢管进行受力分析,并根据虚功原理得到钢桶、各钢管的倾角与约束力(作为 吃水深度 h 的函数) ;之后,根据锚链形状为一悬链线的假设,求解锚链在吃水 深度为 h 时的形状方程;最后,计算锚链、钢桶、钢管、浮标在水下部分的竖直 方向的高度作为 h 的函数,并根据水深为 18 m 的条件计算出 h 的大小,进而计算 得到题目要求的各个参量。结果为: (1)风速为 12 m / s 的情况下,钢桶倾斜角 度为 1.202°;从下至上各钢管倾斜角度依次为:1.184°,1.176°,1.168°, 1.160°;锚链形状方程为: s 3.98 tan ;浮标吃水深度 0.681 m ,游动范围为 一半径 14.65 m 的圆; (2)风速为 24 m / s 的情况下,钢桶倾斜角度为 4.569°; 从下至上各钢管倾斜角度依次为:4.502°,4.473°,4.444°,4.415°;锚链 形状方程为: s 15.74 tan 1.24 ;浮标吃水深度 0.695 m ,游动范围为一半径 17.78 m 的圆。 针对问题二,将风速 36 m / s 代入问题一的模型中,得到钢桶倾斜角度为 9.452°; 从下至上各钢管倾斜角度依次为:9.323°, 9.267°, 9.211°, 9.157°; 锚链末端与海床夹角为 20.905°,形状方程为: s 34.80 tan 13.29 ;浮标吃 水深度 0.718 m , 游动范围为一半径 18.87 m 的圆。 由于钢桶的倾斜角度超过 5°, 且锚链末端与海床夹角超过 16°,因此需要将重物球的质量作为自变量,两个 角度作为因变量,建立控制模型求解。通过控制重物球的质量,使得钢桶倾角小 于 5°且锚链末端与海床夹角小于 16°。调整后的结果为:重物球的质量大于 2262.9kg 时钢桶的倾斜角度小于 4.5°,锚链末端切线与海床夹角小于 16°。 针对问题三,首先对问题一及问题二中使用的模型进行改进,在受力分析过 程中引入水流力;随后,构建以钢球质量 M 、水深 H 、风速 v 、水流速 V 、风 速与水流速之间的夹角β、锚链的线密度ρ、以及锚链的总长度 L 为自变量的函 数,函数的因变量为钢桶以及各节钢管的倾角、浮标的吃水深度 h 、以及用于确 定锚链形状方程 s k tan b 的参数 k 和 b ;之后,考虑到水深大小波动的影响, 在人为给定海面风速以及浅海水流速之后,讨论锚链的型号、总长度以及重物球 的质量对钢桶及各钢管倾角、浮标吃水深度、锚链形状以及游动区域的影响,并 在人为给定的风速与水流速 36 m / s ,1.5 m / s 且同向的条件下,使用遗传算法得 到最优的系泊系统设计为:选用 V 型锚链 20.78m,重物球质量为 4560kg. 最后,将模型应用于青岛市胶州湾浅海海域,根据区域的实际海水流速、海 风风向,得到系泊系统的最优设计。对模型进行客观评价,对模型的实用性进行 评估,并给出针对模型缺陷的改进方案。
2016年全国大学生数学建模竞赛B题解题分析与总结

2016年全国大学生数学建模竞赛B题解题分析与总结2016年全国大学生数学建模竞赛B题解题分析与总结一、题目分析2016年全国大学生数学建模竞赛B题是一个与经济学、金融学相关的问题,要求参赛者通过对问题的深入分析和建模,以及对模型的求解和结果的解释,提出合理的结论。
二、问题描述本题的题目为《贷款利率调控模型》。
题目给出了一组数据,包括贷款利率、消费者价格指数、人均可支配收入、外汇储备等指标,要求参赛者针对这些指标进行分析,并建立合适的模型来解释这些指标之间的关系。
三、解题思路1. 数据分析:首先,我们需要对给定的数据进行分析。
通过绘制图表和计算一些统计量,我们可以对这些数据的变化和趋势进行初步了解。
2. 建立模型:在了解了数据的基本特征之后,我们需要以此为基础,建立起合适的数学模型。
这个模型应该能够描述贷款利率与消费者价格指数、人均可支配收入、外汇储备之间的关系,并能够进行预测。
3. 参数估计:建立好模型之后,我们需要对模型中的参数进行估计。
这需要依赖于数学推导和数据拟合的方法,通过最小二乘法等方法,确定模型的参数。
4. 模型求解:有了模型和参数之后,我们可以使用计算机软件进行模型的求解。
通过数值计算的方法,我们可以得到模型的解析解或数值解,并进行结果的分析和解释。
5. 结论与反思:最后,我们需要根据模型的结果,对问题进行结论和反思。
我们可以分析模型的合理性、可靠性,以及对解决实际问题的指导意义。
同时,我们也可以对模型的不足之处进行总结,并提出改进的建议。
四、模型建立与结果解释在解题的过程中,我们可以考虑建立如下的模型:贷款利率=消费者价格指数+人均可支配收入+外汇储备。
通过对这三个指标的分析,我们可以发现它们之间存在着一定的关系。
消费者价格指数和人均可支配收入可以反映经济的收入水平和购买力,而外汇储备可以反映国家的经济实力。
在建立了模型之后,我们可以对模型进行求解,并得到相应的结果。
根据模型的求解结果可以得出以下结论:贷款利率与消费者价格指数、人均可支配收入和外汇储备之间存在着一定的关系。
2016全国大学生数学建模竞赛获奖名单

2016高教社杯全国大学生数学建模竞赛获奖名单(初稿)(异议期:2016年11月7日-2016年11月20日)
本科组高教社杯获得者:张滕翔、夏智康、郑安琪(东南大学)
专科组高教社杯获得者:吴伟龙、杨婷、段玲(湖南化工职业技术学院)
本科组MATLAB创新奖获得者:王毅然、纪昀红、张伟(中国人民大学)
专科组MATLAB创新奖获得者:刘苏生、祝王缘、王柏熙(海军蚌埠士官学校)
[注]以下每一获奖等级内,按赛区顺序排列(同一赛区内,按学校笔画顺序排列)。
本科组一等奖(共294名)
本科组二等奖(共1621名)
曹小
专科组一等奖(共60名)。
2016全国大学生数学建模竞赛获奖名单
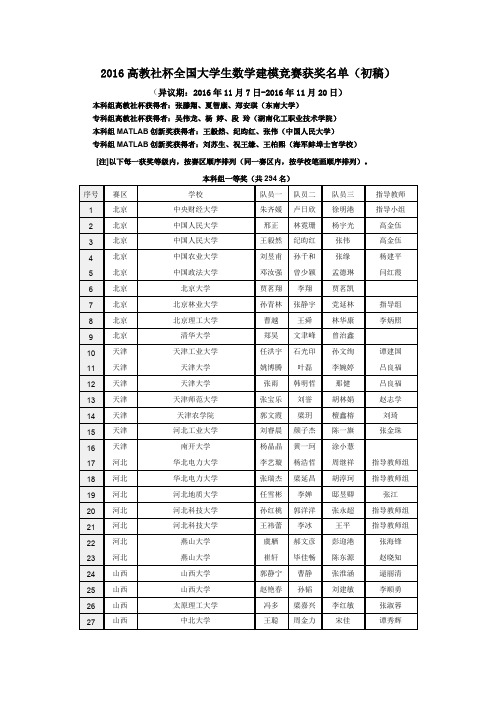
2016高教社杯全国大学生数学建模竞赛获奖名单(初稿)(异议期:2016年11月7日-2016年11月20日)
本科组高教社杯获得者:张滕翔、夏智康、郑安琪(东南大学)
专科组高教社杯获得者:吴伟龙、杨婷、段玲(湖南化工职业技术学院)
本科组MATLAB创新奖获得者:王毅然、纪昀红、张伟(中国人民大学)
专科组MATLAB创新奖获得者:刘苏生、祝王缘、王柏熙(海军蚌埠士官学校)
[注]以下每一获奖等级内,按赛区顺序排列(同一赛区内,按学校笔画顺序排列)。
本科组一等奖(共294名)
本科组二等奖(共1621名)
曹小
专科组一等奖(共60名)。
2016年全国大学生数学建模竞赛浙江赛区获奖名单(A组)

序号 队号 1 A201611141015 2 A201611117011 3 A201611141006 4 A201611117010 5 A201611136024 6 A201611117002 7 A201611141001 8 A201611168017 9 A201611117015 10 A201611119010 11 A201611119007 12 A201611160015 13 A201611102010 14 A201611102007 15 A201611136012 16 A201611168018 17 A201611160011 18 A201611168011 19 A201611160014 20 A201611104005 21 A201611140020 22 A201611117018 23 A201611117012 24 A201611117007 25 A201611141014 26 A201611117026 27 A201611141017 28 A201611168022 29 A201611168020 30 A201611168012 31 A201611104029 32 A201611155004 33 A201611102030 34 A201611137008 35 A201611136007 36 A201611167004 37 A201611127013 38 A201611102020 39 A201611153002 40 A201611149004 41 A201611127004 42 A201611117023 43 A201611117025 44 A201611117016 45 A201611117009 46 A201611117021 47 A201611117022 48 A201611141031 49 A201611141012 50 A201611141016 51 A201611137004 52 A201611102021 53 A201611168051 54 A201611153004 55 A201611122029 队员1 黄逸尘 赵璐铭 徐志豪 鲍刘璐 张遵明 徐俊 唐洁琪 肖耀 陈家琦 聂大惟 邵凯丽 陈秉权 程晓君 任胜苗 梅红艳 王淑怡 潘小芳 曾京乐 朱诗勇 杜飞龙 王筱倩 徐胜男 汤佳逸 郭雨霞 卢方伟 杨星宇 王奕舒 赵雪娇 徐伟袖 裘银浩 李瑞翔 王达 王健 臧泽林 蒋烁予 吴思佳 王鹏 袁家兴 池皓然 刘翔 李科杰 郭佳梅 潘婉儿 杨雪萍 方楚冰 谭栋 潘娜 陈冀潇 陈妃 徐军亮 陈倩怡 马诗卉 汤卓翰 胡旭孟 余清奖 队员2 队员3 廖亮 江渔 安巡 杨鹏 龚鑫 葛鑫鑫 徐辉 李一鸣 陈宁 金萧 魏倩 邱华辉 黄成斌 蔡依辰 王哲 崔震 杨汉晨 张晗 汪玲芳 朱兴宝 黄文娜 吴华鑫 彭佳瑜 许芷晴 吴志伟 朱晨睿 应芝 杨碧姣 李佳毅 王竞康 张超 施康康 胡智慧 丁桔 潘伟 甘甜 林琳 郑舒 吴丽燕 陆嘉泓 泮玲玲 吴青青 林心代 吴良碧 杨鑫建 叶林杰 朱佳丽 刘江 林瑞豪 施佳 苏铉琳 李文豪 郭燕玉 林朗星 董志超 张嘉荟 徐颖 陈璐 许青山 周佳儿 陈鹏 李盈盈 黄灵耀 林申君 宋江胜 岳振东 王惠洁 翟丹妮 李静航 高慧靖 姚锦权 王晨 王金鑫 吴汉魏 于子青 许弘 华一泓 黄睿希 周汀鹏 张思悦 钱可可 倪昊 陈娴静 姜晓红 彭双 朱增钢 郑晓颖 王侠侠 诸葛晨曦刘嵩 叶晋 吴思思 葛雨静 赵一明 蒋锦鹏 陈潜 潘宇婷 童珺怡 林恒屹 任浩杰 王心愉 李媛媛 陈卓琳 滕安超 高程玲 朱康钧 方子明 张怡帆 俞红燕 张逃 指导教师 院校 邓爱珍 浙江工业大学 王松静 宁波大学 周明华 浙江工业大学 王松静 宁波大学 数模组 浙江大学 张晓敏 宁波大学 宋军全 浙江工业大学 数模组 中国计量大学 王立洪 宁波大学 蔡军伟 宁波工程学院 陈军 宁波工程学院 数模组 浙江师范大学 数模组 杭州电子科技大学 数模组 杭州电子科技大学 数模组 浙江大学 数模组 中国计量大学 数模组 浙江师范大学 数模组 中国计量大学 数模组 浙江师范大学 黄越夏 杭州师范大学 数模组 浙江工商大学 罗文昌 宁波大学 王松静 宁波大学 徐晨东 宁波大学 周明华 浙江工业大学 李茂华 宁波大学 邓爱珍 浙江工业大学 数模组 中国计量大学 数模组 中国计量大学 数模组 中国计量大学 何颖俞 杭州师范大学 数模组 浙江理工大学 数模组 杭州电子科技大学 数模组 浙江大学城市学院 数模组 浙江大学 金伟锋 浙江中医药大学 陈文海 温州大学 数模组 杭州电子科技大学 数模组 浙江警察学院 数模组 浙江外国语学院 数模组 温州大学 李卫华 宁波大学 李茂华 宁波大学 王立洪 宁波大学 徐晨东 宁波大学 李卫华 宁波大学 李卫华 宁波大学 周明华 浙江工业大学 邬学军 浙江工业大学 周明华 浙江工业大学 数模组 浙江大学城市学院 数模组 杭州电子科技大学 数模组 中国计量大学 数模组 浙江警察学院 祝汉灿 绍兴文理学院 奖项 推荐全国一等奖 推荐全国一等奖 推荐全国一等奖 推荐全国一等奖 推荐全国一等奖 推荐全国一等奖 推荐全国一等奖 推荐全国一等奖 推荐全国一等奖 推荐全国一等奖 推荐全国一等奖 推荐全国一等奖 推荐全国一等奖 推荐全国一等奖 推荐全国一等奖 推荐全国一等奖 推荐全国一等奖 推荐全国一等奖 推荐全国一等奖 推荐全国一等奖 推荐全国一等奖 推荐全国二等奖 推荐全国二等奖 推荐全国二等奖 推荐全国二等奖 推荐全国二等奖 推荐全国二等奖 推荐全国二等奖 推荐全国二等奖 推荐全国二等奖 推荐全国二等奖 推荐全国二等奖 推荐全国二等奖 推荐全国二等奖 推荐全国二等奖 推荐全国二等奖 推荐全国二等奖 推荐全国二等奖 推荐全国二等奖 推荐全国二等奖 推荐全国二等奖 省一等奖 省一等奖 省一等奖 省一等奖 省一等奖 省一等奖 省一等奖 省一等奖 省一等奖 省一等奖 省一等奖 省一等奖 省一等奖 省一等奖
2016高教社杯全国大学生数学建模竞赛题目A题解题思路

2016高教社杯全国大学生数学建模竞赛题目A题系泊系统的设计分析初稿,旨在交流,有各种做题思路,大家自由发挥!不保证正确,如有错误,欢迎指正!注意1:程序为最初稿,只是证明解的存在性,可以使用二分法、牛顿法等进行进一步求解!2:剩下的可以使用锚链线等更复杂的理论:请继续查阅文献,给文章加分3:此外可以化下面的流程图,解释求解程序,给文章加分4:剩下题目问题原则上是把问题做的更复杂,考虑更多的受力,请大家自行脑补。
5:第一天说了对系缆力的计算,目前主要有三种模型:悬链线模型(我们下面说的第三种静力学分析)、以多体动力学理论为基础的集中质量一弹簧模型(我们下面说的第二种,需要matlab做常微分方程数值解)以及细长杆模型(我们下面说的第一种,力学有限元分析))。
查阅参考文献《深海系泊系统动力特性研究进展》,请大家自行选择各类方法。
1. 某型传输节点选用II型电焊锚链22.05m,选用的重物球的质量为1200kg。
现将该型传输节点布放在水深18m、海床平坦、海水密度为1.025×103kg/m3的海域。
若海水静止,分别计算海面风速为12m/s和24m/s时钢桶和各节钢管的倾斜角度、锚链形状、浮标的吃水深度和游动区域。
1. 某型传输节点选用II型电焊锚链22.05m,选用的重物球的质量为1200kg。
现将该型传输节点布放在水深18m、海床平坦、海水密度为1.025×103kg/m3的海域。
若海水静止,分别计算海面风速为12m/s和24m/s时钢桶和各节钢管的倾斜角度、锚链形状、浮标的吃水深度和游动区域。
分析:为简化起见, 按平浮处理,风引起的水平力x F()()220.625,0.6252x F v S h r h h v θ'==⨯-浮力f F 为2f F g r h ρπ'=其中h '为正浮吃水深度。
则对浮标的方程有 1111011011sin ,cos sin ,cos x f x f F T F T G F T F G T θθθθ==+=-= (1)其中0G 为浮标自重,00G m g =,0m 为浮标的质量为1000kg 。
2016年数学建模国赛a题
2016年数学建模国赛a题一、2016年数学建模国赛A题的一些了解哎呀,2016年数学建模国赛A题可真是个挺有挑战性的题目呢。
当时很多同学都对这个题目下了不少功夫。
这个A题大概是和什么相关的呢?我印象里好像是和一些实际的物理或者工程现象有关的建模问题。
就好比是把现实中的某个复杂情况,用数学的模型去表示出来,然后再用数学的方法去解决相关的问题。
比如说,可能是关于某种物体的运动轨迹建模呀,或者是某个工程系统中的资源分配优化建模之类的。
这就需要我们把实际的问题转化成数学语言,像是建立方程啦,设定变量啦,然后再去求解这个数学模型。
这过程就像是在玩一个超级复杂的拼图游戏,每个小的数学元素就是一块拼图,要把它们都拼对了,才能得出正确的答案。
而且在这个过程中,要考虑到各种实际的限制条件,就像拼图有边界一样,数学模型也有它的边界条件,不能随便乱设。
二、如果把它当成一道试卷题来做要是把这个题目当成一张试卷里的题目,满分100分的话。
我觉得可以这样来出题。
1. 第一部分可以出个20分的题目,就是让大家简单描述这个问题的数学模型的基本框架。
比如说这个模型应该包含哪些变量呀,哪些参数是已知的,哪些是需要求解的。
答案呢,就是根据对这个题目实际问题的理解,准确列出这些变量和参数,解析就是解释为什么要这样列,这些变量和参数在实际问题里代表着什么。
2. 然后再出个30分的题目,让大家根据给定的一些简化条件,去求解这个模型的初步结果。
答案就是具体的数值或者表达式,解析就是每一步计算的依据和用到的数学原理。
3. 还有个30分的题目,可以是让大家对这个模型进行优化,考虑更多的实际因素进去,看看模型会有什么变化。
答案就是优化后的模型表达式或者参数值,解析就是说明优化的思路和每个优化步骤的数学依据。
4. 最后20分的题目,可以是让大家讨论这个模型在实际应用中的局限性和可能的改进方向。
答案就是列出局限性和改进方向,解析就是解释为什么这些是局限性,以及改进方向的合理性。
2016数学建模竞赛山东赛区获奖名单公示
娄鹤 徐玉莹 郭小铭 欧阳勖 毛艳雪 刘兆珂 王衍春 马栋梁 于晓晓 路宝国 刘文君 王仲倩 于璐 李宇 李昂 王晓玲 徐嘉宾 孙蓓 牛彦昭 胡聪 李卓 胡雪卿 崔馨月 马传震 李清新 周生远 解子阳 刘天雨 宋来振 赵冬雪 张辉 刘越 王经元 孙红梅 刘星 王兵兵 杨欣欣 许国梁 孙芮 胡大明 朱雯婷 任尊超 王惠 王学贞 李小鹏 李体鉴 刘胜男 杨学英 吴仪 张凯颖 王思琪 孔浩强
孙鹏举 吴鸿华 刘艳 吴鸿华 许振宇 吴鸿华 邱保建 邱保建 邱保建 屈忠锋 李尚友 李尚友 刘艳 吴鸿华 邱保建 何燕玲 何燕玲 屈忠锋 邱保建 李尚友 许振宇 何燕玲 李西成 何燕玲 许振宇 刘春燕 吴鸿华 刘春燕 李西成 邱保建 吴鸿华 刘艳 刘艳 李西成 吴鸿华 刘艳 孙鹏举 许振宇 屈忠锋 李尚友 孙鹏举 李西成 屈忠锋 吴鸿华 李西成 吴鸿华 刘春燕 刘春燕 孙鹏举 李西成 屈忠锋 邱保建
队员三 段金鹏 薛盼盼 杨锐 牛聪 苑赛楠 张璇 尚雪丽 周润欣 全鑫 王永东 刘鹏宇 魏春艳 任九洲 张凤霞 金玉静 李西娜 吴炫霏 胡倩 苏金凤 陈永威 刘治 徐洁 纪卫克 丁雪梅 刘鸿基 刘佳星 王娜 郜泽新 郭红晓 王颖 陈洋 杨云瑞 王庆松 刘晓桐 王子健 尚宇航 马月阳 高畅 于江兴 魏久桐 刘云飞 赵伊然 穆尧 王宇辰 陶福建 黄中元 谢路毅 徐德晨 郭林坡 廖晓玲 张岩
许桢 徐明玉 麻敏超 许立鹤 周纯年 何泽津 丛晓杨 李学峰 吴泽涛 潘剑 陈少华 李国豪 金铮 王艾浩 胡金朋 徐富 郭俊鹏 黄帅 袁欣益 陈诚 易觉 全闻捷 方李晟 张凯洋 曹竞之 方国伟 殷海尧 李泽政 陶俊权 何雨山 马小然 吴按毅 陈发赢 何云风 姜雅馨 王平 刘明霞 胡晓梦 郭蓉 党兆盈 郑雪园 杨玙璠 刘红巧 田金辉 李舒豫 郁越 万鉴辉 张婷 倪慧宇 张莹 张海啸 高爽 栾娜娜
2016电工杯数模大赛a题
2016电工杯数模大赛a题
2016年电工杯数学建模大赛A题是一个涉及数学建模和解决实际问题的竞赛题目。
根据我的了解,A题的具体内容可能涉及到某个具体的实际问题,可能涉及到数学模型的建立和求解,也可能需要进行数据分析和结果的解释等方面。
在这个题目中,参赛者可能需要考虑如何利用数学工具和方法对所提出的问题进行建模,可能需要运用概率统计、微积分、线性代数等数学知识,结合实际情况进行分析和求解。
此外,A题可能还需要参赛者具备一定的编程能力,能够利用计算机对模型进行仿真和求解。
在参赛者回答A题时,需要从实际问题出发,分析问题的背景和意义,明确问题的求解目标,提出合理的数学假设和模型假设,选择合适的数学方法进行建模和求解,并对结果进行合理的解释和分析。
同时,还需要考虑模型的合理性和稳定性,以及对结果的敏感性分析等方面。
总的来说,2016年电工杯数学建模大赛A题是一个综合性较强的竞赛题目,需要参赛者具备扎实的数学基础知识、良好的建模能
力和分析能力,以及较强的团队合作能力和创新思维。
希望我的回答能够对你有所帮助。
2016年数学建模国赛A题
2016年高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)A题系泊系统的设计近浅海观测网的传输节点由浮标系统、系泊系统和水声通讯系统组成(如图1所示)。
某型传输节点的浮标系统可简化为底面直径2m、高2m的圆柱体,浮标的质量为1000kg。
系泊系统由钢管、钢桶、重物球、电焊锚链和特制的抗拖移锚组成。
锚的质量为600kg,锚链选用无档普通链环,近浅海观测网的常用型号及其参数在附表中列出。
钢管共4节,每节长度1m,直径为50mm,每节钢管的质量为10kg。
要求锚链末端与锚的链接处的切线方向与海床的夹角不超过16度,否则锚会被拖行,致使节点移位丢失。
水声通讯系统安装在一个长1m、外径30cm 的密封圆柱形钢桶内,设备和钢桶总质量为100kg。
钢桶上接第4节钢管,下接电焊锚链。
钢桶竖直时,水声通讯设备的工作效果最佳.若钢桶倾斜,则影响设备的工作效果。
钢桶的倾斜角度(钢桶与竖直线的夹角)超过5度时,设备的工作效果较差。
为了控制钢桶的倾斜角度,钢桶与电焊锚链链接处可悬挂重物球。
图1 传输节点示意图(仅为结构模块示意图,未考虑尺寸比例) 系泊系统的设计问题就是确定锚链的型号、长度和重物球的质量,使得浮标的吃水深度和游动区域及钢桶的倾斜角度尽可能小。
问题1某型传输节点选用II型电焊锚链22。
05m,选用的重物球的质量为1200kg。
现将该型传输节点布放在水深18m、海床平坦、海水密度为1。
025×103kg/m3的海域。
若海水静止,分别计算海面风速为12m/s和24m/s时钢桶和各节钢管的倾斜角度、锚链形状、浮标的吃水深度和游动区域。
问题2在问题1的假设下,计算海面风速为36m/s时钢桶和各节钢管的倾斜角度、锚链形状和浮标的游动区域。
请调节重物球的质量,使得钢桶的倾斜角度不超过5度,锚链在锚点与海床的夹角不超过16度.问题3 由于潮汐等因素的影响,布放海域的实测水深介于16m~20m之间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016年数学建模
【原创实用版】
目录
1.2016 年数学建模竞赛简介
2.竞赛的难度和挑战
3.我国高校在竞赛中的表现
4.数学建模对学生的意义
5.未来数学建模竞赛的发展趋势
正文
【2016 年数学建模竞赛简介】
2016 年数学建模竞赛,全名为国际数学建模竞赛,英文名为International Mathematical Modeling Contest,简称为 MCM。
这是一项全球范围内的大学生数学建模竞赛,旨在通过数学方法解决实际问题,考验参赛选手的数学、物理、计算机等多方面能力。
【竞赛的难度和挑战】
数学建模竞赛的难度在于,参赛选手需要在规定时间内(通常为 72 小时)独立完成对一个问题的深入理解、数学模型的建立和求解、计算程序的编写以及论文的撰写。
这对选手的智力、体力和意志都是极大的挑战。
【我国高校在竞赛中的表现】
我国高校在数学建模竞赛中的表现一直非常出色。
2016 年的比赛中,我国高校共有 46 支队伍获得一等奖,成绩斐然。
这充分展示了我国高校在数学建模领域的教育水平和实力。
【数学建模对学生的意义】
数学建模不仅是一项竞赛,更是一种对学生综合能力的锻炼。
通过数
学建模,学生不仅可以提高自己的数学水平,还可以锻炼自己的逻辑思维、问题分析和解决能力,以及团队协作和创新能力。
【未来数学建模竞赛的发展趋势】
随着科技的发展,数学建模竞赛在未来将会更加重要。
