重庆市巴蜀中学2018届高三适应性月考(九)文科综合试题(图片版)
重庆市2018届巴蜀中学高考适应性月考卷(九)理综-答案
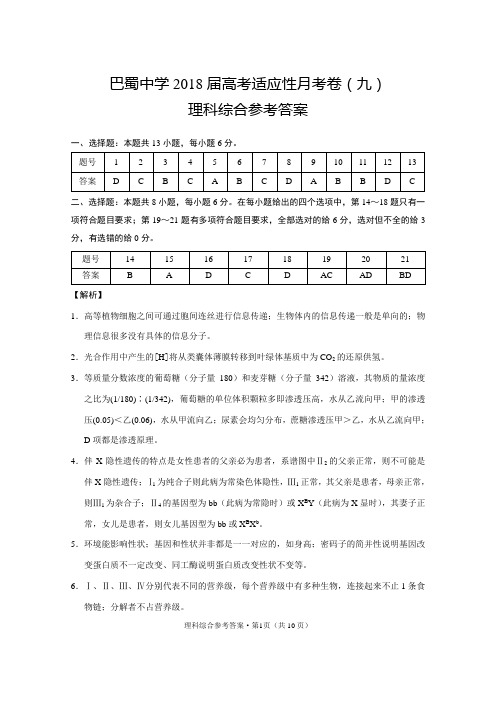
巴蜀中学2018届高考适应性月考卷(九)理科综合参考答案一、选择题:本题共13小题,每小题6分。
二、选择题:本题共8小题,每小题6分。
在每小题给出的四个选项中,第14~18题只有一项符合题目要求;第19~21题有多项符合题目要求,全部选对的给6分,选对但不全的给3分,有选错的给0分。
【解析】1.高等植物细胞之间可通过胞间连丝进行信息传递;生物体内的信息传递一般是单向的;物理信息很多没有具体的信息分子。
2.光合作用中产生的[H]将从类囊体薄膜转移到叶绿体基质中为CO2的还原供氢。
3.等质量分数浓度的葡萄糖(分子量180)和麦芽糖(分子量342)溶液,其物质的量浓度之比为(1/180)∶(1/342),葡萄糖的单位体积颗粒多即渗透压高,水从乙流向甲;甲的渗透压(0.05)<乙(0.06),水从甲流向乙;尿素会均匀分布,蔗糖渗透压甲>乙,水从乙流向甲;D项都是渗透原理。
4.伴X隐性遗传的特点是女性患者的父亲必为患者,系谱图中Ⅱ2的父亲正常,则不可能是伴X隐性遗传;Ⅰ1为纯合子则此病为常染色体隐性,Ⅲ1正常,其父亲是患者,母亲正常,则Ⅲ1为杂合子;Ⅱ4的基因型为bb(此病为常隐时)或X B Y(此病为X显时),其妻子正常,女儿是患者,则女儿基因型为bb或X B X b。
5.环境能影响性状;基因和性状并非都是一一对应的,如身高;密码子的简并性说明基因改变蛋白质不一定改变、同工酶说明蛋白质改变性状不变等。
6.Ⅰ、Ⅱ、Ⅲ、Ⅳ分别代表不同的营养级,每个营养级中有多种生物,连接起来不止1条食物链;分解者不占营养级。
理科综合参考答案·第1页(共10页)7.A项,用食醋浸泡有水垢(主要成分为CaCO3)的水壶,可以清除其中的水垢,这是利用了醋酸的酸性;B项,葡萄糖为单糖,不能发生水解反应;C项,地沟油在碱性条件下水解可以生成高级脂肪酸盐和甘油,正确;D项,铜制品在潮湿的空气中生锈,其主要原因是发生了吸氧腐蚀。
2018届重庆市巴蜀中学高三适应性月考(九)英语试题及答案

巴蜀中学2018届高考适应性月考卷(九)英语参考答案第一部分听力(共两节,满分30分)1~5 CBBCA 6~10 CBCCC 11~15 BAABA 16~20 ACAAB第二部分阅读理解(共两节,满分40分)第一节(共15小题;每小题2分,满分30分)21~25 CAADA 26~30 BDBCC 31~35 AADCB第二节(共5小题;每小题2分,满分10分)36~40 FABED第三部分语言知识运用(共两节,满分45分)第一节(共20小题;每小题1.5分,满分30分)41~45 BDACB 46~50 ACDCB 51~55 ADDAB 56~60 ACDBC第二节(共10小题;每小题1.5分,满分15分)61.but 62.intentionally 63.reasons 64.who65.itself 66.was considered 67.the 68.inspiring 69.have combined 70.dating第四部分写作(共两节,满分35分)第一节短文改错(共10小题;每小题1分,满分10分)With the summer vacation came round again,I am happy that I could forget about school at①comingleast for a while.In case of I would fool around all through this summer vacation,I have made a plan ②as to how to spent it.First,I think I should go over all the things which my teachers taught me in the③spend ④thatprevious term.So,I could have∧better understanding of it.Then I think I should take up some⑤a ⑥themexercises,such as walking,running and rowing,to keep me physical strong.Undoubtedly,with so ⑦exercise ⑧physically ⑨sucha good plan I will make the best of my vacation time.And I am sure I will live up to that I have planned.⑩what第二节书面表达(满分25分)【参考范文】Dear fellow students,I’m Li Hua,president of the Students Union.To help you have a better understanding of China,a contest on Chinese traditional culture is going to be held in the lecture hall this Sunday evening.As scheduled,in the first section,you are to answer questions about Chinese culture quickly to get more points.And then a speech delivered in Chinese is required,in which both pronunciation and accuracy will be evaluated.For the last part,you can choose an art form to show your talent for Chinese learning and knowledge of the culture.Winners of the contest will be awarded an e-dictionary that can help with your Chinese learning.More importantly,I think this is a great opportunity for you to challenge yourself and deepen your understanding of Chinese culture.You can contact the Students Union for more detailed information about the contest.Yours,Li Hua【解析】第二部分阅读理解第一节A21.C 推理判断题。
重庆市巴蜀中学2018届高三适应性月考(九)数学(理)试题(精编含解析)

巴蜀中学2018届高考适应性月考卷(九)理科数学第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 若集合,则()A. B. C. D.【答案】C【解析】分析:首先根据一元二次不等式的解法以及绝对值的解法,项确定出集合P,Q中的元素,最后根据集合的交集中元素的特征,求得,即得结果.详解:解不等式,可得,结合,可得,解不等式,可得,所以,所以,故选C.点睛:该题以集合为载体,考查了一元二次不等式的解法以及绝对值不等式的解法,注意交集中元素的特征,最后求得结果.2. 若复数满足,则的共轭复数的虚部为()A. B. C. D.【答案】B【解析】分析:首先利用复数的模以及复数的除法运算,求得复数,之后应用共轭复数的定义,求得,从而确定其虚部的值,求得结果.详解:根据题意,有,所以,故其虚部为,故选B.点睛:该题考查的是有关复数的除法运算以及共轭复数的定义,在求解的过程中,注意对复数的除法运算法则要掌握,最后一定要看清题意,是其共轭复数的虚部,从而正确求得结果.3. 已知等比数列满足,,则该数列的公比为()A. B. C. D.【答案】A【解析】分析:首先根据等比数列的性质,确定出,之后应用等比数列的通项公式求得,因为题中没有关于限定公比的条件的语句,所以应该是两个值,得到结果.详解:根据等比数列的性质可得,所以,即,故选A.点睛:该题考查的是有关等比数列的性质的问题,在求解的过程中,注意对数列的通项公式的应用,得到其公比q所满足的等量关系式,求得结果.4. 阅读如图1所示的程序框图,运行相应的程序,则输出的S 的值为()A. B. C. D.【答案】C【解析】分析:首先分析该程序框图的作用以及要完成的任务,从中可以发现就是求几个数的和,要看清条件,到什么时候结束,最后通分,求得结果.详解:根据题中所给的框图,可知输出的,故选C.点睛:该题考查的是有关程序框图的输出结果的求解问题,在解题的过程中,需要明确其要求,以及对应的量有哪些,算到什么时候就结束了,一定要注意条件,最后求得结果即可.5. 函数的图象向左平移个单位长度后得到函数的图象,则下列选项中的函数的一条对称轴的是()A. B. C. D.【答案】B【解析】分析:首先根据题意,结合左右平移的规律,得到的解析式,再利用正弦型函数的性质求得图像的对称轴方程,之后对各个选项逐一验证,即可得结果.详解:依题意,,令,解得,逐项对比,可以求得满足条件,故选B.点睛:该题考查的是有关三角函数图像的平移变换以及对称性,在解题的过程中,需要明确左右平移对函数解析式中量的变化,以及对应函数图像的对称轴位置的确定以及对称轴方程的求解问题.6. 下列命题中,正确的选项是()A. 若为真命题,则为真命题B. ,使得C. “平面向量与的夹角为钝角”的充分不必要条件是“”D. 在锐角中,必有【答案】D【解析】分析:首先对各个选项的内容进行分析,对于A项,要明确复合命题的真值表,两个命题都是真命题,才会有为真命题,而只要有一个真命题,则就为真命题,在研究指数函数的图像的时候,发现,当时,在y轴右侧,当底数越小的时候,图像越靠近于x轴,对于时,除了夹角为钝角,还有反向共线的时候,所以都是不正确的,利用锐角三角形三个内角的大小,以及正弦函数的单调性还有诱导公式,可以确定D项是正确的,从而求得结果.详解:因为若为真命题的条件是至少有一个是真命题,而为真命题的条件为两个都是真命题,所以当一个真一个假时,为假命题,所以A不正确;当时,都有成立,所以B不正确;“”是“平面向量与的夹角为钝角”的必要不充分条件,所以C不正确;因为在直角三角形中,,有,所以有,即,故选D.点睛:该题考查的内容比较多,每一个知识点都是相互独立的,所以需要对各选项逐一分析,涉及到的知识点有复合命题的,有向量的,有函数的,有三角的,所以需要我们对基础知识比较扎实,才能做好本题.7. 已知圆,若圆刚好被直线平分,则的最小值为()A. B. C. D.【答案】C【解析】分析:首先要明确圆被直线平分的条件,就是直线过圆心,将圆心坐标代入直线的方程,得到关于两个正数的整式形式的和为定值,而目标式是关于两个正数的分式形式和的最值,将两式相乘,利用基本不等式求得结果.详解:根据题意,有圆心在直线上,所以有,所以有,故选C.点睛:该题考查的是有关利用基本不等式求最值的问题,在解题的过程中,涉及到的知识点有圆被直线平分的条件是直线过圆心,之后应用点在直线上的条件,点的坐标满足直线方程,从而求得所满足的关系,之后应用利用基本不等式求最值的方法求解.8. 已知抛物线,直线与抛物线交于两点,若中点的坐标为,则原点到直线的距离为()A. B. C. D.【答案】D【解析】分析:首先根据题意设出直线的方程,之后与抛物线的方程联立,利用韦达定理求得两根和,之后借助于中点坐标公式求得关于k所满足的等量关系式,从而确定出直线的方程,接着应用点到直线的距离公式求得结果.详解:根据抛物线的对称性,可知该直线的斜率是存在的,设直线的方程为,与抛物线方程联立,化简可得,因为是弦的中点,所以有,解得,所以直线方程为,所以原点到直线的距离为,故选D.点睛:该题考查的是有关抛物线的中点弦所在直线的问题,在求解的过程中,注意有关直线与曲线相交的统一解法,再者注意韦达定理的应用以及中点坐标公式的应用,最后求出直线方程之后注意点到直线的距离公式的正确使用.9. 已知,则()A. B. C. D.【答案】B【解析】分析:首先注意与的关系,想到用到倍角公式,求得的值,之后分析与的关系,从而应用诱导公式求得结果.详解:依题意,,故选B.点睛:该题考查的是有关应用倍角公式以及诱导公式求三角函数值的问题,在解题的过程中,需要认真分析角之间的关系,以及已知量与待求量的联系,应用相应的公式求得结果.10. 2018年俄罗斯世界杯将于2018年6月14日至7月15日在俄罗斯境内座城市的座球场内举行,共有支球队参加比赛,其中欧洲有支球队参赛,中北美球队有支球队参赛,亚洲、南美洲、非洲各有支球队参赛,所有参赛球队被平均分入个小组.已知小组的支队伍来自不同的大洲,东道主俄罗斯(俄罗斯属于欧洲球队)和墨西哥(墨西哥属于中北美球队)在小组中,那么南美洲球队巴西队在小组的概率为()A. B. C. D.【答案】A【解析】分析:首先要明确A组球队所满足的条件,来自不同的洲,所以得需要先确定选的哪个洲的球队,之后再确定选定洲之后对应的球队的选法,接着需要明确当南美洲球队巴西队选定之后另一个球队有几种选法,从而得到满足条件的基本事件与总的基本事件数,最后作除法运算求得结果.详解:根据题意有,A组剩余两个球队需要从亚洲、南美洲、和非洲三个洲中选两个洲,有种选法,每个洲选定之后从5个球队中任选1个球队,共有5种选法,所以另两个球队共有种选法,若南美洲球队巴西队在A组,则另一个球队有种选法,所以南美洲球队巴西队在小组的概率为,故选A.点睛:该题考查的是有关古典概型的问题,在求解的时候,需要明确实验所对应的基本事件数,以及满徐条件的基本事件数,在此过程中,需要时刻注意题中所给的组队的要求,之后借助于相关公式求得结果. 11. 已知定义在上的偶函数满足,且当时,,那么函数在区间上的所有零点之和为()A. B. C. D.【答案】D【解析】分析:首先从题的条件得到函数的图像关于直线对称,借助偶函数,得到图像关于y轴对称,从而得到函数是周期函数,借助于两个函数在相应区间上的图像,应用数形结合求得结果. 详解:根据,可得是函数图像的对称轴,又因为是偶函数,所以其图像关于y轴对称,所以其为最小正周期为2的周期函数,又函数也是偶函数,并且其图像也关于直线对称,在同一个坐标系中,画出函数的图像和的图像,可以发现在区间上一共有6个交点,且是关于对称的三对,所以留个零点的和为,故选D.点睛:该题考查的是有关函数的零点的问题,在解决之前,需要明确函数的相关性质,一是函数图像的对称性,二是函数的周期性,三是数形结合思想的应用,之后借助于中点坐标公式求得相应的结果.12. 已知某几何体的三视图如图2所示(小正方形的边长为),则该几何体的外接球的表面积为()A. B. C. D.【答案】A【解析】分析:首先根据题中所给的三视图,还原几何体,得到该几何体是由正方体切割而成的,找到该几何体的顶点有三个是正方体的棱的中点,一个就是正方体的顶点,之后将几何体补体,从而得到该三棱锥的外接球是补成的棱柱的外接球,利用公式求得结果.详解:根据题中所给的三视图,可以将几何体还原,可以得到该几何体是由正方体切割而成的,记正方体是,则记的中点为E,CD中点为F,中点为G,题中所涉及的几何体就是三棱锥,经过分析,将几何体补体,取棱中点H,再取正方体的顶点,从而得到该三棱锥的外接球即为直三棱柱的外接球,利用正弦定理可以求得底面三角形的外接圆的半径为,棱柱的高为4,所以可以求得其外接球的半径,所以其表面积为,故选A.点睛:该题考查的是有关利用三视图还原几何体,求其外接球的体积的问题,在解题的过程中,最关键的一步就是还原几何体,再者就是将其补成一个直三棱柱,之后应用直三棱柱的外接球的球心在上下底面外心的连线的中点处,利用公式求得结果.第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13. 的展开式中的常数项为__________.【答案】.【解析】分析:首先利用二项式定理得到二项展开式的通项,令x的幂指数等于零,求得r的值,即可求得展开式中常数项的值.详解:的展开式的通项为,令,得,所以展开式中的常数项为,故答案是216.点睛:该题考查的是有关二项式定理的问题,涉及到的知识点为求其展开式中的某一项,在求解的过程中,需要先求得展开式中的通项,之后令x的幂指数等于题中所要求的量,从而求得结果.14. 已知实数满足条件则的最小值为__________.【答案】.【解析】分析:首先根据题中所给的约束条件作出相应的可行域,结合表示的是区域内的点到坐标原点的距离的平方,结合图形,根据其几何意义,可以得到其结果为原点到直线的距离的平方,应用点到直线的距离公式求得结果.详解:根据约束条件画出可行域,其为直线的右下方,直线的右上方和直线的右上方,表示的是区域内的点到原点的距离的平方,从图中可以发现,距离最小时为原点到边界线的距离,即,而其平方为,所以的最小值为.点睛:该题考查的是有关线性规划的升级问题,约束条件是线性的,目标函数是非线性的,在解题的过程中,需要先根据约束条件画出相应的可行域,之后结合其几何意义,应用相应的公式求得结果.15. 已知双曲线的左、右焦点分别为,过且斜率为的直线与双曲线的两条渐近线分别交于两点,若,则双曲线的离心率为__________.【答案】.【解析】分析:首先根据题意,设出直线的方程,之后与双曲线的渐近线联立,分别求出A,B两点的坐标,之后根据题中条件,得出A是的中点,根据中点坐标公式,得出其坐标间的关系,借助双曲线中的关系,求得该双曲线的离心率.详解:设直线的方程为,两条渐近线的方程分别为和,分别联立方程组,求得,根据,可以得到A是的中点,所以有,整理得,结合双曲线中的关系,可以的到,所以答案为.点睛:该题考查的是有关双曲线的离心率问题,在解题的过程中,需要做的就是根据题中条件,想办法寻找的关系,利用题中条件,找到坐标间的关系,从而求得结果.16. 如图3,正方形的边长为,顶点分别在轴的非负半轴,轴的非负半轴上移动,为的中点,则的最大值是__________.【答案】.【解析】分析:首先根据题意,以及题中所给的图,设出正方形四个顶点的坐标,之后应用中点坐标公式,求得点E的坐标,接下来应用向量数量积坐标公式,将其转化为关于的三角函数式,从而求得结果.详解:根据题意,设,根据正方形的特点,可以确定出,根据中点坐标公式,可以求得,所以有,所以其最大值为.点睛:该题考查的是有关向量的数量积的最值问题,在求解的时候,关键是将正方形的顶点坐标求出,之后将向量的数量积转化为关于角的三角函数式,借助于倍角公式和辅助角公式,从而求得结果.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. 已知在数列中,.(1)求数列的通项公式;(2)设,求的前项和.【答案】(1).(2) .【解析】分析:第一问首先应用题中所给的数列的递推公式,类比着写出个相邻两项差的式子,之后累加得出结果,注意对首项的验证;第二问利用对数的运算法则求得的通项,之后求和时利用分组求和法以及裂项相消法求和即可得结果.详解:(Ⅰ),,,.时,.(Ⅱ)令的前项和为.的前项和为.点睛:该题考查的是有关数列的问题,一是应用累加法求通项的问题,二是应用对数的运算法则求通项公式的问题,三是对数列求和,采用的方法就是分组求和法以及裂项相消法,在用累加法求和时需要对进行验证.18. 支付宝作为一款移动支付工具,在日常生活中起到了重要的作用.巴蜀中学高2018届学生为了调查支付宝在人群中的使用情况,在街头随机对名市民进行了调查,结果如下.(1)对名市民按年龄以及是否使用支付宝进行分组,得到以下表格,试问能否有的把握认为“使用支付宝与年龄有关”?岁以上岁以下(2)现采用分层抽样的方法,从被调查的岁以下的市民中抽取了位进行进一步调查,然后从这位市民中随机抽取位,求至少抽到位“使用支付宝”的市民的概率;(3)为了鼓励市民使用支付宝,支付宝推出了“奖励金”活动,每使用支付宝支付一次,分别有的概率获得元奖励金,每次支付获得的奖励金情况互不影响.若某位市民在一周使用了次支付宝,记为这一周他获得的奖励金数,求的分布列和数学期望.附:,其中.【答案】(1)不能有99%的把握认为“使用支付宝与年龄有关”.(2)(3)分布列见解析;.【解析】分析:第一问首先应用题中所给的列联表,利用公式求得观测值的值,之后与临界值比较大小,从而得到相应的结论;第二问利用相关知识求得所抽取的12人中,使用和不使用支付宝的人数分别是多少,之后借助于组合数求得相应的概率;第三问根据题意,求得随机变量X的取值以及相对应的概率,列出分布列,利用期望公式求得其期望.详解:(Ⅰ)不能有99%的把握认为“使用支付宝与年龄有关”.(Ⅱ)12位中,使用支付宝的人数为(人),不使用支付宝的人数为(人),.(Ⅲ)的分布列如下:点睛:该题考查的是有关统计、独立检验以及离散型随机变量的分布列的问题,在求解的过程中,需要明确独立检验的步骤,以及观测值的求解公式,再者对随机事件发生的概率求解时,需要对其对应的基本事件数弄清楚,最后在求随机变量的分布列及期望的时候,需要对变量的可取值以及对应的概率要算对.19. 如图4,在四棱锥中,底面,底面为直角梯形,,过作平面分别交线段于点.(1)证明:;(2)若直线与平面所成的线面角的正切值为,则当点在线段的何处时,直线与平面所成角为?【答案】(1)见解析.(2)当在线段靠近的三分点位置时,直线与平面所成的线面角为45°.【解析】分析:第一问利用梯形的条件,结合线面平行的判定以及性质定理,证得线线垂直;第二问建立相应的空间直角坐标系,设出对应点的坐标,将线面角转化为有关向量所成的角,利用向量所成角的余弦公式求得结果.详解:(Ⅰ)证明:底面为直角梯形,,平面,平面,平面,平面,平面平面,.(Ⅱ)解:平面,,为直线与平面所成的线面角,,,.以点为原点,,,为轴建立空间直角坐标系,(2,0,0),(2,1,0),(0,2,0),(0,0,2),设,则,∴.设平面的法向量为,则令,则,,当在线段靠近的三分点位置时,直线与平面所成的线面角为45°.点睛:该题考查的是有关立体几何的问题,在解题的过程中,注意空间关系的转化,有关线线平行、线面平行之间的关系,利用相关的判定和性质定理证得结果,有关空间角的问题,大多应用空间向量来完成,注意相关公式的正确使用.20. 已知椭圆的左右焦点分别为,上顶点为,右顶点为,的外接圆半径为.(1)求圆的标准方程;(2)设直线与椭圆交于两点,若以为直径的圆经过点,求面积的最大值.-【答案】(1).(2) .【解析】分析:第一问首先应用正弦定理求得三角形的外接圆的直径,结合椭圆的性质,以及三角形的特征,求得短半轴;第二问设出直线的方程,与椭圆方程联立,利用韦达定理,结合题中的条件,最后应用导数研究函数的单调性,求得其最值.详解:(Ⅰ)右顶点为,,,椭圆的标准方程为.(Ⅱ)设直线的方程为,与椭圆联立得.以为直径的圆经过点,①,代入①式得或(舍去),故直线过定点.,令,则在上单调递减,时,.点睛:该题考查的是有关直线与椭圆的综合题,在解题的过程中,需要明确焦点三角形的有关特征,以及正弦定理的内容和常数的意义,再者就是有关直线与椭圆相交的问题,需要联立消元,韦达定理紧跟其后,将三角形的面积表示成有关变量的函数关系,结合函数的解题思想,求得结果.21. 已知.(1)当时,若函数在处的切线与函数相切,求实数的值;(2)当时,记.证明:当时,存在,使得.【答案】(1).(2)见解析.【解析】分析:第一问将代入解析式,之后对函数求导,从而可以求得,结合,利用点斜式写出切线的方程,之后再结合直线与抛物线相切的有关特征求得参数b的值;第二问结合题中的条件,转化函数解析式,利用导数研究函数的性质,向最值靠拢即可证得结果.详解:(Ⅰ)解:当时,,,故切线方程为.设切线与相切的切点为,故满足方程组解得,故.(Ⅱ)证明:,令,则在上单调递增,在上单调递减.即恒成立,或,在上单调递减,在上单调递增,.只需证时,即可,令则,恒成立,在上单调递减.,在上单调递增,上单调递减,点睛:该题考查的是应用导数研究函数的问题,在解题的过程中,需要用到导数的几何意义,求函数图像的切线方程,之后应用抛物线与直线相切,寻找关系,求得结果,至于第二问,利用导数研究函数的单调性,向最值靠拢证得结果.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22. 选修4-4:坐标系与参数方程以平面直角坐标系的原点为极点,轴的正半轴为极轴,建立极坐标系,且两种坐标系中采取相同的单位长度.曲线的极坐标方程是,直线的参数方程是(为参数).(1)求曲线的直角坐标方程与直线的普通方程;(2)设点,若直线与曲线交于两点,求的值.【答案】(1);.(2) .【解析】分析:第一问利用极坐标与平面直角坐标之间的关系,将其极坐标方程转化为平面直角坐标方程,将参数方程消参,将其转化为普通方程;第二问将直线的参数方程代入曲线方程中,化简,结合直线参数方程中参数的几何意义结合韦达定理求得结果.详解:(Ⅰ)曲线C的直角坐标方程为,直线的普通方程为.(Ⅱ)将直线的参数方程代入曲线C的直角坐标方程得,得,,异号,.点睛:该题考查的是有关坐标系与参数方程的问题,在解题的过程中,需要明确极坐标方程与平面直角坐标方程的转换关系以及参数方程向普通方程的转化,再者就是需要明确直线的参数方程中参数的几何意义,将直线的参数方程代入曲线的方程中,结合韦达定理求得结果.23. 已知函数(且).(1)当时,解不等式;(2)若的最大值为,且正实数满足,求的最小值.【答案】(1);(2)2【解析】分析:第一问首先利用零点分段法,将绝对值符号去掉,将其转化为三个不等式组,将不等式组的解集取并集,求得结果;第二问利用三角不等式求得其最小值,可以转化为,得到之后将式子变形,利用基本不等式求得结果.详解:(Ⅰ)①当时,;②当时,;③当时,综上所述,不等式的解集为.(Ⅱ)由三角不等式可得的最小值为2,当且仅当时取等号.点睛:该题考查的是有关不等式的问题,在求解的过程中,需要明确绝对值不等式的解法,再者就是利用三角不等式求得其最值,之后借助于基本不等式求得其最值,在解题的过程中,一定要注意相关的条件.。
【英语】重庆市巴蜀中学2018届高三适应性月考(九)英语试题

巴蜀中学2018届高考适应性月考卷(九)英语参考答案第一部分听力(共两节,满分30分)1~5 CBBCA 6~10 CBCCC 11~15 BAABA 16~20 ACAAB第二部分阅读理解(共两节,满分40分)第一节(共15小题;每小题2分,满分30分)21~25 CAADA 26~30 BDBCC 31~35 AADCB第二节(共5小题;每小题2分,满分10分)36~40 FABED第三部分语言知识运用(共两节,满分45分)第一节(共20小题;每小题1.5分,满分30分)41~45 BDACB 46~50 ACDCB 51~55 ADDAB 56~60 ACDBC第二节(共10小题;每小题1.5分,满分15分)61.but 62.intentionally 63.reasons 64.who 65.itself 66.was considered 67.the 68.inspiring 69.have combined 70.dating第四部分写作(共两节,满分35分)第一节短文改错(共10小题;每小题1分,满分10分)With the summer vacation came round again,I am happy that I could forget about school at①comingleast for a while.In case of I would fool around all through this summer vacation,I have made a plan②as to how to spent it.First,I think I should go over all the things which my teachers taught me in the③spend ④thatprevious term.So,I could have∧better understanding of it.Then I think I should take up some⑤a ⑥themexercises,such as walking,running and rowing,to keep me physical strong.Undoubtedly,with so⑦exercise ⑧physically⑨sucha good plan I will make the best of my vacation time.And I am sure I will live up to that I have planned.⑩what第二节书面表达(满分25分)【参考范文】Dear fellow students,I’m Li Hua,president of the Students Union.To help you have a better understanding of China,a contest on Chinese traditional culture is going to be held in the lecture hall this Sunday evening.As scheduled,in the first section,you are to answer questions about Chinese culture quickly to get more points.And then a speech delivered in Chinese is required,in which both pronunciation and accuracy will be evaluated.For the last part,you can choose an art form to show your talent for Chinese learning and knowledge of the culture.Winners of the contest will be awarded an e-dictionary that can help with your Chinese learning.More importantly,I think this is a great opportunity for you to challenge yourself and deepen your understanding of Chinese culture.You can contact the Students Union for more detailed information about the contest.Yours,Li Hua【解析】第二部分阅读理解第一节A21.C 推理判断题。
重庆市巴蜀中学2018届高考理综9月适应月考试题(扫描版)

重庆市巴蜀中学2018届高考理综9月适应月考试题(扫描版)
尊敬的读者:
本文由我和我的同事在百忙中收集整编出来,本文档在发布之前我们对内容进行仔细校对,但是难免会有不尽如人意之处,如有疏漏之处请指正,希望本文能为您解开疑惑,引发思考。
文中部分文字受到网友的关怀和支持,在此表示感谢!在往后的日子希望与大家共同进步,成长。
This article is collected and compiled by my colleagues and I in our busy schedule. We proofread the content carefully before the release of this article, but it is inevitable that there will be some unsatisfactory points. If there are omissions, please correct them. I hope this article can solve your doubts and arouse your thinking. Part of the text by the user's care and support, thank you here! I hope to make progress and grow with you in the future.。
重庆市巴蜀中学高考适应性月考(九)语文试

2022届重庆市巴蜀中学高考适应性月考(九)语文试题注意事项:1.答题前,考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写清楚。
2.每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
在试题卷上作答无效。
3.考试结束后,请将本试卷和答题卡一并交回。
满分150分,考试用时150分钟。
一、现代文阅读(35分)(一)现代文阅读Ⅰ(本题共5小题,19分)阅读下面的文字,完成1~5题。
从立春到大寒,中国古人通过观察太阳周年运动,参照天象、气象和物象等自然现象,总结一年中时令、气候等方面的变化规律,形成了二十四节气的时间知识体系。
二十四节气是古人对自然时间与农耕生产关系的精准把握,体现了中华民族传统农耕社会的生活经验和文化记忆,蕴含着中国人传统的生存智慧与生命哲学。
作为中华优秀传统文化的一部分,二十四节气如何融入当代生活?花知时而开,人顺势而为,与天地唱和,与万物相谐——二十四节气体现出的“天人合一”理念,如何助益当代人的生活?多年来,有关部门从多层面、多维度深入实施二十四节气相关文化遗产的保护传承工作,促进各地活态传承节气文化。
尤其近年来伴随中华优秀传统文化升温,人们文化自觉意识日渐增强,二十四节气以多种面貌和形态在当代生活中展现出蓬勃生机。
结合节庆民俗,实现价值聚力。
二十四节气不仅自身内涵丰富,而且与春节、端午、中秋等传统节庆、传统民俗之间存在密切关系。
传承发展二十四节气文化,应结合重要节庆与各地民俗,拓展文化内涵,强化情感纽带。
每到立秋,湖南省花垣县都会迎来盛大的赶秋节。
庄稼成熟,丰收在即,人们吹笙、歌唱、舞蹈,庆丰年、祈幸福。
而今,花垣赶秋活动丰富多彩,周边群众也纷纷聚集在“秋场”,观赏和参与舞龙舞狮、八人秋千、上刀梯、武术等活动。
花垣赶秋还与中国农民丰收节、全域旅游等相结合,吸引众多游客参与其间。
在礼敬“秋”的节气文化基础上,焕发更多文化活力,创造更多经济价值。
重庆市巴蜀中学2018届高三适应性月考(九)理综生物试题扫描版附详细答案
矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
【数学】重庆市巴蜀中学2018届高三适应性月考(九)试题(理)(扫描版)
重庆市巴蜀中学2018届高三适应性月考(九)数学试题(理)【参考答案】12.【解析】几何体还原为如图1所示的三棱锥A BCD -,把此几何体补全为如图2所示的三棱柱,所以三棱锥的外接球即为三棱柱111ABC A B C -的外接球,在ABC △中,202084cos 2205A +-==⨯, 3sin 5A =,∴2sin BC r A ==∴A .二、填空题16π04ϕ⎛⎫∈- ⎪⎝⎭,,故当π22θϕ+=时,OE OD 的最大值为5+三、解答题17.解:(Ⅰ)112n n n a a --=+∵,2122n n n a a ---=+,,212a a =+,12112(12)222321(2)12n n n n a a n ---=++++=+=+-≥∴.1n =∵时,11321a ==+, 21n n a =+∴.(Ⅱ)1212log (1)log (211)1n n n b a n ++=-=+-=+,令122112(1)(2)12n n n c b b n n n n +⎛⎫===- ⎪+⨯+++⎝⎭,n b ∴的前n 项和为2(21)322n n n n++⨯+=.n c 的前n 项和为1111111122233412222n n n n n ⎛⎫⎛⎫-+-++-=-= ⎪ ⎪++++⎝⎭⎝⎭,2322n n n nT n +=++∴.18.解:(Ⅰ)2250(2510105)4006.349 6.6353515203063K ⨯⨯-⨯==≈<⨯⨯⨯,∴不能有99%的把握认为“使用支付宝与年龄有关”.(Ⅱ)12位中,使用支付宝的人数为251210255⨯=+(人),不使用支付宝的人数为5122255⨯=+(人),2131210210102331212C C +C C C 211=C C 22P ==-∴.(Ⅲ)1119(0.2)22436P X ==⨯==,11112(0.3)223336P X ==⨯⨯==,2111510(0.4)22631836P X ⎛⎫==⨯⨯+== ⎪⎝⎭,19.(Ⅰ)证明:底面平面平面以点为原点,,0,0),(2,1,0),(0,2,0),(0,0,2),0220y x y z =⎧⎨--+=⎩,,令1x =(101)n =,,∴,1sin |cos |32(22)DE n θλλ=〈〉==⇒=-,,∴∴当E 在线段PC 靠近C 的三分点位置时,直线DE 与平面PBC 所成的线面角为45°.20. 解:(Ⅰ)∵右顶点为(20),,∴2a =,122MF MF ==,∵121sin 2MO b b MF F MF a ∠===,2122424sin 2MF R b MF F b ====∠,∴1b =,∴椭圆的标准方程为2214x y +=.(Ⅱ)设直线l 的方程为my x b =+,1122()()A x y B x y ,,,,与椭圆联立得222(4)240m y mby b +-+-=, ∴21212222444mb b y y y y m m -+==++,. ∵以AB 为直径的圆经过点N ,∴0NA NB =, ∵1122(2)(2)NA x y NB x y =-=-,,,, ∴1212122()40x x x x y y -+++=,①∵121228()24b x x m y y b m -+=+-=+,2222121212244()4b m x x m y y mb y y b m -=-++=+,代入①式得2516120b b ++=,∴65b =-或2b =-(舍去),故直线l 过定点605⎛⎫⎪⎝⎭,.∴121622||255ABN S y y ⎛⎫=⨯-⨯-= ⎪⎝⎭△,令222564()[0)(4)t h t t m t +==∈+∞+,,,则228()0251281120425h t t t t ⎛⎫'>⇒++<⇒∈-- ⎪⎝⎭,,∴()h t 在[0)t ∈+∞,上单调递减,max ()(0)4h t h ==, ∴0m =时,max 1625ABN S =△.21.(Ⅰ)解:当3a =时,()(3)e x f x x =-,()e (3)e (2)e x x xf x x x '=+-=-,∴(0)3(0)2f f =-'=-,,故切线方程为23y x =--.设切线与()g x 相切的切点为00(23)x x --,, 故满足方程组0020000()21()232g x x b g x x bx x '=-=-⎧⎪⎨=-=--⎪⎩,,解得0x =2b =. (Ⅱ)证明:()()e xf x x a =-,21()(1)2g x x a x =--,∴21()()e (1)2x h x x a ax a a x =--+-,()e ()e (1)(e )[(1)]x x x h x x a ax a a a x a '=+--+-=---,令()ln 1m a a a =-+,则1()101m a a a '=->⇒<,∴()m a 在(01)a ∈,上单调递增,在(1)a ∈+∞,上单调递减. ∵max ()(1)0m a m ==,∴ln 10a a -+≤,即ln 1a a -≤恒成立, ∴()01h x x a '>⇒>-或ln x a <,∴()h x 在(ln 1)x a a ∈-,上单调递减,在(1)x a ∈-+∞,上单调递增,∴12min 1()(1)e (1)2a h x h a a a -=-=-+-. 只需证104a ⎛⎫∈ ⎪⎝⎭,时,min ()0h x <即可, 令121()e (1)2a a a a ϕ-=-+-,则121()e (341)2a a a a ϕ-'=-+-+,1()e 320a a a ϕ-"=-+-<恒成立, ∴()a ϕ'在104a ⎛⎫∈ ⎪⎝⎭,上单调递减. ∵11(0)02e ϕ'=->,3413e 0432ϕ-⎛⎫'=-< ⎪⎝⎭,∴0010()04a a ϕ⎛⎫∃∈'= ⎪⎝⎭,,使得,∴()a ϕ在0(0)a a ∈,上单调递增,014a a ⎛⎫∈ ⎪⎝⎭,上单调递减,∴1232max 00000011()()e (1)(551)0.22a a a a a a a a ϕϕ-==-+-=-+-<,故证毕22. 解:(Ⅰ)曲线C 的直角坐标方程为22(2)(2)8x y -+-=, 直线l的普通方程为1y -.(Ⅱ)将直线l 的参数方程代入曲线C的直角坐标方程得221221282t ⎛⎫⎛⎫+-++-= ⎪ ⎪ ⎪⎝⎭⎝⎭,得270t -=,121270t t t t +=-<∴,12t t ,∴异号,12121212111111||||||||t t PA PB t t t t t t +-=-=+==.23.解:(Ⅰ)①当12x ≤时,1()122f x x x =-⇒-≥≤;②当112x <<时,16()43127f x x x x =-⇒<≥≤;③当1x ≥时,1()1122f x x x =⇒≥≤,≤综上所述,不等式的解集为6(2]27x ⎡⎤∈-∞-⎢⎥⎣⎦,,.(Ⅱ)由三角不等式可得||21||2|||(21)(2)||1|1x x a x x a a a ------=-=-≤,∴12(1)1a Ma ab c+=-=--=⇒121b c +=⇒2cb c =-,∴2121122122212c c b c c c c +=+=-+------≥,2112b c +--∴的最小值为2,当且仅当1232c c c -==-⇒时取等号.。
重庆市巴蜀中学高三适应性月考(九)理科综合答案
a1t v0 a2t
⑤
理科综合参考答案·第 3 页(共 10 页)
(1)大于
(2)
1 2
mv 2A
1 2
(FO
+FA
)xA
(3
分)
(3) W
Ek
(或
1 2
(
FO
+FA
)
xA
1 2
mv
2 A
)
24.(12 分)
解:(1)设小物块和小车的加速度分别为 a1 和 a2
µmg ma1
①
得 a1 2.5m/s2
②
F mg Ma2
③
得 a2 1m/s2
④
(2)设经过 t 时间两者达到相同速度
理科综合参考答案·第 2 页(共 10 页)
21. t
0 时,
1
2
BS1
B0S2
2 0.8 0.3 1
π (0.2)2 2
0.42Wb ,故
A
错误。由楞
次定律可知
B
正确。bc
边所受安培力 F安
B0I
2r,I
E R
,E
t
B t
S1 ,代入数据
可得 E 1.2V,I 0.4A ,则 F安 0.16N ,故 C 错误。线框开始滑动时,有 f F安ad F安bc ,
5.环境能影响性状;基因和性状并非都是一一对应的,如身高;密码子的简并性说明基因改
变蛋白质不一定改变、同工酶说明蛋白质改变性状不变等。
6.Ⅰ、Ⅱ、Ⅲ、Ⅳ分别代表不同的营养级,每个营养级中有多种生物,连接起来不止 1 条食
物链;分解者不占营养级。
理科综合参考答案·第 1 页(共 10 页)
