二次函数动点问题
二次函数动点问题的解题技巧

二次函数动点问题的解题技巧
以下是 8 条关于二次函数动点问题的解题技巧:
1. 大胆设未知数呀!比如在一个直角坐标系里,有个二次函数图像上有个动点 P,那咱就大大方方设它的坐标为(x,y),这样不就能更好地分析啦!就像给这个动点取了个名字,好指挥它呀!
2. 把条件都用上呀!可别漏了,像找到某个线段长度与动点坐标的关系,哎呀呀,这可是关键呢!比如已知一个线段的长度是 5,和动点 P 的横坐标有关,那可不能放过这个线索,得好好挖掘挖掘!
3. 找等量关系呀!这就好比寻宝,到处去找那些能关联起来的等量哦。
比如说一个三角形面积和另一个图形面积相等,这不就找到宝贝线索啦!
4. 注意特殊位置呀!嘿,动点有时候会跑到一些特殊的点呢,那可有意思啦。
比如它跑到对称轴上时,那说不定会有惊喜发现呢!像突然发现一些对称关系,多神奇呀!
5. 画画图呀!通过图形能更直观地看到动点的运动呀,这就像给你一双眼睛看着它怎么跑。
看看它跑到不同地方时整个图形发生的变化,多好玩呀!
6. 多试试分类讨论呀!有时候动点的情况不唯一呢,那咱就别怕麻烦,一种一种来。
难道还能被它难住不成?像动点在不同区间时可能有不同的结果,咱就一个个算清楚嘛!
7. 利用函数解析式呀!这可是个好宝贝,通过它能知道很多信息呢。
比如知道了二次函数的解析式,那动点在上面的一些性质不就清楚啦?
8. 要敢想敢做呀!别犹豫,大胆去尝试各种方法。
不试试看怎么知道行不行呢?就像冒险一样,多刺激呀!
总之,面对二次函数动点问题,别怕!勇敢地去探索,一定能找到答案的!。
二次函数动点问题

5.如图,等腰直角三角形ABC以2m/s的速度沿直线L向 正方形移动,直到AB与CD重合。设xs时,三角形与正 方形重叠部分的面积为ym² 。 (1)写出y与x的函数关系式; (2)当x=2,3.5时,y分别是多少?
(3)当重叠部分的面积是正方形的面积的一半时, 三角形移动了多长时间?
动面问题
6.如图(1)等腰直角三角形ABC以2m/s的速度沿矩形 DEFG的GF边向右移动,直到BC与GF重合。已知 BC=GF=12m,EF=6m,设xs时,三角形与矩形重叠部分的 面积为ym² (1)参考图②,图③写出y与x之间的关系式; (2)当x1=2.5,x2=5时,y分别是多少? 7 (3)当重叠部分的面积为矩形面积的 时,三角形 18 移动了多长时间?
图(1)
图(2)
图(3)
P
B
Q
C
3.在梯形ABCD,AD∥BC,AB=BC=10cm,CD=6cm ∠c=90°,点P从A点出发沿线段AB以每秒Icm/s的速 度向终B点运动;动点Q同时从B点出发沿线段BC以每 秒2cm/s的速度向终点C运动.设运动的时间为t秒 (0<t<5). (1)求AD的长. (2)t为何值时,△PBQ为直角三角形. (3)设△PBQ的面积为y,求y与t之间的函数关系式 (4)是否存在某一时刻t,使△PБайду номын сангаасQ面积等于梯形形 ABCD面积的2/5?若存在, 求出此时的t值;若不存在, 说明理由;
A
P BP=12-2t,BQ=4t △PBQ的面积: S=1/2(12-2t) •4t B 即S=- 4t² +24t=- 4(t-3)² +36
Q
C
2.已知:如图,△ABC是边长3cm的等边三角形, 动点P、Q同时从A、B两点出发,分别沿AB、 BC方向匀速移动,它们的速度都是1cm/s,当点 P到达点B时,P、Q两点停止运动.设点P的运动 时间为t(s), (1)当t为何值时,△PBQ是直角三角形? (2)设四边形APQC的面积为y(cm2),求y与t 的关系式; (3)是否存在某一时刻t,使四边形APQC的面积 是△ABC面积的三分之二?若存在求出t的值,若 不存在说明理由 A
中考数学二次函数动点问题-因动点产生的平行四边形问题
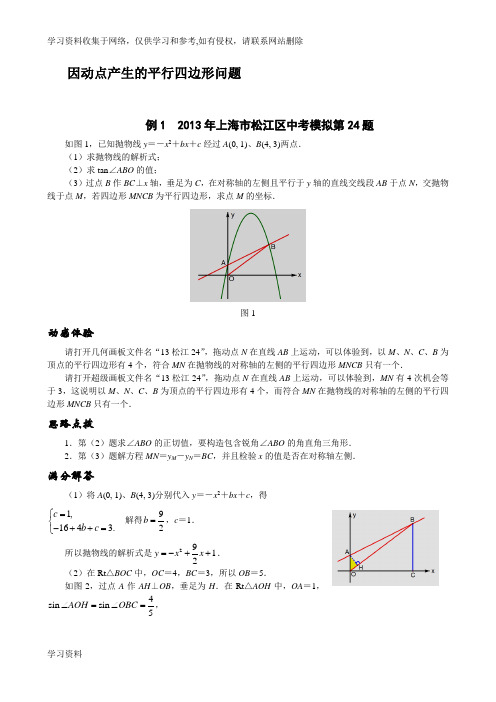
因动点产生的平行四边形问题例1 2013年上海市松江区中考模拟第24题如图1,已知抛物线y =-x 2+bx +c 经过A (0, 1)、B (4, 3)两点. (1)求抛物线的解析式; (2)求tan ∠ABO 的值;(3)过点B 作BC ⊥x 轴,垂足为C ,在对称轴的左侧且平行于y 轴的直线交线段AB 于点N ,交抛物线于点M ,若四边形MNCB 为平行四边形,求点M 的坐标.图1动感体验请打开几何画板文件名“13松江24”,拖动点N 在直线AB 上运动,可以体验到,以M 、N 、C 、B 为顶点的平行四边形有4个,符合MN 在抛物线的对称轴的左侧的平行四边形MNCB 只有一个.请打开超级画板文件名“13松江24”,拖动点N 在直线AB 上运动,可以体验到,MN 有4次机会等于3,这说明以M 、N 、C 、B 为顶点的平行四边形有4个,而符合MN 在抛物线的对称轴的左侧的平行四边形MNCB 只有一个.思路点拨1.第(2)题求∠ABO 的正切值,要构造包含锐角∠ABO 的角直角三角形. 2.第(3)题解方程MN =y M -y N =BC ,并且检验x 的值是否在对称轴左侧.满分解答(1)将A (0, 1)、B (4, 3)分别代入y =-x 2+bx +c ,得1,164 3.c b c =⎧⎨-++=⎩ 解得92b =,c =1. 所以抛物线的解析式是2912y x x =-++. (2)在Rt △BOC 中,OC =4,BC =3,所以OB =5.如图2,过点A 作AH ⊥OB ,垂足为H .在Rt △AOH 中,OA =1,4sin sin 5AOH OBC ∠=∠=,所以4sin 5AH OA AOH =⋅∠=. 图2 所以35OH =,225BH OB OH =-=.在Rt △ABH 中,4222tan 5511AH ABO BH ∠==÷=.(3)直线AB 的解析式为112y x =+.设点M 的坐标为29(,1)2x x x -++,点N 的坐标为1(,1)2x x +,那么2291(1)(1)422MN x x x x x =-++-+=-+.当四边形MNCB 是平行四边形时,MN =BC =3.解方程-x 2+4x =3,得x =1或x =3.因为x =3在对称轴的右侧(如图4),所以符合题意的点M 的坐标为9(1,)2(如图3).图3 图4考点伸展第(3)题如果改为:点M 是抛物线上的一个点,直线MN 平行于y 轴交直线AB 于N ,如果M 、N 、B 、C 为顶点的四边形是平行四边形,求点M 的坐标.那么求点M 的坐标要考虑两种情况:MN =y M -y N 或MN =y N -y M .由y N -y M =4x -x 2,解方程x 2-4x =3,得27x =±(如图5).所以符合题意的点M 有4个:9(1,)2,11(3,)2,57(27,)2--,57(27,)2++.图5例2 2012年福州市中考第21题如图1,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD//BC,交AB于点D,联结PQ.点P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动的时间为t秒(t≥0).(1)直接用含t的代数式分别表示:QB=_______,PD=_______;(2)是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由,并探究如何改变点Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q的速度;(3)如图2,在整个运动过程中,求出线段PQ的中点M所经过的路径长.图1 图2动感体验请打开几何画板文件名“12福州21”,拖动左图中的点P运动,可以体验到,PQ的中点M的运动路径是一条线段.拖动右图中的点Q运动,可以体验到,当PQ//AB时,四边形PDBQ为菱形.请打开超级画板文件名“12福州21”,拖动点Q向上运动,可以体验到,PQ的中点M的运动路径是一条线段.点击动画按钮的左部,Q的速度变成1.07,可以体验到,当PQ//AB时,四边形PDBQ为菱形.点击动画按钮的中部,Q的速度变成1.思路点拨1.菱形PDBQ必须符合两个条件,点P在∠ABC的平分线上,PQ//AB.先求出点P运动的时间t,再根据PQ//AB,对应线段成比例求CQ的长,从而求出点Q的速度.2.探究点M的路径,可以先取两个极端值画线段,再验证这条线段是不是点M的路径.满分解答(1)QB=8-2t,PD=43t.(2)如图3,作∠ABC的平分线交CA于P ,过点P作PQ//AB交BC于Q,那么四边形PDBQ是菱形.过点P作PE⊥AB,垂足为E,那么BE=BC=8.在Rt△ABC中,AC=6,BC=8,所以AB=10.图3在Rt△APE中,23cos5AEAAP t===,所以103t=.当PQ//AB时,CQ CPCB CA=,即106386CQ-=.解得329CQ=.所以点Q的运动速度为3210169315÷=.(3)以C为原点建立直角坐标系.如图4,当t=0时,PQ的中点就是AC的中点E(3,0).如图5,当t=4时,PQ的中点就是PB的中点F(1,4).直线EF的解析式是y=-2x+6.如图6,PQ的中点M的坐标可以表示为(62t-,t).经验证,点M(62t-,t)在直线EF上.所以PQ的中点M的运动路径长就是线段EF的长,EF=25.图4 图5 图6考点伸展第(3)题求点M的运动路径还有一种通用的方法是设二次函数:当t=2时,PQ的中点为(2,2).设点M的运动路径的解析式为y=ax2+bx+c,代入E(3,0)、F(1,4)和(2,2),得930,4,42 2.a b ca b ca b c++=⎧⎪++=⎨⎪++=⎩解得a=0,b=-2,c=6.所以点M的运动路径的解析式为y=-2x+6.例3 2012年烟台市中考第26题如图1,在平面直角坐标系中,已知矩形ABCD的三个顶点B(1, 0)、C(3, 0)、D(3, 4).以A为顶点的抛物线y=ax2+bx+c过点C.动点P从点A出发,沿线段AB向点B运动,同时动点Q从点C出发,沿线段CD向点D运动.点P、Q的运动速度均为每秒1个单位,运动时间为t秒.过点P作PE⊥AB交AC 于点E.(1)直接写出点A的坐标,并求出抛物线的解析式;(2)过点E作EF⊥AD于F,交抛物线于点G,当t为何值时,△ACG的面积最大?最大值为多少?(3)在动点P、Q运动的过程中,当t为何值时,在矩形ABCD内(包括边界)存在点H,使以C、Q、E、H为顶点的四边形为菱形?请直接写出t的值.图1动感体验请打开几何画板文件名“12烟台26”,拖动点P在AB上运动,可以体验到,当P在AB的中点时,△ACG的面积最大.观察右图,我们构造了和△CEQ中心对称的△FQE和△ECH′,可以体验到,线段EQ 的垂直平分线可以经过点C和F,线段CE的垂直平分线可以经过点Q和H′,因此以C、Q、E、H为顶点的菱形有2个.请打开超级画板文件名“12烟台26”,拖动点P在AB上运动,可以体验到,当P在AB 的中点时,即t=2,△ACG的面积取得最大值1.观察CQ,EQ,EC的值,发现以C、Q、E、H为顶点的菱形有2个.点击动画按钮的左部和中部,可得菱形的两种准确位置。
二次函数动点问题解题技巧

二次函数动点问题解题技巧
《二次函数动点问题解题技巧》
一、概述
在数学中,二次函数动点问题是用来求解一个二次函数满足某点移动的情况。
这是一个经典的问题,一般涉及到二次函数的开根号法等技巧,因此在解决动点问题上要有所准备。
本文将介绍二次函数动点问题的解题技巧,指导考生正确解答此类问题。
二、解题技巧
1、把问题转化为动点方程。
首先,我们要把问题转化为一个动点方程:y=ax^2+bx+c。
其中a,b,c代表着不同的变量,它们分别代表着二次函数的三个系数。
2、求解动点方程。
接下来,我们要求解动点方程,首先需要解出各个变量的值,即a,b,c的值。
可以使用开根号法来求解,具体的步骤如下:
①把动点方程化为一元二次方程
②使用开方法求出a、b、c的值
3、求解动点问题。
最后,我们要求解动点问题,就是找到动点移动后的位置。
这时可以使用同样的方法,即把二次函数带入动点方程,使用开根号法求出动点移动后的位置。
三、总结
本文介绍了二次函数动点问题的解题技巧,涉及到动点方程的求解和动点移动后位置的求解。
由此可见,要正确解答二次函数动点问
题,必须具备良好的开根号法的技巧,并熟练掌握求解动点方程和动点问题的解题技巧。
二次函数动点问题的解题思路

2023年12月下半月㊀解法探究㊀㊀㊀㊀二次函数动点问题的解题思路◉江苏省连云港市海头初级中学㊀王小路㊀㊀摘要:二次函数动点问题难度较大,常作为测试中的压轴题,分值较高.部分学生常因不得法㊁无明确的解题思路,失分较为严重.授课中应结合学情以及经验,做好二次函数动点问题教学设计,展示习题情境以及解题思路,给类似问题的解答提供针对性解题指引.关键词:二次函数;动点问题;解题思路㊀㊀二次函数动点问题对学生的想象能力要求较高[1].解决该类习题需从题干以及图形出发寻找突破口,尤其应注重 化动为静 ,全面考虑各种满足题设条件的情境.1求解参数范围图1例1㊀(2021年 河南 统考中考真题)如图1,抛物线y =x 2+m x 和直线y =-x +b 交于点A (2,0)和点B .(1)求m 和b 的值;(2)求点B 的坐标,并结合图象写出不等式x 2+m x >-x +b 的解集;(3)M 为直线A B 上的一个动点,将点M 向左平移3个单位长度得到点N .当线段MN 和抛物线只有一个公共点时,直接写出点M 的横坐标x M 的取值范围.思路剖析:问题(1)将点A 坐标分别代入到抛物线和直线解析式中,构建两个方程求出m 和b 的值;问题(2)将抛物线和直线解析式联立求出点B 的坐标,运用数形结合法求出不等式的解集;问题(3)先确定线段MN 的长度和方向,以点M 为研究对象,从点A 右侧开始逐渐沿着直线A B 运动,分析不同情况下MN 和抛物线的交点,得出结论.解:(1)将点A (2,0)分别代入到抛物线和直线解析中,得4+2m =0,-2+b =0,{解得m =-2,b =2.{(2)由(1)得抛物线为y =x 2-2x ,其顶点坐标为(1,-1);直线为y =-x +2.联立y =x 2-2x ,y =-x +2,{解得x =-1,y =3,{或x =2,y =0,{所以点B 的坐标为(-1,3).不等式x 2+m x >-x +b 表示抛物线y =x 2-2x 在直线y =-x +2的上方,对应的解集为x <-1或x >2.(3)由题意可得,A ,B 两点的水平距离为3.根据题意,直线MN 为一条与x 轴平行的直线,且线段MN 的长为3.由于M 为动点,坐标未知,因此,需要分类讨论.①当点M 在点A 的右侧,线段M N 和抛物线只有一个公共点时,线段M N 经过抛物线的顶点(1,-1).令-x +2=-1,解得x =3,此时x M =3.②当点M 在线段A B 上时,要想满足题意,则应满足-1ɤx M <2.③当点M 在点B 的左侧,则线段MN 和抛物线不会有交点.综上分析,满足题意的x M 的取值范围为-1ɤx M <2或x M =3.点评:例1情境较为复杂,吃透题设情境,准确判断线段MN 的走向,以点A 和点B 为分类讨论的界限是解题的关键.2求解点的坐标图2例2㊀如图2,已知抛物线y =-14x 2+32x +4和坐标轴分别交于A ,B ,C 三点,其中点M 在直线B C 下方的抛物线上运动,则当øA B C =øM C B 时,点M 的坐标为.思路剖析:由øA B C 为锐角,知点M 只能在直线B C 下方右侧抛物线上.先假设出点M ,作出辅助线,运用øA B C =øM C B 得出线段C N 和N B 的相等关系,再设出O N 的长,借助勾股定理求出点N 的坐标.最后,在此基础上求出直线C N 的解析式,与抛物线解析式联立解出点M 的坐标.解:对于抛物线y =-14x 2+32x +4,令x =0,得y =4,所以点C (0,4);令y =0,解得x 1=-2,x 2=38解法探究2023年12月下半月㊀㊀㊀8,则A (-2,0),B (8,0).因此O A =2,O C =4,O B =8.在直角三角形C O B 中,由勾股定理可得B C =42+82=45.图3设点M 的位置如图3所示,连接C M 和x 轴交于点N .由øA B C =øM C B ,则C N =N B .令O N =x ,则C N =N B =8-x .在直角三角形C O N 中,由勾股定理可得x 2+42=(8-x )2,解得x =3,则点N (3,0).设直线C N 的解析式为y =k x +4,将N (3,0)代入得k =-43,则C N 的解析式为y =-43x +4.将其和抛物线y =-14x 2+32x +4联立,解得x 1=0(舍去),x 2=343.将x =343代入y =-43x +4,得y =-1009.综上,点M 的坐标为(343,-1009).点评:根据题意假设出点M 的位置,将给出的角度关系转化为线段间的相等关系,灵活运用勾股定理求出点N 的坐标,求出直线表达式后与抛物线解析式联立求得最终结果.3求解最值问题图4例3㊀(2022年 广东 统考中考真题)如图4,抛物线y =x 2+b x +c (b ,c 是常数)的顶点为C ,与x 轴交于A ,B 两点,A (1,0),AB =4,P 为线段A B 上的动点,过点P 作P Q ʊBC 交A C 于点Q .(1)求该抛物线的解析式;(2)求әC P Q 面积的最大值,并求此时点P 的坐标.思路剖析:问题(1)根据已知条件求出点B 的坐标,运用待定系数法即可求出结果.问题(2)首先求出抛物线顶点C 的坐标,使用待定系数法分别求出直线B C 和A C 的解析式,然后根据P Q 和B C 的平行关系,设出直线P Q 解析式,求出点P 的坐标,最后结合图形通过图形面积关系表示出әC P Q 的面积,运用二次函数性质,求出最值.解:(1)由A (1,0),A B =4,得到B (-3,0).由抛物线过A ,B 两点,将两点坐标代入抛物线解析式得1+b +c =0,9-3b +c =0,{解得b =2,c =-3,{则抛物线的解析式为y =x 2+2x -3.(2)由(1)可得y =x 2+2x -3=(x +1)2-4,则点C (-1,-4).根据A ,B ,C 三点的坐标,容易求得直线B C 的解析式为y =-2x -6,直线A C 的解析式为y =2x -2.由P Q ʊB C ,设直线P Q 的解析式为y =-2x +m ,令y =0,解得x =m 2,则点P 的坐标为(m2,0).联立y =-2x +m ,y =2x -2,{解得x =m +24,y =m -22,ìîíïïïï所以点的坐标为Q(m +24,m -22).又点P 是线段A B 上的动点,则-3<m2<1,解得-6<m <2.由图4可知S әC P Q =S әA P C -S әA P Q ,而S әA P C =12|y C ||A P |,S әA P Q =12|y Q ||A P |,则S әC P Q =12ˑ4ˑ(1-m2)-12ˑ(1-m2)ˑ(-m -22)=-18(m +2)2+2.由二次函数性质可得,当m =-2时,S әC P Q 取得最大值2,此时点P 的坐标为(-1,0).点评:该题综合性较强,求解时需认真观察图形,既要注重数形结合,又要会运用已知条件进行灵活转化,适当设出参数,搭建已知与未知参数之间的桥梁,化陌生为熟悉[2].4总结上述三道例题情境较为典型,解题思路具有较强的代表性.从解题过程不难看出,二次函数动点问题的思路灵活多变,需在深刻理解题意的基础上,敢于大胆假设,借助所学知识 化动为静 ,运用题设条件抽丝剥茧,严谨推理,认真计算,得出结果[3].参考文献:[1]王微.初中数学二次函数动点问题教学模式分析[J ].数理天地(初中版),2023(9):46G48.[2]单小燕.二次函数动点问题的解法及教学策略探究[J ].数学之友,2022,36(22):4G6.[3]冯玲玉.初中数学动点问题的教学策略研究 以二次函数为例[J ].数理天地(初中版),2022(16):36G38.Z48。
【中考数学压轴题专题突破02】二次函数中的动点问题
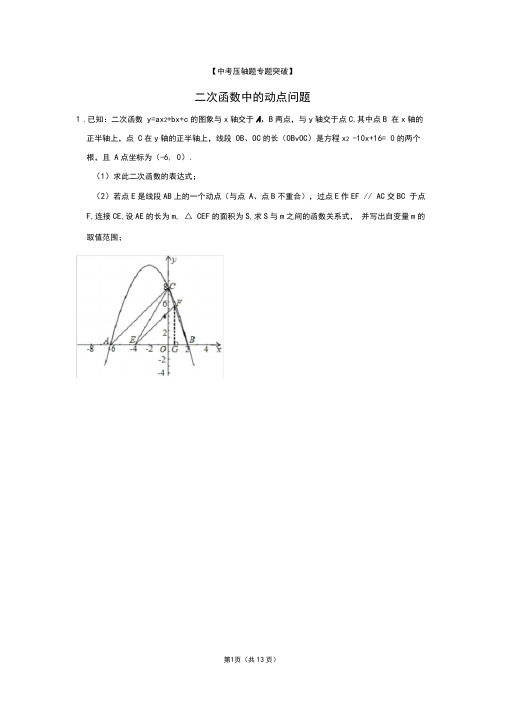
【中考压轴题专题突破】二次函数中的动点问题1.已知:二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,其中点B 在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OBvOC)是方程x2 -10x+16= 0的两个根,且A点坐标为(-6, 0).(1)求此二次函数的表达式;(2)若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF // AC交BC 于点F,连接CE,设AE的长为m, △ CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;2.如图是二次函数y= ( x+m) 2+k的图象,其顶点坐标为M (1, -4).(1)求出图象与x轴的交点A, B的坐标;(2)在二次函数的图象上是否存在点P,使S APAB=—S;AMAB?若存在,求出P点的坐标,4若不存在,请说明理由;(3)点C在x轴上一动点,以BC为边作正方形BCDE ,正方形BCDE还有一个顶点(除点B外)在抛物线上,请写出满足条件的点E的坐标;(4)将二次函数的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线y=x+b与此图象至少有三个公共点时,请直接写出b的取值范围是 .即圄2 邺3.如图,二次函数图象的顶点为坐标系原点O,且经过点A (3, 3), 一次函数的图象经过点A和点B (6, 0).(1)求二次函数与一次函数的解析式;(2)如果一次函数图象与y轴相交于点C,点D在线段AC上,与y轴平行的直线DE 与二次函数图象相交于点巳/ CDO = / OED ,求点D的坐标;(3)当点D在直线AC上的一个动点时,以点O、C、D、E为顶点的四边形能成为平行四边形吗?请说明理由.4.如图,二次函数y=ax2+bx+c (a^0)的图象与x轴交于A (- 3, 0)、B (1, 0 与y轴相交点C (0,近).(1)求该二次函数解析式;(2)连接AC、BC,点M、N分别是线段AB、BC上的动点,且始终满足BM = 接MN.①将4BMN沿MN翻折,B点能恰好落在AC边上的P处吗?若能,请判断四边形的形状并求出PN的长;若不能,请说明理由.②将^ BMN沿MN翻折,B点能恰好落在此抛物线上吗?若能,请直接写出此时于MN的对称点Q的坐标;若不能,请说明理由.两点,BN,连BMPNB点关5.如图,在平面直角坐标系中,抛物线y=』!x2-2F3x-代与x轴交于A、B两点(点3 3(1)判断△ ABC的形状,并说明理由;(2)如图(1),点P为直线BC下方的二次函数图象上的一个动点(点P与B、C不重合),过点p作Y轴的平行线交X轴于点E.当△ PBC面积的最大值时,点F为线段BC 一点(不与点BC重合),连接EF,动点G从点E出发,沿线段EF以每秒1个单位的速度运动到点F,再沿FC以每秒2工3个单位的速度运动到点C后停止,当点F的坐标| 3是多少时,点G在整个运动过程中用时最少?(3)如图2,将4ACO沿射线CB方向以每秒个单位的速度平移,记平移后的△ ACO 为AA l C l O l连接AA1,直线AA1交抛物线与点M,设平移的时间为t秒,当^ AMC 1为等腰三角形时,求t的值.6.如图,二次函数y=—x2+bx- -的图象与x轴交于点A (-3, 0)和点B,以AB为边在2 2x轴上方作正方形ABCD ,点P是x轴上一动点,连接DP ,过点P作DP的垂线与y轴交于点E.(1)b=;点D的坐标:;(2)线段AO上是否存在点P (点P不与A、。
二次函数动点问题(提高篇)(最新整理)
数学压轴题 二次函数动点问题1.如图,抛物线y =ax2+bx +c (a ≠0)与x 轴交于A (-3,0)、B 两点,与y 轴相交于点C (0,).当x =-4和x =2时,二次函数y =ax 2+bx +c (a ≠0)的函数值y 相等,连结AC 、3BC .(1)求实数a ,b ,c 的值;(2)若点M 、N 同时从B 点出发,均以每秒1个单位长度的速度分别沿BA 、BC 边运动,其中一个点到达终点时,另一点也随之停止运动.当运动时间为t 秒时,连结MN ,将△BMN 沿MN 翻折,B 点恰好落在AC 边上的P 处,求t 的值及点P 的坐标;(3)在(2)的条件下,抛物线的对称轴上是否存在点Q ,使得以B ,N ,Q 为顶点的三角形与△ABC 相似?若存在,请求出点Q 的坐标;若不存在,请说明理由.解:(1)由题意得⎪⎩⎪⎨⎧++=+-==+-c b a c b a c c b a 244163039 解得a =-,b =-,c =.333323(2)由(1)知y =-x 2-x +,令y =0,得-x 2-x +=0.333323333323解得x 1=-3,x 2=1.∵A (-3,0),∴B (1,0).又∵C (0,),∴OA =3,OB =1,OC =,33∴AB =4,BC =2.∴tan ∠ACO ==,∴∠ACO =60°,∴∠CAO =30°.OCOA3同理,可求得∠CBO =60°,∠BCO =30°,∴∠ACB =90°.∴△ABC 是直角三角形.又∵BM =BN =t ,∴△BMN 是等边三角形.∴∠BNM =60°,∴∠PNM =60°,∴∠PNC =60°.∴Rt △PNC ∽Rt △ABC ,∴=.NC PN BCAB由题意知PN =BN =t ,NC =BC -BN =2-t ,∴=.t t 224∴t =.∴OM =BM -OB =-1=.343431如图1,过点P 作PH ⊥x 轴于H ,则PH =PM ·sin60°=×=.3423332MH =PM ·cos60°=×=.∴OH =OM +MH =+=1.3421323132∴点P 的坐标为(-1,).332(3)存在.由(2)知△ABC 是直角三角形,若△BNQ 与△ABC 相似,则△BNQ 也是直角三角形.∵二次函数y =-x 2-x +的图象的对称轴为x =-1.∴点P 在对称轴上.333323∵PN ∥x 轴,∴PN ⊥对称轴.又∵QN ≥PN ,PN =BN ,∴QN ≥BN .∴△BNQ 不存在以点Q 为直角顶点的情形.①如图2,过点N 作QN ⊥对称轴于Q ,连结BQ ,则△BNQ 是以点N 为直角顶点的直角三角形,且QN >PN ,∠MNQ =30°.∴∠PNQ =30°,∴QN ===.o 30cos PN 2334938∴==.∵=tan60°=,∴≠.BN QN 34938332BC AC 3BN QN BC AC ∴当△BNQ 以点N 为直角顶点时,△BNQ 与△ABC 不相似.②如图3,延长NM 交对称轴于点Q ,连结BQ ,则∠BMQ =120°.∵∠AMP =60°,∠AMQ =∠BMN =60°,∴∠PMQ =120°.∴∠BMQ =∠PMQ ,又∵PM =BM ,QM =QM .∴△BMQ ≌△PMQ ,∴∠BQM =∠PQM =30°.∵∠BNM =60°,∴∠QBN =90°.∵∠CAO =30°,∠ACB =90°.∴△BNQ ∽△ABC .∴当△BNQ 以点B 为直角顶点时,△BNQ ∽△ABC .设对称轴与x 轴的交点为D .∵∠DMQ =∠DMP =60°,DM =DM ,∴Rt △DMQ ≌Rt △DMP .∴DQ =PD ,∴点Q 与点P 关于x 轴对称.∴点Q 的坐标为(-1,-).332综合①②得,在抛物线的对称轴上存在点Q (-1,-),使得以B ,N ,Q 为顶点的三角332形与△ABC 相似.2.如图①,已知抛物线y =ax 2+bx +3(a ≠0)与x 轴交于点A (1,0)和点B (-3,0),与y 轴交于点C .(1)求抛物线的解析式;(2)设抛物线的对称轴与x 轴交于点M ,问在对称轴上是否存在点P ,使△CMP 为等腰三角形?若存在,请直接写出所有符合条件的点P 的坐标;若不存在,请说明理由;(3)如图②,若点E 为第二象限抛物线上一动点,连接BE 、CE ,求四边形BOCE 面积的最大值,并求此时E 点的坐标.解:(1)由题意得解得⎩⎨⎧033903=+=++-b a b a ⎩⎨⎧21--==b a ∴所求抛物线的解析式为y =-x 2-2x +3;(2)存在符合条件的点P ,其坐标为P (-1,)或P (-1,)1010-或P (-1,6)或P (-1,);35(3)解法一:过点E 作EF ⊥x 轴于点F ,设E (m ,-m 2-2m +3)(-3< a <0)则EF =-m 2-2m +3,BF =m +3,OF =-m .∴S 四边形BOCE =S △BEF +S 梯形FOCE =BF ·EF +(EF +OC )·OF 2121=(m +3)(-m 2-2m +3)+(-m 2-2m +6)(-m ).2121=-m 2-m +=-(m +)2+2329292323863∴当m =-时,S 四边形BOCE 最大,且最大值为.23863此时y =-(-)2-2×(-)+3=∴此时E 点的坐标为(-,).232341523415解法二:过点E 作EF ⊥x 轴于点F ,设E (x ,y )(-3< x <0)则S 四边形BOCE =S △BEF +S 梯形FOCE =BF ·EF +(EF +OC )·OF 2121=(3+x )· y +(3+y )(-x )=(y -x )=(-x 2-3x +3)21212323=-(x +)2+2323863∴当x =-时,S 四边形BOCE 最大,且最大值为.23863此时y =-(-)2-2×(-)+3=∴此时E 点的坐标为(-,).2323415234153.如图,已知抛物线y =ax 2+bx +c 与x 轴交于A 、B 两点,与y 轴交于点C .其中点A 在x 轴的负半轴上,点C 在y 轴的负半轴上,线段OA 、OC 的长(OA <OC )是方程x 2-5x +4=0的两个根,且抛物线的对称轴是直线x =1.(1)求A 、B 、C 三点的坐标;(2)求此抛物线的解析式;(3)若点D 是线段AB 上的一个动点(与点A 、B 不重合),过点D 作DE ∥BC 交AC 于点E ,连结CD ,设BD 的长为m ,△CDE 的面积为S ,求S 与m 的函数关系式,并写出自变量m 的取值范围.S 是否存在最大值?若存在,求出最大值并求此时D 点坐标;若不存在,请说明理由.解:(1)∵OA 、OC 的长是方程x 2-5x +4=0的两个根,OA <OC .∴OA =1,OC =4.∵点A 在x 轴的负半轴,点C 在y 轴的负半轴∴A (-1,0),C (0,-4).∵抛物线y =ax 2+bx +c 的对称轴为x =1∴由对称性可得B 点坐标为(3,0).∴A 、B 、C 三点的坐标分别是:A (-1,0),B (3,0),C (0,-4).(2)∵点C (0,-4)在抛物线y =ax 2+bx +c 图象上,∴c =-4.4分将A (-1,0),B (3,0)代入y =ax 2+bx -4得 解得⎩⎨⎧043904=+=---b a b a ⎪⎪⎩⎪⎪⎨⎧3834-==b a ∴此抛物线的解析式为y =x 2-x -4.3438(3)∵BD =m ,∴AD =4-m .在Rt △BOC 中,BC 2=OB 2+OC 2=3 2+4 2=25,∴BC =5.∵DE ∥BC ,∴△ADE ∽△ABC .∴=,即=.∴DE =.BC DE AB AD 5DE 44m-4520m -过点E 作EF ⊥AB 于点F ,则sin ∠EDF =sin ∠CBA ==.BC OC 54∴=,∴EF =DE =×=4-m .DE EF 5454544520m -∴S =S △CDE =S △ADC -S △ADE =(4-m )×4-(4-m )(4-m )=-m 2+2m 212121=-(m -2)2+2(0<m <4).21∵-<0 ∴当m =2时,S 有最大值2.21此时OD =OB -BD =3-2=1.∴此时D 点坐标为(1,0).4.如图,抛物线y =a (x +3)(x -1)与x 轴相交于A 、B 两点(点A 在点B 右侧),过点A 的直线交抛物线于另一点C ,点C 的坐标为(-2,6).(1)求a 的值及直线AC 的函数关系式;(2)P 是线段AC 上一动点,过点P 作y 轴的平行线,交抛物线于点M ,交x 轴于点N .①求线段PM 长度的最大值;②在抛物线上是否存在这样的点M ,使得△CMP 与△APN 相似?如果存在,请直接写出所有满足条件的点M 的坐标(不必写解答过程);如果不存在,请说明理由.解:(1)由题意得6=a (-2+3)(-2-1),∴a =-2∴抛物线的解析式为y =-2(x +3)(x -1),即y =-2x 2-4x +6令-2(x +3)(x -1)=0,得x 1=-3,x 2=1∵点A 在点B 右侧,∴A (1,0),B (-3,0)设直线AC 的函数关系式为y =kx +b ,把A (1,0)、C (-2,6)代入,得 解得⎩⎨⎧620=+=+-b k b k ⎩⎨⎧22==-b k ∴直线AC 的函数关系式为y =-2x +2(2)①设P 点的横坐标为m (-2≤ m ≤1),则P (m ,-2m +2),M (m ,-2m 2-4m +6)∴PM =-2m 2-4m +6-(-2m +2)=-2m 2-2m +4=-2(m +)2+2129∴当m =-时,线段PM 长度的最大值为2129②存在. M 1(0,6), M 2(-,)41855ⅰ)如图1,当M 为直角顶点时,连结CM ,则CM ⊥PM ,△CMP ∽△ANP ∵点C (-2,6),∴点M 的纵坐标为6,代入y =-2x 2-4x +6得-2x 2-4x +6=6,∴x =-2(舍去)或x =0∴M 1(0,6)(此时点M 在y 轴上,即抛物线与y 轴的交点,此时直线MN 与y 轴重合,点N 与原点O 重合)ⅱ)如图2,当C 为直角顶点时,设M (m ,-2m 2-4m +6)(-2≤ m ≤1)过C 作CH ⊥MN 于H ,连结CM ,设直线AC 与y 轴相交于点D 则△CMP ∽△NAP又∵△HMC ∽△CMP ,△NAP ∽△OAD ,∴△HMC ∽△OAD ∴=OD CH OAMH∵C (-2,6),∴CH =m +2,MH =-2m 2-4m +6-6=-2m 2-4m 在y =-2x +2中,令x =0,得y =2∴D (0,2),∴OD =2 ∴=22+m 1422m m --整理得4m 2+9m +2=0,解得m =-2(舍去)或m =-41当m =-时,-2m 2-4m +6=(-)2-4×(-)+6= ∴M 2(-,)41414185541855。
初中数学二次函数动点问题
动点问题1:相似三角形问题例1:如图①,在△ABC 中,AB=AC ,BC=acm ,∠B=30°.动点P 以1cm/s 的速度从点B 出发,沿折线B ﹣A ﹣C 运动到点C 时停止运动.设点P 出发x s 时,△PBC 的面积为y cm 2.已知y 与x 的函数图象如图②所示.请根据图中信息,解答下列问题:(1) 试判断△DOE 的形状,并说明理由;(2) 当a 为何值时,△DOE 与△ABC 相似?例2:矩形OABC 在平面直角坐标系中位置如图所示,A 、C 两点的坐标分别为A (6,0),C (0,-3),直线y =-43x 与BC 边相交于D 点. (1) 求点D 的坐标; (2) 若抛物线y =ax 2-49x 经过点A ,试确定此抛物线的表达式; (3) 设(2)中的抛物线的对称轴与直线OD 交于点M ,点P 为对称轴上一动点,以P 、O 、M 为顶点的三角形与△OCD例3.如图,抛物线的顶点为A(2,1),且经过原点O,与x轴的另一个交点为B.(1)求抛物线的解析式;(2)在抛物线上求点M,使△MOB的面积是△AOB面积的3倍;(3)连结OA,AB,在x轴下方的抛物线上是否存在点N,使△OBN与△OAB相似?若存在,求出N点的坐标作业1.如图,已知抛物线y =x 2-1与x 轴交于A 、B 两点,与y 轴交于点C . (1)求A 、B 、C 三点的坐标.(2)过点A 作AP ∥CB 交抛物线于点P ,求四边形ACBP 的面积.(3)在x 轴上方的抛物线上是否存在一点M ,过M 作MG ⊥x 轴于点G ,使以A 、M 、G 三点为顶点的三角形与△PCA 相似?若存在,请求出M 点的坐标;否则,请说明理由.2.如图,已知抛物线y =43x 2+bx +c 与坐标轴交于A 、B 、C 三点,A 点的坐标为(-1,0),过点C 的直线y =t43x -3与x 轴交于点Q ,点P 是线段BC 上的一个动点,过P 作PH ⊥OB 于点H .若PB =5t ,且0<t <1.(1)填空:点C 的坐标是___________,b =_______,c =_______;(2)求线段QH 的长(用含t 的式子表示);(3)依点P 的变化,是否存在t 的值,使以P 、H 、Q 为顶点的三角形与△COQ 相似?若存在,求出所有t3.已知,如图1,过点B (0,-1)作平行于x 轴的直线l ,抛物线y =41x2上的两点A 、B 的横坐标分别为-1和4,直线AB 交y 轴于点F ,过点A 、B 分别作直线l 的垂线,垂足分别为点C 、D ,连接CF 、DF .(1)求点A 、B 、F 的坐标;(2)求证:CF ⊥DF ; (3)点P 是抛物线y =41x 2对称轴右侧图象上的一动点,过点P 作PQ ⊥OP 交x 轴于点Q ,是否存在点P 使得△OPQ 与△CDF 相似?若存在,请求出所有符合条件的点P 的坐标;若不存在,请说明理由.(备用图)(图1)。
二次函数动点问题类型
二次函数动点问题类型二次函数是高中数学中重要的一部分,随着时代的发展,二次函数的应用越来越广泛。
其中,二次函数动点问题类型是考试中出现频率较高的一类题目,也是值得我们深入学习和掌握的内容。
一、什么是二次函数动点问题类型?二次函数动点问题类型指的是给定二次函数及其图象上的一点(即动点),通过对动点运动过程中的相关数据进行分析,解答与动点有关的问题。
通常情况下,动点的运动路径为直线或曲线,并按给定规律进行移动,以便更好地探究相关知识点。
二、二次函数动点问题类型的解题步骤二次函数动点问题类型的解题步骤可以分为以下几个方面:1. 给出图象并写出二次函数式首先,我们需要学会根据图象写出二次函数式,同时标注出图象上给定的动点位置,包括横纵坐标等。
2. 设定动点运动规律根据题意,我们设定动点运动规律,并标注出相关数据(如起点、终点、速度等等)。
3. 计算动点运动路径上的中点坐标根据所给出的动点运动路径,我们可以计算出该路径上所有中点的坐标,并标注出来。
4. 求解动点的最高/最低点和极值通过对动点运动路径上的中点坐标进行计算,我们可以得到动点的最高/最低点和极值,并将其标出。
5. 解答相关问题在完成以上步骤后,我们可以根据题目所给的要求,解答相关问题,例如:求动点在何时到达最高/最低点,求解动点的最大/最小值,求出动点最终到达的位置等等。
三、二次函数动点问题类型的应用二次函数动点问题类型是高中数学中常见的考察点,同时也广泛地应用于实际生活中。
以下是几个常见的应用案例:1. 抛物线切线问题抛物线切线问题是二次函数动点问题类型中应用广泛的一种。
通过设定动点的运动规律,我们可以计算出与抛物线相切的直线方程,从而进一步探究相关知识点。
2. 自由落体问题自由落体问题也是二次函数动点问题类型的重点之一。
通过设定动点的初始高度和运动规律,我们可以计算出物体的落地时间,最高高度等等,从而更好地探究物理知识。
3. 弹道问题弹道问题也是二次函数动点问题类型中应用广泛的一种。
二次函数动点问题解答方法技巧(含例解标准答案)
下面就此问题的常见题型作简单介绍,解题方法、关键给以点拨。
二、抛物线上动点
5、(湖北十堰市)如图①,已知抛物线 (a≠0)与 轴交于点A(1,0)和点B(-3,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)设抛物线的对称轴与 轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
(3)当 为何值时,四边形 的面积 有最大值,并求出此最大值;
(4)在运动过程中,四边形 能否形成矩形?若能,求出此时 的值;若不能,请说明理由.
[解](1)点 ,点 ,点 关于原点的对称点分别为 , , .
设抛物线 的解析式是
,
则
解得
所以所求抛物线的解析式是 .
(2)由(1)可计算得点 .
过点 作 ,垂足为 .
⑶ 根据图象的位置判断二次函数ax²+bx+c=0中a,b,c的符号,或由二次函数中a,b,c的符号判断图象的位置,要数形结合;
⑷ 二次函数的图象关于对称轴对称,可利用这一性质,求和已知一点对称的点坐标,或已知与x轴的一个交点坐标,可由对称性求出另一个交点坐标.
⑸ 与二次函数有关的还有二次三项式,二次三项式ax²+bx+c﹙a≠0﹚本身就是所含字母x的二次函数;下面以a>0时为例,揭示二次函数、二次三项式和一元二次方程之间的内在联系:
当运动到时刻 时, , .
根据中心对称的性质 ,所以四边形 是平行四边形.
所以 .
所以,四边形 的面积 .
因为运动至点 与点 重合为止,据题意可知 .
所以,所求关系式是 , 的取值范围是 .
(3) ,( ).
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数动点问题
动点问题是中考中的热点也是难点,这类问题的关键在于不要被动点牵着鼻子走,而是要根据图形的特性先确定要求的点的位置再根据几何关系求出点的坐标。
对于涉及函数的动点问题,还应考虑到借助代数的方法,通过建立方程、构建函数模型等方法来求解。
比较典型的动点问题类型一般有:求等腰三角形、直角三角形、相似三角形、平行四边形、梯形、特殊角(或其三角函数)的存在性、求线段或面积的最值等。
类型一:求线段或面积的最值
要点:求面积或线段的最值时,关键在于将长度或面积用代数式表示出来,构建一个函数关系式,再利用函数关系式求出最值。
例1 如图1,已知抛物线经过坐标原点O 和x 轴上另一点E ,顶点M 的坐标为 (2,4);矩形ABCD 的顶点
A 与点O 重合,AD 、A
B 分别在x 轴、y 轴上,且AD=2,AB=3. (1)求该抛物线的函数关系式;
(2)将矩形ABCD 以每秒1个单位长度的速度
从图1所示的位置沿x 轴的正方向匀速平行移动,同时一动点P 也以相同的速度.....从点A 出发向B 匀速移动,设它们运动的时间为t 秒(0≤t ≤3),直线AB 与该抛物线的交点为N (如图2所示) ① 当t=
时,判断点P 是否在直线ME 上,并说明理由;
② 设以P 、N 、C 、D 为顶点的多边形面积为S ,试问S 是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
2
5
图2
B
C
O
A D E
M
y
x
P
N
· 图1
B
C
O (A )
D
E M
y
x
类型二:等腰三角形或直角三角形的存在性
要点:证明等腰三角形或直角三角形的存在性需要注意分类讨论,即讨论直角顶点或者两腰的情况。
例2 如图,已知抛物线y=ax2+bx+c的顶点坐标为Q(2,-1),且与y轴交于点C(0,3),与x轴交于A、B两点(点A在点B的右侧),点P是该抛物线上一个动点,从点C沿抛物线向点A 运动(点P与A不重合),过点P作PD∥y轴,交AC于点D.
(1)求该抛物线的函数关系式;
(2)当△ADP是直角三角形时,求点P的坐标.
例3 已知:如图,在平面直角坐标系xOy中,矩形OABC的边OA在y轴的正半轴上,OC 在x轴的正半轴上,OA=2,OC=3,过原点O作 AOC的平分线交AB于点D,连接DC,过点D作DE⊥DC,交OA于点E.
(1)求过点E、D、C的抛物线的解析式;
(2)将△EDC绕点D按顺时针方向旋转后,角的一边与y轴的正半轴交于点F,另一边与
线段OC交于点G.如果DF与(1)中的抛物线交于另一点M,点M的横坐标为6
5
,那么
EF=2GO是否成立?若成立,请给予证明;若不成立,请说明理由;
(3)对于(2)中的点G,在位于第一象限内的该抛物线上是否存在点Q,使得直线GQ与AB的交点P与点C、G构成的△PCG是等腰三角形?若存在,请求出点Q的坐标;若不存在成立,请说明理由.
要点:证明相似三角形的存在性时,本质是要注意三角形的内角的变化情况。
例4 如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C
(1)求抛物线的函数解析式.
(2)P是抛物线上第一象限内的动点,过点P作PM⊥x轴,垂足为M,是否存在点P,使得以P,M,A为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.
要点:要注意平行四边形的判定,使用较多的是一组对边平行且相等以及两组对边分别相等这两个判定,解题过程中可能需要建立方程来求解。
例5 在平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4),C(2,0)三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值;
(3)若点P是抛物线上的动点,点Q是直线y=-x上的动点,判断有几个位置能使以点P、Q、
B、0为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
y P (x ,y ) A
B
C
O
N
D
x
y =kx +4
类型五:求特殊的三角函数值
要点:先求出要求的图形,然后根据三角函数的定义求解。
例6 如图,抛物线y =ax 2+bx +c 经过原点O ,与x 轴交于另一点N ,直线y =kx +4与两坐标轴分别交于A 、D 两点,与抛物线交于点B (1,m )、C (2,2). (1)求直线与抛物线的解析式.
(2)若抛物线在x 轴上方的部分有一动点P (x ,y ),设∠PON =α,求当△PON 的面积最大时tan α的值.
类型六:梯形的存在性
要点:此类问题要注意结合梯形的定义,特别需要注意直角梯形和等腰梯形这两种特殊情况。
例7 如图,二次函数y = -x 2+ax +b 的图像与x 轴交于A (-
2
1
,0)、 B (2,0)两点,且与y 轴交于点C ;
(1) 求该拋物线的解析式,并判断△ABC 的形状; (2) 在x 轴上方的拋物线上有一点D ,且以A 、C 、D 、B 四点为顶点的四边形是等腰梯形,请直接写出D 点的坐标;
(3) 在此拋物线上是否存在点P ,使得以A 、C 、B 、P 四点为顶点的四边形是直角梯形?若存在,求出P 点的坐标;若不存在,说明理由。
y A B C O x
参考答案
例1
解:(1)(2)①点P 不在直线ME 上②依题意可知:P (,),N (,)
当时,以P 、N 、C 、D 为顶点的多边形是四边形PNCD ,依题意可得:
=
+=+==
∵抛物线的开口方向:向下,∴当=
,且时,=当时,点P 、N 都重合,此时以P 、N 、C 、D 为顶点的多边形是三角形.依题意可得,==3综上所述,
以P 、N 、C 、D 为顶点的多边形面积S 存在最大值21/4.
例2 解:
x x y 42+-=t t t t t 42
+-30
t PNC PCD S S S +=OD CD ⋅21BC PN ⋅21
2321⨯⨯()
242
12⋅-+-t t t 332++-t t 4
21
)23(2+--t t 233230 =t 最大S 4
21
03或=t ABCD
S S 矩形2
1=322
1
⨯
⨯
例3 解:
例4解:
例5 解:
例6
解:
例7
解:
(1) 根据题意,将A(-
2
1
,0),B(2,0)代入y= -x2+ax +b 中,得
⎪⎩
⎪
⎨
⎧
=
+
+
-
=
+
-
-
2
4
2
1
4
1
b
a
b
a
,解这个方程,得a=
2
3
,
b=1,∴该拋物线的解析式为y= -x2+
2
3
x+1,当x=0时,y=1,∴点C的坐标为(0,1)。
∴在△AOC中,AC=
2
2OC
OA+=2
21
)
2
1
(+=
2
5。
在△BOC中,BC=2
2OC
OB+=2
21
2+=5。
AB=OA+OB=
2
1
+2=
2
5
,∵AC2+BC2=
4
5
+5=
4
25
=AB2,∴△ABC是直角三角形。
(2) 点D的坐标为(
2
3
,1)。
(3) 存在。
由(1)知,AC⊥BC。
若以BC为底边,则BC//AP,如图1所示,可求得直线BC的解析式为y= -
2
1
x+1,直线AP可以
看作是由直线BC平移得到的,所以设直线AP的解析式为y= -
2
1
x+b,把点A(-
2
1
,0)代入直线
AP的解析式,求得b= -
4
1
,∴直线AP的解析式为y= -
2
1
x-
4
1。
∵点P既在拋物线上,又在直线
AP上,∴点P的纵坐标相等,即-x2+
2
3
x+1= -
2
1
x-
4
1
,解得x1=
2
5
,x2= -
2
1
(舍去)。
当x=
2
5
时,
y
A B
C
O
x
y = -
2
3, ∴点P (25,-23)。
若以AC 为底边,则BP //AC ,如图2所示。
可求得直线AC 的解析式为y =2x +1。
直线BP 可以看作是由直线AC 平移得到的,所以设直线BP 的解析式为y =2x +b ,把点B (2,0)代入直线BP 的解析式,求得b = -4,
∴直线BP 的解析式为y =2x -4。
∵点P 既在拋物线上,又在直线BP 上,∴点P 的纵坐标相等,即-x 2+23x +1=2x -4,解得x 1= -25,x 2=2(舍去)。
当x = -25时,y = -9,∴点P 的坐标为(-2
5,-9)。
综上所述,满足题目条件的点P 为(25,-23)或(-2
5,-9)。
