高中数学导数及微积分练习题
微积分练习题带答案

微积分练习题带答案微积分是数学的分支之一,它研究的是函数的变化规律。
在微积分中,经常会出现各种各样的练习题,这些练习题有助于我们加深对微积分概念和原理的理解。
在这篇文章中,我们将分享一些微积分练习题,并附带答案,希望对你的学习有所帮助。
1. 求函数f(x) = 2x^3 - x^2 + 3x - 5的导数。
答案:f'(x) = 6x^2 - 2x + 32. 求函数g(x) = e^x * sin(x)的导数。
答案:g'(x) = e^x * sin(x) + e^x * cos(x)3. 求函数h(x) = ln(x^2)的导数。
答案:h'(x) = 2/x4. 求函数i(x) = ∫(0到x) t^2 dt的导数。
答案:i'(x) = x^25. 求函数j(x) = ∫(x到1) t^2 dt的导数。
答案:j'(x) = -x^26. 求函数k(x) = ∫(0到x) e^t * sin(t) dt的导数。
答案:k'(x) = e^x * sin(x)7. 求函数l(x) = e^(-x)的不定积分。
答案:∫ e^(-x) dx = -e^(-x) + C (C为常数)8. 求函数m(x) = 1/(x^2+1)的不定积分。
答案:∫ 1/(x^2+1) dx = arctan(x) + C (C为常数)9. 求函数n(x) = 2x * cos(x^2)的不定积分。
答案:∫ 2x * cos(x^2) dx = sin(x^2) + C (C为常数)10. 求函数o(x) = ∫(1到x) e^(t^2) dt的原函数。
答案:o(x) = ∫(1到x) e^(t^2) dt + C (C为常数)以上是一些微积分练习题及其答案。
通过解答这些题目,我们可以巩固对微积分概念和原理的理解,并提升解题能力。
微积分是应用广泛的数学工具,在物理、工程、经济等领域都有重要的应用,掌握微积分对于进一步深入学习这些领域十分必要。
导数与微分练习题及解析

导数与微分练习题及解析在微积分学中,导数和微分是最基本的概念之一。
它们可以帮助我们研究函数的变化率和性质,广泛应用于物理、经济、工程等各个领域。
为了帮助你更好地理解导数和微分的概念,以下是一些练习题及其解析。
练习题1:求函数f(x) = x^2 + 3x + 2在x = 2处的导数和切线方程。
解析:首先,我们求函数f(x)的导数。
使用求导法则,对于多项式函数来说,可以将每一项的指数与系数相乘,并将指数减一,得到函数的导数。
f'(x) = 2x + 3接下来,我们计算x = 2处的导数值。
f'(2) = 2(2) + 3 = 7切线方程的一般形式为y = mx + b,其中m代表斜率,b代表截距。
根据导数的定义,导数即为切线的斜率。
所以切线的斜率为m = 7。
将切点的坐标代入切线方程,我们可以得到b的值。
2 = 7(2) + b2 = 14 + bb = -12最终的切线方程为y = 7x - 12。
练习题2:求函数f(x) = e^x * sin(x)的导数。
解析:考虑到函数f(x) = e^x * sin(x)是两个函数的乘积,我们可以使用乘积法则来求导。
乘积法则的公式为:(uv)' = u'v + uv'对于e^x和sin(x)两个函数,它们的导数分别为e^x和cos(x)。
根据乘积法则,我们可以将这两个导数与原函数进行组合,得到最终的导数为:f'(x) = (e^x * cos(x)) + (e^x * sin(x))练习题3:求函数f(x) = ln(x^2 + 1)的导数和微分。
解析:首先,我们求函数f(x)的导数。
根据链式法则,可以分别计算外函数和内函数的导数。
设内函数为u = x^2 + 1,则内函数的导数为du/dx = 2x。
外函数为f(u) = ln(u),则外函数的导数为df/du = 1/u。
根据链式法则,函数f(x)的导数为:f'(x) = df/du * du/dx= (1/u) * (2x)= 2x / (x^2 + 1)接下来,我们计算函数f(x)的微分。
掌握函数的导数与微分练习题

掌握函数的导数与微分练习题函数的导数与微分是微积分的重要内容,对于学习者而言,掌握这一部分知识对于提高解题能力和理解数学概念非常重要。
本文将通过练习题的方式,帮助读者巩固对函数的导数与微分的理解,并培养解题的思维能力。
1. 求解下列函数的导数:(1) f(x) = 3x² - 2x + 1解答:f'(x) = 6x - 2(2) g(x) = 5sin(x) + 2cos(x)解答:g'(x) = 5cos(x) - 2sin(x)2. 对下列函数进行微分:(1) h(x) = x³ - 4x² + 2x解答:dh(x) = 3x² - 8x + 2(2) k(x) = 2e^x + 3ln(x)解答:dk(x) = 2e^x + 3/x3. 求解给定函数在指定点的导数:(1) y = 2x³,求导数在x=2处的值。
解答:y' = 6x²y'(2) = 6(2)² = 24(2) y = x^4 - 2x²,求导数在x=-1处的值。
解答:y' = 4x³ - 4xy'(-1) = 4(-1)³ - 4(-1) = -44. 求解给定函数的极值点:(1) y = x³ - 12x² + 36x解答:为求取极值点,先求导数:y' = 3x² - 24x + 36令y' = 0,求解方程得:x = 2 或 x = 6将以上两个x值代入原函数求y值得到极值点:当x=2时,y = 2³ - 12(2)² + 36(2) = 16 - 48 + 72 = 40当x=6时,y = 6³ - 12(6)² + 36(6) = 216 - 432 + 216 = 0因此,函数y = x³ - 12x² + 36x在x = 2处有极小值,极小值为40,在x = 6处有极大值,极大值为0。
高中数学 第1章 导数及其应用 1.6 微积分基本定理练习 新人教A版选修2-2-新人教A版高二选修

§1.6 微积分基本定理[限时50分钟,满分80分]一、选择题(每小题5分,共30分) 1.⎠⎛122x 2+x +1xd x 的值为A .1+ln 2B .2+ln 2C .3+ln 2D .4+ln 2解析 ∵f (x )=2x 2+x +1x =2x +1+1x,取F (x )=x 2+x +ln x , 则F ′(x )=2x +1+1x,∴⎠⎛122x 2+x +1xd x =(x 2+x +ln x )⎪⎪⎪21=4+ln 2.答案D2.直线y =4x 与曲线y =x 3在第一象限内围成的封闭图形的面积为 A .2 2 B .4 2 C .2D .4解析 首先求出两曲线的交点,画出图形,确定出被积函数,再用积分求出面积.令4x =x 3,解得x =0或x =±2,∴S =⎠⎛02(4x -x 3)=⎝ ⎛⎭⎪⎫2x 2-x 44|)20=8-4=4,故选D.答案D3.已知f (x )=⎩⎪⎨⎪⎧x 2,x ∈[0,1),1x ,x ∈[1,e 2)(其中e 为自然对数的底数),则⎰2e 0d )(x xf 的值为 A.43 B.53 C.73D.83解析⎰2e 0d )(x x f =⎠⎛01x 2d x +⎰2e 0d 1x x=13x 3|1+ln x |2e 0=13+2=73. 答案C4.⎠⎛02||1-x )d x 等于A .0B .1C .2D .-2解析⎠⎛01(1-x )d x +⎠⎛12(x -1)d x=⎝ ⎛⎭⎪⎫x -12x 2⎪⎪⎪10+⎝ ⎛⎭⎪⎫12x 2-x ⎪⎪⎪21=⎝ ⎛⎭⎪⎫1-12+⎝ ⎛⎭⎪⎫12×4-2-⎝ ⎛⎭⎪⎫12-1=1. 答案B5.设f (x )=⎠⎛0x sin t d t ,则f ⎝ ⎛⎭⎪⎫f ⎝ ⎛⎭⎪⎫π2等于A .-1B .1C .-cos 1D .1-cos 1解析f (x )=⎠⎛0xsin t d t =-cos t |x=-cos x +1,∴f ⎝ ⎛⎭⎪⎫π2=-cos π2+1=1.∴f ⎝ ⎛⎭⎪⎫f ⎝ ⎛⎭⎪⎫π2=f (1)=-cos 1+1.答案D6.若⎠⎛1a ⎝⎛⎭⎪⎫2x +1x d x =3+ln 2,且a >1,则a 的值是A .6B .4C .3D .2解析 因为⎠⎛1a ⎝⎛⎭⎪⎫2x +1x d x =(x 2+ln x )|1a =a 2+ln a -1,所以a 2+ln a -1=3+ln 2,所以a =2.答案D二、填空题(每小题5分,共15分)7.已知α∈⎣⎢⎡⎦⎥⎤0,π2,则当⎠⎛0α(cos x -sin x )d x 取最大值时,α=________.解析⎠⎛0α(cos x -sin x )d x=(sin x +cos x )⎪⎪⎪α=sin α+cos α-1=2sin ⎝⎛⎭⎪⎫α+π4-1, 上式取最大值时,sin ⎝ ⎛⎭⎪⎫α+π4=1,∵α∈⎣⎢⎡⎦⎥⎤0,π2,∴α=π4.答案π48.F (x )是一次函数,且⎠⎛01F (x )d x =5,⎠⎛01F (x )x d x =176,则F (x )=________.解析 ∵F (x )是一次函数, ∴设F (x )=kx +b (k ≠0). ∴⎠⎛01F (x )d x =⎠⎛01(kx +b )d x=⎝ ⎛⎭⎪⎫k 2x 2+bx ⎪⎪⎪1=k 2+b , ∴k2+b =5.① ∴⎠⎛01F (x )x d x =⎠⎛01(kx +b )x d x =⎠⎛01(kx 2+bx )d x=⎝ ⎛⎭⎪⎫k 3x 3+b 2x 2⎪⎪⎪1=k 3+b2.∴k 3+b 2=176.② 由①②,得k =4,b =3. ∴F (x )=4x +3. 答案 4x +39.设函数y =f (x )=ax 2+c (a ≠0).若⎠⎛01f (x )d x =f (x 0),0≤x 0≤1,则x 0的值为________.解析 ∵⎠⎛01f (x )d x =⎠⎛01(ax 2+c )d x=⎝ ⎛⎭⎪⎫13ax 3+cx ⎪⎪⎪10=a 3+c =ax 20+c ,0≤x 0≤1, ∴x 0=33. 答案33三、解答题(本大题共3小题,共35分) 10.(10分)求下列定积分.(1)⎰20π⎣⎢⎡⎦⎥⎤e x +sin ⎝ ⎛⎭⎪⎫2x -π3d x ; (2)⎰-ππ3cos ⎝⎛⎭⎪⎫x -π6d x .解析 (1)∵(e x)′=e x,⎣⎢⎡⎦⎥⎤12cos ⎝ ⎛⎭⎪⎫2x -π3′ =12·⎣⎢⎡⎦⎥⎤-sin ⎝ ⎛⎭⎪⎫2x -π3⎝ ⎛⎭⎪⎫2x -π3′=-sin ⎝ ⎛⎭⎪⎫2x -π3 ∴⎰20π⎣⎢⎡⎦⎥⎤e x +sin ⎝⎛⎭⎪⎫2x -π3d x =⎰20πe xd x +∫π20sin ⎝⎛⎭⎪⎫2x -π3d x =e x|20π-12cos ⎝ ⎛⎭⎪⎫2x -π3|2π=(e π2-e 0)-12⎣⎢⎡⎦⎥⎤cos ⎝ ⎛⎭⎪⎫π-π3-cos π3=e π2-1-12⎝ ⎛⎭⎪⎫-12-12=e π2-12.(2)因为cos ⎝ ⎛⎭⎪⎫x -π6=cos x cos π6+sin x sin π6=32cos x +12sin x ,又因为(sin x )′=cos x ,(-cos x )′=sin x , 所以⎰ππ3cos ⎝ ⎛⎭⎪⎫x -π6d x =⎰ππ3⎝ ⎛⎭⎪⎫32cos x +12sin x d x=|3cos 21sin 23ππ⎪⎪⎭⎫ ⎝⎛-x x =0. 11.(12分)求函数f (x )=⎩⎨⎧x 3x ∈[0,1)x x ∈[1,2)2xx ∈[2,3]在区间[0,3]上的定积分.解析 由积分性质知⎠⎛03f (x )d x =⎠⎛01f (x )d x +⎠⎛12f (x )d x +⎠⎛23f (x )d x =⎠⎛01x 3d x +⎠⎛12x d x +⎠⎛232xd x=⎠⎛01x 3d x +⎠⎛12x 12d x +⎠⎛232xd x=⎪⎪⎪x 441+⎪⎪⎪23x 3221+⎪⎪⎪2xln 232 =14+432-23+8ln 2-4ln 2 =-512+432+4ln 2.12.(13分)求由曲线y =x 2+4与直线y =5x ,x =0,x =4所围成平面图形的面积. 解析 由图形可得S =⎠⎛01(x 2+4-5x )d x +⎠⎛14(5x -x 2-4)d x =⎝ ⎛⎭⎪⎫13x 3+4x -52x 2⎪⎪⎪10+⎝ ⎛⎭⎪⎫52x 2-13x 3-4x ⎪⎪⎪41 =13+4-52+52×42-13×43-4×4-52+13+4=193.。
导数微积分练习题
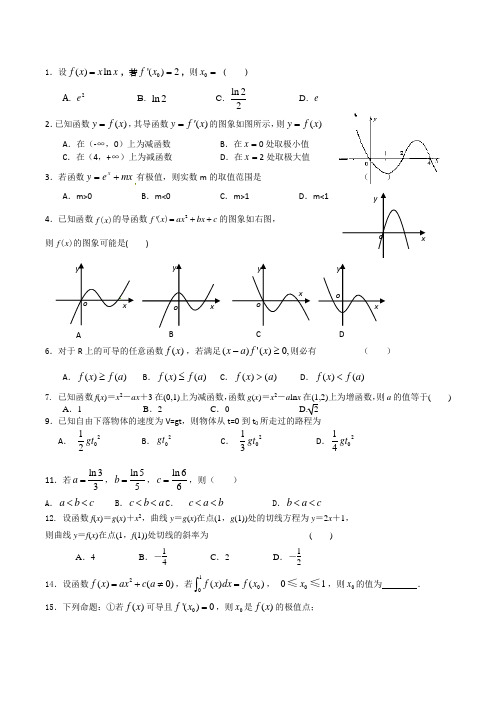
x yo 1.设()ln f x x x =,若0'()2f x =,则0x =( )A. 2eB. ln 2C. ln 22 D. e2.已知函数)(x f y =,其导函数)(x f y '=的图象如图所示,则)(x f y =A .在(-∞,0)上为减函数B .在=x 0处取极小值C .在(4,+∞)上为减函数D .在=x 2处取极大值3.若函数mx e y x +=有极值,则实数m 的取值范围是 ( )A .m>0B .m<0C .m>1D .m<1 4.已知函数f x ()的导函数2f x ax bx c '=++()的图象如右图,则f x ()的图象可能是( )6.对于R 上的可导的任意函数)(x f ,若满足,0)(')(≥-x f a x 则必有 ( )A .)()(a f x f ≥B .)()(a f x f ≤C .)()(a x f >D .)()(a f x f <7. 已知函数f (x )=x 2-ax +3在(0,1)上为减函数,函数g (x )=x 2-a ln x 在(1,2)上为增函数,则a 的值等于() A .1 B .2 C .0 D. 29.已知自由下落物体的速度为V=gt ,则物体从t=0到t 0所走过的路程为A . 2012gt B .20gt C . 2013gt D .2014gt11.若ln 33a =,ln 55b =,ln 66c =,则( )A .a b c <<B .c b a <<C . c a b <<D .b a c <<12. 设函数f (x )=g (x )+x 2,曲线y =g (x )在点(1,g (1))处的切线方程为y =2x +1,则曲线y =f (x )在点(1,f (1))处切线的斜率为 ( )A .4B .-14C .2D .-1214.设函数2()(0)f x ax c a =+≠,若100()()f x dx f x =⎰, 001x ≤≤,则0x 的值为 .15.下列命题:①若()f x 可导且0'()0f x =,则0x 是()f x 的极值点; o y x x o y xoyxo y A B C DO y x (16题图)②函数(),[2,4]x f x xe x -=∈的最大值为22e -; ③424168x dx π--=⎰ ④一质点在直线上以速度243(/)v t t m s =-+运动,从时刻0()t s =到4()t s =时质点运动的路程为4()3m 。
导数的练习题及答案

导数的练习题及答案导数是微积分中的一个重要概念,它描述了函数在某一点上的变化率。
掌握导数的概念对于解决各种数学和物理问题至关重要。
在这篇文章中,我们将给出一些关于导数的练习题及其答案,帮助读者更好地理解和应用导数。
练习题一:求函数 $f(x) = 2x^3 - 5x^2 + 3x - 1$ 在 $x = 2$ 处的导数。
解答一:根据导数的定义,我们知道导数可以通过函数的极限来求解。
在这个例子中,我们可以使用直接求导的方法来计算导数。
首先,我们对每一项使用求导法则。
对于 $2x^3$,它的导数是$6x^2$;对于 $-5x^2$,它的导数是 $-10x$;对于 $3x$,它的导数是$3$;对于常数项 $-1$,它的导数是 $0$。
然后,将这些导数相加,得到函数 $f(x)$ 的导数 $f'(x)$。
所以,$f'(x) = 6x^2 - 10x + 3$。
接下来,我们求函数 $f(x)$ 在 $x = 2$ 处的导数。
将 $x$ 替换为 $2$,得到 $f'(2) = 6(2)^2 - 10(2) + 3 = 28$。
所以,函数 $f(x) = 2x^3 - 5x^2 + 3x - 1$ 在 $x = 2$ 处的导数为 $f'(2) = 28$。
练习题二:求函数 $y = e^x \sin(x)$ 的导数。
解答二:这个问题涉及到两个函数的乘积,所以我们需要使用乘积规则来求解。
首先,我们将函数 $y = e^x \sin(x)$ 分解为两个函数的乘积:$y =u(x) v(x)$,其中 $u(x) = e^x$,$v(x) = \sin(x)$。
然后,我们求出每个函数的导数。
对于 $u(x) = e^x$,它的导数仍然是 $e^x$;对于 $v(x) = \sin(x)$,它的导数是 $\cos(x)$。
根据乘积规则,函数 $y$ 的导数为 $y' = u'v + uv'$。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.求导:(1)函数y= 2cosxx的导数为--------------------------------------------------------
(2)y=ln(x+2)-------------------------------------;(3)y=(1+sin x)2------------------------ ----------------------
(4)y=3x2+xcos x------------------------------------ ;(5)y=x2cos(2x-π3)---------------------------------------- .
(6)已知y=ln 3xex,则y′|x=1=________.
2.设1ln)(2xxf,则)2('f( ).
(A).54 (B).52 (C).51 (D).53
3.已知函数dcxbxaxxf23)(的图象与x轴有三个不同交点)0,(),0,0(1x,)0,(2x,
且)(xf在1x,2x时取得极值,则21xx的值为( )
(A).4 (B).5 (C).-6 (D).不确定
3
4.()34([0,1])1()1()()0()12fxxxxABCD函数的最大值是( )
5.设底面为等边三角形的直棱柱的体积为V,则其表面积最小时,底面边长为( ).
(A).3V (B).32V (C).34V (D).32V
6.由抛物线xy22与直线4xy所围成的图形的面积是( ).
(A).18 (B).338 (C).316 (D).16
7.曲线3xy在点)0)(,(3aaa处的切线与x轴、直线ax所围成的三角形的面积为61,
则a_________ 。
8.已知抛物线2yxbxc在点(12),处的切线与直线20xy垂直,求函数
2
yxbxc
的最值.
9.已知函数xbxaxxf3)(23在1x处取得极值.(1)讨论)1(f和)1(f是函数
)(xf的极大值还是极小值;(2)过点)16,0(A作曲线)(xfy
的切线,求此切线方程.
10、已知f(x)=x3+ax2+bx+c,在x=1与x=-2时,都取得极值。
⑴求a,b的值;⑵若x[-3,2]都有f(x)>112c恒成立,求c的取值范围。
11.设a为实数,函数axxxxf23。(1)求xf的极值;(2)当a在什么范围内
取值时,曲线xfy与x轴仅有一个交点?
12.设a为实数,函数axxxf33。(1)求xf的极值;(2)是否存在实数a,使
得方程0xf恰好有两个实数根?
1. 已知函数()fx在1x处的导数为3,则()fx的解析式可能为 ( )
A.(x-1)3+3(x-1) B.2(x-1)2 C.2(x-1) D.x-1
2.函数)0,4(2cos在点xy处的切线方程是 ( )
A.024yx B.024yxC.024yx D.024yx
3.曲线3cos(0)2yxx与坐标轴围成的面积是 ( )
A.4 B. 52 C.3 D.2
4.函数313yxx 有 ( )
A.极小值-1,极大值1 B. 极小值-2,极大值3
C. 极小值-1,极大值3 D. 极小值-2,极大值2
5.函数32yxxx的单调区间为_________________________________。
6.设函数32()2fxxaxx, (1)f=9,则a_______________________.
7.220(3)10,xkdxk则 ,
8
3
1xdx
__________________.
8、已知对任意实数x,有()(),()()fxfxgxgx。且0x时,
''
()0,()0fxgx
则0x时 ( )
A ''()0,()0fxgx B ''()0,()0fxgx
C ''()0,()0fxgx D ''()0,()0fxgx
9、曲线3cos(0)2yxx与两坐标轴所围成图形的面积为( )
A . 4 B . 2 C . 52 D. 3
10、设2(01)()2(12)xxfxxx,则20()fxdx等于( )
A 34 B 45 C 56 D不存在
11、已知1220()(2)faaxaxdx,则()fa的最大值是()
A 23 B 29 C 43 D 49
12、已知函数2()321fxxx,若11()2()fxdxfa成立,则a=__________.
13、()fx是一次函数,且110017()5,()6fxdxxfxdx,那么()fx的解析式是
________________.
14、已知二次函数2()fxaxbxc的导数为''(),(0)0fxf,对于任意实数x,有
()0fx
,则'(1)(0)ff的最小值为________.
15.计算下列定积分。 (1)34|2|xdx (2)1211edxx
16、设两抛物线222,yxxyx所围成的图形为M,求:(1)M的面积;(2)将
M
绕x轴旋转一周所得旋转体的体积。
17.求由抛物线42xy与直线2xy所围成图形的面积。
18、已知函数03acbxaxxf为奇函数,其图像在点1,1f处的切线与直线
076yx
垂直,导函数xf/的最小值为-12。
(1)求a、b、c的值;
(2)求函数xf的单调递增区间,并求函数xf在3,1上的最大值和最小值。
