手拉手模型
手拉手模型的特点及结论

手拉手模型的特点及结论一、手拉手模型的定义。
手拉手模型呀,就像是两个有共同顶点的全等或相似三角形,通过绕着这个顶点旋转,让它们的边手拉手连在一起,形成一种特殊的几何图形结构。
比如说,有两个等腰三角形,它们共用一个顶点,这就可能构成手拉手模型啦。
想象一下,就好像两个小伙伴手拉手一起玩耍,是不是还挺形象的 。
二、手拉手模型的特点。
1. 图形结构特点。
有一个公共顶点。
这个顶点就像是两个图形的连接点,所有的神奇变化都围绕它展开。
比如说,在两个等腰直角三角形构成的手拉手模型中,那个公共顶点就是直角顶点。
对应边相等或成比例。
如果是全等三角形构成的手拉手模型,那对应边肯定是相等的;要是相似三角形构成的呢,对应边就是成比例的啦。
就好比两个相似的三角形小伙伴,它们的边虽然长度可能不一样,但比例是固定的 。
夹角相等。
两个三角形拉手的那两条边所夹的角是相等的哦。
这个夹角相等的特点在解决很多角度相关的问题时可是非常有用的呢。
2. 位置关系特点。
两个三角形的相对位置比较特殊。
它们通过公共顶点相连,并且在旋转过程中,保持着一种特定的位置关系。
有时候是一个三角形绕着公共顶点旋转一定角度后和另一个三角形拉手,这种旋转的特性让图形充满了变化和趣味 。
三、手拉手模型的结论。
1. 全等结论。
如果是全等三角形构成的手拉手模型,那么可以得到新的全等三角形。
已知三角形ABC和三角形ADE是全等的等腰三角形(AB = AC,AD = AE,∠BAC = ∠DAE),当它们构成手拉手模型时,连接BD和CE,那么三角形ABD和三角形ACE就是全等的。
这是因为AB = AC,AD = AE,而且∠BAD = ∠CAE(都是∠BAC加上或者减去同一个角得到的),根据全等三角形的判定定理(SAS)就可以得出这个结论啦。
这个结论在证明线段相等、角相等的问题中经常会用到哦 。
2. 相似结论。
当是相似三角形构成的手拉手模型时,会得到新的相似三角形。
比如说,三角形ABC和三角形ADE是相似三角形(对应边成比例,对应角相等),它们构成手拉手模型,连接BD和CE,那么三角形ABD和三角形ACE也是相似的。
【北师大版】八年级数学专题手拉手几何模型 课件

巩固训练
1.如图,△ABC和△DEC都是等边三角形,点C是它们的公共顶点 求证:AE=BD
2.已知:如图△ABC和△ADE都是等腰直角三角形, ∠BAC=∠DAE=90°. 求证:(1)BD=CE.(2)BD⊥CE
巩固训练
3.如图,△ABD和△BCE是等边三角形,连接AE与CD 求证: (1)△ABE≌△DBC (2)AE=DC (3)AE与DC的夹角为60° (4)AE与DC的交点设为H,BH平分∠AHC
过点b分别往hahc作垂线运用等积法得出两垂线段相等hl判定三角形全等解决4初三时亦可用behc四点共圆证明此结论二发散思维二发散思维例2
初二数学手拉手几何模型
学习目标
1.了解手拉手模型的基本概念 2.掌握手拉手模型的全等与相关结论 3.运用手拉手模型解决实际问题 学习重点: 熟练的找出手拉手模型中的全等三角形及其 相关结论 学习难点: 利用手拉手模型的结论解决问题
(二)发散思维
例2:如图,△ADC和△EDG是等腰直角三角形,连接AG,CE,交 点为H。 (1)证明:△ADG≌△CDE; (2)证明:AG=CE (3)求AG与CE之间的夹角为多少度。 (4)HD是否平分∠AHE?
分析:
等腰直角三角形,两腰相等,两底角相等为45°,其余同例
(三)举一反三
例3:如图,△ADB和△BCE是等腰三角形,其中 AB=BD,CB=EB,∠ABD=∠CBE=α,连接AE与CD,交点为H。 (1)证明:△ABE≌△DBC (2)证明:AE=CD (3)求AE与CD之间的夹角为多少度。 (4)HB是否平分∠AHC?
复习引入
如图,△ABC和△ADE为等腰三角形,其中,∠BAC=∠DAE=α。从中 你能得到哪些结论?
我们重点研究△ABD和△ACE,这两个三 角形是否全等?有哪些边和角对应相等 ?还有什么共同特征?旋转α得到
手拉手模型(解析版)
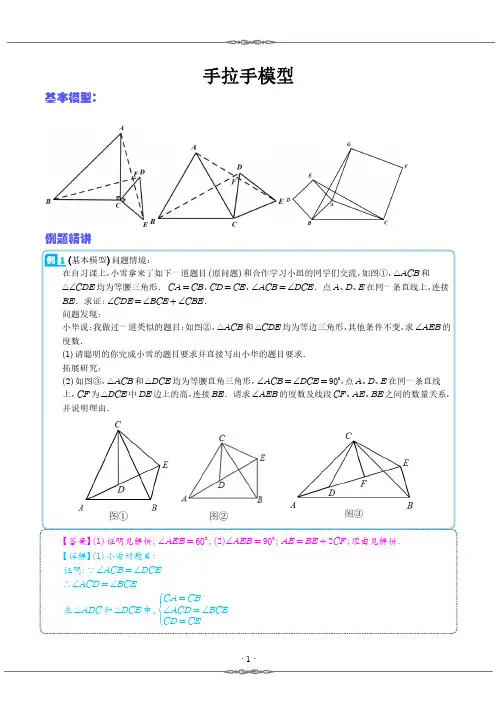
手拉手模型基本模型:例题精讲1(基本模型)问题情境:在自习课上,小雪拿来了如下一道题目(原问题)和合作学习小组的同学们交流,如图①,△ACB和△∠CDE均为等腰三角形.CA=CB,CD=CE,∠ACB=∠DCE.点A、D、E在同一条直线上,连接BE.求证:∠CDE=∠BCE+∠CBE.问题发现:小华说:我做过一道类似的题目:如图②,△ACB和△CDE均为等边三角形,其他条件不变,求∠AEB的度数.(1)请聪明的你完成小雪的题目要求并直接写出小华的题目要求.拓展研究:(2)如图③,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一条直线上,CF为△DCE中DE边上的高,连接BE.请求∠AEB的度数及线段CF、AE、BE之间的数量关系,并说明理由.【答案】(1)证明见解析;∠AEB=60°;(2)∠AEB=90°;AE=BE+2CF;理由见解析.【详解】(1)小雪的题目:证明:∵∠ACB=∠DCE∴∠ACD=∠BCE在△ADC和△DCE中,CA=CB∠ACD=∠BCECD=CE∴△ADC≅△BEC SAS∴∠CAD=∠CBE又∵∠ACD=∠BCE,∠CDE=∠CAD+∠ACD ∴∠CDE=∠CBE+∠BCE;小华的题目:解:∵∠ACB=∠DCE∴∠ACD=∠BCE在△ADC和△DCE中,CA=CB∠ACD=∠BCE CD=CE∴△ADC≅△BEC SAS∴∠ADC=∠BEC∵△CDE为等边三角形∴∠CDE=∠CED=60°又∵点A、D、E在同一条直线上∴∠ADC=∠BEC=120°∴∠AEB=∠BEC-∠CED=60°(2)∠AEB=90°;AE=BE+2CF;理由如下:∵△ACB和△DCE均为等腰直角三角形,∴AC=BC,CD=CE,∠ACB=∠DCE=90°,∠CDE=∠CED=45°,∴∠ACB-∠DCB=∠DCE-∠DCB即∠ACD=∠BCE在△ADC和△DCE中,CA=CB∠ACD=∠BCE CD=CE∴△ADC≅△BEC SAS∴BE=AD,∠BEC=∠ADC,∵点A、D、E在同一直线上∴∠ADC=180°-45°=135°∴∠BEC=135°∴∠AEB=∠BEC-∠CED=135°-45°=90°∵∠DCE=90°,CD=CE,CF⊥DE∴CF=DF=EF∴DE=DF+EF=2CF∴AE=AD+DE=BE+2CF .2(培优综合)(1)如图1,△ABC和△DCE都是等边三角形,且B,C,D三点在一条直线上,连接AD,BE相交于点P,求证:BE=AD.(2)如图2,在△BCD中,若∠BCD<120°,分别以BC,CD和BD为边在△BCD外部作等边△ABC,等边△CDE,等边△BDF,连接AD、BE、CF恰交于点P.①求证:AD=BE=CF;②如图2,在(2)的条件下,试猜想PB,PC,PD与BE存在怎样的数量关系,并说明理由.【答案】(1)详见解析;(2)①详见解析;②PB+PC+PD=BE,理由详见解析【详解】(1)证明:∵△ABC和△DCE都是等边三角形,∴BC=AC,CE=CD,∠ACB=∠DCE=60°,∴∠ABC+∠ACE=∠DCE+∠ACE,即∠BCE=∠ACD,∴△BCE≌△ACD(SAS),∴BE=AD;(2)①证明:∵△ABC和△DCE是等边三角形,∴AC=BC,CD=CE,∠ACB=∠DCE=60°,∴∠ACB+∠BCD=∠DCE+∠BCD,即∠ACD=∠BCE,∴△ACD≌△BCE(SAS),∴AD=BE,同理:△ABD≌△CBF(SAS),∴AD=CF,即AD=BE=CF;②解:结论:PB+PC+PD=BE,理由:如图2,AD与BC的交点记作点Q,则∠AQC=∠BQP,由①知,△ACD≌△BCE,∴∠CAD=∠CBE,在△ACQ中,∠CAD+∠AQC=180°-∠ACB=120°,∴∠CBE+∠BQP=120°,在△BPQ中,∠APB=180°-(∠CBE+∠BQP)=60°,∴∠DPE=60°,同理:∠APC=60°,∴∠CPE=60°, ∠CPD=120°,在PE上取一点M,使PM=PC,∴△CPM是等边三角形,∴CP=CM=PM,∠PCM=∠CMP=60°,∴∠CME=120°=∠CPD,∵△CDE是等边三角形,∴CD=CE,∠DCE=60°=∠PCM,∴∠PCD=∠MCE,∴△PCD≌△MCE(SAS),∴PD=ME,∴BE=PB+PM+ME=PB+PC+PD.【变式训练】1现有一块含30°角的直角三角板AOB,点N在其斜边AB上,点M在其最短直角边OA所在直线上.以MN为边作如图所示的等边△MNP.(1)如图1,当M在线段OA上时,证明:AM-AN=AP;(2)如图2当M在射线OA上时,试探究AM、AN、AP三者之间的数量关系并给出证明.【答案】(1)见解析;(2)AM+AN=AP,理由见解析【详解】证:(1)由题意可知,∠BAO=60°,如图所示,在AB上取点C,使得AC=AM,则△ACM为等边三角形,MC=MA,∠CMA=60°,∵△NMP为等边三角形,∴MN=MP,∠NMP=60°,∴∠CMA=∠NMP,∴∠CMA-∠NMA=∠NMP-∠NMA,∴∠CMN=∠AMP,在△CMN和△AMP中,MC=MA∠CMN=∠AMP MN=MP∴△CMN≌△AMP(SAS),∴CN=AP,∴CN+AN=AP+AN=AC,∵AC=AM,∴AP+AN=AM,∴AM-AN=AP;(2)AM+AN=AP,理由如下:如图所示,在射线AO上取点D,使得AN=AD,∵∠BAO=60°,∴△AND 为等边三角形,ND =NA ,∠DNA =60°,∵△NMP 为等边三角形,∴NM =NP ,∠MNP =60°,∴∠DNA =∠MNP ,∴∠DNA +∠ANM =∠MNP +∠ANM ,∴∠DNM =∠ANP ,在△DNM 和△ANP 中,ND =NA∠DNM =∠ANPNM =NP∴△DNM ≌△ANP (SAS ),∴AP =DM ,∵AN =AD ,DA +AM =DM ,∴AN +AM =AP .2如图1,在△ABC 中,AE ⊥BC 于E ,AE =BE ,D 是AE 上一点,且DE =CE ,连接BD ,CD .(1)判断BD 与AC 的位置关系和数量关系,并证明;(2)如图2,若将△DCE 绕点E 旋转一定的角度后,BD 与AC 的位置关系和数量关系是否发生变化?并证明;(3)如图3,将(2)中的等腰直角三角形都换成等边三角形,其他条件不变,求BD 与AC夹角的度数.【答案】(1)BD ⊥AC ,BD =AC ;(2)BD ⊥AC ,BD =AC ;(3)60°.【详解】解:(1)BD 与AC 的位置关系是:BD ⊥AC ,数量关系是BD =AC .理由如下:如图1,延长BD 交AC 于点F .∵AE ⊥BC 于E ,∴∠BED =∠AEC =90°.∵AE =BE ,DE =CE ,∴△DBE ≅△CAE ,∴BD =AC ,∠DBE =∠CAE ,∠BDE =∠ACE .∵∠BDE =∠ADF ,∴∠ADF =∠ACE .∵AE ⊥BC∴∠ACE +∠CAE =90°,∴∠ADF +∠CAE =90°,∴BD ⊥AC .(2)BD 与AC 的位置关系是:BD ⊥AC ,数量关系是BD =AC .如图,线段AC 与线段BD 交于点F ,线段AE 与线段BD 交于点G,∵∠AEB =∠DEC =90°,∴∠AEB +∠AED =∠DEC +∠AED ,即∠BED =∠AEC .∵AE =BE ,DE =CE ,∴△BED ≅△AEC ,∴BD =AC ,∠DBE =∠CAE .∵AE ⊥BC∴∠DBE +∠BGE =90°,又∵∠FGA =∠BGE∴∠FGA +∠CAE =90°,∴BD ⊥AC .(3)如图,线段AC 与线段BD 交于点F ,∵△ABE 和△DEC 是等边三角形,∴AE =BE ,DE =EC ,∠EDC =∠DCE =60°,∠BEA =∠DEC =60°,∴∠BEA +∠AED =∠DEC +∠AED ,∴∠BED =∠AEC ,在△BED 和△AEC 中,BE =AE∠BED =∠AECDE =EC∴△BED ≅△AEC ,∴∠BDE =∠ACE ,∴∠BED +∠ACD =∠ACE +∠ACD =60°,∴∠DFC =180°-(∠EDC +∠BDE +∠ACD )=60°∴BD 与AC 的夹角度数为60°.3在△ABC 中,AB =AC ,点D 是直线BC 上一点(不与B ,C 重合),以AD 为一边在AD 的右侧作△ADE ,使AD =AE ,∠DAE =∠BAC ,连接CE.(1)(请直接写出你的结论)如图1,当点D 在线段BC 上:①如果∠BAC =90°,则∠BCE =°;②如果∠BAC =100°,则∠BCE =°;(2)设∠BAC =α,∠BCE =β.①如图2,当点D 在线段BC 上移动,则α、β之间有怎样的数量关系?请说明理由;②当点D 在直线BC 上移动,则α、β之间有怎样的数量关系?请画出图形,并直接写出你的结论.【答案】(1)①90;②80;(2)①α+β=180°,理由见解析;②图见解析,α+β=180°或α=β【详解】解:(1)①∵AB=AC,∠BAC=90°,∴∠ABC=∠ACB=45°,∵∠DAE=∠BAC,∴∠BAD=∠CAE,∵AB=AC,AD=AE,∴△BAD≌△CAE(SAS)∴∠ABC=∠ACE=45°,∴∠BCE=∠ACB+∠ACE=90°,故答案为:90;②∵∠BAC=100°,AB=AC,∴∠ABD=∠ACB=40°,∵∠BAC=∠DAE,∴∠BAD=∠CAE,在△ABD和△ACE中,∵∠BAD=∠CAE,∵AB=AC,AD=AE,∴△ABD≌△ACE(SAS),∴∠ABD=∠ACE=40°,∴∠BCE=∠ACE+∠ACB=40°+40°=80°,故答案为:80.(2)①α+β=180°,理由:∵∠BAC=∠DAE,∴∠BAC-∠DAC=∠DAE-∠DAC.即∠BAD=∠CAE.在△ABD与△ACE中,AB=AC∠BAD=∠CAE AD=AE,∴△ABD≌△ACE(SAS),∴∠B=∠ACE.∴∠B+∠ACB=∠ACE+∠ACB.∵∠ACE+∠ACB=β,∴∠B+∠ACB=β,∵α+∠B+∠ACB=180°,∴α+β=180°.②如图1:当点D在射线BC上时,α+β=180°,连接CE,∵∠BAC=∠DAE,∴∠BAD=∠CAE,在△ABD 和△ACE 中,AB =AC∠BAD =∠CAE AD =AE,∴△ABD ≌△ACE (SAS ),∴∠ABD =∠ACE ,在△ABC 中,∠BAC +∠B +∠ACB =180°,∴∠BAC +∠ACE +∠ACB =∠BAC +∠BCE =180°,即:∠BCE +∠BAC =180°,∴α+β=180°,如图2:当点D 在射线BC 的反向延长线上时,α=β.连接BE ,∵∠BAC =∠DAE ,∴∠BAD =∠CAE ,又∵AB =AC ,AD =AE ,∴△ABD ≌△ACE (SAS ),∴∠ABD =∠ACE ,∴∠ABD =∠ACE =∠ACB +∠BCE ,∴∠ABD +∠ABC =∠ACE +∠ABC =∠ACB +∠BCE +∠ABC =180°,∵∠BAC =180°-∠ABC -∠ACB ,∴∠BAC =∠BCE .∴α=β;综上所述:点D 在直线BC 上移动,α+β=180°或α=β.4如图1,在△ABC 中,CA =CB ,∠ACB =90°.点D 是AC 中点,连接BD ,过点A 作AE ⊥BD 交BD 的延长线于点E ,过点C 作CF ⊥BD 于点F .(1)求证:∠EAD =∠CBD ;(2)求证:BF =2AE ;(3)如图2,将△BCF 沿BC 翻折得到△BCG ,连接AG ,请猜想并证明线段AG 和AB的数量关系.【答案】(1)见解析;(2)见解析;(3):AG =AB ,理由见解析【详解】(1)证明:∵AE ⊥BD ,∴∠AED =90°,∴∠EAD +∠ADE =90°,∵∠ADE =∠BDC ,∴∠EAD +∠BDC =90°,∵∠ACB=90°,∴∠CBD+∠BDC=90°,∴∠EAD=∠CBD;(2)证明:如图1,连接CE,在BF上截取BP=AE,连接CP,∵∠EAD=∠CBD,AC=BC,∴△AEC≌△BPC(SAS),∴CE=CP,∠ACE=∠BCP,∴∠ACE+∠DCP=∠BCP+∠DCP,∴∠ECP=∠DCB=90°,∵CE=CP,CF⊥BD,∴∠CEP=∠CPF=∠PCF=45°,∴CF=PF,∵点D是AC的中点,∴AD=CD,∵∠AED=∠CFD=90°,∠ADE=∠CDF,∴△AED≌△CFD(AAS),∴AE=CF,∴AE=PF,∴BF=BP+PF=2AE;(3)结论:AG=AB,证明如下:如图2,取BG的中点H,连接CE,CH,AH,∴BH=12BG=12BF=AE,∵∠HBC=∠PBC=∠EAC,∴∠EAC+∠CAB=∠HBC+∠CBA,∴∠EAB=∠HBA,∵AB=BA,∴△AEB≌△BHA(SAS),∴∠BHA=∠AEB=90°,∴AH⊥BG,∵BH=HG,∴AG=AB.课后训练5如图,在Rt△ABC中,∠ABC=90°,AB=BC,点D为三角形右侧外一点.且∠BDC=45°.连接AD,若△ACD的面积为98,则线段CD的长度为.【答案】32【详解】解:过点B 作BE ⊥BD ,交DC 的延长线于点E ,连接AE ,如图所示:∵∠ABC =90°,∴∠ABE +∠EBC =∠EBC +∠CBD =90°,∴∠ABE =∠CBD ,∵∠BDC =45°,∠EBD =90°,∴△EBD 是等腰直角三角形,∴∠BDC =∠BED =45°,BE =BD ,∵AB =BC ,∴△BCD ≌△BAE (SAS ),∴∠BDC =∠BEA =45°,AE =CD ,∴∠AED =∠AEB +∠BED =90°,∵S △ACD =12CD ⋅AE =98,∴CD 2=94,∴CD =32;故答案为32.6如图1,在Rt △ABC 中,∠A =90°,AB =AC ,点D 、E 分别在边AB ,AC 上,AD =AE ,连接DC ,点M ,P ,N 分别为DE ,DC ,BC 的中点.(1)观察猜想:图中,线段PM 与PN 的数量关系是,位置关系是;(2)探究证明:把△ADE 绕点A 逆时针方向旋转到图2的位置,连接MN ,BD ,CE ,判断△PMN 的形状,并说明理由;(3)拓展延伸:把△ADE 绕点A 在平面内自由旋转,若AD =4,AB =10,请直接写出△PMN 面积的最大值.【答案】(1)PM =PN ,PM ⊥PN(2)△PMN 是等腰直角三角形(3)S △PMN 最大=492【详解】(1)∵点P ,N 是BC ,CD 的中点,∴PN ∥BD ,PN =12BD ,∵点P,M是CD,DE的中点,∴PM∥CE,PM=12CE,∴AB=AC,AD=AE,∴BD=CE,∴PM=PN,∵PN∥BD,∴∠DPN=∠ADC,∵PM∥CE,∴∠DPM=∠DCA,∵∠BAC=90°,∴∠ADC+∠ACD=90°,∴∠MPN=∠DPM+∠DPN=∠DCA+∠ADC=90°,∴PM⊥PN,故答案为:PM=PN,PM⊥PN;(2)△PMN是等腰直角三角形,理由如下:由旋转知,∠BAD=∠CAE,∵AB=AC,AD=AE,∴△ABD≅△ACE(SAS),∴∠ABD=∠ACE,BD=CE,利用三角形的中位线得,PN=12BD,PM=12CE,∴PM=PN,∴△PMN是等腰三角形,同(1)的方法得,PM∥CE,∴∠DPM=∠DCE,同(1)的方法得,PN∥BD,∴∠PNC=∠DBC,∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC,∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC=∠BCE+∠DBC=∠ACB+∠ACE+∠DBC=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC,∵∠BAC=90°,∴∠ACB+∠ABC=90°,∴∠MPN=90°,∴△PMN是等腰直角三角形;(3)由(2)知,△PMN是等腰直角三角形,PM=PN=12BD,∴PM最大时,△PMN面积最大,∴点D在BA的延长线上,∴BD=AB+AD=14,∴PM=7,∴S △PMN 最大=12PM 2=12×72=492.7【问题发现】(1)如图1,△ABC 和△ADE 均为等边三角形,点B ,D ,E 在同一直线上,连接CE ,容易发现:①∠BEC 的度数为;②线段BD 、CE 之间的数量关系为;【类比探究】(2)如图2,△ABC 和△ADE 均为等腰直角三角形,∠BAC =∠DAE =90°,点B ,D ,E 在同一直线上,连接CE ,试判断∠BEC 的度数以及线段BE 、CE 、DE 之间的数量关系,并说明理由;【问题解决】(3)如图3,∠AOB =∠ACB =90°,OA =4,OB =8,AC =BC ,则OC 2的值为.【答案】(1)①60°;②BD =CE ;(2)∠BEC =90°,BE =CE +DE ,见解析;(3)8【详解】解:(1)∵△ABC 和△ADE 均为等边三角形,∴AB =AC ,AD =AE ,∠BAC =∠DAE =60°,∴∠BAC -∠DAC =∠DAE -∠DAC ,即∠BAD =∠CAE ,在△BAD 和△CAE 中,AB =AC∠BAD =∠CAE AD =AE,∴△ABD ≌△ACE (SAS ),∴BD =CE ,∠AEC =∠ADB =180°-∠ADE =120°,∴∠BEC =∠AEC -∠AED =120°-60°=60°,故答案为:60°,BD =CE ;(2)∠BEC =90°,BE =CE +DE ,理由如下:∵∠BAC =∠DAE =90°,△ABC 和△ADE 均为等腰直角三角形,∴AB =AC ,AD =AE ,∠BAC =∠DAE =90°,∠ADE =∠AED =45°∠BAC -∠DAC =∠DAE -∠DAC ,即∠BAD =∠CAE ,在△ABD 和△ACE 中,AB =AC∠BAD =∠CAE AD =AE,∴△ABD ≌△ACE (SAS ),∴BD =CE ,∠AEC =∠ADB =135°,∴∠BEC =∠AEC -∠AED =135°-45°=90°,∵BE =BD +DE ,∴BE =CE +DE ;(3)如图3,过点C 作EF ∥OB ,交AO 的延长线于F ,过点B 作BE ⊥EF 于E ,∴∠F=∠AOB=∠BOF=90°,∠E=90°,∴四边形BOFE是矩形,∴OB=EF=8,BE=OF,∵∠ACB=90°,∴∠BCE+∠ACF=90°,∵∠ACF+∠CAF=90°,∴∠CAF=∠BCE,∵∠F=∠E=90°,AC=BC,∴△ACF≌△CBE(AAS),∴CF=BE,AF=CE,设OF=x,则AF=4+x,CE=8-x,∴4+x=8-x∴x=2,∴OF=2,AF=CE=6,∴CF=BE=OF=2,∴在Rt△COF中,OC2=OF2+CF2=22+22=8.故答案为:8.8已知在△ABC中,AB=AC,过点B引一条射线BM,D是BM上一点【问题解决】(1)如图1,若∠ABC=60°,射线BM在∠ABC内部,∠ADB=60°,求证:∠BDC=60°,小明同学展示的做法是:在BM上取一点E使得AE=AD,通过已知的条件,从而求得∠BDC的度数,请你帮助小明写出证明过程;【类比探究】(2)如图2,已知∠ABC=∠ADB=30°.①当射线BM在∠ABC内,求∠BDC的度数②当射线BM在BC下方,如图3所示,请问∠BDC的度数会变化吗?若不变,请说明理由,若改变,请求出∠BDC的度数;【答案】(1)见解析(2)①∠BDC=120°②;∠BDC的度数会变化,理由见解析【详解】(1)证明:如图1,在BM上取一点E,使AE=AD,∵∠ADB=60°,∴△ADE是等边三角形,∴∠EAD=60°,∵AB=AC,∠ABC=60°,∴△ABC是等边三角形,∴∠BAC=60°,∴∠BAC=∠EAD,∴∠BAC-∠EAC=∠EAD-∠EAC,即∠BAE=∠CAD,∵在△BAE和△CAD中AB=AC∠BAE=∠CAD AE=AD,∴△BAE≌△CAD SAS,∴∠ADC =∠AEB =120°,∴∠BDC =120°-60°=60°;(2)证明:①在BD 上取一点E ,AE =AD ,如图所示:∵∠ABC =∠ADB =30°,AB =AC ,∴∠ABC =∠ACB =30°,∠AED =∠ADE =30°,∴∠BAC =∠EAD =120°,∴∠BAE =∠CAD ,∵在△BAE 和△CAD 中AB =AC∠BAE =∠CAD AE =AD,∴△BAE ≌△CAD SAS ,∴∠ADC =∠AEB =180°-30°=150°,∴∠BDC =150°-30°=120°;②∠BDC 的度数会变化,理由如下:在DB 延长线上取一点E ,使得AE =AD ,如图所示:同理①的方法可证:△BAE ≌△CAD ,∴∠ADC =∠E =30°,∴∠BDC =∠ADE +∠ADC =30°+30°=60°.9(1)如图1,△ABC 与△CDE 均为等腰直角三角形,∠ACB =∠DCE =90°,猜想并证明:线段AE 、BD的数量关系和位置关系.(2)在(1)的条件下,若点A ,E ,D 在同一直线上,CM 为△DCE 中DE 边上的高,请判断∠ADB 的度数及线段CM ,AD ,BD 之间的数量关系,并说明理由.【答案】(1)AE =BD ,AE ⊥BD ,证明见解析.(2)∠ADB =90°,AD =2CM +BD .证明见解析【详解】解:(1)如图1中,延长AE 交BD 于点H ,AH 交BC 于点O ,∵△ACB 和△DCE 均为等腰直角三角形,∠ACB =∠DCE =90°,∴AC =BC ,CD =CE ,∴∠ACE =∠BCD ,∴△ACE ≌△BCD (SAS ),∴AE =BD ,∠CAE =∠CBD,∵∠CAE+∠AOC=90°,∠AOC=∠BOH,∴∠BOH+∠CBD=90°.∴∠AHB=90°,∴AE⊥BD.故答案为AE=BD,AE⊥BD;(2)∠ADB=90°,AD=2CM+BD,理由如下:如图2中,∵△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,∴∠CDE=∠CED=45°,∴∠AEC=180°-∠CED=135°,由(2)可知:△ACE≌△BCD,∴AE=BD,∠BDC=∠AEC=135°,∴∠ADB=∠BDC-∠CDE=135°-45°=90°;在等腰直角三角形DCE中,CM为斜边DE上的高,∴CM=DM=ME,∴DE=2CM,∴AD=DE+AE=2CM+BD .10已知△ABC,分别以AB、AC为边作△ABD和△ACE,且AD=AB,AC=AE,∠DAB=∠CAE,连接DC与BE,G、F分别是DC与BE的中点.(1)如图1,若∠DAB=60°,则∠AFG=;(2)如图2,若∠DAB=90°,则∠AFG=;(3)如图3,若∠DAB=α,试探究∠AFG与α的数量关系,并给予证明.【答案】(1)60°;(2)45°;(3)12(180°-α),证明见解析【解析】(1)连接AG.∵∠DAB=∠CAE,∴∠DAB+∠BAC=∠CAE+∠BAC,∴∠DAC=∠BAE.在△ADC和△ABE中,AD=AB∠DAC=∠BAE AC=AE,∴△ADC≌△ABE(SAS),∴DC =BE ,∠ADC =∠ABE .∵G 、F 分别是DC 与BE 的中点,∴DG =12DC ,BF =12BE ,∴DG =BF .在△ADG 和△ABF 中,AD =AB∠ADC =∠ABE DG =BF,∴△ADG ≌△ABF (SAS ),∴AG =AF ,∠DAG =∠BAF ,∴∠AGF =∠AFG ,∠DAG -∠BAG =∠BAF -∠BAG ,∴∠DAB =∠GAF .∵∠DAB =60°,∴∠GAF =60°.∵∠GAF +∠AFG +∠AGF =180°,∴∠AFG =60°;故答案为60°,(2)连接AG ,如图2,∵∠DAB =90°,∠DAB =∠GAF ,(已证)∴∠GAF =90°,∵AG =AF ,∴∠AFG =12×(180°-90°)=45°;故答案为45°,(3)连接AG ,如图3,∵∠DAB =α,∠DAB =∠GAF ,(已证)∴∠GAF =α,∵AG =AF ,∴∠AFG =12(180°-α).11△ACB 和△DCE 是共顶点C 的两个大小不一样的等边三角形.(1)问题发现:如图1,若点A,D,E在同一直线上,连接AE,BE.①求证:△ACD≌△BCE;②求∠AEB的度数.(2)类比探究:如图2,点B、D、E在同一直线上,连接AE,AD,BE,CM为△DCE中DE边上的高,请求∠ADB的度数及线段DB,AD,DM之间的数量关系,并说明理由.(3)拓展延伸:如图3,若设AD(或其延长线)与BE的所夹锐角为α,则你认为α为多少度,并证明.【答案】(1)①见解析;②∠AEB=60°;(2)∠ADB=60°,2DM+BD=AD,理由见解析;(3)α=60°,证明见解析【解析】(1)①证明:∵△ACB和△DCE是等边三角形,∴AC=BC,CD=CE,∠ACB=∠DCE=60°,∴∠ACD=60°-∠DCB=∠BCE,∴△ACD≌△BCE(SAS);②∵△ACD≌△BCE,∴∠ADC=∠BEC=180°-∠CDE=120°,又∵∠CED=60°,∴∠AEB=60°;(2)解:∠ADB=60°,2DM+BD=AD,理由如下;∵AC=BC,CD=CE,∠ACD=60°+∠DCB=∠BCE,∴△ACD≌△BCE(SAS),∴∠CDA=∠CED=60°;∵∠ADB+∠CDA=∠DCE+∠CED,∴∠ADB=60°;又∵CM⊥BE,且△CDE为等边三角形,∴DE=2DM,∴2DM+BD=BE=AD;(3)解:α=60°,理由如下:同理可证△ACD≌△BCE,∴∠BEC=∠ADC,∴∠CDF+∠CEF=180°,∴∠ECD+∠DFE=180°,而α+∠DFE=180°,∴α=∠ECD=60°.12(1)问题发现:如图1,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,连接AD,BE,点A、D、E在同一条直线上,则∠AEB的度数为,线段AD、BE之间的数量关系;(2)拓展探究:如图2,△ACB 和△DCE 均为等腰直角三角形,∠ACB =∠DCE =90°,连接AD ,BE ,点A 、D 、E 不在一条直线上,请判断线段AD 、BE 之间的数量关系和位置关系,并说明理由.(3)解决问题:如图3,△ACB 和△DCE 均为等腰三角形,∠ACB =∠DCE =α,则直线AD 和BE 的夹角为.(请用含α的式子表示)【答案】(1)90°,AD =BE ;(2)AD =BE ,AD ⊥BE ;(3)α【详解】(1)∵△ACB 和△DCE 均为等腰直角三角形,∠ACB =∠DCE =90°,∴AC =BC ,CD =CE ,∠CDE =45°∴∠CDA =135°∵∠ACB -∠DCB =∠DCE -∠DCB ,∴∠ACD =∠BCE .在△ACD 和△BCE 中,AC =BC∠ACD =∠BCE CD =CE,∴△ACD ≌△BCE (SAS ),∴∠BEC =∠ADC =135°,AD =BE∴∠AEB =90°故答案为:90°,AD =BE(2)AD =BE ,AD ⊥BE ,理由如下,同理可得△ACD ≌△BCE ,则AD =BE ,延长AD 交BE 于点F ,设∠FAB =α,则∠CAD =∠CBE =45°-α∴∠ABE =45°+45°-α=90°-α∴∠AFB =180°-∠FAB -∠ABE =180°-α-(90°-α)=90°∴AD ⊥BE(3)如图,延长BE 交AD 于点G ,∵△ACB 和△DCE 均为等腰三角形,∴AC =BC ,CD =CE ,∵∠ACB =∠DCE =α,∵∠ACB +∠ACE =∠DCE +∠ACE ,∴∠ACD =∠BCE .CD =CE∴△ACD ≌△BCE (SAS ),∴∠CBE =∠CAD∵∠ACB =∠DCE =α∴∠CBA =∠CAB =12180°-α =90°-12α∴∠GAB +∠GBA =∠CAD +∠CAB +∠ABC -∠CBE ,=∠ABC +∠CAB =180°-α,∴∠AGB =180°-(∠GAB +∠GBA )=α,即直线AD 和BE 的夹角为α.故答案为:α.13已知,在△ABC 中,∠A =90°,AB =AC ,点D 为BC 的中点.(1)观察猜想如图①,若点E 、F 分别是AB 、AC 的中点,则线段DE 与DF 的数量关系是;线段DE 与DF 的位置关系是.(2)类比探究如图②,若点E 、F 分别是AB 、AC 上的点,且BE =AF ,上述结论是否仍然成立,若成立,请证明:若不成立,请说明理由;(3)解决问题如图③,若点E 、F 分别为AB 、CA 延长线的点,且BE =AF =13AB =2,请直接写出△DEF 的面积.【答案】(1)DE =DF ,DE ⊥DF ;(2)成立,证明见解析;(3)17【详解】解:(1)∵点E 、F 、D 分别是AB 、AC 、BC 的中点,∴ED =12AC ,DF =12AB ,ED ∥AC ,DF ∥AB ,∵AB =AC ,∠A =90°,∴DE =DF ,∠BDE =∠FDC =∠C =45°,∴∠EDF =90°即DE ⊥DF ,故答案为:DE =DF ,DE ⊥DF ;(2)结论成立:DE =DF ,DE ⊥DF ,证明:如图所示,连接AD ,∵AB =AC ,∠BAC =90°,D 为BC 的中点,∴AD =12BC =BD =CD ,且AD 平分∠BAC ,∠B =∠C =45°,∴∠BAD =∠CAD =45°,BE =AF∴△BDE ≌△ADF SAS ,∴DE =DF ,∠BDE =∠ADF ,∵∠BDE +∠ADE =90°,∴∠ADF +∠ADE =90°,即∠EDF =90°,即DE ⊥DF ;(3)如图所示,连接AD ,∵AB =AC ,∠BAC =90°,D 为BC 的中点,∴AD =12BC =BD =CD ,且AD 平分∠BAC ,∠ABC =∠C =45°,∴∠BAD =∠CAD =45°,∴∠FAD =180°-∠CAD =135°,∠EBD =180°-∠ABC =135°,∴∠FAD =∠EBD ,在在△BDE 和△ADF 中,BD =AD∠EBD =∠FAD BE =AF,∴△BDE ≌△ADF (SAS ),∴S △BDE =S △ADF ,∴S △DEF =S △ABD +S △AEF =12S △ABC +S △AEF,∵BE =AF =13AB =2,∴AB =AC =6,∴AE =AB +BE =8,∴S △DEF =12S △ABC +S △AEF =12×2×8+12×12×6×6=1714如图,在等边三角形ABC 右侧作射线CP ,∠ACP =α<60°,点A 关于射线CP 的对称点为点D ,连接BD 交CP 于点E ,连接AD ,CD ,AE .(1)用含α的式子表示∠BCD ;(2)求∠BEC 的度数;(3)试探究线段BD 、AE 、CE 之间的数量关系,并证明.【答案】(1)∠BCD =60°+2α;(2)60°;(3)BD =2AE +CE ,证明见解析【详解】(1)∵点A 关于射线CP 的对称点为点D ,∴PC 垂直平分AD ,∴AC=DC,∠ACP=∠DCP=α,∴∠ACD=2α,∵△ABC是等边三角形,∴∠ACB=60°,∴∠BCD=∠BCA+∠ACD=60°+2α,(2)由(1)得∠BCD=60°+2α,∵△ABC是等边三角形,∴BC=AC,又∵AC=DC,∴BC=DC,∴∠DBC=∠BDC=180°-60°-2α2=60°-α,∴∠BEC=180°-∠DBC-∠BCE=180°-(60°-α)-(60°+α)=60°;(3)答:BD=2AE+CE;证明:在BE上取点F,使得EF=EC,连接FC,∵∠BEC=60º,∴△EFC是等边三角形,∴∠ECF=∠ACB=60°,EF=FC=EC,∴∠ECF-∠ACF=∠ACB-∠ACF即∠BCF=∠ACE,在△BCF和△ACE中,AC=BC∠ACE=∠BCF FC=EC,∴△BCF≌△ACE(SAS),∴BF=AE,∵PC垂直平分AD,∴DE=AE,∴BD=BF+EF+DE,即BD=2AE+CE.·21·。
全等五边形模型之手拉手模型

全等五边形模型之手拉手模型
模型介绍
全等五边形模型是一种立体几何模型,由五个全等的五边形构成。
手拉手模型是一种特殊的全等五边形模型,通过将五个全等五边形相互连接形成一个有趣的结构。
模型制作步骤
1. 准备五个全等五边形的模型。
可以使用纸板、塑料或其他材料制作。
确保五个五边形的边长、角度和相邻边的长度完全相同。
2. 将五个全等五边形排列成一个闭合的环状。
确保每个五边形的边与相邻五边形的边紧密相连。
3. 选择任意一个五边形,将其一边平行地连接到另一个五边形的对应边。
这样,两个五边形就通过一条共同的边连接在一起了。
4. 重复第3步,将其他剩下的五边形不断地连接在一起,直到所有五边形都相互连接成一个大的结构。
5. 最后,检查手拉手模型是否已完全连接,并确保没有松动的部分。
应用与拓展
手拉手模型可以用作教学工具,用于教授几何学和立体几何的相关概念。
它展示了全等五边形的特性,并引发学生们对立体几何的兴趣。
此外,手拉手模型还可以通过改变五边形的材料、颜色或尺寸来创造不同的效果。
例如,可以使用透明的材料制作手拉手模型,从而展示内部结构。
还可以尝试使用更多的全等五边形来构建更复杂的结构。
手拉手模型的制作过程可以激发学生们的创造力和问题解决能力。
他们可以尝试探索不同的组合方式,寻找更多可能的结构。
结论
全等五边形模型的手拉手模型是一个有趣而简单的立体几何项目。
通过制作和探索这个模型,学生们可以进一步理解全等五边形的特性,并培养他们的几何学习兴趣和创造力。
专题12.19 三角形全等几何模型-“手拉手”模型(知识讲解)
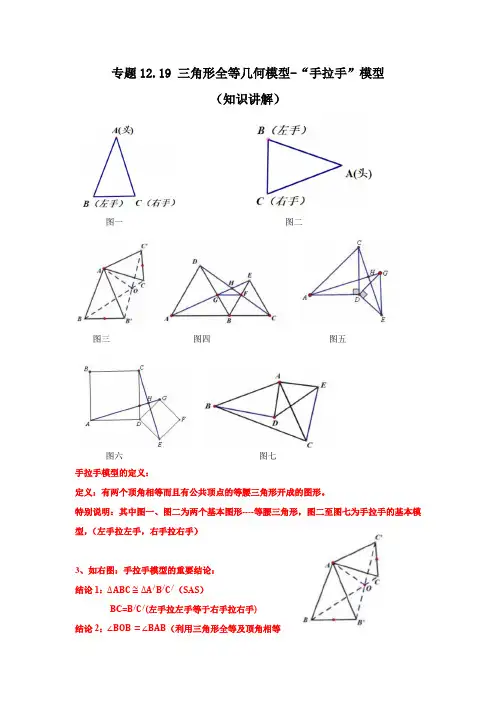
专题12.19 三角形全等几何模型-“手拉手”模型(知识讲解)图一图二图三图四图五图六图七手拉手模型的定义:定义:有两个顶角相等而且有公共顶点的等腰三角形开成的图形。
特别说明:其中图一、图二为两个基本图形----等腰三角形,图二至图七为手拉手的基本模型,(左手拉左手,右手拉右手)3、如右图:手拉手模型的重要结论:结论1:∆ABC≅∆A/B/C/(SAS)BC=B/C/(左手拉左手等于右手拉右手)结论2:∠BOB=∠BAB(利用三角形全等及顶角相等的等腰三角形底角相等)结论3:AO平分∠B O C/(利用三角形全等面积相等,再利用角平分线性质定理证明)典型例题讲练:在学习全等三角形知识时、教学兴趣小组发现这样一个模型:它是由两个共顶点且顶角相等的等腰三角形构成.在相对位置变化的同时,始终存在一对全等三角形.通过资料查询,他们得知这种模型称为“手拉手模型” 兴趣小组进行了如下操究:(1)如图1、两个等腰三角形△ABC和△ADE中,AB=AC,AE=AD,△BAC=△DAE,连接BD、CE、如果把小等腰三角形的腰长看作小手,大等腰三角形的腰长看作大手,两个等腰三角形有公共顶点,类似大手拉着小手,这个就是“手拉手模型”,在这个模型中,和△ADB 全等的三角形是,此线BD和CE的数量关系是(2)如图2、两个等腰直角三角形△ABC和△ADE中,AB=AC,AE=AD,△BAC=△DAE=90°,连接BD,CE,两线交于点P,请判断线段BD和CE的数量关系和位置关系,并说明理由:(3)如图3,已知△ABC、请完成作图:以AB、AC为边分别向△ABC外作等边△ABD和等边△ACE(等边三角形三条边相等,三个角都等于60°),连接BE,CD,两线交于点P,并直接写出线段BE和CD的数量关系及△PBC+△PCB的度数、【答案】(1)△AEC,BD=CE;(2)BD=CE且BD△CE,理由见解析;(3)作图见解析,BE=CD,△PBC+△PCB=60°.【分析】(1)根据SAS证明两个三角形全等即可证明;(2)通过条件证明△DAB△△EAC(SAS),得到△DBC+△ECB=90°,即可证明BD△CE,从而得到结果;≅即可得到证明;(3)根据已知条件证明DAC BAE解:(1)△AB=AC,AE=AD,△BAC=△DAE,∠+∠=∠+∠,△DAE EAB BAC EAB即DAB EAC ∠=∠,△()△△ADB AEC SAS ≅,△BD=CE ;(2)BD=CE 且BD△CE ;理由如下:因为△DAE=△BAC=90°,如图2.所以△DAE+△BAE=△BAC+△BAE .所以△DAB=△EAC .在△DAB 和△EAC 中,,,.AD AE DAB EAC AB AC =⎧⎪∠=∠⎨⎪=⎩所以△DAB△△EAC (SAS ).所以BD=CE ,△DBA=△ECA .因为△ECA+△ECB+△ABC=90°,所以△DBA+△ECB+△ABC=90°.即△DBC+△ECB=90°.所以△BPC=180°-(△DBC+△ECB )=90°.所以BD△CE .综上所述:BD=CE 且BD△CE .(3)如图3所示,BE=CD ,△PBC+△PCB=60°.由图可知60DAB EAC ∠=∠=︒,AD=AB ,AE=AC ,△+DAB BAC EAC BAC ∠∠=∠+∠,即DAC BAE ∠=∠,△()△DAE △BAE SAS ≅,△BE=CD ,ABE ADC ∠=∠,又△60BDA ∠=︒,△60ADC BDC ABE BDC ∠+∠=∠+∠=︒,△120BPC ABP BDC BDA ∠=∠+∠+∠=︒,△△PBC+△PCB=60°.【点拨】本题主要考查了全等三角形的知识点应用,准确分析图形是解题的关键. 举一反三变式1:如图,AC △BC ,DC △EC ,AC =BC ,DC =EC ,AE 与BD 交于点F .(1)求证:AE =BD ;(2)求△AFD 的度数.【答案】(1)详情见解析;(2)90AFD ∠=︒【分析】(1)利用角的等量代换求出ACE BCD ∠=∠,再判断ACE ≌BCD △即可求解; (2)利用全等三角形的性质得到E D ∠=∠,再通过角的等量代换求解即可.解:(1)△AC BC ⊥,DC EC ⊥△90ACB ECD ∠=∠=︒△ACB BCE ECD BCE ∠+∠=∠+∠△ACE BCD ∠=∠在ACE 和BCD △中AC BC ACE BCD DC EC =⎧⎪∠=∠⎨⎪=⎩△ACE ≌BCD △(SAS)△AE BD =(2)设BD 与CE 的交点为G ,如图所示:△ACE ≌BCD △△E D ∠=∠△180EFG FGE E ++=︒∠∠∠,180GCD CGD D ++=︒∠∠∠,且BGE CGD ∠=∠△90EFG GCD ==︒∠∠△90AFD ∠=︒【点拨】本题主要考查了全等三角形的性质和判定,灵活运用角的等量代换是解题的关键.例题2.已如:如图1,B ,C ,D 三点在一条直线上,△ABC 和△ECD 均为等边三角形,连接BE ,AD 交于点F ,BE 交AC 于点M ,AD 交CE 于点N .(1)以下结论正确的有 ;△AD =BE △△EFD =60° △MC =NC △△AMB =△END(2)探究:将图1中的△ECD 绕点C 顺时针旋转一个角度(旋转角小于60°),如图2所示. △问:(1)中的正确结论哪些还成立?若成立,请说明理由;△连接FC ,如图3所示,求证:FC 平分△BFD【答案】(1)△△△;(2)△ △△;△见解析.【分析】(1)△根据等边三角形的性质得CA =CB ,CD =CE ,△ACB =60°,△DCE =60°,则△ACE =60°,利用“SAS ”可判断△ACD △△BCE ,则AD =BE ;△根据三角形外角关系得△EFD =△EBC +△ADC =△DAC +△ADC =△ACB =60°,从而可得结论; △连接MN ,证明△MCN 是等边三角形即可得出结论;△60,60AMB EBC END NDC ∠=︒+∠∠=︒+∠,而AC ≠CD 得CAD CDA ∠≠∠,从而可得出结论;(2)△方法同(1),逐个结论进行证明即可;△作,CG BE CH AD ⊥⊥于点G ,H ,证明△BGC △△AHC ,△CGF △△CHF 可得△CFG CFH =∠,从而可得结论.解:(1)△△ABC ,△ECD 是等边三角形,△AC=BC ,CE=CD ,△ACB=△ECD=60°△△ACD=△BCE=△120°△△ACD△△BCE△AD=BE ,故△正确;△△FEN=△NDC又△△ENF=△CND△△EFD=△ECD=60°,故△正确;又△△ACE=△NCD=60°△MEC=△NDCEC=CD△△EMC△△DNC△MC=NC ,故△正确;又△△AMB=△ACB+△ECB=60°+△ECB ,△END=△ECD+△NDC=60°+△NDC而AC CD ≠△CAD CDA ∠≠∠△MBC NDC ∠≠∠△MBC END ∠≠∠,故△错误;故答案为:△△△;(2)△△ACB=△ECD=60°△△BCE=△ACD又AC=BC ,CE=CD△△ACD△△BCE△AD=BE,故△正确;△△ADC=△BEC又△ENF=△CND△△EFD=△ECD=60°,故△正确△△ACE≠60°=△ECD△△EMC 不全等于△DNC ,△MC≠NC ,故△错误(3),CG BE CH AD ⊥⊥于点G ,H ,如图,由(2)△知,△CBG=△CAHAC=BC△BGC=△AHC=90°△△BGC△△AHC△CG=CH又CF=CF ,△CGF=△CHF=90°△△CGF△△CHF△△CFG=△CFH△FC 平分△BFD【点拨】本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS ”、“SAS ”、“ASA ”、“AAS ”;全等三角形的对应边相等.也考查了等边三角形的判定与性质.举一反三变式:如图,在ABC∆中,分别以AC,BC为边作等边三角形ACD和等边三角形BCE,连接AE,BD交于点O,则AOB∠的度数为()A.100︒B.120︒C.130︒D.150︒【答案】B【分析】先证明△DCB△△ACE,求出△CAE=△CDB,再利用“8字型”证明△AOH=△DCH =60°即可解决问题.解:如图:AC与BD交于点H,△△ACD,△BCE都是等边三角形,△CD=CA,CB=CE,△ACD=△BCE=60°,△△DCB=△ACE,在△DCB和△ACE中,CD CADCB ACECB CE⎧⎪∠∠⎨⎪⎩===,△△DCB△△ACE,△△CAE=△CDB,△△DCH+△CHD+△BDC=180°,△AOH+△AHO+△CAE=180°,△DHC=△OHA,△△AOH=△DCH=60°,△△AOB=180°−△AOH=120°.故选:B.【点拨】本题考查全等三角形的判定和性质、等边三角形的性质等知识,解题的关键是正确寻找全等三角形,学会利用“8字型”证明角相等,属于中考常考题型.例题3.(阅读材料)小明同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的项角的顶点,并把它们的底角顶点连接起来则形成一组全等的三角形,小明把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小明发现若△BAC=△DAE,AB=AC,AD=AE,则△ABD△△ACE.(材料理解)(1)在图1中证明小明的发现.(深入探究)(2)如图2,△ABC和△AED是等边三角形,连接BD,EC交于点O,连接AO,下列结论:△BD=EC;△△BOC=60°;△△AOE=60°;△EO=CO,其中正确的有.(将所有正确的序号填在横线上).(延伸应用)(3)如图3,AB=BC,△ABC=△BDC=60°,试探究△A与△C的数量关系.【答案】(1)证明见解析;(2)△△△;(3)△A+△C=180°.【分析】(1)利用等式的性质得出△BAD=△CAE,即可得出结论;(2)同(1)的方法判断出△ABD△△ACE,得出BD=CE,再利用对顶角和三角形的内角和定理判断出△BOC=60°,再判断出△BCF△△ACO,得出△AOC=120°,进而得出△AOE=60°,再判断出BF<CF,进而判断出△OBC>30°,即可得出结论;(3)先判断出△BDP是等边三角形,得出BD=BP,△DBP=60°,进而判断出△ABD△△CBP(SAS ),即可得出结论.(1)证明:△△BAC=△DAE ,△△BAC+△CAD=△DAE+△CAD , △△BAD=△CAE ,在△ABD 和△ACE 中,AB AC BAD CAE AD AE ⎧⎪∠∠⎨⎪⎩=== ,△△ABD△△ACE ;(2)如图2,△△ABC 和△ADE 是等边三角形, △AB=AC ,AD=AE ,△BAC=△DAE=60°, △△BAD=△CAE ,在△ABD 和△ACE 中,AB AC BAD CAE AD AE ⎧⎪∠∠⎨⎪⎩=== ,△△ABD△△ACE ,△BD=CE ,△正确,△ADB=△AEC , 记AD 与CE 的交点为G ,△△AGE=△DGO ,△180°-△ADB -△DGO=180°-△AEC -△AGE , △△DOE=△DAE=60°,△△BOC=60°,△正确,在OB上取一点F,使OF=OC,△△OCF是等边三角形,△CF=OC,△OFC=△OCF=60°=△ACB,△△BCF=△ACO,△AB=AC,△△BCF△△ACO(SAS),△△AOC=△BFC=180°-△OFC=120°,△△AOE=180°-△AOC=60°,△正确,连接AF,要使OC=OE,则有OC=12 CE,△BD=CE,△CF=OF=12 BD,△OF=BF+OD,△BF<CF,△△OBC>△BCF,△△OBC+△BCF=△OFC=60°,△△OBC>30°,而没办法判断△OBC大于30度,所以,△不一定正确,即:正确的有△△△,故答案为△△△;(3)如图3,延长DC至P,使DP=DB,△△BDC=60°,△△BDP 是等边三角形,△BD=BP ,△DBP=60°,△△BAC=60°=△DBP ,△△ABD=△CBP ,△AB=CB ,△△ABD△△CBP (SAS ),△△BCP=△A ,△△BCD+△BCP=180°,△△A+△BCD=180°.【点拨】此题考查三角形综合题,等腰三角形的性质,等边三角形的性质,全等三角形的判定和性质,构造等边三角形是解题的关键.举一反三变式:如图,C 为线段AE 上一动点(不与点,A E 重合),在AE 同侧分别作等边三角形ABC 和等边三角形,CDE AD 与BE 交于点O ,AD 与BC 交于点P ,BE 与CD 交于点Q ,连结PQ .以下结论:①AD BE =;①//PQ AE ;①60AOB ∠=︒;①CPQ 是等边三角形,恒成立的是______.【答案】△△△△【分析】△由△ABC 和△CDE 都是等边三角形,可知AC=BC ,CD=CE ,△ACB=△DCE=60°,所以△ACD=△BCE=120°,所以△ACD△△BCE (SAS ),从而AD=BE ,故△正确;△△由△ACD△△BCE 得△CBE=△DAC ,加之AC=BC ,易得△ACB=△BCQ=60°,可证△CQB△△CPA (ASA ),从而CP=CQ ,再加之△PCQ=60°,可推出△PCQ 为等边三角形,易得△PQC=60°=△DCE ,根据内错角相等,两直线平行,可知△△正确;△结合△ACD△△BCE 和三角形的外角的性质,可得△AOB=60°,故△正确.解:△△等边△ABC 和等边△CDE ,△AC=BC ,CD=CE ,△ACB=△DCE=60°,△△ACB+△BCD=△DCE+△BCD ,即△ACD=△BCE ,△在△ACD 与△BCE 中,AC BC ACD BCE CD CE ⎧⎪∠∠⎨⎪⎩===△△ACD△△BCE (SAS ),△AD=BE ,故△正确;△△△△ACD△△BCE ,△△CBE=△DAC ,△由△ACB=△DCE=60°得△BCD=60°,△△ACP=△BCQ ,又△AC=BC ,△△CQB△△CPA (ASA ),△CP=CQ ,又△△PCQ=60°△△PCQ 为等边三角形,△△PQC=60°,△△PQC=60°=△DCE△PQ△AE故△△正确;△△△ACD△△BCE (SAS ),△△CAD=△CBE ,△△AOB=△CAD+△CEB=△CBE+△CEB ,又△△ACB=△CBE+△CEB=60°,△△AOB=△ACB=60°,故△正确.故答案为:△△△△.【点拨】本题考查了等边三角形的性质、全等三角形的判定与性质、三角形外角的性质,熟练应用三角形全等的判定是解题的关键.。
几何必会模型:手拉手模型

本文为word 版资料,可以任意编辑修 本文为word 版资料,可以任意编辑修手拉手模型模型手拉手如图,△ ABC 是等腰三角形、△ ADE 是等腰三角形,AB = AC, AD = AE ,/ BAC = Z DAE =:-. 结论:连接 BD 、CE ,则有△ BADCAE . 模型分析 如图①,/ BAD = Z BAC-Z DAC ,/ CAE =Z DAE-Z DAC . •••/ BAC =Z DAE =:-, •••Z BAD = Z CAE . 在厶BAD 和厶CAE 中, 【AB =AC , ■' /BAD - • CAE , AD =AE ,图②、图③同理可证. (1)这个图形是由两个共顶点且顶角相等的等腰三角形构成. 在相对位置变化的同时, 始终存在一对全等三角形.(2) 如果把小等腰三角形的腰长看作小手,大等腰三角形的腰长看作大手,两个等腰 三角形有公共顶点,类似大手拉着小手,所以把这个模型称为手拉手模型.(3) 手拉手模型常和旋转结合,在考试中作为几何综合题目出现.EDBC图①BC图②BC图③模型实例例1如图,△ ADC与厶EDG都为等腰直角三角形,连接AG、CE,相交于点H,问:(1)AG与CE是否相等?(2)AG与CE之间的夹角为多少度?解答:(1)AG = CE.理由如下:•••/ ADG = Z ADC + Z CDG , / CDE = Z GDE + Z CDG , / ADC = Z EDG = 90°,•••/ ADG = Z CDE .在厶ADG和厶CDE中,AD 二 CD ,■■: /ADG 二■ CDE ,DG 二DE ,• AG = CE .(2)v^ ADG 也厶 CDE ,•••/ DAG = Z DCE .•••/ COH = Z AOD ,•••/ CHA = Z ADC = 90°.• AG与CE之间的夹角是90°.例2如图,在直线AB的同一侧作△ 形,连接AE、CD,二者交点为 H .求证:(1 )△ ABE◎△ DBC ;(2)AE = DQ ;(3)/ DHA = 60°(4) A AGB ◎△ DFB ;(5) A EGB ◎△ CFB ;(6)连接 GF , GF // AC ; ABD和厶BCE,A ABD和厶BCE都是等边三角G(7)连接 HB, HB 平分/ AHC .证明:(1 )Z ABE = 120° / CBD = 120° 在厶ABE和厶DBC中,BA 二 BD ,/ABE ZDBC ,BE =BC ,•••△ ABE◎△ DBC .(2)T A ABE◎△ DBC ,•AE= DC.(3) A ABE◎△ DBC,•••/ 1 = Z 2.•••/ DGH =Z AGB .•••/ DHA =Z 4= 60°(4)vZ 5= 180° — / 4-Z CBE= 60°•4=/ 5.•/△ ABE也厶 DBC ,•/ 1 = / 2.又••• AB = DB,•△ AGB◎△ DFB (ASA).(5)同(4)可证△ EGB也厶 CFB ( ASA ).(6)如图①所示,连接 GF .由(4)得,△ AGB◎△ DFB .•BG= BF.又•••/ 5 = 60°•△ BGF是等边三角形.•/ 3= 60°••/ 3=/ 4 .• GF // AC .(7)如图②所示,过点 B作BM丄DC于M,过点B作BN丄AE于点N .•/△ ABE◎△ DBC ,•S^ABE = S A DBC .1 1•••丄X AE X BN=丄X CD X BM .2 2•/ AE= CD,•BM = BN .•••点B在/ AHC的平分线上. A B C图②••• HB 平分/ AHC . 练习: 1.在厶ABC 中,AB= CB,Z ABC = 90 ° F 为AB 延长线上一点,点 E 在BC 上,且 AE =CF .(1) 求证:BE= BF ;(2) 若/ CAE = 30° 求/ ACF 度数.答案:(1) 证明:/ ABC = 90° . 在 Rt △ ABE 和 Rt △ CBF 中, CF = AE , AB 二CB ,• Rt △ ABE 也 Rt △ CBF (HL ). • BE= BF.(2) v AB = CB,Z ABC = 90° • / BAC =Z BCA = 45° • / CAE = 30°• / BAE = 45° — 30° = 15° . •/ Rt △ ABE 也 Rt △ CBF , • / BCF = Z BAE = 15° .• / ACF = Z BCF + Z BCA = 15° + 45° = 60° .2. 如图,△ ABD 与厶BCE 都为等边三角形,连接 求证:(1) AE= DC ;(2) Z AHD = 60°(3) 连接 HB, HB 平分/ AHC .答案:(1)vZ ABE =Z ABD — Z EBD ,/ DBC =Z EBC —Z EBD ,/ ABD = Z EBC = 60° • / ABE =Z DBC . 在厶ABE 和厶DBC 中,AE 与CD ,延长AE 交CD 于点H .CAB 二 DB , M ABE Z DBC , BE =BC ,• AE= DC.(2):公 ABE◎△ DBC ,•••/ EAB =Z CDB .又•••/ OAB + Z OBA = Z ODH +Z OHD ,•••/ AHD =Z ABD = 60°(3)过B作AH、DC的垂线,垂足分别为点 M、N .ABE也厶 DBC ,--S^ABE= S A DBC .1 1即—AE • BM = - CD • BN.2 2又••• AE = CD,•BM = BN .•HB 平分/ AHC .3.在线段AE同侧作等边△ ABC和等边△ CDE (/ ACEv 120 ° ,点P与点M分别是线段BE和AD的中点.求证:△ CPM是等边三角形.答案:证明:•••△ ABC和厶CDE都是等边三角形, • AC = BC, CD = CE . •••/ ACB =Z ECD = 60°.• / BCE =Z ACD .•△ BCE◎△ ACD .•/ CBE =Z CAD , BE = AD .又•••点P与点M分别是线段 BE和AD的中点, • BP= AM .在厶BCP和厶ACM中,BC =AC ,CBE = CAD ,BP = AM ,• △ BCP◎△ ACM .CPD•PC = MC,Z BCP =Z ACM .•/ PCM =Z ACB = 60°.•△ CPM是等边三角形.4.将等腰Rt△ ABC和等腰Rt△ ADE按图①方式放置,/ A= 90° AD边与AB边重合,AB= 2AD = 4.将△ ADE 绕A 点逆时针方向旋转一个角度 a (0 °< a < 180 °, BD 的 延长线交CE 于P.(1) 如图②,求明: BD = CE, BD 丄CE; (2)如图③,在旋转的过程中,当 AD 丄BD 时,求CP 长.答案:(1) v 等腰 Rt △ ABC 和等腰 Rt △ ADE ,••• AB= AC, AD = AE,Z BAC =Z DAE = 90° •••/ DAB = 90° — / CAD ,/ CAE= 90° — / CAD , •••/ DAB = / CAE . • △ ABD ◎△ ACE . • BD = CE. • / DBA = / ECA.• / CPB =/ CAB . ( 8 字模型) • BD 丄CE. (2)由(1)得 BP 丄 CE .又••• AD 丄 BD ,/ DAE = 90° AD = AE, •四边形ADPE 为正方形. AD = PE= 2.• / ADB = 90° AD = 2, AB= 4, BD = CE= 2 .3 .• CP= CE —PE= 2 3-2 .图①E图②。
(完整版)全等六边形模型之手拉手模型
(完整版)全等六边形模型之手拉手模型
1. 简介
全等六边形模型是一种由相等边长和相等内角的六边形构成的特殊几何模型。
在这份文档中,我们将介绍一个由全等六边形组成的手拉手模型。
2. 模型构建
手拉手模型的构建是基于全等六边形的特性进行设计的。
下面是构建手拉手模型的步骤:
2.1 准备材料
首先,需准备以下材料:
- 六个相等的六边形图案,材质可以选择纸张、塑料等。
- 适当的胶水或胶带。
2.2 组装手拉手模型
以下步骤详细描述了如何组装手拉手模型:
1. 将一个六边形图案放置在桌面上作为模型的底部。
2. 在六边形图案的边缘涂抹一层胶水或使用胶带固定。
3. 取另一个六边形图案,将其一个边缘对齐并与底部六边形图案的边缘相连接。
重复此步骤,直到所有六边形连接成一个环形。
4. 检查每个连接处的稳固性,并确保六边形图案完全闭合形成一个环。
5. 等待胶水干燥或胶带粘合牢固后,手拉手模型便可使用。
3. 模型应用
全等六边形手拉手模型的应用可以有多种形式。
以下是几个常见的应用场景:
- 教育用途:该模型可用于学生研究六边形的性质和特点,以及了解全等形的概念。
- 模型展示:手拉手模型具有美观的外观和独特的几何结构,可以用作展示或展览的装饰品。
- 创意手工:制作手拉手模型是一项有趣的手工活动,可以锻炼孩子们的动手能力和创造力。
4. 结论
全等六边形手拉手模型是一种能够展示六边形特性和全等形概念的几何模型。
通过简单的构建步骤,我们可以制作出一个美观且有趣的模型,适用于教育、展示和手工等多种场景。
(完整版)计算机模型手拉手模型
(完整版)计算机模型手拉手模型1. 模型简介计算机模型手拉手模型是一种基于计算机科学的模型,用于描述计算机系统中各个组件之间的相互协作和通信方式。
该模型的设计灵感源自实际生活中的手拉手,形象地展示了计算机系统中各个组件之间通过通信协议进行数据交互的过程。
2. 模型结构计算机模型手拉手模型由以下几个主要组成部分构成:2.1. 手拉手接口手拉手接口是模型的核心部分,它通过模拟计算机系统中的通信协议,实现不同组件之间的连接和数据传输。
手拉手接口包含了发送和接收数据的功能,以及数据传输的控制逻辑。
2.2. 组件模块模型中的每个组件模块代表了计算机系统中的一个具体组件,例如CPU、内存、硬盘等。
每个组件模块都通过手拉手接口与其他组件进行连接,实现数据的传输和协作。
2.3. 数据线数据线是模型中的另一个重要部分,它用于在不同组件之间传输数据。
数据线不仅连接了不同组件的手拉手接口,还承载了数据的传输和传递。
3. 模型原理计算机模型手拉手模型的原理是模拟计算机系统中的数据交互过程。
当一个组件需要与另一个组件进行数据交换时,它会通过手拉手接口将数据发送给对应的组件。
接收组件收到数据后,会进行相应的处理,并通过手拉手接口将处理结果返回给发送组件。
模型通过手拉手接口和数据线的连接实现了组件之间的通信和协作。
数据线的拓扑结构可以灵活地调整,以适应不同计算机系统的需求。
4. 应用场景计算机模型手拉手模型可以被广泛应用于计算机科学领域的教学和研究工作中。
通过模型,学生可以直观地了解计算机系统中各个组件之间的数据交互方式,加深对计算机系统原理的理解。
此外,这个模型还可以作为一种通信协议的教学工具,帮助学生更好地理解通信协议的原理和实现方式。
5. 结论计算机模型手拉手模型通过形象生动的手拉手形态,展示了计算机系统中各个组件之间的通信和协作方式。
它可以被广泛应用于计算机科学教学和研究领域,有助于提升学生对计算机科学原理的理解和应用能力。
专题06 手拉手模型(解析版)
专题06 手拉手模型基本模型:例题精讲例1.(等腰三角形)【阅读材科】小明同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的项角的顶点,并把它们的底角顶点连接起来则形成一组全等的三角形,小明把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小明发现若∠BAC=∠DAE,AB=AC,AD=AE,则△ABD≌△ACE.【材料理解】(1)在图1中证明小明的发现.【深入探究】(2)如图2,△ABC和△AED是等边三角形,连接BD,EC交于点O,连接AO,下列结论:①BD=EC;②∠BOC=60°;③∠AOE=60°;④EO=CO,其中正确的有.(将所有正确的序号填在横线上).【延伸应用】(3)如图3,AB=BC,∠ABC=∠BDC=60°,试探究∠A与∠C的数量关系.【答案】(1)证明见解析;(2)①②③;(3)∠A+∠C=180°.【详解】(1)证明:∵∠BAC=∠DAE,∴∠BAC+∠CAD=∠DAE+∠CAD,∴∠BAD=∠CAE,在△ABD和△ACE中,AB ACBAD CAEAD AE⎧⎪∠∠⎨⎪⎩===,∴△ABD≌△ACE;(2)如图2,∵△ABC和△ADE是等边三角形,∴AB=AC,AD=AE,∠BAC=∠DAE=60°,∴∠BAD=∠CAE,在△ABD和△ACE中,AB ACBAD CAEAD AE⎧⎪∠∠⎨⎪⎩===,∴△ABD≌△ACE,∴BD=CE,①正确,∠ADB=∠AEC,记AD与CE的交点为G,∵∠AGE=∠DGO,∴180°-∠ADB-∠DGO=180°-∠AEC-∠AGE,∴∠DOE=∠DAE=60°,∴∠BOC=60°,②正确,在OB上取一点F,使OF=OC,∴△OCF是等边三角形,∴CF=OC,∠OFC=∠OCF=60°=∠ACB,∴∠BCF=∠ACO,∵AB=AC,∴△BCF≌△ACO(SAS),∴∠AOC=∠BFC=180°-∠OFC=120°,∴∠AOE=180°-∠AOC=60°,③正确,连接AF,要使OC=OE,则有OC=12CE,∵BD=CE,∴CF=OF=12BD,∴OF=BF+OD,∴BF<CF,∴∠OBC>∠BCF,∵∠OBC+∠BCF=∠OFC=60°,∴∠OBC>30°,而没办法判断∠OBC大于30度,所以,④不一定正确,即:正确的有①②③,故答案为①②③;(3)如图3,延长DC 至P ,使DP=DB ,∵∠BDC=60°,∴△BDP 是等边三角形,∴BD=BP ,∠DBP=60°,∵∠BAC=60°=∠DBP ,∴∠ABD=∠CBP ,∵AB=CB ,∴△ABD ≌△CBP (SAS ),∴∠BCP=∠A ,∵∠BCD+∠BCP=180°,∴∠A+∠BCD=180°.例2.(等边三角形)如图,B ,,三点在一条直线上,和均为等边三角形,与交于点,与交于点.(1)求证:;(2)若把绕点任意旋转一个角度,(1)中的结论还成立吗?请说明理由.【答案】(1)见解析(2)成立,理由见解析.【详解】解:(1)证明:如图1中,与都是等边三角形,,,,,,,即.在和中,,(SAS)..即AE=BD ,(2)成立;理由如下:如图2中,、均为等边三角形,,,,,即,C E ABC ∆DCE ∆BD AC M AE CDN AE BD =DCE ∆C ABC ∆DCE∆AC BC ∴=CD CE =60ACB DCE ∠=∠=︒180ACB ACD DCE ∠+∠+∠=60ACD ∴∠=︒ACB ACD ACD DCE ∠+∠=∠+∠BCD ACE ∠=∠BCD ∆ACE ∆BC AC BCD ACE CD CE =⎧⎪∠=∠⎨⎪=⎩BCD ACE ∴∆≅∆BD AE ∴=AE BD =ABC ∆DCE ∆BC AC ∴=CD CE =60BCA DCE ∠=∠=︒BCA ACD DCE ACD ∴∠+∠=∠+∠BCD ACE ∠=∠在和中,,,.例3.(正方形)综合与实践特例研究:将矩形ABCD 和Rt CEF 按如图1放置,已知90,,,FCE AD CD CE CF CF CD ∠=︒==>,连接',BF DE .()1如图1,当点D 在CF 上时,线段BF 与DE 之间的数量关系是__ ;直线BF 与直线DE 之间的位置关系是_ ;拓广探索:()2图2是由图1中的矩形ABCD 绕点C 顺时针旋转一定角度得到的,请探索线段BF 与DE 之间的数量关系和直线BF 与直线DE 之间的位置关系,并说明理由.【答案】(1),BF DE BF DE =⊥;(2),BF DE BF DE =⊥,理由见解析【详解】解:()1,BF DE BF DE =⊥,延长ED 交B F 于点G ,∵四边形ABCD 为矩形,且AD=DC ,∴BC=CD ,F D BC CE ∴∠=∠=90º,由旋转的FC=EC ,∴△FBC ≌△EDC (SAS ),,BF DE CED CFB =∠=∠,∵∠DCE=90º,∴∠DEC+∠CDE=90º,∴∠FDG+∠GFD=90º∠FGD=90º,ACE ∆BCD ∆AC BC BCD ACE CD CE =⎧⎪∠=∠⎨⎪=⎩()ACE BCD SAS ∴∆≅∆AE BD ∴=()2,BF DE BF DE =⊥,理由如下:如答图,延长ED 交CF 于点,M 交FB 于点N ,90FCE ∠=︒,四边形ABCD 为矩形,BCD FCE ∴∠=∠,FCB FCD ECD FCD ∠+∠=∠+∠,FCB ECD ∴∠=∠,AD CD =,∴矩形ABCD 为正方形.CD CB ∴=,在DCE 和BCF △中,,,CD CB ECD FCB CE CF =⎧⎪∠=∠⎨⎪=⎩,()DCE BCF SAS ∴≅.,BF DE CED CFB ∴=∠=∠.90,FCE ∠=︒90CME CED ∴∠+∠=︒.,CME FMN ∠=∠90,FMN CFB ∴∠+∠=︒90,FNE ∴∠=︒BF DE ∴⊥.课后训练1.如图,在ABC ∆中,分别以AC ,BC 为边作等边三角形ACD 和等边三角形BCE ,连接AE ,BD 交于点O ,则AOB ∠的度数为( )A .100︒B .120︒C .130︒D .150︒【答案】B 【解析】解:如图:AC 与BD 交于点H ,∵△ACD ,△BCE 都是等边三角形,∴CD =CA ,CB =CE ,∠ACD =∠BCE =60°,∴∠DCB =∠ACE ,在△DCB 和△ACE 中,CD CA DCB ACE CB CE ⎧⎪∠∠⎨⎪⎩===,∴△DCB ≌△ACE ,∴∠CAE =∠CDB ,∵∠DCH +∠CHD +∠BDC =180°,∠AOH +∠AHO +∠CAE =180°,∠DHC =∠OHA ,∴∠AOH =∠DCH =60°,∴∠AOB =180°−∠AOH =120°.故选:B.2.如图,C 为线段AE 上一动点(不与点,A E 重合),在AE 同侧分别作等边三角形ABC 和等边三角形,CDE AD 与BE 交于点O ,AD 与BC 交于点P ,BE 与CD 交于点Q ,连结PQ .以下结论:①AD BE =;②//PQ AE ;③60AOB ∠=︒;④CPQ 是等边三角形,恒成立的是______.【答案】①②③④【解析】解:①∵等边△ABC 和等边△CDE ,∴AC=BC ,CD=CE ,∠ACB=∠DCE=60°,∴∠ACB+∠BCD=∠DCE+∠BCD ,即∠ACD=∠BCE ,∵在△ACD 与△BCE 中,AC BC ACD BCE CD CE ⎧⎪∠∠⎨⎪⎩===∴△ACD ≌△BCE (SAS ),∴AD=BE ,故①正确;④②∵△ACD ≌△BCE ,∴∠CBE=∠DAC ,∵由∠ACB=∠DCE=60°得∠BCD=60°,∴∠ACP=∠BCQ ,又∵AC=BC ,∴△CQB ≌△CPA (ASA ),∴CP=CQ ,又∵∠PCQ=60°∴△PCQ 为等边三角形,∴∠PQC=60°,∴∠PQC=60°=∠DCE ∴PQ ∥AE故②④正确;③∵△ACD ≌△BCE (SAS ),∴∠CAD=∠CBE ,∴∠AOB=∠CAD+∠CEB=∠CBE+∠CEB ,又∵∠ACB=∠CBE+∠CEB=60°,∴∠AOB=∠ACB=60°,故③正确.故答案为:①②③④.3.如图1,在线段BE 上取一点C ,分别以CB ,CE 为腰作等腰直角△BCA 和等腰直角△DCE ,连接BD 和AE .(1)请判断线段BD 和线段AE 的数量关系,并说明理由;(2)如图2,若B ,C ,E 三点不共线,(1)中的结论还成立吗?请说明理由.【答案】(1)BD =AE ,理由见解析;(2)成立,理由见解析【详解】解:(1)∵△BCA 和△DCE 均为等腰直角三角形,∴BC =AC ,DC =CE ,∠BCD =∠ACE =90°.在△BCD 和△ACE 中,,,BC AC BCD ACE DC CE =⎧⎪∠=∠⎨⎪=⎩∴△BCD ≌△ACE .∴BD =AE .(2)成立.∵△BCA 和△DCE 均为等腰直角三角形,∴BC =AC ,DC =CE ,∠BCD =∠ACE =90°. ∴∠BCA +∠ACD =∠DCE +∠ACD ,即∠BCD =∠ACE .在△BCD 和△ACE 中,,,,BC AC BCD ACE DC CE =⎧⎪∠=∠⎨⎪=⎩∴△BCD ≌△ACE .∴BD =AE .4.已知:如图1,在和中,,,.(1)证明.(2)如图2,连接和,,与分别交于点和,,求的度数.(3)在(2)的条件下,若,请直接写出的度数.ABC ∆ADE ∆C E ∠=∠CAE DAB ∠=∠BC DE =ABC ADE ∆∆≌CE BD DE AD BC M N 56DMB ∠=︒ACE ∠CN EM =CBA ∠【答案】(1)证明见解析;(2)∠ACE =62°;(3)∠CBA =6°.【详解】解:(1)∵∠CAE =∠DAB ,∴∠CAE +∠CAD =∠DAB +∠CAD ,即∠CAB =∠EAD ,在△ABC 和△ADE 中,∴△ABC ≌△ADE (AAS ),(2)∵△ABC ≌△ADE ,∴∠CBA=∠EDA ,AC=AE ,在△MND 和△ANB 中,∵∠EDA +∠MND+∠DMB =,∠CBA +∠ANB +∠DAB =,又∵ ∠MND=∠ANB ,∴ ∠DAB=∠DMB=,∴∠CAE =∠DAB=,∵AC=AE ,∴∠ACE =∠AEC=,∴∠ACE =, (3)∠CBA=,如图所示,连接AM ,,CN=EM,CA=EA,(SAS),AM=AN,,=即, 由(2)可得:,=, ∠CAE =∠DAB==-= .4.已如:如图1,B ,C ,D 三点在一条直线上,△ABC 和△ECD 均为等边三角形,连接BE ,AD 交于点F ,BE 交AC 于点M ,AD 交CE 于点N .(1)以下结论正确的有 ;①AD =BE ②∠EFD =60° ③MC =NC ④∠AMB =∠END(2)探究:将图1中的△ECD 绕点C 顺时针旋转一个角度(旋转角小于60°),如图2所示.C E CAB EAD BC DE ∠=∠⎧⎪∠=∠⎨⎪=⎩180︒180︒56︒56︒1(18056)622︒︒︒-=62︒6︒NCA MEA ∠=∠∴NCA MEA ≅∴EAM CAN ∠=∠∴EAM CAM ∠-∠CAN CAM ∠-∠EAC MAN ∠=∠=56EAC MAN ︒∠=∠∴ANM ∠1(18056)622︒︒︒-=56︒∴CBA ANM DAB ∠=∠-∠62︒56︒6︒①问:(1)中的正确结论哪些还成立?若成立,请说明理由;②连接FC ,如图3所示,求证:FC 平分∠BFD【答案】(1)①②③;(2)① ①②;②见解析.【解析】 解:(1)∵△ABC ,△ECD 是等边三角形,∴AC =BC ,CE =CD ,∠ACB =∠ECD =60°,∴∠ACD =∠BCE=∠120°,∴△ACD ≌△BCE ,∴AD =BE ,故①正确;∴∠FEN =∠NDC又∵∠ENF =∠CND ,∴∠EFD =∠ECD =60°,故②正确;又∵∠ACE =∠NCD =60°,∠MEC =∠NDC ,EC =CD∴△EMC ≌△DNC ,∴MC =NC ,故③正确;又∵∠AMB =∠ACB +∠ECB =60°+∠ECB ,∠END =∠ECD +∠NDC =60°+∠NDC而AC CD ≠ ,∴CAD CDA ∠≠∠,∴MBC NDC ∠≠∠ ,∴MBC END ∠≠∠,故④错误; 故答案为:①②③;(2)∵∠ACB =∠ECD =60°,∴∠BCE =∠ACD又AC =BC ,CE =CD ,∴△ACD ≌△BCE ,∴AD =BE ,故①正确;,∴∠ADC =∠BEC又∠ENF =∠CND ,∴∠EFD =∠ECD =60°,故②正确∵∠ACE ≠60°=∠ECD ,∴△EMC 不全等于△DNC ,∴MC ≠NC ,故③错误(3),CG BE CH AD ⊥⊥于点G ,H ,如图,由(2)②知,∠CBG =∠CAH ,AC =BC∠BGC =∠AHC =90°∴△BGC ≌△AHC∴CG =CH又CF =CF ,∠CGF =∠CHF =90°∴△CGF ≌△CHF∴∠CFG =∠CFH∴FC 平分∠BFD5.已知:如图1,在和中,,,.(1)证明.(2)如图2,连接和,,与分别交于点和,,求的度数.(3)在(2)的条件下,若,请直接写出的度数.【答案】(1)证明见解析;(2)∠ACE =62°;(3)∠CBA =6°.【详解】解:(1)∵∠CAE =∠DAB ,∴∠CAE +∠CAD =∠DAB +∠CAD ,即∠CAB =∠EAD ,在△ABC 和△ADE 中,∴△ABC ≌△ADE (AAS ),(2)∵△ABC ≌△ADE ,∴∠CBA=∠EDA ,AC=AE ,在△MND 和△ANB 中,∵∠EDA +∠MND+∠DMB =,∠CBA +∠ANB +∠DAB =, 又∵ ∠MND=∠ANB ,∴ ∠DAB=∠DMB=,∴∠CAE =∠DAB=,∵AC=AE ,∴∠ACE =∠AEC=,∴∠ACE =, (3)∠CBA=, ABC ∆ADE ∆C E ∠=∠CAE DAB ∠=∠BC DE =ABC ADE ∆∆≌CE BD DE AD BC M N 56DMB ∠=︒ACE ∠CN EM =CBA∠C E CAB EAD BC DE ∠=∠⎧⎪∠=∠⎨⎪=⎩180︒180︒56︒56︒1(18056)622︒︒︒-=62︒6︒如图所示,连接AM ,,CN=EM,CA=EA,(SAS),AM=AN,,=即, 由(2)可得:,=, ∠CAE =∠DAB==-= .6.已知△ABC 与ΔADE 均为等腰直角三角形,且∠BAC =∠DAE =90°,点D 在直线BC 上.(1)如图1,当点D 在CB 延长线上时,求证:BE ⊥CD ;(2)如图2,当D 点不在直线BC 上时, BE 、CD 相交于M ,①直接写出∠CME 的度数;②求证:MA 平分∠CME【答案】(1)见解析(2)①90°;②见解析【解析】(1)解:∵△ABC 与ΔADE 均为等腰直角三角形,且∠BAC =∠DAE =90°,∴AB =AC ,AE =AD ,∠DAE +∠DAB =∠CAB +∠DAB ,∴∠CAD =∠BAE ,∠C =∠ABC =45°, ∴△CAD ≌△BAE (SAS ),∴∠ABE =∠C =45°,∴∠EBC =∠ABE +∠ABC =90°,即EB ⊥CD ;(2)解:①同理可证△BAE ≌△CAD ,∠ABC =∠ACB =90°,∴∠ABE =∠ACD ,∵∠EMC =∠EBC +∠BCD ,∴∠EMC =∠ABE +∠ABC +∠ACD +∠BCD =90°;NCA MEA ∠=∠∴NCA MEA ≅∴EAM CAN ∠=∠∴EAM CAM ∠-∠CAN CAM ∠-∠EAC MAN ∠=∠=56EAC MAN ︒∠=∠∴ANM ∠1(18056)622︒︒︒-=56︒∴CBA ANM DAB ∠=∠-∠62︒56︒6︒②如图,过点A 作AG ⊥BE 于G ,AF ⊥CD 于F ,∵△BAE ≌△CAD ,∴AG =AF ,在Rt △AGM 和Rt △AFM 中,AG AF AM AM =⎧⎨=⎩,∴Rt △AGM ≌Rt △AFM (HL ), ∴∠AMG =∠AMF ,即AM 平分∠EMC .7.正方形ABCD 和正方形AEFG 的边长分别为6和2,将正方形AEFG 绕点A 逆时针旋转.(1)当旋转至图1位置时,连接BE ,DG ,线段BE 和DG 是否相等且垂直?请说明理由;(2)在图1中,连接BD ,BF ,DF ,请直接写出在旋转过程中BDF 的面积最大值;(3)在旋转过程中,当点G ,E ,D 在同一直线上时,请求出线段BE 的长.【答案】(1)相等且垂直,理由见解析;(2)30;(3)BE 【解析】(1)解:(1)数量关系:BE DG =,位置关系:BE DG ⊥,理由如下:如图,设BE 与DG 交于点H ,连接BD ,∵四边形ABCD 、四边形AEFG 都是正方形,∴90BAD EAG ∠=∠=︒,AB AD =,AE AG =,∴BAD DAE DAE EAG ∠+∠=∠+∠即BAE DAG ∠=∠,在BAE ∆和DAG ∆中,AB AD BAD DAG AE AG =⎧⎪∠=∠⎨⎪=⎩, ()BAE DAG SAS ∴∆≅∆,BE DG ∴=,ABE ADG ∠=∠,90ABE EBD BDA ∴∠+∠+∠=︒, 90ADG EBD BDA ∠+∠+∠=︒即90HBD BDH ∠+∠=︒,BE DG ∴⊥, 故BE 与DG 的数量关系为:BE DG =,位置关系为:BE DG ⊥;(2)解:如图,取BD 的中点O ,连接AF 、AO 、FO ,过点F 作FH BD ⊥于点H ,AB AD =,O 为BD 中点,90BAD ∠=︒,12AO BD ∴=,2BD ==AO ∴=四边形AEFG是正方形AF ==AF AO FO FH ∴+≥≥,FH ∴≤=FH 的最大值为12BDF S BD FH ∆∴=⋅=,∴当FG 最大时,BDF ∆的面积也最大,BDF ∴∆面积的最大值为30=;(3)解:当点E 在线段DG 上时,如图,连接AF 交DG 于点P ,四边形AEFG 是正方形,AF GE∴=,12GPAPAF ===在Rt APD ∆中,由勾股定理得DP =DG DP GP =+=BE ∴ 当点E 在线段DG 的延长线上时,如图,连接AF 交DG 于点P ,同理可得:12GP AP AF ==在Rt APD ∆中,由勾股定理得DP =DG DP GP ∴=-=BE ∴=BE。
(完整版)心理学模型手拉手模型
(完整版)心理学模型手拉手模型心理学模型手拉手模型概述心理学模型手拉手模型是一种有效的心理治疗方法,旨在帮助个人理解和管理自己的情绪和行为。
这种模型结合了心理学理论和实践,通过身体、情绪和思维三个层面的综合训练,促进个人的内在平衡和健康成长。
模型框架心理学模型手拉手模型基于以下几个关键要素:1.身体层面这一层面的训练旨在通过身体运动和呼吸练,促进身体的放松和平衡。
例如,深呼吸、瑜伽和身体冥想等练可以帮助个人减轻压力、放松身心,并提高自我意识。
2.情绪层面情绪是我们内在体验的一部分,而情绪的管理对心理健康至关重要。
手拉手模型通过情绪识别、表达和调节的训练,帮助个人更好地处理情绪,减少消极情绪的影响,提升积极情绪的体验。
3.思维层面思维是影响我们行为和情绪的关键因素之一。
手拉手模型通过认知重塑和思维模式的调整,帮助个人改善负面思维模式,培养积极的信念和态度,并在面对挑战时更加应对灵活。
实施过程心理学模型手拉手模型的实施过程一般包括以下几个步骤:1. 确定目标:与个人合作,明确希望达到的目标和所需改变的领域。
2. 认知评估:通过与个人的对话和评估工具,了解其目前的思维、情绪和行为模式,并识别不健康的模式和问题领域。
3. 训练计划制定:根据评估结果,制定个性化的训练计划,包括身体、情绪和思维层面的综合训练。
4. 实施训练:与个人合作,按照计划进行训练,定期评估进展,并根据需要进行调整。
5. 评估和总结:定期评估个人的进展和成效,为后续训练提供参考,并总结经验和教训。
适用范围心理学模型手拉手模型适用于各个年龄段的个人,无论是面对情绪困扰、心理压力或行为问题,都能从中受益。
此外,该模型还可用于个人成长发展、情绪管理、焦虑和抑郁症等心理疾病的治疗。
结论心理学模型手拉手模型通过综合训练身体、情绪和思维三个层面,帮助个人理解和管理自己的情绪和行为。
它是一种简单且有效的心理治疗方法,可以帮助个人实现内在平衡和健康成长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例1.如图在直线ABC的同一侧作两个等边三角形ABD与BCE,连结AE与CD,证明
(1)DBCABE
(2)DCAE
(3)AE与DC之间的夹角为60
(4)DFBAGB
(5)CFBEGB
(6)BH平分AHC
(7)ACGF//
变式精练1:如图两个等边三角形ABD与BCE,连结AE与CD,
证明(1)DBCABE
(2)DCAE
(3)AE与DC之间的夹角为60
(4)AE与DC的交点设为H,BH平分AHC
变式精练2:如图两个等边三角形ABD与BCE,连结AE与CD,
证明(1)DBCABE
(2)DCAE
(3)AE与DC之间的夹角为60
(4)AE与DC的交点设为H,BH平分AHC
例2:如图,两个正方形ABCD与DEFG,连结CEAG,,二者相交于点H
问:(1)CDEADG是否成立?
(2)AG是否与CE相等?
(3)AG与CE之间的夹角为多少度?
(4)HD是否平分AHE?
例3:如图两个等腰直角三角形ADC与EDG,连结CEAG,,二者相交于点H
问:(1)CDEADG是否成立?
(2)AG是否与CE相等?
(3)AG与CE之间的夹角为多少度?
(4)HD是否平分AHE?
例4:两个等腰三角形ABD与BCE,其中BDAB,,EBCBCBEABD,
连结AE与CD,
问:(1)DBCABE是否成立?
(2)AE是否与CD相等?
(3)AE与CD之间的夹角为多少度?
(4)HB是否平分AHC?
