NS335特性及应用领域概述
2019 年度国家科学技术奖自然科学奖提名公示内容

3)Nature 的 Asia Materials 的〈research highlight〉栏目以“Carbon cubes” 为题用一个版面对该项目新型碳纳米结构的工作进行了评述:“这种碳纳米结构 是第一次被观测到”、“发光特性使得这些纳米碳方块在兰-紫色纳米发光器件中 有着巨大的潜在应用”(附件:其它 2);国际著名光学材料学家国际 Otto-Schott 奖和美国陶瓷学会 G. W. Morey 奖获得者浙江大学“长江”“杰青”邱建荣教授 在 Nanoscale 中 评 价 :“ 杨 研 究 组 在 新 型 碳 纳 米 结 构 领 域 做 出 了 先 驱 性 (pioneering)的贡献,他们通过液相激光熔蚀技术合成多种碳纳米结构,并提 出了相应的合成机理”(代表引文 3)。
细菌胞外多糖的特性及应用研究

细菌胞外多糖的特性及应用研究李明源;王继莲;魏云林;季秀玲【摘要】不论是在自然或病理条件下,多数细菌均被胞外多糖所包被,胞外多糖对细菌的粘附及在竞争环境中的存活和生长都具有重要作用。
近年来细菌胞外多糖以其独特的生物学活性和广阔的应用前景而备受人们关注。
系统介绍了细菌胞外多糖的结构性质、特性及生理功能,重点阐述了几种多糖的应用现状,并对今后细菌胞外多糖在工业上的发展趋势进行了展望,为深入开发利用多糖功能菌资源,进一步扩展其在工业领域上的应用奠定理论基础。
%The majority of bacteria are packaged by extracellular polysaccharides,which play an important role in their survival and growth,whether in nature or pathological conditions.The unique bioactivities of bacterial expolysaccharides and their application prospects were paid great attention by the concerned people.The structure,physical and chemical characteristics,biological activities of polysaccharides produced by bacterium were introduced in detail in this paper,especially the application of several bacterial expolysaccharides in industry.The future development of bacteria polysaccharides was envisaged.It provides theoretical basis for the further development of functional bacteria and expansion of application of bacterial exopolysaccharides in industrial.【期刊名称】《生物技术通报》【年(卷),期】2014(000)006【总页数】6页(P51-56)【关键词】细菌胞外多糖;生物学活性;应用【作者】李明源;王继莲;魏云林;季秀玲【作者单位】喀什师范学院生物与地理科学系叶尔羌绿洲生态与生物资源研究重点实验室,喀什 844006;喀什师范学院生物与地理科学系叶尔羌绿洲生态与生物资源研究重点实验室,喀什 844006;昆明理工大学生命科学与技术学院,昆明650500;昆明理工大学生命科学与技术学院,昆明 650500【正文语种】中文多糖(Polysaccharide,PS)是生物体内普遍存在的一种聚合糖高分子碳水化合物,是维持生命活动正常运转必不可少的重要组成成分。
28335概述

得益于F28335浮点运算单元,从 而简化 软件开发,缩短开发周期。降低开发成本。
DSP技术应用
采用高性能的静态CMOS技术 主频达150MHZ(6.67ns)
低功耗设计,1.9V内核电压,3.3V
Flash编程电压为3.3V
I/O电压
支持JTAG边界扫描接口
高性能32位CPU
16*16位和32*32位的乘法累加操作
C28x
TM
GPIO 16/32-bit
EMIF SPI
88
32x32-bit
Multiplier
通讯接口 32-bit Timers (3) Each McBSP configurable as SPI Real CAN 2.0b with 32 mailboxes Time 2C at 400 Kbps JTAG I 开发套件 SEED-DEC28335+SEED-XDSusb2.0 Code Composer Studio™ IDE V3.3 DSP技术应用 Software libraries
2个增强型的eCAN2.0B接口模块
DSP技术应用
2个多通道缓冲串口(MBSP) 1个12C总线接口 12位模数转换模块
80ns转换时间
2X8通道复用输入接口
两个采样保持电路
单/连续通道转换
高达88个可配置通用目的I/O引脚
先进的仿真调试功能
DSP技术应用
硬件支持适时仿真功能
16*16位的双乘法累加器 哈佛总线结构
DSP技术应用
快速中断响应和处理能力 统一寻址模式 4M的程序/数据寻址空间
高效的代码转换功能
片上存储器
最多达256K
最多达128K
NbSin,NbSin +,NbSin -(n=1~6)团簇稳定性和电子结构特性的研究

Nb i , S n , S S 咒 Nb i Nb i +
n
( n=1~6 团簇 )
稳定 性 和 电子 结构 特 性 的研 究
赵普举 , 李 婷, 郭 平 , 兆玉 任
70 6 ) 10 9
( E 西j 大学 物理学系 , 陕西 西安
摘要 : 目的
研 究 N S N S, 以及 N S ̄ n=l~ ) b i, bi + , bi ( - 6 团簇的稳 定性 和 电子 结构特 性 。方法
究 随着硅 原子 数 目的增 大 N b掺杂 s 团簇 的性质 变 i 化情 况 , 文对 N S n:1~ ) 本 bi( 6 团簇 中最稳 定 的构 型及 其正 负离 子 的稳 定 性和 电子 结构特 性进 行 了研
究。
发现 , 掺入过渡金属元素不仅 可以有效地改善纯硅 团簇 的稳定 性 , 得 它 们 具 有 较 大 的 H MOL MO 使 O —U
收 稿 日期 :0 80 . 20 -91 0
=
1 研 究 方 法
本文 所用 的 计 算 工 具 是 G us3 此 程 序 是 一 as0 , 种 专门用 于进 行 分 子 轨 道 从 头 计 算 ( biio 、 a t ) 密 ni
1~5 团 簇 的研 究 发 现 MS ) i 的是 相 对 最 稳 定 条件 下 对 N i as 团簇 的研 究 发 现 , 电子
西北大学学报 ( 自然科 学版 ) 20 0 8年 l , 3 2月 第 8卷第 6期 , e.2 0 , o.8 N . D c ,0 8 V 13 , o6 Jun l f ot et nvr t N trl c neE io ) ora o r w s u i sy( aua Si c d i N h ei e tn
HastelloyB-3物性参数HastelloyB3执行标准
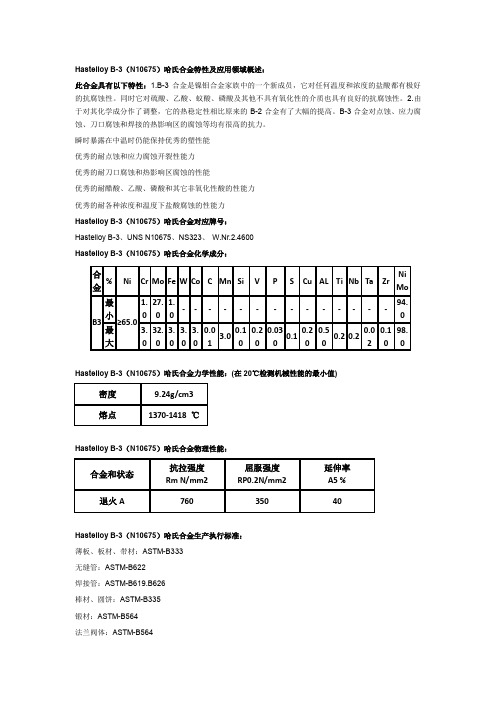
Hastelloy B-3(N10675)哈氏合金特性及应用领域概述:此合金具有以下特性:1.B-3合金是镍钼合金家族中的一个新成员,它对任何温度和浓度的盐酸都有极好的抗腐蚀性。
同时它对硫酸、乙酸、蚁酸、磷酸及其他不具有氧化性的介质也具有良好的抗腐蚀性。
2.由于对其化学成分作了调整,它的热稳定性相比原来的B-2合金有了大幅的提高。
B-3合金对点蚀、应力腐蚀、刀口腐蚀和焊接的热影响区的腐蚀等均有很高的抗力。
瞬时暴露在中温时仍能保持优秀的塑性能优秀的耐点蚀和应力腐蚀开裂性能力优秀的耐刀口腐蚀和热影响区腐蚀的性能优秀的耐醋酸、乙酸、磷酸和其它非氧化性酸的性能力优秀的耐各种浓度和温度下盐酸腐蚀的性能力Hastelloy B-3(N10675)哈氏合金对应牌号:Hastelloy B-3、UNS N10675、NS323、W.Nr.2.4600Hastelloy B-3(N10675)哈氏合金化学成分:Hastelloy B-3(N10675)哈氏合金力学性能:(在20℃检测机械性能的最小值)Hastelloy B-3(N10675)哈氏合金物理性能:Hastelloy B-3(N10675)哈氏合金生产执行标准:薄板、板材、带材:ASTM-B333无缝管:ASTM-B622焊接管:ASTM-B619.B626棒材、圆饼:ASTM-B335锻材:ASTM-B564法兰阀体:ASTM-B564Hastelloy B-3(N10675)哈氏合金金相组织结构:Hastelloy B-3为面心立方晶格结构。
该合金的铁和铬含量被控制在最小值,因此阻碍了其在700-800℃间沉淀析出Ni4Mo相,从而降低了加工脆化的风险。
应用范围B-3合金可适用于先前B-2合金所有用途,同B-2合金我一样,B-3也不推荐使用于三价铁盐和二价铜盐存在的环境中,因为这些盐会很快引起腐蚀破坏。
当盐酸接触到铁和铜时,会与之发生化学反应生成三价铁盐和二价铜盐。
2023年二亚乙基三胺的理化性质和危险特性

中文名:二亚乙基三胺;二乙(撑)三胺
危险货物编号:82025
英文名:Bis(2-aminoethy1;
amine;Diethy1enetriamine
UN编号:2079
分子式:C1Ih3Ns
分子量:103.17
CAS号:111-40-0
理化性质
外观与性状
无色或黄色透明液体,略有氨的气味。
灭火方法
消防人员必须佩戴过滤式防毒面具(全面革)或隔离式呼吸器、穿全身防火防毒服,在上风向灭火。尽可能将容器从火场移至空旷处。喷水保持火场容器冷却,直至灭火结束。处在火场中的容器假设已变色或从平安泄压装置中产生声音,必须马上撤退。灭火剂:雾状水、泡沫、干粉、二氧化碳、砂土。
急救方法
①皮肤接触:马上脱去污染的衣着,用大量流动清水冲洗至少15分钟。就医。②眼睛接触:马上提起眼畛,用大量流动清水或生理盐水彻底冲洗至少15分钟。就医。③吸入:迅速脱离现场至空气新奇处。保持呼吸道通畅。如呼吸困难,给输氧。如呼吸停止,马上进行人工呼吸。就医。④食入:用水漱口,给饮牛奶或蛋清。就医。
强氧化剂、强酸、铝、二氧化碳。
储运条件与泄漏处理
储运条件:储存于阴凉、通风的库房。远离火种、热源。应与氧化剂、酸类、食用化学品分开存放,切忌混储。配备相应品种和数量的消防器材。储区应备有泄漏应急处理设备和适宜的收容材料。泄漏处理:迅速撤退泄漏污染区人员至平安区,并进行隔离,严格限制出入。切断火源。建议应急处理人员戴自给正压式呼吸器,穿防酸碱工作服。尽可能切断泄漏源。预防流入下水道、排洪沟等限制性空间。小量泄漏:用砂土、蛭石或其它惰性材料汲取。也可以用大量水冲洗,洗水稀释后放入废水系统。大量泄漏:构筑围堤或挖坑收容。用泵转移至槽车或专用搜集器内,回收或运至废物处理园地处置。
TDC_GP21中文数据手册
3
Time-to-Digital-Converter
TDC-GP21
4
acam-messelectronic gmbh - Am Hasenbiel 27 - D-76297 Stutensee-Blankenloch - Germany - www.acam.de
TDC-GP21
1
概述
TDC-GP21为TDC-GP2的下一代升级产品.这颗芯片提供了对于TDC-GP2的管脚完全兼容的功能,
0.06
0.04
0,02% < 0.01%
0.012 0.0082
单位 Bit dB
%/V %/10 K
acam-messelectronic gmbh - Am Hasenbiel 27 - D-76297 Stutensee-Blankenloch - Germany - www.acam.de
1-1
2-1 2-2 2-3 2-6 2-7 2-8
3-1 3-11 3-13 3-14
4-1 4-7 4-14 4-16
5-1 5-4 5-7 5-7
6-1
7-1
acam-messelectronic gmbh - Am Hasenbiel 27 - D-76297 Stutensee-Blankenloch - Germany - www.acam.de
如果应用tdcgp21的模拟部分那么一个超声波热量表的典型测量功耗可以下降到22ua11特性测量范围2?单通道90ps典型精度?双精度模式45ps四精度模式22ps?测量范围500ns到4ms?2xclkhs脉冲最小间隔最多可以接受3个脉冲?3个脉冲每个都可以设定精准的时间窗口窗口精确度达10ns模拟输入部分?斩波稳定低噪声比较器?2个模拟开关作为输入选择?外部电路仅需要2个电阻和2个电容特殊功能?脉冲产生器可以产生最多127个脉冲?可以选则上升沿和或下降沿敏感?通过窗口功能精确接受stop脉冲?低功耗32khz振荡器500na?时钟标定单元?7x32位eeprom温度测量单元?2或4个传感器?pt500pt1000或者更高?集成的施密特触发器?应用外部施密特触发器为16位有效精度对于铂电阻来说0004c分辨率应用内部集成低噪声施密特触发器为17
柱坐标系和球坐标系下NS方程的直接推导
Derivation of 3D Euler and Navier-Stokes Equationsin Cylindrical CoordinatesDingxi WangSchool of Engineering, Durham UniversityContents1. Derivation of 3D Euler Equation in Cylindrical coordinates2. Derivation of Euler Equation in Cylindrical coordinates moving at ω in tangential direction3. Derivation of 3D Navier-Stokes Equation in Cylindrical Coordinates1. Derivation of 3D Euler Equation in Cylindrical coordinatesEuler Equation in Cartesian coordinates0=∂∂+∂∂+∂∂+∂∂zGy F x E t U (1.1) WhereU → Conservative flow variables E → Inviscid/convective flux in x direction F → Inviscid/convective flux in y directionG → inviscid/convective flux in z directionAnd their specific definitions are as follows⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=E w v u U ρρρρρ,⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+=Hu wu vu p uu u E ρρρρρ,⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+=Hv wv p vv uv v F ρρρρρ,⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛+=Hw p ww vw uw w G ρρρρρ()ww vv uu CvT E +++=21()ρp E ww vv uu CpT H +=+++=21H → Total enthalpySome relationshipWe want to perform the following coordinates transformation()()r x z y x ,,,,θ→Because1=∂∂∂∂+∂∂∂∂rzz r r y y r0=∂∂∂∂+∂∂∂∂θθzz r y y rAccording to Cramer’s ruler, w e haveθθθθ∂∂=∂∂∂∂∂∂∂∂∂∂∂∂=∂∂z J z y r z r yzr z y r 101 (1.2.1)θθθθ∂∂-=∂∂∂∂∂∂∂∂∂∂∂∂=∂∂y J z y r z r yy r y z r 101(1.2.2)Whereθθ∂∂∂∂∂∂∂∂=z y r z ry j Similar to the above0=∂∂∂∂+∂∂∂∂rzz r y y θθ1=∂∂∂∂+∂∂∂∂θθθθzz y yr z J z y r z r y zr z y∂∂-=∂∂∂∂∂∂∂∂∂∂∂∂=∂∂110θθθθ (1.2.3) ryJ z y r z r y y r y z∂∂=∂∂∂∂∂∂∂∂∂∂∂∂=∂∂110θθθθ(1.2.4) In addition, the following relations hold between cylindrical coordinate and Cartesiancoordinateθcos r y =,θsin r z =⇒θcos =∂∂r y ,θsin =∂∂rz ,θθsin r y -=∂∂,θθcos r z =∂∂, (1.3) r r r z y r zryJ =-=∂∂∂∂∂∂∂∂=θθθθθθcos sin sin cos()()θθθθθθθθθsin cos F Fr r r z F z F r rz F z r F y F y r r F J y FJ∂∂-∂∂=⎪⎭⎫⎝⎛∂∂∂∂-⎪⎭⎫ ⎝⎛∂∂∂∂=∂∂∂∂-∂∂∂∂=⎪⎪⎭⎫ ⎝⎛∂∂∂∂+∂∂∂∂=∂∂(1.4.1)()()θθθθθθθθθcos sin G Gr r r y G y G r r y G y r G z G z r r G J z G J∂∂+∂∂=⎪⎭⎫ ⎝⎛∂∂∂∂+⎪⎭⎫ ⎝⎛∂∂∂∂-=∂∂∂∂+∂∂∂∂-=⎪⎭⎫⎝⎛∂∂∂∂+∂∂∂∂=∂∂(1.4.2) DerivationMultiplying the both side of equation (1.1) by J and applying equalities (1.4.1) and (1.4.2) gives,()()()()()()0sin cos sin cos cos sin sin cos =-∂∂++∂∂+∂∂+∂∂=∂∂+∂∂+∂∂-∂∂+∂∂+∂∂=∂∂+∂∂+∂∂+∂∂=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂+∂∂θθθθθθθθθθθF G Gr Fr r x E r t U r G Gr r F Fr r x E r t U r z GJ y F J x E J t U J z G y F x E t U J (1.5) Differentiating the following w.r.t. time givesθcos r y =,θsin r z =dt d r dt dr dt dy θθθsin cos -=,dtd r dt dr dt dz θθθcos sin +=w dtdz v dt d r v dt dr v dt dy r ====,,,θθ r v w v =+θθsin cos (1.6.1) θθθv w v =+-cos sin (1.6.2)Expanding the term ()θθsin cos Gr Fr + and applying the relationships (1.6) yields,()()()()()()rr r r r r rG Hv p wv p vv uv v r w v H p w v w p w v v w v u w v r r Hw p ww vw uw w r Hv wv p vv uv v Gr Fr =⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛++=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+++++++=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛++⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+=+ρθρθρρρθθρθθθρθθθρθθρθθρθρρρρρθρρρρρθθsin cos sin cos sin sin cos cos sin cos sin cos sin cos sin cos sin cos (1.7.1)Expanding the term ()θθsin cos F G - and applying the relationships (1.6) yields,()()()()()()θθθθθθρθρθρρρθθρθθθρθθθρθθρθθρθρρρρρθρρρρρθθF Hv p wv p vv uv v w v H p w v w p w v v w v u w v Hv wv p vv uv v Hw p ww vw uw w F G =⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛+-=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+-++--+-+-+-=⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛+-⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+=-cos sin cos sin cos cos sin sin cos sin cos sin cos sin sin cos sin cos (1.7.2)Substituting relationships (1.7) into equation (1.5) and rearranging gives,()()0sin cos sin cos =∂∂+∂∂+∂∂+∂∂=-∂∂++∂∂+∂∂+∂∂r rG F x E r t U r F G Gr Fr r x E r t U rr θθθθθθθ(1.8)As we can see from expressions (1.7), the momentum equations in radial and tangential directions contain velocities in Cartesian coordinate; we need to replace them with corresponding variables in cylindrical coordinate. Writing down the momentum equations in radial and tangential directions as follows,()()0sin cos =∂-∂+∂+∂+∂∂+∂∂θθρθρρρθp vv r p vv r x vu r t v r r (1.9.1)()()0cos sin =∂+∂+∂+∂+∂∂+∂∂θθρθρρρθp wv r p wv r x wu r t w rr (1.9.2) Multiplying (1.9.1) by θcos and (1.9.2) by θsin , then summing up and applying expressions (1.6) and rearranging yields()()()()()pv v p wv p vv p wv p vv v v r p v v r x u v t v r r r r r r +=++--=∂∂++∂∂-=∂∂+∂+∂+∂∂+∂∂θθθθθθθρθθρθθρθθθρθθθρθρρρρcos cos sin sin sin cos cos sin (1.10.1)Multiplying (a) by θsin - and (b) by θcos , then summing up and applying expressions (1.6) yields,()()()()()()θθθθθθθθθθρθθρθθρθθθρθθθρθρρρρv v p wv p vv p wv p vv p v v r p v v r x u v t v r r r -=+---=∂∂++∂∂--=∂+∂+∂+∂+∂∂+∂∂sin cos cos sin cos cos sin sin (1.10.2)Replacing (1.10) with (1.9) and rearranging equation (1.8) givesS rr rGr F x E t U =∂∂+∂∂+∂∂+∂∂θ (1.11) Where⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=E v v u U r ρρρρρθ,⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛+=Hu u v u v p uu u E r ρρρρρθ,,⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+=θθθθθθρρρρρHv v v p v v uv v F r ⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛+=rr r r r rHvp v v v v uv v G ρρρρρθ,⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+-=0002r p v r v v S r θθρρNote: different from Euler equation in Cartesian coordinates, the Euler equation in cylindrical coordinates contains source terms from momentum equations in radial and tangential equations.2. Derivation of Euler Equation in Cylindrical coordinates moving atω in tangential direction()()t r x t r x ''''→,,,,,,θθWherer r '=,t '+'=ωθθ,x x '=,t t '=⇒r r =',t ωθθ-=',x x =',t t ='t tt t t x x t t r r t '∂∂++'∂∂-=∂'∂'∂∂+∂'∂'∂∂+∂'∂'∂∂+∂'∂'∂∂=∂∂00ωθθθ,000+++'∂∂=∂'∂'∂∂+∂'∂'∂∂+∂'∂'∂∂+∂'∂'∂∂=∂∂r rt t r x x r r r r r θθ00++'∂∂+=∂'∂'∂∂+∂'∂'∂∂+∂'∂'∂∂+∂'∂'∂∂=∂∂θθθθθθθθt t x x r r ,00+'∂∂++=∂'∂'∂∂+∂'∂'∂∂+∂'∂'∂∂+∂'∂'∂∂=∂∂x x t t x x x x x r r x θθθω'∂∂-'∂∂=∂∂U t U t U ,r r G r r r rG '∂''∂=∂∂,θθ'∂'∂=∂∂r F r F ,x Ex E '∂∂=∂∂ Then equation (1.11) can be written as followsS r r G r r F x E U t U ='∂''∂+'∂'∂+'∂∂+'∂∂-'∂∂θθω ⇒()S r r Gr r r U F x E t U ='∂''∂+'∂'-∂+'∂∂+'∂∂θω (2.1) Where ⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛'-'+=0002r v v r p v S r θθρρEquation (2.1) adopts rotating coordinates but the variables are measured in absolute cylindrical coordinates.3. Derivation of 3D Navier-Stokes Equation in Cylindrical Coordinates3D Navier-Stokes Equations in Cartesian coordinates()()()0=∂-∂+∂-∂+∂-∂+∂∂zV G y V F x V E t U z y x (3.1) Where⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=E w v u U ρρρρρ,⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+=Hu wu vu p uu u E ρρρρρ,⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+=Hv wv p vv uv v F ρρρρρ,⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+=Hw p ww vw uw w G ρρρρρ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-++=x zx yx xx zx yx xx x q w v u V ττττττ0,⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-++=y zy yy xy zy yyxy y q w v u V ττττττ0, ⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-++=z zz yz xzzz yz xz z q w v u V ττττττ0 ⎪⎭⎫ ⎝⎛⋅∇-∂∂=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂-∂∂=V x u z w y v x u xx322232μμτ, ⎪⎪⎭⎫⎝⎛∂∂+∂∂==x v y u xy yx μττ,⎪⎭⎫⎝⎛∂∂+∂∂==x w z u xz zx μττ, ⎪⎪⎭⎫ ⎝⎛⋅∇-∂∂=⎪⎪⎭⎫⎝⎛∂∂-∂∂-∂∂=V y v z w x u y v yy 322232μμτ, ⎪⎭⎫ ⎝⎛⋅∇-∂∂=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂-∂∂=V z w x u y v z w zz322232μμτ,⎪⎪⎭⎫⎝⎛∂∂+∂∂==z v y w zy yz μττx T kq x ∂∂-=,y T k q y ∂∂-=,zTk q z ∂∂-= In the following derivation, only viscous terms will be derived from Cartesian coordinates to cylindrical coordinates, those inviscid terms having been derived in section 1 will be not repeated.()()θθθsin cos F Fr r y F J∂∂-∂∂=∂∂ Replacing F with y V gives()()θθθsin cos y y y V r V r yV J∂∂-∂∂=∂∂ ()()θθθcos sin G Gr r z G J∂∂+∂∂=∂∂ (3.2.1) Replacing G with x V gives()()θθθcos sin z z z V r V r z V J ∂∂+∂∂=∂∂ (3.2.2) Multiplying equation (3.1) by J , the viscous terms are gives as follows (omitting the negative sign before it from simplicity),()()()()()()θθθθθθθθθθθsin cos sin cos cos sin sin cos y z z y x z z y y x z y x V V r V r V r x V r V r V r V r V r x V r z V J y V J x V J -∂∂++∂∂+∂∂=∂∂+∂∂+∂∂-∂∂+∂∂=∂∂+∂∂+∂∂ (3.3)()()()()()⎥⎦⎤⎢⎣⎡∂∂-∂∂-∂∂=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛∂∂+∂∂-⎪⎭⎫ ⎝⎛∂∂-∂∂-∂∂=⎪⎪⎭⎫⎝⎛∂∂-∂∂-∂∂=θμθθθθθθμμτθr v r r rv x u w r wr r v r vr r x u z w y v x u r xx 232cos sin 1sin cos 1232232 (3.4.1) ()()⎥⎦⎤⎢⎣⎡∂∂+⎪⎭⎫ ⎝⎛∂∂-∂∂=⎪⎪⎭⎫⎝⎛∂∂+∂∂==x v u r ur r x v y uxy yx θθθμμττsin cos 1, (3.4.2)()()⎥⎦⎤⎢⎣⎡∂∂+⎪⎭⎫ ⎝⎛∂∂+∂∂=⎪⎭⎫⎝⎛∂∂+∂∂==x w u r ur r x w z u xz zx θθθμμττcos sin 1, (3.4.3)()()()()()()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛∂∂+∂∂-∂∂-⎪⎭⎫ ⎝⎛∂∂-∂∂=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛∂∂+∂∂-∂∂-⎪⎭⎫ ⎝⎛∂∂-∂∂=⎪⎪⎭⎫⎝⎛∂∂-∂∂-∂∂=θθθθθθμθθθθθθμμτcos sin 1sin cos 1232cos sin 1sin cos 1232232w r wr r x u v r vr r w r wr r x u v r vr r z w x uy vyy ,(3.4.4) ()()()()⎥⎦⎤⎢⎣⎡∂∂-⎪⎭⎫ ⎝⎛∂∂-∂∂-⎪⎭⎫ ⎝⎛∂∂+∂∂=⎪⎪⎭⎫⎝⎛∂∂-∂∂-∂∂=x u v r vr r w r wr r x u y vz wzz θθθθθθμμτsin cos 1cos sin 1232232 (3.4.5)()()()()()()⎪⎭⎫ ⎝⎛∂-∂-∂+∂=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛∂∂+∂∂+⎪⎭⎫ ⎝⎛∂∂-∂∂=⎪⎪⎭⎫⎝⎛∂∂+∂∂==θθθθθμθθθθθθμμττcos sin sin cos 1cos sin 1sin cos 1v w r vr wr r v r vr r w r wr r z v y w zy yz (3.4.6)Expanding expression (3.3) gives,()()()()()()()()⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-++-++-++-+-+-+-∂∂+⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--++++++++∂∂+⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-++∂∂=-∂∂++∂∂+∂∂θθθτθτθτθτθτθτθτθτθτθτθτθτθθθθτθτθτθτθτθτθτθτθτθτθτθτττττττθθθθθcos sin cos sin cos sin cos sin cos sin cos sin cos sin 0sin cos sin cos sin cos sin cos sin cos sin cos sin cos 00sin cos sin cos z y zz zy yzyy xz xy zz zy yz yy xz xy z y zz zy yz yy xz xy zz zy yz yy xz xy x zx yx xx zx yx xx y z z y x q q w v u q q w v u r r q w v u x r V V r V r V r x V r(3.5)()()()()()()⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡∂∂+∂∂∂∂=⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡∂∂+⎪⎭⎫ ⎝⎛-∂∂∂∂=⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡∂∂+⎪⎭⎫ ⎝⎛∂∂+∂∂+⎥⎦⎤⎢⎣⎡∂∂+⎪⎭⎫ ⎝⎛∂∂-∂∂∂∂=+∂∂x v r u r r x v u r ur r r r x w u r ur r x v u r ur r r r rrr r xz xy μμθθθθμθθθθμθτθτ1sin cos sin 1cos sin cos 1sin cos =〉⎥⎦⎤⎢⎣⎡∂∂+∂∂==x v r u r rx xr μττ (3.6.1)()()()()()⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡∂∂+∂∂∂∂=⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡∂∂+⎪⎭⎫ ⎝⎛∂∂+∂∂+⎥⎦⎤⎢⎣⎡∂∂+⎪⎭⎫ ⎝⎛∂∂-∂∂-∂∂=+-∂∂x v r u x w u r ur r x v u r ur r xz xy θθμθθθθθμθθθθμθθτθτθcos cos sin 1sin sin cos 1cos sin =〉⎥⎦⎤⎢⎣⎡∂∂+∂∂==x v r u x x θθθθμττ (3.6.2)()()()()()()()()()()()()()()()x rx r r r rr r rr r r r r r zxyx v v x v r u v x v r u v x v v x v v v r u v ru x v v x v v v u rv r u r x v v v v v u uv v r ur r x ww vv w u v u w r ur v r ur r x w w x v v w u r ur v u r ur r x w u r ur r w x v u r ur r v w v θθθθθθθθθθθθθττθμμμθμμμθμμθμμθθθθθθμμμθθθθθθμθθθμθθθμττ+=⎪⎭⎫ ⎝⎛∂∂+∂∂+⎪⎭⎫ ⎝⎛∂∂+∂∂=∂∂+∂∂+⎥⎦⎤⎢⎣⎡∂∂+∂∂=∂∂+∂∂+⎥⎦⎤⎢⎣⎡∂∂+∂∂=∂+∂+⎥⎦⎤⎢⎣⎡∂∂+-∂∂=∂+∂+⎥⎦⎤⎢⎣⎡∂∂+∂∂-⎪⎭⎫ ⎝⎛∂∂+∂∂=∂∂+∂∂+⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛∂∂+∂∂+⎪⎭⎫ ⎝⎛∂∂-∂∂=⎥⎦⎤⎢⎣⎡∂∂+⎪⎭⎫ ⎝⎛∂∂+∂∂+⎥⎦⎤⎢⎣⎡∂∂+⎪⎭⎫ ⎝⎛∂∂-∂∂=+121121cos sin sin cos 1cos sin sin cos 1cos sin 1sin cos 1 (3.6.3)()()()()()()()⎥⎦⎤⎢⎣⎡∂∂+∂∂+∂∂=⎥⎦⎤⎢⎣⎡+-∂∂++∂∂+∂∂=⎥⎦⎤⎢⎣⎡∂∂+∂∂+⎥⎦⎤⎢⎣⎡∂∂-∂∂+∂∂=∂∂+∂∂+∂∂θθθθθθθθθθθθθv rv r r x u w v wr vr r r x u w wr r r v vr r r x u z w y v x u r 1cos sin sin cos 1cos sin 1sin cos 1 (3.7.1)Divergence in Cartesian Coordinateszwy v x u V ∂∂+∂∂+∂∂=⋅∇ (3.7.2)Divergence in cylindrical coordinates()θθ∂∂+∂∂+∂∂=⋅∇r v rv r r x u V r (3.7.3)()()()()()()()()()()()()()rrr r r r r r r r r r r r zz yy yz zz zy yz yy v v V r v v r v r v r r rv v Vv v v v v v v r rv v r rv v r Vv w r wr r w v r vr r v w v v w r vr wr r V z w w V y v v w v v w r vr wr r w v w v w v ττμθμμθμμθθθθμθθθθμθθθθθθθμθμθμθθθθθθθμθτθτθθτθτθτθτθτθθθθθθθθθθ+=⎪⎭⎫ ⎝⎛⋅∇-∂∂+⎪⎭⎫ ⎝⎛-∂∂+∂∂=⋅∇-⎪⎭⎫⎝⎛--∂∂+∂∂+∂∂=⋅∇-⎪⎭⎫ ⎝⎛∂∂+∂∂+⎪⎭⎫ ⎝⎛∂∂-∂∂++⎪⎭⎫⎝⎛∂-∂-∂+∂=⎥⎦⎤⎢⎣⎡⋅∇-∂∂+⎥⎦⎤⎢⎣⎡⋅∇-∂∂++⎪⎭⎫ ⎝⎛∂-∂-∂+∂=+++=+++ 32232222132cos sin 1sin 2sin cos 1cos 2cos sin cos sin sin cos 1322sin 322cos cos sin cos sin sin cos 1sin cos cos sin sin cos sin cos (3.8.1)()()()()()()()()()()()()()()()()()()()()θθθθθθθθθθθθθθθθθθθθθθθθθθθθθθθττμθμθμμθμθμμθμθμμθθμμθθμμθθμθθθθμθθθθμμθθθθθθθμθμθμθθθθθθθμθτθτθθτθτθτθτθτv v V r v r v v r v r v r v v V r v v r v r v r v r v v V r v v r r rv r v v v V v v v v r rv v r v V v v v v v v r rv v r v V ww vv v v r rv v r w r wr r w v r vr r v v V w v v w r vr wr r V z w w V y v v w v v w r vr wr r w v w v w v r r r r r r r r r r r r r r r r zzyy yz zz zy yz yy +=⎥⎦⎤⎢⎣⎡⋅∇-⎪⎭⎫ ⎝⎛+∂∂+⎪⎭⎫ ⎝⎛-∂∂+∂∂=⎪⎭⎫ ⎝⎛⋅∇-∂∂+⎪⎭⎫ ⎝⎛+-∂∂+∂∂=⎪⎭⎫ ⎝⎛⋅∇-∂∂+⎪⎭⎫ ⎝⎛∂∂+∂∂=⋅∇-⎥⎦⎤⎢⎣⎡∂∂+∂∂+∂∂=⋅∇-⎥⎦⎤⎢⎣⎡∂+∂+∂∂+∂∂=⋅∇-⎥⎦⎤⎢⎣⎡∂+∂+∂∂+∂∂=⎪⎭⎫ ⎝⎛∂∂+∂∂+⎪⎭⎫ ⎝⎛∂∂-∂∂-⋅∇--⎪⎭⎫ ⎝⎛∂-∂-∂+∂=⎥⎦⎤⎢⎣⎡⋅∇-∂∂+⎥⎦⎤⎢⎣⎡⋅∇-∂∂--⎪⎭⎫ ⎝⎛∂-∂-∂+∂=+--=+-++- 32232223223221322113221211cos sin 1cos 2sin cos 1sin 232sin cos cos sin sin cos 1322cos 322sin sin cos cos sin sin cos 1cos sin sin cos cos sin cos sin (3.8.2)()()()()()rz y q r T k T r Tr r k T r Tr r k T r Tr r k zT k y T kq q -=∂∂=⎥⎦⎤⎢⎣⎡-∂∂=⎥⎦⎤⎢⎣⎡∂∂+∂∂+⎥⎦⎤⎢⎣⎡∂∂-∂∂=∂∂+∂∂=--1sin cos sin 1cos sin cos 1sin cos sin cos θθθθθθθθθθθθ(3.9.1)()()()()θθθθθθθθθθθθθθq T r k T r Tr r k T r Tr r k zT k y T kq q z y -=∂∂=⎥⎦⎤⎢⎣⎡∂∂+∂∂+⎥⎦⎤⎢⎣⎡∂∂-∂∂-=∂∂+∂∂-=-1cos cos sin 1sin sin cos 1cos sin cos sin (3.9.2) As we can see from the above that viscous terms in expression (3.5) for the momentum equation in axial/x direction and energy equation can be expressed in variables in cylindrical coordinates, while the viscous terms in (3.5) for momentum equations in radial and tangential directions still contain variables in Cartesian coordinates. Similar manipulation to (1.10) will be adopted in the following. Writing out the viscous terms for momentum equations in radial and tangential coordinates as follows,()()θθτθτθτθττ∂+-∂+∂+∂+∂∂cos sin sin cos yz yy yz yy yx rr xr (3.10.1)()()θθτθτθτθττ∂+-∂+∂+∂+∂∂cos sin sin cos zz zy zz zy zx r r x r(3.10.2) Multiplying (3.10.1) by θcos and multiplying (3.10.2) by θsin , then summing up and rearranging gives,()()()[]()()[]()()[]θθτθτθθτθτθθθτθτθθτθτθθτθτθθτθτθτθτcos cos sin sin cos sin sin cos sin cos cos sin sin sin cos cos sin cos sin cos zz zy yz yy zz zy yz yy zz zy yz yy zx yx rr x r +-++---∂+-++-∂+∂+++∂+∂+∂(3.11.1)Multiplying (3.10.1) by θsin - and multiplying (3.10.2) by θcos , then summing up and rearranging gives,()()()[]()()[]()()[]θθτθτθθτθτθθθτθτθθτθτθθτθτθθτθτθτθτsin cos sin cos cos sin cos cos sin sin cos sin cos sin cos sin sin cos cos sin zz zy yz yy zz zy yz yy zz zy yz yy zx yx rr x r +--+---∂+-++--∂+∂+++-∂+∂+-∂(3.11.2)()()()()()()()()()()()()()()()()rrr r r r r zz yy zy zz zy yz yyr v r v x u r v V r v Vv r rv r Vw v v w wr vr vr wr r r V w wr r v vr r r v w r vr wr r V z w y v v w r vr wr r V z w V y v v w r vr wr r τθμμμμμμθθθθθθθθθθθθθθθθθθθθθθθθθμμθθθθθθθθθθμθθθθθθθμμθθθθμθθθθθθθμθθμθθμθθθθθθθμθθτθθτθθτθθτθτθθτθτθ=⎪⎭⎫ ⎝⎛-∂∂-∂∂-∂∂=⋅∇-∂∂=⋅∇-⎪⎭⎫⎝⎛-∂∂=⋅∇-⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡∂∂+∂∂-∂-∂-+++∂∂=⋅∇-⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡∂∂+∂∂+⎥⎦⎤⎢⎣⎡∂∂-∂∂+⎪⎭⎫ ⎝⎛∂-∂-∂+∂=⋅∇-⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+⎪⎭⎫⎝⎛∂-∂-∂+∂=⎪⎭⎫ ⎝⎛⋅∇-∂∂+⎪⎪⎭⎫ ⎝⎛⋅∇-∂∂+⎪⎭⎫ ⎝⎛∂-∂-∂+∂=++=+++232322321232sin sin cos cos cos sin cos sin cos sin sin sin sin cos cos cos cos sin sin cos sin cos 1232sin sin cos sin 2cos cos sin cos 21cos sin cos sin sin cos 1232sin sin 2cos cos 2cos sin cos sin sin cos 12sin sin 322cos cos 322cos sin cos sin sin cos 12sin sin cos cos cos sin 2sin sin cos cos sin cos (3.12.1)()()()()()()()()()()()()()()()()()θθθθθτθμθμθθθθθθθθμθθθθθθθθθμθθμθθθθθθθθθμθθμμθθθθθθθθθμθθττθθθθτθθτθτθθτθτr r r zz yy zy zz zy yz yy r v r v r vv v r rv r w wr r v vr r r v w r vr wr r z w y v v w r vr wr r V z w V y v v w r vr wr r =⎪⎭⎫ ⎝⎛-∂∂+∂∂=⎪⎭⎫⎝⎛-∂∂+∂∂=⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡∂∂+∂∂+⎥⎦⎤⎢⎣⎡∂∂-∂∂-+-⎪⎭⎫ ⎝⎛∂-∂-∂+∂=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂-+-⎪⎭⎫⎝⎛∂-∂-∂+∂=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛⋅∇-∂∂+⎪⎪⎭⎫ ⎝⎛⋅∇-∂∂-+-⎪⎭⎫ ⎝⎛∂-∂-∂+∂=+-+-=+++-21cos sin cos sin sin cos 12sin sin cos cos cos sin sin cos 1cos sin 2sin sin cos cos cos sin sin cos 1cos sin 322322sin sin cos cos cos sin sin cos 1cos sin sin sin cos cos cos sin cos sin sin cos (3.12.2)()()()()[]()()[]()()[θθθθθτθτθτθτθθτθτθμθθθτθτθθτθτθθθτθτθθτθτθθθτθτθθθτθτ-∂∂=+-++---⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-∂∂+∂∂∂∂=+-++---∂+-++-∂=∂+-∂+∂+-∂r zz zy yz yy r zz zy yz yy zz zy yz yy zz zy yz yy r v r v r v cocos sin sin cos sin cos cos sin sin cos sin sin cos sin cos cos sin sin cos sin cos cos sin (3.12.3)()()()()()()()()θθθτμθμθθθθθθθμθθθθθθθθθθμθθτθθθθμθθτθθμθθμθθτθτθθτθτ=⋅∇-⎪⎭⎫ ⎝⎛+∂∂=⎪⎭⎫ ⎝⎛∂-∂-∂+∂-⎭⎬⎫⎩⎨⎧⋅∇-⎥⎦⎤⎢⎣⎡∂∂+∂∂+⎥⎦⎤⎢⎣⎡∂∂-∂∂=-⎪⎪⎭⎫ ⎝⎛⋅∇-∂∂+∂∂=-⎪⎭⎫ ⎝⎛⋅∇-∂∂+⎪⎪⎭⎫ ⎝⎛⋅∇-∂∂=+-++--Vv v r v w r vr wr r V w wr r r v vr r r V z w y v V z w V y v r yz yz zz zy yz yy 3212sin cos cos sin sin cos 1232cos cos cos sin 12sin sin sin cos 12sin cos 232cos cos 2sin sin 2sin cos 2cos cos 322sin sin 322cos cos sin sin cos sin (3.12.4)Substituting (3.6.1), (3.6.2) and (3.12) into expressions (3.11) and rearranging yields,()θθθτθτττ-∂∂+∂∂+∂∂r rr rx r r x r (3.13.1) ()θθθθθτθτττr r x r r x r+∂∂+∂∂+∂∂ (3.13.2) Making use of expressions (3.4.1), (3.6.1), (3.6.2), (3.8.1), (3.8.2), (3.9.1), (3.9.2), (3.13.1) and (3.13.2), we can get the final expression of 3D Navier-Stokes Equation in cylindrical coordinates as follows,3D Navier-Stokes Equation in cylindrical coordinates()()()S rr V G r r V F x V E t U r x =∂-∂+∂-∂+∂-∂+∂∂θθ ⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=E v v u U r ρρρρρθ,⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛+=Hu u v u v p uu u E r ρρρρρθ,⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+=θθθθθθρρρρρHv v v p v v uv v F r ,⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛+=rr r r r rHvp v v v v uv v G ρρρρρθ, ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-++=x rx r x xx rx x xx x q v v u V ττττττθθθ0,⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-++=θθθθθθθθθθθττττττq v v u V r r x r x 0, ⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-++=r rr r r xrrr rxr r q v v u V ττττττθθθ0 ⎪⎭⎫ ⎝⎛∂∂-∂∂-∂∂=⎪⎭⎫ ⎝⎛⋅∇-∂∂=θμμτθr v r r rv x u V x u r xx 232322⎪⎭⎫⎝⎛∂∂+∂∂==θμττθθθr u x v x x ⎪⎭⎫ ⎝⎛-∂∂+∂∂=⎪⎭⎫⎝⎛∂∂+∂∂==r u r r ru x vr u x v r r rx xr μμττ r v x u r r rv r v V v v r r r r 22323212μθμμθμτθθθθ+⎪⎭⎫ ⎝⎛∂∂-∂∂-∂∂=⋅∇-⎪⎭⎫ ⎝⎛+∂∂=r v r v r r rvr v r v r v r r r r θθθθθθμθμθμττ2-⎪⎭⎫ ⎝⎛∂∂+∂∂=⎪⎭⎫⎝⎛-∂∂+∂∂==rv x u r v r r rv V r v r r r rrμθμμμτθ2232322-⎪⎭⎫ ⎝⎛∂∂-∂∂-∂∂=⋅∇-∂∂=θθ∂∂+∂∂+∂∂=⋅∇r v r r rv x u V r⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-++-=000r p v v rv v S r r θθθθθθτρτρIf the moment of momentum equation is adopted to replace the tangential momentum equation, its expression will be simpler. Now for the moment equation, there is no source term.()()()S rr V G r r V F x V E t U r x =∂-∂+∂-∂+∂-∂+∂∂θθ ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=E v r v u U r ρρρρρθ,⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛+=Hu u v ur v p uu u E r ρρρρρθ,⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+=θθθθθθρρρρρHv v v pr r v v uv v F r ,⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+=rr r r r r Hv p v v r v v uv v G ρρρρρθ,⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-++=x rx r x xx rx x xx x q v v u r V ττττττθθθ0,⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-++=θθθθθθθθθθθττττττq v v u r V r r x r x 0, ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-++=r rr r r xr rr rxr r q v v u r V ττττττθθθ0⎪⎭⎫ ⎝⎛∂∂-∂∂-∂∂=⎪⎭⎫ ⎝⎛⋅∇-∂∂=θμμτθr v r r rv x u V x u r xx 232322 ⎪⎭⎫⎝⎛∂∂+∂∂==θμττθθθr u x v x x ⎪⎭⎫ ⎝⎛-∂∂+∂∂=⎪⎭⎫ ⎝⎛∂∂+∂∂==r u r r ru x v r u x v r r rx xr μμττ r v x u r r rv r v V v v r r r r 22323212μθμμθμτθθθθ+⎪⎭⎫ ⎝⎛∂∂-∂∂-∂∂=⋅∇-⎪⎭⎫ ⎝⎛+∂∂= r v r v r r rv r v r v r v r r r r θθθθθθμθμθμττ2-⎪⎭⎫ ⎝⎛∂∂+∂∂=⎪⎭⎫⎝⎛-∂∂+∂∂== rv x u r v r r rv V r v r r r rr μθμμμτθ2232322-⎪⎭⎫ ⎝⎛∂∂-∂∂-∂∂=⋅∇-∂∂= θθ∂∂+∂∂+∂∂=⋅∇r v r r rv x u V r ⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-+=0000r p v v S θθθθτρ For 2D axisymmetric flow field, the tangential momentum equation or moment equation can be omitted as follows, 2D axisymmetric equation in cylindrical coordinate()()S rr V G r x V E t U r x =∂-∂+∂-∂+∂∂ ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=E v u U r ρρρρ,⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+=Hu u v p uu u E r ρρρρ,,⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+=r r r r r Hv p v v uv v G ρρρρ,⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-+=x rx r xx rx xx x q v u V ττττ0,⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-+=r rr r xr rr xr r q v u V ττττ0 ⎪⎭⎫ ⎝⎛∂∂-∂∂=⎪⎭⎫ ⎝⎛⋅∇-∂∂=r r rv x u V x u r xx 232322μμτ ⎪⎭⎫ ⎝⎛-∂∂+∂∂=⎪⎭⎫ ⎝⎛∂∂+∂∂==r u r r ru x v r u x v r r rx xrμμττ ()rv x u r r rv V v r r r r 2323212μμμμτθθ+⎪⎭⎫ ⎝⎛∂∂-∂∂-=⋅∇-= rv x u r r rv V r v r r r rr μμμμτ2232322-⎪⎭⎫ ⎝⎛∂∂-∂∂=⋅∇-∂∂= rr rv x u V r ∂∂+∂∂=⋅∇ ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=000r p S θθτ [分享]CFD 中的湍流模型流体力学是力学的一个重要分支,它是研究流体(包括液体和气体)这样一个连续介质的宏观运动规律以及它与其他运动形态之间的相互作用的学科,在现代科学工程中具有重要的地位。
耐火材料9
第九章不定型耐火材料9.1 不定型耐火材料概述定义:不定型耐火材料是由耐火骨料和粉料、结合剂或另掺外加剂一定比例组成的混合料,能直接使用或加适当的液体调配后使用,是一种不经煅烧的新型耐火材料,其耐火度不低于1580摄氏度。
分类:不定型耐火材料种类繁多。
按工艺特性分类:浇注料,可塑料,捣打料,喷射料,投射料,火泥,涂抹料。
按原料材质分类:硅质,粘土质,高铝质,镁质,白云石质,铬质,含铬质等。
按结合剂品种分类:水玻璃结合,铝酸盐水泥结合,硅酸盐结合,焦油沥青结合,酚醛树脂结合等。
按施工方法和材料性质,不定形耐火材料可分为浇灌料、可塑料、捣打料、喷补料、投射料和涂料等。
矿物组成:其化学矿物组成取决于所用的颗粒料,粉状耐火材料,并与结合剂的品种及数量有关。
其制品的密度与组成材料及配比相关,与施工相关。
不定型耐火材料主要优点: 195页 1段9.2 不定型耐火材料的结合剂和外加剂9.2.1 有机结合剂要求:结合剂具备较好的粘结性能;高温性能;较好的流动性;浸润性;分散度;凝结硬化性质。
同时具备硬化时的体积稳定性,硬化后的耐火性及其他高温性能。
把由耐火粗颗粒料和粉料组成的散状耐火材料胶结在一起的物质,又称“胶结剂”。
用作耐火材料的结合剂,不但要求具有较好的冷态和热态结合强度,而且要求具有较好的施工(成型)性能和使用性能。
分类耐火材料,尤其是不定形耐火材料所用的结合剂,随被结合材料的性能及用途不同而不同,品种繁多,一般按结合剂的化学性质和结合剂的硬化条件分类。
1. 水溶性结合剂按化学性质分有机和无机结合剂:产生粘着结合的结合剂多数为有机结合剂,其中有的为暂时性结合剂,即在常温下或低温下起结合作用,经中温和高温热处理后会燃烧掉,如糊精、羧甲基纤维素、环氧树脂、纸浆废液等;水溶性结合剂——糊精、粉状羧甲基纤维素、粉状及液状木质素磺酸类材料、聚乙烯乙醇粉状晶体等。
这是一类大分子结构的有机物,存在极性基,吸附水分子形成水化膜,这类结合剂一般不与耐火材料产生化学反应,具有保水性,施工方便,所用量占5%,以后的干燥过程中,收缩小,加热易分解,挥发,不产生对高温性能影响的残留物。
超导体的特性、原理及应用
中国科学技术大学电磁学小论文论文题目:超导体的特性、原理及应用作者:蒋哥学号:PB13206***指导老师:周**日期:2014.6.9超导体的特性、原理及应用一、摘要超导是指导电材料在温度接近绝对零度的时候,物体分子热运动下材料的电阻趋近于0的性质;“超导体”是指能进行超导传输的导电材料。
零电阻和抗磁性是超导体的两个重要特性。
自从超导发现至今,超导的研究和超导体的研制已迅速发展,超导体的物质结构及性质已逐渐研究清楚,超导的临界温度已从开始的几开升至二百多开,超导材料得到广泛应用,特别是高温超导材料的广泛应用将会给社会带来的巨大变革。
二、关键词超导体零电阻效应迈斯纳效应应用实验验证三、引言及背景人类最初发现物体的超导现象是在1911年。
当时荷兰科学家卡·翁纳斯等人发现,某些材料在极低的温度下,其电阻完全消失,呈超导状态。
使超导体电阻为零的温度,叫超导临界温度。
经过近100年的发展,临界温度已大大提高,现有的高温超导体用液态氮来冷却即可应用于实际。
高温超导材料的用途非常广阔,大致可分为三类:大电流应用(强电应用)、电子学应用(弱电应用)和抗磁性应用。
大电流应用即超导发电、输电和储能;电子学应用包括超导计算机、超导天线、超导微波器件等;抗磁性主要应用于磁悬浮列车和热核聚变反应堆等。
四、正文1、超导体的特性及原理1.1零电阻效应超导体在一定温度以下,其电阻降为零的现象称为材料的超导电现象。
1911 年荷兰著名低温物理学家昂纳斯发现在 T=4.1K下汞具有零电阻效应。
采用四引线电阻测量法可测出超导体的R-T 特性曲线,如图所示。
图中的 Rn为电阻开始急剧减小时的电阻值,对应的温度称为起始转变温度 Ts;当电阻减小到 Rn/2 时的温度称为中点温度 Tm;当电阻减小至零时的温度为零电阻温度T0。
由于超导体的转变温度还与外部环境条件有关,定义在外部环境条件(电流,磁场和应力等)维持在足够低的数值时,测得的超导转变温度称为超导临界温度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
NS335特性及应用领域概述:
该合金是一种奥氏体低碳镍-钼-铬合金。Nicrofer6616hMo和其他早期开发的相似化学成分的合金的
主要区别是低碳、硅、铁、钨含量。这样的化学成分使其在650-1040℃时表现出极好的稳定性,提高了
抗晶间腐蚀的能力,在适当的制造条件下可以避免刃线腐蚀敏感性和焊缝热影响区腐蚀。合金应用于烟气
脱liu系统、suan洗和suan再生工厂、乙suan和农用化学品生产、二yang化钛生产(lv法)、电解电
镀等。
NS335相近型号:
HastelloyC-4UNSNO6455(mei国)W.Nr.2.4610NiMo16Cr16Ti(德国)
NS335化学成份:(GB/T14992-2005)
合金
型号
%
镍Ni铬Cr铁Fe钼Mo铌Nb钴Co碳C锰Mn硅SiliuS磷P铝Al钛
Ti
NS335
小
余量
14.514.0
标准17.53.017.02.00.0091.00.050.010.020.7
NS335物理性能:
密度
g/cm3
熔点℃热导率λ/(W/m•℃)比热容J/kg•℃弹性模量GPa剪切模量GPa电阻率μΩ•m泊松比线膨胀系数
a/10-6℃-1
8.61335138010.1(100℃)4082111.2410.9(20~100℃)
NS335力学性能:(在20℃检测机械性能的小值)
热处理方式
抗拉强度σb/MPa屈服强度σp0.2/MPa延伸率σ5/%布氏硬度HBS
固溶处理69027540
NS335生产执行标准:
标准
化学成份棒材锻件板材丝材管材
国家标准GB/T15002GB/T15008GB/T15008GB/T15009GB/T15010GB/T15012GB/T15062
航空工业标准
国家标准
NS335金相组织结构:
合金为面心立方晶格结构,其化学成分保证了金相稳定性和抗敏化性。
NS335工艺性能与要求:
1、在热处理过程中不能接触liu、磷、铅及其它低熔点金属,否则合金会变脆,应注意清除诸如标记漆、
温度指示漆、彩色蜡笔、润滑油、燃料等污物。燃料中的含liu量越低越好,天然气中的liu含量应少于
0.1%,重油中liu含量应少于0.5%。电炉加热是较好的选择,因为电炉可以精确控温,炉气干净。若燃气
炉的炉气足够纯净,也可以选择。
2、合金的热加工温度范围1080℃~900℃,冷却方式为水冷或其他快速冷却方式。为保证良好的防腐性
能,热加工后应进行固溶热处理。
