数字信号处理chapt2_rev
合集下载
数字信号处理ppt课件

23
三.自相关函数与 自协方差函数的性质
24
性质1 :相关函数与协方差函数的关系
Cxx m rxx m mx 2
Cxy m rxy m m*xmy
当 mx 0
Cxx m rxx m Cxy m rxy m
25
性质2:均方值、方差与相关函数和协方差函数
rxx
0
E
xn
2
Cxx 0 rxx 0 mx 2
五、功率谱密度
44
维纳——辛钦定理
1. 复频域
rxx
(m)
1
2
j
c Sxx (z)zm1dz,
Sxx
(z)
m
rxx
(m)z
m
C (Rx , Rx )
45
2. 频域
{ rxx(m)
1
2
Pxx (e j )e jm d
2
Pxx (e j ) rxx (m)e jm
m
46
3.性质
实平稳随机信号 rxx m rxx m
rxx m E x x n1 n1m
x1x2 p x1 , x2 ; m dx1dx2
18
自协方差函数
Cxx (m) E (xn1 mx )*(xn2 mx ) E (xn1 mx )*(xn1m mx )
rxx m mx 2
19
对于均值为零的随机过程 rxx m Cxx m
①偶函数
Pxx e j Pxx e j
②实函数
Pxx e j Pxx e j
③极点互为倒数出现
Sxx
z
Sxx
1 z
47
④功率谱在单位圆上的积分等于平均功率
E
x2
三.自相关函数与 自协方差函数的性质
24
性质1 :相关函数与协方差函数的关系
Cxx m rxx m mx 2
Cxy m rxy m m*xmy
当 mx 0
Cxx m rxx m Cxy m rxy m
25
性质2:均方值、方差与相关函数和协方差函数
rxx
0
E
xn
2
Cxx 0 rxx 0 mx 2
五、功率谱密度
44
维纳——辛钦定理
1. 复频域
rxx
(m)
1
2
j
c Sxx (z)zm1dz,
Sxx
(z)
m
rxx
(m)z
m
C (Rx , Rx )
45
2. 频域
{ rxx(m)
1
2
Pxx (e j )e jm d
2
Pxx (e j ) rxx (m)e jm
m
46
3.性质
实平稳随机信号 rxx m rxx m
rxx m E x x n1 n1m
x1x2 p x1 , x2 ; m dx1dx2
18
自协方差函数
Cxx (m) E (xn1 mx )*(xn2 mx ) E (xn1 mx )*(xn1m mx )
rxx m mx 2
19
对于均值为零的随机过程 rxx m Cxx m
①偶函数
Pxx e j Pxx e j
②实函数
Pxx e j Pxx e j
③极点互为倒数出现
Sxx
z
Sxx
1 z
47
④功率谱在单位圆上的积分等于平均功率
E
x2
数字信号处理第二章

x[n]
Input sequence Discrete-time system
y[n]
O Output sequence
§2.2 2 2 Operations O ti on Sequences S
• For example, the input may be a signal p with additive noise corrupted • Discrete-time system is designed to generate an output by removing the noise component from the input • In most cases, the operation defining a particular discrete-time discrete time system is composed of some basic operations
§2.1 Discrete-Time Signals: g Time-Domain Representation
• A complex sequence {x[n]} can be written as {x[n]} ]}={ {xre[n]} ]}+j{xim[n]} where xre and xim are the real and imaginary parts of x[n] • The complex conjugate sequence of {x[n]} is given by {x*[n]}={xre[n]} - j{xim [n]} • Often Of the h b braces are i ignored d to d denote a sequence if there is no ambiguity
Input sequence Discrete-time system
y[n]
O Output sequence
§2.2 2 2 Operations O ti on Sequences S
• For example, the input may be a signal p with additive noise corrupted • Discrete-time system is designed to generate an output by removing the noise component from the input • In most cases, the operation defining a particular discrete-time discrete time system is composed of some basic operations
§2.1 Discrete-Time Signals: g Time-Domain Representation
• A complex sequence {x[n]} can be written as {x[n]} ]}={ {xre[n]} ]}+j{xim[n]} where xre and xim are the real and imaginary parts of x[n] • The complex conjugate sequence of {x[n]} is given by {x*[n]}={xre[n]} - j{xim [n]} • Often Of the h b braces are i ignored d to d denote a sequence if there is no ambiguity
最新版《数字信号处理(英)》精品课件Chap.9 IIR Digital Filter Design(P366)

Spectral Transformations of IIR Filters
IIR Filter Design Using Matlab
1
9.1 Introduction(P366)
Stages for filters design:
stage 1: specification of desired system Hd(e
T
In such cases, conversion from specifications on the effective continuous-time filter to specifications on the discrete-time filter through the relation T .
p pT 0.4
s sT 0.6
Passband Transition Stopband
jT H (e ), | | T H eff ( j) 0, | | T
s
0
p
s
H (e ) H eff ( j
j
6
s (9.2)
C. Typical Specifications for DT filters (II)
Magnitude in log-domain: (dB)
20log10(1+p) 20log10(1-p) 20log10 s
ωp ωs
--- peak passband ripple
3
B. Example
Consider a DT filter that is to be used to lowpass filter a CT signal using the basic configuration of Fig.1. Specifically, we want the overall system of Fig.1 to have the following properties when the sampling rate is 104 samples/s (T=10-4 s): (1) The gain H ( j) should be within ±0.01(0.086dB) of unity 0 2 (2000) . (zero dB) in the frequency band
2010数字信号处理第4章-review
y[n]= x[n]* h[n]
e.g . y[n] = a0 x[n] + a1 x[n − 1] − b1 y[ n − 1]
y[n] = x[n] ∗ h[n] =
Frequency response
k =−∞
∑ x[k ]h[n − k ]
Y(e jω ) = H(e jω )X (e jω )
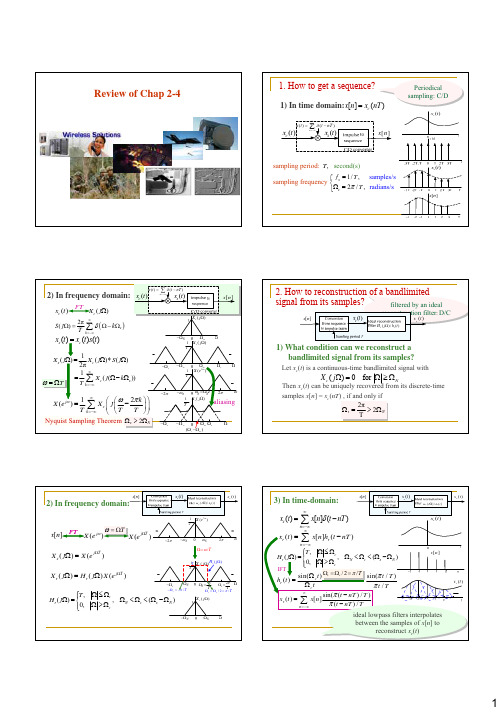
1) What condition can we reconstruct a bandlimited signal from its samples?
Ωs
Ω
−Ω s
−Ω N
1 T
X (e jω )
ΩN
Let xc(t) is a continuous-time bandlimited signal with Then xc(t) can be uniquely recovered from its discrete-time samples x[n] = xc(nT) , if and only if 2π Ωs = > 2Ω N T
−2π
−M ωN
M ωN
2π
ω
π
2π M ωN
ω
−2π
−π
π
2π
ω
c) General system for downsampling by M
2) Sampling rate increasing by an integer L —— upsampling a) In time domain: b) In frequency domain:
x[n] T{ ·· }} T{ y[n]
Periodicity of sinusoidal sequence:
数字信号处理-第2章-精品文档精选文档PPT课件

第2章. 连续时间信号的离散处理
2.1、数字信号处理系统的基本组成
•大多数数字信号处理的应用中,信号为来自不同模拟信号源,这些模拟 信号(电压或电流)通常为连续时间信号。
•应用数字信号处理(DSP)主要有三个原因: 1)滤波:滤除信号中来自周围环境的干扰或噪声; 2)检测:检测淹没在噪声中的特定信号(如雷达或声纳系统中),当检测 到的信号超过给定的阈值则认为目标信号存在,反之认为不存在; 3)压缩:当信号转换到另外一个域后,在变换域上更容易分辨信息的重 要程度,对重要部分分配多的比特数,次要部分分配尽可能少的比特 数,达到压缩的目的(如DCT算法)。
的是离散时间信号。将连续时间信号转换成离散时间信号的过程叫抽样。
抽样可由称为A/D变换器的器件完成:
量化结果
声卡
5
模拟输入 xa (t)
Ts
抽样器
抽样输出
xˆa (t)
xˆa(t) xa(t)•P (t)
xa(t)(t nTs)
n
xˆa (t)
周期性抽样函数 P (t )
xˆa (t)
Ts
P(t) (tnTs)
是否可以根据抽样后的离散时间序列恢复原始信号? •奈奎斯特抽样频率:能够再恢复出原始信号的最低抽样频率(使 抽样后的信号频谱不发生混叠的最低抽样频率,即信号最高频率的 二倍)
0 s/2 s2 0
•满足奈奎斯特抽样频率的抽样信号可由理想低通滤波器恢复出原 始信号。此后将推导这个过程。
xˆa(t) G (j )/g (t( ) 低 通 y滤 (t) 波 xa) (t)
X a ( j)
xa
(t )e
jt dt
[xa
(t )
•
P
(t )]e
2.1、数字信号处理系统的基本组成
•大多数数字信号处理的应用中,信号为来自不同模拟信号源,这些模拟 信号(电压或电流)通常为连续时间信号。
•应用数字信号处理(DSP)主要有三个原因: 1)滤波:滤除信号中来自周围环境的干扰或噪声; 2)检测:检测淹没在噪声中的特定信号(如雷达或声纳系统中),当检测 到的信号超过给定的阈值则认为目标信号存在,反之认为不存在; 3)压缩:当信号转换到另外一个域后,在变换域上更容易分辨信息的重 要程度,对重要部分分配多的比特数,次要部分分配尽可能少的比特 数,达到压缩的目的(如DCT算法)。
的是离散时间信号。将连续时间信号转换成离散时间信号的过程叫抽样。
抽样可由称为A/D变换器的器件完成:
量化结果
声卡
5
模拟输入 xa (t)
Ts
抽样器
抽样输出
xˆa (t)
xˆa(t) xa(t)•P (t)
xa(t)(t nTs)
n
xˆa (t)
周期性抽样函数 P (t )
xˆa (t)
Ts
P(t) (tnTs)
是否可以根据抽样后的离散时间序列恢复原始信号? •奈奎斯特抽样频率:能够再恢复出原始信号的最低抽样频率(使 抽样后的信号频谱不发生混叠的最低抽样频率,即信号最高频率的 二倍)
0 s/2 s2 0
•满足奈奎斯特抽样频率的抽样信号可由理想低通滤波器恢复出原 始信号。此后将推导这个过程。
xˆa(t) G (j )/g (t( ) 低 通 y滤 (t) 波 xa) (t)
X a ( j)
xa
(t )e
jt dt
[xa
(t )
•
P
(t )]e
数字信号处理_课件__数字信号分析-绪论课件共88页

数字信号处理实现方法
➢ 1.采用大、中小型计算机和微机。 ➢ 2.用单片机。 ➢ 3.利用通用DSP芯片 ➢ 4.利用特殊用途的DSP芯片
(1)采用大、中小型计算机和微机
➢ 工作站和微机上各厂家的数字信号软件,如有各 种图象压缩和解压软件。
➢ 用这一方法优点:可适用于各种数字信号处理的 应用场合,很灵活。
➢ 主要参考教材: ➢ (1) 程佩青著,数字信号处理教程(第三版),清华大学出版社,2007 ➢ (2) S. K. Mitra, Digital Signal Processing: A Computer-Based Approach,
Third Edition, Mcgraw-Hill,2001 ➢ (3) John G. Proakis, Dimitris G. Manolakis, Digital Signal Processing,
MATLAB, 2003. ➢ (5) 胡广书,数字信号处理:理论、算法与实现,清华大学出版社,2003
一、数字信号处理的基本概念
DSP(Digital Signal Processing)是近几十年发展起来 的一门新兴学科。
DSP是利用计算机或专用设备,以数值计算的 方法对信号进行采集、变换、综合、估值、识别等 加工处理,借以达到提取信息和便于应用的目的的 一门学科。
取离散值,且通常用二进制编码表示。
模拟信号和数字信号 (Analog Signal and Digital Signal )
➢ 模拟信号:指幅度连续的信号,通常指 时间和幅度上都是连续的信号。
➢ 数字信号:时间和幅度上都是离散的信 号。
x(t)
x(tn)
Байду номын сангаас
数字信号处理 DSP_Chapter2_SM
(a) Consider the sequence defined by x[ n] = ∑ δ[ k ]. If n < 0, then k = 0 is not included in the sum and hence, x[n] = 0 for n < 0. On the other hand, for n ≥ 0, k = 0 is included in the sum, and as a result, x[n] =1 for n ≥ 0. Therefore, n 1, n ≥ 0, x[ n] = ∑ δ[ k ] = ⎧ ⎨0, n < 0, = µ[ n]. ⎩ k = −∞
x[n]
+
_
w[n]
_ z 1
0.6
+
0.3
u[n]
+
y[n+1]
_ z 1
0.8
+
w[n _ 1]
_ z 1
_ 0.5
+
0.4
y[n]
0.2
w[n _ 2]
Not for sale.
3
The second-order section can be redrawn as shown below without changing its inputoutput relation.
Not for sale.
= −4µ[ n + 3] + 9µ[ n + 2] − 4µ[ n + 1] − 3µ[ n] − µ[ n − 1] + 3µ[ n − 2] + 2µ[ n − 3] − 2µ[ n − 4],
2.7
(a)
x[n]
+
_
w[n]
_ z 1
0.6
+
0.3
u[n]
+
y[n+1]
_ z 1
0.8
+
w[n _ 1]
_ z 1
_ 0.5
+
0.4
y[n]
0.2
w[n _ 2]
Not for sale.
3
The second-order section can be redrawn as shown below without changing its inputoutput relation.
Not for sale.
= −4µ[ n + 3] + 9µ[ n + 2] − 4µ[ n + 1] − 3µ[ n] − µ[ n − 1] + 3µ[ n − 2] + 2µ[ n − 3] − 2µ[ n − 4],
2.7
(a)
数字信号处理课件ppt
p
p
前向预测: e (n ) x (n ) x ˆ(n ) x (n )a px ( k n k )a px ( k n k )
k 1
k 0
E[|
e(n)|2]min
E[e*(n)(x(n)
xˆ(n))]E[e*(n)x(n)]
PART 1
Ex*(n) p apkx*(nk)x(n)
k1
p
rxx(0) apkrxx(k) k1
p
rxx(0) apkrxx(k)E[|e(n)|2]m in k1
p
rx
x得(l)到下ap面krx的x(k方l)程0组l:1,2,,
k1
p
rxx(0)
rxx(1)
rrxxx(x将W(01a))方lk程e r方组写程rr成)xxxx((矩pp阵)形1)式(Yau1pl1e- E[
|e(n)|2]m 0
in
rxx(p) rxx(p1) rxx(0) app
0
p
y (n ) s ˆ(n p ) x ˆ(n p ) a p kx [n (p k)] k 1
p
后向预测: b (n ) x (n p ) x ˆ(n p ) x (n p )a p k x (n p k ) k 1
[Lrxex (vpi)nsona p-1Drxxu( prbkin)] 算法:
kp
k 1
2 p 1
k p ap,p
a p ,k a p 1,Lk eviknspoan-pD1u,rpbikn的k一般1递,2推,3公,式如, p下:1
相关卷积定理:
卷积的相关函数等于相关函数的卷积
e(n)=a(n)*b(n) f(n)=c(n)*d(n)
数字信号处理第四章(南理工)
n=−∞
(4.12)
• According to the modulation theorem of CTFT 1 Gp (jΩ) = Ga (jΩ)*∆p (jΩ) 2π
1 +∞ = ∑ Ga (j(Ω+ kΩT )) T k=−∞ (4.16)
9
Effect of sampling in the frequency-domain ─ Gp(jΩ) is a periodic function of frequency Ω Ω consisting of a sum of shifted and scaled replicas of Ga(jΩ), shifted by integer of ΩT and Ω scaled by 1/T. ─ Baseband signal: the term on the right-hand side of Eq.(4.16) for k=0 is called baseband portion of Gp(jΩ). ─ Baseband / Nyquist band: frequency range −ΩT /2≤ Ω< ΩT /2
a
+∞
(4.11)
8
CTFT Gp(jΩ) of gp(t) Ω • According to the definition of CTFT +∞ +∞ − jΩt Gp (jΩ) = ∫ ∑ ga (nT)δ (t − nT) e dt −∞ n=−∞ +∞ = ∑ ga (nT)e− jΩnT
• Most signals in the real world are continuous in time; • DT signal processing algorithms are being used increasingly; • Digital processing of a CT signal involves 3 basic steps: ─ Sample a CT signal into a DT signal; (analog-to-digital (A/D) converter) ─ Process the DT signal (binary word); ─ Convert the processed DT signal back into CT signal. (digital-to-analog (D/A) converter)
(4.12)
• According to the modulation theorem of CTFT 1 Gp (jΩ) = Ga (jΩ)*∆p (jΩ) 2π
1 +∞ = ∑ Ga (j(Ω+ kΩT )) T k=−∞ (4.16)
9
Effect of sampling in the frequency-domain ─ Gp(jΩ) is a periodic function of frequency Ω Ω consisting of a sum of shifted and scaled replicas of Ga(jΩ), shifted by integer of ΩT and Ω scaled by 1/T. ─ Baseband signal: the term on the right-hand side of Eq.(4.16) for k=0 is called baseband portion of Gp(jΩ). ─ Baseband / Nyquist band: frequency range −ΩT /2≤ Ω< ΩT /2
a
+∞
(4.11)
8
CTFT Gp(jΩ) of gp(t) Ω • According to the definition of CTFT +∞ +∞ − jΩt Gp (jΩ) = ∫ ∑ ga (nT)δ (t − nT) e dt −∞ n=−∞ +∞ = ∑ ga (nT)e− jΩnT
• Most signals in the real world are continuous in time; • DT signal processing algorithms are being used increasingly; • Digital processing of a CT signal involves 3 basic steps: ─ Sample a CT signal into a DT signal; (analog-to-digital (A/D) converter) ─ Process the DT signal (binary word); ─ Convert the processed DT signal back into CT signal. (digital-to-analog (D/A) converter)
数字信号处理chapter272页PPT
2
2.1 Fourier Transform
Signal Analysis and Processing (1)Time Domain Analysis: t-A (2)Frequency Domain Analysis: f-A
Fourier Transform
x t in time-domain x xt sin n2 2 5 f0 0t t2randn
2020/4/17
7
4) Conclusion
(1)Sampling in time domain brings periodicity in frequency domain.
(2)Sampling in frequency domain brings periodicity in time domain.
Q3: HOW to DFT?
HOW to realize DFT? How to use DFT to solve the practical problems?
2020/4/17
1
Basic contents of this chapter
2.1 Review of Fourier Transform 2.2 Discrete Fourier Series 2.3 Discrete Fourier Transform 2.4 Relationship between DFT, z-Transform and sequence’s
Three Questions about Discrete Fourier Transform
Q1: WHAT is DFT?
WHAT is relationship between DFT and other kinds of Fourier Transform?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Y (e jω ) FT [ y (n)] =
[
∞ m =−∞
x(m)h(n − m)]e − jω
k=n-m Y (e jω ) =
=
∞ k =−∞ jω
h(k )e − jω k x(m)e − jωk e− jω x(m)e − jω k
k =−∞
h(k )e − jωk
jω
= H (e ) X (e )
X ( k )e
j
X ( k ) = N ⋅ ak
(2.3.6)
x ( n)
(2.3.7)
DFS N
X (k )
2
2.3.1 8
x(n)=R4(n)
x ( n)
7 n =0
x(n) 2.3.1(a)
N=8
x ( n)
3 n =0 − kn 4
DFS
X (k ) = =
x ( n )e
− j k ⋅4 4 −j k 4
2
(2.2.11) (2.2.12)
* xo (n) = − xo ( − n)
(2.2.13)
2
7
2
2.2.2 x(n) n -n
x(n)=x*(-n)
(2.2.10)
x(n)
x(n)=cos( n)+j sin( n) (END)
2
x(n) = xe (n) + xo (n)
xe(n), xo(n) (2.2.16) (2.2.16) n -n x(n)
h(n)=he(n)+ho(n) h(n)+h(-n) h(n)-h(-n)
h(n) = 0, n < 0
he(n)
ho(n)
h(o),
n=0
(2.2.27)
he ( n ) =
1 h ( n ), n > 0 2 1 h ( − n ), n < 0 2
12
2
0,
n=0
(2.2.28)
ho (n ) =
FT FT xe(n) FT xo(n) =1/2 =1/2 X(ej )+X*(ej ) =Re X(ej ) =XR(ej ) =jXI(ej ) X(ej )-X*(ej ) =jIm X(ej )
(2.2.18)
(2.2.19)
10
2
xe(n) xo(n)
FT FT
XR(ej ) j XI(ej ) ( j)
(2.2.23) (2.2.24)
x(n) = xr (n) + jxi (n)
FT X(e j )=Xe(e j )+Xo(e j )
X e (e jω ) = FT [ xr (n)] =
∞ n =−∞
xr (n)e − jωn =X e* (e- jω )
* xi (n)e − jω n = − X o (e- jω )
X o (e jω ) = FT [ jxi (n)] = j
∞ n =−∞
9
2
• • j
FT FT
2
(b)
xe(n) x(n)=xe(n)+xo(n)
xo(n) (2.2.25)
1 1 xe (n) = [ x(n) + x∗ (−n)], xo (n) = [ x(n) − x∗ (− n)] 2 2
2
h(n) i.e.,
FT
He(ej )
H(ej )
11
2
X (e jω ) = X (e − jω ) =
h[n] ⋅ e − jnω h[n] ⋅ e jnω
h[ n]
X (e jω ) = X * (e − jω )
2
(2.2.18) he(n)=1/2 ho(n)=1/2 h(n)
(2.2.19)
=
1 n a ,n > 0 2 1 − a −n , n < 0 2
13
2
2.2.3
2.2.3
2
5. y(n)=x(n)*h(n), Y(e j )=X(e j )·H(e j )
y (n) =
∞ m =−∞
(2.2.32)
x ( m) h( n − m)
∞ n =−∞ ∞ ∞ m =−∞ ∞ m =−∞
1 h(n), n > 0 2 1 − h(−n), n < 0 2
h(n) he(n) ho(n)
h(n)= he(n)u+(n) h(n)= ho(n)u+(n)+h(o) (n)
(2.2.29) (2.2.30)
2
2.2.3
x(n)=an u(n); 0<a<1; xo(n) (2.2.xx)
15
2
7.
∞ n =−∞
2
(Parseval)
1 2π
∞ n =−∞
x ( n) =
π
−π
X (e jω ) d ω
(2.2.34)
2
∞ n =−∞
2
x ( n) =
x ( n ) x* ( n ) =
π
−π
∞ n =−∞
x* (n)[
1 2π
π
−π
X (e jω )e jω n d ω )]
1 2π 1 = 2π =
n =−∞
e
jω ( m − n )
dω = 2πδ (n − m)
π
−π
DTFT (2.2.3)
x ( m) =
1 2π
X (e jω )e jω m dω
m≠n
m=n
3
2
FT (2.2.2)
(2.2.1) FT
(2.2.4)
Common DTFT pairs
MMTICA DEMO
2
2.2.1
x(n)=RN(n)
(2.2.16)
(2.2.17) (2.2.17) (2.2.18) (2.2.19)
1 xe ( n ) = [ x (n ) + x ∗ ( −n )] 2 1 xo (n ) = [ x ( n ) − x ∗ ( −n )] 2
8
2
xe(n) X(ej ) X(ej )=Xe(ej )+Xo(ej ) Xe(ej ) Xo(ej )
∞ n =−∞ ∞ n =−∞
x(n)h(n)e − jω n x( n)[ 1 2π
π
−π
H (e jθ )e jθ n dθ ]e − jω n
Y (e ) =
jω
∞ 1 π H (e jθ )[ x(n)e − j (ω −θ ) n ]dθ 2π −π n =−∞ π 1 = H (e jθ ) X (e j (ω −θ ) )dθ − π 2π 1 = H (e jω ) * H (e jω ) 2π
(2.2.2)
2
2
DTFT Definition in Mathematica
2
FT - ~
π
−π
ej
n
(2.2.1)
X (e jω )e jω m d ω = =
π
−π
π
−π ∞
[
∞ n =−∞
x(n)e − jω n ]e jω m dω
∞ −∞
x(n)
e jω ( m − n ) d ω
(2.2.3) (2.2.4)
X ( e jω )
∞ n =−∞
x ∗ ( n )e jω n dω 1 2π
π
−π
π
−π
X ( e jω ) X * ( e jω )dω =
X ( e jω ) dω
2
1/(2 )
|X(e j )|2 2.2.1 FT
2 2.2.1
x(n)e jnωo → X (ω − ω0 )
16
2
2.3
2
2
2.1 2.2 2.3 2.4 2.5 2.6 Z Z
2
2.1
t
(
)
1
2
Z
DTFT
Z
Z
2
2.2
2.2.1 DTFT
X (e jω ) =
x(n) DTFT
∞ n =−∞
∞ n =−∞
x ( n )e − jω n
(2.2.1)
,
FT(Fourier Transform) x(n)
x(n) < ∞
2.3.1
x ( n)
(DFS) N
∞ k =−∞ j 2π kn N
x ( n) =
ak
2π − j mn N
ak e
(2.3.1)
ak
e
n
N
2
N −1 n =0 N −1 n =0
x ( n )e
−j
2π mn N
=
N −1 n=0
[
∞ k =−∞
ak e =
−j
2π mn N
=
∞ k =−∞
ak
,
e
j 2π kl N
DFS (Discrete Fourier Series k
j 2π kn N j 2π kl N
X ( k )e
= e
j
[
N −1 n =0
x ( n )e
]e
=
N −1 n =0
x ( n)
N −1 k =0
2π (l −n ) k N
= x(l )
j 2π kn N
x ( n) =
xe(n)
x(n)=xe(n)+xo(n),
x (0),
