线性规划课后题答案(张干宗)
线性规划题及答案

线性规划题及答案线性规划是一种数学优化方法,用于解决最大化或最小化线性目标函数的问题,同时满足一组线性约束条件。
在这个任务中,我们将提供一道线性规划题目,并给出相应的答案。
题目描述:某公司生产两种产品A和B,每个单位的产品A利润为10元,产品B利润为15元。
公司有两个生产部门,分别是部门X和部门Y。
部门X每天最多能生产200个单位的产品A或150个单位的产品B;部门Y每天最多能生产100个单位的产品A或120个单位的产品B。
公司每天的生产时间为8小时,部门X生产一个单位的产品A需要1小时,生产一个单位的产品B需要2小时;部门Y生产一个单位的产品A需要2小时,生产一个单位的产品B需要1小时。
公司希望在满足生产能力和时间限制的情况下,最大化每天的利润。
解题步骤:1. 定义变量:- 设产品A的产量为x,产品B的产量为y。
2. 建立目标函数:- 目标函数表示每天的利润,即最大化10x + 15y。
3. 建立约束条件:- 部门X的生产能力限制:x ≤ 200,y ≤ 150。
- 部门Y的生产能力限制:x ≤ 100,y ≤ 120。
- 时间限制:x + 2y ≤ 8。
- 非负约束:x ≥ 0,y ≥ 0。
4. 求解线性规划问题:- 将目标函数和约束条件带入线性规划模型,使用线性规划求解器求解得到最优解。
答案:根据上述线性规划模型,我们可以使用线性规划求解器求解得到最优解。
经过计算,最优解如下:- 产品A的产量为100个单位。
- 产品B的产量为120个单位。
- 每天的最大利润为(100 * 10) + (120 * 15) = 3100元。
因此,公司在满足生产能力和时间限制的情况下,每天的最大利润为3100元,最佳的生产方案是生产100个单位的产品A和120个单位的产品B。
这个线性规划问题的求解过程可以帮助公司在生产过程中做出最佳的决策,以最大化利润。
同时,通过调整约束条件和目标函数,可以应用线性规划方法解决其他类似的优化问题。
线性规划题及答案

线性规划题及答案一、问题描述某公司生产两种产品A和B,每一个产品的生产需要消耗不同的资源,并且每一个产品的销售利润也不同。
公司希翼通过线性规划来确定生产计划,以最大化利润。
已知产品A每一个单位的生产需要消耗2个资源1和3个资源2,每一个单位的销售利润为10元;产品B每一个单位的生产需要消耗4个资源1和1个资源2,每一个单位的销售利润为15元。
公司目前有10个资源1和12个资源2可供使用。
二、数学建模1. 假设生产产品A的数量为x,生产产品B的数量为y。
2. 根据资源的消耗情况,可以得到以下约束条件:2x + 4y ≤ 10 (资源1的消耗)3x + y ≤ 12 (资源2的消耗)x ≥ 0, y ≥ 0 (生产数量为非负数)3. 目标是最大化利润,即最大化销售收入减去生产成本:最大化 Z = 10x + 15y三、线性规划求解1. 将目标函数和约束条件转化为标准形式:目标函数:最大化 Z = 10x + 15y约束条件:2x + 4y ≤ 103x + y ≤ 12x ≥ 0, y ≥ 02. 通过图形法求解线性规划问题:a. 绘制约束条件的图形:画出2x + 4y = 10和3x + y = 12的直线,并标出可行域。
b. 确定可行域内的顶点:可行域的顶点为(0, 0),(0, 2.5),(4, 0),(2, 3)。
c. 计算目标函数在每一个顶点处的值:分别计算Z = 10x + 15y在(0, 0),(0, 2.5),(4, 0),(2, 3)四个顶点处的值。
Z(0, 0) = 0Z(0, 2.5) = 37.5Z(4, 0) = 40Z(2, 3) = 80d. 比较所有顶点处的目标函数值,确定最优解:最优解为Z = 80,即在生产2个单位的产品A和3个单位的产品B时,可以获得最大利润80元。
四、结论根据线性规划的结果,公司在资源充足的情况下,应该生产2个单位的产品A和3个单位的产品B,以最大化利润。
线性规划习题答案-推荐下载
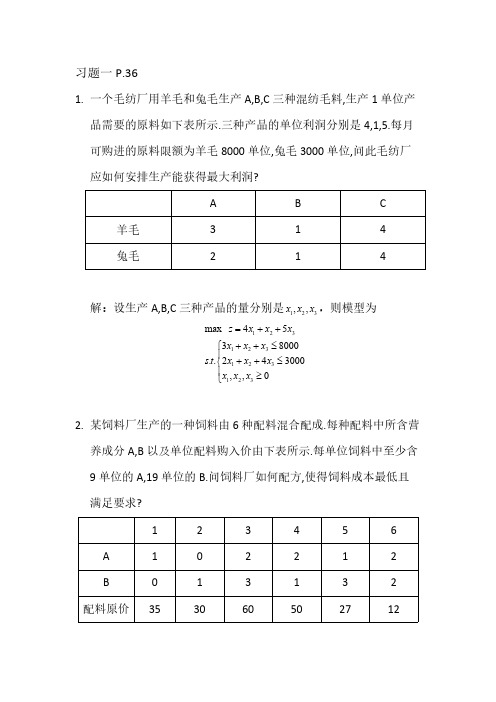
习题一P.361.一个毛纺厂用羊毛和兔毛生产A,B,C 三种混纺毛料,生产1单位产品需要的原料如下表所示.三种产品的单位利润分别是4,1,5.每月可购进的原料限额为羊毛8000单位,兔毛3000单位,问此毛纺厂应如何安排生产能获得最大利润?A B C 羊毛314兔毛214解:设生产A,B,C 三种产品的量分别是,则模型为123,,x x x 123123123123max 4538000..243000,,0z x x x x x x s t x x x x x x =++++≤⎧⎪++≤⎨⎪≥⎩2.某饲料厂生产的一种饲料由6种配料混合配成.每种配料中所含营养成分A,B 以及单位配料购入价由下表所示.每单位饲料中至少含9单位的A,19单位的B.问饲料厂如何配方,使得饲料成本最低且满足要求?123456A12212B 013132配料原价353060502712解:设每单位饲料中每种配料所需的量为,则有()1,2,3,4,5,6i x i =1234561345623456123456min 3530605027122229..33219,,,,,0z x x x x x x x x x x x s t x x x x x x x x x x x =+++++++++≥⎧⎪++++≥⎨⎪≥⎩4.某产品的一个完整单位包括四个A 零件和三个B 零件.这两种零件(A 和B)由两种不同的原料制成,而这两种原料可利用的数量分别是100单位和200单位.三个车间进行生产,而每个车间制造零件的方法各不相同.下表中给出每个生产班组的原料耗用量和每一种零件的产量.目标是要确定每一个车间的生产班组数使得产品的配套数达到最大.车间每班进料每班产量/个数原料1原料2零件A 零件B 186752596933884解:设每个车间的生产组数分别为,则可生产123,,x x x 个单位产品,则线性规划如()()123123768594min ,43x x x x x x y ++++⎧⎫=⎨⎬⎩⎭下:123123123123123max 853*********..76845943,,0yx x x x x x s t x x x y x x x yx x x ++≤⎧⎪++≤⎪⎪++≥⎨⎪++≥⎪⎪≥⎩6.设三地各有某种纺织原料90,30,70吨,需要调运给123,,,A A A 五地,后者各需要80,10,30,50,20吨.从到12345,,,,B B B B B ()1,2,3i A i =的路程(千米)如下表所示.现要求设计一个调拨方案,(1,2,3,4,5)j B j =使得总运输吨公里数最少.B1B2B3B4B5A1130286240523153A26422074457309A3718518146443解: 设从运往的运量为,则线性规划()1,2,3i A i =()1,2,3,4,5j B j =ij x 模型为如下形式,其中表示从到的运价。
线性规划题及答案

线性规划题及答案一、问题描述假设某公司生产两种产品:产品A和产品B。
每天生产的产品A需要花费3小时的人工时间和2小时的机器时间,每天生产的产品B需要花费2小时的人工时间和4小时的机器时间。
公司每天有8小时的人工时间和10小时的机器时间可供使用。
产品A的利润为200元/件,产品B的利润为300元/件。
公司希望通过合理安排生产计划,使得每天的总利润最大化。
二、数学建模1. 定义变量:设产品A的生产量为x,产品B的生产量为y。
2. 建立目标函数:总利润最大化,即Maximize Z = 200x + 300y。
3. 建立约束条件:3x + 2y ≤ 8(人工时间约束)2x + 4y ≤ 10(机器时间约束)x ≥ 0,y ≥ 0(非负约束)三、线性规划模型Maximize Z = 200x + 300ysubject to3x + 2y ≤ 82x + 4y ≤ 10x ≥ 0, y ≥ 0四、求解线性规划问题通过线性规划求解器进行计算,得到最优解。
1. 求解目标函数最大值:Z = 200x + 300y最大值为Z = 200 * 2 + 300 * 1 = 700。
2. 求解最优生产量:当x = 2,y = 1时,总利润最大,即每天生产2件产品A和1件产品B,总利润为700元。
五、结论根据线性规划模型的计算结果,为了使得公司每天的总利润最大化,应该安排每天生产2件产品A和1件产品B。
这样可以获得每天700元的总利润。
六、灵敏度分析在线性规划问题中,灵敏度分析可以帮助我们了解模型的稳定性和可行性。
下面对人工时间和机器时间的变化进行灵敏度分析。
1. 人工时间的变化:当每天的人工时间增加1小时,即约束条件变为3x + 2y ≤ 9时,重新求解线性规划问题。
结果显示,最大总利润仍然为700元,最优生产量为每天生产2件产品A和1件产品B。
2. 机器时间的变化:当每天的机器时间增加1小时,即约束条件变为2x + 4y ≤ 11时,重新求解线性规划问题。
线性规划练习题

作业1.第7题A.AB.BC.CD.D答案:D标准答案:D您的答案:题目分数:1.0此题得分:0.02.第8题下列不满足线性规划问题的典式要求的是()。
A. 线性规划模型必须是标准形B. 基必须是单位矩阵。
C. 基变量可以出现在目标函数中D. 非基变量可以出现在目标函数中。
A.AB.BC.CD.D答案:C标准答案:C您的答案:题目分数:1.0此题得分:0.03.第13题A.AB.BC.CD.D答案:B标准答案:B 您的答案:题目分数:1.0 此题得分:0.04.第14题A.AB.BC.CD.D答案:D标准答案:D 您的答案:题目分数:1.0此题得分:0.05.第15题A.AB.BC.CD.D答案:A标准答案:A 您的答案:题目分数:1.0 此题得分:0.06.第16题A.AB.BC.CD.D答案:B标准答案:B 您的答案:题目分数:1.0 此题得分:0.07.第17题A.AB.BC.CD.D答案:A标准答案:A您的答案:题目分数:1.0此题得分:0.08.第18题若用二阶段法求没有可行解的线性规划问题,则在最后一张单纯表上()。
A. 人工变量的检验数没有正数B. 人工变量的检验数没有负数C. 非基变量中有人工变量D. 基变量中有人工变量A.AB.BC.CD.D答案:D标准答案:D您的答案:题目分数:1.0此题得分:0.09.第19题A.AB.BC.CD.D答案:D标准答案:D您的答案:题目分数:1.0此题得分:0.010.第20题若目标函数求极小值的线性规划问题没有最优解,则在最后一张单纯表上()。
A. 对应非基变量的列上的系数没有正数B. 基变量的取值有负数C. 检验数没有负数D. 检验数为负的非基变量对应的列上的系数没有正数A.AB.BC.CD.D答案:D标准答案:D您的答案:题目分数:1.0此题得分:0.011.第21题A.AB.BC.CD.D答案:D标准答案:D您的答案:题目分数:1.0 此题得分:0.012.第26题A.AB.BC.CD.D答案:B标准答案:B您的答案:题目分数:1.0 此题得分:0.013.第28题A.AB.BC.CD.D答案:A标准答案:A您的答案:题目分数:1.0 此题得分:0.014.第33题A.AB.BC.CD.D答案:D标准答案:D您的答案:题目分数:1.0 此题得分:0.015.第34题A.AB.BC.CD.D答案:D标准答案:D您的答案:题目分数:1.0 此题得分:0.016.第35题A.AB.BC.CD.D答案:D标准答案:D您的答案:题目分数:1.0此题得分:0.017.第36题A.AB.BC.CD.D答案:A标准答案:A您的答案:题目分数:1.0此题得分:0.018.第46题检验有无迂回时,必须对()进行。
线性规划题及答案

线性规划题及答案线性规划是一种数学优化方法,用于解决在给定约束条件下求解线性目标函数的最优解的问题。
本文将介绍一个线性规划题及其答案,以帮助您更好地理解和应用线性规划。
题目描述:某工厂生产两种产品A和B。
每单位产品A需要3个工时和2个材料单位,每单位产品B需要4个工时和1个材料单位。
工厂每天有总共24个工时和10个材料单位可用。
产品A的利润为100元/单位,产品B的利润为80元/单位。
问工厂每天应该生产多少单位的产品A和产品B,以最大化利润?解答步骤:1. 确定决策变量:设工厂每天生产的产品A的单位数为x,产品B的单位数为y。
2. 建立目标函数:目标是最大化利润,因此目标函数为:Z = 100x + 80y。
3. 建立约束条件:根据题目描述,工厂每天可用的工时为24个,每单位产品A需要3个工时,每单位产品B需要4个工时,因此工时的约束条件为:3x + 4y ≤ 24。
工厂每天可用的材料单位为10个,每单位产品A需要2个材料单位,每单位产品B需要1个材料单位,因此材料单位的约束条件为:2x + y ≤ 10。
另外,生产的产品数量不能为负数,即:x ≥ 0,y ≥ 0。
4. 构建线性规划模型:综合考虑目标函数和约束条件,可以得到线性规划模型如下:Maximize Z = 100x + 80ySubject to:3x + 4y ≤ 242x + y ≤ 10x ≥ 0y ≥ 05. 解答最优解:通过线性规划求解器或图形法等方法,可以求解出最优解。
假设最优解为x*和y*,则工厂每天应该生产x*单位的产品A和y*单位的产品B,以最大化利润。
答案解析:通过线性规划求解器求解上述线性规划模型,得到最优解为x* = 4,y* = 4。
即工厂每天应该生产4个单位的产品A和4个单位的产品B,以最大化利润。
利润最大化时的最优解下,工厂每天使用的工时为3x* + 4y* = 3*4 + 4*4 = 24个,使用的材料单位为2x* + y* = 2*4 + 4 = 12个。
线性规划题及答案
线性规划题及答案线性规划是一种数学优化方法,用于解决线性约束条件下的最优化问题。
在线性规划中,我们需要确定一组变量的取值,以使得目标函数达到最大或最小值,同时满足一系列线性约束条件。
以下是一道线性规划题及其答案,供您参考:题目:某工厂生产两种产品A和B,每单位产品A的利润为10元,每单位产品B的利润为15元。
工厂的生产能力为每天生产100个单位的产品A和80个单位的产品B。
每单位产品A需要消耗1个单位的原材料X和2个单位的原材料Y,每单位产品B需要消耗3个单位的原材料X和1个单位的原材料Y。
工厂每天可获得的原材料X和Y的数量分别为120个单位和110个单位。
请问,工厂应该如何安排生产,以使得利润最大化?答案:首先,我们需要定义决策变量。
设x为生产的产品A的数量(单位:个),y 为生产的产品B的数量(单位:个)。
其次,我们需要建立目标函数和约束条件。
目标函数:利润最大化目标函数为:Z = 10x + 15y约束条件:1. 生产能力约束:x ≤ 100y ≤ 802. 原材料X的约束:x + 3y ≤ 1203. 原材料Y的约束:2x + y ≤ 1104. 非负约束:x ≥ 0y ≥ 0现在,我们可以根据以上目标函数和约束条件进行线性规划求解。
首先,我们绘制出目标函数和约束条件的图形表示:目标函数:Z = 10x + 15y约束条件:1. x ≤ 1002. y ≤ 803. x + 3y ≤ 1204. 2x + y ≤ 1105. x ≥ 06. y ≥ 0通过图形表示,我们可以找到目标函数和约束条件的可行解区域,并确定最优解点。
根据图形表示,我们可以得出以下结论:1. 目标函数的等值线是一条直线,其斜率为-10/15=-2/3。
随着等值线向右上方移动,目标函数的值逐渐增加。
2. 可行解区域是由约束条件所确定的多边形区域。
根据图形表示,我们可以确定最优解点为多边形区域的顶点之一。
通过计算,我们可以得到最优解点的坐标。
《运筹学》_习题_线性规划部分练习题及_答案
一、思考题1. 什么是线性规划模型,在模型中各系数的经济意义是什么? 2. 线性规划问题的一般形式有何特征?3. 建立一个实际问题的数学模型一般要几步?4. 两个变量的线性规划问题的图解法的一般步骤是什么?5. 求解线性规划问题时可能出现几种结果,那种结果反映建模时有错误?6. 什么是线性规划的标准型,如何把一个非标准形式的线性规划问题转化成标准形式。
7. 试述线性规划问题的可行解、基础解、基础可行解、最优解、最优基础解的概念及它们之间的相互关系。
8. 试述单纯形法的计算步骤,如何在单纯形表上判别问题具有唯一最优解、有无穷多个最优解、无界解或无可行解。
9. 在什么样的情况下采用人工变量法,人工变量法包括哪两种解法?10.大M 法中,M 的作用是什么?对最小化问题,在目标函数中人工变量的系数取什么?最大化问题呢? 11.什么是单纯形法的两阶段法?两阶段法的第一段是为了解决什么问题?在怎样的情况下,继续第二阶段? 二、判断下列说法是否正确。
1. 线性规划问题的最优解一定在可行域的顶点达到。
2. 线性规划的可行解集是凸集。
3. 如果一个线性规划问题有两个不同的最优解,则它有无穷多个最优解。
4. 线性规划模型中增加一个约束条件,可行域的范围一般将缩小,减少一个约束条件,可行域的范围一般将扩大。
5. 线性规划问题的每一个基本解对应可行域的一个顶点。
6. 如果一个线性规划问题有可行解,那么它必有最优解。
7. 用单纯形法求解标准形式(求最小值)的线性规划问题时,与0>j σ对应的变量都可以被选作换入变量。
8. 单纯形法计算中,如不按最小非负比值原则选出换出变量,则在下一个解中至少有一个基变量的值是负的。
9. 单纯形法计算中,选取最大正检验数k σ对应的变量k x作为换入变量,可使目 标函数值得到最快的减少。
10. 一旦一个人工变量在迭代中变为非基变量后,该变量及相应列的数字可以从单纯形表中删除,而不影响计算结果。
线性规划题及答案
线性规划题及答案一、题目描述:假设某公司生产两种产品:A和B。
产品A每单位利润为10元,产品B每单位利润为8元。
生产一单位产品A需要消耗2个单位的原材料X和3个单位的原材料Y;生产一单位产品B需要消耗4个单位的原材料X和1个单位的原材料Y。
公司的生产能力限制为每天生产产品A不超过100个单位,生产产品B不超过80个单位。
原材料X每天供应量为180个单位,原材料Y每天供应量为150个单位。
为了最大化利润,公司应如何安排生产计划?二、解题思路:本题是一个线性规划问题,可以使用线性规划模型来解决。
首先,我们需要确定决策变量、目标函数和约束条件。
1. 决策变量:设产品A的生产数量为x,产品B的生产数量为y。
2. 目标函数:公司的利润最大化是我们的目标。
由于产品A每单位利润为10元,产品B每单位利润为8元,因此目标函数可以表示为:maximize 10x + 8y。
3. 约束条件:a) 生产能力限制:根据题目描述,每天生产产品A不超过100个单位,生产产品B不超过80个单位,可以得到以下约束条件:x ≤ 100y ≤ 80b) 原材料供应量限制:根据题目描述,原材料X每天供应量为180个单位,原材料Y每天供应量为150个单位,可以得到以下约束条件:2x + 4y ≤ 1803x + y ≤ 150c) 非负约束:生产数量不能为负数,可以得到以下约束条件:x ≥ 0y ≥ 0综上所述,我们可以得到线性规划模型如下:maximize 10x + 8ysubject to:x ≤ 100y ≤ 802x + 4y ≤ 1803x + y ≤ 150x ≥ 0y ≥ 0三、求解线性规划问题:通过线性规划求解器,我们可以得到最优解。
假设使用某线性规划求解软件,输入上述模型后,运行求解器,得到最优解如下:x = 50,y = 30利润最大值为:10 * 50 + 8 * 30 = 860元四、答案解析:根据线性规划求解结果,为了最大化利润,公司应按照以下生产计划进行生产:每天生产50个单位的产品A和30个单位的产品B,此时公司的利润最大化为860元。
线性规划题及答案
线性规划题及答案线性规划是一种优化问题的数学建模方法,用于求解最大化或者最小化目标函数的线性约束条件下的最优解。
在实际应用中,线性规划常用于资源分配、生产计划、运输问题等领域。
下面将为您提供一道线性规划题及其详细解答。
题目描述:某公司生产两种产品A和B,每天的生产时间为8小时。
产品A每单位利润为200元,产品B每单位利润为300元。
生产产品A需要1小时,生产产品B需要2小时。
公司希翼通过合理的生产安排最大化每天的利润。
解答步骤:1. 定义变量:设产品A的生产数量为x,产品B的生产数量为y。
2. 建立目标函数:目标函数为最大化每天的利润,即maximize Z = 200x + 300y。
3. 建立约束条件:a) 生产时间的约束:x + 2y ≤ 8。
b) 非负约束:x ≥ 0,y ≥ 0。
4. 绘制可行域:将约束条件绘制在坐标系中,得到一个可行域。
5. 求解最优解:a) 在可行域内找到目标函数的最大值点。
b) 根据最大值点的坐标值得到最优解。
解答过程:1. 建立目标函数:目标函数为最大化每天的利润,即maximize Z = 200x + 300y。
2. 建立约束条件:a) 生产时间的约束:x + 2y ≤ 8。
b) 非负约束:x ≥ 0,y ≥ 0。
3. 绘制可行域:将约束条件绘制在坐标系中,得到一个可行域。
可行域为一个三角形,顶点分别为(0,0),(0,4),(8,0)。
4. 求解最优解:a) 在可行域内找到目标函数的最大值点。
计算可行域内的所有顶点的目标函数值,得到以下结果:- (0,0):Z = 200(0) + 300(0) = 0。
- (0,4):Z = 200(0) + 300(4) = 1200。
- (8,0):Z = 200(8) + 300(0) = 1600。
b) 根据最大值点的坐标值得到最优解。
最大值点为(8,0),即在生产时间充分的情况下,只生产产品A能够获得最大利润1600元。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P11.3(1)将下列线性规划模型化成标准形式:
⎩⎨
⎧=+≤+--=10
352..3max 212121x x x x t s x x z 解:令"
2'
22"
1'
11,,'x x x x x x z z -=-=-=,代入上面的线性规划,得标准形式
⎪⎩⎪⎨⎧≥=-+-=+-++--++-=0,,,,10335
22..33'min 3"
2'2"1'1"
2'2"1'
13"
2'2"1'1"
2
'2"1'1x x x x x x x x x x x x x x t s x x x x z P14:
1、用图解法求解下列线性规划问题:
⎪⎪⎪⎩⎪
⎪⎪⎨⎧≥≥≤-≤-≤+-≤++-=0
,01
37210
42242..23min 212
121212121x x x x x x x x x x t s x x f 利用图解法:
于是得最优解为(4,1),最优值为-10。
P15:2
⎪⎪⎩⎪⎪⎨⎧≥≤≤≥-≥+-=0
6063222..26max 2121
2121x x x x x x t s x x z 解:利用图解法
于是最优解为(6,0),最优值为36。
P15.3
⎪⎪⎩⎪⎪⎨⎧≥≥≥+≤+≤+--=0
,0121272172..27min 212121
21210x x x x x x x x t s x x x 解:利用图解法求得
有无穷多最优解,都落在一个线段上,该线段的两个端点是:
)3/7,3/7(),0,3()2()1(==x x
于是全部的最优解可以表示成)
1(x
与)
2(x
的凸组合,即
.10,)1()2()1(*≤≤-+=αααx x x
最优值都是-21。
P16:
1、 解:设ij x 表示第i 台机床加工第j 类产品的产量,于是可得数学模型
⎪⎪⎪⎩⎪
⎪⎪
⎨⎧=≥≤+≤+≤+≤++++++++++++++++=.
6,5,4,3,2,1,0900
600700850..)(80)(64)(72)(32)(28)(40max 46
4335322421161514131211461635152414431332122111j x x x x x x x x x x x x x t s x x x x x x x x x x x x f j P16:
2、 解:设j x 表示第j 食品的采购量,于是可得数学模型
13、某养鸡场有一万只鸡,用动物饲料和谷物饲料混合喂养,每天每只鸡平均吃混合饲料0.5公斤,其中动物饲料占的比例不得少于1/5。
动物饲料每公斤0.2元,谷物饲料每公斤0.16元。
饲料公司每周只保证供应谷物饲料21000公斤。
问饲料应怎样混合,才能使每天的总成本最低?试建立问题的数学模型并求解(图解法)。
解:设养鸡场每天用动物饲料和谷物饲料分别为12,x x 公斤,则问题模型为
⎪⎪⎩⎪⎪⎨
⎧≥≥≤≥=++=.
0,0300010005000
16.02.0min 2121212
1x x x x x x x x f
用图解法:
求得其最优解为
122000,3000x x ==。
P19:14
解:
设甲乙厂各处理21x x 、万立方米/天;总费用 z 元/天;考虑 工厂1与工厂2所在的两点: 工厂1:
工厂2:
1
≥10002≤500211x x ⇒-1000
2
≤700)4.1()2(8.021x x -+-6.1≥8.021x x +⇒
于是建立数学模型为:
目标函数
⎪⎩
⎪
⎨⎧≤≤≤≤≥+≥+=4
.10,2016
8.01
..8001000min 212112
1x x x x x t s x x z
利用图解法,画图
求得其最优解为:
T x )8.0,1(*=
最优值为:
.1640*
=z P37:1
解:线性规划问题
⎪⎩⎪
⎨⎧=≥=++=++++=)3,2,1(03334
22..24min 321321321j x x x x x x x t s x x x f j
由第一个约束的3倍减去第二个约束的2倍,得 64332=+-x x 即
,2≤01x ≤显然:4.1≤02x ≤
对偶问题的最优解为:
).1,1(*=u
下面利用互补松弛性求解原问题的最优解。
由于 01,01*
2*
1>=>=u u 因此它们的互补约束均为紧约束,即
⎪⎩⎪⎨⎧=++=++4032230
33*
3*2*1*3*2*1x x x x x x (1) 又由于
4523*
2*
1>=+u u 于是其对偶约束也是紧约束,即
0*1=x (2) 将(2)带入(1),得
⎪⎩⎪⎨⎧=+=+403230
3*
3*2*
3*2x x x x
得对偶规划的最优解为:
).6.0,2.0(*
=u 最优值为
.17*=g
下面利用互补松弛性求解原问题的最优解:首先由于6.0,2.0*
2*
1==u u ,都严格大于零,因此它们的对偶约束都为紧约束,即:
⎪⎩⎪⎨⎧=++=++2054325536*
3*2*1*3*2*1x x x x x x (1)
另一方面,将最优解*u 代入对偶的约束中,得:
⎪⎩
⎪⎨⎧=+>=+=+.4551343336*2*1*
2*1*
2*1u u u u u u
由于第二个约束为松约束,因此其对偶约束应该是紧约束,于是 .0*
2=x 将上式代入方程组(1),得
⎪⎩⎪⎨⎧=+=+20532556*3*1*3*1x x x x。
