(完整word版)正交试验的方差分析实例1
正交检验的极差分析和方差分析

计算各样本平均数 y i 如下:
型号
yi
表 8-2
A
B
C
D
E
F
9.4 5.5 7.9 5.4 7.5 8.8
4.1 方差分析的基本概念和原理
两个总体平均值比较的检验法 把样本平均数两两组成对:
y
(
C
2 6
1与
y
2,
y
与
1
y
15)对。
3,…
y
1与 y
6
,
y
2与 y
3
,…, y
参数 假设 检验 的假 设条 件
观测值(i=1,2,…,k;j=1,2,…,m) 相互独立
在水平Ai条件下, Yij(j=1,2,…m)
服从正态分布N (i ,2)
4.2.4 显著性检验
要判断在因素A的k个水平条件下真值之间是否 有显著性差异, 即检验假设
H0: 12k, H1: 不全相等
我们还可以证明 , i , i分别是参数 ,i ,i 的无
偏估计量。
将和 i 分别用它们的估计量代替,可以得到试 验误差 ij 的估计量 e ij ,
eij Yij Yi
(4-10)
4.2.3 分解定理 自由度
为了由观测值的偏差中分析出各水平的效应,我们 研究三种偏差:Y ij Y ,Yi Y 和 Yij Y i. 根据前面参数估计的讨论,它们分别表示
数学模型和数据结构 参数点估计 分解定理 自由度 显著性检验 多重分布与区间估计
4.2.1 数学模型和数据结构
在单因素试验中,为了考察因素A的k个水平A1, A2,…,Ak对Y的影响(如k种型号对维修时间的影响), 设想在固定的条件Ai下作试验.所有可能的试验结果 组成一个总体Yi,它是一个随机变量.可以把它分解
卫生统计学第八章正交试验方差分析

WENKU DESIGN
正交试验设计定义与原理
正交试验设计定义
正交试验设计是研究多因素多水平的一种设计方法,它是根 据正交性从全面试验中挑选出部分有代表性的点进行试验, 这些有代表性的点具备了“均匀分散,齐整可比”的特点。
正交试验设计原理
正交试验设计是利用正交表来安排与分析多因素试验的一种 设计方法。它是由试验因素的全部水平组合中,挑选部分有 代表性的水平组合进行试验的,通过对这部分试验结果的分 析,了解全面试验的情况。
THANKS
感谢观看
REPORTINGΒιβλιοθήκη https://VS
正交表特点
每列中不同数字出现的次数相等;任意两 列中数字的排列方式齐全而且均衡。
正交试验设计步骤
挑因素,选水平
根据试验的目的和专业知识,挑选出与考察指标有关的因素。对选出的因素要分清主次,合理安排。 选取的水平数应根据实际情况而定,过少会导致结果不准确,过多则可能数据分布的规律性较差,代 表性差;
通过建立线性模型来描述各因素 与结果之间的关系,从而进行方 差分析和参数估计。
PART 03
正交试验方差分析步骤
REPORTING
WENKU DESIGN
数据整理与描述性统计
整理试验数据
按照试验因素和水平整理数据,列出试验指标的观察值。
计算总均值和总变异
计算所有观察值的总和、均值、离差平方和等描述性统计量。
选正交表,进行表头设计
根据确定的列数(C)与水平数(t)选择相应的正交表。选择的原则是首先满足列数,其次是水平数。若 有2个或2个以上正交表满足条件时则应选取行数最少的一个;
正交试验设计步骤
明确试验方案,进行试验;
正交设计与方差分析

正交设计适用于多因素、多水平的试验安排,而方差分析 适用于检验数据间的差异和因素显著性。
04
正交设计与方差分析的实例
正交设计实例
实验设计
正交设计是一种实验设计方法, 通过选择合适的正交表,安排多 因素多水平的实验,以最小实验 次数获得尽可能多的信息。
特点
正交设计具有均衡分散、整齐可 比的特点,能够快速有效地找到 最优方案。
THANKS
感谢观看
复合正交设计
适用于多个因素,每个因素有多个水平的实验。
混合水平正交设计
适用于某些因素水平较多,而其他因素水平较少 的实验。
02
方差分析简介
方差分析的定义
• 方差分析(ANOVA)是一种统计分析方法,用于比较两 个或多个组之间的平均值差异是否显著。它通过分析数据 的变异来源,将总变异分解为组间变异和组内变异,从而 评估不同组之间的差异是否具有统计意义。
适用范围有限
正交设计主要适用于多因素、多水平的实验设计,对于其他类型 的实验可能不太适用。
对实验条件要求较高
正交设计要求实验条件相同,对于实验条件不易控制的情况可能不 太适用。
对实验结果分析要求较高
正交设计需要对实验结果进行复杂的统计分析,对于数据分析能力 要求较高。
正交设计与方差分析的发展趋势
多元化
正交设计与方差分析在未来的应用前景
科学研究
正交设计与方差分析在科学研究领域的应用将会越来越广泛,特别是在生物、化学、物理 等领域。
工业生产
工业生产中需要进行大量的实验研究和数据分析,正交设计与方差分析可以为工业生产提 供有效的实验设计和数据分析方法。
数据分析
正交设计与方差分析作为一种统计分析方法,在数据分析领域的应用将会越来越广泛。
正交实验作业Word版
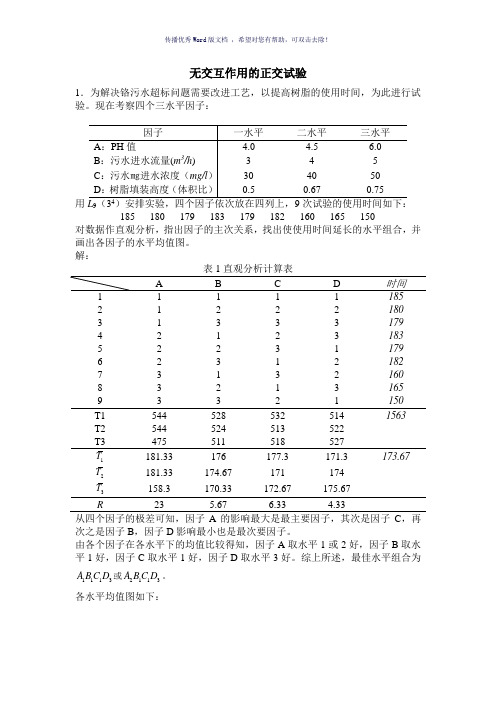
无交互作用的正交试验1.为解决铬污水超标问题需要改进工艺,以提高树脂的使用时间,为此进行试验。
现在考察四个三水平因子:用9185 180 179 183 179 182 160 165 150对数据作直观分析,指出因子的主次关系,找出使使用时间延长的水平组合,并画出各因子的水平均值图。
解:2 1 2 2 2 1803 1 3 3 3 1794 2 1 2 3 1835 2 2 3 1 1796 2 3 1 2 1827 3 1 3 2 1608 3 2 1 3 1659 3 3 2 1 150 T2 544 524 513 522 T3 475 511 518 527 1T 181.33 176 177.3 171.3 173.672T 181.33 174.67 171 174 3T158.3170.33172.67175.67R 23 5.67 6.33 4.33次之是因子B ,因子D 影响最小也是最次要因子。
由各个因子在各水平下的均值比较得知,因子A 取水平1或2好,因子B 取水平1好,因子C 取水平1好,因子D 取水平3好。
综上所述,最佳水平组合为1113A B C D 或2113A B C D 。
各水平均值图如下:图 1各水平均值图由上图可以直观的看出,因子A 的水平1或2一样高,因子B 的水平1高,因子C 的水平1高,因子D 的水平3高,最佳水平组合为1113A B C D 或2113A B C D ,得到的结论与直观分析计算表得到的是一致的。
2.某化工厂生产的一种产品的收率较低,为此希望通过试验提高效率。
在试验用951 61 58 72 69 59 87 85 84 (1)对数据作直观分析,画出各因子的水平均值图;(2)在数据满足等方差正态分布的前提下,对数据作方差分析;(3)找出使收率达到最高的水平组合,并求该水平组合下平均收率的95﹪置信区间;(4)对数据作贡献率分析 解:(1)对数据做直观分析表如下:2 1 2 2 2 613 1 3 3 3 584 2 1 2 3 725 2 2 3 1 696 2 3 1 2 597 3 1 3 2 878 3 2 1 3 859 332184 T1 170 210 195 204 626 T2 200 215 217 207 T312T 66.66667 71.66667 72.33333 69 3T85.33333 67 71.33333 71.66667 R28.666674.6666677.3333333.666667由上表可知,每一因子最好水平分别为322A ,B ,C ,而且知道每个因子水平间的最大差异,其中因子A 差异最大是最主要因子,因子B 差异最小是最次要因子。
第五章 方差分析和正交试验

r
i 表示组内理论均值, eij 表示随机误差, eij ~ N (0, 2 ), i 称为效应值. ni i 0.
单因素方差分析的数学模型为 : Yij i eij (i 1, 2, , r; j 1, 2, , ni ) 2 e ~ N ( 0 , ), eij 互相独立; ij n n 0. i i i 1
•步骤2:表头设计.见下表:一般至少安排有一个空列.
17
结束
•步骤3:制订试验方案, 见下表:
18
结束
•步骤4:作试验得到得率 yi .填入表中.作试验时采用随机顺序. •步骤5:计算统计量,填入表5.4.5中.
水平数r 3, 每水平在 1列中出现次数 m 3, 试验数n rm 9, 试验结果为Y1 , Y2 , , Yn , K jl为j列中水平为l (l 1,2, , r )的试验结果之和 . 这里K11 y1 y2 y3 , K 23 y3 y6 y9 . 记K K jl , 显然, K Yi , 与j无关.
l 1 i 1 n 1 2 1 r 2 2 2 P K , Q j K jl , S j Q j P, Q Yi 2 , ST Q P. n m l 1 i 1 r n
S Yi Y
2 T j 1
r
2
1 2 2 2 2 S , Y K , 这里, ST S12 S 2 S3 S4 . n j 1
EYi i , EY ,
2 总离差平方和 ST Yij Y , r ni 2 i 1 r j 1
组间差平方和 S 组内差平方和 S
正交试验设计中的方差分析例题分析优秀

15
3
1
3(9 ml) 3(17 ml) 3
20
4
2(7 ml)
1
5
2
2
6
2
3
7
3(10 ml)
1
2
3
22
3
1
29
1
2
17
3
2
21
8
3
2
9
3
3
1
3
2
1
19 19 4
这里看出 A2B2C3的结果最好。 第四步, 计算各因素平均试验指标以及极差 :
A
B
C
D
K1
48
56
49
61
K2
68Βιβλιοθήκη 635653K3
59
14
可见: F0.05(2,4)≥FA>F0.10(2,4), F0.05(2,4)≥FC>F0.10(2,4), 因此 A 和C属于影响显著的因素,要重点考察。 而B 的F值小于 F0.25(2,4) ,因此 B 因素对指标没什么 影响,可以忽略。 因此其加入体积可以在给定范围内 任意变化。 这是用方差分析和前面直观分析以及极差分析得出的 一个比较重要的不同结论。 当然,在实际分析中,因素 B还要用其他试验指标进 一步确定,以保证得到准确的结果。
2
7
12
1:1HCl(ml)
21.5
21
20.5
Abs
20
19.5
19
18.5
2
4
6
8
10
0.5% 8-OH喹啉 (ml)
24
23
22
21
Abs
20 19
正交检验的极差分析和方差分析
第十九页,编辑于星期二:二十二点 五十九分。
第四章 方差分析
4.2.2 参数点估计 并由此得 的i 估计量
ˆi ˆˆi Yi
至此,求得参数 ,i,的i估计量
ˆ Y, ˆi Yi Y, ˆi Yi (4-9)
第二十页,编辑于星期二:二十二点 五十九分。
第四章 方差分析
4.2.2 参数点估计
按照上述原则求参数估计量的方法称为最小二乘法,
并且称
i i
为第i个水平Ai的效应.它表示水平的真值比一般水平
差多少。满足约束条件
(4-6)
12k0
可得
Yiji ij;
i 0
i=1,2,…,k ;j=1,2,…,m
第十五页,编辑于星期二:二十二点 五十九分。
第四章 方差分析
4.2.1 数学模型和数据结构
找出参数 ,1,2,...k.,
要
和 2的估计量
解
决 的
分析观测值的偏差
问
题
检验各水平效应 1,2,...,k
有无显著差异
第十六页,编辑于星期二:二十二点 五十九分。
第四章 方差分析
4.2.2 参数点估计
用最小二乘法求参数 ,1,2,...k.的, 估计量,然后寻
求 的 无2 偏估计量.
须使参数 ,1,2,...的k.,估计值能使在水平Ai下求得 的观测值Yij与真值 之间 i的偏差尽可能小。
第二十八页,编辑于星期二:二十二点 五十九 分。
第四章 方差分析
4.2.4 显著性检验
利用(8-17)式来检验原假设H0是否成立.对于给定
的显著水平 ,可以从F分布表查出临界值
据样本观测值算出FA的值.
F(k再1,k根(m1)),
第六章 方差分析与正交试验设计(4)1
S e = S e / f e = 703.13
S A× B = S 3 / f 3 = 78.13 / 1 = 78.13 < S e
S D = S 7 / f 7 = 78.13 / 1 = 78.13 < S e
故将 S A×B , S D 并入误差平方和 S e 中,得
S e = S e + S A× B + S D = 703.13 + 78.13 + 78.13 = 859.39
S T = 67.34
K2 j
Rj
Sj
42.78 18.30 0.91
列为空白列, 由于第 3 列、第 7 列为空白列,其方差 S 3 , S 7 是由随机 误差引起的, 误差引起的,因此
S e = S 3 + S 7 = 0.91 + 0.03 = 0.94
fe = f3 + f7 = 1 + 1 = 2
通过前面的分析可以看出, 设计试验时若正交表上 通过前面的分析可以看出, 没有空白列,一般不能做方差分析。 没有空白列,一般不能做方差分析。为了做方差分析 通常是把因素的偏差平方和明显偏小的列作为误差列 来处理,或是取较大的正交表做试验, 来处理,或是取较大的正交表做试验,但这要增加试 验次数,因此在实际问题中应视具体情况采用相应的 验次数, 数据分析方法。 数据分析方法。
∆
FA×C
S5 / f 5 3828.13 / 1 = ∆ = = 13.36 > F0.05 (1,3) = 10.13 ∆ 859.39 / 3 Se / f e
故因素 A、B 对试验结果的影响是高度显著的,而交互 、 对试验结果的影响是高度显著的, 作用 A×C 对试验结果的影响是显著的。因素 C、D 和 × 对试验结果的影响是显著的。 、 交互作用 A×B 对试验结果无显著影响。 × 对试验结果无显著影响。
第八章方差分析与正交试验设计
nj i 1
X ij—数据的总平均 Nhomakorabeas nj
ST
( X ij X )2 —总偏差平方和(总变差)
j1 i1
1 nj
X•j
nj
X ij
i 1
— 水平Aj下的样本平均值
定理一(平方和分解定理)在单因素方差分 析模型中,平方和有如下的恒等式,
ST SE SA
注: 定理一的意义是将试验中的总偏差平方和 分解为试验随机误差的平方和与因素A的偏 差平方和.
其二,当假设 H0 不成时, Xij ~ N ( j , 2 ) ,各
个 Xij 的数学期望不同,当然取值也不会一致.
因此,我们想用一个量来刻划各个
X
之间
ij
的波动程度,并且把引起波动的两个原因区分
开来,这就是方差分析的总偏差平方和分解方
法,并由此构造检验用的统计量.
平方和的分解
X
1 n
s j 1
A4
75.8 71.5
58.2 51.0
48.7 41.4
试验指标: 射程
因素: 推进器和燃料
水平: 推进器有3个,燃料有4个 双因素试验
试验目的: 考察推进器和燃料两因素对射程有 无显著的影响.
数学模型
设因素A有s个水平A1 , A2 , , As ,在水平Aj ( j
1,2, , s)下,进行nj (nj 2)次独立试验,得到如下表
表 电路的响应时间
类型Ⅰ 类型Ⅱ 类型Ⅲ 类型Ⅳ
19 15
22 20 18
20 40
21 33 27
16 17 18
15
22
18
19
26
试验指标:电路的响应时间 因素:电路类型
正交设计试验资料的方差分析
数据整理
将收集到的数据整理成 表格形式,便于后续分 析。
数据筛选
对异常值进行筛选和处 理,确保数据质量。
正交设计试验资料的方差分析过程
确定试验因素和水平
明确试验因素和各因素的水平, 为后续分析提供基础。
计算各因素的效应值
根据试验结果,计算各因素的效 应值。
计算误差平方和
根据效应值和水平,计算误差平 方和。
跨学科融合
标准化与规范化
结合其他学科的理论和方法,拓展正交设 计试验的应用领域,推动多学科交叉融合 发展。
制定和完善正交设计试验的标准和规范, 提高试验的可靠性和可比性。
正交设计试验资料方差分析的实际应用价值
科学研究
在科学研究领域,正交设计 试验资料方差分析可用于探 索和验证科学假设,揭示现 象背后的机制和规律。
正交试验设计的基本原理
1 2
正交性原理
正交试验设计基于正交性原理,即每个因素在试 验中出现的次数相同,且各次出现的概率相等。
均匀分散原理
正交试验设计通过均匀分散原理,确保每个水平 在试验中都有均衡的分布,从而减少结果的偏差。
3
代表性原理
正交试验设计通过代表性原理,选取具有代表性 的样本点进行试验,以反映整体情况。
正交设计试验资料的方差 分析
• 正交设计试验概述 • 方差分析基础 • 正交设计试验资料的方差分析方法 • 实例分析 • 总结与展望
01
正交设计试验概述
正交试验设计的基本概念
正交试验设计是一种统计技术,用于 在多因素、多水平条件下进行试验, 以最小化试验次数,同时最大化信息 收集。
它利用正交表来安排试验,确保每个 因素的每个水平都被等可能地选取, 从而得到全面而均衡的试验结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正交试验设计实例分析
正交试验设计是使用正交表来安排多因素、多水平试表验,并采用统计学方法分析实验结果的一种实验设计方法[1]。
对于多因素、多水平的问题,人们一般希望通过若干次的实验找出各因素的主次关系和最优搭配条件,用正交表合理地安排实验,可以省时、省力、省钱,同时又能得到基本满意的实验效果。
因此,这种方法在改进产品质量、优化工艺条件及研发新产品等诸多方面广泛应用。
但是,很多研究人员在使用该方法时,有些细节往往容易被忽视。
作者以姜黄素的提取为例具体阐述这一方法的使用和注意事项。
1.实例:
姜黄素是姜黄中的主要活性成分,在优化其提取工艺时,首先应确定正交试验需要考察的因素和水平。
尤本明等[2]考察了三个因素,因素A(作为溶媒的乙醇浓度)、因素 B(溶媒的量)、因素C(渗漉速度),每个因素取三个水平。
试验设计时,一般还应考虑各因素间的交互作用,也就是因素之间的联合作用,这点不可忽视。
根据以往经验可知,本例中因素之间的交互作用可以忽略,故采用 L9(34)正交表来安排试验(见表1)。
该表共有4列,将因素 A 、B 、C 分别安排在正交表的第2、3、4列上,第1列为空白列。
在试验前,各因素及水平在正交表中的位置必须交待清楚,以确定各次试验的条件,避免不必要的错误。
1 正交试验设计与结果
2 .直观分析法:
表1中的 K1、K2、K3分别表示在各因素各水平下姜黄素提取量的总和,K分别表示在各因素各水平下姜黄素提取量的平均值。
由于有时会遇到各因素水平数不等的情况,因此,一般用提取量的平均值大小来反映同一个因素的各个不同水平对试验结果(提取量)影响的大小,并以此确定该因素应取的最佳水平。
用同一因素各水平下平均提取量的极差R(极差=平均提取量
的最大值-平均提取量的最小值)来反映各因素的水平变动对试验结果(提取量)影响的大小。
极差大就表示该因素的水平变动对试验结果的影响大,极差小就表示该因素的水平变动对试验结果的影响
小。
由表1得到因素的主次顺序依次为乙醇浓度(因素A )、渗漉速度(因素C)、提取溶媒的量(因素B)。
主要因素应取最好的水平,而次要因素则可根据成本、时间、收益等方面的统筹考虑选取适当的水平。
由此得到各因素的最佳搭配为A2B3C2,即最佳工艺为9倍体积的70%乙醇,以3mL速度渗漉。
按此条件的试验在正交表的9次试验中并没有出现,通过做补充试验,结果得到姜黄素的提取量达到4812mg ,大于正交试验结果中的最高值461.25mg ,说明利用正交试验优化姜黄素的提取工艺是成功的。
3 .方差分析法:[3 ]
正交试验的直观分析法简便、直观、计算量小,但不能估计试验误差,即不能区分试验结果的差异是由各因素的水平变化而导致,还是由试验的随机波动而导致。
很多正交试验都没能考虑这一问题。
要解决此问题,可以对试验结果做方差分析。
在对正交试验做方差分析时,必须估计随机误差,而随机误差是通过正交表上空白列得到的。
由于空白列中没有因素作用,因此正好反映随机因素所引起的误差,该空白列在方差分析中常被称为误差列。
因此,在做正交试验方差分析时,正交表的表头中必须留下空白列,以确定随机误差引起的离差平方和;若没有空白列,则需做重复试验,或者选择离差平方和中最小者做近似估计。
当空白列多于一列时,随机误差平方和等于所有空白列的离差平方和之和,而其自由度也等于各空白列自由度的总和,见表2
由表2可知,因素A的P值<0.01,即因素A对试验结果影响极显著;因素C的P值<0.05,即因素 C 对试验结果影响显著;因素 B 的P值<0.10,即因素 B 对试验结果有一定影响。
因此,因素 A 为主要因素,因素C 和因素 B 为次要
因素。
按方差分析法的观点.只需对有显著影响的因素选择最佳水平,而其他对试验结果影响较小的因素,则可按实际需要选择适当的水平。
因此,本例中试验各因素的最佳搭配为A2 B3 C2,即最佳工艺为9倍体积的70%乙醇,以3m L / min 速度渗漉,结论与直观分析法相同。
4. 讨论[4]
在利用直观分析法分析正交试验结果后,由于所得的最佳搭配只是相对于被选因素和水平而言的,不是绝对的“最佳”,因此通常需作进一步讨论,而这一点恰恰容易被研究人员忽
视。
从表1可看出:对因素 A 而言,乙醇浓度太大或太小,姜黄素提取量都不高,在以后的试验中,可考虑细化实验条件,选取适当乙醇浓度,比如乙醇浓度为60%? 、80%等,再观察姜黄素提取量的变化情况。
对因素 B 而言,取9倍体积的溶媒,姜黄素提取量较高,而取4倍体积或6倍体积时,姜黄素提取量较低,在以后的试验中,溶媒的量可取12倍或15倍体积,姜黄素提取量也许还会提高。
对因素 C 而言,渗漉速度太快或太慢,姜黄素提取量都不高,因此在以后的试验中,可适当选取渗漉速度,比如选取渗漉速度为2.5m L/min或3.5m L/min。
通过上述分析能方便地得出一些改进的思路,为获得更优的工艺条件提供了线索。
参考文献:
[1]周怀梧,倪永兴.医药应用概率统计[M ]?.上海:百家出版社,
1990?:235.
[2]尤本明,王忠壮,胡晋红.姜黄中姜黄素的提取及分离工艺研究[J ].药学服务与研究,2006,6(4):277唱279.
[3]刘定远.医药数理统计方法[M ].北京:人民卫生出版社,1999?:
174唱175.
[4]祝国强,刘庆欧.医药数理统计方法[M ].北京:高等教育出版社,2004:201唱222.[收稿日期]2007唱08唱15[修回日期]2007唱11唱09[本文编辑]兰、姚春芳。
