数学初中二年级上册试卷 2017年下学期八年级数学测试题1
2017年哈尔滨市名校八年级下学期月考数学试卷(无答案)四边形与勾股定理

2016-2017学年度下学期八年级4月份月考数学试题一、选择题(共30分,每题3分)1. 以下列各组数据为三角形三边,能构成直角三角形的是( ) A.4cm ,8cm ,7cm B.2cm ,2cm ,2cm C .2cm ,2cm ,4cm D .13cm ,12cm ,5cm2.在下面给出的条件中,能判定四边形ABCD 是平行四边形的是( ) A.AB =BC ,AD =CD B.AB ∥CD ,AD =BC C.AB ∥CD ,AB =CD D.∠A =∠B ,∠C =∠D3.如图,□ABCD 中,对角线AC 、BD 交于点O ,点E 是BC 的中点.若OE=3cm ,则CD 的长为 ( ) cmA. 3B.4C. 5D.64.如图,在□ABCD 中,∠B=80º,AE 平分∠BAD 交BC 于点E ,CF//AE 交AD 于点 F ,则∠1=( ) A. 40º B. 50º C. 60º D. 80º5. 已知一个直角三角形的两边长分别为3和4,则第三边长是( ) A .5 B .25 C .7 D .5或76. 如图,长方形ABCD 中,AB=3,AD=9,将此长方形折叠,使点B 与点D 重合,折痕为EF ,则AE 的长为( )A .3B .4C .5D .6 7.如图,在△ABC 中,AD⊥BC 于D ,AB=3,BD=2,DC=1,则AC=( ) A. 6 B. 6 C. 5 D. 48.下列说法错误的是( ) A. 四个角都相等的四边形是矩形;B. 一组对边平行且一组对角相等的四边形是平行四边形;C. 两条对角线相等的四边形是矩形;D. 三角形的中位线平行于三角形的第三边且等于第三边的一半.9. 如图,矩形ABCD 中,AB =3,AD =4,点P 在AD 上,PE⊥AC 于E ,PF⊥BD 于F ,则PE+PF 等于( ) A .75 B .125 C .135 D .2第3题图第4题图第7题图ADBcEFPC /F ECDBA第6题图线段AD 的延长线于G ,下面结论:①BE ; ②∠A=∠BHE ; ③AB=BH ; ④∠BHD=∠BDG;其中正确的个数是( )A.1B.2C.3D.4 二、填空题(共30分,每题3分)11. 在平行四边形ABCD 中,∠A :∠B=3:2,则∠C=______.12. 三角形三边长分别为6,8,10,那么它最长边上的高等于 .13. 矩形的一条边长是32,一条对角线的长是4,则这个矩形的面积是___ ___.14. 如图,一个长为10米的梯子AB ,斜靠在一竖直的墙AO 上,这时AO 的长为8米,如果梯子的顶端A 沿墙下滑2米到点C 处,那么梯子底端B 将外移到D ,则线段BD 的长为__________米. 15.如图,所示,DE 是△ABC 的中位线,△ABC 的周长为8,则△A DE 的周长为________.16. 如图,在平行四边形ABCD 中,DE 平分∠ADC ,AD=6,BE=2,则平行四边形ABCD 的周长是 .17.等边三角形的边长为2,则该三角形的面积为__________.18.如图,在矩形ABCD 中,AE ⊥BD 于E ,BE:DE=1:3,则∠EAD=_____ .第18题图 第20题图19.矩形的一个角的平分线分一边为3cm 和4cm 两部分,则这个矩形的对角线的长度是___ ___cm.20.如图,在四边形ABCD 中,∠B =30°,∠BA D=120°,点E 为AB 的中点, DE ⊥CE ,若BC=4,CD=132,则AD=___ _ ____.三、解答题(共60分) 21. (本题6分)先化简,再求代数式22424412x x xx x x x -+÷--++-的值,其中x =2+2.B AC在正方形网格中,每个小正方形的边长为1.=90°,使它的三条边均为整数,且较短的直角边长为3,要求它的顶点均在 (1)在图①中,画直角△ABC ,C格点上.(2)在图②中,画平行四边形ABCD,使它的面积为12 且有一锐角为45°,要求它的顶点均在格点上.①②23.(本题8分)如图,某港口P位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.他们离开港口一个半小时后分别位于点Q、R 处,且相距30海里.已知“远航”号沿北偏东60°方向航行.(1)说明“海天”号沿哪个方向航行?(2)请直接写出此时“海天”号到海岸线的距离.如图,△ABC中,D、E分别是AB、AC的中点,延长DE到点F,使得EF=2DE,连接CF.(1)求证:四边形BCFE是平行四边形;(2)若BE=EF,CE=4,∠BCF=120°,求平行四边形BCFE的面积.25.(本题10分)某服装店老板到厂家选购A、B两种品牌的儿童服装,每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装的数量是用750元购进B种服装数量的2倍.(1)求A、B两种品牌服装每套进价分别是多少元?(2)若A品牌服装每套售价为130元,B品牌服装每套售价为95元,服装店老板决定,购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套,两种服装全部售出后,要使总的获利不少于1200元,则最少购进A品牌服装多少套?图1图2图3D 26.(本题10分)如图,AD 是△ABC 的中线,AE∥BC,BE 交AD 于点F ,且AF=DF . (1)如图1,求证:四边形ADCE 是平行四边形;(2)如图2,在(1)的条件下,∠ADB=120°,设对角线AC 、DE 交于点O ,过点O 作OQ⊥AC 交∠A DB 的角平分线于点Q. OQ 与AD 交于P 点.求证:AD-DC=DQ ;(3)如图3,在(2)的条件下,若CE=3,QD=1,求AP 的长.27. (本题10分)如图,在平面直角坐标系中,矩形OABC的顶点A、C分别落在x轴、y轴正半轴上,点E在边OA上,点F在2).边OC上,且AE=EF,已知B(6,8),F(0,3(1)求点E的坐标;(2)点E关于点A的对称点为点D,点P从C点出发,以每秒1个单位的速度沿射线CB运动,设P点的运动时间为t秒,△PBD的面积为S,用含t的代数式表示S;(3)在(2)的条件下,点M为平面内一点,点P在线段BC上运动时,作∠PDO的平分线交y轴于点N,t为何值时,四边形DPNM为矩形?并求此时点M的坐标.。
2017年秋八年级数学上册期末检测题二新版新人教版20170704169

期末检测题(二)(时间:120分钟满分:120分)一、选择题(每小题3分,共30分)1.以下列各组线段长为边能组成三角形的是( B)A.1 cm 2 cm 4 cm B.8 cm 6 cm 4 cmC.12 cm 5 cm 6 cm D.2 cm 3 cm 6 cm2.下面的图形是天气预报使用的图标,从左到右分别代表“霾”、“大雪”、“扬沙”、“阴”,其中是轴对称图形的是( A)3.(2017·莒县模拟)参观“12·12”海口冬交会的总人数约为589000人,将589000用科学记数法表示为( B)A.58.9×104 B.5.89×105 C.5.89×104 D.0.589×1064.(2016·贵港)下列运算正确的是( B)A.3a+2b=5ab B.3a·2b=6abC.(a3)2=a5 D.(ab2)3=ab65.线段MN在平面直角坐标系中的位置如图,若线段M′N′与MN关于y轴对称,则点M的对应点M′的坐标为( D)A.(4,2) B.(-4,2)C.(-4,-2) D.(4,-2)6.a4b-6a3b+9a2b分解因式的正确结果是( D)A.a2b(a2-6a+9) B.a2b(a+3)(a-3)C.b(a2-3)2 D.a2b(a-3)27.已知(m-n)2=32,(m+n)2=4000,则m2+n2的值为( C)A.2018 B.2017 C.2016 D.40328.张老师和李老师住在同一个小区,离学校3000米,某天早晨,张老师和李老师分别于7点10分、7点15分离家骑自行车上班,刚好在校门口遇上,已知李老师骑车的速度是张老师的1.2倍,为了求他们各自骑自行车的速度,设张老师骑自行车的速度是x米/分,则可列得方程为( A)A.3000x-30001.2x=5 B.3000x-30001.2x=5×60C.30001.2x-3000x=5 D.3000x+30001.2x=5×609.如图,∠ABC ,∠ACB 的平分线相交于点F ,过点F 作DE∥BC,交AB 于D ,交AC 于E ,那么下列结论正确的是:①△BDF,△CEF 都是等腰三角形;②DE=BD +CE ;③△ADE 的周长为AB +AC ;④BD=CE.( C )A .③④B .①②C .①②③D .②③④10.在平面直角坐标系中,任意两点A(x 1,y 1),B(x 2,y 2),规定运算:①A⊕B=(x 1+x 2,y 1+y 2);②A ⊗B =x 1x 2+y 1y 2;③当x 1=x 2,且y 1=y 2时,A =B ,有下列四个命题:(1)若A(1,2),B(2,-1),则A⊕B=(3,1),A ⊗B =0;(2)若A⊕B=B⊕C,则A =C ;(3)对任意A ,B ,C 均有(A⊕B)⊕C=A⊕(B⊕C)成立.其中正确命题的个数为( C )A .1个B .2个C .3个D .0个 二、填空题(每小题3分,共18分)11.若分式x 2-12x +2的值为0,则实数x 的值为__1__.12.等腰三角形的一个外角是140°,则其底角是__70°或40°__.13.已知点P(1-a ,a +2)关于y 轴的对称点在第二象限,则a 的取值范围是__-2<a <1__.14.若4x 2+kx +9是完全平方式,则k =__±12__.15.如图,在△ABC 中,∠A =36°,AB =AC ,BD 是∠ABC 的角分线,若在边AB 上截取BE =BC ,连接DE ,则图中共有__5__个等腰三角形.16.如图,在Rt △ABC 中,∠BAC =90°,AD ⊥BC 于D ,BE 平分∠ABC 交AC 于E ,交AD 于F ,FG ∥BC ,FH ∥AC ,下列结论:①AE=AF ;②AF=FH ;③AG=CE ;④AB+FG =BC ,其中正确的结论有__①②③④__.(填序号)三、解答题(共72分) 17.(8分)计算:(1)[(x -y)2+(x +y)(x -y)]÷2x; (2)(a a +2+2a -2)÷1a 2-4.解:x -y 解:a 2+418.(8分)解下列分式方程:(1)32x -2+11-x =3; (2)3x -1-x +2x (x -1)=0. 解:x =76,经检验x =76是原方程的解 解:解得x =1,经检验x =1不是原方程的解,原 方程无解19.(7分)(2016·毕节)已知A =(x -3)÷(x +2)(x 2-6x +9)x 2-4-1. (1)化简A ;(2)若x 满足不等式组⎩⎪⎨⎪⎧2x -1<x ,1-x 3<43,且x 为整数时,求A 的值.解:(1)A =1x -3 (2)⎩⎪⎨⎪⎧2x -1<x ①,1-x 3<43 ②,由①得:x <1,由②得:x >-1,∴不等式组的解集为-1<x <1,即整数x =0,则A =-1320.(7分)如图,在△ABC 中,AC =BC ,D ,E 分别在BC ,AC 上,AD 和BE 相交于点F ,连接CF 交AB 于点P ,若∠CAD=∠CBE,求证:点P 是AB 的中点.解:∵AC =BC ,∴∠CAB =∠C BA ,∵∠CAD =∠CBE ,∴∠DAB =∠EBA ,∴FA =FB ,又∵AC =BC ,∴CF 是AB 的中垂线,∴P 是AB 的中点21.(7分)回答下列问题:(1)填空:x 2+1x 2=(x +1x )2-__2__=(x -1x )2+__2__;(2)若a +1a =5,则a 2+1a2=__23__;(3)若a 2-3a +1=0,求a 2+1a2的值.解:∵a 2-3a +1=0且a≠0,两边同除以a 得:a -3+1a =0,移项得:a +1a=3,∴a 2+1a 2=(a +1a)2-2=722.(8分)在等边△ABC 中,AO 是角平分线,D 为AO 上一点,以CD 为一边,在CD 下方作等边△CDE,连接BE.(1)求证:△ACD≌△BCE;(2)过点C 作CH⊥BE,交BE 的延长线于H ,若BC =8,求CH 的长.解:(1)∵△ABC ,△CDE 为等边三角形,∴AC =BC ,CD =CE ,∠ACB =∠DCE =60°,∴∠ACB -∠DCO =∠DCE -∠DCO ,即∠ACD =∠BCE ,易证△ACD≌△BCE (SAS ) (2)∵△ACD≌△BCE ,∴∠HBC =∠DAC ,∵AO 平分∠BAC ,∴∠DAC =30°,∴∠HBC =30°,∴CH =12BC =423.(9分)如图,已知△ABC 中AB =AC ,BD ,CD 分别平分∠EBA,∠ECA ,BD 交AC 于F ,连接AD.(1)当∠BAC=50°时,求∠BDC 的度数; (2)请直接写出∠BAC 与∠BDC 的数量关系; (3)求证:A D∥BE.解:(1)∵AB =AC ,∠BAC =50°,∴∠ACB =∠ABC =65°,∴∠ACE =115°,∵BD ,CD 分别平分∠EBA ,∠ECA ,∴∠DBC =12∠ABC =32.5°,∠DCE =12∠ACE =57.5°,∴∠BDC =∠DCE -∠DBC =25° (2)∠BAC =2∠BDC (或∠BDC =12∠BAC ) (3)如图,过点D 作DN⊥BA ,DK ⊥AC ,DM ⊥BC ,垂足分别为点N ,K ,M.∵BD ,CD 分别平分∠EBA ,∠ECA ,DN ⊥BA ,DK ⊥AC ,DM⊥BC ,∴DM =DN =DK ,∴AD 平分∠GAC ,∠ABD =∠DBC ,∴∠GAD =∠DAC ,∵∠GAC =∠ABC +∠ACB ,∴∠GAD =∠ABC ,∴AD ∥BE24.(8分)某商店第一次用3000元购进某款书包,很快卖完,第二次又用2400元购进该款书包,但这次每个书包的进价是第一次进价的1.2倍,数量比第一次少了20个.(1)求第一次每个书包的进价是多少元?(2)若第二次进货后按80元/个的价格销售,恰好销售完一半时,根据市场情况,商店决定对剩余的书包按同一标准一次性打折销售,但要求这次的利润不少于480元,问最低可打几折?解:(1)设第一次每个书包的进价是x 元,则3000x -20=24001.2x.解得x =50.经检验,x =50是原分式方程的解,且符合题意.答:第一次书包的进价是50元 (2)设最低可以打x 折,则2400÷(50×1.2)=40(个).80×20+80·x10·20-2400≥480.解得x≥8.故最低可打8折25.(10分)在等腰Rt△ABC中,∠BAC=90°,AB=AC,点A,点B分别是y轴,x轴上两个动点,直角边AC交x轴于点D,斜边BC交y轴于点E.(1)如图①,已知C点的横坐标为-1,直接写出点A的坐标;(2)如图②,当等腰Rt△ABC运动到使点D恰为AC中点时,连接DE,求证:∠ADB=∠CDE;(3)如图③,若点A在x轴上,且A(-4,0),点B在y轴的正半轴上运动时,分别以OB,AB为直角边在第一、二象限作等腰直角△BOD和等腰直角△ABC,连接CD交y轴于点P,问当点B在y轴的正半轴上运动时,BP的长度是否变化?若变化请说明理由,若不变化,请求出BP的长度.解:(1)点A的坐标是(0,1) (2)如图②,过点C作CG⊥AC交y轴于点G,∵CG⊥AC,∴∠ACG=90°,∠CAG+∠AGC=90°,∵∠AOD=90°,∴∠ADO+∠DAO=90°,∴∠AGC =∠ADO,易证△ACG≌△BAD(AAS),∴CG=AD=CD,∠ADB=∠G,∵∠ACB=45°,∠ACG=90°,∴∠DCE=∠GC E=45°,易证△DCE≌△GCE(SAS),∴∠CDE=∠G,∴∠ADB=∠CDE (3)BP的长度不变,理由如下:如图③,过点C作CE⊥y轴于点E.∵∠ABC=90°,∴∠CBE+∠ABO=90°.∵∠BAO+∠ABO=90°,∴∠CBE=∠BAO.∵∠CEB=∠AOB=90°,AB=AC,∴△CBE≌△BAO(AAS),∴CE=BO,BE=AO=4,∵BD=BO,∴CE=BD.∵∠CEP=∠DBP=90°,∠CPE=∠DPB,∴△CPE≌△DPB(AAS),∴BP=EP=2。
广西桂平市2017-2018年八年级下学期期中考试数学试题

2017-2018学年广西贵港市桂平市八年级(下)期中数学试卷一、选择题(本大题共12小题,每小题3分,共36分)1.(3分)在Rt△ABC中,∠C=90°,∠A=70°,则∠B的度数为()A.20°B.30°C.40°D.70°2.(3分)在Rt△ABC中,斜边上的中线CD=2.5cm,则斜边AB的长是()A.2.5cm B.5cm C.7.5cm D.10cm3.(3分)以下列长度的线段为边,不能构成直角三角形的是()A.3,4,5B.5,12,13C.2,3,4D.8,15,17 4.(3分)如图,▱ABCD的周长是28cm,△ABC的周长是22cm,则AC的长为()A.6cm B.12cm C.4cm D.8cm5.(3分)在线段、角、等腰三角形、平行四边形、矩形、菱形、正方形这几个图形中,既是轴对称图形又是中心对称图形的个数是()A.3个B.4个C.5个D.6个6.(3分)如图,在△ABC中,∠ACB=90°,AC=8,AB=10,DE垂直平分AC交AB于点E,则DE的长为()A.6B.5C.4D.37.(3分)如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC长是()A.3B.4C.6D.58.(3分)下列判断错误的是()A.两组对边分别相等的四边形是平行四边形B.四个内角都相等的四边形是矩形C.四条边都相等的四边形是菱形D.两条对角线垂直且平分的四边形是正方形9.(3分)菱形ABCD的对角线交于点O,则下列结论不一定正确的是()A.AB=BC B.OA=OC C.OA⊥OB D.AC=BD 10.(3分)如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A 重合,则下列结论错误的是()A.AF=AE B.△ABE≌△AGF C.EF=2D.AF=EF11.(3分)已知直角三角形两直角边的和为,斜边长为2,则这个直角三角形的面积是()A.B.C.3D.412.(3分)如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为()A.B.C.4D.5二、填空题(本大题共6小题,每小题3分,共18分)13.(3分)在▱ABCD中,∠A,∠B的度数之比为5:4,则∠C等于度.14.(3分)在某直角三角形中,其中一个锐角为30°,斜边和较小的边的和为12cm,则较大的直角边的长为.15.(3分)如图,已知∠AOB=30°,P是∠AOB平分线上一点,CP∥OB,交OA于点C,PD⊥OB,垂足为点D,且PC=8,则PD的长为.16.(3分)如图,在菱形ABCD中,边长AB=6,∠ABD=30°,则菱形ABCD的面积是.17.(3分)如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,P为AB边上不与A,B 重合的一动点,过点P分别作PE⊥AC于点E,PF⊥BC于点F,则线段EF的最小值是.18.(3分)如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E 作EF∥BC,分别交BD,CD于点G,F两点,若M,N分别是DG,CE的中点,则MN 的长是.三、解答题(本大题共8小题,共计66分)19.(6分)已知一个多边形的内角和比其外角和的2倍多180°,求这个多边形的边数及对角线的条数?20.(6分)若a,b,c为△ABC的三边长,且a,b,c满足等式|a﹣3|+(4﹣b)2+=0,△ABC是直角三角形吗?请说明理由.21.(8分)已知:如图,在平行四边形ABCD中,E,F是对角线BD上的两点,且BF=DE.求证:(1)AE=CF;(2)四边形AECF是平行四边形.22.(6分)如图,求作一点P,使PM=PN,并且使点P到∠AOB的两边OA,OB的距离相等.23.(8分)已知:如图,一轮船一直由西向东航行,早上8点,在A处测得小岛P的方向是北偏东75°,以每小时15海里的速度继续向东航行,10点到达B处,并测得小岛P 的方向是北偏东60°,若小岛周围25海里内有暗礁,问该轮船一直向东航行是否有触礁的危险?24.(10分)如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DE,连接CE、AF.(1)证明:AF=CE;(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.25.(10分)如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN 交∠ACB的平分线于点E,交∠ACB的外角平分线于点F(1)若CE=12,CF=5,求OC的长;(2)当点O在边AC上运动到何处且△ABC满足什么条件时,四边形AECF是正方形?并说明理由.26.(12分)如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.(1)证明:PC=PE;(2)求∠CPE的度数;(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.2017-2018学年广西贵港市桂平市八年级(下)期中数学试卷参考答案与试题解析一、选择题(本大题共12小题,每小题3分,共36分)1.【解答】解:∵在Rt△ABC中,∠C=90°,∴∠A+∠B=90°,∴∠B=90°﹣∠A=90°﹣70°=20°,故选:A.2.【解答】解:∵Rt△ABC中,斜边AB的中线CD=2.5cm,∴2CD=AB,∴AB=5cm.故选:B.3.【解答】解:在A中,32+42=252=52,故能构成直角三角形,故A不符合题意;在B中,52+122=169=132,故能构成直角三角形,故B不符合题意;在C中,22+32=13≠42,故不能构成直角三角形,故C符合题意;在D中,82+152=289=172,故能构成直角三角形,故D不符合题意;故选:C.4.【解答】解:∵▱ABCD的周长是28cm,∴AB+BC=14cm,∵AB+BC+AC=22cm,∴AC=22﹣14=8 cm.故选:D.5.【解答】解:既是轴对称图形又是中心对称图形的是:线段、矩形、菱形、正方形,共4个,故选:B.6.【解答】解:∵在Rt△ACB中,∠ACB=90°,AC=8,AB=10,∴BC=6.又∵DE垂直平分AC交AB于点E,∴DE∥BC,∴DE是△ACB的中位线,∴DE=BC=3.故选:D.7.【解答】解:作DH⊥AC于H,如图,∵AD是△ABC中∠BAC的角平分线,DE⊥AB,DH⊥AC,∴DH=DE=2,∵S△ABC=S△ADC+S△ABD,∴×2×AC+×2×4=7,∴AC=3.故选:A.8.【解答】解:A、两组对边分别相等的四边形是平行四边形,正确,故本选项错误;B、四个内角都相等的四边形是矩形,正确,故本选项错误;C、四条边都相等的四边形是菱形,正确,故本选项错误;D、两条对角线垂直且平分的四边形是正方形,错误,应该是菱形,故本选项正确.故选:D.9.【解答】解:∵四边形ABCD是菱形,∴AB=BC,OA=OC,OA⊥OB.故不一定正确的是AC=BD.故选:D.10.【解答】解:设BE=x,则CE=BC﹣BE=8﹣x,∵沿EF翻折后点C与点A重合,∴AE=CE=8﹣x,在Rt△ABE中,AB2+BE2=AE2,即42+x2=(8﹣x)2解得x=3,∴AE=8﹣3=5,由翻折的性质得,∠AEF=∠CEF,∵矩形ABCD的对边AD∥BC,∴∠AFE=∠CEF,∴∠AEF=∠AFE,∴AE=AF=5,∴A正确;在Rt△ABE和Rt△AGF中,,∴△ABE≌△AGF(HL),∴B正确;过点E作EH⊥AD于H,则四边形ABEH是矩形,∴EH=AB=4,AH=BE=3,∴FH=AF﹣AH=5﹣3=2,在Rt△EFH中,EF=2,∴C正确;∵△AEF不是等边三角形,∴EF≠AF,故D错误;故选:D.11.【解答】解:设直角三角形两直角边分别为a、b,由题意得,a+b=,a2+b2=22,则2ab=(a+b)2﹣(a2+b2)=3,∴直角三角形的面积=ab=,故选:B.12.【解答】解:设BN=x,由折叠的性质可得DN=AN=9﹣x,∵D是BC的中点,∴BD=3,在Rt△BDN中,x2+32=(9﹣x)2,解得x=4.故线段BN的长为4.故选:C.二、填空题(本大题共6小题,每小题3分,共18分)13.【解答】解:根据平行四边形两邻角此补,可得:∠A+∠B=180°又∵∠A,∠B的度数之比为5:4,可得两角分别是100°,80°,∴平行四边形的对角相等,∴∠C等于100度.故答案为100.14.【解答】解:设较小直角边是xcm,则斜边是2xcm.根据题意,得x+2x=12,解得x=4.则2x=8.根据勾股定理,较大直角边==4(cm).故答案为4cm.15.【解答】解:作PE⊥OA于E,∵P是∠AOB平分线上一点,∴∠AOP=∠BOP=15°,∵PC∥OB,∴∠POD=∠OPC,∴∠PCE=∠POC+∠OPC=∠POC+∠POD=∠AOB=30°,∴PE=PC=4,∵P是∠AOB平分线上一点,PD⊥OB,PE⊥OA,∴PD=PE=4,故答案为:4.16.【解答】解:连接CA交BD于点O,∵四边形ABCD是菱形,∴AC⊥BD,AO=OC,BO=OD,在RT△ABO中,∵∠AOB=90°,AB=6,∠ABO=30°,∴AO=AB=3,BO=AO=3,∴AC=6,BD=6,∴S菱形ABC D=•BD•AC=18.故答案为18.17.【解答】解:如图,连接CP.∵∠C=90°,AC=6,BC=8,∴AB==10,∵PE⊥AC,PF⊥BC,∠C=90°,∴四边形CFPE是矩形,∴EF=CP,由垂线段最短可得CP⊥AB时,线段EF的值最小,此时,S△ABC=BC•AC=AB•CP,即×8×6=×10•CP,解得CP=4.8.故答案为:4.818.【解答】解:过M作MK⊥CD于K,过N作NP⊥CD于P,过M作MH⊥PN于H,则MK∥EF∥NP,∵∠MKP=∠MHP=∠HPK=90°,∴四边形MHPK是矩形,∴MK=PH,MH=KP,∵NP∥EF,N是EC的中点,∴=1,==∴PF=FC=BE=2,NP=EF=3,同理得:FK=DK=1,∵四边形ABCD为正方形,∴∠BDC=45°,∴△MKD是等腰直角三角形,∴MK=DK=1,NH=NP﹣HP=3﹣1=2,∴MH=2+1=3,在Rt△MNH中,由勾股定理得:MN==;故答案为:.三、解答题(本大题共8小题,共计66分)19.【解答】解:设这个多边形的边数为n,根据题意,得:(n﹣2)×180°=360°×2+180°,解得n=7,则这个多边形的边数是7,七边形的对角线条数为:×7×(7﹣3)=14(条),答:所求的多边形的边数为7,这个多边形对角线为14条.20.【解答】解:△ABC是直角三角形.理由是:∵|a﹣3|+(4﹣b)2+=0,∴a﹣3=0,4﹣b=0,c﹣5=0,∴a=3,b=4,c=5,∴a2+b2=32+42=25,c2=52=25,∴a2+b2=c2,由勾股定理的逆定理可知,△ABC是直角三角形.21.【解答】证明:(1)∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD∠ABE=∠CDF.又∵BF=DE,∴BF﹣EF=DE﹣EF,即:BE=DF,在△ABE和△CDF中,,∴△ABE≌△CDF(SAS).∴AE=CF.(2)∵△ABE≌△CDF,∴∠AEB=∠CFD,∴∠AEF=∠CFE,∴AE∥CF∵AE=CF,∴四边形AECF是平行四边形.22.【解答】解:如图所示:点P即为所求.23.【解答】解:过点P作PD⊥AB于点.∵在A处测得小岛P的方向是北偏东75°,∴∠PAB=90°﹣75°=15°又∵在B处测得小岛P的方向是北偏东60°,∴∠PBD=90°﹣60°=30°,∵∠PBD=∠PAB+∠APB,∴∠APB=∠PBD﹣∠P AB=30°﹣15°=15°,∴∠APB=∠PAB,∴AB=PB=2×15=30(海里),在Rt△BDP中,∠PBD=30°,∴PD=BP=15(海里)<25 (海里)∴该轮船一直向东航行是有触礁的危险.24.【解答】(1)证明:∵点D,E分别是边BC,AB上的中点,∴DE∥AC,AC=2DE,∵EF=2DE,∴EF∥AC,EF=AC,∴四边形ACEF是平行四边形,∴AF=CE;(2)解:当∠B=30°时,四边形ACEF是菱形;理由如下:∵∠ACB=90°,∠B=30°,∴∠BAC=60°,AC=AB=AE,∴△AEC是等边三角形,∴AC=CE,又∵四边形ACEF是平行四边形,∴四边形ACEF是菱形.25.【解答】解:(1)∵OF是∠BCA的外角平分线,∴∠OCF=∠FCD,又∵MN∥BC,∴∠OFC=∠FCD,∴∠OFC=∠OCF,∴OF=OC,∴OE=OF;∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F ∴∠ECF=90°,∵CE=12,CF=5,∴EF==13,∵CE是∠ACB的角平分线,∴∠ACE=∠BCE,又∵MN∥BC,∴∠NEC=∠ECB,∴∠NEC=∠ACE,∴OE=OC,∴CO是△ECF上的中线,∴CO=EF=6.5;(2)点O是AC的中点且∠ACB=90°,理由:∵O为AC中点,∴OA=OC,∵由(1)知OE=OF,∴四边形AECF为平行四边形;∵∠1=∠2,∠4=∠5,∠1+∠2+∠4+∠5=180°,∴∠2+∠5=90°,即∠ECF=90°,∴▱AECF为矩形,又∵AC⊥EF.∴▱AECF是正方形.∴当点O为AC中点且△ABC是以∠ACB为直角三角形时,四边形AECF是正方形.26.【解答】(1)证明:在正方形ABCD中,AB=BC,∠ABP=∠CBP=45°,在△ABP和△CBP中,,∴△ABP≌△CBP(SAS),∴PA=PC,∵PA=PE,∴PC=PE;(2)由(1)知,△ABP≌△CBP,∴∠BAP=∠BCP,∴∠DAP=∠DCP,∵PA=PE,∴∠DAP=∠E,∴∠DCP=∠E,∵∠CFP=∠EFD(对顶角相等),∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E,即∠CPF=∠EDF=90°;(3)在菱形ABCD中,AB=BC,∠ABP=∠CBP,在△ABP和△CBP中,,∴△ABP≌△CBP(SAS),∴PA=PC,∠BAP=∠BCP,∴∠DAP=∠DCP,∵PA=PE,∴PC=PE,∵PA=PE,∴∠DAP=∠E,∴∠DCP=∠E,∵∠CFP=∠EFD,∴∠CPF=∠EDF∵∠ABC=∠ADC=120°,∴∠CPF=∠EDF=180°﹣∠ADC=60°,∴△EPC是等边三角形,∴PC=CE,∴AP=CE;。
2017八年级数学试题
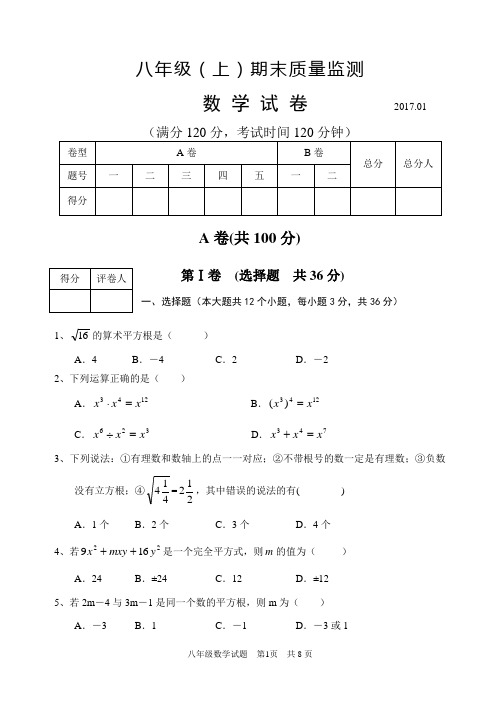
八年级(上)期末质量监测数 学 试 卷 2017.01A 卷(共100分)第Ⅰ卷 (选择题 共36分)一、选择题(本大题共12个小题,每小题3分,共36分)1、16的算术平方根是( )A .4B .-4C .2D .-22、下列运算正确的是( )A .1243x x x =⋅ B .1243)(x x =C .326x x x =÷D .743x x x =+3、下列说法:①有理数和数轴上的点一一对应;②不带根号的数一定是有理数;③负数没有立方根;④414=212,其中错误的说法的有( )A .1个B .2个C .3个D .4个4、若22169y mxy x ++是一个完全平方式,则m 的值为( )A .24B .±24C .12D .±125、若2m -4与3m -1是同一个数的平方根,则m 为( )A .-3B .1C .-1D .-3或16、下列各式中,不能用平方差公式计算的是( )A .(-a -1)(-a+1)B .(a -1)(-a -1)C .(a -1)(1+a)D .(a+1)(-a -1)7、不能确定两个三角形全等的条件是( )A .三边对应相等B .两边及其夹角相等C .两角和任一边对应相等D .三个角对应相等8、如图1,△ABC 中,∠C=90°,AC=BC ,AD 平分∠CAB 交BC 于点D ,DE ⊥AB 于E ,且AB=6cm ,则△DEB 的周长为( ) A .40 cm B .6 cm C .8 cm D .10 cm 9、如图2,AE ⊥AB 且AE=AB ,BC ⊥CD 且BC=CD ,按图中所标示的数据,图中实线所围成的图形的面积是( )A .50B .62C .65D .68 10、下列命题中,其逆命题是真命题的个数是( )①相等的两个角是对顶角;②到线段两端距离相等的点在线段的垂直平分线上; ③全等三角形三个对应角相等; ④-3是9的平方根。
八年级数学测试题及答案

八年级数学测试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是等腰三角形的性质?A. 三条边相等B. 两条边相等C. 三个角相等D. 两个角相等答案:B2. 一个数的平方根是4,那么这个数是:A. 16B. 8C. 4D. 2答案:A3. 一个圆的半径是5,那么它的周长是:A. 10πB. 20πC. 25πD. 50π答案:B4. 下列哪个选项表示的是一次函数?A. y = 2x + 3B. y = x^2 + 1C. y = 3x^3D. y = 1/x答案:A5. 一个等差数列的首项是2,公差是3,那么第5项是:A. 14B. 17C. 20D. 23答案:A6. 如果一个三角形的两边长分别是3和4,那么第三边的长x满足:A. 1 < x < 7B. 0 < x < 7C. 1 < x < 7D. 0 < x < 7答案:A7. 一个正数的倒数是1/4,那么这个数是:A. 4B. 1/4C. 1/2D. 2答案:A8. 一个数的绝对值是5,那么这个数可能是:A. 5B. -5C. 5或-5D. 0答案:C9. 下列哪个选项是二次函数的图像?A. 一条直线B. 一个点C. 一个抛物线D. 一个圆答案:C10. 一个数的立方根是2,那么这个数是:A. 8B. 6C. 2D. 4答案:A二、填空题(每题4分,共20分)1. 一个数的平方是25,那么这个数是____。
答案:±52. 一个等腰三角形的底边长是6,两腰长是5,那么它的周长是____。
答案:163. 一个圆的直径是10,那么它的半径是____。
答案:54. 一个数列的前三项是2,4,8,那么第四项是____。
答案:165. 如果一个三角形的两边长分别是5和12,那么第三边的长x满足的条件是____。
答案:7 < x < 17三、解答题(每题10分,共50分)1. 已知一个等差数列的前三项分别是2,5,8,求第10项的值。
人教版八年级上册数学 数学试题2017 10 1 优质试题

A BDCMN2017-2018学年度第一学期初二第一次数学检测题 2017.10.12一、选择题(共12道题,每道题3分,共36分.请将正确答案填涂在答题卡上)1.下列交通标志中,是轴对称图形的是 ( )2.在△ABC 中,若∠B =∠C=2∠A ,则∠A 的度数为 ( ) A.72° B.45° C.36° D.30°3.等腰三角形的两边分别为3和6,则这个三角形的周长是 ( ) A.12 B.15 C.9 D.12或154. 木工师傅在做完门框后,为防止变形常常像图中所示那样钉上两条斜拉的木板条(即图中的AB 和CD ),这样做的根据是 ( ) A .矩形的对称性 B .矩形的四个角都是直角 C .三角形的稳定性 D .两点之间线段最短5.如图,∠ACB >90°,AD ⊥BC ,BE ⊥AC ,CF ⊥AB ,垂足分别为点D 、点E 、点F ,△ABC 中AC 边上的高是 ( ) A .CF B .BE C .AD D .CD6.如图,DE ⊥AC ,垂足为E ,CE =AE.若AB =12cm ,BC =10cm ,则△BCD 的周长是 ( ) A.22cm B.16cm C.23cm D.25cm7.如图,在Rt △ACD 和Rt △BEC 中,若AD=BE ,DC=EC ,则不正确的结论是 ( )A .Rt △ACD 和Rt △BCE 全等 B.OA=OBC .AE=BD D.E 是AC 的中点 8.一个正多边的内角和是外角和的3倍,这个正多边形的边数是 ( )A .7 B.8 C.9 D.109.如图,在△ABC 中,AB=4,AC=3,AD 平分∠BAC ,则S △ABD :S △ADC 为 ( )A.4:3B.16:19C.3:4D.不能确定10. 在△ABC 中,∠B =∠C ,与△ABC 全等的三角形有一个角是100°,那么在△ABC 中与这100°角对应相等的角是 ( )A.∠AB.∠BC.∠CD.∠B 或∠C11.如右图,图中显示的是从镜子中看到背后墙上的电子钟读数,由此你可以推断这时的实际时间是()A 、10:05 B 、20:01 C 、20:10 D、10:0212. 如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是 ( )A.∠M=∠NB. AM∥CNC.AB=CDD. AM=CN二、填空题(共5小题,每小题3分,计15分)13.已知点P(-3,4),关于y 轴对称的点的坐标为 。
2017八年级上册第一次月考试题(数学、答题卡、答案)
第6题第8题 第7题 2017—2018学年度第一学期第一次月考试题八 年 级 数 学(时间:120分钟 满分:150分)一.选择题(共12小题)1.下列各组数中,不可能成为一个三角形三边长的是( )A .2,3,4B .5,7,7C .5,6,12D .6,8,102.一个三角形的三个内角的度数之比为1:2:3,则这个三角形一定是( )A .锐角三角形B .直角三角形C .钝角三角形D .等腰直角三角形3.如图,△ABC 中,∠A=60°,∠B=40°,则∠C 等于( )A .100°B .80°C .60°D .40°4.已知一个多边形的内角和是900°,则这个多边形是( )A .五边形B .六边形C .七边形D .八边形5.下列四个图形中,线段BE 是△ABC 的高的是( )A B C D6.如图,在△ABC 中,D 、E 分别是AC 、BC 上的点,若△ADB ≌△EDB ≌△EDC ,则∠C 的度数是( )A .15°B .20°C .25°D .30°7.如图,已知∠ABC=∠DCB ,下列所给条件不能证明△ABC ≌△DCB 的是( )A .∠A=∠DB .AB=DC C .∠ACB=∠DBCD .AC=BD8.某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的 玻璃,那么最省事方法是( )A .带①去B .带②去C .带③去D .①②③都带去9.如图,△ABC 的三边AB 、BC 、AC 的长分别12,18,24,O 是△ABC 三条角平分 线的交点,则S △OAB :S △OBC :S △OAC =( )A .1:1:1B .1:2:3C .2:3:4D .3:4:510.如图,OP 平分∠MON ,PA ⊥OA 于点A ,点Q 是射线OM 上的一个动点,若PA=2, 则PQ 的值为( )A .1B .2C .大于2D .不小于211.如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=( )A .90°B .135°C .150°D .180°12.如图,直线l 、l′、l″表示三条相互交叉的公路,现计划建一个加油站,要求它到 三条公路的距离相等,则可供选择的地址有( )A .一处B .二处C .三处D .四处二.填空题(共6小题)13.如图示在△ABC 中∠B= . 14.若正多边形的一个外角是40°,则这个正多边形的边数是.15.如图,已知△ABC ≌△ADE ,若AB=10,AC=4,则BE 的值为 .16.如图,已知∠AOB=30°,P 是∠AOB 平分线上一点,CP ∥OB ,交OA 于点C , PD ⊥OB ,垂足为点D ,且PC=4,则PD 等于 .17.如图,五角星的顶点分别是A ,B ,C ,D ,E ,那么∠A +∠B +∠C +∠D +∠E= .18.△ABC 中,AB=AC=12厘米,∠B=∠C ,BC=8厘米,点D 为AB 的中点.如果点P 在线段BC 上以2厘米/秒的速度由B 点向C 点运动,同时,点Q 在线段CA 上由C 点向A 点运动.若点Q 的运动速度为v 厘米/秒,则当△BPD 与△CQP 全等时,v 的值为 .三.解答题(共9小题)19.一个多边形的内角和比四边形的内角和多720°,并且这个多边形的各内角都相第9题 第10题 第11题 第12题 第13题 第16题 第17题第15题等,这个多边形的每个内角是多少度?20.化简求值: 3a2b﹣[2ab2﹣2(﹣a2b+4ab2)]﹣5ab2,其中a=﹣2,b=.21.如图所示,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=63°,求∠DAC的度数.22.如图,已知AB=DC,AC=DB.求证:∠1=∠2.23.已知:如图,∠A=∠D=90°,AC=BD.求证:OB=OC.24.如图,在△ABC中,AD⊥BC,AE平分∠BAC.(1)若∠B=72°,∠C=30°,求①∠BAE的度数;②∠DAE的度数;(2)探究:如果只知道∠B=∠C+42°,也能求出∠DAE的度数吗?若能,请你写出求解过程;若不能,请说明理由.25.如图,在△ABC中,∠ABC、∠ACB的平分线相交于点O(1)若∠A=60°,则∠BOC=;(2)若∠A=n°,求∠BOC的度数;(3)若∠BOC=3∠A,求∠A的度数.26.如图所示,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,延长AE交BC的延长线于点F.(1)判断FC与AD的数量关系,并说明理由;(2)若AB=BC+AD,则BE⊥AF吗?为什么?(3)在(2)的条件下,若EC⊥BF,EC=3,求点E到AB的距离.27.如图,已△ABC中,AB=AC=12厘米,BC=9厘米,点D为AB的中点.(1)如果点P在线段BC上以3厘米/秒的速度由B向C点运动,同时点Q在线段CA上由C点向A点运动.①若点Q的运动速度与点P的运动速度相等,1秒钟时,△BPD与△CQP是否全等,请说明;②点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD≌△CPQ?(2)若点Q以②的运动速度从点C出发点P以原来运动速度从点B同时出发,都逆时针沿ABC的三边运动,求多长时间点P与点Q第一次在△ABC的哪条边上相遇?育才中学2017年秋季学期第一次月考八年级数学答题卡一:选择题(共36分):1、【A】【B】【C】【D】2、【A】【B】【C】【D】3、【A】【B】【C】【D】4、【A】【B】【C】【D】5、【A】【B】【C】【D】6、【A】【B】【C】【D】7、【A】【B】【C】【D】8、【A】【B】【C】【D】9、【A】【B】【C】【D】10、【A】【B】【C】【D】11、【A】【B】【C】【D】12、【A】【B】【C】【D】二、填空题:(共24分)13、14、15、16、17、18、三、简答题(共90分)19.(6分)20.(8分)化简求值:3a2b﹣[2ab2﹣2(﹣a2b+4ab2)]﹣5ab2,其中a=﹣2,b=.21、(8分)22(10分)23、(10分)24、(10分)25、(12分)27、(14分)26、(12分)2017年秋季学期八年级数学第一次月考试题参考答案一、选择题:二、填空题:13、25°14、九15、616、217、180°18、2或3三、解答题:19、解:设这个多边形边数为n,则(n﹣2)•180=360+720,解得:n=8,∵这个多边形的每个内角都相等,∴它每一个内角的度数为1080°÷8=135°.答:这个多边形的每个内角是135度.20、解:(1)原式=3a2b﹣2ab2﹣2a2b+8ab2﹣5ab2=a2b+ab2,当a=﹣2,b=时,原式=2﹣=;21、解:设∠1=∠2=x,则∠3=∠4=2x.因为∠BAC=63°,所以∠2+∠4=117°,即x+2x=117°,所以x=39°;所以∠3=∠4=78°,∠DAC=180°﹣∠3﹣∠4=24°.22、证明:在△ABC和△DCB中,,∴△ABC≌△DCB(SSS),∴∠1=∠2.23、证明:∵∠A=∠D=90°,AC=BD,BC=BC,∴Rt△BAC≌Rt△CDB(HL)∴∠ACB=∠DBC.∴∠OCB=∠OBC.∴OB=OC(等角对等边).24、解:(1)①∵∠B+∠C+∠BAC=180°,∴∠BAC=180°﹣72°﹣30°=78°,∵AE平分∠BAC,∴∠BAE=∠BAC=39°;②∵AD⊥BC,∴∠ADB=90°,∴∠BAD=90°﹣∠B=18°,∴∠DAE=∠BAE﹣∠BAD=39°﹣18°=21°;(2)能.∵∠B+∠C+∠BAC=180°,∠B=∠C+42°,∴∠C=∠B﹣42°,∴2∠B+∠BAC=222°,∴∠BAC=222°﹣2∠B,∵AE平分∠BAC,∴∠BAE=111°﹣∠B,在△ABD中,∠BAD=90°﹣∠B,∴∠DAE=∠BAE﹣∠BAD=(111°﹣∠B)﹣(90°﹣∠B)=21°.25、解:(1)∵∠A=60°,∴∠ABC+∠ACB=180°﹣∠A=120°.∵∠ABC、∠ACB的平分线相交于点O,∴∠CBO=∠ABC,∠BCO=∠ACB,∴∠BOC=180°﹣(∠CBO+∠BCO)=180°﹣(∠ABC+∠ACB)=120°.故答案为:120°.(2)由(1)可知:∠BOC=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣∠A)=90°+∠A=90°+n°.(3)由(2)可知:∠BOC=90°+∠A,∵∠BOC=3∠A,∴3∠A=90°+∠A,解得:∠A=36°.26、证明:(1)∵AD∥BC,∴∠ADC=∠ECF,∵E是CD的中点,∴DE=EC,∵在△ADE与△FCE中,,∴△ADE≌△FCE(ASA),∴FC=AD;(2)由(1)知△ADE≌△FCE,∴AE=EF,AD=CF,∵AB=BC+AD,∴AB=BC+CF,即AB=BF,在△ABE与△FBE中,,∴△ABE≌△FBE,∴∠AEB=∠FBE=90°,∴BE⊥AE;(3)在(2)的条件下有△ABE≌△FBE,∴∠ABE=∠FBE,∴E到BF的距离等于E到AB的距离,∵CE⊥BF,CE=3,∴点E到AB的距离为3.27、解:(1)①∵t=1(秒),∴BP=CQ=3(厘米)∵AB=12,D为AB中点,∴BD=6(厘米)又∵PC=BC﹣BP=9﹣3=6(厘米)∴PC=BD ∵AB=AC,∴∠B=∠C,在△BPD与△CQP中,,∴△BPD≌△CQP(SAS),②∵V P≠V Q,∴BP≠CQ,又∵∠B=∠C,要使△BPD≌△CPQ,只能BP=CP=4.5,∵△BPD≌△CPQ,∴CQ=BD=6.∴点P的运动时间t===1.5(秒),此时V Q===4(厘米/秒).(2)因为V Q>V P,只能是点Q追上点P,即点Q比点P多走AB+AC的路程设经过x秒后P与Q第一次相遇,依题意得4x=3x+2×12,解得x=24(秒)此时P运动了24×3=72(厘米)又∵△ABC的周长为33厘米,72=33×2+6,∴点P、Q在BC边上相遇,即经过了24秒,点P与点Q第一次在BC边上相遇.。
2017年1月历下八上期末数学教学质量检测试题
历下区八年级数学教学质量检测试题(2017.1)班级: 学号: 姓名:一、选择题(本大题共12小题,每小题5分,满分60分.)1.9的平方根是( )A .3 B .﹣3 C .±3 D .±√3 2.如图,已知直线a ∥b ,若∠1=110°,则∠2=( ) A .60° B .70° C .80° D .90°3.若a >b ,则下列各式中一定..成立的是( ) A .a +1>b +1 B .3a <3bC .−a >−bD .4.在平面直角坐标系中,点P (-1,5)所在的象限是( )A .第一象限B .第二象限C .第三象限D .第四象限 5.一次函数y =2x +1的图象不经过( )A .第一象限B .第二象限C .第三象限D .第四象限 6.下列长度的三条线段能.组成直角三角形的是( ) A .3,4,4 B .6,8,10 C .5,5,5 D .6,7,87.某市五月份连续五天的日最高气温分别为23、20、20、21、26(单位:C ︒),这组 数据的中位数和众数分别是( )A .22C ︒,26C ︒B .22C ︒,20C ︒ C .21C ︒,26C ︒D .21C ︒,20C ︒8.如图,直线AB ∥CD ,∠A =70︒,∠C =40︒,则∠E 等于() A .30° B .40° C .60° D .70°9.若线段CD 是由线段AB 平移得到的,点A (﹣1,3)的对应点 为C (2,2),则点B (﹣3,﹣1)的对应点D 的坐标是( ) A .(0,﹣2) B .(1,﹣2) C .(﹣2,0) D .(4,6)10.已知方程组{2m +n =6m +2n =5,则m ﹣n 的值是( )A .﹣1 B .0 C .1 D .211.如图,△ABC 的顶点A 、B 、C 在边长为1的正方形网格的格点上,BD ⊥AC 于点D .则BD 的长为( ) A . B C D12.已知点11()A x y , 、22()B x y , 是一次函数2(0)y kx k =+> 图象上不同的两点,若1212()()t x x y y =-- ,则( )A .t <0B .t =0C .t >0D .t ≤0bc ac < A CB DE第2题图第11题图第8题图二、填空题(本大题共4个小题,每小题4分,共16分.) 13.8的立方根是 .14.不等式4x -6≥3x -5的解集为 .15.如图,一只蚂蚁沿着边长为1的正方体表面从点A 出发,经过3个面爬到点B ,如果它运动的路径是最短的,则最短路径的长为 .16.正方形A 1B 1C 1O ,A 2B 2C 2C 1,A 3B 3C 3C 2,…按如图 所示的方式放置.点A 1,A 2,A 3,…和点C 1,C 2, C 3,…分别在直线y=kx +b (k >0)和x 轴上,已知点 B 1(1,1),B 2(3,2),则B n 的坐标是 . 三、解答题(本大题共8题,满分74分) 17. (本小题满分8分)已知方程组{ax +2y =72x +y =3与{3x −y =25x +by =4有相同的解,求代数式a —4b 的值.18.(本小题满分8分)已知,如图,BCE 、AFE 是直线,AB ∥CD ,∠1=∠2,∠3=∠4.求证:AD ∥BE证明: ∵AB ∥CD (已知)∴∠4= ( ) ∵∠3=∠4(已知)∴∠3= ( ) ∵∠1=∠2(已知)∴∠1+∠CAF =∠2+∠CAF( )即 = ∴∠3=∠DAC∴AD ∥BE ( ) 19.(本小题满分8分)为增强学生的身体素质,教育行政部门规定学生每天参加户外活动的平均时间不少于1小时.为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制作成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:第15题图第16题图第18题图(1)在这次调查中共调查了多少名学生?(2)求户外活动时间为1.5小时的人数,并补充频数分布直方图;(3)求户外活动时间的众数和中位数是多少?(4)本次调查中学生参加户外活动的平均时间是否符合要求?说明理由.20.(本小题满分9分)阅读对话后,完成下面的要求:张老师:王芳,你怎么哭了?王芳:张老师,我还没来得及记下来,李兵就把这道题后面的擦掉了.张老师:是这么回事呀!如果我告诉你这道题的答案是x≥—4,而且后面被擦掉的是一个常数,你能把这个常数补上吗?王芳:…,我知道了,谢谢老师(笑).根据以上信息,你能否求出被擦掉的常数?试试看!21.(本小题满分9分)某蔬菜公司收购到某种蔬菜104吨,准备加工后上市销售.该公司加工该种蔬菜的能力是:每天可以精加工4吨或粗加工8吨.现计划用16天正好完成加工任务,则该公司应安排几天精加工,几天粗加工?22.(本小题满分10分)李明骑自行车去上学途中,经过先上坡后下坡的一条路段,在这段路上所走的路程S(米)与时间t(分钟)之间的函数关系如图所示.根据图象,解答下列问题:(1)求李明上坡时所走的路程S1(米)与时间t(分钟)之间的函数关系式和下坡时所走的路程S2(米)与时间t(分钟)之间的函数关系式;(2)若李明放学后按原路返回,且往返过程中,上坡的速度相同,下坡的速度也相同,时走这段路所用的时间为多少分钟?问李明返回..历下区八年级数学教学质量检测试题(2017.1)班级:学号:姓名:23.(本小题满分10分)如图,在长方形ABCD中,点E、F分别在边AB和BC上,∠AEF的平分线与边AD交于点G,线段EG的反向延长线与∠EFB的平分线交于点H.(1)当∠BEF=50°(图1),试求∠H的度数.(2)当E、F在边AB和BC上任意移动时(不与点B重合)(图2),∠H的大小是否变化?若变化,请说明理由;若不变化,求出∠H的度数.图1 图224.(本小题满分12分)张老师给爱好数学的小林提出这样一个问题:如图①,在△ABC 中,AB =AC ,点P 为边BC 上的任意一点,过点P 作PD ⊥AB ,PE ⊥AC ,垂足分别为D 、E ,过点C 作CF ⊥AB ,垂足为F .求证:PD +PE =CF .小林的证明思路是:如图②,连接AP ,由△ABP 与△ACP 面积之和等于△ABC 的面积可以证得:PD +PE =CF .【变式探究】如图③,当点P 在BC 延长线上时,其余条件不变,求证:PD ﹣PE =CF ;【结论运用】请运用上述解答中所积累的经验和方法完成下题:如图④,在平面直角坐标系中有两条直线l 1:y =34x +3、l 2:y =﹣3x +3,若l 2上的一点M 到l 1的距离是1,请运用上述的结论求出点M 的坐标.。
初中二年级上册数学试卷【含答案】
初中二年级上册数学试卷【含答案】专业课原理概述部分一、选择题(每题1分,共5分)1. 如果一个数的平方根是9,那么这个数是:A. 81B. 9C. -9D. 32. 下列哪个数是负数?A. -5B. 0C. 3.5D. 1003. 一个等腰三角形的底边长是10cm,腰长是12cm,那么这个三角形的周长是:A. 22cmB. 32cmC. 34cmD. 44cm4. 如果一个数的立方根是2,那么这个数是:A. 2B. 6C. 8D. 105. 下列哪个数是有理数?A. √3B. πC. 0.333D. √2二、判断题(每题1分,共5分)1. 任何数都有立方根。
()2. 负数没有平方根。
()3. 0的立方根是0。
()4. 等腰三角形的两腰相等。
()5. √9 = 3,所以-√9 = -3。
()三、填空题(每题1分,共5分)1. 如果一个数的平方根是4,那么这个数是______。
2. 0的立方根是______。
3. 一个等腰三角形的底边长是10cm,腰长是12cm,那么这个三角形的周长是______cm。
4. 下列哪个数是无理数?______5. 如果一个数的立方根是8,那么这个数是______。
四、简答题(每题2分,共10分)1. 请解释什么是有理数。
2. 请解释什么是无理数。
3. 请解释等腰三角形的性质。
4. 请解释什么是平方根。
5. 请解释什么是立方根。
五、应用题(每题2分,共10分)1. 一个正方体的体积是64cm³,那么这个正方体的边长是多少?2. 如果一个数的平方根是5,那么这个数的立方根是多少?3. 一个等腰三角形的底边长是8cm,腰长是10cm,那么这个三角形的周长是多少?4. 如果一个数的立方根是3,那么这个数的平方根是多少?5. 请计算√(27 + 64)的值。
六、分析题(每题5分,共10分)1. 请分析有理数和无理数的区别。
2. 请分析等腰三角形和等边三角形的区别。
七、实践操作题(每题5分,共10分)1. 请测量一个正方体的体积,并计算其边长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017年下学期八年级数学测试题(1)
一.选择题(每小题3分,共30分)
1.下列式子(1)yxyxyx122;(2)cabaacab;(3)1baab;
(4)yxyxyxyx,其中正确的有 ( )
A 、1个 B 、2 个 C、 3 个 D、 4 个
2. 能使分式122xxx的值为零的所有x的值是 ( )
A 0x B 1x C 0x 或1x D 0x或1x
3.将分式yxx2中的x、y的值同时扩大3倍,则 扩大后分式的值( )
A、扩大3倍; B、缩小3倍; C、保持不变; D、无法确定。
4.计算()ababbaa的结果为( )
A.abb B.abb C.aba D.aba
5、如果三角形的一个外角和与它不相邻的两个内角的和为180°,那么与这个外
角相邻的内角的度数为( )
A、30° B、60° C、90° D、120°
6.用3cm、5cm、7cm、9cm、11cm的五根木棒可组成不同的三角形的个数是( )
A.5个 B.6个 C.7个 D.8个
7.如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下述
结论错误的是( )
A、BD平分∠ABC B、△BCD的周长等于AB+BC
C、AD=BD=BC D、点D是线段AC的中点
8.下列句子中,不是命题的是( )
A.三角形的内角和等于180度; B.对顶角相等;
C.过一点作已知直线的平行线; D.两点确定一条直线.
9.
若 ,则a、b、c、d的大小关系是( ).
A. a
10.一件工作,甲独做a小时完成,乙独做b小时完成,则甲、乙两人合作完成需要
( )小时.
A.11ab; B.1ab; C.1ab; D.abab
二.填空题(每小题3分,共24分)
11.当____x时,23xx无意义,当____x时,这个分式的值为零。
12.某种感冒病毒的直径是0.00000012米,用科学记数法表示为
13.如图,已知△ABC是等边三角形,点B、C、D、E在同一直线上,
且CG=CD,DF=DE,则∠E= 度.
14.已知311yx,则分式yxyxyxyx2232的值为 ___ .
15.如图,在△ABC中,D为AB上的一点,连接CD,AD=CD,∠B=115°,
且∠ACD:∠BCD=5:3,则∠ACB= 度。
16.等腰三角形的两边长分别为5 cm和12 cm,则三角形的周长为 cm.
17.分式方程3x+61x=27xx的解为x= 。
18.某市对一段全长1500米的道路进行改造.原计划每天修x米,为了尽量减少施工对城
市交通所造成的影响,实际施工时,每天修路比原计划的2倍还多35米,那么修这条路实
际用了 天。
三.解答题:(46分)
19.先化简:(212xx-2144xx)÷222xx,再选择一个你喜欢的x值代入求值。(6
分)
21.如图,在△ABC中,AB=AC,D是AB上一点,DE⊥BC,E是垂足,ED的延长线交CA的延
长线于点F,求证:AD=AF. (6分)
22.如图,在AB=AC的△ABC中,D点在AC边上,使BD=BC,E点在AB边上,使AD=DE=EB,
求∠EDB.(6分)
23.在2008年春运期间,我国南方出现大范围冰雪灾害,导致某地电路断电.该地供电局组
织电工进行抢修.供电局距离抢修工地15千米.抢修车装载着所需材料先从供电局出发,15
分钟后,电工乘吉普车从同一地点出发,结果他们同时到达抢修工地.已知吉普车速度是抢
修车速度的1.5倍,求这两种车的速度。(7分)
24.(7分)某一工程,在工程招标时,接到甲、乙两个工程队的投标书.施工一天,需付甲
工程队工程款1.2万元,乙工程队工程款0.5万元.工程领导小组根据甲、乙两队的投标书
测算,有如下方案:(1)甲队单独完成这项工程刚好如期完成;
(2)乙队单独完成这项工程要比规定日期多用6天;
(3)若甲、乙两队合做3天,余下的工程由乙队单独做也正好如期完成.
试问:在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理由.
25.计算)1999x)(1998x(1.....)3x)(2x(1)2x)(1x(1)1x(x1
并求当x=1时,该代数式的值.(6分)
26.(8分)如图⑴,AB⊥BD,DE⊥BD,点C是BD上一点,且BC=DE,CD=AB.
⑴试判断AC与CE的位置关系,并说明理由.
⑵如图⑵,若把△CDE沿直线BD向左平移,使△CDE的顶点C与B重合,此时第⑴问中AC
与BE的位置关系还成立吗?说明理由。(注意字母的变化)
