6-4一阶电路的全响应及阶跃响应剖析
电路分析基础(金波)1-6章 (6)

(6-16)
第6章 一阶电路 串联电容的等效电容为
1 1 1 1
Ceq C1 C2
Cn
(6-17) 等效初始电压为
u(0)=u1(0)+u2(0)+…+un(0)
(6-18)
第6章 一阶电路
自测题6-1 电路中的储能元件是指
(A) 电阻元件 (B) 电感元件 (C) 电容元件
【例6-3】 一个电容元件如图6-5所示。电容C=4 μF,已 知t=0时,uC(0)=0,iC=2 A,求t=20 ms
第6章 一阶电路 图6-5 例6-3的电路
第6章 一阶电路
解 电容电压为
uC
uC (0)
1 C
0t iCdt
1 C
2t
uC (20
ms )
2 20103 C
0.04 C
V
电容的储能为
第6章 一阶电路 图6-7 电感元件串联
第6章 一阶电路 并联电感有相同的电压,每个电感元件的电流为
i1
1 L1
t
0
udt
i1(0) ,i2
1 L2
0t udt
i2 (0) ,i3
1 L3
t
0
udt
i3(0)
总电流为
i
i1
i2
i3
(1 L1
1 L2
1 L3
)0t
udt
i1(0)
i2 (0)
i3(0)
即电容量的大小是电容极板上的电荷与所加电压之比。 其中, q为电荷,当C 设电容元件端电压和电流为关联参考方向,则有
(6-7)
iC
C
duC dt
上式表示电容元件的伏安关系,电容电流是与其电压的变
一阶电路详解

ab
都等于
ab
u C (t 0 )
' u C (t 0 )
U 0e
t0
(U 0 e
(
1
))
④ =RC,可用改变电路的参数的办法加以调节或控制;
⑤ 能量转换关系:电容不断放出能量,电阻不断消耗能量,最 后,原来储存在电容的电场能量全部为电阻吸收并转换为热能。
例7-1:下图所示电路中, t = 0 时,开关 S 由 a 投向 b, 在此以前电容电压为 U0 ,试求 t 0 时,电容电压及电流。
从而得到所求变量(电流或电压)的方法。 用经典法求解常微分方程时,必须根据电路的初始条件确定解
答中的积分常数。
电路独立初始条件:uC(0+)和 iL(0+)
二. 电路的初始条件 1. 电容的电荷和电压
q (t ) q C (t 0 ) C u (t ) u (t ) C 0 C
V
二. RL电路的零输入响应
t = 0 , 换路; t <0,S1与 b 端相接, S2 打开,L通电; t > 0,S1 投向 c 端, S2 同时闭合.
电路的微分方程及其解为
di L R iL 0 L dt i (0) I 0 L
i( t ) I 0 e L
2 S
能量与
R 的大小无关
又因
WC
1 CU 2
2 S
, 可见
WC W R
二. RL电路的零状态响应
类似于RC电路,可求出零状态响应为
iL (t ) U
S
R
(1 e
R t L
《电路分析》阶跃函数和阶跃响应

在上一节的讨论中,我们看到直流一阶电路中的各种 开关,可以起到将直流电压源和电流源接入电路或脱离电 路的作用,这种作用可以描述为分段恒定信号对电路的激 励。
随着电路规模的增大和计算工作量增加,有必要引入 阶跃函数来描述这些物理现象,以便更好地建立电路的物 理模型和数学模型,也有利于用计算机分析和设计电路。
一、阶跃函数
单位阶跃函数(t)的定义为
(t)
0 1
t0 t 0
(8 26)
波形如图(a)所示。当t=0时,(t)从0跃变到1。当跃变量是k
个单位时,可以用阶跃函数k(t)来表示,其波形如图(b)所
示。当跃变发生在t=t0时刻,可以用延迟阶跃函数 (t-to) 表 示,其波形如图(c)所示。函数(-t)表示t<0时,(-t)=1,t>0
时,(-t)=0,如图(d)所示。
图8-30 阶跃函数
当直流电压源或直流电流源通过一个开关的作用施加 到某个电路时,有时可以表示为一个阶跃电压或阶跃电流 作用于该电路。
例如图 (a)所示开关电路,就其端口所产生的电压波形
u(t)来说,等效于图(b)所示的阶跃电压源U0(t)。
图(c)所示开关电路,就其端口所产生的电流波形i(t)来
图8-33
例8-15 用阶跃电流源表示图8-33(b)所示的方波电流,再次 求解电路中电感电流的响应,并画出波形曲线。
图8-33
解:图(b)所示的方波电流,可以用两个阶跃函数
iS(t)=[10 (t)-10 (t-1ms)]mA 表示。
由于该电路是线性电路,根据动态电路的叠加定理,
其零状态响应等于10(t)和-10 (t-1ms)两个阶跃电源单独作
值iL()=1,时间常数为=L/R。
4-2一阶电路的阶跃响应
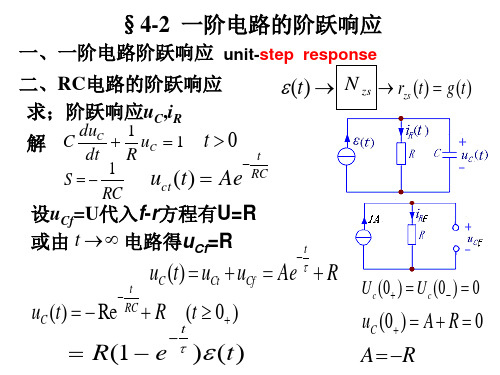
uC ( t ) = uC ( 2 + ) e = 5R(1 e = 5R ( e
t 2 RC
)e
e
t RC
)
时的L 作业 4-6 (t>0时的 eq,Req) 时的 4-8 rzS(t),g(t) 间的线性时不变性) 4-11 (rzS(t)与f(t)间的线性时不变性 与 间的线性时不变性
�
τ
)ε ( t )
uC(0+) = A+R=0
A = R
u C ( t ) = R (1 e
t
τ
)ε ( t )
t 1 τt τt duC iC = C = CR( e )ε (t) + (1 e τ )δ (t) = e ε (t) dt τ t uC (t ) iR (t ) = 1 iC (t ) = = (1 e τ )ε (t ) R
t RC
)ε (t )
)ε (t 2)
t 2 RC
当i (t ) = 5ε (t 2) A时, 零状态响应
′′ uC (t ) = 5 R (1 e
t 2 RC
′ ′ uc (t ) = uc (t ) + uc′(t ) = 5R(1 e
t RC
)ε (t ) 5R(1 e
)ε (t 2)
R
四,对于一阶电路阶跃响应中的电容电压和电感 电流变量可表示为
r (t ) = rf (1 e τ#43; rf )
只要求出电容电压(或电感电流) 只要求出电容电压(或电感电流)的稳态值和电 路的时间常数,即可根据上式写出电容电压( 路的时间常数,即可根据上式写出电容电压(或 电感电流)的函数式. 电感电流)的函数式.
Re τ ε (t)
《电路分析基础》第六章:一阶电路

t ≥ t0 -
R i''(t) a
+
C
uC'' (t)
b
+-u1''(t)
零输入响应
零状态响应
信息学院电子系
6
2. RC电路的零状态响应
t=0时,开关由打开到闭合
中uC(0−) =0
¾ 定性分析
国 uC
i
K (t = 0)
R
i+
+
C
Us
uC
−
−
海洋 O τ 2τ 3τ 4τ t O τ
uC
(t
)
=
uC
−1
(0)e τ
t
t ≥ 0 τ=RC
−1t
iL (t) = iL (0)e τ
t ≥ 0 τ=L/R
¾ 零输入响应线性 ¾零输入响应形式也适用于非状态变量
信息学院电子系
18
6.5 线性动态电路的叠加定理
中全响应
电路的初始状态不为零,同时又有外加激励 源作用时电路中产生的响应。
国 线性动态电路的叠加定理
中电容储存能量:WC
=
1 2
CU
2 S
+
C
Us
uC
−
−
国 ∫ ∫ e 电阻消耗能量:WR =
∞i2Rdt =
0
∞ (US 0R
−
t
RC
)2
R
dtΒιβλιοθήκη =1 CU 22 S
海 电源提供能量:WS = WC + WR = CUS2
注意
洋 •电源提供的能量一半消耗在电阻上,一半转换成电场能 大 量储存在电容中。 学 • uc由0开始按照指数规律上升趋向稳态值
吉林大学电路分析课件第6章修

6-1 分解的方法在动态电路分析中的应用
一、把一阶电路的动态元件分离出来,可以得到典 把一阶电路的动态元件分离出来, 型的一阶电路: 型的一阶电路:
其中N为一般的线性含源单口网络。 其中N为一般的线性含源单口网络。而N可以化简 为戴维南等效电路或诺顿等效电路,如图( 为戴维南等效电路或诺顿等效电路,如图(b)。 这样一阶电路的分析问题,转化为图( 这样一阶电路的分析问题,转化为图(b) RC或RL电路的分析问题。 RC或RL电路的分析问题。 电路的分析问题
电路在没有外界输入的情况下, 电路在没有外界输入的情况下,只由电路中动 态元件初始储能作用而产生的响应为零输入响应。 态元件初始储能作用而产生的响应为零输入响应。 输入为零) 一、RC 电路的零输入响应(输入为零) 所示电路, 图(a)所示电路,开关原来在 端,电容电压已 所示电路 开关原来在1端 经达到U 时开关由1端转换到 经达到 0,在t=0时开关由 端转换到 端,如图 时开关由 端转换到2端 如图(b) 求: uC(t);iC(t), t ≥ 0
X h ( t ) = Ke
At
齐次方程特解 特解: 2)非齐次方程特解:
W=Q
常数*
确定: 3)K确定: X ( t ) = Ke At + Q 由初始条件解出K 由初始条件解出K
特解的形式: 特解的形式:
输入W (t )的形式 特解x p (t )的形式 P Pt P0 + P t 1 P0 + P t + P2t 2 1 Pe (λ ≠ A) Pe (λ = A) P sin bt P cos bt
利用分解方法分析一阶电路的方法: 把电路分解为一个动态元件和一个单口网络; 把单口网络化为最简单的形式,得到RC或RL 电路; 布列RC或RL电路的微分方程,解出状态变 量; 用电压源或电流源置换动态元件,得到纯电 阻电路; 分析纯电阻电路,求解余下变量。 以上方法可以处理所有一阶电路。
电路2
§6-1 动态电路的方程及其初始条件正误判断题1.动态电路换路时,如果在换路前后电容电流和电感电压为有限值的条件下,则换路前后瞬间有:a)b)2.电路如图所示,电路原已达稳态,t =0时开关S 由1合向2,则、为:a) OA , 24Vb) 4A , 20V3.电路如图所示,电路原已达稳态,t=0时开关S 闭合,则、为:a) -1mA , 0Vb) +1mA , 0V打开,则,4A , 4S b) 2A , 0.25S-0.8e -t Ab) 0.8e -t Aa) Vb)打开,电路时间常数和 2S, 1A b) 0.5S , 1A时,电压a)b)闭合,已知,则时电压a)b)§6-4 一阶电路的全响应正误判断题1.电路如图所示,电路原处于稳态,t=0时开关S 闭合,则,和为:a) 4V ,2V , 1Sb) 2V , 4V , 1S2.电路如图所示,电路原处于稳态,t=0时开关S 闭合,则,和为:a) 3A, 4.5A ,b) 3A , 4.5A , 2S3.电路如图所示,电路原已达稳态,t=0时开关S 由1合向2,则时为: a)b)4.电路如图所示,电路原已达稳态,t=0时开关S闭合,则时为:a) Ab) A§7-1 二阶电路的零输入响应正误判断题1.图中电路是否为二阶电路a) 是b) 否2.二阶方程的通解形式为a)b)3.已知零输入的RLC 串联电路的微分方程形式为,则电路的放电过程a)非振荡b)振荡§7-2 二阶电路的零状态响应和阶跃响应正误判断题1.某二阶电路的微分方程形式为,则方程的特解为a) =0.5b) =1§8-1复数正误判断题1.已知 A ,V ,则u与i的相位差为a) b)2.等于a)i b)-ia)超前b) 滞后超前滞后§8-4 电路定律的相量形式正误判断题1.电容上的电压相量和电流向量满足a)b)2.当ω等于零时,电感相当于a)短路b)开路§9-1阻抗和导纳正误判断题1 .电容的导纳为( A )( B )2 .已知一阻抗为1+jΩ,则该阻抗为( A )容性阻抗( B )感性阻抗a)b)a) 2+2j Sb) 2-2j Sa)b)§9-5 正弦稳态电路的功率正误判断题1.有功功率中的ω是a)电压与电流的相位差b)阻抗角2.视在功率的单位是a) Varb) VA§9-6 复功率正误判断题1.正弦稳态电路的复功率a)守恒b)不守恒2.复功率的定义为a)b)§9-7 最大传输功率正误判断题1.正弦交流电路含源一端口向终端负载传输功率,已知含源一端口的戴维宁等效阻抗为,则负载获得最大有功功率的条件是负载阻抗等于a)b)2.在上题中,负载获得的最大功率为a)b)§9-8 串联电路的谐振正误判断题1.正弦稳态电路发生串联谐振时阻抗a)最大b)最小2.串联谐振时阻抗为纯电阻,此时电容两端a)电压为零b)电压不为零§9-9 并联谐振电路正误判断题1.并联谐振的条件是a)b)2.下图为正弦稳态电路的一部分,发生并联谐振时,电容和电感两端相当于a)短路b)开路§10-1 互感正误判断题1.两个具有耦合的线圈如图所示,则端子1的同名端为(a )端子 2(b )端子2'2 .电路如图所示,则感应电压为(a )(b )(a )(b )(b )不一定相等))§11-1 三相电路正误判断题1.图 11 -1-1所示的电压相序为2.三相四线制常用于 ( A ) Y-Y 接法 ( B ) Y-接法.对称三相电路星形接法 与的相位差为) ).对称三相电路三角形负载的线电流 与相电流 的相位差)))倍.图示电路是一种相序比较器,图中电阻是用两个相同的灯泡,在相电压对称的情况下,( A ) A 相 ( B ) C 相11-4-2图( A )正确( B )不正确11-5-2图第六章一阶电路路后,分别为:,S,S时电容电压为:)))),则时为))))时开关打开,时电压为:))))则时电压为:))))则时开关中电流为:))))图,已知,则的阶跃响应())))图所示,已知,则的冲激响应为:))))时开关闭合,则时电压为:))))已知输入电压,))))第七章二阶电路t=0开关闭合,则可得到初始条件为时,开关闭合,)))),初始条件为V,,,则当时,为))))所示,已知VA 时开关闭合,则为))))))))第八章相量法.已知正弦电压的相量为 A2 A -2 A2 A -2 A .某一元件的电压、电流(关联方向)分别为V A已知,并以作为参考10 A10 A10 A 10 A。
一阶电路和二阶电路
iL Is
t
iL Ae L R
iL
=
I (1 S
e-
R L
t
)
A由初值: A Is
uL
=
L diL dt
=
IS Re- RLt
佛山科§学7技-术3学院 一阶电路的零状态响应
现代制造装备工程技术开发中心
佛山科§学技7术-学2院 一阶电路的零输入响应
现代制造装备工程技术开发中心
t=0时 , 打开开关K,求uv。
电压表量程:50V 现象 :电压表坏了
分析
iL (0+) = iL(0-) 1 A
iL e t /
L 4 4104 s
R RV 10000
uV RV i L 10000e 2500t t 0
uV (0+)= - 10000V 造成 V 损坏。
佛山科§学7技-术2学院 一阶电路的零输入响应
现代制造装备工程技术开发中心
四、小结 <一阶电路零输入响应的求解>
+
P
C Uc
P
iL
-
u(0 ) uc (0 ) U0
iL (0 ) iL (0 ) I0
分析:戴维南定理化简
佛山科§学技7术-学2院 一阶电路的零输入响应
3)作 0 等效电路
L 用一电流为 iL (0 )的电流源代替 C 用一电压为 uc (0 )的电压源代替
4) 求解0电路。求出其它 f (0 )
佛山科§学技7术-学1院动态电路的方程及其初始条件
现代制造装备工程技术开发中心
(1) 由0-电路求 uC(0-) 或 iL(0-) uC(0-)=8V
电路分析中的阶跃响应
时,(-t)=0,如图(d)所示。
图8-27 阶跃函数
当直流电压源或直流电流源通过一个开关将电压或电流施加 到某个电路时,可以表示为一个阶跃电压或一个阶跃电流作 用于该电路。引入阶跃电压源和阶跃电流源可以省去电路中 的开关,使电路的分析研究变得更加方便。
阶跃函数可以用来表示时间上分段恒定的电压或电流信号。 对于线性电路来说,这种表示方法的好处在于可以应用叠加 定理来计算电路的零状态响应,在此基础上,采用积分的方 法还可以求出电路在任意波形激励时的零状态响应。
§8-5 阶跃响应
在上一节的讨论中,我们看到直流一阶电路中的各种 开关,可以起到将直流电压源和电流源接入电路或脱离电 路的作用,这种作用可以描述为分段恒定信号对电路的激 励。
随着电路规模的增大和计算工作量增加,有必要引入 阶跃函数来描述这些物理现象,以便更好地建立电路的物 理模型和数学模型,也有利于用计算机分析和设计电路。
iL (t ) iL' (t) iL" (t) {10(1 e1000t )ε (t ) 10[1 e1000(t1ms) ]ε (t 1ms )} mA
分别画出 iL' (t ) 和 i"L (t )的波形, 如曲线1和2所示。然后它们相加得 到iL(t)波形曲线,如曲线3所示。
图83023424321sttttttttttu??????其电容电压uct的零状态响应可以表示为e1e1e1e1e12342443322114321c4321ttttsttttsttttsttttsttsttsttsttsttststurcttrcttrcttrcttrct????????????????????????????????????????????????????????其中图830rc串联电路在分段恒定信号激励下的零状态响应名称时间名称时间1电容器的放电过程2
一阶电路暂态分析
返节目录
电路分析基础
8.1 换路定律
3、暂态:动态元件L的磁场能量WL=0.5LI2和C的电场能
量WC=0.5CUC2,在电路发生换路时必定产生 变化,由于这种变化持续的时间非常短暂,通 常称为“暂态”。
4、零输入响应:电路发生换路前,动态元件中已储有
原始能量。换路时,外部输入激励为零,仅在 动态元件原始能量作用下引起的电路响应。
联,元件向电路吸取电能建立
电场。
iC(U0+S) 0.632US
uC iC
0 τ
t
返节目录
电路分析基础
RC零状态响应电路中的计算公式
S
+
t≥0
US
-
R
由RC零状态响应电路图可得
iC
+
过渡过程结束时电容的极间
C -uC 电压(即换路后的新稳态值)
uC () US
则电容电压的零状态响应为:
t
t
换路定律用公式可表示为:
iL (0) iL (0) uC (0) uC (0)
换路发生在t=0时刻,(0-)为换路前一瞬间,该时刻电 路还未换路;(0+)为换路后一瞬间,此时刻电路已经换 路。
返节目录
电路分析基础
暂态过程产生的原因
电阻电路
S
I
(t = 0)
+
I
_US
R
0
t
电阻元件是耗能元件,其电压、电流在任一瞬 间均遵循欧姆定律的即时对应关系。因此,电阻元 件上不存在暂态过程。
1. 根据换路前一瞬间的电路,应用电路
基本定律确定iL(0+)和uC(0+)。
2. 根据换路后的等效电路,应用电路基
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第6章 一阶电路
讲授 板书
1、理解一阶电路的全响应和阶跃响应概念和物理意义。
2、掌握一阶电路的全响和阶跃响应的计算方法
一阶电路的全响的计算方法
一阶电路的阶跃响的计算方法、求解初始值的方法
1. 组织教学 5分钟
3. 讲授新课 70分钟
2. 复习旧课 5分钟
基尔霍夫定律
4. 巩固新课 5分钟
5. 布置作业 5分钟
一、学时:2
二、班级:06电气工程(本)/06数控技术(本)
三、教学内容:
[讲授新课]:
§6.4 一阶电路的全响应
一阶电路的全响应是指换路后电路的初始状态不为零,同时又有外加激励源作
用时电路中产生的响应。
1.全响应
以图 6.19 所示的 RC 串联电路为例:
图 6.19 图 6.20
电路微分方程为:
方程的解为: uC(t)=uC'+ uC"
令微分方程的导数为零得稳态解:uC"=US
暂态解 , 其中τ= RC
因此
由初始值定常数A,设电容原本充有电压:uC(0-)= uC(0+)=U0
代入上述方程得:uC(0+)= A + US = U0
解得:A = U0 - US
所以电路的全响应为:
2. 全响应的两种分解方式
(1)上式的第一项是电路的稳态解,第二项是电路的暂态解,因此一阶电路的
全响应可以看成是稳态解加暂态解,即:全响应 = 强制分量 ( 稳态解 )+ 自由分
量 ( 暂态解 )
(2)把上式改写成:
显然第一项是电路的零状态解,第二项是电路的零输入解,因此一阶电路的全
响应也可以看成是零状态解加零输入解,即:全响应 = 零状态响应 + 零输入响应
此种分解方式便于叠加计算,如图 6.21 所示。
图 6.21
3. 三要素法分析一阶电路
一阶电路的数学模型是一阶微分方程 :
其解答为稳态分量加暂态分量,即解的一般形式为 :
t= 0+ 时有 :
则积分常数:
代入方程得:
注意直流激励时 :
以上式子表明分析一阶电路问题可以转为求解电路的初值 f(0+),稳态值
f
(¥)及时间常数τ的三个要素的问题。求解方法为:
f
(0+):用 t → ¥ 的稳态电路求解;
f
(¥): 用 0+ 等效电路求解;
时间常数τ:求出等效电阻,则电容电路有τ=RC ,电感电路有:τ= L/R。
例6-13 图示电路原本处于稳定状态,t=0时开关闭合,求t>0后的电容电压
u
C
并画出波形图。
例 6-13 图(a)
解:这是一个一阶 RC 电路全响应问题,应用三要素法,
电容电压的初始值为:
稳态值为:
时间常数为:
代入三要素公式:
所以:
图( b )
电容电压随时间变化的波形如图(b)所示。
例6-15 图示电路原本处于稳定状态,t=0时开关由1扳到2,求换路后的电容电压
uC(t
)。
例 6-15 图(a)
解:这是一个一阶 RC 电路全响应问题,应用三要素法,
三要素为:
由于含有受控源所以应用图(b)电路求等效电阻:
则时间常数为:
代入三要素公式得:
图( b )
例6-16 图示电路原本处于稳定状态,t=0 时开关闭合,求换路后的电流i(t) 。
例 6-16 图
解:开关闭合后电路分为两个一阶电路,应用三要素法,
电容电路的三要素为:
电感电路的三要素为:
代入三要素公式得:
因此:
§6.5 一阶电路的阶跃响应
1.单位阶跃函数
1)单位阶跃函数的定义
单位阶跃函数是一种奇异函数,如图6.22 所示。函数在 t=0 时发生了阶跃。
可定义为:
图 6.22
任一时刻 t0 起始的阶跃函数如图 6.23 所示,也称为延迟的单位阶跃函数,
可定义为:
图 6.23
2)单位阶跃函数的作用
(1)可以用来描述图 6.24 所示的开关动作,如图6.25所示,表示 t=0 时把
电路接到直流电源。
图 6.24
图 6.25
(2)可以用来起始一个任意函数,即:
图 6.26 为单位阶跃函数起始一个正弦函数
图 6.26
(3)可以用来延迟一个函数,如图 6.27 所示。
图 6.27
(4)可以用来表示复杂的信号,如图 6.28 所示函数可以写为:
图 6.28
2.一阶电路的阶跃响应
阶跃响应是指激励为单位阶跃函数时,电路中产生的零状态响应。以图6.29
所示RC 电路受直流阶跃激励为例加以说明。
图 6.29 图 6.30 图 6.31
根据阶跃函数的性质得: ,
所以阶跃响应为:
响应的波形如图 6.30 和图 6.31 所示。
注意: (初值为零) 和 (初值可以不为零)的
区别。
若上述激励在t = t0 时加入,如图6.32所示,则响应从t = t0 开始。即:
图 6.32
注意: 上式为延迟的阶跃响应,不要写为
例6-18 用阶跃函数表示图示函数 f(t)。
例 6 — 18 ( a ) ( b )
例 6 — 18 ( c )
解:(a)
(b)
(c)
例6-20 求图(a)所示电路中电流iC(t),已知电压源波形如图(b)所示。
例 6 — 20 ( a )
( b )
解:把电路等效为图(c)中的左图,
( c )
时间常数为:
等效电路的阶跃响应为:
图(b)所示电压源波形可以用阶跃函数表示为:
即:电源可以看成是阶跃激励和延迟的阶跃激励的叠加,因此等效电路可以用
图(c)中右边两分电路图表示。由齐次性和叠加性得实际响应为:
上式用分段函数可表示为:
响应的波形如图(d)所示。
图( d )
四、预习内容 向量法
五、作业
6.4 全响应 求解步骤: 6.5 阶跃响应 例 15.2
例 15.3
