5.2 转动定律
合集下载
05--2、转动定律、转动能量

T=T’ …(5)
v v v aτ = β ×r
β+ r T m2 T’
T
m1
N r
T’
m1g - T= m1a….(1) T’r=Jβ…(2) β
1 2 J = mr …(3) 2
a+
m1g
m2g
a = rβ…(4) β
Jβ β T=T’= r 代入(1)式 代入 式: Jβ β m1g = m1a r Jβ β m1g = m1rβ β r m1gr β = 所以: 所以 m1r2+J 由(2)式: 式
v F // v r
v F v ⊥ F
转动定律说明了J 3)转动定律说明了J是物体转动惯性大小的量 因为: 度。因为: M一 时 ↑Lβ ↓ J ↓Lβ ↑ 定 J 越大的物体, 即J越大的物体,保持原来转动状态的性质就 越大的物体 越强,转动惯性就越大;反之, 越小 越小, 越强,转动惯性就越大;反之,J越小,越容 易改变状态,保持原有状态的能力越弱。 易改变状态,保持原有状态的能力越弱。或 者说转动惯性越小。 者说转动惯性越小。
基本步骤 (1)隔离法选择研究对象; )隔离法选择研究对象; (2)受力分析和运动情况分析; )受力分析和运动情况分析; (3)对质点用牛顿定理,对刚体用转动定理; )对质点用牛顿定理,对刚体用转动定理; (4)建立角量与线量的关系,求解方程; )建立角量与线量的关系,求解方程; (5)结果分析及讨论。 )结果分析及讨论。
r
r
T ' m3g T ' 1 v 2 a1 m
1
v mg 1
m2
m L 2g.T ' m 2 2 m L 3g.N THale Waihona Puke .T2 m 1 3v a2
转动定律精品文档

工程应用:转动定律在机械工程、航空航天、交通运输等领域有着广泛的应用,为各种旋转机 械和运动机构的设计、分析和优化提供了重要的理论支持。
科学研究方法:转动定律的发现和研究过程中所采用的科学方法,如实验观测、数学建模和逻 辑推理等,为科学研究提供了重要的方法和思路。
科学发展进程:转动定律的发展历程展示了科学知识的不断积累和进步,推动了人类对自然界 的认识和理解。
土木工程:在桥梁和建筑设计 中,转动定律用于分析结构的
稳定性和安全性。
自行车轮转动:通过脚踏产生动 力,使自行车前进
风扇工作原理:通过电机转动, 使扇叶产生风流,实现降温效果
汽车方向盘:驾驶员转动方向盘, 使车辆转向或掉头
洗衣机工作原理:电机转动,带 动内桶旋转,实现洗涤功能
物理学中的基 本定律之一, 用于描述旋转 运动的规律。
适度。
航空航天:在航空航天 领域,转动定律的应用 将有助于实现更加稳定 和精确的飞行姿态控制。
体育运动:在体育装备和 训练中,转动定律的应用 将有助于提高运动员的转 动速度和灵活性,从而提
高是物理学中的基本定律之一, 深入理解其原理和应用有助于推
动物理学领域的进步。
汇报人:XX
转动定律:描述刚体绕固 定点转动的运动规律
刚体:转动过程中形状和 大小保持不变的物体
固定点:刚体上的一点, 绕其转动
运动规律:转动速度和转 动角加速度之间的关系
转动定律的定义:描述 转动物体运动状态的物
理定律
转动定律的表述方式: 力矩等于转动惯量乘以
角加速度
转动定律的物理意义: 揭示了转动物体运动
探索更高温度下的转动定律特性
研究转动定律与量子力学之间的 联系
探索转动定律在新型材料中的应 用
科学研究方法:转动定律的发现和研究过程中所采用的科学方法,如实验观测、数学建模和逻 辑推理等,为科学研究提供了重要的方法和思路。
科学发展进程:转动定律的发展历程展示了科学知识的不断积累和进步,推动了人类对自然界 的认识和理解。
土木工程:在桥梁和建筑设计 中,转动定律用于分析结构的
稳定性和安全性。
自行车轮转动:通过脚踏产生动 力,使自行车前进
风扇工作原理:通过电机转动, 使扇叶产生风流,实现降温效果
汽车方向盘:驾驶员转动方向盘, 使车辆转向或掉头
洗衣机工作原理:电机转动,带 动内桶旋转,实现洗涤功能
物理学中的基 本定律之一, 用于描述旋转 运动的规律。
适度。
航空航天:在航空航天 领域,转动定律的应用 将有助于实现更加稳定 和精确的飞行姿态控制。
体育运动:在体育装备和 训练中,转动定律的应用 将有助于提高运动员的转 动速度和灵活性,从而提
高是物理学中的基本定律之一, 深入理解其原理和应用有助于推
动物理学领域的进步。
汇报人:XX
转动定律:描述刚体绕固 定点转动的运动规律
刚体:转动过程中形状和 大小保持不变的物体
固定点:刚体上的一点, 绕其转动
运动规律:转动速度和转 动角加速度之间的关系
转动定律的定义:描述 转动物体运动状态的物
理定律
转动定律的表述方式: 力矩等于转动惯量乘以
角加速度
转动定律的物理意义: 揭示了转动物体运动
探索更高温度下的转动定律特性
研究转动定律与量子力学之间的 联系
探索转动定律在新型材料中的应 用
大学物理 第5章刚体定轴转动

赵 承 均
转动平面 某质点所在的圆周平面,称为转动平面。
参考线
转心 矢径
转动平面内任一过转轴的直线,如选 x 轴。
某质点所在的轨迹圆的圆心,称为转心。 某质点对其转心的位矢,称为该质点的矢径。
第一篇
力学
重 大 数 理 学 院
显然:转动刚体内所有点有相同的角量,故用角量描述刚体 的转动更方便,只需确定转动平面内任一点的角量即可。 1.角坐标— 描写刚体转动位臵的物理量。 角坐标 转动平面内刚体上任一点 P 到转轴 O 点的连线与 参考线间的夹角 。
赵 承 均
第二类问题:已知J和力矩M:求出运动情况和 b及 F 。
第三类问题:已知运动情况和力矩M,求刚体转动惯量 J 。
第一篇
力学
重 大 数 理 学 院
第一类问题:已知运动情况和 J ,确定运动学和动力学的联 系 例 :长为 l,质量为 m 的细杆,初始时的角速 度为 ωo ,由于细杆与 桌面的摩擦,经过时间 t 后杆静止,求摩擦力 矩 Mf 。
Fi cos i Fi cos i mi ain mi ri 2 法向:
e i
第一篇
力学
重 大 数 理 学 院
由于法向力的作用线穿过转轴,其力矩为零。可在切向 方程两边乘以 ri ,得到:
Fi e ri sin i Fi i r i sin i mi ri 2
4.角加速度— 描写角速度变化快慢和方向的物理量。 ⑴ 平均角加速度 t
即:刚体的角速度变化与发生变化所用的时间之比。
赵 承 均
⑵ 角加速度 ①用平均角加速度代替变化的角加速度; ②令 t 0 取极限;
d d lim 2 t 0 t dt dt
§5.2-力矩---刚体绕定轴转动微分方程
F f m a i i
的切向加速度,质元沿
法向运动的科里奥里加
i
i
速度(定轴转动刚体没 有这种运动)
圆周轨迹切线投影
Fi fi miai
同乘以 ri
Fi ri fi ri miai ri miri2β ai=ri
对所有质元求和
Fi ri fi ri ( miri2 )β
根据牛顿第二定律,第 i 个质元
外内
力 Fi
力 fi
miai
圆周轨迹切线投影
同乘以 ri
Fi fi miai Fi ri fi ri miai ri miri2β
ai=ri
对所有质元求和
Fi ri fi ri ( miri2 )β
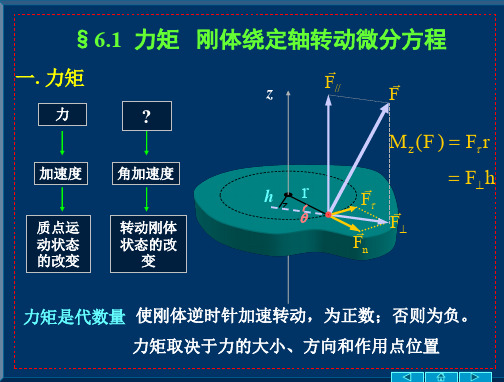
§6.1 力矩
一. 力矩
力
?
加速度 角加速度
质点运 动状态 的改变
转动刚体 状态的改
变
刚体绕定轴转动微分方程
z
F//
F
hr
M z (F ) F r
F F Fn
Fh
力矩是代数量 使刚体逆时针加速转动,为正数;否则为负。 力矩取决于力的大小、方向和作用点位置
二. 刚体定轴转动微分方程
它在水平位置
求 它由此下摆 角时的 解 dm 质元 dm m dx
l
dm 重力矩 dM gdm x cos
O
ml
x
M
dM
1 2
mgl cos
gdm
重力对整个棒的合力矩等于重力全部 集中于质心所产生的力矩
转动定律 M
J J 1 ml2
3
的切向加速度,质元沿
法向运动的科里奥里加
i
i
速度(定轴转动刚体没 有这种运动)
圆周轨迹切线投影
Fi fi miai
同乘以 ri
Fi ri fi ri miai ri miri2β ai=ri
对所有质元求和
Fi ri fi ri ( miri2 )β
根据牛顿第二定律,第 i 个质元
外内
力 Fi
力 fi
miai
圆周轨迹切线投影
同乘以 ri
Fi fi miai Fi ri fi ri miai ri miri2β
ai=ri
对所有质元求和
Fi ri fi ri ( miri2 )β
§6.1 力矩
一. 力矩
力
?
加速度 角加速度
质点运 动状态 的改变
转动刚体 状态的改
变
刚体绕定轴转动微分方程
z
F//
F
hr
M z (F ) F r
F F Fn
Fh
力矩是代数量 使刚体逆时针加速转动,为正数;否则为负。 力矩取决于力的大小、方向和作用点位置
二. 刚体定轴转动微分方程
它在水平位置
求 它由此下摆 角时的 解 dm 质元 dm m dx
l
dm 重力矩 dM gdm x cos
O
ml
x
M
dM
1 2
mgl cos
gdm
重力对整个棒的合力矩等于重力全部 集中于质心所产生的力矩
转动定律 M
J J 1 ml2
3
5.2 刚体定轴转动定律
因为各质元角动量方向相同, 因为各质元角动量方向相同, 所以合矢量的大小就是分矢量 大小的直接相加 因为 L = L = rmυ S
mi
α r P
r
i
i i
υi = riω
L = ω(∑ mi ri2 )
i
定义刚体对定轴 定义刚体对定轴 J = 的转动惯量
3
∑m r
i
2
i i
r r L = Jω
对于转轴z,
r ri α
A
r F τ
r r r M z = ri × F⊥
不产生对z轴的力矩
α
Fn
r r F ⊥
M z = ri F⊥ sin α = F⊥ h
F ——平行于z轴 平行于 //
在转动平面内 F ——在转动平面内 产生对z轴的力矩 ⊥
r rz
O
r r
α
r F ⊥
y
x
力对任意点的力矩, 力对任意点的力矩,在通过该点的任一轴上的投影 等于该力对该轴的力矩
2 第5章 刚体的定轴转动
质点对定点 的动量矩 角动量) 质点对定点o的动量矩 角动量 定点 的动量矩(角动量
r r r r r L = r × P = r × mv = Lx x + Ly y + Lz z
2. 任一质量元的定轴角动量大小为
对z轴的 轴的 动量矩
r LO
Liz = ri miυi
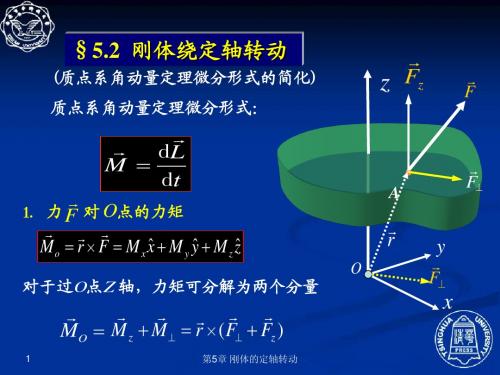
§5.2 刚体绕定轴转动
(质点系角动量定理微分形式的简化) 质点系角动量定理微分形式的简化) 质点系角动量定理微分形式: 质点系角动量定理微分形式:
r z Fz
r F
r r dL M = dt
r 1. 力 F 对 O点的力矩
mi
α r P
r
i
i i
υi = riω
L = ω(∑ mi ri2 )
i
定义刚体对定轴 定义刚体对定轴 J = 的转动惯量
3
∑m r
i
2
i i
r r L = Jω
对于转轴z,
r ri α
A
r F τ
r r r M z = ri × F⊥
不产生对z轴的力矩
α
Fn
r r F ⊥
M z = ri F⊥ sin α = F⊥ h
F ——平行于z轴 平行于 //
在转动平面内 F ——在转动平面内 产生对z轴的力矩 ⊥
r rz
O
r r
α
r F ⊥
y
x
力对任意点的力矩, 力对任意点的力矩,在通过该点的任一轴上的投影 等于该力对该轴的力矩
2 第5章 刚体的定轴转动
质点对定点 的动量矩 角动量) 质点对定点o的动量矩 角动量 定点 的动量矩(角动量
r r r r r L = r × P = r × mv = Lx x + Ly y + Lz z
2. 任一质量元的定轴角动量大小为
对z轴的 轴的 动量矩
r LO
Liz = ri miυi
§5.2 刚体绕定轴转动
(质点系角动量定理微分形式的简化) 质点系角动量定理微分形式的简化) 质点系角动量定理微分形式: 质点系角动量定理微分形式:
r z Fz
r F
r r dL M = dt
r 1. 力 F 对 O点的力矩
5-刚体的定轴转动

L1 L2
刚体定轴转动的角动量 L=?
z
v
ri mi
O
刚体 定轴
L Li mirivi
m iri(ri) ( miri2)
J M=0的原因,可能
1)F=0(不受外力) 2)外力作用于转轴上 3)外力作用线通过转轴
4)外力作用线与转轴平行
刚体定轴转动的角动量守恒
L1 L2
J11J22
位置,求它由此下摆角时的角速度。
解:如图建立坐标
x
杆受到的重力矩为:
O
M = gxd g m xdm
X
dm
据质心x定 d= m 义 mCx MmgxC
xc
1l 2
cos
M1mgclos
2
dmg
MJJdJ d d J d M dJd
dt d dt d
0 1 2mc go lds 0 Jd
mglsin
端点 o 且与桌面垂直的固定光滑轴转动,另有 一水平运动的质量 m2为的小滑块,从侧面垂直 与杆的另一端 A 相碰撞,设碰撞时间极短,已知 小滑块在碰撞前后的速度分别为 v1 和 v2 ,方 向如图所示,求碰撞后从细杆开始转动到停止 转动过程所需时间,(已知杆绕点 o 的转动惯 量 J= ml2/ 3 )
dLR J2J0m0d2 其中 Jo 12moR2
J J1J2 1 3m LL 21 2m oR 2m o(LR )2
2.对薄平板刚体的正交轴定理
z
Jz miri2
yi
xi
ri
y
m i(x2y2) m ix 2 m iy 2
x
Δmi
Jz JxJy
z
应用
例:已知圆盘
大学物理第5章刚体的定轴转动
d ctdt
对上式两边积分得
d c td t
0 0
t
1 2 ct 2
2 2 600π π 3 rad s 由给定条件, c 2 t 300 2 75
d π 2 由角速度的定义,则任意 t 时刻的角速度可写为: d t 150
得到: 转子转数:
A M d E K
a b
动能定理
动量定理
A F ds E K
动能定理 角动量定理 角动量 守恒
t 0Fdt P
t
动量守恒
F 0, P 0
t 0 M z dt Lz
t
M 0, L 0
§5.1 刚体、刚体运动
一、一般运动 二、刚体的定轴转动 三、解决刚体动力学问题的一般方法
基本方法: 加
质点系运动定理 刚体特性 平动:动量定理
刚体定轴转动的 动能定理 角动量定理
F mac
可以解决刚体的一般运动(平动加转动)
一、一般运动
1. 刚体 特殊的质点系, 形状和体积不变化 —— 理想化模型 在力作用下,组成物体的所有质点间的距离始终保持不变 2. 自由度 确定物体的位置所需要的独立坐标数 —— 物体的自由度数 z
刚体平面运动可看做刚体的平动与定轴转动的合成。 例如:车轮的滚动可以看成车轮随轮 轴的平动与绕轮轴的转动的组合。 描述刚体平面运动的自由度:3个
定点转动 刚体运动时,刚体上的一点固定不动,刚体绕过定点的一 瞬时转轴的转动,称作定点转动。
描述定点转动的自由度:3个
刚体的一般运动 质心的平动
+
绕质心的转动
z
描述刚体绕定轴转动的角量: 角坐标
大学物理 刚体的定轴转动
⑶ t =6 ·0 s 时转过的角度为
6s
0
6s
d t 0
0(1et)dt
0 [te t]6 0 s 9 [6 ( 2 0 0) 5 (0 2 )]369rad
则 t =6 ·0 s
时电动机转过的圈数
N 587圈 2
5.2 5.4 刚体的转动定律及应用
5.2.1力对转轴的力矩
转轴
§5.1 刚体的运动的描述 §5.2 刚体定轴转动 §5.3 转动惯量的计算 §5.4 转动定律应用 §5.5 角动量守恒 §5.6 定轴转动中的功和能
5.1 刚体的运动的描述
•刚体(rigid body)
任何情况下形状和体积都不改变的物体(理想化模型)。 刚体是特殊的质点系。 刚体可以看作是由许多质点组成,每一个质点叫做 刚体的一个质元,刚体这个质点系的特点是,在外 力作用下各质元之间的相对位置保持不变。
2、刚体定轴转动的转动定律
M d(J )dL J
dt dt
刚体绕定轴转动时,它的角加速度与作用于刚体上的 合外力矩成正比,与刚体对转轴的转动惯量成反比。
刚体定轴转动的转动定律
M=J 与 F ma地位相当 m反映质点的平动惯性,J 反映刚体的转动惯性
力矩是使刚体转动状态发生改变而产生角加速度的原因。力
ri
即 F itfitΔ m iri
则刚体转动定律为
变形有 F ir tifir tiΔm iri2
M J
对所有质元求和:
F ir ti fir ti (m ir i2 ) 上式表明:
这里 FitriM i M外
刚体绕定轴转动时,刚
fitri 0 定义 JΔmiri2 叫转动惯量
体的角加速度与它所 受的合外力矩成正比.
大学物理 第五章.
时,
刚体定轴转动的 角动量守恒定律
35
§5.4 刚体的角动量定理及守恒定律
例5.6:如图,质量为M,半径为R的转台,可绕通过中心竖直轴
转动,阻力忽略不计,质量为m的人站在台的边缘,人和台原来都 静止,如果人沿转台的边缘绕行了一周,问相对地面转台转过了多 少角度?
解:把人和转台看做一个系统
系统的角动量守恒 规定:逆时针转动为正方向,以 地面为参考系。 设人的角速度为ω,转台的角速度为Ω。
或
A = ∫ Mdθ = Mθ
42
例5.9:一质量为m,长为 l的匀质杆,两端用绳悬挂杆处于水平 状态,现突然将杆右端的悬线剪断,求(1)此瞬间另一根绳受到 的张力 ;(2)剪断绳子之后任一时刻杆的角速度 ω与转过角度 θ之 间的关系。 解: (1)首先考虑杆绕O点的的转动 根据转动定律: T O
匀变速运动
6
§5.1 刚体及其定轴转动描述
例5.1:一汽车发动机的转速在5s内由200r(转)/min均匀地增加 到3000r(转)/min。(1)求在这段时间内的初角速度、末角速 度和角加速度;(2)求这段时间内转过的角度;(3)发动机轴 上装有一半径为R=0.15m的飞轮,求轮边缘上一点在这第5s末的 切向加速度、法向加速度和总加速度。
24
§5.3 刚体转动的功和能
回顾: 质点 质量 牛顿运动定律
M = Jβ
刚体 转动惯量 转动定律
力做功
力矩做功
25
§5.3 刚体转动的功和能
一、力矩的功
轴
dθ dr α r
α
F 在转动平面内
ω
元功: dA = F • dr = F dr cos α = F ( rdθ ) cos α F ( r cos α )dθ = Mdθ
52--定轴转动定律
dt
Mdt d(J) 刚体定轴转动角动量定理微分形式
t
J
Mdt
t0
J00 d(J) J J00
刚体定轴转动角动量定理积分形式
4
L (miviri ) (miri2 ) ( miri 2 ) J
J miri 2 称为刚体对转轴的转动惯量
3
L J
于是有 M d(J) J d J
dt
dt
刚体定轴转动定理: M J
F ma
对 M d (J) 进行处理得到:
大小:M Fr sin
M
F
Or
d
Pr
z
F∥
or
F θ F⊥
转轴
转动平面 2
二、刚体定轴转动定理
在以角速度ω作定轴转动的刚体
内取一质点 mi ,则其对OZ轴
的角动量为:
o ri
v
P
Li miviri
对于整个刚体,各质点对定轴的角动量都具有相同的 方向。则定轴转动刚体的角动量就是对组成刚体的所 有质点的角动量求和。
刚体转动定律
1
一、作用于定轴刚体的外力矩
1 .力对固定点的矩
M
rF
2 .力对固定轴的矩
(1)力直于转轴
这种情况相当于质点绕固 定点O转动的情形。
(2)力与转轴不垂直 可以把力分解为平行于转轴
的分量和垂直于转轴的分量。
平行转轴的力不产生转动效果,
该力对转轴的 力矩 为零。 M r F
Mdt d(J) 刚体定轴转动角动量定理微分形式
t
J
Mdt
t0
J00 d(J) J J00
刚体定轴转动角动量定理积分形式
4
L (miviri ) (miri2 ) ( miri 2 ) J
J miri 2 称为刚体对转轴的转动惯量
3
L J
于是有 M d(J) J d J
dt
dt
刚体定轴转动定理: M J
F ma
对 M d (J) 进行处理得到:
大小:M Fr sin
M
F
Or
d
Pr
z
F∥
or
F θ F⊥
转轴
转动平面 2
二、刚体定轴转动定理
在以角速度ω作定轴转动的刚体
内取一质点 mi ,则其对OZ轴
的角动量为:
o ri
v
P
Li miviri
对于整个刚体,各质点对定轴的角动量都具有相同的 方向。则定轴转动刚体的角动量就是对组成刚体的所 有质点的角动量求和。
刚体转动定律
1
一、作用于定轴刚体的外力矩
1 .力对固定点的矩
M
rF
2 .力对固定轴的矩
(1)力直于转轴
这种情况相当于质点绕固 定点O转动的情形。
(2)力与转轴不垂直 可以把力分解为平行于转轴
的分量和垂直于转轴的分量。
平行转轴的力不产生转动效果,
该力对转轴的 力矩 为零。 M r F
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x
r
y
dm
• 薄圆盘绕直径转动惯量? 1 2 I mR Ix I y ? z 2
y
m
R
x
垂直轴定理
Iz Ix I y
z
Iz 1 1 1 2 I x I y mR mR 2 2 2 2 4
圆环转轴沿直径
圆环转轴通过中心 与环面垂直
1 2 J mr How ? 2
dm
R
m
例3 薄圆盘 (质量 m,半径 R ),求 J
解:把盘分成大量同心圆环。
R
dm
dr
r
dS
任一圆环(半径 r,宽 dr,质量 dm) 转动惯量 dJ = r2dm = r2 (m/ R2) 2rdr 整个盘的转动惯量 J = dJ = 0R r2dm = mR2 / 2
Hale Waihona Puke 1 2 J mR (圆柱体 ?) 2
= σR4/(4)(2θ/2)│02π = mR2 /4
2 2 J mr 3
六 转动定律的应用
• 选择刚体(如杆或圆盘),受力分析 • 求合外力矩 M (动力矩取正,阻力矩取负) • 求 J • 代入 M J • 利用
v r at r
角加速度α 例 4 求细杆在图中各个位置时的 角速度ω
l 解:在水平位置1时力矩 M mg 2 1 2 杆对端点的转动惯量 J ml
圆盘
• F1 为 F 平行于转轴 oz 的分力。 • F2 为 F 垂直于转轴 oz 的分力。 MO在OZ 轴上的投影
M OZ M O cos r F2 rF2 sin F2 d
o
MZ
5)M 合内力矩 ≡ 0
垂直 oz 的平面
二 定轴转动定律
合外力 合内力
对组元 i,牛顿定律 Fi + fi =Δmi a i 切向 Fit+ fit=Δmi ait=Δmi riα
J mr
2
薄圆盘转轴通过中心 与盘面垂直
圆筒转轴沿几何轴
1 2 J mr 2
1 2 2 J m(r1 r2 ) 2
圆柱体转轴沿几何轴
圆柱体转轴通过中 心与几何轴垂直
1 2 J mr 2
1 2 1 2 J mr ml 4 12
球体转轴沿直径
球壳转轴沿直径
2 2 J mr 5
讨论: 一般 T1≠T2
若滑轮质量 m = 0,则 T1= T2 *** 注意此题的解题方法!!! END
1 2 I x I y mR 4
2Rcos θ
根据定义计算 r = Rsinθ dr = Rcosθdθ
dr
dm d θ dS r θ O R
dS = 2Rcosθdr = 2R2cos2θdθ dm = σdS = σ2R2cos2θdθ J = ∫r2dm = ∫02πσ 2R4sin2θcos2θdθ = (σR4/2)∫02πsin22θdθ σ = m/(πR2)
2
1 2 1 J O mL MR 2 M ( L R) 2 3 2
在平行轴中,对 质心的转动惯量 JC最小
五 垂直轴定理 (只适用于均匀薄板)
证明
2
Jz Jx J y
2 2
J z r dm ( x y )dxdy x 2dxdy y 2dxdy J x J y
(1) 与质量 m、质量分布及转轴位置有关。
o
o ´
o 1 ml 2 J = 12 m , J o ´
m3
2 1 J = ml 3
(2) 意义:反映刚体转动惯性的大小. J 大 转动惯性 大 (3) J 的计算 • 质点组:J =∑Δmi ri2 =∑Ji
i 3 i 1
r1 m1
r3
J mi ri 2 m1r12 m2r22 m3r32
r2
m2
2 J dJ r • 连续体: dm 方法 ?
• 几个刚体组合 J
Ji
r dm
例1 求一个质量均匀分布的细杆(m,l) 对于通 过杆的一端而与杆垂直的轴的转动惯量。
方法:r 处取dm,
2 J r dm
解:在x 处取线元 dx,质量 dm = mdx x / l,距转 轴的垂直距离 x 0 m m1 3 l 1 2 2 2 J x dm x dx x 0 ml l l l l 3 3 • 通过杆的中点而与杆垂直的轴的转动惯量。
四
平行轴定理(任意刚体,普适) JD = JC + m d2
质心 C
D
• 由均匀细杆和均匀圆盘组 成的刚体对 O 轴的 J
过 过 刚 C 体 JD O J1 J 2 点 平 质 轴 1 行2 量 J的 mL 1 轴 3 的 J J 平 行 轴 距 离
m
C
d
J 2 J 2c M ( L R)
3 转动定律 M = Jβ,角加速度
l mg M 3g 2 1 2 2l J ml 3
1
0
3
2
l 转动到2位置时,力矩 M mg cos 2 l
M J m g cos 3g cos 2 1 2 2l ml 3
在竖直位置3时, M
0
0
求ω :
3g cos 2l
例5 一轻绳跨过定滑轮悬有质量分别为 m, r m1 和 m2 的物体, 滑轮的质量为m ,半 径为 r, 绳与滑轮之间无相对滑动,无 摩擦。求物体的加速度和绳的张力。 解: m1 m2 m
T1
m1
T1-m1g = m1 a m2g-T2 = m2 a T2r -T1r = Jα at = a = rα
d d d d dt d dt d
0
3 g cos 1 2 3g d d d sin 0 0 2 2l 2l
θ 角的角速度 转到竖直位置3(θ=
3g sin l
900)时角速度
3g l
*** 注意此题的解题方法!!!
m1g N f
a
T2
m2
a
β T2
m2g
J=
mr2/2
T1
mg
∴
(m 2 m1 )g a m1 m 2 m/ 2
2m 2 m/ 2 T1 m1 (g a) m1g m1 m 2 m/ 2
2m1 m/ 2 T2 m 2 (g a) m 2g m1 m 2 m/ 2
第 2 节 刚体的定轴转动定律
一 力 矩 M
1)力F 对O点的力矩 M O r F
3) 连续力对O点的力矩 4)力F 对轴的力矩 积分
i
M
O
F
2)多个力 对O点的力矩 M O M i
r
m
R
M dM r dF MO r F r (F1 F2 ) r F1 r F2
两边乘 ri ,求和
fi F i
C
ri
Δmi
∑Fitri + ∑fitri = ∑Δmi ri2α
i i i
合外力矩 令
i
0
Ft
r F
内力矩之和 ≡ 0
J =∑ ri2 Δmi
— 刚体对转轴的转动惯量
M = Jα — 转动定律
合外力矩等于转动惯量 J 乘以角加速度。
三
转动惯量 J =∑ ri2 Δmi
取杆的中点为坐标原点0,把积分上下限换一下 l m m 1 1 2 2 3 2 J x dm x dx x l ml2 l l l l 3 12 2
dx
X
例2 质量为m的细圆环,求对对称轴的 J
解:把环分成多个质量为dm的小段, dJ = R2dm 整个环 J = dJ = R2dm = mR2
