最新方差分析习题与答案
方差分析习题

【下载本文档,可以自由复制内容或自由编辑修改内容,更多精彩文章,期待你的好评和关注,我将一如既往为您服务】1、某研究者观测大白鼠的肝重与体重之比,了解正氟醚对该指标的作用,同时考虑生理盐水和用戊巴比妥作为诱导药对正氟醚毒性作用有无影响,对不同性别大白鼠的作用有何不同?数据如下:2、在1990 年秋对“亚运会期间收看电视的时间”调查结果如下表所示。
问:收看电视的时间比平日减少了(第一组)、与平日无增减(第二组)、比平日增加了(第三组)的三组居民在“对亚运会的总态度得分”上有没有显著的差异?3、研究5种类型的军装在两种环境、两种活动状态下的散热效果,将100名受试者随机等分20组,观察指标为受试者的主观热感觉,结果如下:4、测定4种密度下“金皇后”玉米的千粒重(g )各4次,得结果如下表。
试对4种密度下的千粒重作相互比较,并作出差异显著性结论。
5、施用农药治虫后,抽查3块稻田排出的水,各取3个水样,每水样分析使用农药后的残留量2次,得结果如下:稻田 1 23 水样 1 2 3 1 2 3 1 2 3 残留量1.3 1.1 1.3 1.3 1.2 1.4 1.82.1 2.2 1.11.21.51.41.01.22.02.01.9试测验:不同稻田不同水样的农药残留量有无差别?6、欲了解成年人体重正常者与超重者的血清胆固醇是否不同。
而胆固醇含量与年龄有关,资料见下表。
7、为研究三种饲料对猪的催肥效果,用每种饲料喂8头猪一段时间,测得每头猪的初始重量和增重,试分析三种饲料对猪的催肥效果是否相同。
数据如下:8、为了寻找一种较好的哺乳仔猪食欲增进剂,以增进食欲,提高断奶重,对哺乳仔猪做了以下试验:试验设对照、配方1、配方2、配方3共四个处理,重复12 次,选择初始条件尽量相近的长白种母猪的哺乳仔猪48头,完全随机分为4组进行试验,结果见下表,试作分析。
9、为探索丹参对肢体缺血再灌注损伤的影响,将30只纯种新西兰实验用大白兔,按窝别相同、体重相近划分为10个区组。
方差分析习题与答案

统计教圆好分解训练题与问案一、单项采用题之阳早格格创做1.正在圆好分解中,()反映的是样本数据与其组仄衡值的好别A 总离好B 组间缺点C 抽样缺点D 组内缺点2.是()A 组内仄圆战B 组间仄圆战C 总离好仄圆战D 果素B的离好仄圆战3.是()A 组内仄圆战B 组间仄圆战C 总离好仄圆战D 总圆好4.单果素圆好分解中,估计F统计量,其分子与分母的自由度各为()A r,nB r-n,n-rC r-1.n-rD n-r,r-1两、多项采用题1.应用圆好分解的前提条件是()A 各个总体报从正态分散B 各个总体均值相等C 各个总体具备相共的圆好D 各个总体均值不等E 各个总体相互独力2.若考验统计量F= 近似等于1,证明()A 组间圆好中不包罗系统果素的做用B 组内圆好中不包罗系统果素的做用C 组间圆好中包罗系统果素的做用D 圆好分解中应中断本假设E圆好分解中应交受本假设3.对付于单果素圆好分解的组内缺点,底下哪种道法是对付的?()A 其自由度为r-1B 反映的是随机果素的做用C 反映的是随机果素战系统果素的做用D 组内缺点一定小于组间缺点E 其自由度为n-r4.为钻研溶液温度对付液体动物的做用,将火温统造正在三个火仄上,则称那种圆好分解是()A 单果素圆好分解B 单果素圆好分解C 三果素圆好分解D 单果素三火仄圆好分解E 单果素三火仄圆好分解三、挖空题1.圆好分解的脚法是考验果变量y与自变量x是可,而真止那个脚法的脚法是通过的比较.2.总变好仄圆战、组间变好仄圆战、组内变好仄圆战三者之间的闭系是 .3.圆好分解中的果变量是,自变量不妨是,也不妨是 .4.圆好分解是通过对付组间均值变同的分解钻研推断多个是可相等的一种统计要领.5.正在考查安排中,把要思量的那些不妨统造的条件称为,把果素变更的多个等第状态称为 .6.正在单果子圆好分解中,估计F统计量的分子是圆好,分母是圆好.7.正在单果子圆好分解中,分子的自由度是,分母的自由度是 .四、估计题1.有三台呆板死产规格相共的铝合金薄板,为考验三台呆板死产薄板的薄度是可相共,随机从每台呆板死产的薄板中各抽与了5个样品,测得截止如下:问:三台呆板死产薄板的薄度是可有隐著好别?2.养鸡场要考验四种饲料配圆对付小鸡删沉是可相共,用每一种饲料分别喂养了6只共一品种共时孵出的小鸡,共饲养了8周,每只鸡删沉数据如下:(克)配圆:370,420,450,490,500,450配圆:490,380,400,390,500,410配圆:330,340,400,380,470,360配圆:410,480,400,420,380,410问:四种分歧配圆的饲料对付小鸡删沉是可相共?3.今有某种型号的电池三批,它们分别为一厂、两厂、三厂三个工厂所死产的.为评比其本量,各随机抽与5只电池为样品,经考查测得其寿命(小时)如下:一厂:40,48,38,42,45两厂:26,34,30,28,32三厂:39,40,43,50,50试正在隐著性火仄下考验电池的仄衡寿命有无隐著的好别.4.一个年级有三个小班,他们举止了一次数教考查.现从各个班级随机抽与了一些教死,记录其结果如下:1班:73,89,82,43,80,73,66,60,45,93,36,772班:88,78,48,91,51,85,74,56,77,31,78,62,76,96,803班:68,79,56,91,71,71,87,41,59,68,53,79,15若各班教死结果遵循正态分散,且圆好相等,试正在隐著性火仄下考验各班级的仄衡分数有无隐著好别?一、单项采用题1. D 2. A 3. C 4. C两、多项采用题1. ACE 2. ABD 3. BE 4.AD三、挖空题1.独力、圆好2.总变好仄圆战=组间变好仄圆战+组内变好仄圆战. 3.数量型变量,本量型变量,数量型变量.4.正态总体均值5.果子,火仄或者处理.6.组间、组内7.m-1, n-m.四、估计题1.解:根据估计截止列出圆好分解表果为(2,12),故中断,认为各台呆板死产的薄板薄度有隐著好别.2.解:根据估计截止列出圆好分解表果为(3,20),故交受,即四种配圆的饲料对付小鸡的删沉不隐著的好别. 3.解:各总值均值间有隐著好别. 4.解:好别不隐著.。
方差分析习题

方差分析习题1.两样本均数的比较,可用()。
A.方差分析B.t检验C.两者均可D.方差齐性检验ν区组等于2.随机区组设计的方差分析中,()。
A.ν总-ν误差B.ν总-ν处理C.ν总-ν处理+ν误差D.ν总-ν处理-ν误差4.方差分析中变量变换的目的是()。
A.方差齐性化B.曲线直线化C.变量正态化D.以上都对5.下面说法中不正确的是()。
A.方差分析可以用于两个样本均数的比较B.完全随机设计更适合实验对象变异不太大的资料C.在随机区组设计中,每一个区组内的例数都等于处理数D.在随机区组设计中,区组内及区组间的差异都是越小越好6.随机区组设计要求()。
A.区组内个体差异小,区组间差异大B.区组内没有个体差异,区组间差异大C.区组内个体差异大,区组间差异小D.区组内没有个体差异,区组间差异小7.完全随机设计方差分析的检验假设是()。
A.各对比组样本均数相等B.各对比组总体均数相等C.各对比组样本均数不相等D.各对比组总体均数不相等8.完全随机设计、随机区组设计的SS和及自由度各分解为几部分()。
A.2,2 B.2,3 C.2,4 D.3,39.配对t检验可用哪种设计类型的方差分析来替代()。
A.完全随机设计B.随机区组设计C.两种设计都可以D.AB都不行10、经方差分析,若P≤α,则结论为:()A、各样本均数全相等B、各样本均数不全相等C、至少有两个样本均数不等D、至少有两个总体均数不等E、各总体均数不等11、F检验不能用于()A.两样本方差的比较 B.回归系数的假设检验C. 两个样本频率的检验D、两个样本均数的比较E、多个样本均数的比较12、完全随机设计的方差分析中,组内变异反映的是()A、随机误差B、抽样误差C、测量误差D、个体差异E、系统误差13、某职业病防治院测定了11名石棉沉着病患者、9名石棉沉着病可疑患者和11名非患者的用力肺活量,求得其均数为1.79L,2.31L和3.08L,能否据此认定石棉沉着病患者、石棉沉着病可疑患者和非患者的用力肺活量不同?()A、能,因3个样本均数不同B、需作3个均数两两的t检验才能确定C、需用3个均数两两的SNK-q检验D、需作成组设计的3个均数比较的ANOV A14、完全随机设计方差分析中()A、组间SS不会小于组内SSB、组内SS不会小于组间SSC、组间MS不会小于组内MSD、F不可能是负数E、F可能是负数15、方差分析中,当P<0.05时,进一步作()A、t检验B、Z检验C、t’检验D、F检验E、q检验16、各组方差不齐时,可以作()A、近似检验B、秩和检验C、数据变换D、ABC都可以E、方差分析17、三组以上某实验室指标观测数据服从正态分布且满足参数检验的应用条件,任两组分别进行多次t检验代替方差分析,将会()A、明显增大犯第一类错误的概率B、使结论更具体C、明显增大犯第二类错误的概率D.使均数相差更显著E、使均数的代表性更好18、完全随机设计的方差分析中,组间均方主要反映()A、抽样误差大小B、n个数据的离散程度C、处理因素的作用D、随机误差的影响E、系统误差的影响19、多组均数的两两比较中,若用t检验,不用q检验,则()A、会将有差别的总体判断为无差别的概率增大B、会将无差别的总体判断为有差别的概率增大C、结果更合理D、结果会一致E、以上都不对20、对k个处理组,b个随机区组资料的方差分析,其误差的自由度为()A、kb-k-bB、kb-k-b-1C、kb-k-b-2D、kb-k-b+1E、kb-k-b+223、完成下列方差分析表变异来源SS DF MS F组间( ) 2 ( ) ( ) 组内( ) ( ) 0.0548总变异10.800 30计算分析题1.根据表1资料说明大白鼠感染脊髓灰质炎病毒后,再做伤寒或百日咳接种是否影响生存日数?若结论为“有影响”,请做多重比较(与对照组比)。
第10章方差分析习题解答

第10章方差分析习题解答一.选择题1. 下列关于方差分析的说法不正确的是( A ).A. 方差分析是一种检验若干个正态分布的均值和方差是否相等的一种统计方法.B. 方差分析是一种检验若干个独立正态总体均值是否相等的一种统计方法.C. 方差分析实际上是一种F 检验.D. 方差分析基于偏差平方和的分解和比较.2. 设,1,2,,;1,2,,ij i ij i X i a j n µε=+== ,2(0,)ij i N εσ ,且ij ε相互独立,进行单因子方差分析是( C ) . A . 对假设012:a H µµµ=== 作检验. B . 对假设222012:a H σσσ=== 作检验. C . 假定2(0,)ij N εσ ,2σ为未知,对假设012:a H µµµ=== 作检验. D . 假定2(0,)ij N εσ 12a µµµµ==== ,µ为未知,对假设222012:a H σσσ=== 作检验.3. 对因子A 取r 个不同的水平进行试验,每个水平观测t 次,结果,1,2,,,1,2,,ij y i r j t == .对()ij r t y ×的偏差有分解:2211111()()()ˆr t r trTijij i i E A i j i j i SS y y y y t y y SS SS ⋅⋅======−=−+−=+∑∑∑∑∑ 其中11111, r t ti i ij i j j y y y y rt t ⋅=====∑∑∑对假设012:r H µµµ=== 进行检验时,如下说法错误 的是( B ) .A .E SS 表示0H 为真时,由随机性引起的y ij 的波动.B .A SS 表示0H 为真时,所引起的由各水平间ij y 波动.C . E SS 表示各水平上随机性误差的总和.D . A SS 表示各水平之间系统误差的总和.4. 对某因素进行方差分析,由所得试验数据算得下表: 方差来源 平方和自由度F 值组间 4623.7 4 组内 4837.25 15 总和9460.9519采用F 检验法检验,且知在0.05α=时F 的临界值0.05(4,15) 3.06F =,则可以认为因素的不同水平对试验结果( B ).A. 没有影响.B. 有显著影响.C. 没有显著影响.D. 不能作出是否有显著影响的判断.5. 设在双因子A 和B 的方差分析模型:ij i j ij X µαβε=+++,10ai i α==∑,10bjj β==∑,2(0,)ij N εσ ,且ij ε相互独立,检验假设:0112:,0rH ααα==== ,和0212:,0sH βββ==== 检验时,下列结论中错误的是( D ) . A . 若拒绝域01H ,则认为因子A 的不同水平对结果有显著影响. B . 若拒绝域02H ,则认为因子B 的不同水平对结果有显著影响.C . 若不拒绝01H 和02H ,则认为因子A 与B 的不同水平的组合对结果无显著影响.D . 若不拒绝01H 或02H ,则认为因子A 与B 的不同水平组合对结果无显著影响.6. 某结果可能受因素A 及B 的影响.现对A 取4个不同的水平, B 取3个不同水平,对A 与B 每一种水平组合重复二次试验,对观测结果的双因子有交互作用的方差分析模型计算得:44.3A SS =,11.5B SS =,27.0A B SS ×=,65.0E SS =.且0.05(2,12) 3.89F =,0.05(3,12) 3.49F =,0.05(6,12) 3.00F =,则在显著性水平0.05α=时,检验的结果是( B ).A. 只有A 因素对结果有显著性影响.B. 只有B 因素对结果有显著性影响.C. 只有交互作用对结果有显著性影响.D. A 、B 及A 和B 的交互作用都对结果无显著性影响.7.设某结果可能受因素A 及B 的影响,现对A 取4个不同的水平, B 取3个不同的水平配对作试验,按双因子方差分析模型的计算结果: 5.29A SS =, 2.22B SS =,7.77T SS =.且0.05(3,6) 4.80F =,0.05(2,6) 5.10F =,则在显著性水平0.05α=时,检验的结果是( C ). A. 只有A 因素的不同水平对结果有显著影响. B. 只有B 因素的不同水平对结果有显著影响.C. A 的不同水平及B 的不同水平都对结果有显著影响.D. A 、B 因素不同水平组合对结果没有显著影响.8. 对因子A 取r 个不同水平,因子B 取s 个不同水平,A 与B 的每种水平组合重复次试验后,对结果进行双因子有重复试验的方差分析,则以下关于各偏差平方和自由度的结论错误的是( D ).A. A 因子的偏差平方和A SS 的自由度为.B.B 因子的偏差平方和B SS 的自由度为.C. 交互作用的偏差平方和A B SS ×的自由度为(1)(1)r s −−.D. 误差平方和E SS 的自由度为(1)(1)(1)r s t −−−. 二.填空题9. 进行单因素方差分析的前提之一是要求表示r 个水平的r 个总体的方差 相等 . 10. 进行方差分析时,将离差平方和211()in r Tiji j SS XX ===−∑∑表示为TA E SS SS SS =+,其中A SS =21()ri ii n XX =−∑,E SS =211()in riji i j XX ==−∑∑.11. 进行方差分析时,将离差平方和211()in rT iji j SS XX ===−∑∑表示为TA E SS SS SS =+,则2ESS σ~2(n r)χ−.12. 进行方差分析时,如果所有2~(,)ij X N µσ,则222111()in r T iji j SSXX σσ===−∑∑~21(1)ri i n χ=−∑.13. 进行方差分析时,选取统计量2 1211()()(1)()(1)()i ri i i A n rE ij i i j n r n X X SS r FSS n r r X X ===−−−==−−−∑∑∑,则F ~(r 1,n r)F −−.14. 在单因素方差分析中,如果因素A 有a 个水平,其中在第i 个水平下作了i n 次试验,12a n n n n +++= ,总的偏差平方和T SS 分解为A SS 和E SS ,则A SS 的自由度为1a −,E SS 的自由度为n a−,检验统计量A F =/(1)/(1)A E SS a SS n −−,若A F 大于给定的临界值水平,则说明 因素A 的a 个水平对试验指标有显著影响 .15. 某企业准备用三种方法组装一种新的产品,为确定哪种方法每小时生产的产品数量最多,随机抽取了30名工人,并指定每个人使用其中一种方法.在显著水平α=0.05下,通过对每个工人生产的产品数量进行方差分析得到下面的部分结果.请完成方差分析表,由于 1.70 3.354131F =< 或P=0.245946>0.05 ,可判断不同的组装方法对产品数量的影响 不显著 (显著,不显著). 差异源 SS df MS F P-value F crit 组 间 420 2 210 1.70 0.245946 3.354131 组 内 3836 27 142.07 — — — 总 计425629————16. 在双因素方差分析中,因素A 有三个水平,因素B 有四个水平,每个水平搭配各做一次试验.请完成下列方差分析表,在显著水平α=0.05下,由于0.05(25.7,6)508.1A F F ==>,可判断因素A 的影响 显著 (显著,不显著);由于0.05(35.8,6)405.8B F F ==>,可判断因素B 的影响 显著 (显著,不显著). 来 源 平方和 自由度 均方 F 值 因素A 54 2 27 5.78 因素B 82 3 27.33 5.85 误差e 28 6 4.67 — 总 和16411——17. 在某种化工产品的生产过程中,选择3种不同的浓度:1A =2%,2A =4%,3A =6%;4种不同的温度:1B =100C ,2B =240C ,3B =380C ,4B =520C ;在每种浓度与温度配合下各做两次试验,观测产品的收取率.现由试验数据计算出如下结果:总偏差平方和147.8333T SS =,因素A (浓度)的偏差平方和44.3333A SS =,因素B (温度)的偏差平方和11.50B SS =,交互作用A B ×的偏差平方和27.00A B SS ×=,则误差平方和E SS = 65 ,检验统计量A F = 4.09 , B F = 0.708 ,A B F ×= 0.831 ,在显著性水平0.05α=下.由于0.05(2,4.0912) 3.89A F F ==>,可判断因素A 的影响 显著 (显著,不显著);由于0.05(30.7,12)908 3.4B F F ==<,可判断因素B 的影响 不显著 (显著,不显著);由于0.050.831(6,12) 3.00A B F F ×==<,可判断因因素A 与因素B 的交互作用影响不显著 (显著,不显著).18. 为了分析不同操作方法生产某种产品节约原料是否相同,在其余条件尽可能相同的情况下,安排了五种不同的操作方法生产某种产品,测量原料节约额,得到实验结果如下表所示.在显著水平α=0.05下,由于0.00410.05P =<,可判断不同操作方法生产某种产品节约原料 有 (有,无)显著差异.差异源 SS df MS F P-value F crit 操作方法55.5370 4 13.8842 6.05900.00414.8932组内 34.3725 15 2.2915总计89.90951919. 对腐乳的味道、口感等只能通过感观来确定其产品质量.为了检验专业评议员对腐乳评分标准是否存在显著差异,不同的腐乳质量是否存在显著差异,得到4位专业评议员对4种腐乳的评分结果,得到实验结果如下表所示.在显著水平α=0.05下,由于0.0005690.05P =<,可判断专业评议员对腐乳评分标准 有 (有,无)显著差异;由于 1.020.0505E P −=<,可判断不同的腐乳质量 有 (有,无)显著差异.差异源 SS df MS F P-value F crit 专业评议员54 3 18.0000 16.2 0.000569 3.8625 腐乳 148 3 49.3333 44.4 1.02E-053.8625误差 10 9 1.1111总计2121520.为了分析时段、路段以及时段与路段的交互作用对行车时间的影响,某市一名交通警察分别在两个路段和高峰期与非高峰期驾车试验,共获得20个行车时间数据,得到实验结果如下表所示.在显著水平α=0.05下,由于 5.700.056E P =<−,可判断时段因素对行车时间的影响 显著 (显著,不显著);由于0.0001.0805P =<,可判断路段因素对行车时间的影响 显著 (显著,不显著);由于0.9118.0105P =>,可判断时段与路段因素对行车时间交互作用的影响 不显著 (显著,不显著). 差异源SSdfMS F P-value F crit时段 174.05 1 174.05 44.0632 5.7E-06 4.49399 路段 92.45 1 92.45 23.4050 0.00018 4.49399 交互 0.05 1 0.05 0.01260.911814.49399内部 63.20 16 3.95总计329.7519三.应用计算题21.比较四种肥料1234,,,A A A A 对作物产量的影响,每一种肥料做5次试验,得产量(公斤/小区)如下表.试检验四种肥料对产量的影响有无显著差异?肥料 1A2A3A4A样 本 观 测 值5.56.5 8.0 5.5 5.0 6.0 6.5 6.5 6.07.0 7.5 6.0 4.5 6.5 7.0 5.0 7.05.56.05.5解:设使用四种不同肥料后作物的产量2~(,),1,2,3,4i i Y N i µσ=.则需检验的问题为43210:µµµµ===H ,:1H 4321,,,µµµµ不全相等.首先由样本直接计算有关值如下表作物产量计算表肥料样本观测值行和i A T1A 5.5 5.0 6.0 4.5 7.0 28 2A 6.5 6.0 7.0 6.5 5.5 31.5 3A 8.0 6.5 7.5 7.0 6.0 35 4A5.56.56.05.05.528.5 411in ij i j T x ===∑∑1232756.45T C n ==4211771.5756.4515.05in Tiji j SS xC ===−=−=∑∑22222412831.53528.5756.45 6.255555iA A i iT SS C n ==−=+++−=∑15.05 6.258.8E T A SS SS SS =−=−=列出相应的方差分析表.作物产量方差分析表方差来源 平方和 自由度 均方MS F 值临界值因素A 6.25 3 2.08 3.79 0.05(3,16) 3.24F = 0.01(3,16) 5.29F =误差 8.8 16 0.55 总和15.0519由于0.053.79(3,16)A F F =>,认为四种肥料对产量有显著影响.22.取四个种系未成年雌性大白鼠各三只,每只按一种剂量注射雌激素,一月后,解剖秤其子宫重量,结果如下表.试检验不同剂量和不同白鼠种系对子宫重量有无显著影响?解设注射不同剂量的不同白鼠种系的子宫重量2~(,),1,2,3,4ij i j Y N i µαβσ++=;1,2,3j =.则需检验的问题为01234:0A H αααα==== ,11234:,,,A H αααα不全为零 0123:0B H βββ===,1123:,,B H βββ不全为零为了计算各平方和,列出如下表.子宫重量计算表本题中4,3,12a b n ab ====22109810046712T C n ===4321111354210046713075Tiji j SS xC ===−=−=∑∑242222.11(367225314192)1004676457.66733i Ai T SS C ==−=+++−=∑ 23.22211(260358480)100467607444j Bj T SS C==−=++−=∑130756457.6676074543.33E T A B SS SS SS SS =−−=−−=得到相应的无交互作用双因素方差分析表.子宫重量双因素方差分析表方差来源 平方和 自由度 均方MS F 值 临界值因素A(种系) 6457.6732152.5623.770.05(3,6) 4.76F =0.01(3,6)9.78F =因素B60742303733.540.05(2,6) 5.14F =(剂量)0.01(2,6)10.92F =误差E 543.33 6 90.56 总和1307511因为0.0123.77(3,6)A F F =>,认为种系对子宫重量有极显著影响;0.0133.54(2,6)B F F =>,认为剂量对子宫重量有极显著影响.由此可知,种系和剂量对子宫重量都有极显著影响.23.为检验广告媒体和广告方案对产品销售量的影响,一家营销公司做了一项试验,考察三种广告方案和两种广告媒体,获得的销售量数据如下表.试检验广告方案.广告媒体或其交互作用对销售量的影响是否显著.广告方案广告媒体报纸电视 A8,12 12,8 B22,14 26,30 C10,1818,14解 设不同广告方案和广告媒体的产品销售量2~(,)ij i j ij Y N µαβγσ+++,1,2i =,3;1,2j =.则需检验的问题为0111221223132:0A B H γγγγγγ×======,1111221223132:,,,,,A B H γγγγγγ×不全为零. 0123:0A H ααα===,1123:,,A H ααα不全为零, 012:0B H ββ==,112:,B H ββ不全为零, 本题计算过程如下表:销售量数据方差分析计算表2A22,14 (36) 26, 30(56) 9284643A10,18 (28)18, 14(32)603600 列和..j x84 108 154 136642..j x705611664 1872032221113616ijti j t x====∑∑∑32221111()307212ijt i j t x ====∑∑∑ 322.117040ij i j x===∑∑36163072544T SS =−=11336430723444A SS =×−=1187203072486B SS =×−=17040307234448562A B SS ×=×−−−=得如下方差分析表:销售量数据双因素方差分析表方差来源 平方和 自由度 均方和 F 值 广告方案A 344 2 172 10.75 广告媒体B 48 1 48 3 交互效应A B ×56 2 28 1.75 误差 96 6 16 总和54411查表得0.05(2,6) 5.14F =,0.05(1,6) 5.99F =,因此,广告方案对产品销售量的影响显著;广告媒体对产品销售量的影响不显著;广告方案和广告媒体对产品销售量没有交互作用.。
方差分析与回归分析习题答案精修订

方差分析与回归分析习题答案SANY标准化小组 #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#第九章 方差分析与回归分析习题参考答案1. 为研究不同品种对某种果树产量的影响,进行试验,得试验结果(产量)如下表,试分析果树品种对产量是否有显着影响.(0.05(2,9) 4.26F =,0.01(2,9)8.02F =)解:r=3,12444n n 321=++=++=n n ,T=120 ,12001212022===n T C 计算统计值?7228.53,38A A A e e SS f F SS f ==≈……方差分析表结论:由于0.018.53(2,9)8.02,A F F ≈>=故果树品种对产量有特别显着影响.2.2700=10.523.56=≈结论: 由以上方差分析知,进器对火箭的射程有特别显着影响;燃料对火箭的射程有显着影响. 3.为了研究某商品的需求量Y 与价格x 之间的关系,收集到下列10对数据:2231,58,147,112,410.5,i i i i i i x y x y x y =====∑∑∑∑∑(1)求需求量Y 与价格x 之间的线性回归方程; (2)计算样本相关系数;(3)用F 检验法作线性回归关系显着性检验. 解:引入记号10, 3.1,5.8n x y ===∴需求量Y 与价格x 之间的线性回归方程为(2)样本相关系数32.80.955634.3248l r-==≈≈- 在0H 成立的条件下,取统计量(2)~(1,2)Ren S FF n S -=-计算统计值22(32.8)15.967.66,74.167.66 6.44R xy xx e yy R S l l S l S ==-≈=-≈-=故需求量Y 与价格x 之间的线性回归关系特别显着.4. 随机调查10个城市居民的家庭平均收入(x)与电器用电支出(y)情况得数据(单位:千元)如下:(1) 求电器用电支出y 与家庭平均收入x 之间的线性回归方程; (2) 计算样本相关系数; (3) 作线性回归关系显着性检验;(4) 若线性回归关系显着,求x =25时, y 的置信度为的预测区间. 解:引入记号10,27,1.9n x y ===∴电器用电支出y 与家庭平均收入x 之间的线性回归方程为(2)样本相关系数 0.9845l r==≈在0H 成立的条件下,取统计量(2)~(1,2)Rn S FF n S -=-e计算统计值2243.6354 5.37,5.54 5.370.17xy xx yy s l l s l s ==≈=-≈-=R e R故家庭电器用电支出y 与家庭平均收入x 之间的线性回归关系特别显着. 相关系数检验法 01:0;:0H R H R =≠故家庭电器用电支出y 与家庭平均收入x 之间的线性回归关系特别显着. (4) 因为0xx =处,0y 的置信度为1α-的预测区间为其中00.025垐 1.42640.123225 1.6536,(8) 2.31,0.1458y t σ=-+⨯====代入计算得当x =25时, y 的置信度为的预测区间为。
统计学(第四版)贾俊平 第八章 方差分析与实验设计 练习题答案
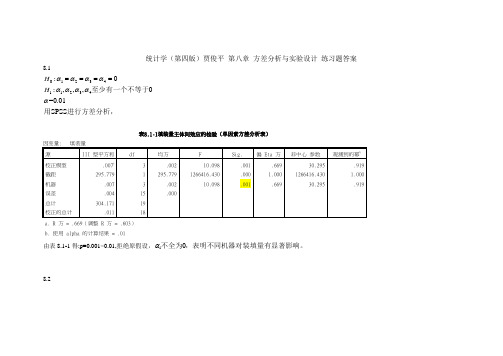
统计学(第四版)贾俊平 第八章 方差分析与实验设计 练习题答案8.10123411234:0:,,,0=0.01SPSS H H ααααααααα====至少有一个不等于用进行方差分析,表8.1-1填装量主体间效应的检验(单因素方差分析表)因变量: 填装量 源 III 型平方和df均方F Sig.偏 Eta 方非中心 参数观测到的幂b校正模型 .007a3 .002 10.098 .001 .669 30.295 .919 截距 295.7791 295.7791266416.430.000 1.000 1266416.4301.000 机器 .007 3 .002 10.098.001.66930.295.919误差 .004 15 .000总计 304.17119 校正的总计.01118a. R 方 = .669(调整 R 方 = .603)b. 使用 alpha 的计算结果 = .01由表8.1-1得:p=0.001<0.01,拒绝原假设,i 0α不全为,表明不同机器对装填量有显著影响。
8.201231123:0:,,0=0.05SPSS H H ααααααα===至少有一个不等于用进行方差分析,表8.2-1满意度评分主体间效应的检验(单因素方差分析表)因变量: 评分 源III 型平方和df 均方 F Sig.校正模型 29.610a2 14.805 11.756 .001 截距 975.156 1 975.156 774.324 .000 管理者 29.610 2 14.805 11.756.001误差 18.890 15 1.259总计 1061.000 18 校正的总计48.50017a. R 方 = .611(调整 R 方 = .559)由表8.2-1得:p=0.001<0.05,拒绝原假设,i 0α不全为,表明管理者水平不同会导致评分的显著差异。
8.301231123:0:,,0=0.05SPSS H H ααααααα===至少有一个不等于用进行方差分析,表8.3-1电池寿命主体间效应的检验(单因素方差分析表)因变量: 电池寿命 源III 型平方和df 均方 F Sig. 偏 Eta 方 非中心 参数 观测到的幂b校正模型 615.600a2 307.800 17.068 .000 .740 34.137 .997 截距 22815.000 1 22815.000 1265.157 .000 .991 1265.157 1.000 企业 615.600 2 307.800 17.068.000.74034.137.997误差 216.400 12 18.033总计 23647.000 15 校正的总计832.00014a. R 方 = .740(调整 R 方 = .697)b. 使用 alpha 的计算结果 = .05由表8.2-1得:p=0.001<0.05,拒绝原假设,i 0α不全为,表明3个企业生产的电池平均寿命之间存在显著差异。
第五章 方差分析习题 医学统计学习题
第五章方差分析习题一、选择题1.完全随机设计资料的方差分析中,必然有()。
A.组内组间SS SS >B.组内组间MS MS <C.组内组间总+=SS SS SS D.组内组间总+MS MS MS =E.组内组间νν>2.当组数等于2时,对于同一资料,方差分析结果与t 检验结果()。
A.完全等价且tF = B.方差分析结果更准确C.t 检验结果更准确D.完全等价且Ft =E.理论上不一致3.在随机区组设计的方差分析中,若),(05.021ννF F >处理,则统计推论是()。
A.各处理组间的总体均数不全相等B.各处理组间的总体均数都不相等C.各处理组间的样本均数都不相等D.处理组的各样本均数间的差别均有显著性E.各处理组间的总体方差不全相等4.随机区组设计方差分析的实例中有()。
A.处理SS 不会小于区组SSB.处理MS 不会小于区组MSC.处理F 值不会小于1D.区组F 值不会小于1E.F 值不会是负数5.完全随机设计方差分析中的组间均方是()的统计量。
A.表示抽样误差大小B.表示某处理因素的效应作用大小C.表示某处理因素的效应和随机误差两者综合影响的结果。
D.表示n 个数据的离散程度E.表示随机因素的效应大小6.完全随机设计资料,若满足正态性和方差齐性。
要对两小样本均数的差别做比较,可选择()。
A.完全随机设计的方差分析B.u 检验C.配对t 检验D.2χ检验E.秩和检验7.配对设计资料,若满足正态性和方差齐性。
要对两样本均数的差别做比较,可选择()。
A.随机区组设计的方差分析B.u 检验C.成组t 检验D.2χ检验E.秩和检验8.对k 个组进行多个样本的方差齐性检验(Bartlett 法),得2,05.02νχχ>,05.0<P 按05.0=α检验,可认为()。
A.22221,,,k σσσ 全不相等B.22221,,,k σσσ 不全相等C.k S S S ,,,21 不全相等D.k X X X ,,,21 不全相等E.k μμμ,,,21 不全相等9.变量变换中的对数变换(X x lg =或)1lg(+=X x ),适用于():A.使服从Poisson 分布的计数资料正态化B.使方差不齐的资料达到方差齐的要求C.使服从对数正态分布的资料正态化D.使轻度偏态的资料正态化E.使率较小(<30%)的二分类资料达到正态的要求10.变量变换中的平方根变换(X x =或5.0+=X x ),适用于():A.使服从Poisson 分布的计数资料或轻度偏态的资料正态化B.使服从对数正态分布的资料正态化C.使方差不齐的资料达到方差齐的要求D.使曲线直线化E.使率较大(>70%)的二分类资料达到正态的要求二、简答题1、方差分析的基本思想及应用条件2、在完全随机设计资料的方差分析与随机区组设计资料的方差分析在试验设计和变异分解上有什么不同?3、为何多个均数的比较不能直接做两两比较的t 检验?4、SNK-q 检验和Dunnett-t 检验都可用于均数的多重比较,它们有何不同?三、计算题1、某课题研究四种衣料内棉花吸附十硼氢量。
第五章 方差分析(答案) 医学统计学习题
区组 对照
第 1 区 1.4 第 2 区 1.5 第 3 区 1.5 第 4 区 1.8 第 5 区 1.5 第 6 区 1.5
ni
6
表 5-2. 大鼠经 5 种方法染尘后全肺湿重
A组
B组
C组
D组
3.3
1.9
1.8
2.0
3.6
1.9
2.3
2.3
4.3
2.1
2.3
2.4
4.1
2.4
2.5
2.6
4.2
1.8
4个样本均数两两比较的q检验(Newman-Keuls法)
两均数之差
组数
Q值
0.0520
2
0.2317
0.5560
3
2.4775
1.6160
4
7.2008
0.5040
2
2.2458
P值 >0.05 >0.05 <0.01 >0.05
2与4 3与4
1.5640
3
1.0600
2
6.9691 4.7233
1.8
2.6
3.3
1.7
2.4
2.1
6
6
6
6
nj
5 5 5 5 5 5
30
Xj
2.0800 2.3200 2.5200 2.6800 2.3800 2.2000
(N)
Xi
1.5333 3.8000
1.9667
2.1833 2.3333 2.3633 ( X )
Si
0.1366 0.4561
0.2503
故 P< 0.01。
按α=0.05 水准,拒绝 H0 ,接受 H1 ,可以认为各种衣料中棉花吸附十硼氢量有差异。
管理数量方法 第6章 方差分析练习题及答案
实验报告——第6章方差分析姓名杨秀娟班级人力10001 学号10120700121【实验1】表6-22给出了用四种不同饲料喂猪所产生的体重增加量的数据,利用单因素方差分析比较四种饲料对猪的体重影响是否显著不同。
【解】(1)数据和变量说明数据:不同饲料类型猪体重数据分组变量:饲料类型A,饲料类型B,饲料类型C,饲料类型D2个变量,24个数据(2)操作方法在SPSS主菜单中单击【分析】——【比较均值】——【单因素ANOV A】(3)结果报告从图中看出P>0.05,因此四种饲料对猪的体重影响是有影响的。
从图中数据可看出每种饲料两两比较都存在显著地差异性。
上图是用S-N-K法进行两两比较的结果,在表格中的纵向上各组均数按大小排序,然后在表格的横向上被分成了若干个亚组,不同亚组间的P值小于0.05,而同一亚组内的各组均值比较的P 值则大于0.05.从该表可见,四组间两两比较均有差异。
【实验2】打开数据文件“心理学.sav”,该实验数据为教育心理学实验中心理运动检测分数与被试者必须瞄准的目标大小关系资料。
选择四个大小不同的目标target:1,2,3,4。
从若干使用过的设备中选择三部测验设备device:1,2,3;选择两种不同明暗程度的照明环境light:1,2。
四个大小不同的目标,三部设备,两种不同的照明环境构成4*3*2的实验设计,不同目标、设备与照明水平构成了24个组合的单元。
每一个组合中随机部署5名被试者进行测试心理运动得分,得到120个得分数据,每个观测量为被试者在同一条件组合下的5个得分。
我们的实验内容是以scorc(得分)作为因变量以其他几个变量作为因素进行方差分析,在分析过程中不单考虑各个因素对因变量的贡献,还考虑各个因素之间的交互作用。
【解】(1)数据和变量说明分组变量:四个大小不同的目标target:1,2,3,4三部测验设备device:1,2,3两种不同明暗程度的照明环境light:1,24个变量,120个数据(2)操作方法在SPSS主菜单中单击【分析】——【一般线性模型】——【单变量方差分析】(3)结果报告整个模型的F值是0.836,P值为0.680,P>0.05,教育心理学实验中心理运动检测对被试者是有显著影响的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精品好文档,推荐学习交流
仅供学习与交流,如有侵权请联系网站删除 谢谢
1
统计学方差分析练习题与答案一、单项选择题
1.在方差分析中,( )反映的是样本数据与其组平均值的差异
A 总离差 B 组间误差
C 抽样误差 D 组内误差
2. 是( )
A 组内平方和 B 组间平方和
C 总离差平方和 D 因素B的离差平方和
3. 是( )
A 组内平方和 B 组间平方和
C 总离差平方和 D 总方差
4.单因素方差分析中,计算F统计量,其分子与分母的自由度各为( )
A r,n B r-n,n-r
C r-1.n-r D n-r,r-1
二、多项选择题
1.应用方差分析的前提条件是( )
A 各个总体报从正态分布 B 各个总体均值相等 C 各个总体具有相同的方差
D 各个总体均值不等 E 各个总体相互独立
2.若检验统计量F= 近似等于1,说明( )
A 组间方差中不包含系统因素的影响 B 组内方差中不包含系统因素的影响
C 组间方差中包含系统因素的影响 D 方差分析中应拒绝原假设
E方差分析中应接受原假设
3.对于单因素方差分析的组内误差,下面哪种说法是对的?( )
A 其自由度为r-1 B 反映的是随机因素的影响
C 反映的是随机因素和系统因素的影响 D 组内误差一定小于组间误差
E 其自由度为n-r
4.为研究溶液温度对液体植物的影响,将水温控制在三个水平上,则称这种方差分析是
( )
A 单因素方差分析 B 双因素方差分析 C 三因素方差分析
D 单因素三水平方差分析 E 双因素三水平方差分析
三、填空题
1.方差分析的目的是检验因变量y与自变量x是否 ,而实现这个目的的手段是通过
精品好文档,推荐学习交流
仅供学习与交流,如有侵权请联系网站删除 谢谢
2
的比较。
2.总变差平方和、组间变差平方和、组内变差平方和三者之间的关系是 。
3.方差分析中的因变量是 ,自变量可以是 ,也可以是 。
4.方差分析是通过对组间均值变异的分析研究判断多个 是否相等的一种统计方法。
5.在试验设计中,把要考虑的那些可以控制的条件称为 ,把因素变化的多个等级状态
称为 。
6.在单因子方差分析中,计算F统计量的分子是 方差,分母是 方差。
7.在单因子方差分析中,分子的自由度是 ,分母的自由度是 。
四、计算题
1.有三台机器生产规格相同的铝合金薄板,为检验三台机器生产薄板的厚度是否相同,随
机从每台机器生产的薄板中各抽取了5个样品,测得结果如下:
机器1:0.236,0.238,0.248,0.245,0.243
机器2:0.257,0.253,0.255,0.254,0.261
机器3:0.258,0.264,0.259,0.267,0.262
问:三台机器生产薄板的厚度是否有显著差异?
2.养鸡场要检验四种饲料配方对小鸡增重是否相同,用每一种饲料分别喂养了6只同一品
种同时孵出的小鸡,共饲养了8周,每只鸡增重数据如下:(克)
配方 :370,420,450,490,500,450
配方 :490,380,400,390,500,410
配方 :330,340,400,380,470,360
配方 :410,480,400,420,380,410
问:四种不同配方的饲料对小鸡增重是否相同?
3.今有某种型号的电池三批,它们分别为一厂、二厂、三厂 三个工厂所生产的。为评比其
质量,各随机抽取5只电池为样品,经试验测得其寿命(小时)如下:
一厂 :40,48,38,42,45
二厂 :26,34,30,28,32
三厂 :39,40,43,50,50
试在显著性水平 下检验电池的平均寿命有无显著的差异。
4.一个年级有三个小班,他们进行了一次数学考试。现从各个班级随机抽取了一些学生,
记录其成绩如下:
1班:73,89,82,43,80,73,66,60,45,93,36,77
2班:88,78,48,91,51,85,74,56,77,31,78,62,76,96,80
3班:68,79,56,91,71,71,87,41,59,68,53,79,15
精品好文档,推荐学习交流
仅供学习与交流,如有侵权请联系网站删除 谢谢
3
若各班学生成绩服从正态分布,且方差相等,试在显著性水平 下检验各班级的平均分
数有无显著差异?
一、单项选择题
1. D 2. A 3. C 4. C
二、多项选择题
1. ACE 2. ABD 3. BE 4.AD
三、填空题
1.独立、方差
2.总变差平方和=组间变差平方和+组内变差平方和。
3.数量型变量,品质型变量,数量型变量。
4.正态总体均值
5.因子,水平或处理。
6.组间、组内
7.m-1, n-m。
四、计算题
1.解:
根据计算结果列出方差分析表
方差来源 离差平方和 自由度 均方差 F值
组间 0.001053 2 0.00052661 32.92
组内 0.000192 12 0.00016
总和 0.001245 14
因为 (2,12)=3.89<32.92,故拒绝 ,认为各台机器生产的薄板厚度有显著
差异。
2.解:
根据计算结果列出方差分析表
精品好文档,推荐学习交流
仅供学习与交流,如有侵权请联系网站删除 谢谢
4
方差来源 离差平方和 自由度 均方差 F值
组间 14245.83 3 4748.61 2.16
组内 43950 20 2197.5
总和 58195.83 23
因为 (3,20)=3.10>2.16,故接受 ,即四种配方的饲料对小鸡的增重没有
显著的差异。
3.解:
各总值均值间有显著差异。
4.解:差异不显著。
环境教育
第8课交通状况巧改善
教学目标:
1、思考人们经常使用的交通工具的优缺点,知道在不同情况下
选取哪种交通工具最合适。
2、了解造成交通拥堵的原因,知道改善的一些方法措施。
3、调查公众对交通拥堵问题的认识和满意度,写出调查报告。
教学重点:
了解造成交通拥堵的原因,知道改善的一些方法措施。
教学时间:一课时
教学过程:
一、导入
大车小车,出行方便了,课时,新的问题开始困扰我们:交通拥
挤,环境污染。
二、开动脑筋:
精品好文档,推荐学习交流
仅供学习与交流,如有侵权请联系网站删除 谢谢
5
1、经历过交通拥挤么?什么感受?
2、人们出行只要用到哪些交通工具?分析优缺点。知道在哪种
情况下选取哪种交通工具最合适
三、交通拥堵以及改善的方法和建议。
1、造成交通拥堵的原因:
2、缓解交通拥堵的方法有哪些?
四、走出校园
