初二下册分式专题全部题型

合集下载

(必考题)初中数学八年级数学下册第五单元《分式与分式方程》测试卷(包含答案解析)(1)

一、选择题1．甲乙两地相距60km ，一艘轮船从甲地顺流到乙地，又从乙地立即逆流到甲地，共用8小时，已知水流速度为5km/h ，若设此轮船在静水中的速度为x km/h ，可列方程为（） A ．6060855x x +=+- B ．120120855x x +=+- C ．6058x += D ．6060855x x +=+- 2．已知一个三角形三边的长分别为5，7，a ，且关于y 的分式方程45233y a a y y++=--的解是非负数，则符合条件的所有整数a 的和为（） A ．24 B ．15 C ．12 D ．73．H7N9病毒直径为30纳米，已知1纳米=0.000 000 001米．用科学记数法表示这个病毒直径的大小，正确的是（）A ．93010-⨯米B ．83.010-⨯米C ．103.010-⨯米D ．90.310-⨯米 4．下列关于分式2x x+的各种说法中，错误的是（）． A ．当0x =时，分式无意义 B ．当2x >-时，分式的值为负数C ．当2x <-时，分式的值为正数D ．当2x =-时，分式的值为0 5．定义：若两个分式的和为n （n 为正整数），则称这两个分式互为“n 阶分式”．例如，分式31x +与31x x+互为“3阶分式”．设正数x ，y 互为倒数，则分式22x x y +与22y y x +互为（）A ．二阶分式B ．三阶分式C ．四阶分式D ．六阶分式6．若数a 关于x 的不等式组()()11223321x x x a x ⎧-≤-⎪⎨⎪-≥-+⎩恰有三个整数解，且使关于y 的分式方程13y 2a 2y 11y--=---的解为正数，则所有满足条件的整数a 的值之和是（） A ．2 B ．3 C ．4 D ．57．下列说法正确的是（）A ．分式242x x --的值为零，则x 的值为2± B ．根据分式的基本性质，m n 可以变形为22mx nxC ．分式32xy x y-中的,x y 都扩大3倍，分式的值不变 D ．分式211x x ++是最简分式8．如果分式11m m -+的值为零，则m 的值是（） A ．1m =- B ．1m = C ．1m =± D ．0m = 9．已知2,1x y xy +==，则y x x y +的值是（） A ．0 B ．1 C ．-1 D ．210．已知：x 是整数，12,21x x M N x +==+．设2y N M =+．则符合要求的y 的正整数值共有（）A ．1个B ．2个C ．3个D ．4个11．不改变分式的值，下列各式变形正确的是（） A ．11x x y y +=+ B ．1x y x y -+=-- C ．22x y x y x y +=++ D ．22233x x y y ⎛⎫-= ⎪⎝⎭12．冬季来临，为防止疫情传播，某学校决定用420元购买某种品牌的消毒液，经过还价，每瓶便宜0.5元，结果比用原价购买多了20瓶，求原价每瓶多少元．设原价每瓶x 元，则可列出方程为（）A ．420420200.5x x -=- B ．420420200.5x x -=+ C ．420420200.5x x -=+ D ．420200.5x =- 二、填空题13．人类进入5G 时代，科技竞争日趋激烈．据报道，我国某种芯片的制作工艺已达到28纳米，居世界前列．已知1纳米＝1×10﹣9米，则28纳米等于多少米？将其结果用科学记数法表示为_____．14．关于x 的分式方程211m x =-+无解，则m 的取值是_______． 15．一艘轮船在静水中的最大航速为60km/h ，它以最大航速沿江顺流航行240km 所用时间与以最大航速逆流航行120km 所用时间相同，则江水的流速为________km/h ．16．已知215a a+=，那么2421a a a =++________．17．使式子2x +有意义的x 的取值范围是______． 18．对于实数a 、b ，定义一种运算“⊗”为：2(1)a a b ab a-⊗=-有下列命题： ①1(3)3⊗-=；②a b b a ⊗=⊗；③方程1102x 的解为12x =；④若函数(2)y x =-⊗的图象经过(1,)A m -，(3,)B n 两点，则m n <，其中正确命题的序号是__．（把所有正确命题的序号都填上）19．某危险品工厂采用甲型、乙型两种机器人代替人力搬运产品．甲型机器人比乙型机器人每小时多搬运10kg ，甲型机器人搬运800kg 所用时间与乙型机器人搬运600kg 所用时间相等．问乙型机器人每小时搬运多少kg 产品？根据以上信息，解答下列问题．（1）小华同学设乙型机器人每小时搬运xkg 产品，可列方程为______小惠同学设甲型机器人搬运800kg 所用时间为y 小时，可列方程为____________．（2）乙型机器人每小时搬运产品_______________kg ．20．如果方程322x m x x-=-- 无解，则m=___________．三、解答题21．先化简，再求值：222444142x x x x x x+-++⎛⎫-÷- ⎪-⎝⎭，其中22150x x +-=． 22．（1）先化简，再求值：2222213214x x x x x x x x -⎛⎫÷-- ⎪+++-⎝⎭，其中12x =．（2）解方程：11322x x x--=--． 23．计算：（1）()()()3223m n m n mn ⋅-÷-；（2）()()()22x y x y x y y ⎡⎤+-+-÷⎣⎦；（3）2269243a a a a a-+-⋅--． 24．（1）化简：22121a a a a a--+÷；（2）把（1）中化简的结果记作A ，将A 中的分子与分母同时加上1后得到B ，问：当1a >时，B 的值与A 的值相比变大了还是变小了？试说明理由．25．先化简，再求值2111x x x x x ⎛⎫-+÷ ⎪++⎝⎭，其中整数x 满足13x -≤<． 26．列分式方程解应用题：2020年玉林市倡导市民积极参与垃圾分类，某小区购进A 型和B 型两种分类垃圾桶，购买A 型垃圾桶花费了2500元，购买B 型垃圾桶花费了2000元，且购买A 型垃圾桶数量是购买B 型垃圾桶数量的2倍，已知购买一个B 型垃圾桶比购买一个A 型垃圾桶多花30元，求购买一个A 型垃圾桶、一个B 型垃圾桶各需多少元？【参考答案】***试卷处理标记，请不要删除一、选择题1．D解析：D【分析】本题关键描述语是：“共用去8小时”．等量关系为：顺流60千米用的时间+逆流60千米用的时间=5，根据等量关系列出方程即可．【详解】解：由题意，得：6060855x x +=+-，故选：D ．【点睛】本题考查分式方程的应用，分析题意，找到关键描述语，找到合适的等量关系是解决问题的关键．注意顺流速度=静水速度+水流速度；逆流速度=静水速度-水流速度． 2．B解析：B【分析】根据三角形的三边关系确定a 的取值范围，再根据分式方程的解是非负数确定a 的取值范围，从而求出符合条件的所有整数即可得结论.【详解】解：45233y a a y y++=-- 去分母得:4526y a a y +-=-移项得:6y a -=-+∴6y a =-∵分式方程的解为非负数，∴60a -≥∴6a ≤，且a≠3∵三角形的三边为:5，7，a ，∴212a <<∴26a <≤，又∵a≠3，且为整数，∴a 可取4，5，6，和为15.故选：B.【点睛】本题考查了三角形的三边关系、分式方程的解，解决本题的关键是根据不等式（组）解集，求出不等式（组）的整数解.3．B解析：B【分析】由于1纳米=10-9米，则30纳米=30×10-9米，然后根据幂的运算法则计算即可．【详解】解：1纳米=0.000 000 001米=10-9米，30纳米=30×10-9米=3×10-8米．故选：B ．【点睛】本题考查了科学记数法-表示较小的数：用a×10n （1≤a ＜10，n 为负整数）表示较小的数． 4．B解析：B【分析】根据分式的定义和性质，对各个选项逐个分析，即可得到答案．【详解】当0x =时，分式无意义，选项A 正确；当2x >-时，分式的值可能为负数，可能为正数，故选项B 错误；当2x <-时，20x +<，分式的值为正数，选项C 正确；当2x =-时，20x +=，分式的值为0，选项D 正确；故选：B ．【点睛】本题考查了分式的知识；解题的关键是熟练掌握分式的性质，从而完成求解． 5．A解析：A【分析】根据题意得出xy ＝1，可以用1x 表示y ，代入22x x y ++22y y x +，计算结果为2即可．【详解】由题意得：xy ＝1，则y ＝1x，把 y ＝1x ，代入22x x y ++22y y x +，得：原式＝221x x x ++221x x x+＝3321x x ++321x +＝2 ∴22x x y +与22y y x +互为“2阶分式”，故选A ．【点睛】本题是一道新定义型题目，主要考查分式的相关计算，有一定难度，熟练掌握分式的运算法则是解题的关键．6．A解析：A【分析】先解不等式得出解集x≤2且x≥2a -，根据其有两个整数解得出0＜2a -≤1，解之求得a 的范围；解分式方程求出y ＝2a −1，由解为正数且分式方程有解得出2a −1＞0且2a － 1≠1，解之求得a 的范围；综合以上a 的范围得出a 的整数值，从而得出答案．【详解】解：()()11223321x x x a x ⎧-≤-⎪⎨⎪-≥--⎩①②，解不等式①得：x≤2，解不等式②得：x≥2a -，∵不等式组恰有三个整数解，∴-1＜2a -≤0，解得12a ≤＜，解分式方程132211y a y y--=---，得：21y a =-，由题意知210211a a ->⎧⎨-≠⎩，解得12a >且1a ≠，则满足12a ≤＜，12a >且1a ≠的所有整数a 的值是2，所有满足条件的整数a 的值之和为2．故选择：A ．【点睛】本题主要考查解一元一次不等式组和求方程的正数解，解题的关键是根据不等式组整数解和方程的正数解得出a 的范围，再求和即可．7．D解析：D【分析】直接利用分式的值为零的条件以及分式的基本性质、最简分式的定义分别分析得出答案．【详解】A 、分式242x x --的值为零，则x 的值为−2，故此选项错误； B 、根据分式的基本性质，等式m n =22mx nx（x≠0），故此选项错误； C 、分式32xy x y -中的x ，y 都扩大3倍，分式的值扩大为3倍，故此选项错误； D 、分式211x x ++是最简分式，正确；故选：D ．【点睛】此题主要考查了分式的值为零的条件以及分式的基本性质、最简分式的定义，正确掌握相关定义和性质是解题关键．8．B解析：B【分析】先根据分式为零的条件列出关于m 的不等式组并求解即可．【详解】解：∵11m m -+=0 ∴m-1=0，m+1≠0，解得m=1．故选B ．【点睛】本题主要考查了分式为零的条件，掌握分式为零的条件是解答本题的关键，同时分母不等于零是解答本题的易错点．9．D解析：D【分析】将y x x y+进行通分化简，整理出含已知条件形式的分式，即可得出答案．【详解】解：2222()2221=21y x y x x y xy x y xy xy ++--⨯+=== 故选D ．【点睛】本题考查了分式的混合运算，熟练运用完全平方公式是解题的关键．10．C解析：C【分析】先求出y 的值，再根据x ，y 是整数，得出x ＋1的取值，然后进行讨论，即可得出y 的正整数值．【详解】解：∵12,21x x M N x +==+ ∴42222221111x x y x x x x ++=+==+++++． ∵x ，y 是整数， ∴21x +是整数， ∴x ＋1可以取±1，±2．当x ＋1＝1，即x ＝0时2241y =+=＞0；当x ＋1＝−1时，即x ＝−2时，2201y =+=-（舍去）；当x ＋1＝2时，即x ＝1时，2232y =+=＞0；当x ＋1＝−2时，即x ＝−3时，2212y =+=-＞0；综上所述，当x 为整数时，y 的正整数值是4或3或1．故选：C ．【点睛】此题考查了分式的加减法，熟练掌握分式的加减运算法则，求出y 的值是解题的关键． 11．B解析：B【分析】根据分式的基本性质即可求出答案．【详解】解：A 、11x x y y ++≠，不符合题意； B 、=1x y x y-+--，符合题意； C 、22x y x y x y+≠++，不符合题意； D 、22239x x y y ⎛⎫-= ⎪⎝⎭，不符合题意；故选：B ．【点睛】本题考查分式的基本性质，解题的关键是熟练运用分式的基本性质，本题属于基础题型． 12．A解析：A【分析】根据“原价买的瓶数-实际价格买的瓶数=20”列出方程即可．【详解】解：原价买可买420x 瓶，经过还价，可买4200.5x -瓶．方程可表示为： 420420200.5x x-=-．故选：A ．【点睛】考查了由实际问题抽象出分式方程．列方程解应用题的关键步骤在于找相等关系．本题要注意还价前后商品的单价的变化．二、填空题13．8×10-8米【分析】科学记数法的表示形式为a×10n 的形式其中1≤|a|＜10n 为整数确定n 的值时要看把原数变成a 时小数点移动了多少位n 的绝对值与小数点移动的位数相同当原数绝对值≥10时n 是正数；解析：8×10-8米【分析】科学记数法的表示形式为a×10n 的形式，其中1≤|a|＜10，n 为整数．确定n 的值时，要看把原数变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n 是正数；当原数的绝对值＜1时，n 是负数．【详解】解：将28纳米用科学记数法表示为2.8×10-8米，故答案为：2.8×10-8米．【点睛】本题考查了科学记数法的表示方法．科学记数法的表示形式为a×10n 的形式，其中1≤|a|＜10，n 为整数，表示时关键要正确确定a 的值以及n 的值．14．【分析】分式方程去分母转化为整式方程由分式方程无解确定出x 的值代入整式方程计算即可求出m 的值【详解】解：去分母得：由分式方程无解得x+1=0即x=-1把x=-1代入得：解得：m=0故答案为：m=0【解析：0m =【分析】分式方程去分母转化为整式方程，由分式方程无解确定出x 的值，代入整式方程计算即可求出m 的值．【详解】解：去分母得：21m x =--，由分式方程无解，得x+1=0，即x=-1，把x=-1代入21m x =--得：2110m =-=，解得：m=0，故答案为：m=0．【点睛】本题主要考查分式方程的解，理解分式方程的增根产生的原因是解题的关键．15．20【分析】由顺水船速＝静水船速+水速逆水船速＝静水船速﹣水速设未知数根据两不同航程时间相同列出方程即可求出答案【详解】解：设江水的流速为根据题意可得：解得：经检验：是原方程的根故答案为20【点睛】解析：20【分析】由顺水船速＝静水船速+水速，逆水船速＝静水船速﹣水速，设未知数根据两不同航程时间相同列出方程即可求出答案．【详解】解：设江水的流速为/x km h ，根据题意可得：2401206060x x=+-，解得：20x ，经检验：20x 是原方程的根，故答案为20．【点睛】此题主要考查了分式方程的应用，正确得出等量关系是解题关键．16．【分析】将变形为=5a 根据完全平方公式将原式的分母变形后代入=5a 即可得到答案【详解】∵∴=5a ∴故答案为：【点睛】此题考查分式的化简求值完全平方公式根据已知等式变形为=5a 将所求代数式的分母变形为解析：124【分析】将215a a+=变形为21a +=5a ，根据完全平方公式将原式的分母变形后代入21a +=5a ，即可得到答案．【详解】 ∵215a a+=， ∴21a +=5a ，∴2421a a a =++()()2222222221242451a a a a a a a a ===-+- 故答案为：124．【点睛】此题考查分式的化简求值，完全平方公式，根据已知等式变形为21a +=5a ，将所求代数式的分母变形为22(1)a a +-形式，再代入计算是解题的关键． 17．且【分析】根据分式的分母不能为0二次根式的被开方数大于或等于0列出式子求解即可得【详解】由题意得：解得且故答案为：且【点睛】本题考查了分式和二次根式有意义的条件熟练掌握分式和二次根式的定义是解题关键解析：3x ≤且2x ≠-【分析】根据分式的分母不能为0、二次根式的被开方数大于或等于0列出式子求解即可得．【详解】由题意得：2030x x +≠⎧⎨-≥⎩，解得3x ≤且2x ≠-，故答案为：3x ≤且2x ≠-．【点睛】本题考查了分式和二次根式有意义的条件，熟练掌握分式和二次根式的定义是解题关键． 18．①④【分析】根据新定义对①②直接进行判断；根据新定义得解得经检验原方程无实数解可对③进行判断；根据新定义得到然后根据一次函数的性质对④进行判断【详解】解：所以①正确；所以②不正确；由于方程所以解得经解析：①④【分析】根据新定义对①②直接进行判断；根据新定义得2111210122x x x ，解得12x =，经检验原方程无实数解，可对③进行判断；根据新定义得到922y x ，然后根据一次函数的性质对④进行判断．【详解】解：2(11)1(3)1(3)31，所以①正确； 2(1)a a b ab a-⊗=-，2(1)b b a ab b ，所以②不正确；由于方程1102x ，所以2111210122x x x ，解得12x =，经检验原方程无实数解，所以③错误；函数2(21)9(2)2222y x x x ，因为(1,)A m -，(3,)B n 在函数922y x =-，所以m n <，所以④正确；综上所述，正确的是：①④；故答案为①④．【点睛】本题考查了命题，新定义下实数的运算，分式方程，一次函数的性质特点，熟悉相关性质是解题的关键．19．【分析】（1）设乙型机器人每小时搬运产品根据甲型机器人搬运所用时间与乙型机器人搬运所用时间相等列方程；设甲型机器人搬运所用时间为小时根据甲型机器人比乙型机器人每小时多搬运列方程；（2）设乙型机器人每解析：80060010x x =+80060010yy =+ 【分析】（1）设乙型机器人每小时搬运xkg 产品，根据甲型机器人搬运800kg 所用时间与乙型机器人搬运600kg 所用时间相等列方程；设甲型机器人搬运800kg 所用时间为y 小时，根据甲型机器人比乙型机器人每小时多搬运10kg 列方程；（2）设乙型机器人每小时搬运xkg 产品，则甲型机器人每小时搬运（x+10）kg ，由题意得80060010x x=+，解方程即可．【详解】（1）设乙型机器人每小时搬运xkg 产品，则甲型机器人每小时搬运（x+10）kg ，由题意得 80060010x x=+，设甲型机器人搬运800kg 所用时间为y 小时，由题意得80060010y y=+，故答案为：80060010x x=+，80060010y y =+；（2）设乙型机器人每小时搬运xkg 产品，则甲型机器人每小时搬运（x+10）kg ，由题意得 80060010x x=+，解得x=30，经检验，x=30是方程的解，答：乙型机器人每小时搬运产品30kg ．故答案为：30．【点睛】此题考查分式方程的实际应用，正确理解题意，利用直接设未知数的方法和间接设未知数的方法列方程解决问题，注意：解分式方程需检验．20．1【分析】先去分母把分式方程转化为整式方程再根据原方程无解可得x=2然后把x=2代入整式方程求解即可【详解】解：去分母得x －3=﹣m ∵原方程无解∴x －2=0即x=2把x=2代入上式得2－3=﹣m 所以解析：1【分析】先去分母把分式方程转化为整式方程，再根据原方程无解可得x =2，然后把x =2代入整式方程求解即可．【详解】解：去分母，得x －3=﹣m ，∵原方程无解，∴x －2=0，即x =2，把x =2代入上式，得2－3=﹣m ，所以m =1．故答案为1．【点睛】本题考查了分式方程的无解问题，属于常考题型，正确理解题意、掌握解答的方法是关键．三、解答题21．242x x +；415【分析】先根据分式混合运算的法则把原式进行化简，再把22150x x +-=变形为2215x x +=，最后代入化简结果中进行计算即可．【详解】解：222444142x x x x x x+-++⎛⎫-÷- ⎪-⎝⎭=22(2)4(2)(2)2x x x x x x x+--+÷-+- =22(2)(2)4(2)2x x x x x x x+-+-+⨯-- =242x x x x+++-=22444(2)x x x x x x ++--+ 242x x=+ 22150x x +-=2215x x ∴+=∴原式415=．【点睛】本题考查了分式的化简求值，解答本题的关键是明确分式化简求值的方法．22．（1）2x x +，15；；（2）3x = 【分析】（1）原式括号中两项通分并利用同分母分式的加法法则计算，同时利用除法法则变形，约分得到最简结果，把12x =代入计算即可求出值；（2）分式方程去分母转化为整式方程，求出整式方程的解得到x 的值，经检验即可得到分式方程的解．【详解】（1）解：原式2222123214x x x x x x x x x +--=÷-+++- ()()()()()22112122x x x x x x x x -+=⋅-++-+ 2222x x x x x x =-=+++ 当12x =原式2x x =+15=；（2）解：去分母得：()1321x x --=-，移项合并得：-2x ＝-6，解得：3x =，经检验3x =是分式方程的解【点睛】此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．23．（1）72m n -；（2）x y +；（3）32a a --+ 【分析】（1）先根据积的乘方和幂的乘方化简原式中的各项后再进行乘除运算即可得到结果；（2）将中括号内的运用完全平方公式和平方差公式把小括号展开合并后，根据多项式除以单项式的运算法则计算出结果即可；（3）把分式中的分子与分母因式分解后约分即可得到答案．【详解】解：（1）()()()3223m n m n mn ⋅-÷- =()63322m n m n m n ⋅-÷=9422m n m n -÷=72m n -；（2）()()()22x y x y x y y ⎡⎤+-+-÷⎣⎦ ()222222x xy y x y y =++-+÷()2222xy y y =+÷x y =+；（3）2269243a a a a a-+-⋅-- ()()()232223a a a a a--=⋅+-- 32a a -=-+．【点睛】此题主要考查了整式的运算和分式的化简，熟练掌握相关运算法则是解答此题的关键． 24．（1）1a a -；（2）B 的值与A 的值相比变小了，理由见解析【分析】（1）把除变乘，同时将除式的分子分母因式分解，约分即可；（2）由1a A a =-先求出1a B a+=，作差1(1)B A a a -=--，然后判断1(1)a a --符号即可．【详解】解：（1）原式221(1)a a a a -=⋅-． 1a a =-；（2）B 的值与A 的值相比变小了．理由如下：1,1a a A B a a+==-．∴21(1)(1)11(1)(1)a a a a a B A a a a a a a ++---=-==----． ∵1a >，∴10a ->，∴()11a a >0-， ∴0B A -<．∴B A <．∴B 的值与A 的值相比是变小了．【点睛】本题考查分式的除法，比较分式的大小，掌握分式的除法法则，和比较分式的大小的方法是解题关键．25．原式1x=，1x =时，原式1=；或2x =时原式12=．【分析】根据分式的减法和除法可以化简题目中的式子，然后从-1≤x ＜3中选取使得原分式有意义的整数代入化简后的式子即可解答本题．【详解】解：2111x x x x x ⎛⎫-+÷ ⎪++⎝⎭ =2(1)(1)11x x x x x x--++⋅+ =221x x x-+ =1x， ∵x （x+1）≠0，∴x≠0，x≠-1，∵整数x 满足-1≤x ＜3，∴x=1或2，当x=1时，原式=11=1，当x=2时，原式=12．【点睛】本题考查分式的化简求值，解答本题的关键是明确分式化简求值的方法．26．一个A 型垃圾桶需50元，一个B 型垃圾桶需80元【分析】设一个A 型垃圾桶需x 元，则一个B 型垃圾桶需（x+30）元，根据购买A 型垃圾桶数量是购买B 品牌足球数量的2倍列出方程解答即可．【详解】解：设购买一个A 型垃圾桶需x 元，则一个B 型垃圾桶需()30x +元由题意得：25002000230x x =⨯+，解得：50x =，经检验：50x =是原方程的解，且符合题意，则：3080x +=，答：购买一个A 型垃圾桶需50元，一个B 型垃圾桶需80元．【点睛】此题考查了分式方程的应用，找出题目蕴含的等量关系列出方程是解决问题的关键．。

(完整版)初二数学分式练习题汇总,推荐文档

1 x 1
x x2 1
，其中：x=-2
23、解方程（1） 2 3 x3 x
（2）
x
3
1x
2
x
x 1
1
25、已知 y= x 1 ，x 取哪些值时： 2 3x
（1）y 的值是零；（2）分式无意义；（3）y 的值是正数；（4）y 的值是负数．
24、中学 2 班和 3 班的学生去河边抬砂到校园内铺路，经统计发
现：162 班比 163 班每小时多抬 30kg，162 班抬 900kg 所用的时间和 163 班抬 600kg 所用的时间相等，两个班长每小时分别抬多少砂？
18. 0 19． x=-5
x
20.
ab 三、解答题
第 16 章分式参考答案
（第一次统测试卷）
一、选择题（每题 3 分，共 30 分.将答案填在表格内）题号 1 2 3 4 5 6 7 8 9 10 答案 B D C B B B C D B D 二、填空题 11. x≠5 12. x=1 13. 1 14. y3
5、化简
的结果是（）
9 m2
m
A、
m3
B、 m m3
m
C、
m3
6、下列分式中,最简分式是（）
m
D、
3m
ab
x2 y2
A.
B.
ba
x y
x2 4
C.
x2
2a
D.
a2 4a 4
a 7、根据分式的基本性质，分式 a b 可变形为（）
a （A） a b
a （B） a b
a （C） a b
3、下列约分正确的是（
）
x6
A、

第五章第03讲分式的加减法(10类热点题型讲练)(解析版)--初中数学北师大版8年级下册

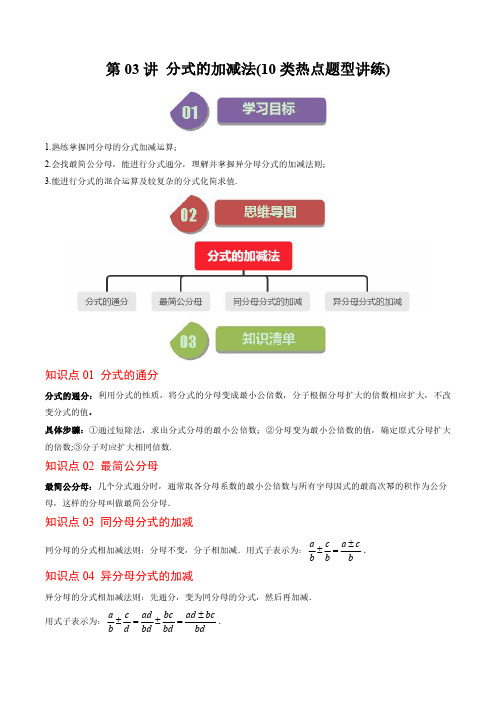
第03讲分式的加减法(10类热点题型讲练)1.熟练掌握同分母的分式加减运算；2.会找最简公分母，能进行分式通分，理解并掌握异分母分式的加减法则；3.能进行分式的混合运算及较复杂的分式化简求值.知识点01分式的通分分式的通分：利用分式的性质，将分式的分母变成最小公倍数，分子根据分母扩大的倍数相应扩大，不改变分式的值。

具体步骤：①通过短除法，求出分式分母的最小公倍数；②分母变为最小公倍数的值，确定原式分母扩大的倍数;③分子对应扩大相同倍数.知识点02最简公分母最简公分母：几个分式通分时，通常取各分母系数的最小公倍数与所有字母因式的最高次幂的积作为公分母，这样的分母叫做最简公分母．知识点03同分母分式的加减同分母的分式相加减法则：分母不变，分子相加减．用式子表示为：a c a cb b b±±=．知识点04异分母分式的加减异分母的分式相加减法则：先通分，变为同分母的分式，然后再加减．用式子表示为：a c ad bc ad bcb d bd bd bd±±=±=．注意：分式是分数的扩展，因此分式的运算法则与分数的运算法则类似.知识点01平面向量基本定理知识点02平面向量的坐标表示知识点03平面向量的坐标运算题型01同分母分式加减法题型02最简公分母题型03通分题型04异分母分式加减法题型05整式与分式相加减题型06已知分式恒等式，确定分子或分母【点睛】本题考查分式的加减，解题关键是掌握分式加法的运算法则．【变式训练】题型07分式加减混合运算题型08分式加减的实际应用【点睛】本题主要考查了分式加减的应用，解题的关键是根据题意列出分式，熟练掌握分式加减运算法则，准确计算．【变式训练】题型09分式加减乘除混合运算题型10分式化简求值一、单选题1．（23-24八年级上·天津红桥·期末）计算2111x x x x --++的结果是（）A ．1B ．1x +C ．11x +D ．1x x +2．（22-23八年级上·贵州黔南·期末）分式22x x -，36x -的最简公分母是（）A ．2x -B ．()2x x -C ．()()323x x --D ．()32x x -【答案】D【分析】本题考查了最简公分母，先因式分解取系数的最小公倍数，字母的最高次幂，1，3的最小公倍数为3，x 的最高次幂为1，2x -的最高次幂为1，则得出最简公分母．A ．2222233y y x x ⎛⎫= ⎪⎝⎭B ．110x y y x-=--C ．3263x x y y ⎛⎫-=- ⎪⎝⎭D ．()111333x y x y +=+将这些防护服尽快投入使用，增加了人手，最后平均每天比原计划多生产了60套，则工厂完成这个订单的时间比原计划提前（）A ．60x x y ⎛⎫- ⎪⎝⎭天B ．60x x y y ⎛⎫- ⎪+⎝⎭天C ．60x x y y ⎛⎫-⎪-⎝⎭天D ．60x x y y ⎛⎫-⎪-⎝⎭天5．（23-24九年级下·湖北武汉·开学考试）已知2220x x --=，计算2121-⎛⎫-÷ ⎪+++⎝⎭x x x x x x 的值是（）A ．1B ．1-C ．0.5D ．0.5-二、填空题6．（2023八年级下·江苏·专题练习）计算：221b a b a b+=-+．7．（23-24八年级上·山东东营·阶段练习）将分式29-a 和93a-进行通分时，最简公分母是【答案】()()333a a -+-【分析】本题考查了分式的通分；先对分式的分母进行因式分解，然后即可确定它们的最简公分母．【详解】解：∵()()2933a a a -=+-，()9333a a -=--，∴最简公分母是()()333a a -+-，故答案为：()()333a a -+-．8．（23-24八年级上·湖南长沙·阶段练习）若2574515x A Bx x x x -=+--+-，A ，B 为常数，则2A B -的值为．9．（2024八年级下·全国·专题练习）小刚在化简22a b M--时，整式M 看不清楚了，通过查看答案，发现得到的化简结果是1a b-，则整式M 是．和，多次重复进行这种运算的过程如下：则第2024次运算的结果2024y =．（用含字母x 的式子表示）三、解答题11．（22-23八年级上·山东济宁·阶段练习）通分：(1)235a b c 与2710c a b；(2)22x x +与21x x-．(1)2111x x x -++；(2)24411a a a a a a -+⎛⎫-÷⎪--⎝⎭．(1)2m n m n n m m n n m -++---(2)22211111 m m mmm m-+-⎛⎫÷--⎪-+⎝⎭14．（23-24八年级上·全国·课时练习）计算：(1)22211x x x -++；(2)3a b a b a b b a -+---；(3)2243164x x+--；(4)222a a a ---．(1)211y y y ---；(2)2221111x x x +--+-；(3)21613962x x x x------；(4)2()a b a b a b+--+．16．（2024九年级下·山东·专题练习）下面是某同学计算11a a ---的解题过程：解：211a a a ---()-=---22111aa a a ……………………①()2211a a a --=-………………………②2211a a a a -+-=-………………………③111a a -==-．……………………………④上述解题过程从第几步开始出现错误？请写出正确的解题过程．17．（23-24八年级上·江苏南通·阶段练习）先化简，再求值：111x x x x x -+⎛⎫÷-+ ⎪++⎝⎭，请从1-，0或2中选择你喜欢的一个数代入求值．18．（22-23八年级下·辽宁本溪·阶段练习）先化简，再求值：111x x x ++⎛⎫-+÷ ⎪++⎝⎭，其中()1013.142x π-⎛⎫=-+ ⎪⎝⎭形式，那么称这个分式为“美好分式”，如：112122111111x x x x x x x x +-+-==+=+-----，则11x x +-是“美好分式”．(1)下列分式中，属于“美好分式”的是______；（只填序号）①6325x x +；②232x x +；③33x x +；④24321x x +-．(2)将“美好分式”2221x x x -+-化成一个整式与一个分子为常数的分式的和的形式；(3)判断2251117x x x x x x x---÷+-的结果是否为“美好分式”，并说明理由．形式，那么称这个分式为“和谐分式”．如：514144111111x x x x x x x x ++++==+=++++++，则51x x ++是“和谐分式”．(1)下列分式中，属于“和谐分式”的是（填序号）；①23x x+；②21x x +；③21x x +-．(2)将“和谐分式”2472y y y -+-化成一个整式与一个分子为常数的分式的和的形式；(3)应用：先化简22321112a a a a a a a-+--÷--，并回答：a 取什么整数时，该式的值为整数？3a ∴=，3a ∴=时，该式的值为整数．。

华东师大版八年级下册第16章《分式》单元测试卷(原卷版+解析版)

华东师大版八年级下册第16章《分式》单元测试卷（原卷版）本试卷三个大题共22个小题，全卷满分120分，考试时间120分钟。

题号一二三全卷总分总分人1718 19 20 21 22 得分1、答题前，请考生务必将自己姓名、考号、班级等写在试卷相应的位置上；2、选择题选出答案后，用钢笔或黑色水笔把答案标号填写在选择题答题卡的相应号上。

一、选择题（本大题共12个小题，每小题4分，共48分.以下每小题都给出了A 、B 、C 、D 四个选项，其中只有一个是符合题目要求的。

）1、在代数式m 1，3b ，π1-x ，y x +2，aa 1+中，分式的个数是（）A 、2B 、3C 、4D 、52、下列各分式中，是最简分式的是（）A 、x x 22B 、1122+++x x xC 、x x 1+ D 、112--x x 3、将分式yx x42-中的x ，y 的值同时扩大为原来的2022倍，则变化后分式的值（）A 、扩大为原来的2022倍B 、缩小为原来的20221C 、保持不变D 、以上都不正确4、已知0132=+-x x ，则xx 1-的值是（） A 、5B 、7±C 、5±D 、35、若b a ≠，则下列分式化简正确的是（）A 、b a b a =--22B 、b a mb a m =+C 、b ab a =22D 、b abab =26、下列运算正确的是（）A 、692432b b a a b =•B 、2323132b a b ab =+ C 、a a a 32121=+ D 、1211112-=+--a a a 7、分式方程13132=----xx x 的解为（） A 、2=xB 、无解C 、3=xD 、3-=x8、若关于x 的分式方程2113+-=--x mx x 产生增根，则m 的值为（） A 、1-B 、2-C 、1D 、29、随着电影《你好，李焕英》热映，其同名小说的销量也急剧上升、某书店分别用400元和600元两次购进该小说，第二次数量比第一次多1倍，且第二次比第一次进价便宜4元，设书店第一次购进x 套，根据题意，下列方程正确的是（）A 、42600400=-x x B 、42400600=-x x C 、46002400=-xx D 、44002600=-xx 10、若关于x 的分式方程21121=----x k x kx 无解，则k 的值为（） A 、31-=kB 、1=kC 、31=k 或2 D 、0=k 11、已知关于x 的分式方程xkx x -=--343的解为负数，则k 的取值范围是（） A 、12-≤k 且3-≠k B 、12->k C 、12-<k 且3-≠k D 、12-<k 12、若关于x 的不等式组()⎪⎩⎪⎨⎧-≤+-≥-+12224131x a x x x 有解，且使关于y 的分式方程32221-=--+--yya y y 的解为非负数、则满足条件的所有整数a 的和为（） A 、9- B 、8- C 、5- D 、﹣4二、填空题（本大题共4个小题，每小题4分，共16分） 13、已知611=+y x ，则yxy x y xy x +-++525的值为； 14、对于实数a 、b ，定义一种新运算“*”为：ba ab a -=*，这里等式右边是实数运算。

专题5.23 分式与分式方程(全章基本概念与性质专题)八年级数学下册基础知识专项讲练(北师大版)

专题5.23分式与分式方程（全章基本概念与性质专题）（专项练习）一、单选题【性质】分式基本性质1．如果将分式xx y2+中的字母x 与y 的值分别扩大为原来的5倍，那么这个分式的值（）A ．扩大为原来的5倍B ．扩大为原来的10倍C ．缩小为原来的15D ．不改变2．如果把分式22x x y-中的x ，y 的值都扩大2倍，那么此分式的值（）A ．扩大2倍B ．扩大4倍C ．扩大6倍D ．不变【概念一】分式3．下列代数式中，属于分式的是（）A ．23-x B ．xπC ．23x +D ．124．在式子1a ，2xy π，2334a b c，56x +，109x y +，78x y +中，分式的个数是（）A ．2B ．3C ．4D ．5【概念二】最简分式5．下列分式中是最简分式的是（）A ．221x x +B ．42xC ．211x x --D ．11x x --6．下列各分式中是最简分式的是（）A ．()()1215x y x y -+B ．2222x y x y xy ++C ．()222x y x y -+D ．22x y x y-+【概念三】约分7．化简222a b a ab--的结果为（）A ．2a b a-B ．a b a-C ．a b a+D ．a b a b-+8．将分236x xy-约分的结果是（）A ．12y-B ．2x y-C ．2xy-D ．x y-【概念四】最简公分母9．分式1x y +、1x y-、221x y -的最简公分母是（）A ．()()x y x y +-B ．()()()22x y x y x y +--C ．()()22x y x y +-D ．()()22x y x y --10．212a b与2a b ab c +的最简公分母为（）A ．222a b cB ．abC ．222a b D ．2abc【概念五】通分11．把12x -，1(2)(3)x x -+，22(3)x +通分的过程中，不正确的是（）A ．最简公分母是2(2)(3)x x -+B ．221(3)2(2)(3)x x x x +=--+C ．213(2)(3)(2)(3)x x x x x +=-+-+D ．22222(3)(2)(3)x x x x -=+-+12．把2121a a a -++与211a -通分后，2121a a a -++的分母为()()211a a -+，则211a -的分子变为（）A ．1a -B ．1a ＋C ．1a --D ．1a-+【概念六】分式方程的增根13．若分式方程311x mx x -=--有增根，则m 等于（）A ．3B ．3-C ．2D ．2-14．关于x 的方程31111x mx x --=++有增根，则方程的增根是（）A ．1-B ．4C ．4-D ．2【概念七】分式方程的无解15．关于x 的方程6122=---ax x x无解，则a 的值为（）A ．1B ．3C ．1或3-D ．1或316．已知关于x 的分式方程2322x mm x x+=--无解，则m 的值是（）A ．1或13B ．1或3C ．13D ．1二、填空题【性质】分式基本性质17．已知32m n =，则m n n+的值为__________．18．不改变分式10.4210.35-+a ba b 的值，若把其分子与分母中的各项系数都化成整数，其结果为______．【概念一】分式19．下列各式：2a b -，3x x -，5y π+，a ba b+-，1()m x y -中，是分式的共有____个．20．将分式121x x ++写成除法的形式：____________________．【概念二】最简分式21．将分式2244x x +-化为最简分式，所得结果是_______．22．下列分式：①233a a ++；②22x y x y --；③22m m n；④21m +，最简分式有______（填序号）．【概念三】约分23．约分：222315a ba b =________．24．约分：22abc b c=____________．【概念四】最简公分母25．分式22a b ，1ab ，3abc的最简公分母是______________；26．分式212a b 与31ab 的最简公分母是________．【概念五】通分27．2121a a a -++与251a -通分的结果是_______．28．把分式22111221(1)x x x ⋅⋅+--通分，最简公分母是_________________．【概念六】分式方程的增根29．若关于x 的分式方程5233x mx x +=---有增根，则常数m 的值是_________．30．若关于x 的分式方程1222x mx x-=---有增根，则m 的值是_______．【概念七】分式方程的无解31．已知关于x 的分式方程11235a xx x --=+-无解，则a 的值为_____．32．若关于x 的方程301ax x+=-无解，则a 的值为______．参考答案1．D 【分析】将xx y2+的字母x 与y 的值分别扩大为原来的5倍，与原式比较即可．【详解】解：xx y2+的字母x 与y 的值分别扩大为原来的5倍得：()25522555x x xx y x y x y⨯⨯==+++所以，分式的值不变．故选D【点拨】本题考查了分式的基本性质，熟练运用分式的基本性质是解题关键．2．A【分析】根据分式的基本性质进行计算即可得出结果．【详解】解：由题意得：()()2222822==2222x x x x y x yx y ⨯---，∴把x ，y 的值都扩大2倍，分式的值扩大了2倍，故选：A ．【点拨】本题考查了分式的基本性质，熟练掌握分式的基本性质是解题的关键．3．C【分析】根据分式的定义逐个判断即可．【详解】解：A ．23-x 分母中不含字母，不是分式，故本选项不符合题意；B ．xπ分母中不含字母，不是分式，故本选项不符合题意；C ．23x +分母中含字母，是分式，故本选项符合题意；D ．12分母中不含字母，不是分式，故本选项不符合题意；故选：C ．【点拨】本题考查了分式的定义，能熟记分式的定义是解此题的关键，式子AB（A 、B 是整式）中，分母B 中含有字母，则AB叫分式．4．B【分析】判断分式的依据是看分母中是否含有字母，如果含有字母则是分式，如果不含有字母则不是分式．【详解】式子2xyπ，2334a b c，78x y +中的分母中均不含有字母，因此它们是整式，而不是分式；1a ，56x+，109x y +中分母中含有字母，因此是分式．故选B ．【点拨】本题主要考查分式的定义，注意π不是字母，是常数，所以2xyπ不是分式，是整式，掌握分母里含有字母是分式区别于整式的标志是解题的关键．5．A【分析】直接利用最简分式的定义，一个分式的分子与分母没有公因式时叫最简分式，进而分析得出答案．【详解】解：A ．221xx +的分子、分母都不能再分解，且不能约分，是最简分式，故此选项符合题意；B ．422x x=，故此选项不符合题意；C ．()()21111111x x x x x x +---==-+，故此选项不符合题意；D ．()11111x x x x ---==---，故此选项不符合题意．故选：A ．【点拨】本题考查最简分式，正确掌握最简分式的定义是解题的关键．6．B【分析】最简分式是分子，分母中不含有公因式，不能再约分的分式．判断的方法是把分子、分母分解因式，并且观察有无公因式．如果有互为相反数的因式，这样的因式可以通过符号变化化为相同的因式从而进行约分．【详解】解：A 、()()()()124155x y x y x y x y --=++，不是最简分式，不符合题意；B 、2222x y x y xy ++是最简分式，符合题意；C 、()()()()2222x y x y x y x yx y x y x y +---==+++，不是最简分式，不符合题意；D 、()()22x y x y x y x y x y x y+--==-++，不是最简分式，不符合题意；故选B ．【点拨】本题考查了最简分式，分式的化简过程，首先要把分子分母分解因式，互为相反数的因式是比较易忽视的问题．在解题中一定要引起注意．7．C【分析】分子、分母分别因式分解，约分即可得到结论．【详解】解：()()()222a b a b a b a ba ab a a b a+--+==--，故选：C ．【点拨】本题考查了分式的化简，解决问题的关键是熟练应用平方差公式．8．C【分析】依据分式的性质约分即可．【详解】解：2362x xxy y-=-故选：C ．【点拨】本题考查了分式的约分；熟练掌握分式的性质是解题的关键．9．A【分析】先把分母因式分解，再找出最简分母即可．【详解】解：221x y-的分母为：()()22x y x y x y -=+-，∴最简公分母为：()()x y x y +-，故选：A ．【点拨】本题主要考查最简公分母的定义，熟练掌握最简公分母的定义是解决本题的关键．10．A【分析】根据最简公分母的确定方法：各分母系数的最小公倍数与字母因式的最高次幂的积，进行判断即可．【详解】解：212a b与2a b ab c +的最简公分母为222a b c ；故选A ．【点拨】本题考查最简公分母．熟练掌握最简公分母的确定方法，是解题的关键．11．D【分析】按照通分的方法依次验证各选项，找出不正确的答案．【详解】A 、最简公分母为2(2)(3)x x -+，正确，该选项不符合题意；B 、221(3)2(2)(3)x x x x +=--+，通分正确，该选项不符合题意；C 、213(2)(3)(2)(3)x x x x x +=-+-+，通分正确，该选项不符合题意；D 、通分不正确，分子应为()222224(3)(2)(3)x x x x x --=+-+，该选项符合题意；故选：D ．【点拨】本题考查根据分数的基本性质，把几个异分母的分式分别化成与原来的分式相等的同分母的分式，叫做分式的通分．解题的关键是通分保证（1）各分式与原分式相等；（2）各分式分母相等．12．B【分析】直接利用已知进行通分运算，进而得出答案．【详解】解∶221111(1)(1)(1)(1)aa a a a a +==--+-+，故211a -的分子为1a +．故选∶B ．【点拨】此题主要考查了通分，正确进行通分运算是解题关键．13．D【分析】方程两边都乘以最简公分母，把分式方程化为整式方程，再求出分式方程的增根，然后代入整式方程，解关于m 的方程即可得解．【详解】解：311x mx x -=--，去分母，得3x m -=，由分式方程有增根，得到10x -=，即1x =，把1x =代入3x m -=，并解得2m =-．故选：D ．【点拨】本题考查了分式方程的增根问题，增根问题可按如下步骤进行：①让最简公分母为0确定增根；②化分式方程为整式方程；③把增根代入整式方程即可求得相关字母的值．14．C【分析】由分式方程有增根，得到10x +=，求出x 的值，将原方程去分母化为整式方程，将x 的值代入即可求出m 的值．【详解】由分式方程有增根，得到10x +=，解得：=1x -，分式方程31111x m x x --=++，去分母得311x m x --=+，将=1x -代入311x m x --=+中，得：3111m ---=-+，解得：4m =-，故选：C ．【点拨】本题考查了分式方程的增根，关键是求出增根的值，代入到分式方程化简后的整式方程中去求未知数参数的值．15．D【分析】分式方程去分母转化为整式方程，再分整式方程无解和整式方程的解是分式方程的增根两种情况进行讨论，即可得出答案．【详解】解：分式方程去分母得：26ax x =-+，整理得：()14a x -=，当a −1＝0，即a ＝1时，此时整式方程无解，分式方程无解；当a −1≠0，即a ≠1时，由()14a x -=得x ＝41a -，若此时分式方程无解，则分式方程有增根，即20x -=，增根为x ＝2，∴421a =-，解得：a ＝3，∴关于x 的方程6122=---ax x x无解时，则a 的值为1或3，故选：D ．【点拨】本题考查了分式方程无解问题，理解分式方程无解有整式方程无解和整式方程的解是分式方程的增根两种情况是解决问题的关键．16．A【分析】根据分式方程无解，需要对化简之后的整式进行讨论，可能是整式方程无解，也可能是整式方程的解是原分式方程的增根，即可求解．【详解】解：去分母得，23(2)x m m x -=-，去括号得，236x m mx m -=-，移项得，326x mx m m -=-，合并同类项得，(13)4m x m -=-，∵分式方程2322x m m x x+=--无解，∴1-3m =0或x =2，∴13m =，将x =2代入(13)4m x m -=-，得2(13)4m m -=-，解得m =1，综上，m 的值是1或13．故选A ．【点拨】本题主要考查的是利用分式方程无解求参数的值，理解分式方程无解的解题方法是解题关键．17．52【分析】设3,2m k n k ==，代入m nn+约分化简．【详解】∵32m n =，∴设3,2m k n k ==，∴32522m n k k n k ++==．故答案为：52．【点拨】本题考查了分式的约分，设3,2m k n k ==是解答本题的关键．18．4523a b a b-+【分析】根据分式的性质“分子分母同时扩大或缩小相同的倍数，分式的值不变”，分子和分母同时乘以10，即可获得答案．【详解】解：分式2110.45221130.35510a b a ba b a b --=++，分子、分母同时乘以10，则有原式4523a b a b -=+．故答案为：4523a ba b-+．【点拨】本题主要考查了分式的性质，理解并掌握分式的性质是解题关键．19．3【详解】解析：判断式子是否是分式就是看分母中是否含有字母，如果含有字母则是分式，如果不含有字母则不是分式．由此可知3x x -，a ba b+-，1()m x y -是分式，共3个．答案：3易错：4错因：误认为π是字母，错误判断5yπ+是分式．满分备考：区分整式与分式的唯一标准就是看分母，分母中不含字母的是整式，分母中含有字母的是分式．注意π是一个数，而不是字母．20．()()121x x +÷+【分析】根据分式的意义将分式写成除法形式即可．【详解】解：将分式121x x ++写成除法的形式为()()121x x +÷+．故答案为：()()121x x +÷+【点拨】本题考查了分式的意义，AB表示A B ÷，其中分数线表示相除的意思．21．22x -【分析】先把分式的分子、分母因式分解，再约分即可．【详解】解：2244x x +-()()()2222x x x +=+-22x =-．故答案为：22x -．【点拨】本题考查的是最简分式，掌握分式的约分法则是解题的关键．22．①④##④①【分析】根据最简分式的定义逐式分析即可．【详解】①233a a ++是最简分式；②22x y x y --=1x y +，不是最简分式；③22m m n =12mn，不是最简分式；④21m +是最简分式．故答案为：①④．【点拨】本题考查了最简分式的识别，与最简分数的意义类似，当一个分式的分子与分母，除去1以外没有其它的公因式时，这样的分式叫做最简分式．23．15b【分析】根据分式的基本性质解答即可．【详解】解：22231155a b a b b=；故答案为：15b．【点拨】本题考查了分式的约分，属于基础题型，熟练掌握分式的基本性质是解题的关键．24．acb【分析】根据分式的性质，分子分母同时乘以或除以相同因式时分式的值不变即可解题解答．【详解】解：22abc ac bc ac b c b bc b== 故答案为：acb【点拨】本题考查了分式的约分，熟悉分式的性质是解题关键，约分的方法是：若分子分母都是单项式，则直接求取分子分母的公因式再化简；若分子或分母是多项式，需要将分子分母因式分解后求取分子分母的公因式再化简25．2a bc【分析】各分母系数的最小公倍数和所有因式的最高次幂的积作为公分母，这样的公分母称为最简公分母，据此即可求解．【详解】解：22a b ，1ab ，3abc的最简公分母是2a bc ，故答案为：2a bc ．【点拨】本题考查了最简公分母，解题的关键是掌握最简公分母．26．232a b 【分析】根据确定最简公分母的步骤找出最简公分母即可．【详解】解：2、1的最小公倍数为2，a 的最高次幂为2，b 的最高次幂为3，所以最简公分母为232a b ．故答案为：232a b ．【点拨】本题考查了分式的基本性质，掌握分式的基本性质是关键．27．222(1)5(1),(1)(1)(1)(1)a a a a a a --++-+-【分析】找到最简公分母，根据分式的结伴行知进行通分即可；【详解】221121(1)a a a a a --=+++ ，225511a a -==--5(1)(1)a a -+-，∴最简公分母为()()211a a +-，∴通分后分别为222(1)5(1),(1)(1)(1)(1)a a a a a a --++-+-．故答案为：222(1)5(1),(1)(1)(1)(1)a a a a a a --++-+-．【点拨】本题主要考查了分式的通分，准确计算是解题的关键．28．22(1)(1)x x +-【分析】根据确定最简公分母的方法：（1）取各分母系数的最小公倍数；（2）凡单独出现的字母连同它的指数作为最简公分母的一个因式确定；（3）同底数幂取次数最高的，得到的因式的积就是最简公分母．【详解】解：∵()2221x x +=+()()2111x x x -=-+，故22x +，21x -，()21x -的最简公分母为：22(1)(1)x x +-．故答案为22(1)(1)x x +-．【点拨】本题主要考查了最简公分母的定义：取各分母系数的最小公倍数与字母因式的最高次幂的积作公分母，这样的公分母叫做最简公分母．29．8【分析】首先把所给的分式方程化为整式方程，然后根据分式方程有增根，得到30x -=，据此求出x 的值，代入整式方程求出m 的值即可．【详解】解：去分母，得：() 523x x m+=-+由分式方程有增根，得到30x -=，即3x =，把3x =代入整式方程，可得： 8m =．故答案为：8．【点拨】此题主要考查了分式方程的增根，解答此题的关键是要明确：（1）化分式方程为整式方程；（2）把增根代入整式方程即可求得相关字母的值．30．1【分析】先把分式方程去分母变为整式方程，然后把2x =代入计算，即可求出m 的值．【详解】解：∵1222x m x x-=---，去分母，得：12(2)x m x -=---；∵分式方程有增根，∴2x =，把2x =代入12(2)x m x -=---，则122(22)m -=---，解得：1m =；故答案为：1．【点拨】此题考查了分式方程的增根，增根确定后可按如下步骤进行：①化分式方程为整式方程；②把增根代入整式方程即可求得相关字母的值．31．5或112【分析】根据分式方程的解法步骤，结合分式方程无解的情况即可得到参数a 的值．【详解】解：11235a x x x --=+-，去分母得()()()()()523235x x a x x x --+-=+-，∴()112310a x a -=-，关于x 的分式方程11235a x x x --=+-无解，∴①当1120a -=时，即112a =，此时()112310a x a -=-无解；②当1120a -≠时，即112a ≠，解()112310a x a -=-得310112a x a -=-，此时分式方程无解，必须有32x =-或5x =，则31031122a x a -==--或3105112a x a-==-，i 当31031122a x a -==--时，方程无解；ii 当3105112a x a-==-时，解得5a =；综上所述，a 的值为5或112，故答案为：5或11 2．【点拨】本题考查解分式方程及由分式方程无解求参数问题，熟练掌握分式方程的解法步骤以及无解情况的分类讨论是解决问题的关键．32．0或-3【分析】先去分母化为整式方程，根据分式方程无解得到x=0或x=1或3+a=0，将解代入整式方程求出a即可．【详解】解：去分母，得3x+a（x-1）=0，∴（3+a）x-a=0，∵原分式方程无解，∴x=0或x=1或3+a=0，当x=0时，a=0；当x=1时，3+0=0，无解；∴a=0，当3+a=0时，解得a=-3，故答案为：0或-3．【点拨】此题考查了根据分式方程解的情况求参数，正确掌握解分式方程的解法是解题的关键．。

(完整版)初二分式练习题及答案

分式练习题1、（1）当x 为何值时，分式2122---x x x 有意义？（2）当x 为何值时，分式2122---x x x 的值为零？2、计算：（1）()212242-⨯-÷+-a a a a （2）222---x x x （3）x x x x x x 2421212-+÷⎪⎭⎫⎝⎛-+-+（4）x y x y x xy x y x x -÷⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--++-3232 （5）4214121111x x x x ++++++-3、计算（1）已知211222-=-x x ，求⎪⎭⎫⎝⎛+-÷⎪⎭⎫ ⎝⎛+--x x x x x 111112的值。

（2）当()00130sin 4--=x 、060tan =y 时，求y x y xy x y x x 3322122++-÷⎪⎪⎭⎫ ⎝⎛+-222y x xy x -++ 的值。

（3）已知02322=-+y xy x （x ≠0，y ≠0），求xyy x x y y x 22+--的值。

（4）已知0132=+-a a ，求142+a a 的值。

4、已知a 、b 、c 为实数，且满足()()02)3(432222=---+-+-c b c b a ，求cb b a -+-11的值。

5、解下列分式方程：（1）xx x x --=-+222；（2）41)1(31122=+++++x x x x（3）1131222=⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛+x x x x （4）3124122=---x x x x6、解方程组：⎪⎪⎩⎪⎪⎨⎧==-92113111y x y x7、已知方程11122-+=---x x x m x x ，是否存在m 的值使得方程无解？若存在，求出满足条件的m 的值；若不存在，请说明理由。

8、某商店在“端午节”到来之际，以2400元购进一批盒装粽子，节日期间每盒按进价增加20%作为售价，售出了50盒；节日过后每盒以低于进价5元作为售价，售完余下的粽子，整个买卖过程共盈利350元，求每盒粽子的进价．9、某书店老板去图书批发市场购买某种图书．第一次用1200元购书若干本，并按该书定价7元出售，很快售完．由于该书畅销，第二次购书时，每本书的批发价已比第一次提高了20%，他用1500元所购该书数量比第一次多10本．当按定价售出200本时，出现滞销，便以定价的4折售完剩余的书．试问该老板这两次售书总体上是赔钱了，还是赚钱了（不考虑其它因素）？若赔钱，赔多少？若赚钱，赚多少？10、进入防汛期后，某地对河堤进行了加固．该地驻军在河堤加固的工程中出色完成了任务．这是记者与驻军工程指挥官的一段对话:11、建筑学要求，家用住宅房间窗户的面积m 必须小于房间地面的面积n ，但窗户的面积与地面面积的比值越大，采光条件越好。

(完整版)初二分式所有知识点总结材料和常考题提高难题压轴题练习(含答案解析汇报)

初二分式所有知识点总结和常考题知识点:1. 分式：形如-,A、B是整式，B中含有字母且B不等于0的整式叫做分式.B其中A叫做分式的分子，B叫做分式的分母.2. 分式有意义的条件：分母不等于0.3. 分式的基本性质：分式的分子和分母同时乘以（或除以）同一个不为0的整式，分式的值不变•4. 约分：把一个分式的分子和分母的公因式（不为1的数）约去，这种变形称为约分.5. 通分：异分母的分式可以化成同分母的分式，这一过程叫做通分6. 最简分式：一个分式的分子和分母没有公因式时，这个分式称为最简分式，约分时，一般将一个分式化为最简分式.7. 分式的四则运算：⑴同分母分式加减法则：同分母的分式相加减，分母不变，把分子相加减.用字母表示为:⑵异分母分式加减法则：异分母的分式相加减，先通分，化为同分母的分式，然后再按同分母分式的加减法法则进行计算.用字母表示为：a c ad cbb d bd⑶分式的乘法法则：两个分式相乘，把分子相乘的积作为积的分子，把分母相乘的积作为积的分母.用字母表示为：a £空b d bd⑷分式的除法法则：两个分式相除，把除式的分子和分母颠倒位置后再与被除式相乘.用字母表示为：————adb d bc bc⑸分式的乘方法则：分子、分母分别乘方.用字母表示为:8. 整数指数幕：⑴a m a n a m n（m、n是正整数）⑵a m n a mn（m、n是正整数）⑶ab " a n b n（n是正整数）⑷ a m a n a m n（a 0，m、n是正整数，m n ）n n⑸a a-（n是正整数）b b nA. 2. A.3. A.4. .选择题（共14小题）肚古壬1 2xy 3/b 在式子丄、a2个B. 3个C. 4个D. 5个 7T6+工 2化简'‘ ”7x-l 1-Xx+1 B . x — 1 C. - x D . x的结果是如果把分式」中的x 和y 都扩大2倍，则分式的值（ xtyB.扩大2倍C.不变扩大4倍D.缩小2倍把分式方程11_1C=1的两边同时乘以 x-2 2-K1 -( 1-x ) =1 B. 1+ (1 - x ) =1 C. （x - 2）,约去分母，得（A. =x - 25.化简 1—( 1 - x ) =x — 2 D. 1+( 1-x )A. 1 a-1 6. A.巴-b7. A. 8. A. a+1 a ~2a+l B.*（ 1+—— ）的结果是 C. D. 1 J+1 丄的结果为（）B. C. D.已知关于x 的分式方程 2 B. 2下列运算正确的是（ 236a? a =a1的解是非负数，则m 的取值范围是（）x-1 1 -xC. 2 且 nn^ 3D.2 且 3)-1=-2 C ..丨：=土4D. | - 6|=69.某服装加工厂计划加工工作效率比原计划提高了加工x 套运动服，根据题意可列方程为（ 400套运动服，在加工完160套后，采用了新技术， 20%结果共用了 18天完成全部任务.设原计划每天）160 . 400-1^0 2 -1R (l + 2O%)5 aoo . 4oo-i$c 2 ■IISR (1+20%)10 .货车行驶25千米与小车行驶35千米所用时间相同，已知小车每小时比货车1⑹a n n （ a 0 , n 是正整数）a9. 分式方程的意义：分母中含有未知数的方程叫做分式方程 10. 分式方程的解法：①去分母（方程两边同时乘以最简公分母，将分式方程化为整式方程）;②按解整式方程的步骤求出未知数的值；③验根（求出未知数的值后必须验根，因为在把分式方程化为整式方程的过程中，扩大了未知数的取值范围，可能产生增根）•常考题：7中，分式的个数有（B. D.多行驶20千米，求两车的速度各为多少？设货车的速度为 x 千米/小时，依题意列方程正确的是（）12 . A , B 两地相距48千米，一艘轮船从A 地顺流航行至B 地，又立即从B 地逆流返回A 地，共用去9小时，已知水流速度为4千米/时，若设该轮船在静水中的速度为x 千米/时，则可列方程（）A .B・ T13 .计算([十斗W(i+_=)的结果为( H -1 x 2-l A . 1B. x+1 C .出 D. -J —x x-1[A^-35填空题（共13小题）计算：| ■「. =一若分式斗有意义，则实数x 的取值范围是 17 .分式方程金-二1的解x= ______ .x+1 18 .若代数式-^--1的值为零，则x= _________x-1 19 .化简（nrf!）的结果是 ______________ .9才十4u+4 xF-4 x-220 .化简: 西二35 x x+2011.如图，设k 哼吕— (a >b >0),则有(甲乙A k >2 B. 1< k v 2 —Di "一C.+4=9 D.9& 卄 96w+4 x-414.若分式諾怎IT 苍影"£（A, B 为常数），则A ，B 的值为（ 15 . 16 . C.23. 已知关于x 的方程彎詡勺解是正数'则m 的取值范围是 24. a 、b 为实数，且 ab=1,设 P= , Q=，，则 PQ （填“〉”a+1 M a+1 b+1 ----------“V” 或“=”.25.如果实数x 满足x 2+2x - 3=0,那么代数式的值为 _______ .26. 某工厂现在平均每天比原计划多生产 50台机器，现在生产600台机器所需时间与原计划生产450台机器所需时间相同，现在平均每天生产 _________ 台机器. 27. 杭州到北京的铁路长1487千米.火车的原平均速度为x 千米/时，提速后平均速度增加了 70千米/时，由杭州到北京的行驶时间缩短了 3小时，则可列方程为 _________ . 三.解答题（共13小题）28. 先化简，再求值：（［— 、十 _，其中^W&.时1 宀1 29.先化简代数式，然后选取一个使原式有意义的a 值3-1a-2a+l a_1代入求值.30. 已知 x - 3y=0，求 .？（ x -y ）的值.31. 解方程：—一•二亠.st-2 2-K 32.先化简，再求值：，其中x 是不等式3x+7> 1的负整数解.233. 先化简空学十（a+1） + ： T ，然后a 在-1、1、2三个数中任选一个合a_1a 2-2a+l 适的数代入求值. 34. 解分式方程：」2 -35. 已知A = ：「-亠 i 2-l 日121. 22.计算（4-希）的结果是若关于x 的方程为占+1无解，则a的值是（1）化简A;（2）当x满足不等式组且x为整数时，求A的值.36. 甲、乙两个工程队共同承担一项筑路任务，甲队单独施工完成此项任务比乙队单独施工完成此项任务多用10天，且甲队单独施工45天和乙队单独施工30 天的工作量相同.(1)甲、乙两队单独完成此项任务需要多少天？(2)若甲、乙两队共同工作了3天后，乙队因设备检修停止施工，由甲队继续施工，为了不影响工程进度，甲队的工作效率提高到原来的2倍，要使甲队总的工作量不少于乙队的工作量的2倍，那么甲队至少再单独施工多少天？37. 某商家预测一种应季衬衫能畅销市场，就用13200元购进了一批这种衬衫，面市后果然供不应求，商家又用28800元购进了第二批这种衬衫，所购数量是第一批购进量的2倍，但单价贵了10元.(1)该商家购进的第一批衬衫是多少件？(2)若两批衬衫按相同的标价销售，最后剩下50件按八折优惠卖出，如果两批衬衫全部售完后利润不低于25% (不考虑其他因素)，那么每件衬衫的标价至少是多少兀？38. 从广州到某市，可乘坐普通列车或高铁，已知高铁的行驶路程是400千米，普通列车的行驶路程是高铁的行驶路程的 1.3倍.(1)求普通列车的行驶路程；(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍，且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时，求高铁的平均速度. 39. 学校计划选购甲、乙两种图书作为“校园读书节”的奖品.已知甲图书的单价是乙图书单价的1.5倍；用600元单独购买甲种图书比单独购买乙种图书要少10本.(1)甲、乙两种图书的单价分别为多少元？(2)若学校计划购买这两种图书共40本，且投入的经费不超过1050元，要使购买的甲种图书数量不少于乙种图书的数量，则共有几种购买方案？40. 某汽车销售公司经销某品牌A款汽车，随着汽车的普及，其价格也在不断下降.今年5月份A款汽车的售价比去年同期每辆降价1万元，如果卖出相同数量的A 款汽车，去年销售额为100万元，今年销售额只有90万元.(1)今年5月份A款汽车每辆售价多少万元？(2)为了增加收入，汽车销售公司决定再经销同品牌的B款汽车，已知A款汽车每辆进价为7.5万元，B款汽车每辆进价为6万元，公司预计用不多于105万元且不少于99万元的资金购进这两款汽车共15辆，有几种进货方案？(3)如果B款汽车每辆售价为8万元，为打开B款汽车的销路，公司决定每售出一辆B款汽车，返还顾客现金a万元，要使(2)中所有的方案获利相同，a 值应是多少？此时，哪种方案对公司更有利？初二分式所有知识点总结和常考题提高难题压轴题练习（含答案解析）参考答案与试题解析一•选择题（共14小题）1. （2012春？潜江期末）在式子丄a 分式的个数有（）A. 2个B. 3个C. 4个D. 5个【分析】判断分式的依据是看分母中是否含有字母，如果含有字母则是分式，如果不含有字母则不是分式.【解答】解：丄、丄、9x+J这3个式子的分母中含有字母，因此是分式.a 6+s y其它式子分母中均不含有字母，是整式，而不是分式. 故选：B.【点评】本题考查的是分式的定义，在解答此题时要注意分式是形式定义，只要是分母中含有未知数的式子即为分式.22. （2014?南通）化简’彳的结果是（）x-1 1-JA. x+1 B . x - 1 C.- x D . x【分析】将分母化为同分母，通分，再将分子因式分解，约分.2 2【解答】解：-二^—--^-x-l 1-J 1-1 旷12=•K-1=-■- - -< -L:x-1=x，故选：D.【点评】本题考查了分式的加减运算.分式的加减运算中，如果是同分母分式，那么分母不变，把分子直接相加减即可；如果是异分母分式，则必须先通分，把异分母分式化为同分母分式，然后再相加减.3. （2012?岳麓区校级自主招生）如果把分式严一中的x和y都扩大2倍，贝扮式的值（）A.扩大4倍B.扩大2倍C.不变D.缩小2倍【分析】把分式王中的x和y都扩大2倍，分别用2x和2y去代换原分式中的x+y x和y，利用分式的基本性质化简即可.【解答】解：原式 a+1 Ca-1a+1 a _l 故选A.【点评】 6. A.巴-1a+本题主要考查分式的混合运算，通分、因式分解和约分是解答的关键. （2008?黄冈）计算：二二的结果为（b a aC.【分析】先算小括号里的，再把除法统一成乘法，约分化为最简. 【解答】解：「=—，故选A.b a a ab a+b b【点评】分式的四则运算是整式四则运算的进一步发展，在计算时, 首先要弄清【解答】解：把分式中的x 和y 都扩大2倍后得:x+y【点评】根据分式的基本性质，无论是把分式的分子和分母扩大还是缩小相同的倍数，都不要漏乘（除）分子、分母中的任何一项.4. （2005?扬州）把分式方程二1的两边同时乘以（x - 2）,约去分母，得（）A. 1 -（ 1-x ） =1B. 1+（ 1 - x ） =1C. 1 -（1 - x ） =x - 2D. 1+（ 1-x ） =x - 2【分析】分母中x - 2与2-x 互为相反数，那么最简公分母为（x - 2）,乘以最简公分母，可以把分式方程转化成整式方程.【解答】解：方程两边都乘（x - 2），得：1+ （1 - x ） =x - 2. 故选：D.【点评】找到最简公分母是解答分式方程的最重要一步；注意单独的一个数也要乘最简公分母；互为相反数的两个数为分母，最简公分母为其中的一个，另一个乘以最简公分母后，结果为-1.2玄吃y =4zy = 2Ci+y) 2 Cz+05. （2013?临沂）化简 a+l 2A. C. a^-Za+l—D.*( 1+—— a _l ] J+1 ）的结果是【分析】首先对括号内的式子通分相加，然后把除法转化成乘法, 进行约分即可. 即分式的值扩大2倍. 故选：B.a+1 Ca-1 )2 a+b楚运算顺序，先去括号，再进行分式的乘除.7. （2014?黑龙江）已知关于x 的分式方程』-丄=1的解是非负数，则 m 的玄一1 1-x 取值范围是（） A. m > 2 B. m > 2C. m > 2 且3 D. m >2 且3【分析】分式方程去分母转化为整式方程，求出整式方程的解表示出 x ,根据方程的解为非负数求出m 的范围即可.【解答】解：分式方程去分母得：m- 3=x - 1，解得：x=mn 2，由方程的解为非负数，得到 m- 2>0,且m- 2工1，解得：m >2且m ^3. 故选：C【点评】此题考查了分式方程的解，时刻注意分母不为 0这个条件. 8. （2009?潍坊）下列运算正确的是（）A 、 a 2? a 3=a 6 B.（丄）-1=-2 C . | ,=±4D. | - 6|=6【分析】幕运算的性质：① 同底数的幕相乘，底数不变，指数相加；② 一个数的负指数次幕等于这个数的正指数次幕的倒数，算术平方根的概念：一个正数的正的平方根叫它的算术平方根， 0的算术平方根是0.绝对值的性质：正数的绝对值等于它本身，负数的绝对值等于它的相反数， 0的绝对值是0.【解答】解：A 、a 2? a 3=a 5,故A 错误； B 、（丄）-1=2,故B 错误；C 、 .「=4,故C 错误；D 根据负数的绝对值等于它的相反数，故 D 正确. 故选D.【点评】本题涉及知识：负指数为正指数的倒数；任何非 0数的0次幕等于1；绝对值的化简；二次根式的化简.9. （2013?本溪）某服装加工厂计划加工400套运动服，在加工完160套后，采用了新技术，工作效率比原计划提高了 20%结果共用了 18天完成全部任务.设原计划每天加工x 套运动服，根据题意可列方程为（160 丄 400 B 160 , 400-160 160 , 400-1611 . . n goo , 400-1^0 .-【分析】关键描述语为：“共用了 18天完成任务” 用的时间+采用新技术后所用的时间=18.A. C.等量关系为：采用新技术前上〔-卜）天-■■ I -:方程可表示为： 4一二・:：.x （1+20%）K故选：B.【点评】列方程解应用题的关键步骤在于找相等关系.找到关键描述语，找到等量关系是解决问题的关键.本题要注意采用新技术前后工作量和工作效率的变化. 10. （2014?黔南州）货车行驶25千米与小车行驶35千米所用时间相同，已知小车每小时比货车多行驶20千米，求两车的速度各为多少？设货车的速度为x 千米/小时，依题意列方程正确的是（）A 25 _ 35B 25C 25 _ 35D 亞二35x _K-20 K-20-x x -乂十20 疋+加-丈【分析】题中等量关系：货车行驶25千米与小车行驶35千米所用时间相同，列出关系式.【解答】解：根据题意，得25 _ 35K ~K+20'故选：C.【点评】理解题意是解答应用题的关键，找出题中的等量关系，列出关系式. 【解答】解：采用新技术前用的时间可表示为: 丄天，采用新技术后所用的时甲图中护幕部2直和乙图中阴影部分面（a>b>0），则有（甲乙A k>2 B. 1< k v 2 C・£g【分析】分别计算出甲图中阴影部分面积及乙图中阴影部分面积, 即可.【解答】解：甲图中阴影部分面积为a2- b2，乙图中阴影部分面积为a （a- b），则k= = •亠=1丄，aka-M aU-W a aI a> b> 0，然后计算比值11. （2013?杭州）如图，设k=••• 1v_+1v 2,••• 1v k v 2 故选B.【点评】本题考查了分式的乘除法，会计算矩形的面积及熟悉分式的运算是解题的关键.12.（2016?本溪一模）A ，B 两地相距48千米，一艘轮船从 A 地顺流航行至B 地，又立即从B 地逆流返回A 地，共用去9小时，已知水流速度为4千米/时，若设该轮船在静水中的速度为x 千米/时，则可列方程（C. 【分析】本题的等量关系为：顺流时间+ 逆流时间=9小时. 【解答】解：顺流时间为：；逆流时间为：_丄. 工+4 x-4所列方程为：+ 亠=9. x+4 *-4故选A.【点评】未知量是速度，有速度，一定是根据时间来列等量关系的.找到关键描述语，找到等量关系是解决问题的关键. 13. （2005?武汉）计算Cl+-fy ）的结果为（）A. 1B. x+1 C .丄 D.—x x-l|【分析】先算括号里的通分，再进行因式分解，将除号换为乘号，最后再进行分式间的约分化简.故选C.【点评】注意：当整式与分式相加减时，一般可以把整式看作分母为 1的分式,与其它分式进行通分运算. 14 （2004?十堰）若分式二十甘（A，B 为常数），则A ，B 的【分析】对等式右边通分加减运算和，再根据对应项系数相等列方程组求解即可.牡-9 仗-1) (3时 R 二0-證)*- (A+2B)C3x+2)(x-l)= C3x+2)(x-l) = (3x+2)(x-l)所以記二4,【解答】<-1 1 -X ■ fl J.丄K —1+1 . S 1一筈_（时1）上—DA +1JK_1' X 2-12X 2值为（A. B.A=7C.A-lD.C A--35【解答】解:A.—+4=9 D.解:解得严I（B=l故选B.【点评】此题考查了分式的减法，比较灵活，需要熟练掌握分式的加减运算.二•填空题（共13小题）15. （2014?陕西）计算：| 一'= 9 .【分析】根据负整数指数幕的运算法则进行计算即可.【解答】解：原式=I =一=9.（斗1■ d丿9故答案为：9.【点评】本题考查的是负整数指数幕，即负整数指数幕等于该数对应的正整数指数幕的倒数.16. （2014?衢州）若分式」=有意义，则实数x的取值范围是x工5 .K-5【分析】由于分式的分母不能为0，x - 5为分母，因此x - 5工0，解得x.【解答】解：•••分式丄有意义，二x - 5工0，即卩x工5. 故答案为：x丰5.【点评】本题主要考查分式有意义的条件：分式有意义，分母不能为0.17. （2013?梅州）分式方程的解x= 1 .【分析】本题的最简公分母是x+1，方程两边都乘最简公分母，可把分式方程转换为整式方程求解.结果要检验.【解答】解：方程两边都乘x+1，得2x=x+1，解得x=1.检验：当x=1时，x+1 0.••• x=1是原方程的解.【点评】（1）解分式方程的基本思想是“转化思想”，方程两边都乘最简公分母, 把分式方程转化为整式方程求解.（2）解分式方程一定注意要代入最简公分母验根.18. （2013?临夏州）若代数式一的值为零，贝U x= 3x-1【分析】由题意得=0,解分式方程即可得出答案./-I【解答】解：由题意得，-1=0,M~1解得：x=3,经检验的x=3是原方程的根. 故答案为：3.【点评】此题考查了分式值为0的条件，属于基础题，注意分式方程需要检验. 19. （2013?凉山州）化简（吋1）的结果是 m .in+1【分析】本题需先把（m+1与括号里的每一项分别进行相乘，再把所得结果相加即可求出答案.【解答】解：」十亠 =（m+1 - 1 =m故答案为：m【点评】本题主要考查了分式的混合运算，在解题时要把（ m+1分别进行相乘是解题的关键.【分析】先将x 2 - 4.Qi［解答】解.丁 --=；+•：：「+ •： ■■- 1= .一 =二答： -7- <I ■ ：' > - ' ■: :- > ■' " ' ■ - ：【点评】本题考查了分式的计算和化简.解决这类题关键是把握好通分与约分. 式加减的本质是通分，乘除的本质是约分. 法则变形，约分即可得到结果.故答案为：丄a-b【点评】此题考查了分式的混合运算，熟练掌握运算法则是解本题的关键. 22. （2013?绥化）若关于x 的方程耳」=+1无解，则a 的值是 2或1 .x-2【分析】把方程去分母得到一个整式方程，把方程的增根 x=2代入即可求得a 的值.【解答】解：x - 2=0,解得：x=2.方程去分母，得：ax=4+x - 2，即（a - 1） x=2X 2-H 4K +4 K=丨2 X 2 -4 Z一2一. 20. （2013?衢州）化简:丄【分析】原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法21. （2015?黄冈）计算宁（1-亠）的结果 a+b【日瓦疋【解答】解: 原式a+b-a = b a+b (耳b) (a-b)b ta+b)(a-b)当a - 1工0时，把x=2代入方程得：2a=4+2- 2, 解得：a=2. 当a -仁0,即a=1时，原方程无解. 故答案是：2或1.【点评】首先根据题意写出a 的新方程，然后解出a 的值.23. （2013?德阳）已知关于x 的方程亠-二已的解是正数，贝U m 的取值范围是m>—6且仃严―4.【分析】首先求出关于x 的方程二:;的解，然后根据解是正数，再解不等式求出m 的取值范围.【解答】解：解关于x 的方程得x=m+6 •••方程的解是正数，二 m+6>0 且 m+O2，解这个不等式得 m> — 6且m^ — 4. 故答案为：m> — 6且m^ — 4.【点评】本题考查了分式方程的解，是一个方程与不等式的综合题目，解关于 x的方程是关键，解关于x 的不等式是本题的一个难点. 24.（2009?枣庄）a 、b 为实数，且 ab=1,设 P= ' ，Q= ，贝UPa+1 b+1a+1 屏 1—Q （填 “〉”、“v” 或“=”）.即可得出结论. :I =1 ；■ ■■.-Ji.=；【点评】解答此题关键是先把所求代数式化简再把已知代入即可.' 1 1 .i - I .1 (a+1) (b+1) ab+a+b+1【分析】将两式分别化简，然后将ab=1代入其中，再进行比较, 【解答】解：：P2+a+b2+a+b =1；，把ab=1代入得: ab=1代入得:【点评】本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键.26. （2013?呼和浩特）某工厂现在平均每天比原计划多生产 50台机器，现在生产600台机器所需时间与原计划生产 450台机器所需时间相同，现在平均每天生产 200台机器.【分析】根据现在生产600台机器的时间与原计划生产450台机器的时间相同.所以可得等量关系为：现在生产600台机器时间二原计划生产450台时间.【解答】解：设：现在平均每天生产x 台机器，则原计划可生产（x - 50）台. 依题意得：丄=^^.解得：x=200.检验：当 x=200 时，x （x - 50）工 0. ••• x=200是原分式方程的解.•••现在平均每天生产200台机器. 故答案为：200.【点评】此题主要考查了分式方程的应用，重点在于准确地找出相等关系，这是列方程的依据.而难点则在于对题目已知条件的分析，也就是审题，一般来说应用题中的条件有两种，一种是显性的，直接在题目中明确给出，而另一种是隐性的，是以题目的隐含条件给出.本题中“现在平均每天比原计划多生产 50台机器”就是一个隐含条件，注意挖掘.27. （2013?舟山）杭州到北京的铁路长1487千米.火车的原平均速度为x 千米 /时，提速后平均速度增加了 70千米/时，由杭州到北京的行驶时间缩短了【点评】此题考查了由实际问题抽象出分式方程，关键是读懂题意，找出题目中的等量关系并列出方程. 三.解答题（共13小题）28. （2013?眉山）先化简，再求值:工-2），其中^W6.【分析】这道求代数式值的题目，不应考虑把x 的值直接代入，通常做法是先把代数式去括号，把除法转换为乘法化简，然后再代入求值. 【解答】解：原式=•■ + （x - 2）（3分）^+1 12【分析】先分别求出提速前和提速后由杭州到北京的行驶时间, 北京的行驶时间缩短了 3小时，即可列出方程. 【解答】解：根据题意得：再根据由杭州到故答案为:迴__迴_=3x K +70 =时，则可列方程为=x （x —1）+ （x —2）=x - 2; （2 分）当X 二后时，贝U 原式的值为（后）2 - 2=4. （2分）【点评】分式混合运算要注意先去括号；分子、分母能因式分解的先因式分解; 除法要统一为乘法运算.29. （2005?徐州）先化简代数式■ -1- |-:,然后选取一个使原式a ?-2a+L 冋有意义的a 值代入求值.【分析】本题考查的化简与计算的综合运算，关键是正确进行分式的通分、约分,【点评】此题考查了分式的化简求值，取合适的值代入原式求值时，要特注意原式及化简过程中的每一步都有意义.30. （2015?甘南州）已知x - 3y=0，求 ? （x - y ）的值.【分析】首先将分式的分母分解因式，然后再约分、化简，最后将 x 、y 的关系式代入化简后的式子中进行计算即可. 【解答】解: 邛V ；（4分）2y 2 【点评】分式混合运算要注意先去括号；分子、分母能因式分解的先因式分解; 除法要统一为乘法运算.31. （2013?普洱）解方程：^―-=—.【分析】观察可得2 - x= -（x - 2），所以可确定方程最简公分母为：（x - 2），然后去分母将分式方程化成整式方程求解.注意检验.（2分）当 x - 3y=0 时，x=3y ; （6分）.（8 分）【解答】解：方程两边同乘以（x-2），得：x - 3+ (X — 2) =-3, 解得x=1, 检验：x=1时，x - 2工0, ••• x=1是原分式方程的解. 【点评】(1)解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解. (2) 解分式方程一定注意要验根.(3) 去分母时有常数项的不要漏乘常数项. 32. (2013?重庆)先化简，再求值: 3x+7> 1的负整数解. 其中x 是不等式【分析】首先把分式进行化简，再解出不等式，确定出 x 的值，然后再代入化简【解答】解：原式=[ (r+2) (i-2) xCx-2) =x-4 乂(耳-2)亠 xCx-2)x-4 ' 年, 后的分式即可.3x+7> 1， 3x >- 6， x >- 2， ••• x 是不等式3x+7> 1的负整数解, ••• x=- 1，把x=- 1代入丄中得： =3. x -1【点评】此题主要考查了分式的化简求值, 分式进行化简. 以及不等式的整数解，关键是正确把 33. (2013?巴中)先化简墮坦十(a+1) a-1 2, + -- -------- ，然后a 在-1、吕-2a+L 1、2三个数中任选一个合适的数代入求值. 【分析】先根据分式混合运算的法则把原式进行化简, 进行计算即可.【解答】解：原式亠鼻？亠+ - ^-1 我 1 (a-1) 2再选取合适的a 的值代入 2 i ^+1 a-1 a _l a+3 a-1当 a=2 (a ^- 1, a ^ 1)时，原式='=5.2-1【点评】本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键.34. (2013?陕西)解分式方程：- ^^=1.【分析】分式方程去分母转化为整式方程，求出整式方程的解得到x 的值，经检验即可得到分式方程的解.【解答】解：去分母得：2+x (x+2) =x 2- 4, 解得：x= - 3,经检验x=- 3是分式方程的解.【点评】此题考查了解分式方程，解分式方程的基本思想是“转化思想” ，把分式方程转化为整式方程求解.解分式方程一定注意要验根.35. (2015?广州)已知 A 」、〕-严-1 日(1) 化简A ;(2) 当x 满足不等式组卩且x 为整数时，求A 的值.【分析】(1)根据分式四则混合运算的运算法则，把 A 式进行化简即可.(2)首先求出不等式组的解集，然后根据 x 为整数求出x 的值，再把求出的x 的值代入化简后的A 式进行计算即可. 【解答】解：(1)A 」+?汁I -—(2)・二仁＜3K x v 3， ••• x 为整数， ••• x=1 或 x=2, ①当x=1时， •/ x - 1工0，&+L) (x-1)R-l K-1实用文档••• A 」一中x 丰1,x-1•••当x=1时，A= I 无意义. K-1②当x=2时，【点评】（1）此题主要考查了分式的化简求值，注意化简时不能跨度太大，而缺少必要的步骤.（2）此题还考查了求一元一次不等式组的整数解问题，要熟练掌握，解决此类问题的关键在于正确解得不等式组或不等式的解集，然后再根据题目中对于解集的限制得到下一步所需要的条件，再根据得到的条件求得不等式组的整数解即可.36. （2013?哈尔滨）甲、乙两个工程队共同承担一项筑路任务，甲队单独施工完成此项任务比乙队单独施工完成此项任务多用 10天，且甲队单独施工45天和乙队单独施工30天的工作量相同.（1）甲、乙两队单独完成此项任务需要多少天？（2）若甲、乙两队共同工作了 3天后，乙队因设备检修停止施工，由甲队继续施工，为了不影响工程进度，甲队的工作效率提高到原来的2倍，要使甲队总的工作量不少于乙队的工作量的 2倍，那么甲队至少再单独施工多少天？【分析】（1）设乙队单独完成此项任务需要x 天，则甲队单独完成此项任务需要（x+10）天，根据甲队单独施工45天和乙队单独施工30天的工作量相同建立方程求出其解即可；（2）设甲队再单独施工a 天，根据甲队总的工作量不少于乙队的工作量的 2倍建立不等式求出其解即可.【解答】解：（1）设乙队单独完成此项任务需要x 天，则甲队单独完成此项任务需要（x+10）天，由题意'得解得：x=20.经检验，x=20是原方程的解，• x+10=30 （天）答：甲队单独完成此项任务需要 30天，乙队单独完成此项任务需要 20天；a 天，由题意，得解得：a >3.答：甲队至少再单独施工3天.【点评】本题是一道工程问题的运用，考查了工作时间x 工作效率 =工作总量的运用，列分式方程解实际问题的运用，分式方程的解法的运用，解答时验根是学生容易忽略的地方.1 -1 =1A L-1 12-1 （2）设甲队再单独施工。

第五章第02讲分式的乘除法(6类热点题型讲练)(解析版)--初中数学北师大版8年级下册

第02讲分式的乘除法(6类热点题型讲练)1.掌握分式的乘除运算法则；2.能够进行分子、分母为多项式的分式乘除法运算.知识点01分式的乘法乘法法则：分式乘分式，用分子的积作为积的分子，分母的积作为积的分母．用式子表示为：a c a cb d b d⋅⋅=⋅．知识点02分式的除法除法法则：分式除以分式，把除式的分子、分母颠倒位置后与被除式相乘．用式子表示为：a c a d a db d bc b c⋅÷=⋅=⋅．知识点03分式的乘方乘方法则：分式的乘方，把分子、分母分别乘方．用式子表示为：((nn n a a n b b=为正整数，0)b ≠．题型01分式的乘法运算题型02分式的除法运算题型03分式乘除混合运算题型04分式的乘方运算题型05含乘方的分式乘除混合运算题型06分式乘除混合运算中化简求值1．（2024上·河南信阳·八年级统考期末）化简2223a b ⎛⎫- ⎪⎝⎭的结果是（）A ．2249a b-B ．2249a bC ．4249a b-D ．4249a b【答案】D【分析】本题考查了分式乘方运算，根据分式性质结合乘方法则进行运算，即可作答．【详解】解：依题意，22422439a a b b ⎛⎫-= ⎪⎝⎭，故选：D ．2．（2023下·四川达州·八年级校考阶段练习）下列运算结果为1x -的是（）A ．211x x --B ．211x x x x -⋅+C ．111x x x +÷-D ．2211x x x +++【答案】B【分析】通过约分化简即可判定A 、D ，根据分式的乘法法则计算判定C ，根据分式除法法则计算判定C ．【详解】解：A ．原式()()1111x x x +-==+-x ，故此选项不符合题意；B ．原式()()1111x xx xx +-=⋅=-+x ，故此选项符合题意；C ．原式()2111x x x x x+-=⋅-=，故此选项不符合题意；D ．原式()2111x x x +==++，故此选项不符合题意．故选：B ．【点睛】本题词考查分式化简和分式乘除法，熟练掌握分式化简与分式乘除法法则是解题的关键．3．（2024上·广西河池·八年级统考期末）下列各式计算错误的是（）A ．2310542114ab xy ax y b x-⋅=-B ．2234283xy x y yyz yz x÷=C ．()221a b a ab a a-÷-=D ．33()a a bb-÷=【答案】D【分析】本题主要考查了分式的乘除运算．根据分式的乘除运算法则计算，即可求解．【详解】解：A 、2310542114ab xy ax y b x-⋅=-，故本选项正确，不符合题意；则第4次运算的结果4y=．。

初二数学下册分式练习题

初二数学下册分式练习题分式是数学中的重要概念，它能够帮助我们更好地理解和解决一些复杂的问题。

在初二数学的下册中，分式是一个重要的内容，这里我们将针对分式进行一些练习题，让我们通过实际的练习，加深对分式的理解和运用能力。

1. 约分与化简(1) 将分式 $\frac{12}{18}$ 进行约分。

解析：我们需要找到分子和分母的最大公因数，然后将分子和分母都除以这个公因数即可。

对于 $\frac{12}{18}$，最大公因数是6，因此可以得到化简后的分式 $\frac{2}{3}$。

(2) 将分式 $\frac{24x^3y^2}{12x}$ 进行化简。

解析：首先，我们可以将分子和分母都进行因式分解。

分子的因式分解为 $24x^3y^2 = 2 \times 2 \times 2 \times 3 \times x \times x \times x\times y \times y$，分母的因式分解为 $12x = 2 \times 2 \times 3 \times x$。

接下来，我们可以将分子和分母的公因式约去，化简得到$\frac{2xy^2}{1}$，也可以简写为 $2xy^2$。

2. 乘法与除法(1) 计算 $\frac{1}{3} \times \frac{4}{5}$。

解析：乘法的原则是将分子相乘，分母相乘。

因此，$\frac{1}{3}\times \frac{4}{5} = \frac{1 \times 4}{3 \times 5} = \frac{4}{15}$。

(2) 计算 $\frac{4}{7} \div \frac{2}{3}$。

解析：除法的原则是将除数取倒数，然后与被除数进行乘法运算。

因此，$\frac{4}{7} \div \frac{2}{3} = \frac{4}{7} \times \frac{3}{2} =\frac{12}{14}$。

再进行约分，得到最简分式 $\frac{6}{7}$。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

分式专题题型一：分式的概念：【例题1】

下列各式：5.043,23,33,,22,22xxyxxxyxxx，其中分式有______个. （） A、1 B、2 C、3 D、4 【练一练】 1. 下列式子中，属于分式的是（） A、1 B、3x C、11x D、52

2. 下列式子中，2a，3x，1mm，23x，5，2aa，23．哪些是整式？哪些是分式？整式有：________________________________；分式有：________________________________；

题型二：分式有意义，分式值为0：【例题2】

下列各式中，（1）2mm；（2）1||2m；（3）239mm．m取何值时，分式有意义？

【练一练】 1. x为任意实数，分式一定有意义的是（）

A、21xx B、112xx C、112xx D、11xx

2. 若代数式4xx有意义，则实数x的取值范围是________________. 3. (1)若分式11x有意义，则x的取值范围是________________； (2)已知分式axxx532，当2x时，分式无意义，则a_______________________. 4. 若不论x取何实数，分式mxxx6322总有意义，则m的取值范围是______________________. 【例题3】当x为何值时，（1）2132xx；（2）221xxx；（3）224xx．各式的值为0．

【练一练】 1. 已知分式11xx的值是零，那么x的值是（） A、-1 B、0 C、1 D、1

2. 若分式112xx的值是零，则x的值为（） A、-1 B、0 C、1 D、1 3.(1)如果分式212xxx的值为零，那么x的值为_____________________；

(2)当x______________时，分式123xx的值是零；(3)当x______________时，分式112xx的值为零. 【例题4】当x满足什么条件时，分式2122xxx的值是负数？正数？

【练一练】 1.(1)若分式1232aa的值为负数，则a的取值范围为__________________； (2)当整数x_____________时，分式16x的值是负整数； (3)已知点)82017,22018(2nnn在第四象限，则n的取值范围是______________________. 2. 当x为何值时，分式232xx的值为正数？负数？题型三：分式的基本性质I(分子、分母同乘或除以一个不等于0的数或整式)：【例题5】

如果把分式中的都扩大3倍，那么分式的值（）

A、扩大3倍 B、不变 C、缩小3倍 D、扩大2倍【例题6】不改变分式的值，将下列分式的分子、分母中的系数化为整数．

（1）0.20.020.5xyxy

（2）11341123xyxy 【练一练】 1. 如果把分式yxxy中的x和y都扩大为原来的2倍，那么分式的值（） A、扩大为原来的4倍 B、扩大为原来的2倍 C、不变 D、缩小为原来的21 2. 如果把分式yxyx2中的x和y都缩小为原来的31，那么分式的值（） A、扩大为原来的3倍 B、缩小为原来的31 C、缩小为原来的91 D、不变 3. 分式x11可变形为（） A、11x B、x11 C、x11 D、11x

yxx232yx,4. 不改变分式的值，将下列分式的分子、分母中的系数化为整数．并将较大的系数化成正数. (1) xxxx24.03.12.001.032

(2) yxyx5.12.041 题型四：分式的基本性质II(约分和通分)：【例题7】

约分：（1）；（2）；

（3）1616822aaa，其中5a （4）yxyx2422，其中1,3yx 【练一练】 1. 约分：

(1) 2323510cbabca (2))(3)(2babbaa (3)32)()(axxa (4)393xx (5)2222222yxyxxyyx (6)2222)1()1()1(xxx 2. 先化简，再求值： (1) 22)2(1)(4xxxx，其中7x (2)已知212yxyx，，求2222222yxyxyx的值.

【例题8】通分： (1)分式abcbaab3,1,22的最简公分母是________；(2)分式222,7nmmnnm的最简公分母是____________； (3)分式122,1441,1232aaaa的最简公分母是______________________； (4)分式2222222,2,babacbababbaa的最简公分母是_____________________________；

(5)分式22941,461,461yyyxyx的最简公分母是_____________________________________； (6)分式acbbaccba107,23,5422的最简公分母是__________，通分时，这三个分式的分子分母依次乘以_______________，____________，_______________. 【练一练】通分：

（1）xzxzyx45,34,2123 （2）32)1(,)1(,1azayax （3）42,882,4422acaabaaa 【例题8】已知xyyx4，求yxyxyxyx2232的值

【练一练】 1. 若2abba，则22224babababa___________；若311yx，则代数式yxyxyxyx22142____________；

2. 已知311yx，求yxyxyxyx2232的值.

题型五：分式的加减：【例题9】计算：

（1）（2）（3）

（4）（5）（6）． 222

22333abababababab222422xxxxx22

2222222aabb

abbaab

21132aab2312224xxxx2

11aaa【练一练】 1. (1)111xxx=_________；(2)xyxyxy=_________；(3)2222235baababa=__________. 2. (1)已知1,3abba，则abba___________；(2)已知0322baba，则abba__________. 3.（1）（2）（3）222442242xxxxxx

【例题10】已知，求整式A，B．

【练一练】 1. 若11)1)(1(3xBxAxxx，求整式A，B.

22256343333abbaababcbaccba22

22()()ab

abba

34(1)(2)12xABxxxx

题型六：分式的乘除：【例题11】计算：

(1) (2) (3) (4)．

【练一练】 1．计算：

（1）32232)()2(yxxy （2）xxxxxx22211

2．先化简，再求值：（1）其中（2）其中＝－1．

3．已知求的值．

422449158abxxabg222441214aaaaaag222324ababccd



22242222xyxyxxyyxxy





,144421422xxxxx14x,ab.bbaababaa222224)()(

,21ab

.0)255(|13|2baba3232322

36().()()aabbabba题型七：分式方程：【例题12】解分式方程：

（1）（2）（3）

【练一练】（1）0122xx （2）22231xxx （3）xxx23123 （4）1132xxxx

题型七：分式方程增根问题：【例题13】

（1）若分式方程有增根，求值；

10522112xx225103xxxx21233xxx



223242mxxxxm（2）若分式方程有增根，求的值．【练一练】 1、若关于x的方程0111xxxm有增根，则m的值是（） A、3 B、2 C、1 D、－1 2、若关于x的分式方程1322mxxx有增根，则m的值是（） A、1m B、2m C、3m D、0m或3m 3、若关于x的方程0552xmxx有增根，则m的值是（） A、-2 B、-3 C、5 D、3

4、如果方程有增根，那么增根是_____．若方程114112xxx有增根，则增根是______．

5、已知分式方程5133xmxx有增根，则m的值为．

6、(1)若关于x的分式方程xxxm2132有增根，则该方程的增根为________________； (2)若关于x的方程2222xmxx有增根，则m的值是__________________.

7、若关于x的分式方程3232xmxx有增根，则2m的值为________________.

题型八：分式方程无解问题：【例题14】若关于x的分式方程6523212xxxax总无解，求a的值。

2221151kkxxxxx

1xk

11322xxx

