现代控制理论试习题(详细答案
现代控制理论试卷及答案

现代控制理论试卷一、简答题(对或错,10分)(1)描述系统的状态方程不是唯一的。
(2)用独立变量描述的系统状态向量的维数不是唯一的。
(3)对单输入单输出系统,如果1()C sI A B --存在零极点对消,则系统一定不可控或者不可观测。
(4)对多输入多数出系统,如果1()sI A B --存在零极点对消,则系统一定不可控。
(5)李雅普诺夫直接法的四个判定定理中所述的条件都是充分条件。
(6)李雅普诺夫函数是正定函数,李雅普诺夫稳定性是关于系统平衡状态的稳定性。
(8)线性定常系统经过非奇异线性变换后,系统的可控性不变。
(9)用状态反馈进行系统极点配置可能会改变系统的可观测性。
(10)通过全维状态观测器引入状态反馈来任意配置系统的闭环极点时,要求系统必须同时可控和可观测。
对一个线性定常的单输入单输出5阶系统,假定系统可控可观测,通过设计输出至输入的反馈矩阵H 的参数能任意配置系统的闭环极点。
二、试求下述系统的状态转移矩阵()t Φ和系统状态方程的解x 1(t)和x 2(t)。
(15分)1122()()012()()()230x t x t u t x t x t ⎡⎤⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎣⎦12(0)0,(),0(0)1tx u t e t x -⎡⎤⎡⎤==≥⎢⎥⎢⎥⎣⎦⎣⎦ 三、设系统的传递函数为()10()(1)(2)y s u s s s s =++。
试用状态反馈方法,将闭环极点配置在-2,-1+j ,-1-j 处,并写出闭环系统的动态方程和传递函数。
(15分) 四、已知系统传递函数2()2()43Y s s U s s s +=++,试求系统可观标准型和对角标准型,并画出系统可观标准型的状态变量图。
(15分)五、已知系统的动态方程为[]211010a x x uy b x ⎧⎡⎤⎡⎤=+⎪⎢⎥⎢⎥⎨⎣⎦⎣⎦⎪=⎩,试确定a ,b 值,使系统完全可控、完全可观。
现代控制理论第版课后习题答案

习题答案Document number : WTWYT-WYWY-BTGTT-YTTYU-2018GT《现代控制理论参考答案》第一章答案1-1试求图1-27系统的模拟结构图,并建立其状态空间表达式。
解:系统的模拟结构图如下:系统的状态方程如下:令0(s) = y,则,=册所以,系统的状态空间表达式及输出方程表达式为1-2有电路如图1-28所示。
以电压"⑴为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻R?上的电压作为输出量的输出方程。
解:由图,令ii =x}J2 =x2,u c =x3l输出量y = R2X2• & 1 1Rg + L, Xj + x y = u有电路原理可知:L2XI+R2X2=X3= x2 +C x3写成矢量矩阵形式为:14两输入也,两输出比,比的系统,其模拟结构图如图1-30所示,试求其状态空间表达式和传递函数阵。
解:系统的状态空间表达式如下所示:1-5系统的动态特性由下列微分方程描述列写其相应的状态空间表达式,并画出相应的模拟结构图。
解:令x, = y,吃=,,兀3 =,,则有相应的模拟结构图如下:并画岀相应的模拟结构图10 £初・ 117/ \ 6(5 + 1) -4 V 3 a解:VV (5)= ------ ---------- = --------- +— + ------------+ 丄s(s + 2)(s + 3y (s + 3y 5 + 3 s + 2 s1- 7给定下列状态空间表达式y = [0 0 1 x 2_V 3_(1) 画出其模拟结构图 (2) 求系统的传递函数解:-1 0(2) W(s) = (s/ — A)= 25 + 31 — 1 5 + 31-8求下列矩阵的特征矢量_0 1 0 _ (3)32-12 -7 -6-1 0解:A 的特征方程 |刀—A|= —3 2-2 =23+6/l 2 + lU + 6 = 0 1272 + 6解之得:入=—1,/?2 = —2,/?3 = —31-6 (2)已知系统传递函数W(s)=6(5 + 1)5(5 +2)(5+ 3)2,试求岀系统的约旦标准型的实现,■ 010 '/AiP113 0 2 P11 =— P21 -12 -7 -6_ ■皿■叽当人=一1时,令內=1Ai-1 (或令Pll =一1,得片=P21 =1 )1■ 0 1 0 ■P\2Pn 3 02 Pll =-2 P22-12 -7 _6. L/^2.解得:”22=一2卩2丿32 =>12'P22 =P\2(或令从2 T,得4 = "22“320 1当人=一3时, 3 0 -12 -71 -2£ 2解得:〃23=-3/心〃33=3门3令戸3 = 1得1・9将下列状态空间表达式化成约旦标准型(并联分解)~4 1 -2■3 fX 2 = 1 0 2X 2 + 2 7⑵-.1-1 d_5 3_得解得:P 2] =^31 =-P\\当人=一2时,令门2 = 2 得P 2 = 2 -41'4 1 -2'当人=3时, 1 02=3 "211 -13 .解之得 Pl2 = P12 + 1,P22 = “32 令 Pl2 =1并联联结(第3版教材)已知如图1・22所示的系统,其中子系统1、2的传递函数阵分别求系统的闭环传递函数_4 1 -2 P11PwT 1 0 2 "21 =3 P21 + 11 -1 3 -■叽丄 当An =3时,解:A 的特征方程2-4 -1 |27 - A| = -12 -1 1 2-2 =(2-1)(2-3)2 =02- 3解之得 P2! =Pj] =P11令/“iPw■fP21 = 1■叽丄当人=1时, 解之得 P13 = °,“23 = 2^33 令 “33 = 1约旦标准型1- 10已知两系统的传递函数分别为W|(s)和W 2(s)试求两子系统串联联结和并联连接时,系统的传递函数阵,并讨论所得结果 解: (D 串联联结MlR = 得10 -1得1-H (第2版教材)已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为求系统的闭环传递函数解:M2已知差分方程为试将其用离散状态空间表达式表示,并使驱动函数I】的系数b(即控制列阵)为⑴b=;解法1 :解法2 :求T,使得厂,;得宀鳥所以T=所以,状态空间表达式为第二章习题答案2-4用三种方法计算以下矩阵指数函数屛‘。
《现代控制理论》第3版课后习题答案.
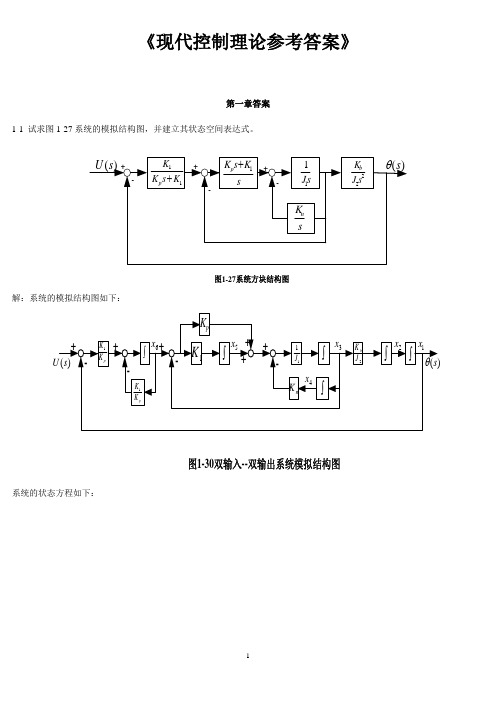
《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
11K s K K p +sK s K p 1+s J 11sK n 22s J K b -++-+-)(s θ)(s U 图1-27系统方块结构图解:系统的模拟结构图如下:)(s U )(s θ---+++图1-30双输入--双输出系统模拟结构图1K pK K 1pK K 1+++pK n K ⎰⎰⎰11J ⎰2J K b ⎰⎰-1x 2x 3x 4x 5x 6x系统的状态方程如下:u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n pb1611166131534615141313322211+--=+-==++--===∙∙∙∙∙∙令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∙∙∙∙∙∙654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp npb1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
R1L1R2L2CU---------Uc---------i1i2图1-28 电路图解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:∙∙∙+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=∙∙∙写成矢量矩阵形式为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。
《现代控制理论》刘豹著(第3版)课后习题答案

《现代控制理论》刘豹著(第3版)课后习题答案《现代控制理论》刘豹著(第3版)课后习题答案第一章习题答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
解:系统的模拟结构图如下:系统的状态方程如下:令,则所以,系统的状态空间表达式及输出方程表达式为1-2有电路如图1-28所示。
以电压为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻上的电压作为输出量的输出方程。
解:由图,令,输出量有电路原理可知:既得写成矢量矩阵形式为:1-3 参考例子1-3. 1-4 两输入,,两输出,的系统,其模拟结构图如图1-30所示,试求其状态空间表达式和传递函数阵。
解:系统的状态空间表达式如下所示:1-5系统的动态特性由下列微分方程描述列写其相应的状态空间表达式,并画出相应的模拟结构图。
解:令,则有相应的模拟结构图如下:1-6 已知系统传递函数,试求出系统的约旦标准型的实现,并画出相应的模拟结构图解:1-7 给定下列状态空间表达式‘画出其模拟结构图求系统的传递函数解:1-8 求下列矩阵的特征矢量解:A的特征方程解之得:当时,解得:令得当时,解得:令得当时,解得:令得1-9将下列状态空间表达式化成约旦标准型解:A的特征方程当时,解之得令得当时,解之得令得当时,解之得令得约旦标准型1-10 已知两系统的传递函数分别为W1(s)和W2(s)试求两子系统串联联结和并联连接时,系统的传递函数阵,并讨论所得结果解:串联联结并联联结1-11 已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为求系统的闭环传递函数解:1-11 已知如图1-22所示的系统,其中子系统1、2的传递函数阵分别为求系统的闭环传递函数解:1-12 已知差分方程为试将其用离散状态空间表达式表示,并使驱动函数u的系数b(即控制列阵)为解法1:解法2:求T,使得得所以所以,状态空间表达式为第二章习题答案2-4 用三种方法计算以下矩阵指数函数。
现代控制理论课后题及答案

第2章 “控制系统的状态空间描述”习题解答2.1有电路如图P2.1所示,设输入为1u ,输出为2u ,试自选状态变量并列写出其状态空间表达式。
图P2.1解 此题可采样机理分析法,首先根据电路定律列写微分方程,再选择状态变量,求得相应的系统状态空间表达式。
也可以先由电路图求得系统传递函数,再由传递函数求得系统状态空间表达式。
这里采样机理分析法。
设1C 两端电压为1c u ,2C 两端的电压为2c u ,则212221c c c du u C R u u dt++= (1) 112121c c c du u duC C dt R dt+= (2) 选择状态变量为11c x u =,22c x u =,由式(1)和(2)得:1121121121212111c c c du R R C u u u dt R R C R C R C +=--+ 2121222222111c c c du u u u dt R C R C R C =--+ 状态空间表达式为:12111211212121212122222221111111R R C x x x u R R C R C R C x x x u R C R C R C y u u x +⎧=--+⎪⎪⎪=--+⎨⎪⎪==-⎪⎩即: 12121121211112222222211111R R C R C R R C R C x x u x x R C R C R C +⎡⎤⎡⎤-⎢⎥⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦--⎢⎥⎢⎥⎣⎦⎣⎦[]11210x y u x ⎡⎤=-+⎢⎥⎣⎦2.2 建立图P22所示系统的状态空间表达式。
1图P2.2解 这是一个物理系统,采用机理分析法求状态空间表达式会更为方便。
令()f t 为输入量,即u f =,1M ,2M 的位移量1y ,2y 为输出量, 选择状态变量1x =1y ,2x = 2y ,3x =1dy dt,24dyx dt =。
现代控制理论习题及答案

现代控制理论习题及答案现代控制理论习题及答案现代控制理论是控制工程领域的重要分支,它研究如何设计和分析控制系统,以实现对动态系统的稳定性、响应速度、精度等方面的要求。
在学习现代控制理论过程中,习题是一个非常重要的环节,通过解答习题可以帮助我们巩固理论知识,提高问题解决能力。
本文将介绍一些常见的现代控制理论习题及其答案,希望对读者有所帮助。
1. 题目:给定一个开环传递函数 G(s) = 10/(s+5),求其闭环传递函数 T(s) 和稳定性判断。
解答:闭环传递函数 T(s) 可以通过公式 T(s) = G(s) / (1 + G(s)) 计算得到。
代入G(s) 的表达式,得到 T(s) = 10/(s+15)。
稳定性判断可以通过判断开环传递函数G(s) 的极点是否在左半平面来进行。
由于 G(s) 的极点为 -5,位于左半平面,因此系统是稳定的。
2. 题目:给定一个系统的状态空间表达式为 dx/dt = Ax + Bu,其中 A = [[-1, 2], [0, -3]],B = [[1], [1]],求系统的传递函数表达式。
解答:系统的传递函数表达式可以通过状态空间表达式进行求解。
首先,计算系统的特征值,即矩阵 A 的特征值。
通过求解 det(sI - A) = 0,可以得到系统的特征值为 -1 和 -3。
然后,将特征值代入传递函数表达式的分母,得到传递函数的分母为 (s+1)(s+3)。
接下来,计算传递函数的分子,可以通过求解 C = D(sI - A)^(-1)B 得到,其中 C 和 D 分别为输出矩阵和输入矩阵。
代入给定的 A、B 矩阵,计算得到 C = [1, 0] 和 D = [0]。
因此,系统的传递函数表达式为 G(s) = C(sI - A)^(-1)B = [1, 0] * [(s+1)^(-1), -2(s+3)^(-1); 0, (s+3)^(-1)] * [1; 1] =(s+1)^(-1) + 2(s+3)^(-1)。
《现代控制理论》第三版_.习题答案
1 0 0 3 1 0 5 2 1 52 7 1 5 2 70 125 3 5 7 5 0 0 1 1 B 2 ; 2 5 5
1 0 a1 0 0 1 0 1 0 0 1 a2 3 7 5
0 B 0 1
C (b0 a0bn ) (bn1 an1bn ) 2 1 0
3 1 a 或者 2 2 1 a1 0 a0
e At I At 1 22 1 33 A t A t 2! 3! t2 t4 t6 t3 t5 1 4 16 64 , 4 16 t 2! 4! 6! 3! 5! 3 5 2 4 6 t t t t t t 4 16 64 , 1 4 16 64 3! 5! 2! 4! 6!
0 0 1 B M 1 0 0 0 0 1 M2
1 0 B 1 M1 B1 M2
1 B1 M1 B1 B2 M2
0
0 0 1 0 C 0 0 0 1
1-5. 根据微分方程, 写状态方程, 画模 拟结构图。
1 a2 a2 2 a1 3 2 a a a 1 2 2 a0
1 a2 a1
1 a2
12 b1 b0
b3 b 2 b1 1 b0
凯莱哈密顿法: 1,2 2 j
0 (t ) 1 1 e1t 1 2(e 2 jt e 2 jt ) (t ) 1 2t 4 2 jt 2 jt e j ( e e ) 2 1
现代控制理论第3课后习题答案
《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
图1-27系统方块结构图解:系统的模拟结构图如下:图1-30双输入--双输出系统模拟结构图系统的状态方程如下:u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n pb1611166131534615141313322211+--=+-==++--===••••••令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡••••••654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp n p b1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
U图1-28 电路图解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。
(完整word版)《现代控制理论》第3版课后习题答案
《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
图1-27系统方块结构图解:系统的模拟结构图如下:图1-30双输入--双输出系统模拟结构图系统的状态方程如下:u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n p b1611166131534615141313322211+--=+-==++--===••••••令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡••••••654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp npb1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
U图1-28 电路图解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。
哈尔滨工业大学《现代控制理论基础》考试题A卷及答案
哈工大2010年春季学期现代控制理论基础 试题A 答案题号 一 二 三 四 五 六 七 八 卷面分 作业分 实验分 总分 满分值 10 10 10 10 10 10 10 10 80 10 10 100 得分值第 1 页 (共 8 页)班号 姓名一.(本题满分10分)如图所示为一个摆杆系统,两摆杆长度均为L ,摆杆的质量忽略不计,摆杆末端两个质量块(质量均为M )视为质点,两摆杆中点处连接一条弹簧,1θ与2θ分别为两摆杆与竖直方向的夹角。
当12θθ=时,弹簧没有伸长和压缩。
水平向右的外力()f t 作用在左杆中点处,假设摆杆与支点之间没有摩擦与阻尼,而且位移足够小,满足近似式sin θθ=,cos 1θ=。
(1)写出系统的运动微分方程; (2)写出系统的状态方程。
【解】(1)对左边的质量块,有()2111211cos sin sin cos sin 222L L LML f k MgL θθθθθθ=⋅-⋅-⋅-对右边的质量块,有()221222sin sin cos sin 22L LML k MgL θθθθθ=⋅-⋅-在位移足够小的条件下,近似写成:()112124f kLML Mg θθθθ=---()21224kLML Mg θθθθ=--即112442kg k f M L M ML θθθ⎛⎫=-+++⎪⎝⎭ 21244k k g M M L θθθ⎛⎫=-+ ⎪⎝⎭(2)定义状态变量11x θ=,21x θ=,32x θ=,42x θ=则122133441344244x x k g k fx x x M L M ML x x k kg x x x M M L =⎧⎪⎛⎫⎪=-+++ ⎪⎪⎝⎭⎨=⎪⎪⎛⎫=-+⎪ ⎪⎪⎝⎭⎩或写成1122334401000014420001000044x x k g k x x M L Mf ML x x x x k kg M M L ⎡⎤⎡⎤⎢⎥⎡⎤⎡⎤⎛⎫⎢⎥⎢⎥-+⎢⎥⎢⎥ ⎪⎢⎥⎢⎥⎝⎭⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎛⎫⎣⎦⎣⎦⎢⎥-+⎣⎦⎢⎥ ⎪⎢⎥⎝⎭⎣⎦二.(本题满分10分)设一个线性定常系统的状态方程为=x Ax ,其中22R ⨯∈A 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
现代控制理论试题B 卷及答案一、1 系统[]210,01021x x u y x ⎡⎤⎡⎤=+=⎢⎥⎢⎥-⎣⎦⎣⎦能控的状态变量个数是,能观测的状态变量个数是cvcvx 。
2试从高阶微分方程385y y y u ++=求得系统的状态方程和输出方程(4分/个) 解 12。
…..233118x x x x y x ==--=010080x ⎡⎢=⎢⎢-⎣分) 00⎣(5分)解 1.答:若存在控制向量序列(),(1),,(1)u k u k u k N ++-,时系统从第k 步的状态()x k 开始,在第N 步达到零状态,即()0x N =,其中N 是大于0的有限数,那么就称此系统在第k 步上是能控的。
若对每一个k ,系统的所有状态都是能控的,就称系统是状态完全能控的,简称能控。
…..….…….(3分)2.[][]320300020012 110-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=CA ………..……….(1分) [][]940300020012 3202=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=CA ……..……….(1分) ⎤⎡⎤⎡110C 1分)0140x ⎡⎤=⎢⎥⎣⎦ ()⎥⎦⎢⎢⎢⎣-=-8181881C U ……..…………..…….…….(1分) 11188P ⎡⎤=-⎢⎥⎣⎦……..………….…..…….…….(1分) ⎦⎤⎢⎣⎡=43412P ……..………….…...…….…….(1分)1314881148P -⎡⎤-⎢⎥=⎢⎥--⎢⎥⎣⎦..………….…...…….…….(1分) 101105C A PAP -⎡⎤==⎢⎥-⎣⎦………….…...…….…….(1分) ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-==1011 43418181Pb b C ……….…...…….…….(1分)1分) 解(3分) 3分)2分)(81分)11121112221222420261p p p p p ⎪-+=⎨⎪-=-⎩………...……....…….…….(1分) 112212743858p p p ⎧=⎪⎪=⎨⎪=⎪⎩………...…………....…….…….(1分)1112122275485388p p P p p ⎡⎤⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦⎣⎦...…………....…….…….(1分) 111211122275717480 det det 05346488p p P p p ⎡⎤⎡⎤⎢⎥=>==>⎢⎥⎢⎥⎣⎦⎣⎦………...(1分) P 正定,因此系统在原点处是大范围渐近稳定的.………(1分)八、给定系统的状态空间表达式为1010x --⎡⎢=-⎢⎢⎣2322213332223321(21)3313332(3)(26)64E E E E E E E E E E E λλλλλλλλλλ=+++++++++++++=+++++++++ -- 2分 又因为 *32()331f λλλλ=+++ ------- 1分列方程32123264126333E E E E E E +++=++=+= ----- 2分1232,0,3E k E =-==- ----------- 1分观测器为10312ˆˆ0110010113x x u y ---⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦------- 1分 方法 2λ⋅分 分分分10ˆ0110x -⎡⎢=-⎢⎢⎣九 分) 1200A tAt A t e e e ⎛⎫= ⎪⎝⎭1A t t e e =…………………………..……….(1分) 11210()12s sI A s ---⎛⎫-= ⎪--⎝⎭101111212s s s s ⎛⎫ ⎪-= ⎪ ⎪- ⎪---⎝⎭………..……….(1分)(){}2112220t A t t t t e e L sI A e ee --⎛⎫=-= ⎪-⎝⎭……….…(1分)()112200000t At tt tt e e L sI A e e e e --⎛⎫ ⎪⎡⎤=-= ⎪⎣⎦ ⎪-⎝⎭……….……….(2分) 222001000001t t tt t t t e e e e e e e ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭……………..……….(2分)一、(( × ( × ( √ ( √二、(的能控标准型、能观标准型和对角线标准型,并画出能控标准型的状态变量图。
解: 能控标准形为能观测标准形为对角标准形为三、(10分)在线性控制系统的分析和设计中,系统的状态转移矩阵起着很重要的作用。
对系统求其状态转移矩阵。
解:解法1。
容易得到系统状态矩阵A 的两个特征值是2,121-=-=λλ,它们是不相同的,故系统) 因此, ⎥⎦⎢⎣+-+-=+==Φ----t t t t At e e e e A t a I t a e t 2210222)()()( 四、(15分)已知对象的状态空间模型Cx y Bu Ax x =+=, ,是完全能观的,请画出观测器设计的框图,并据此给出观测器方程,观测器设计方法。
解 观测器设计的框图:观测器方程:其中:x ~是观测器的维状态,L 是一个n ×p 维的待定观测器增益矩阵。
观测器设计方法:由于 )](det[])(det[)](det[T T T T L C A I LC A I LC A I --=--=--λλλ因此,可以利用极点配置的方法来确定矩阵L ,使得T T T L C A -具有给定的观测器极点。
具体的方法有:直接法、变换法、爱克曼公式。
五、(P 。
I PA -=⎥⎦⎤⎣⎦⎣12/12212p p 根据塞尔维斯特方法,可得 045det 02321>==∆>=∆P 故矩阵P 是正定的。
因此,系统在原点处的平衡状态是大范围渐近稳定的。
六、(10分)已知被控系统的传递函数是试设计一个状态反馈控制律,使得闭环系统的极点为-1 ± j 。
解 系统的状态空间模型是将控制器 []x k k u 10-= 代入到所考虑系统的状态方程中,得到闭环系统状态方程该闭环系统的特征方程是 )2()3()det(012k k A I c ++++=-λλλ期望的闭环特征方程是 22)1)(1(2++=++-+λλλλj j通过 22)2()3(2012++=++++λλλλk kT 八、( 解: 极点配置可以改善系统的动态性能,如调节时间、峰值时间、振荡幅度。
极点配置也有一些负面的影响,特别的,可能使得一个开环无静差的系统通过极点配置后,其闭环系统产生稳态误差,从而使得系统的稳态性能变差。
改善的方法:针对阶跃输入的系统,通过引进一个积分器来消除跟踪误差,其结构图是构建增广系统,通过极点配置方法来设计增广系统的状态反馈控制器,从而使得闭环系统不仅保持期望的动态性能,而且避免了稳态误差的出现。
《现代控制理论》复习题2一、(10分,每小题2分)试判断以下结论的正确性,若结论是正确的,则在其左边的括号里打√,反之打×。
( ×( √ ( × ( × ( √ 二、((1)(2) 答:(1⎩⎨⎧=+-=11113x y u x x 和⎩⎨⎧+-=+-=1212255u x y u x x ? 由于11u y =,故可得给定传递函数的状态空间实现是:将其写成矩阵向量的形式,可得:对应的状态变量图为:串连分解所得状态空间实现的状态变量图(2)将G (s )写成以下形式: 它可以看成是两个环节35.0+-s 和55.2+s 的并联,每一个环节的状态空间模型分别为: 和由此可得原传递函数的状态空间实现:三、(方法一方法二方法三方法四根据凯莱-哈密尔顿定理和,可导出At e 具有以下形式:其中的)(),(),(120t t t n -ααα 均是时间 t 的标量函数。
根据矩阵A 有n 个不同特征值和有重特征值的情况,可以分别确定这些系数。
举例:利用拉普拉斯变换法计算由状态矩阵所确定的自治系统的状态转移矩阵。
由于故四、(10分)解释状态能观性的含义,给出能观性的判别条件,并举例说明之。
答:状态能观性的含义:状态能观性反映了通过系统的输出对系统状态的识别能力,对一个零输入的系统,若它是能观的,则可以通过一段时间内的测量输出来估计之前某个时刻的系统状态。
1.2.举例:的秩为五、((1)(2)简单叙述两种极点配置状态反馈控制器的设计方法;(3)试通过数值例子说明极点配置状态反馈控制器的设计。
答:(1)能够通过状态反馈实现任意极点配置的条件:系统是能控的。
(2)极点配置状态反馈控制器的设计方法有直接法、变换法、爱克曼公式法。
①直接法验证系统的能控性,若系统能控,则进行以下设计。
设状态反馈控制器u =?Kx ,相应的闭环矩阵是A ?BK ,闭环系统的特征多项式为 由期望极点n λλ,,1 可得期望的闭环特征多项式通过让以上两个特征多项式相等,可以列出一组以控制器参数为变量的线性方程组,由这组线性方程可以求出极点配置状态反馈的增益矩阵K 。
②(3) 其特征多项式为由期望的闭环极点? 2和?3,可得闭环特征多项式通过可得由此方程组得到因此,要设计的极点配置状态反馈控制器六、(20分)给定系统状态空间模型Axx=(1)试问如何判断该系统在李雅普诺夫意义下的稳定性?(2)试通过一个例子说明您给出的方法;(3)给出李雅普诺夫稳定性定理的物理解释。
答:(1A T+P解矩阵(2将矩阵即(3)李雅普诺夫稳定性定理的物理意义:针对一个动态系统和确定的平衡状态,通过分析该系统运动过程中能量的变化来判断系统的稳定性。
具体地说,就是构造一个反映系统运动过程中能量变化的虚拟能量函数,沿系统的运动轨迹,通过该能量函数关于时间导数的取值来判断系统能量在运动过程中是否减少,若该导数值都是小于零的,则表明系统能量随着时间的增长是减少的,直至消耗殆尽,表明在系统运动上,就是系统运动逐步趋向平缓,直至在平衡状态处稳定下来,这就是李雅普诺夫意义下的稳定性《现代控制理论》复习题3一、(10分,每小题2分)试判断以下结论的正确性,若结论是正确的,则在其左边的括号里打√,反之打×。
( ×( × ( × ( √ ( √ 器。
二、((2解:(1)单输入单输出线性时不变系统传递函数的一般形式是若0≠n b ,则通过长除法,传递函数)(s G 总可以转化成将分解成等效的两个特殊环节的串联:可得一个状态空间实现串联法 其思想是将一个n 阶的传递函数分解成若干低阶传递函数的乘积,然后写出这些低阶传递函数的状态空间实现,最后利用串联关系,写出原来系统的状态空间模型。
