07--数数图形
三年级数学思维训练导引(奥数)第07讲周期问题

第七讲周期问题1.如图7-1,由一系列黑、白三角形按一定的规律排成一行,请问:第26个图形应该是什么样子?2.在学校运动会的开幕式上,46名同学组成仪仗队站成一排.如图7-2所示,每人手里都举着一面彩旗,从左到右颜色依次是红、黄、蓝、绿四种颜色依次循环.最右侧的同学手里的彩旗是什么颜色的?3.如图713所示,将自然数从1开始顺次写在A、B、C、D、E这五个字母下面,问:208会出现在哪个字母下面?4.在一根绳子上依次穿2个红珠、3个白珠、5个黑珠,并按此方式重复,如果从头开始一共穿了77颗珠子,那么这77颗珠子中白珠比黑珠少多少颗?5.如图7-4,四只小动物不断交换座位,一开始,小鼠坐第1号椅子,小猴坐第2号椅子,小兔坐第3号椅子,小猫坐第4号椅子.第一次前后两排交换,第二次在第一次交换的基础上左右两列交换,第三次又是前后两排交换,第四次再左右两列交换……这样一直换下去.第十次交换座位后,四只小动物分别坐在第几号椅子上?6.将一些自然数排成一列,其中任意相邻的五个数之和都等于15.已知第一个数等于1,第二个数等于2,第三个数等于3,第四个数等于4.问:(1)请写出这个数列的前十项;(2)第一百个数等于多少?7. lOO位同学从左到右排成一行,然后按如下规律从左向右报数:先让第一位同学报1,然后从第二位同学开始,每位同学都把前一位同学所报的数乘以7,再报出乘积的个位来.请问:第100个同学报的是几?8.(1)如图7-5所示,甲、乙两只蚂蚁,分别沿正方形ABCD和AEFG按照顺时针的方向爬行.甲2分钟能爬完正方形的一条边,乙1分钟能爬完正方形的一条边,现在两只蚂蚁在A点同时出发,那么50分钟后甲、乙分别在什么位置?(2)如图7-5所示,如果蚂蚁甲从C点出发,沿着C→D→A→E→F→G→A→B→C的路线爬行,1分钟能爬完正方形的一条边;蚂蚁乙从F点出发,沿着F→G→A→B→C→D→A→E→F的路线爬行,2分钟能爬完正方形的一条边,它们同时出发,90分钟后甲、乙分别在什么位置?9.一只蜗牛从深30米的井底向上爬,第一天向上爬了6米;第二天休息,于是向下滑了4米;第三天再向上爬6米;第四天又向下滑4米……按这样的规律进行下去,蜗牛第几天才能爬到井口?10.(1)今天是星期六,再过60天是星期几?(2) 2008年6月1日是星期日,2008年8月1日是星期几?(3) 2008年2月8日是星期五,2009年2月8日是星期几?1.图7-6是一行按规律排列的图形.请问:第88个图形应该是什么?2.观察图7-7中黑、白两色三角形的变化规律.请问:前200个图形中有多少个白色三角形?3.如图7-8所示,表格中每行的文字都是循环出现的:第一行是“黎曼假设”4个汉字不断重复,第二行是“庞加莱猜想”5个汉字不断重复,第三行则是“哥德巴赫猜想”6个汉字不断重复.第200列从上到下依次是哪3个汉字?4.阿奇和其他5个小朋友围成一圈,圆圈中央摆放着55个乒乓球.从阿奇开始,小朋友们沿逆时针方向依次拿球,每人每次拿3个,直到把乒乓球全部拿完为止(最后剩下的球不足3个就全拿).阿奇总共拿到了几个球?5.如图7-9,电子跳蚤每跳一步,可从一个圆圈跳到相邻的圆圈.现在,一只红跳蚤从标有数“1”的圆圈按顺时针方向跳了100步,落在一个圆圈里.一只黑跳蚤也从标有数“l”的圆圈起跳,但它是沿着逆时针方向跳了200步,落在另一个圆圈里,这两个圆圈里的数的乘积是多少?6.(1)工厂的仓库里有80吨货物,这些货物都由同一辆卡车负责运输.第一天卡车往仓库里运进50吨,第二天运出了60吨,第三天又运进50吨,第四天再运出60吨……如此不停地运下去.第几天的时候,仓库里的货物恰好被运完?(2)工厂的仓库里有80吨货物,同样是由一辆卡车负责货物的运输.第一天,卡车从仓库里运出60吨,第二天再运进50吨,第三天又运出60吨,第四天再运进50吨……如此不停地运下去.第几天的时候,仓库里的货物恰好被运完?7.如图7-10所示,16幅图按规律排成一排.其中前三幅图已经画出,请按规律画出第16幅图的样子.8.甲、乙、丙、丁兄弟四人各收藏了一些宝石.每天早上他们都要聚在一起,重新分配宝石,分配的规则就是:拥有宝石最多的人分给其他三人每人l颗.如果第1天早上分配完之后,甲、乙、丙、丁四人分别有10、7、5、4颗宝石,那么第100天早上分完宝石后,四个人手中分别有几颗宝石?9.500名士兵排成一排,第一次从左到右1至3循环报数,第二次从左到右1至4循环报数.请问:既报过1又报过4的士兵有多少名?10.如图7-11,伸出左手,然后从大拇指起开始数数.当数到200的时候,正好数到哪根手指?11.今天是2008年3月16日星期日,阿奇研究日历时,发现再过1天是2008年3月17日星期一,再过2天则是2008年3月18日星期二……请问:(1)再过多少天才是2008年儿童节呢?(2) 2008年的儿童节是星期几?12.哥哥比妹妹大5岁,而且两人生日相同.如果哥哥是1982年6月17日星期四出生的,那么妹妹是在星期几出生的?妹妹出生后第一次在星期二过生日的时候是哪一年?1.观察图7-12中图形的规律,第200个图形应该是下面A、B、C、D四个图形中的哪一个?2.如图7-13所示,7个小朋友围成一圈,沿顺时针方向依次编号为1—7.然后,按如下方法给他们发糖:先给l号小朋友1块糖;然后沿顺时针方向隔过一个人后,给3号小朋友1块糖;再沿顺时针方向隔过两个人后,给6号小朋友l 块糖;接着又沿顺时针方向隔过一个人后,给1号小朋友1块糖……如此反复地间隔一个人、两个人,直到1997块糖全部分完,那么最先发到糖的那位小朋友一共得到了多少块糖?3.如图7-14所示,用红、黄、蓝3种颜色的彩笔,按规律给表格染色,第20行和第30列交叉处的方格所染的颜色是什么?4.(1)某月有31天,有4个星期二和4个星期五,那么这个月的20日是星期几?(2)某月的星期二比星期一多,那么这个月的25日是星期几?5.500名士兵排成一排,第一次从左到右1-5循环报数,第二次从右到左1—4循环报数.请问:既报1又报5的士兵有多少名?6.有六十多人站成一行,从左到右由1开始按l、2、3、4依次循环报数,然后从右到左由1开始按1、2、3依次循环报数,最后发现刚好有12个人既报了1又报了2.请问:这一行最少有多少人?最多有多少人?7.实验室里有两只不同的怪钟,每只钟只有一个指针,而且都是每分钟跳一次,第一只钟一圈有12个格,格线上依次标着0—11,指针一次跳过2个格(例如从4跳到6).第二只钟一圈有7个格,格线上依次标着0至6,指针一次跳过3个格.开始时两个指针都指向0,如果把这看作两个指针第1次指向同一个标数,那么当两个指针第30次指向同一个标数时,它们的指针指着哪个数字?8.如图7-15,在A、B两地之间有7个车站,一辆列车不停地往返于A、B两地之间.它从A出发,每天行驶到下一站,到达B地后的下一天又回到7号站,如此反复.已知列车第4次驶入4号站时是星期六,那么它第20次驶入5号站时是星期几?。
几何图形(39张PPT)数学

第6章 图形的初步知识
6.1 几何图形
学习目标 1.在具体情况中认识立方体、长方体、圆柱体、圆锥体、球体,并能理解和描述它们的某些特征,进一步认识点、线、面、体,体验几何图形是怎样从实际情况中抽象出来的.2.了解几何图形、立体图形与平面图形的概念.掌握重点 认识常见几何体并能描述它们的某些特征.突破难点 体验几何图形与现实生活中图形的关系,区分立体图形与平面图形.
解
返回
解 立方体由6个面围成,它们都是平的;圆柱由3个面围成,其中有2个平的,1个曲的.解 圆柱的侧面和两个底面相交成2条线,它们都是曲的.解 立方体有8个顶点,经过每个顶点有3条线段(棱).
典例精析
例1 (教材补充例题)如图所示的图形.平面图形有_____________;立体图形有_____________.
答案
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
①,②,⑥
③,④
⑤
②,③,⑤
①,④,⑥
19
13.如图是一个三棱柱,观察这个三棱柱,请回答下列问题:(1)这个三棱柱共有多少个面?(2)这个三棱柱一共有多少条棱?(3)这个三棱柱共有多少顶点?
解 这个三棱柱共有5个面.解 这个三棱柱一共有9条棱.解 这个三棱柱共有6个顶点.
C
解析 观察图形可知,其中一面、两面、三面涂色的小正方体的个数分别为x1=6,x2=12,x3=8,则x1-x2+x3=2.故选C.
1
2
3
4
5
6
7
8
9
10
11
12
初中几何43模型解题 模型【07】 图形变化类(附解析)

模型【07】图形变化类【模型分析】解决图形规律题的步骤:(1)标序数——按图号标序;(2)找规律——观察图形,随着序号增加,后一个图形与前一个图形相比,找出图形变化规律,注意变量与不变量,将每个图中所求量的个数表示成与序数有关的式子;(3)验证——代入序号验证所归纳的式子是否正确;【经典例题】例1.(2021·重庆渝北区·八年级期末)如图是一组有规律的图案,第①个图案中有4个三角形,第②个图案中有7个三角形,第③个图案中有10个三角形……,依此规律,第⑧个图案中有()个三角形.A.19B.21C.22D.25【分析】由题意可知:第①个图案有3+1=4个三角形,第②个图案有3×2+1=7个三角形,第③个图案有3×3+1=10个三角形,…依此规律,第n个图案有(3n+1)个三角形,代入n=8即可求得答案.【解析】∵第①个图案有3+1=4个三角形,第②个图案有3×2+1=7个三角形,第③个图案有3×3+1=10个三角形,…∴第n个图案有(3n+1)个三角形.当n=8时,3×8+1=25,选D.【小结】考查图形的变化规律,解题的关键是找出图形之间的变化规律,利用规律解决问题.例2.(2021·北京东城区·八年级期末)如图,30MON ∠=︒,点1234,,,A A A A ,…在射线ON 上,点123,,B B B ,…在射线OM 上,且112223334,,A B A A B A A B A △△△,…均为等边三角形,以此类推,若11OA =,则202120212022A B A △的边长为_______.【分析】根据30MON ∠=︒,11OA =,112A B A △是等边三角形,得11260∠=︒B A A ,进而得1130∠=︒OB A ,1111A O B A ==,可得22OA =,以此类推即可求解.【解析】∵30MON ∠=︒,11OA =,112A B A △是等边三角形,∴11260∠=︒B A A ∴1130∠=︒OB A ∴1111A OB A ==∴22OA =同理:223A B A △,334A B A △,…均为等边三角形,2222B A OA ==,233342B A OA ===…则202120212022A B A △的边长为20202.【小结】本题考查了规律型-图形的变化类,解决本题的关键是观察图形的变化寻找规律.例3.(2021·安徽芜湖市·七年级期末)如图,同一行的两个图形中小正方形的个数相等,但它们的排列方式不一样,根据不同的排列方式可以得到一列等式.(12)223+⨯=⨯(123)234++⨯=⨯(1234)245+++⨯=⨯(1)第n 个图形中对应的等量关系是()21231n +++⋯++⨯=⎡⎤⎣⎦______.(2)根据(1)的结论,求24650+++⋅⋅⋅+的值.【分析】(1)根据前三幅图可知右边的式子等于左边括号内最大的数与比它大1数的积;(2)先逆用乘法分配律变形,然后根据(1)中结论计算即可;【解析】(1)∵(12)223+⨯=⨯,(123)234++⨯=⨯,(1234)245+++⨯=⨯,…,∴[]123(1)2(1)(2)n n n +++++⨯=++ (2)246501(5)2322+++⋅⋅⋅+=+++⋅⋅⋅+⨯2526650=⨯=【小结】本题考查了规律型—图形类规律与探究,要求学生通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题.也考查了有理数的混合运算.【巩固提升】1.(2020·浙江台州市·七年级期末)如图,用大小相等的黑色三角形按一定规律拼成如图的图案,其中第①个图案中有1个黑色三角形,第②个图案中有3个黑色三角形,第③个图案中有6个黑色三角形…,依照此规律,第⑩个图案中黑色三角形的个数为()A .50B .55C .58D .61【分析】根据前3个图案中黑色三角形的个数找出规律,利用规律解题即可.【解析】第①个图案中有1个黑色三角形,第②个图案中有3个黑色三角形,312=+,第③个图案中有6个黑色三角形,6123=++,……第⑩个图案中黑色三角形的个数为1234567891055+++++++++=,选B【小结】本题注意考查图形类规律探索,找到规律是解题的关键.2.(2021·北京房山区·八年级期末)如图甲,直角三角形ABC 的三边a ,b ,c ,满足222+=a b c 的关系.利用这个关系,探究下面的问题:如图乙,OAB 是腰长为1的等腰直角三角形,90OAB ∠=︒,延长OA 至1B ,使1AB OA =,以1OB 为底,在OAB 外侧作等腰直角三角形11OA B ,再延长1OA 至2B ,使121A B OA =,以2OB 为底,在11OA B 外侧作等腰直角三角形22OA B ,……,按此规律作等腰直角三角形n n OA B (1n ≥,n 为正整数),则22A B 的长及20212021OA B 的面积分别是()A .2,20202B .4,20212C .20202D .2,20192【分析】根据题意结合等腰直角三角形的性质,即可判断出22A B 的长,再进一步推出一般规律,利用规律求解20212021OA B 的面积即可.【解析】由题意可得:11OA AB AB ===,12OB =,∵11OA B 为等腰直角三角形,且“直角三角形ABC 三边a ,b ,c ,满足222+=a b c 关系”,∴根据题意可得:111OA A B ==,∴212OB OA ==,∴22222OA A B ===, ,∴总结出n n OA =,∵111122△OAB S =⨯⨯=,11112△OA B S =,2212222△OA B S =⨯⨯=,∴归纳得出一般规律:1122n n n n n OA B S -=⨯⨯= ,∴2021202120202OA B S = ,选A【小结】本题考查等腰直角三角形的性质,图形变化类的规律探究问题,立即题意并灵活运用等腰直角三角形的性质归纳一般规律是解题关键.3.(2021·山东青岛市·七年级期末)下列图形均是用长度相同的火柴棒按一定的规律搭成,搭第1个图形需要4根火柴棒,搭第2个图形需要10根火柴棒,…,依此规律,搭第10个图形需要________根火柴棒.【分析】由题意,分别求出前面几个的火柴棒数量,然后得到数量的规律,再求出第10个图形的数量即可.【解析】根据题意可知:第1个图案需4根火柴,()4113=⨯+,第2个图案需10根火柴,()10223=⨯+,第3个图案需21根火柴,()18333=⨯+,……,第n 个图案需()3n n +根火柴,则第10个图案需:()10103130⨯+=(根).【小结】此题考查了平面图形,图形变化规律,主要培养学生的观察能力和空间想象能力.4.(2021·全国七年级)如图,△ABC 是边长为1的等边三角形,取BC 边中点E ,作ED ∥AB ,EF ∥AC ,得到四边形EDAF ,它的周长记作C 1;取BE 中点E 1,作E 1D 1∥FB ,E 1F 1∥EF ,得到四边形E 1D 1FF 1,它的周长记作C 2.照此规律作下去,则C 2020=__.【分析】先计算出C 1、C 2的长,进而得到规律,最后求出C 2020的长即可.【解析】∵E 是BC 的中点,ED ∥AB ,∴DE 是△ABC 的中位线,∴DE =12AB =12,AD =12AC =12,∵EF ∥AC ,∴四边形EDAF 是菱形,∴C 1=4×12,同理C 2=4×12×12=4×212,…C n =4×12n ,∴20202020201811422C =⨯=.【小结】本题考查了中位线的性质,菱形的判定与性质,根据题意得到规律是解题关键.5.(2021·山东青岛市·七年级期末)(问题提出)以长方形ABCD 的4个顶点和它内部的n 个点,共(4)n +个点作为顶点,可把原长方形分割成多少个互不重叠的小三角形?(问题探究)为了解决上面的问题,我们将采取一般问题特殊化的策略,先从简单的情形入手:(探究一)以长方形ABCD 的4个顶点和它内部的1个点P (如图①),共5个点为顶点显然,此时可把长方形ABCD 分割成________个互不重叠的小三角形.(探究二)以长方形ABCD 的4个顶点和它内部的2个点P 、Q ,共6个点为顶点,可把长方形ABCD 分割成多少个互不重叠的小三角形?在探究一的基础上,我们可看作在图①长方形ABCD 的内部,再添加1个点Q ,那么点Q 的位置会有两种情况:一种情况是,点Q 在图①分割成的小三角形的某条公共边上不妨设点Q 在PB 上(如图②);另一种情况是,点Q 在图①分割成的某个小三角形内部.不妨设点Q 在PAB △的内部(如图③).显然,不管哪种情况,都可把长方形ABCD 分割成________个互不重叠的小三角形.(探究三)长方形ABCD 的4个顶点和它内部的3个点P 、Q 、R ,共7个点为顶点,可把长方形ABCD 分割成________个互不重叠的小三角形请在图④中画出一种分割示意图.(问题解决)以长方形ABCD 的4个顶点和它内部的n 个点,共(4)n +个点作为顶点,可把原长方形分割成________个互不重叠的小三角形.(实际应用)以梯形的4个顶点和它内部的2021个点作为顶点,可把梯形分割成________个互不重叠的小三角形.(拓展延伸)以五边形的5个顶点和它内部的m 个点,共(5)m +个点作为顶点,可把原五边形分割成________个互不重叠的小三角形.【分析】探究一:根据图形可回答;探究二:根据图形可回答;探究三:根据图形可回答;n ,进而解决问题;问题解决:由探究活动可得规律为2(1)实际应用:把2021代入所得规律,求值即可;拓展延伸:由四边形的规律可得五边形的规律.【解析】探究一:以长方形ABCD的4个顶点和它内部的1个点P,共5个点为顶点显然,此时可把长方形ABCD 分割成4个互不重叠的小三角形.故答案为:4;探究二:如图,不管哪种情况,都可把长方形ABCD分割成6个互不重叠的小三角形.故答案为;6;探究三:长方形ABCD的4个顶点和它内部的3个点P、Q、R,共7个点为顶点,可把长方形ABCD分割成8个互不重叠的小三角形问题解决:以长方形ABCD 的4个顶点和它内部的1个点,共5个点作为顶点,可把原长方形分割成互不重叠的小三角形个数为:4=2(1+1).以长方形ABCD 的4个顶点和它内部的2个点,共6个点作为顶点,可把原长方形分割成互不重叠的小三角形个数为:6=2(2+1).以长方形ABCD 的4个顶点和它内部的3个点,共7个点作为顶点,可把原长方形分割成互不重叠的小三角形个数为:8=2(3+1).所以,以长方形ABCD 的4个顶点和它内部的n 个点,共(4)n +个点作为顶点,可把原长方形分割成互不重叠的小三角形个数为:2(n +1).实际应用:当n =2021时,以梯形的4个顶点和它内部的2021个点作为顶点,可把梯形分割成互不重叠的小三角形2(2021+1)=4044个.拓展延伸:根据前面的解决问题可知:以五边形的5个顶点和它内部的m 个点,共(5)m +个点作为顶点,可把原五边形分割成互不重叠的小三角形个数为(2m +3)个.故答案为:(2m +3)【小结】本题考查了应用与设计作图,图形的变化规律的问题,读懂题目信息,根据前四个探究得到每多一个点,则三角形的个数增加2是解题的关键.6.(2021·青岛实验学校九年级期末)在平面直角坐标系中,点A 从原点O 出发,沿x 轴正方向按半圆形弧线不断向前运动,其移动路线如图所示,其中半圆的半径为1个单位长度,这时点1234,,,A A A A 的坐标分别为()()()()12340,0,1,12,03,1A A A A -,按照这个规律解决下列问题:()1写出点5678,,,,A A A A 的坐标;()2点2018A 的位置在_____________(填“x 轴上方”“x 轴下方”或“x 轴上”);()3试写出点n A 的坐标(n 是正整数).【分析】()1可根据点在图形中的位置及前4点坐标直接求解;()2根据图形可知点的位置每4个数一个循环,20184504...2÷=,进而判断2018A 与2A 的纵坐标相同在x 轴上方,即可求解;()3根据点的坐标规律可分4种情况分别写出坐标即可求解.【解析】(1)由数轴可得:()54,0A ,()65,1A ,()76,0A ,()87,1A -;(2)根据图形可知点的位置每4个数一个循环,20184504...2÷=,2018A ∴与2A 的纵坐标相同,在x 轴上方,故答案为:x 轴上方;(3)根据图形可知点的位置每4个数一个循环,每个点的横坐标为序数减1,纵坐标为0、1、0、-1循环,∴点n A 的坐标(n 是正整数)为A (n -1,0)或()1,1A n -或()1,0A n -或()1,1A n --.【小结】本题主要考查找点的坐标规律,点的坐标的确定,方法,根据已知点的坐标及图形总结点坐标的变化规律,并运用规律解决问题是解题的关键.。
三年级数学思维训练导引(奥数)第07讲 周期问题
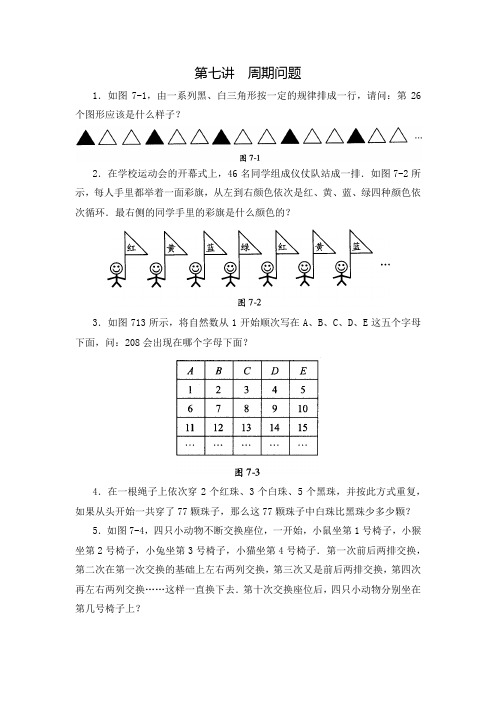
第七讲周期问题1.如图7-1,由一系列黑、白三角形按一定的规律排成一行,请问:第26个图形应该是什么样子?2.在学校运动会的开幕式上,46名同学组成仪仗队站成一排.如图7-2所示,每人手里都举着一面彩旗,从左到右颜色依次是红、黄、蓝、绿四种颜色依次循环.最右侧的同学手里的彩旗是什么颜色的?3.如图713所示,将自然数从1开始顺次写在A、B、C、D、E这五个字母下面,问:208会出现在哪个字母下面?4.在一根绳子上依次穿2个红珠、3个白珠、5个黑珠,并按此方式重复,如果从头开始一共穿了77颗珠子,那么这77颗珠子中白珠比黑珠少多少颗?5.如图7-4,四只小动物不断交换座位,一开始,小鼠坐第1号椅子,小猴坐第2号椅子,小兔坐第3号椅子,小猫坐第4号椅子.第一次前后两排交换,第二次在第一次交换的基础上左右两列交换,第三次又是前后两排交换,第四次再左右两列交换……这样一直换下去.第十次交换座位后,四只小动物分别坐在第几号椅子上?6.将一些自然数排成一列,其中任意相邻的五个数之和都等于15.已知第一个数等于1,第二个数等于2,第三个数等于3,第四个数等于4.问:(1)请写出这个数列的前十项;(2)第一百个数等于多少?7. lOO位同学从左到右排成一行,然后按如下规律从左向右报数:先让第一位同学报1,然后从第二位同学开始,每位同学都把前一位同学所报的数乘以7,再报出乘积的个位来.请问:第100个同学报的是几?8.(1)如图7-5所示,甲、乙两只蚂蚁,分别沿正方形ABCD和AEFG按照顺时针的方向爬行.甲2分钟能爬完正方形的一条边,乙1分钟能爬完正方形的一条边,现在两只蚂蚁在A点同时出发,那么50分钟后甲、乙分别在什么位置?(2)如图7-5所示,如果蚂蚁甲从C点出发,沿着C→D→A→E→F→G→A→B→C 的路线爬行,1分钟能爬完正方形的一条边;蚂蚁乙从F点出发,沿着F→G→A→B→C→D→A→E→F的路线爬行,2分钟能爬完正方形的一条边,它们同时出发,90分钟后甲、乙分别在什么位置?9.一只蜗牛从深30米的井底向上爬,第一天向上爬了6米;第二天休息,于是向下滑了4米;第三天再向上爬6米;第四天又向下滑4米……按这样的规律进行下去,蜗牛第几天才能爬到井口?10.(1)今天是星期六,再过60天是星期几?(2) 2008年6月1日是星期日,2008年8月1日是星期几?(3) 2008年2月8日是星期五,2009年2月8日是星期几?1.图7-6是一行按规律排列的图形.请问:第88个图形应该是什么?2.观察图7-7中黑、白两色三角形的变化规律.请问:前200个图形中有多少个白色三角形?3.如图7-8所示,表格中每行的文字都是循环出现的:第一行是“黎曼假设”4个汉字不断重复,第二行是“庞加莱猜想”5个汉字不断重复,第三行则是“哥德巴赫猜想”6个汉字不断重复.第200列从上到下依次是哪3个汉字?4.阿奇和其他5个小朋友围成一圈,圆圈中央摆放着55个乒乓球.从阿奇开始,小朋友们沿逆时针方向依次拿球,每人每次拿3个,直到把乒乓球全部拿完为止(最后剩下的球不足3个就全拿).阿奇总共拿到了几个球?5.如图7-9,电子跳蚤每跳一步,可从一个圆圈跳到相邻的圆圈.现在,一只红跳蚤从标有数“1”的圆圈按顺时针方向跳了100步,落在一个圆圈里.一只黑跳蚤也从标有数“l”的圆圈起跳,但它是沿着逆时针方向跳了200步,落在另一个圆圈里,这两个圆圈里的数的乘积是多少?6.(1)工厂的仓库里有80吨货物,这些货物都由同一辆卡车负责运输.第一天卡车往仓库里运进50吨,第二天运出了60吨,第三天又运进50吨,第四天再运出60吨……如此不停地运下去.第几天的时候,仓库里的货物恰好被运完?(2)工厂的仓库里有80吨货物,同样是由一辆卡车负责货物的运输.第一天,卡车从仓库里运出60吨,第二天再运进50吨,第三天又运出60吨,第四天再运进50吨……如此不停地运下去.第几天的时候,仓库里的货物恰好被运完?7.如图7-10所示,16幅图按规律排成一排.其中前三幅图已经画出,请按规律画出第16幅图的样子.8.甲、乙、丙、丁兄弟四人各收藏了一些宝石.每天早上他们都要聚在一起,重新分配宝石,分配的规则就是:拥有宝石最多的人分给其他三人每人l 颗.如果第1天早上分配完之后,甲、乙、丙、丁四人分别有10、7、5、4颗宝石,那么第100天早上分完宝石后,四个人手中分别有几颗宝石?9.500名士兵排成一排,第一次从左到右1至3循环报数,第二次从左到右1至4循环报数.请问:既报过1又报过4的士兵有多少名?10.如图7-11,伸出左手,然后从大拇指起开始数数.当数到200的时候,正好数到哪根手指?11.今天是2008年3月16日星期日,阿奇研究日历时,发现再过1天是2008年3月17日星期一,再过2天则是2008年3月18日星期二……请问:(1)再过多少天才是2008年儿童节呢?(2) 2008年的儿童节是星期几?12.哥哥比妹妹大5岁,而且两人生日相同.如果哥哥是1982年6月17日星期四出生的,那么妹妹是在星期几出生的?妹妹出生后第一次在星期二过生日的时候是哪一年?1.观察图7-12中图形的规律,第200个图形应该是下面A、B、C、D四个图形中的哪一个?2.如图7-13所示,7个小朋友围成一圈,沿顺时针方向依次编号为1—7.然后,按如下方法给他们发糖:先给l号小朋友1块糖;然后沿顺时针方向隔过一个人后,给3号小朋友1块糖;再沿顺时针方向隔过两个人后,给6号小朋友l 块糖;接着又沿顺时针方向隔过一个人后,给1号小朋友1块糖……如此反复地间隔一个人、两个人,直到1997块糖全部分完,那么最先发到糖的那位小朋友一共得到了多少块糖?3.如图7-14所示,用红、黄、蓝3种颜色的彩笔,按规律给表格染色,第20行和第30列交叉处的方格所染的颜色是什么?4.(1)某月有31天,有4个星期二和4个星期五,那么这个月的20日是星期几?(2)某月的星期二比星期一多,那么这个月的25日是星期几?5.500名士兵排成一排,第一次从左到右1-5循环报数,第二次从右到左1—4循环报数.请问:既报1又报5的士兵有多少名?6.有六十多人站成一行,从左到右由1开始按l、2、3、4依次循环报数,然后从右到左由1开始按1、2、3依次循环报数,最后发现刚好有12个人既报了1又报了2.请问:这一行最少有多少人?最多有多少人?7.实验室里有两只不同的怪钟,每只钟只有一个指针,而且都是每分钟跳一次,第一只钟一圈有12个格,格线上依次标着0—11,指针一次跳过2个格(例如从4跳到6).第二只钟一圈有7个格,格线上依次标着0至6,指针一次跳过3个格.开始时两个指针都指向0,如果把这看作两个指针第1次指向同一个标数,那么当两个指针第30次指向同一个标数时,它们的指针指着哪个数字?8.如图7-15,在A、B两地之间有7个车站,一辆列车不停地往返于A、B 两地之间.它从A出发,每天行驶到下一站,到达B地后的下一天又回到7号站,如此反复.已知列车第4次驶入4号站时是星期六,那么它第20次驶入5号站时是星期几?。
三年级奥数第07讲-填数游戏(教)

学科教师辅导讲义学员编号:年级:三年级课时数:3 学员姓名:辅导科目:奥数学科教师:授课主题第07讲-填数游戏授课类型T同步课堂P实战演练S归纳总结教学目标①经历填数游戏活动,初步提高分析推理能力。
②在探索、尝试、交流等活动中,体会填数游戏的乐趣,激发学习兴趣。
授课日期及时段T(Textbook-Based)——同步课堂本讲有两部分主要内容:1、幻方的概念和性质,简单幻方的编制;2、把一些数字按照一定要求排列成相应的图形,叫做数阵图。
大致分为三类:(1)封闭型数阵图(2)辐射型数阵图(3)复合型数阵图幻方的概念:所谓幻方是指在正方形方格表的每个方格内填入数,使得每行、每列和两条对角线上的各数之和相等;而阶数是指每行、每列所包含的方格数。
幻方题可以粗略的分为两种(1)限制了所填入的数字,或者给出了需要填入的各个数字,或者已经填入一个或几个数字;(2)另一种是对填入的数字没有任何限制,填对即可。
幻方问题主要方法:(1)累加法:利用累加的方法可以求出“幻和”和关键位置上的数字。
通常将若干个“幻和”累加在一起,再计算每一个位置上的重数,从而求出“幻和”和关键位置上的数字。
(2)求出“幻和”和关键位置上的数字后,结合枚举法完成数阵图的填写,在填写数阵图的过程中注意从特殊的数字和位置入手。
(3)比较法:利用比较的方法可以直接填出某些位置的数字。
注意观察数阵图中相关联的“幻和”之间的关系,注意它们之间共同的部分,去比较不同的部分知识梳理本讲还有一部分内容是数阵图拓展,也就是在三年级数阵图初步的基础上继续学习数阵图问题的解题方法。
数阵图问题方法多样且特殊,我们将在例题中详细讲解。
其实这些方法和幻方是一致的,大家可以在下面的学习中体会到这一点。
例1、在下图中分别填入1—9,使两条直线上五个数的和相等,和是多少呢?【解析】我们可以这样想,把1——9中间的5填到中心的○内,剩下八个数,一大一小,搭配成和都是10的四组,这样两条直线上五个数的和都是5+10×2=25。
高中数学一轮复习课件:第七章 不等式、推理与证明(必修5、选修1-2)7-4

2.数列 2,5,11,20,x,47,…中的 x 等于( ) A.28 B.32 C.33 D.27
[解析] 从第 2 项起每一项与前一项的差构成公差为 3 的等 差数列,所以 x=20+12=32.故选 B.
[答案] B
3.(选修 1-2P30 练习 T1 改编)已知数列{an}中,a1=1,n≥2 时,an=an-1+2n-1,依次计算 a2,a3,a4 后,猜想 an 的表达式 是( )
[对点训练] 1.(2019·山东日照模拟)对于实数 x,[x]表示不超过 x 的最大 整数,观察下列等式: [ 1 ]+[ 2 ]+[ 3 ]=3; [ 4 ]+[ 5 ]+[ 6 ]+[ 7 ]+[ 8 ]=10; [ 9 ]+[ 10 ]+[ 11 ]+[ 12 ]+[ 13 ]+[ 14 ]+[ 15 ] =21; … 按照此规律第 n 个等式的等号右边的结果为________.
主干知识梳理 Z
主干梳理 精要归纳
1.合情推理
[知识梳理]
2.演绎推理 (1)定义:从一般性的原理出发,推出某个特殊情况下的结论, 我们把这种推理称为演绎推理.简言之,演绎推理是由一般到 特殊 的推理. (2)“三段论”是演绎推理的一般模式,包括: ①大前提——已知的一般原理; ②小前提——所研究的特殊情况; ③结论——根据一般原理,对特殊情况作出的判断.
[解析] 根据题图(1)所示的分形规律,可知 1 个白圈分形为 2
个白圈 1 个黑圈,1 个黑圈分形为 1 个白圈 2 个黑圈,把题图(2)
中的树形图的第 1 行记为(1,0),第 2 行记为(2,1),第 3 行记为(5,4),
第 4 行的白圈数为 2×5+4=14,黑圈数为 5+2×4=13,所以第
07正方形展开图50题
正方体展开图一、左边给定的是纸盒的外表面,下面哪一项能由它所折叠而成( )二、左边给定的是纸盒的外表面,下面哪一项能由它所折叠而成( )三、左边给定的是纸盒的外表面,下面哪一项能由它折叠而成?四、左边给定的是纸盒的外表面,下面哪一项能由它折叠而成?五、如图是一个正方体的展开图,图上已经标出了正方体的上面和后面,那么B的位置应该是正方体的()面.A.前B.左C.右D.下六、七、八、九、十、下两幅图是不完整的正方体展开图,请分别把它们补充成完整的正方体展开图.十一、如图是一个平面图形,在顶点处标有数字,当把它折成正方体时,与13重合的数字是_____.十二、如图所示的硬纸板沿虚线折叠成正方体后,与A面相对的面是()面.A.EB.CC.DD.F十三、图二是图一的表面展开图.将这个正方体先向前翻滚一个面,再向右翻滚一个面,这时正方体朝上一面的数字是_____.十四、下面都是正方体展开后的图形,在每一个展开图上用相同的符号标出相对的面.十五、下面哪些能折成一个正方体,画“√”.十六、一个正方小木块,六个面上分别写着不同的数值1、2、3、4、5、6,从3个不同的侧面观看,结果如图,那么与2相对的面是_____.十七、如图是一个长方体展开图,请说出1号、2号、3号相对的各是几号面?并与同学交流.十八、有下面的材料若干份,请你选择一些组成正方体或长方体.十九、韩老师特制了4个同样的立方块,并将它们如图(a)放置,然后又如图(b)放置.则图(b)中四个底面正方形中的点数之和为()A.11B.13C.14D.16二十、如图是一个正方体的展开图,与4号相对的面是()面.A.2B.6C.5D.1二十一、一个正方体展开成一个平面图形,边缘是一个多边形,边数最少是( )条.二十二、如图是一个正方形纸盒的展开图,当折叠成正方体纸盒时,C点与()点重合.A.AB.BC.E D、D二十三、将下图沿虚线折成一个正方体,相对的两个面数字之和最大是( )。
北师大版数学五年级上册-07六 组合图形的面积-033 公顷、平方千米-教案01
教学重点与难点:教学重点:知道1公顷=10000平方米,会进行简单的单位换算,体会1公顷的实际大小
教学难点:知道1公顷=10000平方米,会进行简单的单位换算,体会1公顷的实际大小
教学方法与学法:情境创设,启发引导法
教具准备:课件,1平方厘米和1平方分米的纸片
(平方百米)
100米1000米
厘米分米米10米100米1000米
师:其实看到平方千米,我们还可以想到公顷还有一个其它名字,是什么呢?平方百米。
师:1平方分米=(100)平方厘米┅1平方千米=(100)公顷 强调:相邻的两个面积单位之间的进率是100.
1分米=10厘米 ┅ 1000米=10个100米
强调:每相邻的两个长度单位之间的进率是10
师:现在大家对1公顷有所了解了吧,那么我们通常在什么情况下用公顷来计算和测量呢?公顷有什么作用?
小结:通常在测量学校、小区、村庄、公共场所时,常常用公顷作单位。
我们认识了公顷,比平方米大吗?它等于多少平方米?
1公顷=10000平方米(齐读两遍)
那么2公顷=( )平方米
3公顷=( )平方米
80000平方米=()公顷
教学内容与板书设计
二次
备课
设计
教
学
过
程
一、创设情境,引入公顷
1、谈话:同学们,我们已经学过哪些面积单位?(让学生回答1平方厘米、1平方分米、1平方米的大小的含义。)
强调:边长是1厘米的正方形的面积是1平方厘米。在黑板上标出1平方米的大小区域。
这三个面积单位你会应用吗?我就用这三个面积单位来考考大家。
一块橡皮的面积大约7()
专题07 一次函数中的面积问题精讲(解析版)
专题07 一次函数中的面积问题精讲一、平面直角坐标系中面积的几种求法面积问题是中考的一个重点知识点,考查方式灵活多样,很多题目有创新性,能很好考查学生的灵活运用知识的能力.我们除了要熟知常见图形的面积公式外,在平面直角坐标系中还要懂得以下几种面积的方法: 方法一、割补法割补方法不仅仅只有一种,要灵活使用.方法二、铅垂高、水平宽法=21=2ABC ABC S CD OAS CE OB⨯⨯⨯⨯△△ 二、典型例题选讲题1. 如图1-1所示,把Rt △ABC 放在直角坐标系内,其中∠CAB =90°,BC =5,点A 、B 的坐标分别为(1,0)、(4,0).将△ABC 沿x 轴向右平移,当点C 落在直线y =2x ﹣6上时,线段BC 扫过的面积为( )图1-1A .4B .8C .16D .12 【答案】C .【解析】如图1-2所示.图1-2设C 点移动到直线y =2x ﹣6上的点为C ’. ∵点A 、B 的坐标分别为(1,0)、(4,0), ∴AB =3.∵∠CAB =90°,BC =5,∴在Rt △ABC 中,由勾股定理得:AC =4. ∴A ′C ′=4.∵点C ′在直线y =2x -6上, ∴2x -6=4,解得 x =5.即OA ′=5, ∴CC ′=5-1=4.∴四边形BB ’C ’C 是平行四边形,面积 =4×4=16. 即线段BC 扫过的面积为16,故答案为:C .题2. 已知一次函数2y x a =+与y x b =-+的图象都经过A (2-,0),且与y 轴分别交于B 、C 两点,则△ABC 的面积为 ( ).A . 4B . 5C . 6D . 7 【答案】C .【解析】因为y =2x +a 与y =-x +b 的图象都经过A (-2,0), 所以0=2×(-2)+a , 解得:a =4, 又因为0=2+b 解得:b =-2y =2x +4、y =-x -2与y 轴分别交于B 、C 两点 ∴B (0.4),C (0,-2),三角形ABC 的面积=2×6÷2=6. 故答案为:C .题3. (河北中考)如图3-1所示,在平面直角坐标系xOy 中,A (0,5),直线x =-5与x 轴交于点D ,直线y =-38x -398与x 轴及直线x =-5分别交于点C ,E .点B ,E 关于x 轴对称,连接AB . (1)求点C ,E 的坐标及直线AB 的解析式; (2)若S =S △CDE +S 四边形ABDO ,求S 的值;(3)在求(2)中S 时,嘉琪有个想法:“将△CDE 沿x 轴翻折到△CDB 的位置,而△CDB 与四边形ABDO 拼接后可看成△AOC ,这样求S 便转化为直接求△AOC 的面积,如此不更快捷吗?”但大家经反复验算,发现S △AOC ≠S ,请通过计算解释他的想法错在哪里.图3-1【答案】见解析【解析】解:(1)y =-38x -398,令y =0,有0=-38x -398,解得:x =-13,即C (-13,0).令x =-5,则有y =-38×(-5)-398=-3,即E (-5,-3).∵点B ,E 关于x 轴对称, ∵B (-5,3). ∵A (0,5),∵设直线AB 的解析式为y =kx +5, ∵-5k +5=3, ∵k =25,∵直线AB 的解析式为y =25x +5.(2)由(1)知E (-5,-3), ∵DE =3. ∵C (-13,0),∵CD =-5-(-13)=8, ∵S ∵CDE =12CD ·DE =12.由题意知OA =5,OD =5,BD =3, ∵S 四边形ABDO =12(BD +OA )·OD =20,∵S =S ∵CDE +S 四边形ABDO =12+20=32.(3)由(2)知S =32,在∵AOC 中,OA =5,OC =13, ∵S ∵AOC =12OA ·OC =652=32.5,∵S ≠S ∵AOC .理由:由(1)知直线AB 的解析式为y =25x +5,令y =0,则0=25x +5,∵x =-252≠-13,∵点C 不在直线AB 上,即点A ,B ,C 不在同一条直线上, ∵S ∵AOC ≠S .题4. 已知一次函数的图象过点(0,3),且与两坐标轴所围成的三角形面积为3, 则其表达式为( ) A . y =1.5x +3B . y =-1.5x +3C . y =1.5x +3或y =-1.5x +3D . y =1.5x -3或y =-1.5x -3【答案】C .【解析】解:设该一次函数与x 轴的交点坐标为(a ,0), 由题意得:1332a ⨯⨯=, 解得:a =±2, 当a =2时,设直线解析式为y =kx +3,将(2,0)代入,求得k =-1.5; 同理求得,当a =-2时,k =1.5.所以函数解析式为:y =1.5x +3或y =-1.5x +3,故答案为C .题5. 如图5-1所示,已知一次函数y =kx +b 的图象经过A (-2,-1),B (1,3)两点,并且交x 轴于点C ,交y 轴于点D .图5-1(1)求该一次函数的解析式;(2)求∵AOB 的面积. 【答案】见解析.【解析】解:(1)把A (-2,-1),B (1,3)代入y =kx +b ,得:⎩⎪⎨⎪⎧-2k +b =-1,k +b =3. 解得⎩⎨⎧k =43,b =53.∵一次函数的解析式为y =43x +53.(2)把x =0代入y =43x +53,得y =53,∵D 点坐标为(0,53).∵S ∵AOB =S ∵AOD +S ∵BOD =12×53×2+12×53×1=52.题6. 已知,一次函数y kx b =+的图像与正比例函数13y x =交于点A ,并与y 轴交于点(0,4)B -,△AOB 的面积为6,则kb = 【答案】203-或4. 【解析】解:因为一次函数y kx b =+的图像与y 轴交于点(0,4)B -, ∴b =-4,OB =4, 设A 点横坐标为a , 因为△AOB 的面积为6, 所以162a OB ⨯⨯=, 即a =3或-3,点A 的坐标为(3,1)或(-3,-1) 将A 点坐标代入4y kx =-,得: k =53或-1 所以kb = 203-或4. 故答案为:203-或4.题7. 如图7-1所示,点G ,D ,C 在直线a 上,点E ,F ,A ,B 在直线b 上,若a ∥b ,Rt △GEF 从如图所示的位置出发,沿直线b 向右匀速运动,直到EG 与BC 重合.运动过程中△GEF 与矩形ABCD 重合部分的面积(S )随时间(t )变化的图象大致是( )图7-1A B C D【解析】根据题意可得:①F、A重合之前没有重叠面积;②F、A重叠之后,重叠部分面积逐渐增大,且增加的速度越来越快;③△EFG完全进入且F与B重合之前,重叠部分的面积是三角形的面积,不变,④F与B重合之后,重叠部分的面积逐渐减小,减小的速度越来越慢,直至最后重叠部分的面积为0.综上所述,只有B选项图形符合.故答案为:B.题8. 如图8-1所示,已知直线y=2x+3与直线y=-2x-1.(1)求两直线交点C的坐标;(2)求∵ABC的面积.(3)在直线BC上能否找到点P,使得S∵APC=6,若能,请求出点P的坐标,若不能请说明理由。
初一数学第二学期名校优选小专题07 平行与旋转问题
初一数学第二学期名校优选小专题07 平行与旋转问题【模型讲解】如图1,将三角板ABC 与三角板ADE 摆放在一起:如图2,其中∠ACB =30°,∠DAE =45°,∠BAC =∠D =90°,固定三角板ABC ,将三角板ADE 绕点A 按顺时针方向旋转,记旋转角∠CAE =ɑ(0°<ɑ<180°)(1)当ɑ为________度时,AD BC ∥.(2)当△ADE 旋转速度为5°/秒时,且它的一边与△ABC 的某一边平行(不共线)时,求出时间t 的所有值. 解:(1)当α=15°时,AD BC ∥,如图:AD BC ∥30DAC ACB ∴∠=∠=︒453015CAE DAE DAC ∴=∠=∠-∠=︒-︒=︒ɑ故答案为15;(2)①当AD ∥BC 时,α=15°,t =3;②当DE ∥AB 时,α=45°,t =9;③当DE ∥BC 时,α=105°,t =21;④当DE ∥AC 时,α=135°,t =27;⑤当AE ∥BC 时,α=150°,t =30;综上,t =3或9或21或27或30.【模型演练】1.如图,将木条a ,b 与c 钉在一起,180∠=︒,250∠=︒,要使木条a 与b 平行,木条a 按图所示方向旋转的度数至少是 __.2.如图,已知PQ MN ∥,点A ,B 分别在MN ,PQ 上,射线AC 自射线AN 的位置开始,以每秒4°的速度绕点A 逆时针旋转至AM 便立即顺时针回转当和AN 重合时停止运动,射线BD 自射线BP 的位置开始,以每秒1°的速度绕点B 逆时针旋转至BQ 后停止运动.若射线BD 先转动30秒,射线AC 才开始转动,当射线AC 与BD 互相平行时,射线BD 的旋转时间为______秒.3.如图,AB ∥CD ,点P ,Q 分别是AB ,CD 上的一点,射线PB 绕点P 顺时针旋转,速度为每秒1度,射线QC 绕点Q 顺时针旋转,速度为每秒2度,旋转至与QD 重合便立即回转,当射线PB 旋转至与PA 重合时,PB 与QC 都停止转动.若射线PB 先转动30秒,射线QC 才开始转动,则射线QC 转动__________秒后,QC 与PB 平行.4.有一道题目“一副直角三角尺如图所示叠放,现将含45°角的三角尺ADE 固定不动,将含30°角的三角尺ABC 绕顶点A 顺时针转动180°,在旋转的过程中,当三角尺ABC 的边BC 与三角尺ADE 的边平行时,求∠BAD .”嘉嘉的结果是∠BAD 为60°或105°;淇淇说:“嘉嘉考虑的不周全,∠BAD 还有另一个不同的值.”下列判断正确的是( )A .淇洪说的对,且∠BAD 的另一个值为15°B .嘉嘉的结果完全正确C .嘉嘉求的结果不对,∠BAD 为30°或105°D .两人都不对,∠BAD 应5有个不同的值5.两块不同的三角板按如图1所示摆放,AC 边重合,45BAC ∠=︒,30DAC ∠=︒.接着如图2保持三角板ABC 不动,将三角板ACD 绕着点C 按顺时针以每秒15︒的速度旋转90︒后停止.在此旋转过程中,当旋转时间t =______________秒时,三角板A CD ''有一条边与三角板ABC 的一条边恰好平行.6.“一带一路”让中国和世界联系更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯.如图所示,灯A 射线从AM 开始顺时针旋转至AN 便立即回转,灯B 射线从BP 开始顺时针旋转至BQ 便立即回转,两灯不停交叉照射巡视若灯A 转动的速度是每秒2︒,灯B 转动的速度是每秒1︒.假定主道路是平行的,即PQ MN ∥,且:2:1BAM BAN ∠∠=.(1)填空:BAN ∠=______︒;(2)若灯B 射线先转动30秒,灯A 射线才开始转动,在灯B 射线到达BQ 之前,A 灯转动几秒,两灯的光束互相平行?(3)若两灯同时开始转动,两灯射出的光束交于点C ,且120ACB ∠=︒,则在灯B 射线到达BQ 之前,转动的时间为______秒.7.长江汛期即将来临,为了便于夜间查看江水及两岸河堤的情况,防汛指挥部在一危险地带两岸各安置了一探照灯(如图1),假定这一带长江两岸河堤是平行的,即PQ MN ∥,连结AB ,且45ABN ∠=︒.灯A 射线自AQ 顺时针旋转至AP 便立即回转,灯B 射线自BM 顺时针旋转至BN 便立即回转,两灯不停交叉照射巡视.若灯A 转动的速度是1度/秒,灯B 转动的速度是3度/秒.(1)若两灯同时转动,在灯B 射线第一次转到BN 之前,两灯射出的光线交于点C .①如图1,当两灯光线同时转动50秒时,求ABC ∠的度数.②如图2,过C 作CD BC ⊥交PQ 于点D ,则在转动过程中,求ABC ∠与ACD ∠的比值,并说明理由.(2)若灯A 射线先转动30秒,灯B 射线才开始转动,在灯A 射线第一次转到AP 之前,B 灯转动几秒,两灯的光线互相平行?8.“一带一路”让中国和世界更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了A ,D 两座可旋转探照灯.假定主道路是平行的,即PQ CN ∥,A ,B 为PQ 上两点,AD 平分CAB ∠交CN 于点D ,E 为AD 上一点,连接BE ,AF 平分BAD ∠交BE 于点F .(1)若40C ∠=︒,求EAP ∠的大小;(2)作AG 交CD 于点G ,且满足113ADC ∠=∠,当621805GAF ∠+∠=︒时,试说明:AC BE ∥; (3)在(1)问的条件下,探照灯A 、D 照出的光线在铁路所在平面旋转,探照灯射出的光线AC 以每秒4度的速度逆时针转动,探照灯D 射出的光线DN 以每秒12度的速度逆时针转动,光线DN 转至射线DC 后立即以相同速度顺时针回转,若它们同时开始转动,设转动时间为t 秒,当光线DN 回到出发时的位置时同时停止转动,则在转动过程中,t 为何值时光线AC 与光线DN 互相平行或垂直,请直接写出t 的值.9.如图1,将一副直角三角板放在同一条直线 AB 上,它们的一边分别与直线AB 重合,其中∠ONM =30°,∠OCD =45°,将图1中的三角板OMN 绕点O 按每秒15°的速度沿逆时针方向旋转α︒.(0°<α︒<180°).(1)当∠AOM =105°时,求旋转角的度数.(2)当两块三角板中至少有一组边互相平行时,求旋转的时间.(3)将图1中的三角板OMN 绕点O 按逆时针方向旋转得到图2,MN 与CD 相交于点E ,若∠CEN =β︒时,试探究αβ与的数量关系,并直接写出结论.10.如图,在△ABC 中,点D 、E 是边BC 上两点,点F 是边AB 上一点,将△ADC 沿AD 折叠得到△ADG ,DG 交AB 于点H ;将△EFB 沿EF 折叠得到△EFH .(1)如图1,当点G 与点H 重合时,请说明BAC EHD ∠=∠;(2)当点G 落在△ABC 外,且HE ∥AD ,:1:3GAB CAD ∠∠=①如图2,请说明4EHD GAB ∠∠=;②如图3,若30B ∠=︒,将△EFH 绕点H 顺时针方向旋转一个角度α()0180α<<,则在这个旋转过程中,当△EFH 的其中一边与△AHG 的某一边平行时,直接写出旋转角α的度数11.在平行的两岸河堤即PQ ∥MN ,各安置了一探照灯A 和B ,且∠BAN =45°,如图1,灯A 射线自AM 顺时针旋转至AN 便立即回转,灯B 射线自BP 顺时针旋转至BQ 便立即回转,两灯不停交叉照射巡视.若灯A 转动的速度是a °/秒,灯B 转动的速度是b °/秒,且a ,b 满足()2310a b -+-=.(1)求a ,b 的值;(2)若灯B 射线先转动20秒,灯A 射线才开始转动,在灯B 射线到达BQ 之前,A 灯转动几秒,两灯的光束互相平行?(3)如图,两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作CD⊥AC交PQ于点D,则在转动过程中,∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系.12.如图,已知AB∥CD,直线MN交AB于点M,交CD于点N.点E是线段MN上一点,P,Q 分别在射线MA,NC上,连接PE,QE,PF平分∠MPE,QF平分∠CQE.(1)如图1,若PE⊥QE,∠EQN=64°,则∠MPE=°,∠PFQ=°.(2)如图2,求∠PEQ与∠PFQ之间的数量关系,并说明理由.(3)如图3,当PE⊥QE时,若∠APE=150°,∠MND=110°,过点P作PH⊥QF交QF的延长线于点H.将直线MN绕点N顺时针旋转,速度为每秒5°,直线MN旋转后的对应直线为M N',同'',当直线时△FPH绕点P逆时针旋转,速度为每秒10°,△FPH旋转后的对应三角形为△F PH'' MN首次落到CD上时,整个运动停止.在此运动过程中,经过t秒后,直线M N'恰好平行于△F PH 的一条边,请直接写出所有满足条件的t的值.13.长江汛期即将来临,防汛指挥部在一危险地带两岸各安置了一探照灯,便于夜间查看江水及两岸河堤的情况.如图,灯A射线自AM顺时针旋转至AN便立即回转,灯B射线自BP顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是a°/秒,灯B转动的速度是b°/秒,且a、b满足|a-3|+(b-1)2=0.假定这一带长江两岸河堤是平行的,即PQ∥MN,且∠BAN=45°.(1)求a、b的值;(2)若灯B射线先转动20秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?(3)如图,两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作CD⊥AC交PQ于点D,则在转动过程中,BACBCD∠∠= .14.如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°.将一把直角三角尺的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方,其中∠OMN=30°.(1)将图1中的三角尺绕点O顺时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,求∠CON的度数;(2)将图1中的三角尺绕点O按每秒6°的速度绕点O沿顺时针方向旋转一周,OC也以每秒1°的速度绕点O顺时针方向旋转,当三角尺停止运动时,OC也停止运动.①在旋转的过程中,问运动几秒时,边MN恰好与射线OC平行;②将图1中的三角尺绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究∠AOM与∠NOC 之间的数量关系(直接写出结果).15.如图,直线PQ MN,一副直角三角板△ABC、△DEF中,∠ACB=∠EDF=90°,∠ABC=∠BAC=45°,∠DFE=30°,∠DEF=60°.(1)若△DEF如图1摆放,当ED平分∠PEF时,则∠DFM=.(2)若图2中△ABC固定,将△DEF沿着AC方向平移,边DF与直线PQ相交于点G,作∠FGQ和∠GF A的角平分线GH、FH相交于点H(如图3),求∠GHF的度数.(3)若图2中△DEF固定,(如图4)将△ABC绕点A顺时针旋转,1分钟转半圈,旋转至AC与直线AN首次重合的过程中,当线段BC与△DEF的一条边平行时,请直接写出旋转的时间.(单位必须化成秒)答案与解析【模型讲解】如图1,将三角板ABC 与三角板ADE 摆放在一起:如图2,其中∠ACB =30°,∠DAE =45°,∠BAC =∠D =90°,固定三角板ABC ,将三角板ADE 绕点A 按顺时针方向旋转,记旋转角∠CAE =ɑ(0°<ɑ<180°)(1)当ɑ为________度时,AD BC ∥.(2)当△ADE 旋转速度为5°/秒时,且它的一边与△ABC的某一边平行(不共线)时,求出时间t 的所有值. 解:(1)当α=15°时,AD BC ∥,如图:AD BC ∥30DAC ACB ∴∠=∠=︒453015CAE DAE DAC ∴=∠=∠-∠=︒-︒=︒ɑ故答案为15;(2)①当AD ∥BC 时,α=15°,t =3;②当DE ∥AB 时,α=45°,t =9;③当DE ∥BC 时,α=105°,t =21;④当DE ∥AC 时,α=135°,t =27;⑤当AE ∥BC 时,α=150°,t =30;综上,t =3或9或21或27或30.【模型演练】1.如图,将木条a ,b 与c 钉在一起,180∠=︒,250∠=︒,要使木条a 与b 平行,木条a 按图所示方向旋转的度数至少是 __.【答案】30°【分析】根据同位角相等,两直线平行,求出旋转后∠2的同位角的度数,然后用∠1减去即可得到木条a 旋转的度数.【解析】解:如图:∵∠AOC=∠2=50°时,OA//b,即a//b,∴要使木条a与b平行,木条a旋转的度数至少是80°﹣50°=30°.故答案为:30°.【点评】本题考查了平行线的判定,根据同位角相等两直线平行求出旋转后∠2的同位角的度数是解题的关键.2.如图,已知PQ MN∥,点A,B分别在MN,PQ上,射线AC自射线AN的位置开始,以每秒4°的速度绕点A逆时针旋转至AM便立即顺时针回转当和AN重合时停止运动,射线BD自射线BP 的位置开始,以每秒1°的速度绕点B逆时针旋转至BQ后停止运动.若射线BD先转动30秒,射线AC才开始转动,当射线AC与BD互相平行时,射线BD的旋转时间为______秒.【答案】0或40或96或180【分析】根据题意,设射线BD的旋转时间为t秒,则PBD t∠=︒,分六种情况讨论,①t=0时,AC∥BD;②当0<t≤30,③当30<t≤75,④当75<t≤120,⑤当120<t<180时,⑥当t=180时,AC∥BD共有4种情形,根据平行线的性质得出角度相等,进而列出方程,解方程即可求解.【解析】∵射线AC自射线AN的位置开始,以每秒4°的速度绕点A逆时针旋转至AM便立即顺时针回转当和AN重合时停止运动,∴射线AC自射线AN的位置旋转至AM,用了180454=︒︒(秒),由AM顺时针回转至AN用了180454=︒︒(秒),∵射线BD自射线BP的位置开始,以每秒1°的速度绕点B逆时针旋转至BQ后停止运动,设射线BD的旋转时间为t秒,则PBD t∠=︒,①∵射线BD先转动30秒,射线AC才开始转动,∴当t=0时,AC∥BD;②当0<t≤30,射线AC与BD不能互相平行;③当30<t≤30+45即30<t≤75时,∠CAN=[4(t-30)]°,若射线AC与BD互相平行,则∠PBD=∠CAN,即t=4(t-30),④当30+45<t≤75+45即75<t≤120时,∠CAN = [180×2-4(t-30)]°=(480-4t)°,若射线AC与BD互相平行,则∠PBD=∠CAN,即t=480-4t,解得:t=96;⑤当120<t<180时,射线AC与BD不能互相平行;⑥当t=180时,AC∥BD,综上所述,当射线AC与BD互相平行时,射线BD的旋转时间为0或40或96或180秒.故答案为:0或40或96或180.【点评】本题考查了平行线的性质,一元一次方程的应用,分类讨论是解题的关键.3.如图,AB∥CD,点P,Q分别是AB,CD上的一点,射线PB绕点P顺时针旋转,速度为每秒1度,射线QC绕点Q顺时针旋转,速度为每秒2度,旋转至与QD重合便立即回转,当射线PB旋转至与PA重合时,PB与QC都停止转动.若射线PB先转动30秒,射线QC才开始转动,则射线QC 转动__________秒后,QC与PB平行.【答案】30或110【分析】设射线QC转动t秒,两射线互相平行,分两种情况进行讨论:当0<t<90时,根据平行线的性质得出方程,解方程即可求解.【解析】设QC转动后与AB交于点M,PB转动后与CD交于点N,当0<t<90时,如图1,∵AB∥CD,∴∠BPN=∠PNC,∵PN∥MQ,∴∠CQM=∠PNC,∴∠CQM=∠BPN∴2t=1•(30+t),②当90<t <150时,如图2,∵AB ∥CD ,∴∠BPN +∠PND =180°,∵PN ∥QM ,∴∠MQD =∠PND∴∠BPN +∠MQD =180°∴1•(30+t )+(2t -180)=180,解得 t =110,综上所述,射线QC 转动30或110秒,两射线互相平行;故答案为:30或110.【点评】本题考查了平行线的性质,一元一次方程的应用,根据题意分类讨论是解题的关键.4.有一道题目“一副直角三角尺如图所示叠放,现将含45°角的三角尺ADE 固定不动,将含30°角的三角尺ABC 绕顶点A 顺时针转动180°,在旋转的过程中,当三角尺ABC 的边BC 与三角尺ADE 的边平行时,求∠BAD .”嘉嘉的结果是∠BAD 为60°或105°;淇淇说:“嘉嘉考虑的不周全,∠BAD 还有另一个不同的值.”下列判断正确的是( )A .淇洪说的对,且∠BAD 的另一个值为15°B .嘉嘉的结果完全正确C .嘉嘉求的结果不对,∠BAD 为30°或105°D .两人都不对,∠BAD 应5有个不同的值【答案】A【分析】分三种情况:①若BC DE ∥,②若BC AD ∥,③若BC AE ∥,由平行线的性质可得出答案.【解析】解:①若BC DE ∥,∴∠CFE =∠E =90°,又∵∠C =30°,∴30BAE ∠=︒,∴∠DAB =45°-30°=15°;②若BC AD ∥,60BAD B ∴∠=∠=︒;③若BC AE ∥,60B BAE ∴∠=∠=︒,4560105BAD ∴∠=︒+︒=︒.综上所述,BAD ∠为15︒或60︒或105︒.故选:A .【点评】本题考查了旋转的性质,平行线的性质,正确画出图形是解题的关键.5.两块不同的三角板按如图1所示摆放,AC 边重合,45BAC ∠=︒,30DAC ∠=︒.接着如图2保持三角板ABC 不动,将三角板ACD 绕着点C 按顺时针以每秒15︒的速度旋转90︒后停止.在此旋转过程中,当旋转时间t =______________秒时,三角板A CD ''有一条边与三角板ABC 的一条边恰好平行.【答案】2或3或5【分析】分三种情况:①当A C '∥AB 时,②当A D ''∥AC 时,③当A D ''∥AB 时,分别根据平行线的性质求出∠A CA '的度数,进而解答即可.【解析】解:分三种情况:①当A C '∥AB 时,如图:∴∠A CA '=∠BAC =45°,∴15t =45,∴t =3;②当A D ''∥AC 时,如图,∴∠A CA '=∠A '=30°,∴15t =30,∴t =2;③当A D ''∥AB 时,如图,过点C 作CE ∥AB ,则CE ∥AB ∥A D '',∴∠ACE =∠A ,∠ECA '=∠A ',∴∠A CA '=∠ACE +∠ECA '=∠A +∠A '=75°,∴15t =75,∴t =5.综上所述,当旋转时间t =2或3或5秒时,三角板A CD ''有一条边与三角板ABC 的一条边恰好平行.故答案为:2或3或5.【点评】本题考查了平行线的性质,熟练掌握两直线平行,内错角相等是解题的关键. 6.“一带一路”让中国和世界联系更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯.如图所示,灯A 射线从AM 开始顺时针旋转至AN 便立即回转,灯B 射线从BP 开始顺时针旋转至BQ 便立即回转,两灯不停交叉照射巡视若灯A 转动的速度是每秒2︒,灯B 转动的速度是每秒1︒.假定主道路是平行的,即PQ MN ∥,且:2:1BAM BAN ∠∠=.(1)填空:BAN ∠=______︒;(2)若灯B 射线先转动30秒,灯A 射线才开始转动,在灯B 射线到达BQ 之前,A 灯转动几秒,两灯的光束互相平行?(3)若两灯同时开始转动,两灯射出的光束交于点C ,且120ACB ∠=︒,则在灯B 射线到达BQ 之前,转动的时间为______秒. 【答案】(1)60(2)30秒或110秒(3)100或140【分析】(1)设BAN x ∠=︒,则2BAM x ∠=︒,根据180BA BAN M ∠+=∠︒,可列出关于x 的等式,解出x 即可求解;(2)设A 灯转动t 秒,两灯的光束互相平行,分两种情况进行讨论:当090t <≤时,根据()2130t t =⋅+,可得30t =;当90150t <<时,根据()()1302180180t t ⋅++-=,可得 110t =; (3)分类讨论①当090t <≤时和②当90180t <<时,画出图形,分别根据平行线的性质结合题意构建方程解决问题即可.(1)设BAN x ∠=︒,则2BAM x ∠=︒,∵180BA BAN M ∠+=∠︒,即2180x x ︒+︒=︒,∴60x =,∴60BAN ∠=︒.故答案为:60;(2)设A 灯转动t 秒,两灯的光束互相平行,由题意可知(2)CAM t ∠=︒,(30)CAM t ∠=+︒.①当090t <≤时,如图1,PQ MN ∥,PBD BDA ∴∠=∠.AC BD ,CAM BDA ∴∠=∠,CAM PBD ∴∠=∠.()230t t ∴=+,解得 30t =;②当90150t <<时,如图2,PQ MN ∥,180PBD BDA ∴∠+∠=︒.AC BD ,CAN BDA ∴∠=∠,180PBD CAN ∴∠+∠=︒.∵(2)CAM t ∠=︒,∴(2180)CAN t ∠=-︒,()()302180180t t ∴++-=,解得 110t =.综上所述,当30秒或110秒时,两灯的光束互相平行;(3)设灯A 射线转动时间为t 秒,①当090t <≤时,过点C 作CK PQ ∥,PQ MN ∥,PQ MN CK ∴∥∥,CBP BCK ∴∠=∠,CAN ACK ∠=∠,ACB BCK ACK CBP CAN ∴∠=∠+∠=∠+∠,(1802)CAN t ∠=-︒,CBP t ∠=︒,又120ACB ∠=︒,∴(1802)120t t +-=,解得:60t =,∴60CAN ∠=︒,此时AC 与AB 共线,不符合题意;②当90180t <<时,同①的图可得(2180)CAN t ∠=-︒,则(2180)120t t -+=,解得:100t =;如图4中,当120ACB ∠=︒时,同①可知ACB MAC QBC ∠=∠+∠.因为此时(3602)(180)MAC t QBC t ∠=-︒∠=-︒,,120(3602)(180)t t ∴=-+-,解得:140t =.综上可知,t 的值为100或140.故答案为:100或140.【点评】本题主要考查平行线的性质,平行公理及推论,一元一次方程的应用.利用数形结合和分类讨论的思想是解题关键.7.长江汛期即将来临,为了便于夜间查看江水及两岸河堤的情况,防汛指挥部在一危险地带两岸各安置了一探照灯(如图1),假定这一带长江两岸河堤是平行的,即PQ MN ∥,连结AB ,且45ABN ∠=︒.灯A 射线自AQ 顺时针旋转至AP 便立即回转,灯B 射线自BM 顺时针旋转至BN 便立即回转,两灯不停交叉照射巡视.若灯A 转动的速度是1度/秒,灯B 转动的速度是3度/秒.(1)若两灯同时转动,在灯B 射线第一次转到BN 之前,两灯射出的光线交于点C .①如图1,当两灯光线同时转动50秒时,求ABC ∠的度数.②如图2,过C 作CD BC ⊥交PQ 于点D ,则在转动过程中,求ABC ∠与ACD ∠的比值,并说明理由.(2)若灯A 射线先转动30秒,灯B 射线才开始转动,在灯A 射线第一次转到AP 之前,B 灯转动几秒,两灯的光线互相平行? 【答案】(1)①15︒;②比值为32,详见解析 (2)A 灯转动15秒或82.5秒时,两灯的光束互相平行【分析】(1)①当转动50秒时,有150MBC ∠=︒,即有18030CBN MBC ∠=︒-∠=︒,根据ABC ABN CBN ∠=∠-∠,即可得解;②过点C 作CH MN ∥,得到3MBC t ∠=,QAC t ∠=,即有ACH QAC t ∠=∠=,()1803HCB CBN t ∠=∠=-,根据ABC ABN CBN ∠=∠-∠,可得()345ABC t ∠=-,再根据ACB ACH BCH ∠=∠+∠,可得()245ACD t ∠=-,即问题得解; (2)设A 灯转动t 秒,两灯的光束互相平行,A 灯先转动30秒,则AQ 转到AP 还需要180-30=150(秒)即150t 0<<,①当B 射线第一次垂直MN 时,用时90÷3=30(秒),此时A 射线共计运动30+30=60秒,即60QAE ∠=,即在灯B 射线到达BN 之前,先证明MBF QAE ∠=∠,即有:330=+t t ,即可求解;②在灯B 射线到达BN 之后,回到BM 前,根据①中,同理有:()30MBF QAE t ∠=∠=+,()3180FBN t ∠=-即有:()318030180t t -++=,即可求解;③在灯B 射线回到BM 后,第二次到BN前,由题意得:336030t t -=+,即可求解,即问题得解.(1)两灯速度为:灯A 转动的速度是1度/秒,灯B 转动的速度是3度/秒.①当转动50秒时,503150MBC ∠=⨯=,∴18030CBN MBC ∠=-∠=,∴453015ABC ABN CBN ∠=∠-∠=-=,故答案为:15°;②比值为:32,理由如下, 如图2,过点C 作CH MN ∥,∵PQ MN ∥,∴CH PQ ∥,设两灯转动时间为t 秒,则3MBC t ∠=,QAC t ∠=,∴ACH QAC t ∠=∠=,()1803HCB CBN t ∠=∠=-,∴ABC ABN CBN ∠=∠-∠,即()()()4518033135345ABC t t t ∠=--=-=-,又∵ACB ACH BCH ∠=∠+∠,即18031802ACB t t t ∠=+-=-,而90BCD ∠=︒,∴()90901802ACD ACB t ∠=-∠=--()()290245t t =-=-.∴()()3453:2245t ABC ACD t -∠∠==-. 即比值为:32; (2)两灯速度为:灯A 转动的速度是1度/秒,灯B 转动的速度是3度/秒.设A 灯转动t 秒,两灯的光束互相平行,A 灯先转动30秒,则AQ 转到AP 还需要180-30=150(秒)即150t 0<<, ①当B 射线第一次垂直MN 时,用时90÷3=30(秒),此时A 射线共计运动30+30=60秒,即60QAE ∠=,即在灯B 射线到达BN 之前,如图3所示,∵PQ MN ∥,BF AE ∥,∴ABF EAB ∠=∠,PAB ABN ∠=∠,∴180180ABN ABF BAP BAE -∠-∠=-∠-∠,∴MBF QAE ∠=∠,即有:330=+t t ,解得:15t =(秒);②如图4,在灯B 射线到达BN 之后,回到BM 前,根据①中,同理有:()30MBF QAE t ∠=∠=+∵()3180FBN t ∠=-即有:()318030180t t -++=,解得:82.5t =.③如图5,在灯B 射线回到BM 后,第二次到BN 前,由题意得:336030t t -=+,解得:195t =(舍去).综上所述,A 灯转动15秒或82.5秒时,两灯的光束互相平行.【点评】本题主要考查了平行线的性质以及角的和差关系,厘清角度之间的关系并注意分类讨论是解答本题的关键.8.“一带一路”让中国和世界更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了A ,D 两座可旋转探照灯.假定主道路是平行的,即PQ CN ∥,A ,B 为PQ 上两点,AD 平分CAB ∠交CN 于点D ,E 为AD 上一点,连接BE ,AF 平分BAD ∠交BE 于点F .(1)若40C ∠=︒,求EAP ∠的大小;(2)作AG 交CD 于点G ,且满足113ADC ∠=∠,当621805GAF ∠+∠=︒时,试说明:AC BE ∥; (3)在(1)问的条件下,探照灯A 、D 照出的光线在铁路所在平面旋转,探照灯射出的光线AC 以每秒4度的速度逆时针转动,探照灯D射出的光线DN以每秒12度的速度逆时针转动,光线DN转至射线DC后立即以相同速度顺时针回转,若它们同时开始转动,设转动时间为t秒,当光线DN回到出发时的位置时同时停止转动,则在转动过程中,t为何值时光线AC与光线DN互相平行或垂直,请直接写出t的值.AD平分CAD∴∠=EAP∴∠=(2)解: ∵PQADC∴∠=113∠=∠113∴∠=∠AF平分BAD∴∠=2 13EAF∴∠=∠GAF∴∠=625∠+∠22∴∠+∠2BAD ∴∠+∠2AEB ∠+∠BAD∴∠=BAD∠=CAD AEB ∴∠=∠,∴AC BE ∥;(3)解: 3601230s ︒÷︒=,当AC DN ∥时,则ACD HDN ∠=∠,如图,∵PB CH ∥,PAC ACD ∴∠=∠,PAC HDN ∴∠=∠,由题意,404PAC t ∠=+,12HDN t ∠=,40412t t ∴+=,5t s ∴=;当AC DN ⊥时,则90CND ∠=︒,如图,∵PA CD ∥,404ACD PAC t ∴∠=∠=+,12NDH t ∠=,18012NDC t ∴∠=-,4041801290t t ∴++-=,654t s ∴=; 当AC DN ⊥时,则90CND ∠=︒,如图,∵PA CD ∥,404ACD PAC t ∴∠=∠=+,12180NDC t ∠=-,4041218090t t ∴++-=,1158t s ∴=;当ND AC ∥时,则NDC ACH ∠=∠,如图,由题意,12180MDN t ∠=-,404PAC t ∠=+,18036012NDC MDN t ∴∠=︒-∠=-,∵PA CD ∥,404ACH PAC t ∴∠=∠=+,40436012t t ∴+=-,20t s ∴=;当DN AC ⊥时,90DNC ∠=︒,如图,36012NDC t ∠=-,90NDC DCN ∴∠+∠=︒,()180404DCN t ∠=-+,()3601218040490t t ∴-+-+=.205.8t s ∴= 综上,t 的值为5s 或654s 或1158s 或20s 或205.8s 【点评】本题考查了平行线的性质和判定,能灵活运用定理进行推理是解此题的关键,注意:平行线的判定定理有:①同位角相等,两直线平行,②内错角相等,两直线平行,③同旁内角互补,两直线平行,反之亦然.9.如图1,将一副直角三角板放在同一条直线 AB 上,它们的一边分别与直线AB 重合,其中∠ONM =30°,∠OCD =45°,将图1中的三角板OMN 绕点O 按每秒15°的速度沿逆时针方向旋转α︒.(0°<α︒<180°).(1)当∠AOM =105°时,求旋转角的度数.(2)当两块三角板中至少有一组边互相平行时,求旋转的时间.(3)将图1中的三角板OMN绕点O按逆时针方向旋转得到图2,MN与CD相交于点E,若∠CEN=β︒与的数量关系,并直接写出结论.时,试探究αβ【答案】(1)15°;(2)2s或3s或5s或11s;(3)α+β=255【分析】(1)找到旋转角,根据平角的定义即可求解;(2)分为MN∥OC、ON∥CD、MN∥CD、MN∥OD和MO∥CD几种情况讨论,求出旋转角的大小,即可求出旋转时间;(3)用含α︒的式子表示出∠DON,即可得到∠DOM,根据对顶角相等得到∠DEM=∠CEN=β︒,根据四边形内角和为360°,代入数据整理即可.(1)解:如图所示,∠AOM=105°时,∠MOB=180°-105°=75°,∵∠MON=60°,∴∠BON=75°-60°=15°,即旋转角为15°;(2)如图,当MN∥OC时,∠COM=∠M=90°,∠BON=180°﹣∠AOM﹣∠MON=30°,此时t=30÷15=2s;当ON∥CD时,∠BON=∠OCD=45°,此时t=45÷15=3s;当MN∥CD时,∴∠D=∠OMN=90°,∴此时点M在OD上,∠BON=180°﹣∠AOM﹣∠MON=75°,此时t=75÷15=5s;如图,设CD与MN相交于点E,当MN∥OD时,∠DEM=∠D=90°,∴∠DOM=360°﹣∠D﹣∠DEM﹣∠M =90°,∴四边形DEMO为矩形,∴MO∥CD,∵∠DON=∠DOM﹣∠NOM =90°﹣60°=30°,∴∠AON=∠COD﹣∠DON =45°﹣30°=15°,∴∠BON=180°﹣∠AON=165°,此时t=165÷15=11s;∴当两块三角板中至少有一组边互相平行时,旋转的时间为2s或3s或5s或11s.(3)由图可得,∠BON为旋转角,即∠BON=α︒,∵∠COD=45°,∴∠DOB=135°,∴∠DON=α︒﹣135°,∵∠MON=60°,∴∠DOM=60°+α︒﹣135°=α︒﹣75°,∵∠DEM+∠D +∠DOM +∠M=360°,∠DEM=∠CEN=β︒,∴β︒+90°+90°+α︒﹣75°=360°,∴α+β=255.【点评】本题是旋转综合题,考查平行线的性质和四边形内角和,注意数形结合思想的应用.10.如图,在△ABC中,点D、E是边BC上两点,点F是边AB上一点,将△ADC沿AD折叠得到△ADG,DG交AB于点H;将△EFB沿EF折叠得到△EFH.(1)如图1,当点G 与点H 重合时,请说明BAC EHD ∠=∠;(2)当点G 落在△ABC 外,且HE ∥AD ,:1:3GAB CAD ∠∠=①如图2,请说明4EHD GAB ∠∠=;②如图3,若30B ∠=︒,将△EFH 绕点H 顺时针方向旋转一个角度α()0180α<<,则在这个旋转过程中,当△EFH 的其中一边与△AHG 的某一边平行时,直接写出旋转角α的度数 【答案】(1)见解析(2)①见解析;②满足条件的旋转角α为15︒或45︒或90︒或105︒【分析】(1)利用翻折变换的性质以及三角形内角和定理证明即可;(2)①由:1:3GAB CAD ∠∠=,可以假设GAB x ∠=,3CAD DAG x ∠=∠=,证明4DHE x ∠=即可; ②分四种情形:如图31-中,当FH AG ∥时.如图32-中,当EH AG ∥时.如图33-中,当EF AB ∥时.如图34-中,当EF AG ∥时,分别求解即可.(1)证明:如图1中,由翻折变换的性质可知,AHD C ∠=∠,B EHB ∠=∠,180B C BAC ∠+∠+∠=︒,180EHB EHD AHD ∠+∠+∠=︒,EHD BAC ∴∠=∠;(2)①证明:如图2中,:1:3GAB CAD ∠∠=,∴设GAB x ∠=,3CAD DAG x ∠=∠=,2DAH DAG GAB x ∴∠=∠-∠=,EH ∥AD ,2EHB DAH x ∴∠=∠=,EHD ADH ADC ∠=∠=∠,2B EHB x ∴∠=∠=,4ADC B DAB x ∠=∠+∠=,4DHE GAB ∴∠=∠;②解:由题意,30B ∠=︒,30B DAB ∴∠=∠=︒,15GAB ∴∠=︒,45DAG DAC ∴∠-∠=︒,75C BAC ∴∠=∠=︒,60ADC ADG BDG ∴∠=∠=∠=︒,90DHB ∴∠=︒,如图31-中,当FH AG ∥时,旋转角15FHB GAB ∠=∠=︒.如图32-中,当EH AG ∥时,旋转角153045FHB ∠=︒+︒=︒.如图33-中,当EF AB ∥时,旋转角90FHB ∠=︒.如图34-中,当EF AG ∥时,旋转角9015105FHB ∠=︒+︒=︒,综上所述,满足条件的旋转角α为15︒或45︒或90︒或105︒.【点评】本题考查翻折变换,旋转变换,平行线的性质,三角形内角和定理等知识,解题的关键是学会用分类讨论的思想思考问题.11.在平行的两岸河堤即PQ ∥MN ,各安置了一探照灯A 和B ,且∠BAN =45°,如图1,灯A 射线自AM 顺时针旋转至AN 便立即回转,灯B 射线自BP 顺时针旋转至BQ 便立即回转,两灯不停交叉照射巡视.若灯A 转动的速度是a °/秒,灯B 转动的速度是b °/秒,且a ,b 满足()2310a b -+-=.(1)求a ,b 的值;(2)若灯B 射线先转动20秒,灯A 射线才开始转动,在灯B 射线到达BQ 之前,A 灯转动几秒,两灯的光束互相平行?(3)如图,两灯同时转动,在灯A 射线到达AN 之前.若射出的光束交于点C ,过C 作CD ⊥AC 交PQ 于点D ,则在转动过程中,∠BAC 与∠BCD 的数量关系是否发生变化?若不变,请求出其数量关系.【答案】(1)a =3,b =1(2)当t =10秒或85秒时,两灯的光束互相平行(3)2∠BAC =3∠BCD分别在射线MA,NC上,连接PE,QE,PF平分∠MPE,QF平分∠CQE.(1)如图1,若PE⊥QE,∠EQN=64°,则∠MPE=°,∠PFQ=°.(2)如图2,求∠PEQ与∠PFQ之间的数量关系,并说明理由.(3)如图3,当PE⊥QE时,若∠APE=150°,∠MND=110°,过点P作PH⊥QF交QF的延长线于点H.将直线MN绕点N顺时针旋转,速度为每秒5°,直线MN旋转后的对应直线为M N',同时△FPH绕点P逆时针旋转,速度为每秒10°,△FPH旋转后的对应三角形为△F PH'',当直线MN首次落到CD上时,整个运动停止.在此运动过程中,经过t秒后,直线M N'恰好平行于△F PH''的一条边,请直接写出所有满足条件的t的值.【答案】(1)26;135;(2)2∠PFQ-∠PEQ=180°,理由见解析;(3)t=163或343或253.【分析】(1)延长PE交CD于G,设PE,FQ交于点H,设∠MPE=2α,则∠FPE=12∠BPE=α,根据AB∥CD可表示出∠PGQ,进而根据三角形内角和推论表示出∠EQC,进而表示出∠EQH,然后结合△EQH和△PFH内角和得出关系式,进一步得出结果;(2)类比(1)的方法过程,得出结果;(3)分为△PF H''的三边分别与NM'平行,分别画出图形求解即可.【解析】解:(1)如图1,延长PE交CD于G,设PE,FQ交于点H,设∠BPE=2α,则∠FPE=12∠BPE=α,∵AB∥CD,∴∠PGQ=∠BPE=2α,∵PE⊥QE,∴∠QEH=QEG=90°,∴∠EQC=∠QEG+∠PGQ=90°+2α,∴∠EQH=12∠EQC=45°+α,∴∠BPE=26°.在△EQH和△PFH中,∵∠HEQ+∠HQE+∠EHQ=180°,∠FPH+∠FHP+∠PFH=180°,∠PHF=∠EHQ,∴∠HEQ+∠HQE=∠FPH+∠PFH,即:90°+45°+α=α+∠PFH,∴∠PFH=135°,故答案为:26;135;(2)2∠PFQ-∠PEQ=180°,理由如下:如图1,延长PE交CD于G,设PE,FQ交于点H,设∠BPE=2α,则∠FPE=12∠BPE=α,∵AB∥CD,∴∠PGQ=∠BPE=2α,∵∠GEQ=180°-∠PEQ,∴∠EQC=∠QEG+∠PGQ=180°-∠PEQ+2α,∴∠HQE=12∠EQC=90°+α-12∠PEQ,在△EQH和△PFH中,∵∠PEQ+∠HQE+∠EHQ=180°,∠FPH+∠FHP+∠PFH=180°,∠PHF=∠EHQ,∴∠PEQ+∠HQE=∠FPH+∠PFH,即:∠PEQ+90°+α-12∠PEQ=α+∠PFQ∴2∠PFQ-∠PEQ=180°;(3)根据题意,需要分三种情况:∵∠APE=150°,∴∠BPE=30°,∵PF平分∠MPE,∴∠FPE=∠BPF=15°,由(2)得2∠PFQ-∠PEQ=180°,又∠PEQ=90°,岸河堤的情况.如图,灯A射线自AM顺时针旋转至AN便立即回转,灯B射线自BP顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是a°/秒,灯B转动的速度是b°/秒,且a、b满足|a-3|+(b-1)2=0.假定这一带长江两岸河堤是平行的,即PQ∥MN,且∠BAN=45°.(1)求a 、b 的值;(2)若灯B 射线先转动20秒,灯A 射线才开始转动,在灯B 射线到达BQ 之前,A 灯转动几秒,两灯的光束互相平行?(3)如图,两灯同时转动,在灯A 射线到达AN 之前.若射出的光束交于点C ,过C 作CD ⊥AC 交PQ 于点D ,则在转动过程中,BAC BCD∠∠= . 【答案】(1)a =3,b =1(2)当x =10秒或85秒时,两灯的光束互相平行(3)3:2【分析】(1)根据非负数的性质即可得答案;(2)设A 灯转动x 秒,两灯的光束互相平行.分三种情况讨论:①在灯A 射线转动到AN 之前,②在灯A 射线转动到AN 之后,未到AM 之前,③在灯A 射线转动到AM 之后,未到AN 之前.分别建立方程求得x 的值即可.(3)设A 灯转动x 秒,根据∠BAC =45°-(180°-3t )=3t -135°,∠BCD =90°-∠BCA =90°-(180°-2t )=2t -90°,可得∠BAC 与∠BCD 的关系.(1)∵2|3|(1)0a b -+-=,又2|3|0,(1)0a b -≥-≥,∴30,10a b∴a =3,b =1.(2)设A 灯转动x 秒,两灯的光束互相平行.①当0<x <60时(60为灯A 转到AN 需要的时间,单位s ),3x =(20+x )×1,解得:x =10;②当60<x <120时,3x -60×3+(20+x )×1=180,解得:x =85;③当120<x <160时,3x -360=x +20,解得:x =190>160(不合题意,舍去).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数数图形 B07-1
提示
我们已经认识了好多图形,如长方形、正方形、三角形等,你会在一个组合图形中,数
出这些图形的个数吗?注意:要按一定的顺序去数,才能数准确。
数图形的个数,不但要有一双好眼睛,还要善于开动脑筋,仔细观察按顺序分类去数,
做到不重复、不遗漏,这样才能数得又快又准。
举例1
数一数,下图中共有多少条线段。
【创造力思维】我们知道,每条线段都有两个端点,以相邻两个端点间的线段为1条基
本线段,图中有AB、BC、CD、DE4条,由两条基本线段组成的线段有:AC、BD、CE3条,由
三条基本线段组成的线段有AD、BE2条,由四条基本线段组成的线段有:AE1条,因此,图
中共有线段:4+3+2+1=10(条)
由此可见:一条大线段上的基本线段和线段总条数之间的关系是:线段总条数是从1开
始的一串自然数之和,其中最大的自然数等于基本线段条数。列式如下:
4+3+2+1=10(条)
答:此图共有10条线段。
快练1
1.数一数,下图中共有多少条线段?
2.观察下图,数一数图中共有多少条线段?
3.北京到上海的火车,除起点、终点外,还要停靠6个站,铁路局要准备几种车票?
举例2
数出下面图形中有多少条线段?
【创造力思维】线段都是直的,因此我们在数的时候,必须将这幅图分成九
A-B;B-E;E-F;H-G这四个部分。每一部分用例1的方法数一数,A-B只有1条线段;B-E有
3+2+1-6(条)线段;E-F有1条线段;G-H有2+1=3(条)线段。因此这幅图共有1+6+1+3=11
(条)线段。
列式如下:1+(1+2+3)+1+(1+2)=11(条)
答:此图共有11条线段。
快练2
1.数一数,下图中共有多少条线段?
2.观察下图,数一数图中共有多少条线段?
3.小红在纸上画了一条线段,小亮又拿起笔,在小红画的线段上点了5个点,然后问小红:
“你知道现在这条线段上又多出了多少条线段吗?”小明一会儿就说出了结果。聪明的小
朋友,你知道小明说的是几吗?
举例3
数一数,下图中共有多少个三角形?
【创造力思维】先数上层,有三角形3+2+1=6(个),再数两层合起来的大三角形,有
3+2+1=6(个),所以一共有6×2=12(个)三角形。
此图共有12个三角形。
快练3
数一数,下列各图中有多少个三角形。
B07-2
1. 2. 3.
( )个 ( )个 ( )个
4. 5.
( )个 ( )个
举例4
数一数下图中共有多少个正方形。
(1) (2)
【创造力思维】图(1)中,由一个基本正方形组成的正方形有10个,由四个基本正方
形组成的正方形有4个,所以,图(1)中共有10+4=14(个)正方形。图(2)中,一个基
本正方形组成的正方形有9个,由四个基本正方形组成的正方形有4个,由9个基本正方形
组成的正方形有1个,所以图(2)中共有正方形9+4+1=14(个)。
图(1)中共有14个正方形。图(2)中共有14个正方形。
快练4
数数下列各图形中有几个正方形。
1. 2.
( )个 ( )个
3. 4.
( )个 ( )个
举例5
下图中有多少个小方块?
【创造力思维】图中每层的块数不一样,上层有2块,中间一层在明处的有1块,被上
层遮住的有2块,共3块;下层在明处有3块,被中间层遮住的有3块,共6块。三层一共
有2+3+6=11(块)。列式如下:
2+3+6=11(块)
答:此图共有11块小方块。
快练5
数数下面图中各有多少个小方块。
1. 2.
( )个 ( )个
3. 4.
( )个 ( )个
