圆中切割线定理
第三课时:切割线定理、割线定理和切线长定理

与圆有关的定理第三课时:切割线定理、割线定理和切线长定理直线与圆有三种位置关系,一是直线与圆无交点,叫相离,二是直线与圆只有一个交点,叫相切,这条直线叫做圆的切线,三是直线和圆有二个交点,叫相交,这条直线就叫做圆的割线。
换个更好理解的就是:把圆的任意一条弦向两方无限延长,这条直线就是圆的割线。
1、切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
如图1,几何语言:∵PT切⊙O于点T,PBA是⊙O的割线∴PT2=PA?PB(切割线定理)如图2,设ABP是⊙O的一条割线,PT是⊙O的一条切线,切点为T,则PT2=PA?PB 证明:连接AT, BT∵∠PTB=∠PAT(弦切角定理) ∠P=∠P(公共角)∴△PBT∽△PTA(两角对应相等,两三角形相似)则PB:PT=PT:AP即:PT2=PB?PA2、推论(割线定理):从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等如图3,几何语言:∵PT是○O切线,PBA,PDC是⊙O的割线∴PD?PC=PA?PB(切割线定理推论)由上可知:PT2=PA?PB=PC?PD3、切线长定理:若已知圆的两条切线相交,则切线长相等;圆外一点与圆心的连线,平分过这点向圆引的两条切线所夹的角。
(1)切线长概念切线长是在经过圆外一点的圆的切线上,这点和切点之间的线段的长度,“切线长”是切线上一条线段的长,具有数量的特征,而“切线”是一条直线,它不可以度量长度。
(2)几点说明对于切线长定理,应明确(1)若已知两条切线平行,则圆上两个切点的连线为直径;(2)经过圆外一点引圆的两条切线,连结两个切点可得到一个等腰三角形;(3)经过圆外一点引圆的两条切线,切线的夹角与过切点的两个半径的夹角互补。
(3)推论:圆的外切四边形对边和相等(圆的外切四边形性质定理,逆定理成立);圆的外切等腰梯形的中位线等于腰长.基础知识运用:例1.如图4,正方形ABCD 的边长为1,以BC 为直径。
切割线定理及推论
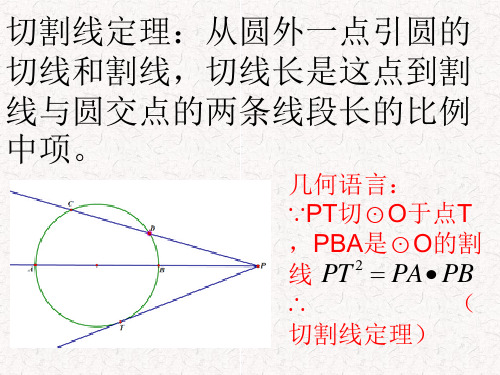
几何语言: ∵PT切⊙O于点T ,PBA是⊙O的割 2 线 PT PA PB ∴ ( 切割线定理)
推论: 从圆外一点引圆的两条割线,这一 点到每条割线与圆的交点的两条线 段长的积相等.
几何语言: ∵PT是⊙O切线, PBA,PDC是⊙O的 割线 ∴PD· PC=PA· PB(切 割线定理推论)(割线 定理)
练:如图,⊙O的两条弦 AB、 CD 相交于点 E, AC和 DB的延长线交 于点 P, 下列结论成立的是( ).
A.PC· CA=PБайду номын сангаас· BD
B.CE· AE=BE· ED C.CE· CD=BE· BA D.PD· PD=PC· PA
例1.如图,⊙O的割线PAB交圆O于点A 和B,PA=6,AB=8,PO=10,求⊙O的半径 。
例2.如图:自圆外一点P作直线PA 切⊙O于A,过PA中点M,作割线 交⊙O于B、C.求证: ∠MPB=∠MCP.
例3.如图,C,D是⊙O的弦AB的三等 分点,弦EF过点C,弦GH过点D。 求证:FC· CE=HD· DG
圆的相关定理

圆幂定理定义圆幂=PO^2-R^2(该结论为欧拉公式)所以圆内的点的幂为负数,圆外的点的幂为正数,圆上的点的幂为零。
相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等。
切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
割线定理:从圆外一点P引两条割线与圆分别交于A、B;C、D,则有PA·PB=PC·PD。
统一归纳:过任意不在圆上的一点P引两条直线L1、L2,L1与圆交于A、B(可重合,即切线),L2与圆交于C、D(可重合),则有PA·PB=PC·PD。
相交弦定理圆内的两条相交弦,被交点分成的两条线段长的积相等。
(经过圆内一点引两条弦,各弦被这点所分成的两段的积相等)相交弦说明几何语言:若弦AB、CD交于点P则PA·PB=PC·PD(相交弦定理)推论:如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的例中项几何语言:若AB是直径,CD垂直AB于点P,则PC^2=PA·PB(相交弦定理推论)切割线定理定义从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
是圆幂定理的一种。
几何语言:∵PT切⊙O于点T,PBA是⊙O的割线∴PT的平方=PA·PB(切割线定理)推论:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等几何语言:∵PT是⊙O切线,PBA,PDC是⊙O的割线∴PD·PC=PA·PB(切割线定理推论)(割线定理)由上可知:PT∧2(平方)=PA·PB=PC·PD证明切割线定理证明:设ABP是⊙O的一条割线,PT是⊙O的一条切线,切点为T,则PT^2=PA·PB证明:连接AT, BT∵∠PTB=∠PAT(弦切角定理)∠P=∠P(公共角)∴△PBT∽△PTA(两角对应相等,两三角形相似)则PB:PT=PT:AP即:PT^2=PB·PA割线定理定义从圆外一点引圆的两条割线,这一点到每条割线与圆交点的距离的积相等。
切割线定理及推论

切割线定理切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
是圆幕定理的一种。
几何语言:••• PT切O O于点T, PBA是O O的割线••• PT A2=PA- PB (切割线定理)推论:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等几何语言:•/ PT是O O切线,PBA , PDC是O O的割线• PD・PC=PA PB (切割线定理推论)(割线定理)由上可知:PT A 2 (平方)=PA・PB=PC PD证明切割线定理证明:T,贝U PTA2=PA PB设ABP是O O的一条割线,PT是O O的一条切线,切点为证明:连接AT, BT•••/ PTB= / PAT(弦切角定理)切割线定理的证明/ P= / P(公共角)•••△ PBTPTA(两角对应相等,两三角形相似)贝U PB : PT=PT:AP即:PT2=PB-PA比较相交弦定理、切割线定理及割线定理(切割线定理推论)以及他们的推论统称为圆幕定理。
一般用于求线段长度。
练:如图,O O的两条弦AB CD相交于点E, AC和DB的延长线交于点P, 下列结论成立的是().A.PC- CA=PB BDB.CE • AE=B E EDC.CE • CD=BE BAD.PD • PD=PC PA例1.如图,O O的割线PAB交圆O于点A和B,PA=6,AB=8,PO=10求OO的半径。
例2.如图:自圆外一点P作直线PA切O O于A,过PA中点M作割线交O O于B、C.求证:/ MPB h MCP例3.如图,C,D是O O的弦AB的三等分点,弦EF过点C,弦GH过点D。
求证:FC- CE=HD DG。
高中数学 1.2.4 切割线定理课件 北师大版选修4-1

∵BC 为⊙O 的直径, ∴∠BAC=90° . 又∵PA 是⊙O 的切线, ∴∠BAP=∠C.
又∵∠P=∠P,∴△ PAB∽△PCA, AP AC 15 ∴ = = =3. BP AB 5 AC ∴在 Rt△ABC 中,tan∠ABC= =3. AB (2)由切割线定理,得 PA2=PB· PC, 即 PA2=PB(PB+BC). 又 PA=15,PB=5, ∴BC=40. 设 AB=x, 则 AC=3x.
2.4 切割线定理
课 标 解 读
1.掌握切割线定理及其推 论. 2.会用切割线定理及推论 解决问题.
1.切割线定理 (1)文字叙述 过圆外一点作圆的一条切线和一条割线, 切线长 是割线 上从 这点到两个交点的线段长 的比例中项.
(2)图形表示
图 1-2-60 如图 1-2-60,⊙O 的切线 PA,切点为 A,割线 PBC,
【答案】 6
定理的综合应用
如图 1-2-67, P 是⊙O 的直径 CB 的延长线上 一点,PA 和⊙O 相切于 A,若 PA=15,PB=5. (1)求 tan∠ABC 的值; (2)弦 AD 使∠BAD=∠P,求 AD 的长.
图 1-2-67
【思路探究】 求 tan∠ABC 可利用△ABC 中边角关系 求出;而 AD 的长,可综合利用切割线定理和图形中的相似 三角形,建立边长关系求出.
图 1-2-62
1.应用切割线定理及其推论的前提条件是什么?
【提示】 只有从圆外一点才可能产生切割线定理或其
推论,切割线定理是指一条切线和一条割线,而其推论则是 指两条割线,只有弄清前提,才能正确运用定理.
2.应用切割线定理应注意什么?
【提示】 出错.
1-2.5.与圆有关的比例线段(切割线定理)

割线定理:从圆外一点引圆的两条割线,这一点到每一条 割线与圆的交点的两条线段长的乘积相等.
应用格式(几何语言描述):
∵PAB,PCD是⊙O 的割线,∴ PA∙PB=PC∙PD.
C
C
B
点P从圆内移动到圆外
D
P
O
D
图5 O
P
A 图3
B A
PA∙PB=PC∙PD
PA∙PB=PC∙PD
使割线PA绕P点
证明:连接AC、AD,同样可以证明
又∵∠ACF=∠AEC. ∴∠CFG=∠ACF. 故FG//AC. ……(6)
你还能推出其他结论吗?
问题3 在图2中,使线段AC继续绕A旋转,使割线CFD 变成切线CD,得到图3. 此时又能推出哪些结论?
B
B
E
D
E
A
D
O 图2
A Q
O 图3
F
G
CG
PC
探究3:可以推出探究1、2中得到的(1)——(6)的所有结论. 此外,
同理可证BD•AE=AC•CE. …………………… (3) ∵AC=AB,∴由(2)(3)可得BE•CD=BD•CE. ………(4)
问题2 在图1中,使线段AC绕A旋转,得到图2.其中EC 交圆于G,DC交圆于F.此时又能推出哪些结论?
问题2 在图1中,使线段AC绕A旋转,得到图2.其中 EC交圆于G,DC交圆于F.此时又能推出哪些结论?
例3 如图,两圆相交于A、B两点,P P 为两圆公共弦AB上任意一点,从P引
D B
两圆的切线PC、PD,求证:PC=PD.
证明:由切割线定理可得:
A
PC2=PA∙PB, PD2=PA∙PB.
C
∴PC2=PD2. 即PC=PD.
圆幂定理切割线定理
圆幂定理切割线定理圆幂定理圆幂定理是解决圆与直线之间关系的重要工具。
它描述了一个点到圆的两条切线段的乘积等于该点到圆心距离的平方减去圆半径的平方。
定义设有一个圆O,其半径为r,圆心为C。
假设有一条直线L穿过点P,并且与圆O相交于点A和B。
则点P到直线L的两条切线段PA和PB 满足以下公式:PA × PB = (PC² - r²)其中,PA和PB分别表示点P到A和B的距离,PC表示点P到C的距离。
证明首先,我们可以通过勾股定理得出三角形OPC中OC² = OP² + PC²。
然后,我们可以使用相似三角形OPA和OPB来证明这个公式。
因为OA和OB是切线,所以∠OPA = ∠OPB = 90°。
同时,因为OA=OB=r,所以三角形OAB是等腰三角形。
因此,在三角形OPA中,我们可以使用勾股定理得出:PA² = OP² - OA²= OP² - r²同样,在三角形OPB中,我们可以使用勾股定理得出:PB² = OP² - OB²= OP² - r²将这两个等式相乘,得到:PA × PB = (OP² - r²) × (OP² - r²)= (OP² - r²)²= PC² - r²因此,圆幂定理得证。
应用圆幂定理在几何学、物理学和工程学中都有广泛的应用。
以下是其中的一些例子:- 在几何学中,圆幂定理可以用来解决关于切线、割线和弦的问题。
- 在物理学中,圆幂定理可以用来计算光线通过透镜或曲面镜时的焦距。
- 在工程学中,圆幂定理可以用来设计机械零件和建筑结构。
切割线定理切割线定理是解决两个相交圆之间关系的重要工具。
它描述了两个相交圆之间的切割线段长度乘积等于该点到两个圆心距离之差的平方。
初中数学重点梳理:切线和割线
切线和割线知识定位切割线定理是初中平面几何中的重要定理,它应用广泛,各地的中考题有相当多的题目都用到它,竞赛题也不例外.且题目新颖,灵活多变,学生往往甚感困难。
因此有计划、有目的、有步骤地对切割线定理进行补充、演化无疑是十分有益的。
知识梳理知识梳理1:切割线定理切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
是圆幂定理的之一。
几何语言:∵PT切⊙O于点T,PDC是⊙O的割线∴PT²=PD·PC(切割线定理)知识梳理2:割线定理从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等几何语言:∵PT是⊙O切线,PBA、PDC是⊙O的割线∴PD·PC=PA·PB(切割线定理推论)(割线定理)由上可知:PT²=PA·PB=PC·PD例题精讲【试题来源】【题目】如图,等边三角形ABC中,边AB与⊙O相切于点H,边BC,CA与⊙O交于点D,E,F,G。
已知AG=2,GF=6,FC=1.则DE=_______.【答案】21【解析】2由切割线定理可知16:4又AH AG AF,AHAC AG=•=∴==2又99故5则25又7,9,AC AG GF FCAB ACBHBD BE BHCE CD CF CG BC AC=++=∴===•==•=•===【知识点】切线和割线【适用场合】当堂例题【难度系数】3【试题来源】【题目】如图,⊙O和⊙O′都经过点A和B,PQ切⊙O于P,交⊙O′于Q,M,交AB的延长线于N.求证:2PN MN NQ=⋅.【答案】【解析】【知识点】切线和割线【适用场合】当堂例题【难度系数】3【试题来源】【题目】如图,已知点P是O外一点,PS,PT是O的两条切线,过点P作O的割线PAB,交O于A.B两点,并交ST于点C,求证:1111()2PC PA PB=+.【答案】【解析】【知识点】切线和割线【适用场合】当堂例题【难度系数】3【试题来源】【题目】如图,设△ABC是直角三角形,点D在斜边BC上,BD=4DC。
圆切线长定理弦切角定理切割线定理相交弦定理
切线长定理、弦切角定理、切割线定理、相交弦定理以及与圆有关的比例线段学习目标1.切线长概念切线长是在经过圆外一点的圆的切线上;这点和切点之间的线段的长度;“切线长”是切线上一条线段的长;具有数量的特征;而“切线”是一条直线;它不可以度量长度..2.切线长定理对于切线长定理;应明确1若已知圆的两条切线相交;则切线长相等;2若已知两条切线平行;则圆上两个切点的连线为直径;3经过圆外一点引圆的两条切线;连结两个切点可得到一个等腰三角形;4经过圆外一点引圆的两条切线;切线的夹角与过切点的两个半径的夹角互补;5圆外一点与圆心的连线;平分过这点向圆引的两条切线所夹的角..3.弦切角:顶点在圆上;一边和圆相交;另一边和圆相切的角..直线AB切⊙O于P;PC、PD为弦;图中几个弦切角呢四个4.弦切角定理:弦切角等于其所夹的弧所对的圆周角..5.弄清和圆有关的角:圆周角;圆心角;弦切角;圆内角;圆外角..6.遇到圆的切线;可联想“角”弦切角;“线”切线的性质定理及切线长定理..7.与圆有关的比例线段定理图形已知结论证法相交弦定理⊙O中;AB、CD为弦;交于P.PA·PB=PC·PD.连结AC、BD;证:△APC∽△DPB.相交弦定理的推论⊙O中;AB为直径;CD⊥AB于P.PC2=PA·PB.用相交弦定理.切割线定理⊙O中;PT切⊙O于T;割线PB交⊙O于APT2=PA·PB连结TA、TB;证:△PTB∽△PAT切割线定理推论PB、PD为⊙O的两条割线;交⊙O于A、CPA·PB=PC·PD过P作PT切⊙O于T;用两次切割线定理圆幂定理⊙O中;割线PB交⊙O于A;CD为弦P'C·P'D=r2-OP'2PA·PB=OP2-r2r为⊙O的半径延长P'O交⊙O于M;延长OP'交⊙O于N;用相交弦定理证;过P作切线用切割线定理勾股定理证8.圆幂定理:过一定点P向⊙O作任一直线;交⊙O于两点;则自定点P到两交点的两条线段之积为常数||R为圆半径;因为叫做点对于⊙O的幂;所以将上述定理统称为圆幂定理..。
圆中切割线定理
圆中切割线定理圆中切割线定理,又称为圆的切线定理,是指一个平面内过圆外一点的直线与圆相交,所得的两条切线长度相等。
这个定理在几何学中非常重要,因为它可以应用于许多不同的问题和证明中。
首先,我们来看一下如何证明这个定理。
假设有一个圆O和一条直线l,在圆外一点P处与圆相交。
现在我们要证明通过P点的两条切线AB和CD长度相等。
首先,我们可以将OP延长到与圆O相交于点E。
这样我们就得到了一个三角形OPE和一个四边形APBE。
由于AE和EB是弧AB的两个端点,所以它们的长度相等。
同样地,由于CE和ED是弧CD的两个端点,它们也具有相等的长度。
接下来,我们观察三角形OPE。
由于OE是半径,并且OP垂直于OE (因为l是过P点且垂直于OE的直线),所以三角形OPE是一个直角三角形。
因此,我们可以使用勾股定理来计算PE和OE之间的关系:$OP^2=OE^2+PE^2$。
现在让我们考虑四边形APBE。
根据正弦定理,我们可以得到:$\frac{AE}{\sin\angle AEP}=\frac{PE}{\sin\angle APE}$。
同样地,$\frac{EB}{\sin\angle BEP}=\frac{PE}{\sin\angle BPE}$。
由于角AEP和角BEP是对顶角,它们的大小相等。
因此,我们可以将上述两个等式相加并整理得到:$\frac{AE+EB}{PE}=\frac{\sin\angle AEP+\sin\angle BEP}{\sin\angle APE}=\frac{\sin(\angleAEP+\angle BEP)}{\sin\angle APE}$。
现在让我们回到三角形OPE。
根据正弦定理,我们可以得到:$\frac{OE}{OP}=\frac{\sin\angle OEP}{\sin\angle OPE}$。
因为OE 是半径,并且OP垂直于OE,所以$\angle OEP$是直角。
因此,$\sin \angle OEP=1$且$\cos \angle OEP=0$。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆中切割线定理
引言:
圆是几何学中的重要概念之一,其性质和定理在几何学中有着广泛的应用。
其中,圆中切割线定理是一条重要的定理,它揭示了圆内部切割线的性质,对于解决与圆相关的问题具有重要意义。
本文将介绍圆中切割线定理的定义、性质和应用,帮助读者更好地理解和应用这一定理。
一、定义:
在圆内部,连接两个圆上的点并且与圆的圆心不重合的线段称为切割线。
圆中切割线定理指出,当一条直线与圆相交于两个不同的点时,这条直线的两个端点与圆心连线的夹角相等。
二、性质:
1. 切割线与半径之间的关系:圆中切割线定理表明,切割线与半径之间存在一定的关系。
具体来说,当一条切割线与圆相交于两个不同的点时,这条切割线与圆的半径垂直相交,并且两条垂直相交线段的乘积等于切割线段的乘积。
即,若AB和CD分别是切割线与圆相交的两个点,O为圆心,则有AO·OB = CO·OD。
2. 切割线夹角的性质:根据圆中切割线定理的定义,切割线的两个端点与圆心连线的夹角相等。
这一性质可以用来证明两条切割线之间的夹角关系。
具体来说,若切割线AB和切割线CD相交于点O,
并且AO与CO在切割线上,BO与DO在切割线上,则∠AOB = ∠COD。
三、应用:
圆中切割线定理在几何学中有着广泛的应用,下面将介绍两个常见的应用场景。
1. 圆的切线问题:当一条直线与圆相交于两个不同的点时,可以利用圆中切割线定理来求解与切线相关的问题。
例如,给定一个圆和一条切割线,求切割线与圆的切点之间的距离。
根据圆中切割线定理,可以先求出切割线与圆心连线的夹角,然后利用三角函数求解切点之间的距离。
2. 圆的切割问题:当一条直线与圆相交于两个不同的点时,可以利用圆中切割线定理来求解与切割线相关的问题。
例如,给定一个圆和一条切割线,求切割线所夹的圆弧的长度。
根据圆中切割线定理,可以先求出切割线与圆心连线的夹角,然后利用圆的周长公式求解圆弧的长度。
四、实例分析:
为了更好地理解圆中切割线定理的应用场景,下面将通过一个具体的实例进行分析。
假设有一个半径为5的圆,一条切割线与该圆相交于两个不同的点
A和B,且切割线与圆心连线的夹角为30度。
我们需要求解切割线所夹的圆弧的长度。
根据圆中切割线定理的性质,切割线与圆心连线的夹角为30度。
由于圆的周长公式为C = 2πr,其中r为半径,所以圆的周长为C = 2π × 5 = 10π。
根据夹角的大小,我们可以计算出切割线所夹的圆弧的长度为10π × 30/360 = π/3。
因此,切割线所夹的圆弧的长度为π/3。
结论:
圆中切割线定理是几何学中的一条重要定理,它揭示了圆内部切割线的性质。
通过掌握圆中切割线定理的定义、性质和应用,我们可以更好地解决与圆相关的问题。
在实际应用中,圆中切割线定理可以帮助我们求解切线和切割线所夹的圆弧的长度等问题。
希望本文的介绍能够对读者理解和应用圆中切割线定理有所帮助。
