自动控制元件作业答案
自动控制原理第三章课后习题 答案()

3-1 设系统的微分方程式如下:(1) )(2)(2.0t r t c= (2) )()()(24.0)(04.0t r t c t c t c=++ 试求系统闭环传递函数Φ(s),以及系统的单位脉冲响应g(t)和单位阶跃响应c(t)。
已知全部初始条件为零。
解:(1) 因为)(2)(2.0s R s sC =闭环传递函数ss R s C s 10)()()(==Φ 单位脉冲响应:s s C /10)(= 010)(≥=t t g单位阶跃响应c(t) 2/10)(s s C = 010)(≥=t t t c(2))()()124.004.0(2s R s C s s =++ 124.004.0)()(2++=s s s R s C `闭环传递函数124.004.01)()()(2++==s s s R s C s φ单位脉冲响应:124.004.01)(2++=s s s C t e t g t 4sin 325)(3-= 单位阶跃响应h(t) 16)3(61]16)3[(25)(22+++-=++=s s s s s s C t e t e t c t t 4sin 434cos 1)(33----=3-2 温度计的传递函数为11+Ts ,用其测量容器内的水温,1min 才能显示出该温度的98%的数值。
若加热容器使水温按10ºC/min 的速度匀速上升,问温度计的稳态指示误差有多大解法一 依题意,温度计闭环传递函数11)(+=ΦTs s 由一阶系统阶跃响应特性可知:o o T c 98)4(=,因此有 min 14=T ,得出 min 25.0=T 。
视温度计为单位反馈系统,则开环传递函数为Tss s s G 1)(1)()(=Φ-Φ=⎩⎨⎧==11v TK !用静态误差系数法,当t t r ⋅=10)( 时,C T Ke ss ︒===5.21010。
解法二 依题意,系统误差定义为 )()()(t c t r t e -=,应有 1111)()(1)()()(+=+-=-==ΦTs TsTs s R s C s R s E s e C T sTs Ts ss R s s e s e s ss ︒==⋅+=Φ=→→5.210101lim )()(lim 203-3 已知二阶系统的单位阶跃响应为)1.536.1sin(5.1210)(2.1o tt et c +-=-试求系统的超调量σ%、峰值时间tp 和调节时间ts 。
自动控制原理答案完全版_第二版
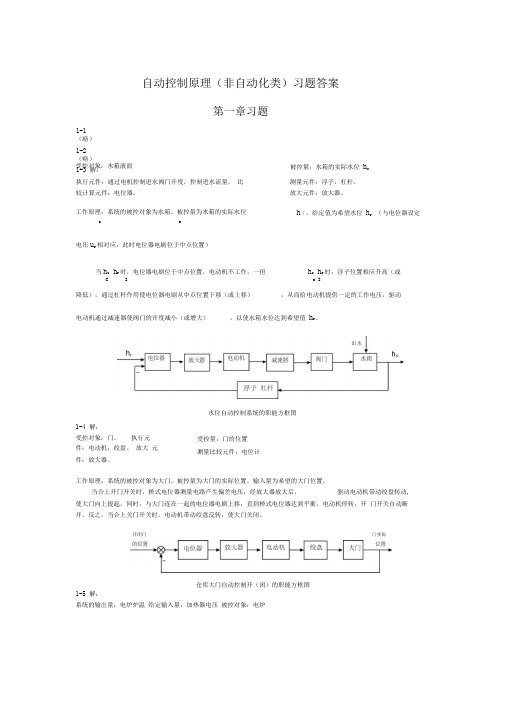
自动控制原理(非自动化类)习题答案第一章习题被控量:水箱的实际水位 h c执行元件:通过电机控制进水阀门开度,控制进水流量。
比较计算元件:电位器。
h 「。
给定值为希望水位 h r (与电位器设定cr电压u r 相对应,此时电位器电刷位于中点位置)当h c h r 时,电位器电刷位于中点位置,电动机不工作。
一但h c h r 时,浮子位置相应升高(或CIc I降低),通过杠杆作用使电位器电刷从中点位置下移(或上移) ,从而给电动机提供一定的工作电压,驱动电动机通过减速器使阀门的开度减小(或增大),以使水箱水位达到希望值 h r 。
水位自动控制系统的职能方框图受控量:门的位置 测量比较元件:电位计工作原理:系统的被控对象为大门。
被控量为大门的实际位置。
输入量为希望的大门位置。
当合上开门开关时,桥式电位器测量电路产生偏差电压,经放大器放大后,驱动电动机带动绞盘转动,使大门向上提起。
同时,与大门连在一起的电位器电刷上移,直到桥式电位器达到平衡,电动机停转,开 门开关自动断开。
反之,当合上关门开关时,电动机带动绞盘反转,使大门关闭。
1-5 解:系统的输岀量:电炉炉温 给定输入量:加热器电压 被控对象:电炉1-1 (略) 1-2(略)1-3 解: 受控对象:水箱液面 测量元件:浮子,杠杆。
放大元件:放大器。
工作原理:系统的被控对象为水箱。
被控量为水箱的实际水位1-4 解:受控对象:门。
执行元件:电动机,绞盘。
放大 元件:放大器。
开闭门门实际仓库大门自动控制开(闭)的职能方框图放大元件:电压放大器,功率放大器,减速器比较元件:电位计测量元件:热电偶职能方框图:KK3 2 Ts (T 1)s s K1K 3电位器电压放大炉温热电偶第二章习题2-1解:对微分方程做拉氏变换:X,(s) R(s) C(s) N,(s)X 2 (s) Q X/s)X 3 (s) X2 (s) X5(s TsX4 (s) X 3 (s)X5 (s) X4 (s) K2 N2(s k 3 X5 (s) s2C (s) sC(s) C(s) / R(s) 功率放大加热器'电机电炉R(s)绘制上式各子方程的方块图如下图所示:C(s) / N i (s) C(s) / R(s),K 2K 3TSTs 3~~T 1)s 2s K 1K 32-2解:对微分方程做拉氏变换X i (s) K[R(s) C (s)] X 2 (s)sR(s)(s 1) X 3(s) X i (s) X 2 (s) (Ts 1)X 4 (s)X 3 (s) X 5 (s)C(s) X 4 (s) N (s) X 5 (s) (Ts 1) N(s)(b) C (s)字红R(s) 1 G 1G 3 G G 4 G 2 G 3 G 2G 4X3(s) 绘制上式各子方程的方块如下图:将方块图连接得出系统的动态结构图:..R(s)1(s 1):Ts 1)C(s)N (s) 02-3解:(过程略)K____________C(s) (s 1)<Js 1) (s 1XTs 1) K ____________ Ts 2(T s1)s (K 1)C(s) / N 2 (s)R(s) ms fs K(c)誤 R(s) G 2 G 1G 2 1 G-i G 2G-I (d 普 R(s)G 1 G 2 1 G 2G 3(e)R^ R(s)G 1G 2G 3G 4 1 G<|G 2 G 2G 3 G 3G 4 G 1G 2G 3G 4 2-4 解:(1)求 C/R ,令 N=0 KK K 3s(Ts 1) C (s) / R(s) G(s)1 G(s) 求C/N ,令R=0,向后移动单位反馈的比较点 K C(s) / N (s) (K n G n K 1 0 ) — J s 1 亠 K 1G(s)K 1K 2 K 3 Ts 2K i K 2 K 3K n K 3s K 1K 2 K 3G K 2 n2 一Ts 2s K 1K 2 K 3 Ts 1 s (2)要消除干扰对系统的影响C(s) / N (s) K n K3s K1K2 K3GnTs 2 s K 1K 2 K 3G n (s) KnsK 1K 22-5 解:(a ) (1 )系统的反馈回路有三个,所以有3L a L 1 L 2 L 3 a 1G 1G 2G 5 G 2G 3G 4 G 4G 2G 5三个回路两两接触,可得 1 L a 1 GG 2G 5 G 2G 3G 4 G 4G 2G 5(2) 有两条前向通道,且与两条回路均有接触,所以P P 2 G 1G 2G 3,11, 2 1(3) 闭环传递函数C/R 为GGG 3 11 G 1G 2G 5 G 2G 3G 4 G 4G 2G 5(b)(1) 系统的反馈回路有三个,所以有3L aa 1L 1L 3 G 1G 2 G 1 G 1三个回路均接触,可得 1 L a 1 G-i G 2 2G-)(2 )有四条前向通道,且与三条回路均有接触,所以R G 1G 2 , 11P 2G, 21PG2,3 1P 4G 1,41(3)闭环传递函数C/R 为C G 1G 2 G 1 G 2 GG-i G 2 G 2 R 1 G 1G 22G 1 1 G-|G 2 2G.2-6解:用梅逊公式求,有两个回路,且接触,可得1L a 1 GG 2G 3 G 2,可得第三章习题采用K 0 , K H 负反馈方法的闭环传递函数为1OK o要使过渡时间减小到原来的 0.1倍,要保证总的放大系数不变,则:(原放大系数为10,时间常数为0.2)3-2解:系统为欠阻尼二阶系统(书上改为“单位负反馈……”,“已知系统开环传递函数”)% e / 1 $100%100% 1C(s) G-|G 2G 3 G 2G 3 R(s) 1 G 1G 2G 3 G 2 C (s)(1 G 2 )G 3N 2 (s) 1 GG 2G 3 G 2 E(s) 1 G 2 G 2G 3 R(s) 1 G-|G 2G :3 G 2 E(s) C(s) (1 G 2 G N 2 (s)N 2 (s)1 G 1G 2G 3 G 2C (s) NQC(s) / R(s)C(s) 1 (1 GG 2G 3 G 2 ) 1N 3 (s) 1 G 1G 2G 3 G 2 E(s) C(s) G 2G 3 G 1G 2G 3 N 1 (s) N 1(s) 1 G 1G 2G 3 G 2E(s)C(s) 1N 3 (s)N 3 (s)3-1解:(原书改为G(s) 100.2s 1)(s)C(s) K G(s) R(s) 01 G(S )K H1 10K H 0.2s1 10K10K 。
自动控制原理C作业答案
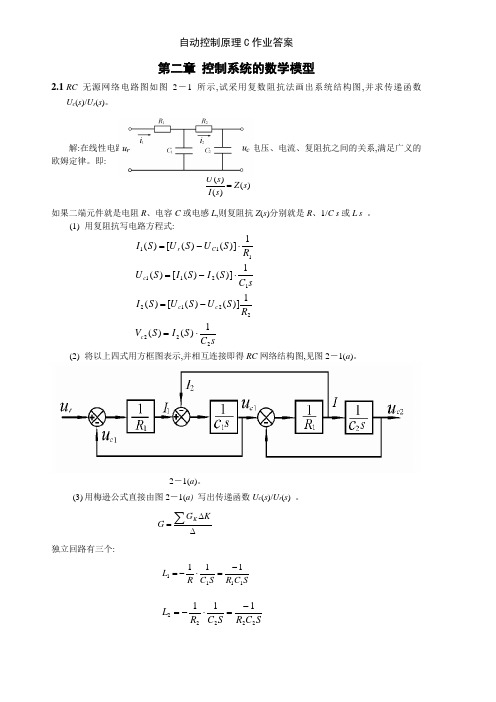
第二章控制系统的数学模型2.1RC无源网络电路图如图2-1所示,试采用复数阻抗法画出系统结构图,并求传递函数U c(s)/U r(s)。
图2-1解:在线性电路的计算中,引入了复阻抗的概念,则电压、电流、复阻抗之间的关系,满足广义的欧姆定律。
即:)()()(sZsIsU=如果二端元件就是电阻R、电容C或电感L,则复阻抗Z(s)分别就是R、1/C s或L s。
(1)用复阻抗写电路方程式:sCSISVRSUSUSIsCSISISURSUSUSIccccCr222221212111111)()(1)]()([)(1)]()([)(1)]()([)(⋅=-=⋅-=⋅-=(2)将以上四式用方框图表示,并相互连接即得RC网络结构图,见图2-1(a)。
2-1(a)。
(3)用梅逊公式直接由图2-1(a)写出传递函数U c(s)/U r(s) 。
∆∆=∑KGG K独立回路有三个:SCRSCRL1111111-=⋅-=SCRSCRL22222111-=⋅-=回路相互不接触的情况只有L 1与L 2两个回路。
则2221121121S C R C R L L L == 由上式可写出特征式为:222111222112132111111)(1S C R C R S C R S C R S C R L L L L L ++++=+++-=∆通向前路只有一条221212*********SC C R R S C R S C R G =⋅⋅⋅=由于G 1与所有回路L 1,L 2, L 3都有公共支路,属于相互有接触,则余子式为Δ1=1代入梅逊公式得传递函数1)(111111121221122121222111222112221111++++=++++=∆∆=s C R C R C R s C C R R s C R C R s C R s C R s C R s C R C R G G 2-2 已知系统结构图如图2-2所示,试用化简法求传递函数C (s )/R (s )。
自动控制原理第三章习题参考答案

Y (s) 1 1 600 ( s) 12 ( ) 2 R( s ) s 10 s 60 s 70 s 600
n 600 24.5
70 70 1.43 2 n 2 24 .5
3-7 简化的飞行控制系统结构图如下,试选择参数K1和Kt, 使系统的ωn=6,ξ=1
S2+5=0
S3 16/3 S2 5
S1 10 S0 25
s1, 2 5 j
有1对纯虚根,系统临界稳定。
3-13单位反馈系统的开环传递函数为:
K (0.5s 1) G( s) 2 s( s 1)(0.5s s 1)
确定使系统稳定的K值范围。 解:闭环传递函数为:
K (0.5s 1) ( s) 0.5s 4 1.5s 3 2 s 2 (1 0.5 K ) s K K ( s 2) 4 s 3s 3 4 s 2 ( 2 K ) s 2 K
K 速度误差系数: P lim sG ( s ) 10
s 0
速度误差:
1 e ss 0.1 Kp
3-11 已知系统的特征方程为:
3s 4 10 s 3 5s 2 s 2 0
用劳斯判据确定系统的稳定性 解:列劳斯列表 S4 3 5 2
S3 10
S2 4.7 S1 -3.26
1
2
S0 2 第1列符号变化两次, 说明有两个正根,系统不稳定。
3-12 已知Βιβλιοθήκη 统的特征方程如下,试求系统在S右半平面的根 数及虚根值。
(1) s 3s 12 s 24 s 32 s 48 0
5 4 3 2
S5 1 S4 3 S3 4 S2 12
自动控制原理作业题 (后附答案)

自动控制原理作业题第一章基本概念一、简答题1 简述自动控制的基本概念2 简述自动控制系统的基本组成3 简述控制系统的基本控制过程4 简述自动控制系统的基本分类5 试比较开环控制和闭环控制的特点6 简述自动控制系统的性能评价指标二、分析计算题1 液位自动控制系统如图所示。
试分析该系统工作原理,画出系统原理框图,指出被控对象、被控参量和控制量2 发动机电压调节系统如图所示,试分析其工作原理,画出系统原理框图,指出其特点。
3液面控制系统如图所示。
试分析该系统的工作原理,指出系统中的干扰量、被控制量及被控制对象,并画出系统的方框图。
4控制系统如图所示。
简述该系统的工作原理,说明该系统的给定值、被控制量和干扰量,并画出该系统的方块图。
图1-7发电机-电动机调速系统操纵电位计发电机伺服电机减速器负载Θr给定值Ur 前置放大器功放执行元件被控量Wm这是一个开环控制的例子+E-EΘrUr操纵电位计R1R2R3R4放大器直流发电机伺服电机Wd Wm发电机-电动机调速系统减速器负载5火炮随动控制系统如图所示。
简述该系统的工作原理,并画出该系统的原理框图。
第二章 线性控制系统的数学模型一、简答题1 简述建立控制系统数学模型的方法及其数学表示形式2 简述建立微分方程的步骤3 简述传递函数的基本概念及其特点4 给出组成控制系统典型基本环节二、分析计算题1 有源电网络如图所示,输入量为)(1t u ,输出量为)(2t u ,试确定该电网络的传递函数2 电枢控制式直流电动机原理图如图所示,输入量为)(1t e ,输出量为)(t o ,试确定其微分方程。
图中,电动机电枢输入电压;电动机输出转角;电枢绕组的电阻;电枢绕组的电感;流过电枢绕组的电流;电动机感应电势;电动机转矩;电动机及负载这和到电动机轴上的转动惯量;电动机及负载这和到电动机轴上的粘性摩擦系数。
3 某RC 电路网络原理图如图所示,电压()i u t 为输入量,()o u t 为输出量,试画出其方块图,并求其传递函数。
(完整版)自动控制原理课后习题答案

第1章控制系统概述【课后自测】1-1 试列举几个日常生活中的开环控制和闭环控制系统,说明它们的工作原理并比较开环控制和闭环控制的优缺点。
解:开环控制——半自动、全自动洗衣机的洗衣过程。
工作原理:被控制量为衣服的干净度。
洗衣人先观察衣服的脏污程度,根据自己的经验,设定洗涤、漂洗时间,洗衣机按照设定程序完成洗涤漂洗任务。
系统输出量(即衣服的干净度)的信息没有通过任何装置反馈到输入端,对系统的控制不起作用,因此为开环控制。
闭环控制——卫生间蓄水箱的蓄水量控制系统和空调、冰箱的温度控制系统。
工作原理:以卫生间蓄水箱蓄水量控制为例,系统的被控制量(输出量)为蓄水箱水位(反应蓄水量)。
水位由浮子测量,并通过杠杆作用于供水阀门(即反馈至输入端),控制供水量,形成闭环控制。
当水位达到蓄水量上限高度时,阀门全关(按要求事先设计好杠杆比例),系统处于平衡状态。
一旦用水,水位降低,浮子随之下沉,通过杠杆打开供水阀门,下沉越深,阀门开度越大,供水量越大,直到水位升至蓄水量上限高度,阀门全关,系统再次处于平衡状态。
开环控制和闭环控制的优缺点如下表1-2 自动控制系统通常有哪些环节组成?各个环节分别的作用是什么?解:自动控制系统包括被控对象、给定元件、检测反馈元件、比较元件、放大元件和执行元件。
各个基本单元的功能如下:(1)被控对象—又称受控对象或对象,指在控制过程中受到操纵控制的机器设备或过程。
(2)给定元件—可以设置系统控制指令的装置,可用于给出与期望输出量相对应的系统输入量。
(3)检测反馈元件—测量被控量的实际值并将其转换为与输入信号同类的物理量,再反馈到系统输入端作比较,一般为各类传感器。
(4)比较元件—把测量元件检测的被控量实际值与给定元件给出的给定值进行比较,分析计算并产生反应两者差值的偏差信号。
常用的比较元件有差动放大器、机械差动装置和电桥等。
(5)放大元件—当比较元件产生的偏差信号比较微弱不足以驱动执行元件动作时,可通过放大元件将微弱信号作线性放大。
自动控制原理课后习题答案第二章

解:由图可得
联立上式消去中间变量U1与U2,可得:
2-8某位置随动系统原理方块图如图2-7所示。已知电位器最大工作角度,功率放大级放大系数为K3,要求:
(1) 分别求出电位器传递系数K0、第一级与第二级放大器得比例系数K1与K2;
(2) 画出系统结构图;
(3) 简化结构图,求系统传递函数。
证明:(a)根据复阻抗概念可得:
即 取A、B两点进行受力分析,可得:
整理可得:
经比较可以瞧出,电网络(a)与机械系统(b)两者参数得相似关系为
2-5 设初始条件均为零,试用拉氏变换法求解下列微分方程式,并概略绘制x(t)曲线,指出各方程式得模态。
(1)
(2)
2-7由运算放大器组成得控制系统模拟电路如图2-6所示,试求闭环传递函数Uc(s)/Ur(s)。
2-10试简化图2-9中得系统结构图,并求传递函数C(s)/R(s )与C(s)/N(s)。
图2-9 题2-10系统结构图
分析:分别假定R(s)=0与N(s)=0,画出各自得结构图,然后对系统结构图进行等效ቤተ መጻሕፍቲ ባይዱ换,将其化成最简单得形式,从而求解系统得传递函数。
解:(a)令N(s)=0,简化结构图如图所示:
可求出:
令R(s)=0,简化结构图如图所示:
所以:
(b)令N(s)=0,简化结构图如下图所示:
所以:
令R(s)=0,简化结构图如下图所示:
2-12 试用梅逊增益公式求图2-8中各系统信号流图得传递函 数C(s)/R(s)。
图2-11 题2-12系统信号流图
解:
(a)存在三个回路:
存在两条前向通路:
所以:
(3)简化后可得系统得传递函数为
New自动控制原理作业2n3 参考答案

自动控制原理作业2 参考答案解:由题设可知,输入信号是由0时刻的阶跃信号a ·1(t )和t 1时刻的阶跃信号b ·1(t – t 1)构成。
选择适当的a 、b 和t 1可以获得图4 (b)所示的响应曲线,它具有有限的调整时间,且没有振荡。
这种控制方法称为重叠控制。
系统在输入信号a ·1(t )作用下的输出为曲线如题6解图(a)所示。
系统在输入信号b ·1(t – t 1)作用下的输出为曲线如题6解图(b)所示。
按题意要求,y a(t )应在t = t 1时取极大值,即题6解图按图4有所以解得(2)列出劳斯阵列(3)由于特征方程缺项,不符合稳定的必要条件。
列出劳斯阵列图6自动控制原理作业3 参考答案解:(1)计算闭环极点。
闭环传递函数为(4)闭环极点的位置图。
题3‐1解图是K →–∞变到K →+∞时闭环极点的位置图。
图中箭头代表增益增加的方向。
该图就是系统的全根轨迹图。
题3-1解图解:(1)写出开环传递函数,在图上标注出开环极点和零点。
(7) 确定根轨迹与虚轴的交点。
从根轨迹的趋势可以看出,根轨迹与虚轴没有 交点。
根据上面的分析和计算,可以画出系统的根轨迹,如题3-2解图所示。
题3-2解图3 – 3试证明3 – 2中不在负实轴上的根轨迹是圆周的一部分。
根轨迹如题3‐4解图中实线所示,其实轴上的根轨迹区段为(–∞, –2)和(–1,0)。
补根轨迹如题3‐4解图中虚线所示,其实轴上的根轨迹区段为(–2, –1)和(0,+∞)。
题3‐4解图(6)画系统的根轨迹。
根轨迹如题3-5解图所示。
题3-5解图题3-6解图题3-6解图中不带圆圈的根轨迹是K = 1,4,9和16时的根轨迹。
题3-6解图表示两个参数同时变化时的根轨迹,称为根轨迹簇。
图8(b)为系统的根轨迹图。
图8(b)根轨迹如图9 (b)所示。
图9 (b)以K = – a为参变量的根轨迹如图10所示,图中箭头表示a从0增加到+∞的方向,也即K从0下降加到–∞的方向。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《自动控制元件》作业
第一章 直流伺服电动机
1-1直流伺服电动机的电磁转矩和控制电流由什么决定?
答:a:由T
em=CmΦIa
知电磁转矩由每极磁通量和绕组电流大小决定。
b:由Tem =T0 +T2 =CmΦIa 控制电流由负载转矩(T2)和空载转矩(T0)大小
决定。
1-2当直流伺服电动机的负载转矩恒定不变时,控制电压升高将使稳态的电磁
转矩、控制电流、转速发生怎样的变化?为什么?
答:a:电磁转矩T
em =T0 +T2可见电磁转矩也不变。由Tem=CmΦIa
知控制电流
Ia 也不变
b:KeKtRaTemKeUan知Tem 不变可见Ua 转速升高理想空载转速变大导致
转速n升高。
1-3已知一台直流电动机,其电枢额定电压Ua=110V,额定运行时电枢电流
Ia=0.4A,转速n=3600rpm,它的电枢电阻Ra=50欧姆,负载阻转矩To=15mN.m。
试问该电动机额定负载转矩是多少?
答:Ea= Ua- IaRa=110-0.4×50=90V
Ea=CeΦn, Ce=0.105Cm CmΦ=0.23836000.10590n105.0Ea
Tem =T0 +T2=CmΦIa→T2=CmΦIa-T0 =0.40.238=0.0952-15×10-3=80.2mN.m
1-6当直流伺服电动机电枢电压、励磁电压不变时,如将负载转矩减少,试问
此时电动机的电枢电流、电磁转矩、转速将怎样变化?并说明由原来的状态到
新的稳态的物理过程。
答:磁转矩T
em =T0 +T2可见T2 ↓电磁转矩也↓。由Tem=CmΦIa知控制电流Ia
↓
Ea= Ua- IaRa可见Ia ↓知Ea↑,由Ea=CeΦn 知Ea↑知n↑
电枢电流减少;电磁转矩减少;转速升高。
第二章 直流测速发电机
2-4某直流测速发电机,其电枢电压U=50V,负载电阻RL=3000Ω,电枢电阻
Ra=180Ω,转速n=3000rpm,求该转速下的空载输出电压Uo和输出电流Ia。
Ea = Ua IaRa Ia=300050=0.0167A Ea=50
Ea =50+300050×180=53 空载Uo =Ea =53
第三章 步进电动机
3-8某五相反应式步进电动机转子有48个齿,试分析其有哪几种运行方式及对
应的步距角,并画出它们的矩角特性曲线族。
答: 5相单5拍A→B→C→D→E→A
Θb=485360NZr3601.5°
TemA =-Tjmaxsin(Θe) TemB =-Tjmaxsin(Θe-52π) TemC =-Tjmaxsin(Θe-54π)
TemD =-Tjmaxsin(Θe-56π) TemE =-Tjmaxsin(Θe-58π)
5相双5拍AB→BC→CD→DE→EA→AB
Θb=485360NZr3601.5°
TemAB=-1.62Tjmaxsin(Θe-5π) TemBC=-1.62Tjmaxsin(Θe-53π)
TemCD =-1.62Tjmaxsin(Θe-π) TemDE=-1.62Tjmaxsin(Θe-57π)
TemEA =-1.62Tjmaxsin(Θe-59π)
5相10拍 A→AB→B→BC→C→CD→D→DE→E→EA→AB
Θb=4810360NZr3600.75°
A
em
T
o
B
BC
B
A
CD
C
D
E
DE
EA
5/3π
5/4π
3-10四相反应式步进电动机,转子有50个齿,试计算各种运行方式的步距角。
并画出其单、双拍制的矩角特性曲线族。若单相通电时的最大静态转矩为
0.1N·m,试计算各种运行方式的起动转矩;并判断转子上负载为0.08N·m时哪
种运行方式可使步进电动机正常运行。
解a:四相单四拍步距角Θ
b=504360NZr360=1.8°, Θbe
= 2π/N=2π/4=2π,如下图
四相单四拍相邻2相矩角特性曲线交点q1转矩
Temq1=Tjmaxcos(π/N)=0.1×cos45°=0.1*0.707=0.0707N·m<0.08N·m
电机不能正常运行
b:四相双四拍步距角Θb=504360NZr360=1.8°,Θbe= 2π,Temq1=
1.414Tjmaxcos4π=1.414×0.0707=0.1N·m>0.08N·m ,电机能正常运行
四相八拍步距角Θb=508360NZr360=0.9°,Θbe= 4π Temq1=
1.414Tjmaxsin4π=1.414×0.0707=0.1N·m>0.08N·m ,电机能正常运行
A
e
em
T
o
B
BC
B
A
C
D
2/π
2/π
4/3π
1
q
2
q
3
q
单拍制时:T1=-Tjmaxsin(ϴe) T2=-Tjmaxsin(ϴe-π/2)
T3=-Tjmaxsin(ϴe-π) T4=-Tjmaxsin(ϴe-3π/2)
双拍制时:TAB=-√2Tjmaxsin(ϴe-π/4) TAB=-√2Tjmaxsin(ϴe-3π/4)
TAB=-√2Tjmaxsin(ϴe-5π/4)TAB=-√2Tjmaxsin(ϴe-7π/4)
第四章 旋转变压器
4-6用正余弦旋转变压器可以构成直角坐标系旋转θ角的变换,接线如图题图
4-1,4-2所示(见书P119)。试分析其工作原理。
解:Uxs= Ussinθ, Uys = Uscosθ, Uxc= Uccosθ, Uyc = Ucsinθ,
∵ Ux= Uxs- Uxc,Uy= Uys +Uyc ,
∴Ux= Ussinθ-Uccosθ,Uy= Uscosθ+Ucsinθ,
如p点与坐标系uov相当于正余弦旋转变压器转子,当其顺时针旋转θ,
坐标系顺uov时针旋转θ就会输出新的坐标(Ux 、Uy )
cossinsinscxysxyUUUUUUco
4-8有一只旋变发送机XF和一只旋变变压器XB定子绕组对应联接作控制式
运行,如题图4-3所示(见书P119),已知:图中的θ1=15°°,θ2=10°°,试求:
(1) 旋变变压器转子的输出绕组的协调位置XT;
解:
21
(2) 失调角r。
5
o
,负号表示逆时针。
第五章 自整角机
5-4三台自整角机如题图5-1所示(见书P147)接线。中间一台为力矩式差动
接收机,左右两台为力矩式发送机,试问:当左右边两台发送机分别转过θ2、
θ1角度时,中间的接收机将转过的角度θ与θ2和θ1之间是什么关系?
解:θ=θ2-θ1 ,
θ2-θ1>0则顺时针转动
θ2-θ1=0则不动
θ2-θ1<0则逆时针转动
5-6某力矩式自整角机接线如题图5-3所示(见书P148)
(1) 画出接收机转子所受的转矩方向:
解:收机转子所受的转矩方向是逆时针方向
(2) 画出接收机的协调位置;
解:接收机转子逆时针旋转转角度:(15-35= -20°)
/
z1
20
(3) 求失调角。
解:r=θ1-θ2=15° -35°=-20°
5-7对于题图5-4所示(见书P148)自整角测量线路,CX为自整角发
送机,CT为自整角变压器,它们的转子的转角分别为θ1和θ2。画出三相
绕组合成磁场轴线的位置,并写出输出电势的有效值Eo和转角θ1、θ2的
关系式。
(1) 合成磁场轴线的位置:
2D
Bfx
2D
1
1
2
Bft
012
4.44sin()EfW
f
为激磁电源交变频率;W为自整角变压器输出绕组有效匝数;
为自整角变压器的主磁通。
6-8 交流伺服电动机的控制方法有几种?幅值控制转速变化的物理过程如
何?
答: 控制方法:幅值控制、相位控制、幅相控制
幅值控制就是将励磁绕组加上恒定的额定励磁电压Ujc,并保持励磁电压和控
制电压的相位差90°不变,改变控制电压的大小,以实现对伺服电动机转速的
控制。
负载不变时,改变控制电压U
k ,如Uk
↑ →a↑ 椭圆磁场越园,其转速n↑,反
之相反
6-13什么是自转现象?为了消除自转现象,交流伺服电动机在单相供电时应具
有怎样的机械特性?
答:控制信号消失后,电动机仍以某个转速稳定运行的现象,就是自转现象。
消除自转将转子电阻足够大,使单相供电时机械特性曲线位于二、四象限。
见书中
图6-28实线所示机械特性。
