工程流体力学-禹华谦-习题答案-第6章
流体力学 第六章

几个概念涵箱加拿大某渠龙羊峡导流洞引渠顺坡(正坡):i>0平坡:i=0逆坡(反坡):i<0明槽槽底沿程降低不变增高顺坡渠道i>0,当渠底坡度较小,如i<0.01或θ很小时,两断面间渠底长度△S与两断面间水平距离△L近似相等,故:此时,过流断面可以看成铅直面(θ很小),水深h可以直接量取,认为h=h’。
§6-1 明渠均匀流的水力学特征一、明渠均匀流特征3.总水头线、测压管水头线及渠底线相互平行,且假定单位面积上所受的阻力损失为流体由断面1流至断面2总阻力损失为11:21由于是明渠紊流,故需要讨论流动的水力半径,根据圆管水力半径的计算,R=d/4,故:谢才公式(1775年):由公式可知,要使明渠中的流动保持均匀流动,则i必须大于0,也就是说只有在顺坡渠道的均匀流动中才有可能满足§6-2 明渠均匀流的基本计算公式§6-3 水力最优断面及允许流速从均匀流的公式可以看出,明渠的输水能力(流量)取决于过水断面的形状、尺寸、底坡和粗糙系数的大小。
设计渠道时,底坡一般依地形条件或其它技术上的要求而定;11:21§6-3 水力最优断面及允许流速从经济的观点来说,总是希望所选定的横断面形状和尺寸在的比值成为边坡系数,表示。
即11:2111:21二、矩形断面的水力最优条件对于矩形断面,m=0故,矩形断面水力最优条件为在一般土渠中,边坡系数m>l,则按水力最优断面求得宽深比<1,即梯形水力最佳断面通常都是窄而深的断面。
11:21内,即:11:21§6-4 明渠均匀流水力计算的几类问题一、校核渠道的输水能力下,将已知值代入公式即可。
11:21m、h,求底坡i。
11:21§6-5 复式断面明渠均匀流水力计算前述梯形、矩形等单式过流断面,如果某一渠道承担着由于渠道主槽左右两侧各有边滩,因此该复式断面可以分为三个部分,主槽、左边滩和右边。
《工程流体力学》习题1~7章参考答案

等
学
校
教
材
过程装备与控制工程专业核心课程教材
工程流体力学
习题参考答案
主讲:陈庆光
化学工业出版社教材出版中心
黄卫星, 陈文梅主编. 工程流体力学, 北京:化学工业出版社教材出版中心,2001.8
习题 1-1 如图 1-9 所示,一个边长 200mm 重量为 1kN 的滑块在 20 斜面的油膜上滑动,油膜 厚度 0.005m,油的粘度 µ = 7 × 10−2 Pa ⋅ s 。设油膜内速度为线性分布,试求滑块的平衡速度。
V= 1000 3 1000 (因为是正方形容器,厚度为 3m) 。 m 的油,使左侧容器中的油的高度增加了 ρ油 g 3ρ油 g
假设此时右侧容器的水位在原来的基础上升高了 ym,则根据左右容器的尺寸关系,左侧的油 柱将下降 2ym。再根据等压面(等压面下降了 2ym 的高度)的性质有: 1000 1000 + ρ油 g h ( y + 2 y ) + (3 − 2) ⇒ y = 9 ρ g ≈ 0.01134m = 11.34mm 3ρ g = ρ水 g 水 油 习题 3-2 在海中一艘满载货物的船,其形态如图 3-10 所示。船底长度 12m,舱体宽度(垂直 于纸面)上下均为 6m,船长两端梯度均为 45 ,并近似取海水的密度为 1000 kg m3 。求船加 上货物的总质量。
参考答案 3
∂v ∂v y ∂vx ∂vz ∂v y ∂vx − − Ω = ∇×v = z − i + j+ ∂y ∂z ∂z ∂x ∂x ∂y ∂v ∂v cz cy j− k = x j+ x k = ∂z ∂y y2 + z2 y2 + z2
流体力学课后习题及答案-第6章
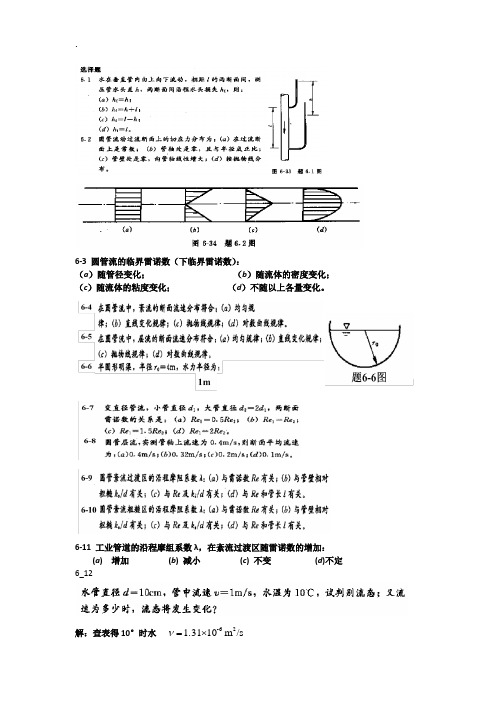
6-3 圆管流的临界雷诺数(下临界雷诺数):(a )随管径变化; (b )随流体的密度变化; (c )随流体的粘度变化; (d )不随以上各量变化。
6-11 工业管道的沿程摩组系数λ,在紊流过渡区随雷诺数的增加: (a ) 增加 (b ) 减小 (c ) 不变 (d )不定 6_12解:查表得10°时水 /s m 101.312-6⨯=ν230076341031.11.01Re 6>=⨯⨯==-νvd紊流m /s 30.01.023001031.1Re 6=⨯⨯==-d v cc ν 流速为0.30m/s 时流态将发生变化6-13解:查表得20°时空气 /s m 101.57 ,kg/m 20.12-53⨯==νρm /s 144.025.023001057.1Re 5=⨯⨯==d v cc νL/s 07.7/s m 00707.0425.014.3144.04322==⨯⨯==d v Q cc π c mQ Q Q >=⨯==/s m 0462.020.136002003v ρ紊流6-14解:查表得10°时水 /s m 101.312-6⨯=ν cm 61522015202=⨯+⨯=+=h b bh R 57568701031.106.015.0Re 6>=⨯⨯==-νvR 紊流6-15解:m/s 2563.0360015.014.33.164422=⨯⨯⨯==d Q v π 1922102.015.02563.0Re 4=⨯⨯==-νvd0333.0192264Re 64===λ m 744.06.192563.015.010000333.0222=⨯⨯==g v d l h f λ6-16见教材 P 137例6-36-17解:先按层流计算,由泊肃叶公式 408πr μρgJ Q =得 cm 97.0298014.3150035013.08884440=⨯⨯⨯⨯⨯===f gh Ql gJ Q r πνπρμ cm 94.120==r d 检验是不是层流 2300176994.114.3013.03544Re <=⨯⨯⨯===d Q vdνπν是层流,说明计算正确6-18解:皮托管测定的是管轴处的速度m/s 35.202.0)190113600(6.19)1(2=⨯-⨯=-=p p h g u ρρ以管轴处速度为特征流速计算雷诺数 23001958109075.035.2Re 5<=⨯⨯==-νud流动是层流 m/s 175.12==uv L/s 19.5/s m 00519.04075.014.3175.14322==⨯⨯==d v Q π6-19解:铸铁管道,取k s =1.25mm (平均值)3101.430025.1-⨯==d k s m/s 236.03.014.33600/604422=⨯⨯==d Q v π 46104.51031.13.0236.0Re ⨯=⨯⨯==-νvd 查穆迪图得 031.0=λ m 176.06.19236.03.0600031.0222=⨯⨯==g v d l h f λ6-20解:查表,取n =0.135m 075.04==d R 002.05001===l h J f 10.4816/1==R nC 管中流速 m /s 59.0==RJ C v6-21解:m/s 2.166.02.13600/42000=⨯==A Q v m 8.0)6.02.1(26.02.144=+⨯⨯==R d e 得由221v d l p e ρλ=∆ 0145.02.1611.15.06.31128.02122=⨯⨯⨯=∆=v p l d e ρλ 6-22解: πAd A AA d e 2 , 44===圆方 (1)层流 v gd lh f 232ρμ= 785.0422===π圆方方圆e e f f d d h h (2)紊流 g v d l h f 22λ= 886.04===π圆方方圆e e f f d d h h6-23解; m/s 702.105.014.300334.04422=⨯⨯==d Q v π 79.126.1215.0702.16.19222=⨯⨯==j h v g ζ 6-24解:由伯努利方程得 gv g v d l g v l H 222222ζλ++=+d l l H g v λζ+++=1)(2222)1()1(2d )(d dl d Hg l v λζλζ++-+=⇒ 当0d )(d 2<lv 时,管中流速随管长增加而减小,因管直径不变,流量也随管长增加而减小,即 01<-+dHλζ小时流量随管长增加而减λζdH )1(+>⇒6-25解:由伯努利方程得 gv v g v h g v 2)(222212221-++= 由连续性方程得 122212v d d v =)1(])1(1[2222122212122221424121d d d d g v d d d d g v h -=---=⇒ ⇒=0)(d )(d 2d h 由0122221=-d d 122d d = g v h 421m ax =6-26解:由伯努利方程得gv d l g v g v H 222222λζ++=进 m/s 36.6025.0602.05.01136.1912=⨯++⨯=++=dlgH v λζ进流量: L/s 12.3/s m 00312.04025.014.336.64322==⨯⨯==d v Q π 65.16.1936.6025.0102.02122=⨯⨯===g v d l h J fλ 切应力: Pa 1.10165.14025.08.910000=⨯⨯⨯==gRJ ρτ6-27解:m/s 06.305.014.3006.04422=⨯⨯==d Q v π m 15.325.06.12)1(=⨯=-=p f h h 水汞ρρ 022.006.3156.1905.015.3222=⨯⨯⨯==gv d l h f λ 6-28解; m/s 28.81.014.3065.04422=⨯⨯==d Q v π 由伯努利方程得gv d l H 2)3(2λζζζζ++++=出阀弯进6.1928.8)1.020042.0126.08.035.0(2⨯⨯+++⨯+=m 9.43=6-29 如图所示,水池中的水经弯管流入大气中。
工程流体力学第六章 管内流动和水力计算 液体出流

由于紊流运动的复杂性,要找出它 的规律还很难。目前所用的都是一 些经验和半经验的公式。
紊流1 紊流2
一. 紊流的发生 紊流发生的机理 扰动使某流 层发生微小 的波动
层流流动的稳定 性丧失(雷诺数 达到临界雷诺数)
流速使波 动幅度加 剧 引起流体 层之间的 混掺 造成 新的 扰动
在横向压差与切 应力的综合作用 下形成旋涡
t l2
t l2
紊流切应力:
t ( t )
d
L
层流边界层
充分发展的流动
紊流边界层
d
L
层流进口段长度: 湍流进口段长度:
粘性底层
L 0 . 058 d Re
L 25 ~ 40 d
第四节 圆管中流体的层流流动
不可压重力流体的定常层流流动 取微元柱体: 半径—r;长度—dl
h
g
mg
w
vl
l
p
dl
受力平衡:
d
r0 r
4 r 2 0 d qV r0 a ( p gh) 8 dl
对于水平圆管,由于h不变,dp/dl=dp/dx= -Δp/L,上式简化为:
d 4 p qV 128L
哈根一泊肃叶(Hagen一poiseuille)公式
由前述沿程损失公式: h f p g 及
, p p p u u u, , www
瞬时速度 平均速度 脉动速度
动画演示: 紊流的脉动
t
时均值定义:
紊流流动在某一空间固定点 上测得的速度随时间的分布
1 ( x, y , z ) T
几何意义:
t
0
工程流体力学课后习题答案

第1章 绪论【1-1】500cm 3的某种液体,在天平上称得其质量为0.453kg ,试求其密度和相对密度。
【解】液体的密度3340.4530.90610 kg/m 510m V ρ-===⨯⨯ 相对密度330.906100.9061.010w ρδρ⨯===⨯ 【1-2】体积为5m 3的水,在温度不变的条件下,当压强从98000Pa 增加到4.9×105Pa 时,体积减少1L 。
求水的压缩系数和弹性系数。
【解】由压缩系数公式10-1510.001 5.110 Pa 5(4.91098000)p dV V dP β-=-==⨯⨯⨯- 910111.9610 Pa 5.110pE β-===⨯⨯ 【1-3】温度为20℃,流量为60m 3/h 的水流入加热器,如果水的体积膨胀系数βt =0.00055K -1,问加热到80℃后从加热器中流出时的体积流量变为多少?【解】根据膨胀系数1t dVV dtβ=则2113600.00055(8020)6061.98 m /ht Q Q dt Q β=+=⨯⨯-+= 【1-4】用200升汽油桶装相对密度0.70的汽油。
罐装时液面上压强为98000Pa 。
封闭后由于温度变化升高了20℃,此时汽油的蒸汽压力为17640Pa 。
若汽油的膨胀系数为0.0006K -1,弹性系数为13.72×106Pa ,(1)试计算由于压力温度变化所增加的体积,(2)问灌装时汽油的体积最多不应超过桶体积的百分之多少?【解】(1)由1β=-=P pdV Vdp E可得,由于压力改变而减少的体积为6200176400.257L 13.7210⨯∆=-===⨯P p VdP V dV E 由于温度变化而增加的体积,可由1β=t t dV V dT得 0.000620020 2.40L β∆===⨯⨯=t t t V dV VdT(2)因为∆∆tp VV ,相比之下可以忽略由压力变化引起的体积改变,则由 200L β+=tV V dT得1198.8%200110.000620β===++⨯t V dT 【1-5】图中表示浮在油面上的平板,其水平运动速度为u =1m/s ,δ=10mm ,油品的粘度μ=0.9807Pa ·s ,求作用在平板单位面积上的阻力。
流体力学第六章

积分常数C1、C2由边界条件确定。
C1 exp( h) C2 exp( h) 0
消去一个常数
C C1 exp(h) C 2 exp(h) 2 C exp ( z h) exp ( z h) Cch ( z h) 2 Cch ( z h)sin x cos t 在 z0
t x x y y z
自由面上的运动边界条件
波浪问题的基本方程和边界条件:
2φ
2φ x
2
2φ y
2
1 t 2
n 0
z p pa
2
2
0
运动学方程 动力学方程
gz 0
=+
pa C (t ) dt
1 p pa gz 0 t 2
在自由面上: z , p pa
1 g 0 t 2
在自由面上:
z ( x, y, t ) , z z ( x x, y y, t t )
流体质点的速度 :
Ach ( z h) u cos x cos t x shh
w Ash ( z h) sin x cos t z shh
波数和频率之间的关系
Ach ( z h) sin x cos t shh
z0
0 在 z h z g 0 在 z 0 t
Ach ( z h) sin x cos t shh
2 gthh
流体质点的运动轨迹(有限水深):
u w
Ach ( z h) sh h Ash ( z h) sh h
[工程流体力学(水力学)] 禹华谦1-5章习题解答
第一章 绪论1-1.20℃的水2.5m 3,当温度升至80℃时,其体积增加多少? [解] 温度变化前后质量守恒,即2211V V ρρ= 又20℃时,水的密度31/23.998m kg =ρ 80℃时,水的密度32/83.971m kg =ρ 321125679.2m V V ==∴ρρ 则增加的体积为3120679.0m V V V =-=∆1-2.当空气温度从0℃增加至20℃时,运动粘度ν增加15%,重度γ减少10%,问此时动力粘度μ增加多少(百分数)? [解] 原原ρννρμ)1.01()15.01(-+==原原原μρν035.1035.1==035.0035.1=-=-原原原原原μμμμμμ此时动力粘度μ增加了3.5%1-3.有一矩形断面的宽渠道,其水流速度分布为μρ/)5.0(002.02y hy g u -=,式中ρ、μ分别为水的密度和动力粘度,h 为水深。
试求m h 5.0=时渠底(y =0)处的切应力。
[解] μρ/)(002.0y h g dydu-=)(002.0y h g dydu-==∴ρμτ 当h =0.5m ,y =0时)05.0(807.91000002.0-⨯⨯=τPa 807.9=1-4.一底面积为45×50cm 2,高为1cm 的木块,质量为5kg ,沿涂有润滑油的斜面向下作等速运动,木块运动速度u=1m/s ,油层厚1cm ,斜坡角22.620 (见图示),求油的粘度。
[解] 木块重量沿斜坡分力F 与切力T 平衡时,等速下滑yu AT mg d d sin μθ== 001.0145.04.062.22sin 8.95sin ⨯⨯⨯⨯==δθμu A mg s Pa 1047.0⋅=μ1-5.已知液体中流速沿y 方向分布如图示三种情况,试根据牛顿内摩擦定律yud d μτ=,定性绘出切应力沿y 方向的分布图。
[解]第二章 流体静力学2-1.一密闭盛水容器如图所示,U 形测压计液面高于容器内液面h=1.5m ,求容器液面的相对压强。
工程流体力学(水力学)] 禹华谦1-5章习题解答
第一章 绪论1-1.20℃的水2.5m 3,当温度升至80℃时,其体积增加多少 [解] 温度变化前后质量守恒,即2211V V ρρ= 又20℃时,水的密度31/23.998m kg =ρ 80℃时,水的密度32/83.971m kg =ρ 321125679.2m V V ==∴ρρ 则增加的体积为3120679.0m V V V =-=∆1-2.当空气温度从0℃增加至20℃时,运动粘度ν增加15%,重度γ减少10%,问此时动力粘度μ增加多少(百分数) [解] 原原ρννρμ)1.01()15.01(-+==Θ原原原μρν035.1035.1==035.0035.1=-=-原原原原原μμμμμμΘ此时动力粘度μ增加了%1-3.有一矩形断面的宽渠道,其水流速度分布为μρ/)5.0(002.02y hy g u -=,式中ρ、μ分别为水的密度和动力粘度,h 为水深。
试求m h 5.0=时渠底(y =0)处的切应力。
[解] μρ/)(002.0y h g dydu-=Θ)(002.0y h g dydu-==∴ρμτ 当h =,y =0时)05.0(807.91000002.0-⨯⨯=τPa 807.9=1-4.一底面积为45×50cm 2,高为1cm 的木块,质量为5kg ,沿涂有润滑油的斜面向下作等速运动,木块运动速度u=1m/s ,油层厚1cm ,斜坡角 (见图示),求油的粘度。
[解] 木块重量沿斜坡分力F 与切力T 平衡时,等速下滑yu AT mg dd sin μθ== 001.0145.04.062.22sin 8.95sin ⨯⨯⨯⨯==δθμu A mg s Pa 1047.0⋅=μ1-5.已知液体中流速沿y 方向分布如图示三种情况,试根据牛顿内摩擦定律yud d μτ=,定性绘出切应力沿y 方向的分布图。
[解]第二章 流体静力学2-1.一密闭盛水容器如图所示,U 形测压计液面高于容器内液面h=1.5m ,求容器液面的相对压强。
(完整版)工程流体力学习题及答案
(完整版)工程流体力学习题及答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第1章 绪论选择题【1.1】 按连续介质的概念,流体质点是指:(a )流体的分子;(b )流体内的固体颗粒;(c )几何的点;(d )几何尺寸同流动空间相比是极小量,又含有大量分子的微元体。
解:流体质点是指体积小到可以看作一个几何点,但它又含有大量的分子,且具有诸如速度、密度及压强等物理量的流体微团。
(d )【1.2】 与牛顿内摩擦定律直接相关的因素是:(a )切应力和压强;(b )切应力和剪切变形速度;(c )切应力和剪切变形;(d )切应力和流速。
解:牛顿内摩擦定律是d d v y τμ=,而且速度梯度d d v y 是流体微团的剪切变形速度d d t γ,故d d t γτμ=。
(b )【1.3】流体运动黏度υ的国际单位是:(a )m 2/s ;(b )N/m 2;(c )kg/m ;(d )N·s/m 2。
解:流体的运动黏度υ的国际单位是/s m 2。
(a )【1.4】理想流体的特征是:(a )黏度是常数;(b )不可压缩;(c )无黏性;(d )符合RTp=ρ。
解:不考虑黏性的流体称为理想流体。
(c )【1.5】当水的压强增加一个大气压时,水的密度增大约为:(a )1/20 000;(b )1/1 000;(c )1/4 000;(d )1/2 000。
解:当水的压强增加一个大气压时,其密度增大约95d 1d 0.51011020 000k p ρρ-==⨯⨯⨯=。
(a )【1.6】 从力学的角度分析,一般流体和固体的区别在于流体:(a )能承受拉力,平衡时不能承受切应力;(b )不能承受拉力,平衡时能承受切应力;(c )不能承受拉力,平衡时不能承受切应力;(d )能承受拉力,平衡时也能承受切应力。
解:流体的特性是既不能承受拉力,同时具有很大的流动性,即平衡时不能承受切应力。
第6章-流体流动微分方程-例题汇编
∂p* = 0, ∂r
∂p* = 0, ∂θ
∂p* ∂z
=
μ r
∂ ∂r
⎛ ⎜⎝
r
∂vz ∂r
⎞ ⎟⎠
(其中 p* = p + ρ gr sinθ )
② 由 r、θ方向运动方程,并考虑稳态条件可知:p* 只能是 z 的函数,即:
p* = p + ρ gr sinθ = C(z)
或
p ρ
+
gh
=
C1 ( z )
工程流体力学——第六章 流体流动微分方程——例题
CH6-2
根据柱坐标系运动方程(6-33),代入本题条件有:
r:
∂∂vt r + vr ∂∂v rr + vrθ
∂∂ vθr − vrθ2 +v z ∂ ∂
vzr = fr −
1 ρ
∂p ∂r
+
μ ρ
⎛⎜⎝∂∂ r ⎜⎛⎝ 1r ∂(∂r rvr ) ⎟⎞⎠ + r 12 ∂∂θ2 v2r − r 22 ∂∂vθ θ + ∂∂ 2zv2
R
该问题所有参数沿 z 方向不变,属 r-θ 平面问
题。其中,因为流动沿切向、稳态且流动对
称,所以有
vr
=
0
,
vθ
=vθ
(r
)
,
∂vθ ∂t
= 0 , ∂vθ ∂θ
=0
图 6-7 例 6-2 附图
又因为忽略重力影响,流动为纯剪切流,故压力沿流动方向不变,所以:
fr = fθ =0 , ∂p / ∂θ = 0 对于 r-θ 平面问题,其连续性方程和运动方程分别为:
工程流体力学——第六章 流体流动微分方程——例题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章理想流体动力学 6-1平面不可压缩流体速度分布为 Vx=4x+1; Vy= =-4y.
(1)该流动满足连续性方程否?(2) 势函数$、流函数p存在否 ?( 3)求$、p Vx 解:(1)由于 Vv 4 4 0 故该流动满足连续性方程
x v
1 (2)由 3 z=(- Vv Vx 1 / / )=—(4 4) = 0, 故流动有势,势函数$存在,由于该流
2 x V 2
动满足连续性方程, 流函数p存在,.
(3 )因 Vx --- -4x+1
x v
Vy= - =-4y V x
d $ - dx+—— dy=Vxdx+Vydy=(4x+1)dx+(-4y)dy
x v
Vxdx+Vydy= (4x+1)dx+(-4y)dy 2 2 =2x -2y +x
d p = --- dx+ ---- dy=-Vydx+Vxdy=4ydx+(4x+1)dy x y
-Vydx+Vxdy= 4ydx+(4x+1)dy =4xy+y 6-2 平面不可压缩流体速度分布 : 2 2 Vx=x -y +x; Vy=_(2xy+y).
(1)流动满足连续性方程否 ? (2) 势函数$、流函数P存在否 ? (3)求$、p 解:(1)由于-Vx =2x + 1—( 2x+ 1)= 0,故该流动满足连续性方程,流动存在 x x
1 Vv Vx 1 (2 2 6( x -;)=:( ^ ( 2y)) = 0,故流动有势,势函数皿在,由
于该流动满足连续性方程,流函数P也存在
—dx+ ——dy= x y
—dx+ ---- dy= x y (3) 因 Vx= —— = ------ =x 2-y 2+x, Vy= ——=- ----- =-(2xy+y). x y y x
2 2 d Q =——dx+ ——dy=Vxdx+Vydy=(x -y +x )dx+(_(2xy+y).)dy
x y
3 =—-xy 2+(x 2-y 2)/2 3
d p = --- dx+ ---- dy=-Vydx+Vxdy x y
p = d p = -- dx+ 一 dy= - Vydx+Vxdy = 2 2
(2xy+y)dx+ (x -y +x)dy x y
=x y+xy-y /3 2 及B(2,2)点处的速度值 6-3平面不可压缩流体速度势函数 Q =x -y -x,求流场上 A(-1,-
1), 及流函数值
解:因 Vx=——= --------- =2x-1 , Vy 一 —— 2y ,由于- + 一 0,该流动满 x y y x x x
足连续性方程,流函数”存在 d p = --- dx+ ----- dy=-Vydx+Vxdy x y
p = d p = -- dx+ - ——dy= -Vydx+Vxdy= 2ydx+(2x-1)dy=2xy-y x y
在点(-1,-
1) 处 Vx=-3; Vy=2; p =3
在点(2,2) 处 Vx=3; Vy=-4; p =6
6-4已知平面流动速度势函数 Q =- Q lnr,写出速度分量 Vr,V e ,q为常数。 2
解:Vr= — =- L, V 0 =——==0
r 2 r r
6-5已知平面流动速度势函数 Q =-m 0 +C ,写出速度分量 Vr、V , m为常数
解:Vr= —— =0, V 0 =——==-
m
r r r
6-6已知平面流动流函数P =x+y,计算其速度、加速度、线变形率& xx, £ yy,求出速度势函数
—dx+ ——dy= x y Vxdx+Vydy =
2 2
(x -y +x )dx+(- (2xy+y))dy Vy= ——= ---------- =-2x y x
d ( = — dx+ — dy=Vxdx+Vydy x y
(= d ( x dx+ 一 —dy= y Vxdx+Vydy= -2ydx+(-2x)dy=-2xy
dVx Vx Vx- Vx Vy Vx 4x
a x=
dt t x y
a yM - Vy Vx Vy Vy- Vy 4y;
dt t x y
6-8 一平面定常流动的流函数为
(j). 解:因 Vx= 一 = 一 = 1
x y
Vy= _ =- ____ =-1 y x
d (=——dx+ ——dy=Vxdx+Vydy x y
(= d (= ——dx+ ——dy= Vxdx+Vydy= dx+(_1)dy=x_y
x y
Vx Vy
xx , yy x y
dVx a x=— dt Vx t
a =dVy a y ----------
dt
Vy t
6-7已知平面流动流函数“ =x2-y2,计算其速度、加速度 ,求出速度势函数(.
解: 因Vx=——
x —=-2y
y (x,y) 、、3x y 试求速度分布,写出通过 A (1, 0),和B (2, 3 )两点的流线方程.
解:v 1 , Vy ——、3
y x
平面上任一点处的速度矢量大小都为、.12 (. 3)2 2,与x和正向夹角都是 arctan( ..3/1) 60°。 A点处流函数值为 ,3? 1 0 ..、3,通过A点的流线方程为 3x y , 3。同
样可以求解出通过 B点的流线方程也是 、、3x y .3。 6-9已知流函数” =V a (ycos a -xsin a ),计算其速度,加速度,角变形率 (xy = yx=X( -匕)),并求速度势函数0 .
2 x y
Vy= ——= -------- =V a sis a y x
d 0 =——dx+ ——dy=Vxdx+Vydy x y
Vxdx+Vydy= V a cos a dx+ sis a dy
6-10.证明不可压缩无旋流动的势函数是调和函数。 解:不可压缩三维流动的连续性方程为
解: 因Vx=——
x -- =V a cos a
y
dx+ ——dy= y
=V a ( COS a x+ sis a y)
dVx x= dt
Vx 、, Vx
Vx --- t x
_dVy y=— dt
Vy VX 卫
t x 0;
xy 亠 v
y )=0 vx vy
x y
vz 0
将关系
v
x, 一
y z x
() () ()0
x x y y z z
2 2 2 或一2 - 2 2
0
x y z
可见不可压缩有势流动的势函数是 调和函数。 6-11 什么样的平面流动有流函数 ?
答: 不可压缩平面流动在满足连续性方程
vx vy 0
x y
或vx (-vy)
x y
的情况下 平面流动 有流函数. 6-12 !什么样的空间流动有势函数 ?
答: 在一空间流动中,如果每点处的旋转角速度矢量
x y z 0,或关系
vz vy
J vx v
z
y z z x
数•
6-13 i已知流函数” =-q ,计算流场速度.
2
解:
Vr= =_ q
r 2 r
V 9 = ----- =0 r 2 6-14
-vz代入上式得到
z
x i+ y j+ z k都是零矢量,即 Vx成立,这样的空间流动有势函
y
=ax(x 2-3y 2),a<0,试确定流速及流函数,并求通过连 接A(0,0)及B(1,1)两点的连线的直线段的流体流量 2 2 解: 因 Vx=—— ——=a(3x -3y )
x y
Vy= —= ----- =-6axy y x
2 2 d p = ------- dx+ ---- dy=-Vydx+Vxdy=6axydx+a(3x -3y )dy
x y
