45分钟课时检测练+10.2
2018年高一北师大版数学必修2(45分钟课时作业与单元测试卷):第1章章末检测 Word版含解析
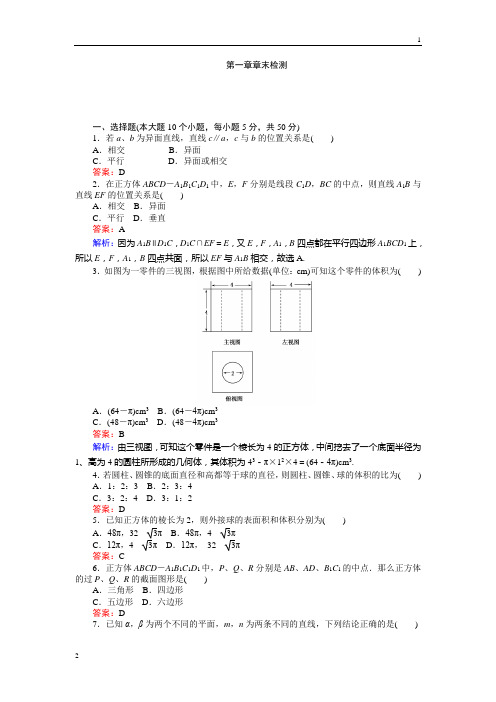
第一章章末检测一、选择题(本大题10个小题,每小题5分,共50分)1.若a、b为异面直线,直线c∥a,c与b的位置关系是()A.相交B.异面C.平行D.异面或相交答案:D2.在正方体ABCD-A1B1C1D1中,E,F分别是线段C1D,BC的中点,则直线A1B与直线EF的位置关系是()A.相交B.异面C.平行D.垂直答案:A解析:因为A1B∥D1C,D1C∩EF=E,又E,F,A1,B四点都在平行四边形A1BCD1上,所以E,F,A1,B四点共面,所以EF与A1B相交,故选A.3.如图为一零件的三视图,根据图中所给数据(单位:cm)可知这个零件的体积为() A.(64-π)cm3B.(64-4π)cm3C.(48-π)cm3D.(48-4π)cm3答案:B解析:由三视图,可知这个零件是一个棱长为4的正方体,中间挖去了一个底面半径为1、高为4的圆柱所形成的几何体,其体积为43-π×12×4=(64-4π)cm3.4.若圆柱、圆锥的底面直径和高都等于球的直径,则圆柱、圆锥、球的体积的比为() A.1:2:3 B.2:3:4C.3:2:4 D.3:1:2答案:D5.已知正方体的棱长为2,则外接球的表面积和体积分别为()A.48π,32 3πB.48π,4 3πC.12π,4 3πD.12π,32 3π答案:C6.正方体ABCD-A1B1C1D1中,P、Q、R分别是AB、AD、B1C1的中点.那么正方体的过P、Q、R的截面图形是()A.三角形B.四边形C.五边形D.六边形答案:D7.已知α,β为两个不同的平面,m,n为两条不同的直线,下列结论正确的是()A .若m ⊥α,m ⊥n ,则n ∥αB .若m ∥α,n ∥α,则m ∥nC .若m β,且α⊥β,则m ⊥αD .若m ⊥β,且α∥β,则m ⊥α 答案:D解析:A 中可能n α;B 中m ,n 还可能相交或异面;C 中m ,α还可能平行或斜交;一条直线垂直于两平行平面中的一个,也垂直于另一个,所以D 正确.8.四面体S -ABC 中,各个面都是边长为2的正三角形,E ,F 分别是SC 和AB 的中点,则异面直线EF 与SA 所成角等于( )A .90°B .60°C .45°D .30° 答案:C9.设m 、n 是两条不同的直线,α,β,γ是三个不同的平面,给出下列四个命题: ①若m ⊥α,n ∥α,则m ⊥n②若α∥β,β∥γ,m ⊥α,则m ⊥γ ③若m ∥α,n ∥α,则m ∥n ④若α⊥γ,β⊥γ,则α∥β 其中正确命题的序号是( ) A .①和② B .②和③ C .③和④ D .①和④ 答案:A10.直线m ⊥平面α,垂足是O ,正四面体ABCD 的棱长为4,点C 在平面α上运动,点B 在直线m 上运动,则点O 到直线AD 的距离的取值范围是( )A .[4 2-52,4 2+52]B .[2 2-2,2 2+2]C .[3-2 22,3+2 22]D .[3 2-2,3 2+2] 答案:B 解析:由题意,直线BC 与动点O 的空间关系: 点O 是以BC 为直径的球面上的点,所以O 到AD 的距离为四面体上以BC 为直径的球面上的点到AD 的距离, 最大距离为AD 到球心的距离(即BC 与AD 的公垂线)+半径=2 2+2. 最小距离为AD 到球心的距离(即BC 与AD 的公垂线)-半径=2 2-2.∴点O 到直线AD 的距离的取值范围是:[2 2-2,2 2+2]. 二、填空题(本大题5个小题,每小题5分,共25分)11.已知圆锥的表面积为6π,且它的侧面展开图是一个半圆,则这个圆锥的底面半径为________.答案: 212.在棱长为2的正方体ABCD -A 1B 1C 1D 1中,E ,F 分别是棱AB ,BC 中点,则三棱锥B -B 1EF 的体积为________.答案:1313.在正方体ABCD -A 1B 1C 1D 1中,M 、N 分别为BB 1和CD 的中点,则直线AM 和D 1N 所成的角为________.答案:90° 14.如图,梯形A ′B ′C ′D ′是水平放置的四边形ABCD 的用斜二测画法画出的直观图.若A ′D ′∥y ′轴,A ′B ′∥C ′D ′,A ′B ′=23C ′D ′=2,A ′D ′=O ′D ′=1,则四边形ABCD 的面积为________.答案:5 解析:如图,建立直角坐标系xOy ,在x 轴上截取OD =O ′D ′=1,OC =O ′C ′=2.过点D 作y 轴的平行线,并在平行线上截取DA =2D ′A ′=2.过点A 作x 轴的平行线,并在平行线上截取AB =A ′B ′=2.连接BC ,即得到了四边形ABCD .可知四边形ABCD 是直角梯形,上、下底边分别为AB =2,CD =3,高AD =2,所以四边形ABCD 的面积S =2+32×2=5.15.如图,在正方体ABCD -A 1B 1C 1D 1中,给出以下四个结论:①直线D 1C ∥平面A 1ABB 1; ②直线A 1D 1与平面BCD 1相交; ③直线AD ⊥平面D 1DB ; ④平面BCD 1⊥平面A 1ABB 1.其中正确结论的序号为________. 答案:①④解析:因为平面A 1ABB 1∥平面D 1DCC 1,D 1C平面D 1DCC 1,所以D 1C ∥平面A 1ABB 1,①正确;直线A 1D 1在平面BCD 1内,②不正确;显然AD 不垂直于BD ,所以AD 不垂直于平面D 1DB ,③不正确;因为BC ⊥平面A 1ABB 1,BC 平面BCD 1,所以平面BCD 1⊥平面A 1ABB 1,④正确.三、解答证明题(本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤.)16.(12分)圆台的一个底面周长是另一个底面周长的3倍,轴截面的面积等于392 cm 2,母线与轴的夹角是45°,求这个圆台的高、母线长和两底面半径.解:x cm,3x cm. 延长AA 1交OO 1的延长线于S , 在Rt △SOA 中,∠ASO =45°,则∠SAO =45°, ∴SO =AO =3x ,∴OO 1=2x ,又S 轴截面=12(6x +2x )·2x =392,∴x =7.故圆台的高OO 1=14 cm ,母线长l = 2O 1O =14 2 cm ,两底面半径分别为7 cm,21 cm.17.(12分)如图,在圆锥SO 中,AB ,CD 为底面圆的两条直径,AB ∩CD =O ,SO =OB =2,P 为SB 的中点.(1)求证:SA ∥平面PCD ; (2)求圆锥SO 的表面积. 解:(1)连接PO ,∵P ,O 分别为SB ,AB 的中点,∴PO ∥SA .又PO 平面PCD ,SA 平面PCD ,∴SA ∥平面PCD .(2)设母线长为l ,底面圆半径为r ,则r =2,l =SB =22, ∴S 底=πr 2=4π,S 侧=πrl =42π, ∴S 表=S 底+S 侧=4(2+1)π.18.(12分)如图,在三棱锥P -ABC 中,P A ⊥底面ABC ,AB ⊥BC ,DE 垂直平分PC ,且分别交AC ,PC 于D ,E 两点,PB =BC ,P A =AB .(1)求证:PC ⊥平面BDE ;(2)试确定线段P A 上点Q 的位置,使得PC ∥平面BDQ . 解:(1)∵PB =BC ,E 为PC 的中点,∴PC ⊥BE . ∵DE 垂直平分PC ,∴PC ⊥DE .又BE 平面BDE ,DE 平面BDE ,且BE ∩DE =E ,∴PC ⊥平面BDE .(2)不妨令P A =AB =1,则有PB =BC =2,计算得AD =33=13AC . ∴点Q 在线段P A 上靠近点A 的三等分点处,即AQ =13AP 时,PC ∥QD ,从而PC ∥平面BDQ .19.(13分)如图,在直三棱柱ADF -BCE 中,AB =AD =DF =a ,AD ⊥DF ,M ,G 分别是AB ,DF 的中点.(1)求该直三棱柱的体积与表面积;(2)在棱AD 上确定一点P ,使得GP ∥平面FMC ,并给出证明.解:(1)由题意,可知该直三棱柱的体积为12×a ×a ×a =12a 3,表面积为12a 2×2+2a 2+a 2+a 2=(3+2)a 2.(2)当点P 与点A 重合时,GP ∥平面FMC . 取FC 的中点H ,连接GH ,GA ,MH .∵G 是DF 的中点,∴GH 綊12CD .又M 是AB 的中点,AB 綊CD ,∴AM 綊12CD .∴GH ∥AM 且GH =AM ,∴四边形GHMA 是平行四边形, ∴GA ∥MH .∵MH 平面FMC ,GA 平面FMC , ∴GA ∥平面FMC ,即当点P 与点A 重合时,GP ∥平面FMC .20.(13分)如图①,有一个等腰直角三角板ABC 垂直于平面α,BC α,AB =BC =5,有一条长为7的细线,其两端分别位于B ,C 处,现用铅笔拉紧细线,在平面α上移动.(1)图②中的PC (PC <PB )的长为多少时,CP ⊥平面ABP ?并说明理由. (2)在(1)的情形下,求三棱锥B -APC 的高. 解:(1)当CP =3时,CP ⊥平面ABP .证明如下:若CP =3,则BP =4,而BC =5, 所以三角形BPC 为直角三角形,且CP ⊥PB . 又平面ABC ⊥平面α,AB ⊥BC ,所以AB ⊥平面α,于是CP ⊥AB .又PB 平面ABP ,AB 平面ABP ,PB ∩AB =B , 所以CP ⊥平面ABP .(2)解法一:如图,过点B 作BD ⊥AP 于点D ,由(1),知CP ⊥平面ABP ,则CP ⊥BD .又AP 平面APC ,CP 平面APC ,AP ∩CP =P , 所以BD ⊥平面APC ,即BD 为三棱锥B -APC 的高. 由于PB =4,AB =5,AB ⊥平面α,所以AP =AB 2+PB 2=25+16=41,由AP ·BD =AB ·PB ,得BD =4×541=204141.即三棱锥B -APC 的高为204141.解法二:由(1),知CP ⊥平面ABP ,所以CP ⊥AP . 又CP =3,BP =4,AB =5,AB ⊥BP , 所以AP =AB 2+PB 2=25+16=41,所以S △APC =12·CP ·AP =3412.设三棱锥B -APC 的高为h ,则V B -APC =13·S △APC ·h =412h .又V A -PBC =13·S △PBC ·AB =13×12×CP ×BP ×AB =10,而V B -APC =V A -PBC ,得412h =10,所以h =204141.即三棱锥B -APC 的高为204141.21.(13分)已知正方形ABCD 所在平面与正方形ABEF 所在平面互相垂直,M 为AC 上一点,N 为BF 上一点,且AM =FN =x ,设AB =a(1)求证:MN ∥平面CBE ; (2)求证: MN ⊥AB ;(3)当x 为何值时,MN 取最小值?并求出这个最小值.证明:(1)在平面ABC 中,作MG ∥AB ,在平面BFE 中,作NH ∥EF ,连接GH ,∵AM =FN ,∴MC =NB ,∵MG AB =MC NC =NBEF∴MG ∥NH ,∴MNHG 为平行四边形,∴MN ∥GH又∵GH ⊆面BEC ,MN 面BEC ,∴MN ∥面BEC (2)∵AB ⊥BC ,AB ⊥BE ,∴AB ⊥面BEC ,∵GH ⊆面GEC ,∴AB ⊥GH ,∵MN ∥GH ,∴MN ⊥AB (3)∵面ABCD ⊥面ABEF ,∴BE ⊥面ABCD ,∴BE ⊥BC∵BG =x2,BH =2a -x 2∴MN =GH =BG 2+BH 2=x 2+x 2-22ax +2a 22=x 2-2ax +a 2(0<a <2a )=⎝⎛⎭⎫x -22a 2+a 22≤22a当且仅当x =22a 时,等号成立;∴当x =22a 时,MN 取最小值22a .。
人教版九年级化学上册年中考45分钟课时检测练(解析版):第十单元酸和碱第2课时中和反应和ph

45分钟课时检测练100分第2课时中和反应和pH一、选择题(本题包括10小题,每小题4分,共40分)1.生活中某些物质的pH近似为西瓜汁5.8、苹果汁3.1、泡菜3.4、鸡蛋清7.6,其中酸性最强的是( )A.苹果汁B.泡菜C.西瓜汁D.鸡蛋清【解析】选A。
pH<7的物质显酸性,数值越小,酸性越强,pH>7的物质显碱性,数值越大,碱性越强,由此确定苹果汁的酸性最强。
2.中和反应在日常生产和生活中有广泛的用途。
下列做法应用了中和反应的是( )A.用生石灰作食品干燥剂B.用熟石灰处理工厂污水中的硫酸C.用碳酸氢钠和柠檬酸等原料自制汽水D.用熟石灰与硫酸铜溶液来配制农药波尔多液【解析】选B。
A.生石灰作干燥剂是利用氧化钙与水的反应,不是酸与碱的反应,故此选项错误;B.用熟石灰处理工厂污水中的硫酸,是氢氧化钙与硫酸的反应,故此选项正确;C.用碳酸氢钠和柠檬酸等原料自制汽水,是利用盐与酸的反应,不是中和反应,故此选项错误;D.用熟石灰与硫酸铜溶液配制波尔多液是利用碱与盐的反应,不是中和反应,故此选项错误。
3.(2016·甘肃兰州模拟)“接叶连枝千万绿,一花两色浅深红”是对玫瑰花生动的写照。
我市苦水玫瑰远近闻名,某同学用“玫瑰花瓣”的汁液自制酸碱指示剂,有关记录如下表:向滴有少量该指示剂的NaOH溶液中逐渐滴加稀盐酸至过量,颜色变化是( )A.由浅红色变红色B.由棕黄色变浅红色C.由浅红色变棕黄色D.由红色变棕黄色【解析】选B。
该指示剂在碱性溶液中呈棕黄色,在酸性溶液中呈浅红色,所以向滴有少量该指示剂的NaOH溶液中逐渐滴加稀盐酸至过量,颜色变化是由棕黄色变浅红色。
4.常温下,下列说法错误的是( )A.pH=2的溶液显酸性B.pH=7的溶液显中性C.溶液的pH由5变成2,其酸性减弱D.pH>10的土壤不适于种植农作物,因为碱性太强【解析】选C。
常温下,pH=7时,溶液显中性;pH>7时,溶液显碱性,且pH数值越大,溶液碱性越强;pH<7时,溶液显酸性,pH数值越小,溶液酸性越大;植物一般生长在pH大约在6.5~7.5的土壤中,酸性太强或碱性太强均不适合植物生长。
10.2直方图练习题带答案

10.2《直方图》同步练习知识点:频数分布直方图①组距:每个小组两个端点之间的距离②组数:组数②频数:数据出现的次数③频率:频数与数据总数的比同步练习1.下表是对某班50名学生如何到校问题进行的一次调查结果,根据表中已知数据填表:频数所占比步行9骑自行车28坐公共汽车20%其他 32.下表是某班学生在一次身高测量中得到的统计结果请回答:(1)这个班总人数是_____人;身高为______m 的人数最多,有____人.(2)身高最高、最低的分别是_____m 、_____m ,他们分别有____人,_____人;最高的与最低的相身高/m 1.40 1.45 1.49 1.54 1.57 1.60 1.62 1.68 1.72 1.78人数/人 1 3 4 6 11 15 96 3 2差______m.3.(25分)七年级13班其中40个同学某次数学测验成绩(单位:分):63 84 91 53 69 81 61 69 91 78 75 81 80 67 76 81 79 94 61 69 89 70 70 87 81 86 90 88 85 67 71 82 87 75 87 95 53 65 74 77 数学老师按10分的组距分段,进行统计分析:解:1、求极差:最高分,最低分。
极差: d2、列频率分布表:分组6050<≤x7060<≤x8070<≤x9080<≤x10090<≤x频数记录正正正频数2 9 14 5所占比例5% 35%4题图(每组含最低分数,但不含最高分数)120人数/人01234567860708090110100分数/分(1)请把频数分布表及频数分布直方图补充完整;(2)绘制频数折线图.4.某中学部分同学参加全国初中数学竞赛,取得了优异的成绩.指导老师统计了所有参赛同学的成绩(成绩都是整数,试题满分为120分),并且绘制了频率分布直方图(如图).请回答:(1)该中学参加本次数学竞赛的有多少名同学?(2)如果成绩在90分以上(含90分)的同学获奖,那么该中学参赛同学的获奖率是多少?(3)图中还提供了其他信息,例如该中学没有获得满分的同学等.请再写出两条信息.10.2《直方图》同步练习题(1)答案:1.10 ;18%;56%; 6 %2.(1)60 ;1.60 ;15 ;(2)1.78 ;1.40 ;2 ; 1 ;0.383. 94 ;53 ;41 ;略4.32 ;43.75%;80到90分的人数最多;80到90分的人数的百分比为25%。
数学人教版七年级下册《10.2直方图》练习

《10.2直方图》练习知识梳理1、频数分布直方图的制作过程:(1)计算最大值与最小值的________;(2)决定组距和________;(3)列________;(4)画________.2、把所有数据分成若干组,每个小组的________之间的距离称为组距.组距和组数________的标准.当数据在100个以内时,按照数据的多少,常分成________组.各个小组内的________叫做频数.3、频数分布直方图中,小长方形的高的比就是各小组________的比.各小组频数的和是________,各小组的频率之和等于________.当堂训练1、某频数分布直方图中,共有A,B,C,D,E五个小组,频数分别为10,15,25,35,10,则直方图中,长方形高的比为( )A.2∶3∶5∶7∶2 B.1∶3∶4∶5∶1 C.2∶3∶5∶6∶2 D.2∶4∶5∶4∶2 2、一个容量为80的样本,最大值为141,最小值为50,取组距为10,则可以分成( )A.10组B.9组C.8组 D.7组3、考察50名学生的年龄,列频数分布表时,这些学生的年龄落在了5个小组中,第一、二、三、五组的数据个数分别是2,8,15,5,则第四组的频数是( )A.20 B.10 C.15 D.304、下图是某班45名同学爱心捐款额的频数分布直方图(每组含前一个边界值,不含后一个边界值),则捐款人数最多的一组是( )A.5~10元 B.10~15元 C.15~20元 D.20~25元5、王老师对本班40名学生的血型作了统计,列出如下的统计表,则本班A型血的人数是( )A.16人B.14人C.4人D.6人6、为绘制一组数据的频数分布直方图,首先要算出这组数据的变动范围,即是指数据的( )A.最大值 B.最小值 C.个数 D.最大值与最小值的差7、在对n个数据进行整理的频数分布表中,各组的频数之和等于( )A.n B.1 C.2n D.3n8、如果一组数据共有30个,那么通常分成( )A.3~5组B.5~12组C.12~20组 D.20~25组9、某棉纺厂为了解一批棉花的质量,从中随机抽取了20根棉花纤维进行测量,其长度x(单位:mm)的数据分布如下表,则棉花纤维长度的数据在8≤x<32,这个范围的频率为( )A.0.8 B.0.7 C.0.4 D.0.210、对某校同龄的70名学生的身高进行测量,得到一组数据,其中最大值是175 cm,最小值是149 cm,对这组数据进行整理时,可得到其极差(最大值与最小值的差)为________,如果确定它的组距为3 cm,那么组数为________.11、为创建“国家园林城市”,某校举行了以“爱我黄石”为主题的图片制作比赛,评委会对200名同学的参赛作品打分发现,参赛者的成绩x均满足50≤x<100,并制作了频数分布直方图,如图:根据以上信息,解答下列问题:(1)请补全频数分布直方图;(2)若依据成绩,采取分层抽样的方法,从参赛同学中抽40人参加图片制作比赛总结大会,则从成绩80≤x<90的选手中应抽多少人?(3)比赛共设一、二、三等奖,若只有25%的参赛同学能拿到一等奖,则一等奖的分数线是多少?12、绵阳农科所为了考察某种水稻穗长的分布情况,在一块试验田里随机抽取了50个谷穗作为样本,量得它们的长度(单位:cm),对样本数据适当分组后,列出了如下频数分布表:(1)在图中画频数分布直方图;(2)请你对这块试验田的水稻穗长进行分析;并计算出这块试验田里穗长在5.5≤x<7范围内的谷穗所占的百分比.参考答案知识梳理1、差 组数 频数分布表 频数分布直方图2、两个端点 没有固定 5~12 数据的个数3、频数 数据总数 1当堂训练1、A2、A3、A4、C5、A6、D7、A8、A9、A 10、26 cm 911、解:(1)200-(35+70+40+10)=45,补图略.(2)设抽了x 人,则20040=40x,解得x =8. (3)依题意知获一等奖的人数为200×25%=50(人),则一等奖的分数线是80分.12、解:(1)补图略.(2)由(1)可知谷穗长度大部分落在5 cm 至7 cm 之间,其他区域较少,长度在6≤x<6.5范围内的谷穗最多,有13个,而长度在4.5≤x<5、7≤x<7.5范围内的谷穗较少,总共只有7个;在这块试验田里穗长在5.5≤x<7范围内的谷穗所占的百分比为(12+13+10)÷50×100%=70%.。
高中北师大版数学必修2(45分钟课时作业与单元测试卷):第1章2 直观图 Word版含解析

2直观图时间:45分钟满分:80分班级________姓名________分数________一、选择题(每小题5分,共5×6=30分)1.水平放置的梯形的直观图是()A.梯形B.矩形C.三角形D.任意四边形答案:A解析:斜二测画法的规则中平行性保持不变,故选A.2.利用斜二测画法可以得到:①水平放置的三角形的直观图是三角形;②水平放置的平行四边形的直观图是平行四边形;③水平放置的正方形的直观图是正方形;④水平放置的菱形的直观图是菱形.以上结论正确的是()A.①②B.①C.③④D.①②③④答案:A解析:因为斜二测画法是一种特殊的平行投影画法,所以①②正确;对于③④,只有平行于x轴的线段长度不变,所以不正确.3.用斜二测画法得到的一个水平放置的平面图形的直观图为如图所示的一个正方形,则原来的图形是()答案:A解析:直观图中的多边形为正方形,对角线的长为2,所以原图形为平行四边形,位于y轴上的对角线的长为2 2.4.已知一条边在x轴上的正方形的直观图是一个平行四边形,此平行四边形中有一边长为4,则原正方形的面积是()A.16 B.64C.16或64 D.以上都不对答案:C解析:根据直观图的画法,平行于x轴的线段长度不变,平行于y轴的线段变为原来的一半,于是直观图中长为4的边如果平行于x ′轴,则正方形的边长为4,面积为16;长为4的边如果平行于y ′轴,则正方形的边长为8,面积是64.5.若用斜二测画法把一个高为10 cm 的圆柱的底面画在x ′O ′y ′平面上,则该圆柱的高应画成( )A .平行于z ′轴且长度为10 cmB .平行于z ′轴且长度为5 cmC .与z ′轴成45°且长度为10 cmD .与z ′轴成45°且长度为5 cm 答案:A解析:平行于z 轴的线段,在直观图中平行性和长度都不变,故选A.6.若一个水平放置的图形的直观图是一个底角为45°且腰和上底均为1的等腰梯形如图所示,则原平面图形的面积是( )A.2+22B.1+22C .2+ 2D .1+ 2 答案:C解析:由题意,知直观图中等腰梯形的下底为2+1,根据斜二测画法规则,可知原平面图形为直角梯形,上底为1,下底为2+1,高为2,所以其面积为2+ 2.二、填空题(每小题5分,共5×3=15分)7.一条边在x 轴上的正方形的面积是4,按斜二测画法所得的直观图是一个平行四边形,则这个平行四边形的面积是________.答案: 2解析:正方形的面积为4,则边长为2,由斜二测画法的规则,知平行四边形的底为2,高为22,故面积为 2.8.一个水平放置的平面图形的直观图是直角梯形ABCD ,如图所示,∠ABC =45°,AB =AD =1,DC ⊥BC ,则这个平面图形的面积为________.答案:4+22解析:由直观图,可知原图形为直角梯形,且上底为1,下底为22+1,高为2,故面积为12×⎝⎛⎭⎫1+22+1×2=2+22.9.给出下列各命题:(1)利用斜二测画法得到的三角形的直观图还是三角形;(2)利用斜二测画法得到的平行四边形的直观图还是平行四边形; (3)利用斜二测画法得到的正方形的直观图还是正方形; (4)利用斜二测画法得到的菱形的直观图还是菱形;(5)在画直观图时,由于选轴的不同所画的直观图可能不同; (6)水平放置的矩形的直观图可能是梯形. 其中正确的命题序号为____________.答案:(1)(2)(5)三、解答题(共35分,11+12+12)10.将图中所给水平放置的直观图绘出原形.解:11.用斜二测画法画出图中水平放置的△OAB 的直观图.解:(1)在已知图中,以O 为坐标原点,以OB 所在的直线及垂直于OB 的直线分别为x 轴与y 轴建立平面直角坐标系,过点A 作AM 垂直x 轴于点M ,如图1.另选一平面画直观图,任取一点O ′,画出相应的x ′轴、y ′轴,使∠x ′O ′y ′=45°.(2)在x ′轴上取点B ′,M ′,使O ′B ′=OB ,O ′M ′=OM ,过点M ′作M ′A ′∥y ′轴,取M ′A ′=12MA .连接O ′A ′,B ′A ′,如图2.(3)擦去辅助线,则△O ′A ′B ′为水平放置的△OAB 的直观图. 12.画正六棱柱的直观图. 解:画法如下:(1)画轴:画x ′轴、y ′轴、z ′轴,使∠x ′O ′y ′=45°,∠x ′O ′z ′=90°; (2)画底面:画正六边形的直观图ABCDEF (O ′为正六边形的中心);(3)画侧棱:过A ,B ,C ,D ,E ,F 各点分别作z ′轴的平行线,在这些平行线上分别截取AA ′,BB ′,CC ′,DD ′,EE ′,FF ′,使AA ′=BB ′=CC ′=DD ′=EE ′=FF ′;(4)连线成图:连接A ′B ′,B ′C ′,C ′D ′,D ′E ′,E ′F ′,F ′A ′,并加以整理(去掉辅助线,将被遮挡的部分改为虚线),就得到正六棱柱ABCDEF -A ′B ′C ′D ′E ′F ′,如图所示.给高中生的建议初中学生学数学,靠的是一个字:练!高中学生学数学靠的也是一个字:悟!学好数学的核心就是悟,悟就是理解,为了理解就要看做想。
七年级数学下10.2 数据的描述课时练
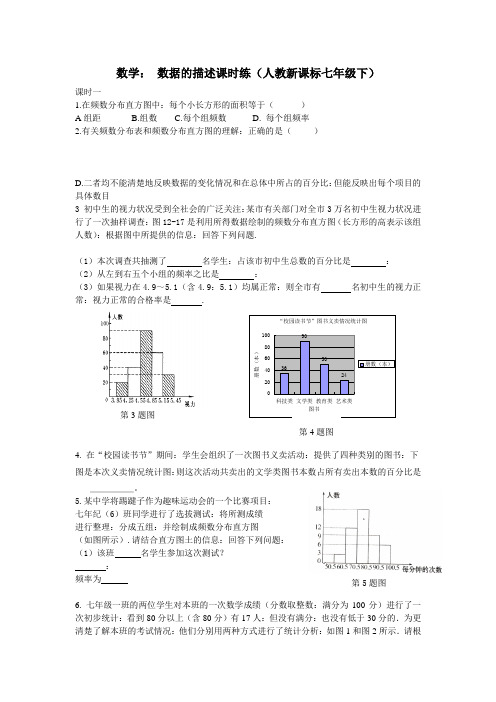
数学: 数据的描述课时练(人教新课标七年级下)课时一1.在频数分布直方图中:每个小长方形的面积等于( ) A 组距 B.组数 C.每个组频数 D. 每个组频率2.有关频数分布表和频数分布直方图的理解:正确的是( )D.二者均不能清楚地反映数据的变化情况和在总体中所占的百分比:但能反映出每个项目的具体数目3 初中生的视力状况受到全社会的广泛关注:某市有关部门对全市3万名初中生视力状况进行了一次抽样调查:图12-17是利用所得数据绘制的频数分布直方图(长方形的高表示该组人数):根据图中所提供的信息:回答下列问题.(1)本次调查共抽测了 名学生:占该市初中生总数的百分比是 : (2)从左到右五个小组的频率之比是 :(3)如果视力在4.9~5.1(含4.9:5.1)均属正常:则全市有 名初中生的视力正常:视力正常的合格率是 .4. 在“校园读书节”期间:学生会组织了一次图书义卖活动:提供了四种类别的图书:下 图是本次义卖情况统计图:则这次活动共卖出的文学类图书本数占所有卖出本数的百分比是_____。
5.某中学将踢踺子作为趣味运动会的一个比赛项目: 七年纪(6)班同学进行了选拔测试:将所测成绩 进行整理:分成五组:并绘制成频数分布直方图(如图所示).请结合直方图土的信息:回答下列问题: (1)该班 名学生参加这次测试? : 频率为6. 七年级一班的两位学生对本班的一次数学成绩(分数取整数:满分为100分)进行了一次初步统计:看到80分以上(含80分)有17人:但没有满分:也没有低于30分的.为更清楚了解本班的考试情况:他们分别用两种方式进行了统计分析:如图1和图2所示.请根第3题图“校园读书节”图书义卖情况统计图3690502420406080100科技类文学类教育类艺术类图书册数(本)册数(本)第4题图第5题图据图中提供的信息回答下列问题:(1)班级共有多少名学生参加了考试? (2)填上两个图中三个空缺的部分: (3)问85分到89分的学生有多少人?7.对某班学生一次数学测验中成绩进行统计分析:各分数段的人数如图(分数取正整数):请观察图形:并回答下列问题: (1)该班有多少名学生?(2)89.5-99.5这一组的频数是多少?8为了了解居民月用水:某市对居民用水进行了抽样调查:并制成如下直方图. (1)这次抽查一共抽查了多少户? (2)用水量不足10吨的有多少户? 用水量超过16吨的有多少户? (3)假设该区有8万户居民:估计用水量不超过10吨的有多少户?9.某校七年级共500名学生参加法律知识测试:从中随机抽取一部分试卷成绩:作统计分析:人数分数2 35 10 11(第6题图1) (第6题图2) 85分~100分60分以下 60分~85分 62%20%% 图中的各部分都只含最低分不含最高分 第7题图 第8题图进行整理后分成五组:并绘制成频数分布直方图:请你结合直方图提供的信息:解答以下问题:(1)随机抽取了多少名学生的测试成绩? (2)70.5-80.5分这一分数段的频率是多少? (3)箬90分以上(不含90分)定为优秀: 则样本的优秀率是多少?(4)请你估计该校七年级这次法律知识测试 获得优秀大约有多少人?课时一答案:1.C :2.D :3. (1)24O O.8% (2)2∶4∶9∶6∶ 6解:(1)(235)20%50++÷=(人)(2)如图所示.(3)85~100分:120%62%18%--=: 所以:含有18%509⨯=(人) 7.(1)4+8+10+16+10=50名:(2)12: 8(1)100户:(2)用水量不足10吨的有55户:用水量超过16吨的有10户: (3)44000户:9.(1)3+8+12+21+6=50(名):(2);24.05012= (3)%12%100506=⨯:(4)500×12%=60(人) 课时二1.已知20个数据如下:25:21:23:25:27:29:25:24:30:29:26:23:25:27:26:22:24:25:26:28:其中24.5-26.6这一组的频率是( ) B.0.35 C2. (08内蒙古赤峰市)如图是光明中学乒乓球队队员年龄分布的条形图.这些年龄的众数、中位数依次分别是( )%A .15:15B .15:15.53 为响应国家要求中小学生每天锻练1小时的号召:某校开展了形式多样的“阳光体育运动”活动:小明对某班同学参加锻炼的情况进行了统计:并绘制了下面的图2和图3:请在图1中将“乒乓球”部分的图形补充完整.4 中小学生的视力状况受到全社会的广泛关注:某市有关部门对全市4万名初中生的视力状况进行一次抽样调查统计:所得到的有关数据绘制成频率分布直方图:如图所示:从左至右五个小组的频率之比依次是2∶4∶9∶7∶3:第五小组的频数是30.(1)本次调查共抽测了多少名学生?(2)本次调查抽测的数据:频数最高的是在哪个范围内? 频率最低的是在哪个范围内?(3)如果视力在4.9~5.1(含4.9:5.1)均属正常: 那么全市初中生视力正常的约有多少人?(4)请你就该市初中生的视力状况:谈一谈你的想法.6.未成年人思想道德建设越来越受到社会的关注.某青少年研究所随机调查了大连市内某校100名学生寒假中花零花钱的数量(钱数取整数元):以便引导学生树立正确的消费观.根据调查数据制成了频率分布表和频率分布直方图(如图12-40所示)分 组 频 数 频 率 ~~20~~30篮球 乒乓球 足球 其他 5 10 15 20 兴趣爱好图2 足球 篮球40%其它 乒 乓球 图3 人数 第4题图 10 8 642 013 14 15 16 17 18 年龄~ 10 ~ 5合 计100(1)补全频率分布表:(2)在频率分布直方图中:长方形ABCD 的面积是 :这次共调查了 人: (3)研究所认为:应对消费150元以上的学生提出勤俭节约的建议.试估计应对该校1000名学生中约多少名学生提出这项建议.6. 为了进一步了解八年级学生的身体素质情况:体育老师对八年级(1)班50位学生进行一分钟跳绳次数测试:以测试数据为样本:绘制出部分频数分布表和部分频数分布直方图.如下所示: 组别 次数x 频数(人数) 第1组 80100x <≤ 6 第2组 100120x <≤ 8 第3组 120140x <≤ a 第4组 140160x <≤ 18第5组 160180x <≤ 6请结合图表完成下列问题:(1)表中的a = :(2)请把频数分布直方图补充完整: (3)这个样本数据的中位数落在第 组: (4)若八年级学生一分钟跳绳次数(x )达标要求是:120x <不合格:120140x <≤为合格:140160x <≤为良:160x ≥为优.根据以上信息:请你给学校或八年级同学提一条合理化建议: .7. 据2007年5月26日《生活报》报道:我省有关部门要求各中小学要把“每天锻炼一小时”写入课表.为了响应这一号召:某校围绕着“你最喜欢的体育活动项目是什么?(只写一项)”的问题:对在校学生进行了随机抽样调查:从而得到一组数据.图1是根据这组数据绘制的条形统计图.请结合统计图回答下列问题: (1)该校对多少名学生进行了抽样调查?18 1512963 050 100 120 140 160 180跳绳次数 频数(人数) 第3题图(2)本次抽样调查中:最喜欢篮球活动的有多少人?占被调查人数的百分比是多少? (3)若该校九年级共有200名学生:图2是根据各年级学生人数占全校学生总人数的百分比绘制的扇形统计图:请你估计全校学生中最喜欢跳绳活动的人数约为多少?8某市教育局在中学开展的“创新素质实践行”中: 进行了小论文的评比。
人教版七年级数学下册 《10.2 直方图》单元测试试卷 含答案解析
人教版七年级下册数学《10.2直方图》课时练1.小聪在做“抛一枚正六面体骰子”的实验时,他连续抛了10次,其中“6”点向上共出现3次,则出现“6”点向上的频率是()A.B.C.D.2.一个班有40名学生,在一次身体素质测试中,测试结果达到优秀的有18人,合格(但没达到优秀)的有17人,则在这次测试中,测试结果不合格人数的频率是()A.0.125B.0.30C.0.45D.1.253.小丽抛一枚硬币10次,其中有6次正面朝上,则反面朝上的频数是()A.6B.0.6C.4D.0.44.将数据83,85,87,89,84,85,86,88,87,90分组,86.5~88.5这组的频数是()A.1B.2C.3D.45.某校九年级随机抽查一部分学生进行了1分钟仰卧起坐次数的测试,并将其绘制成如图所示的频数直方图.那么仰卧起坐次数在25~30次的人数占抽查总人数的百分比是()A.40%B.30%C.20%D.10%6.一组数据共100个,分为6组,第1~4组的频数分别为10,14,16,20,第5组的频率为0.20,则第6组的频数为()A.20B.22C.24D.307.“早发现,早报告,早隔离,早治疗”是我国抗击“新冠肺炎”的宝贵经验,其中“早”字出现的频率是()A.B.C.D.8.有40个数据,共分成6组,第1﹣4组的频数分别是10,5,7,6,第5组的频率为0.10,则第6组的频率为()A.0.25B.0.30C.0.15D.0.209.小文同学统计了他所在小区部分居民每天微信阅读的时间,绘制了直方图.得出了如下结论:①样本中每天阅读微信的时间没人超过1小时,由此可以断定这个小区的居民每天阅读微信时间超过1小时的很少;②样本中每天微信阅读不足20分钟的人数大约占16%;③选取样本的样本容量是60;④估计所有居民每天微信阅读35分钟以上的人数大约占总居民数的一半左右.其中正确的是()A.①②③B.①②④C.①③④D.②③④10.为提高学生的课外阅读水平,我市各中学开展了“我的梦,中国梦”课外阅读活动,某校为了解七年级学生每日课外阅读所用的时间情况,从中随机抽取了部分学生,进行了统计分析,整理并绘制出如图所示的频数分布直方图,有下列说法:①这次调查属于全面调查②这次调查共抽取了200名学生③这次调查阅读所用时间在2.5﹣3h的人数最少④这次调查阅读所用时间在1﹣1.5h的人数占所调查人数的40%,其中正确的有()A.②③④B.①③④C.①②④D.①②③11.某校抽查部分九年级学生1分钟垫球测试成绩(单位:个),将测试成绩分成4组,得到如图不完整的频数直方图(每一组含前一个边界值,不含后一个边界值),已知在120﹣150组别的人数占抽测总人数的40%,则1分钟垫球少于90个的有人.12.生活委员小刚对本班50名学生所穿校服尺码的数据统计如下:尺码S M L XL XXL XXXL 频率0.050.10.20.3250.30.025则该班学生所穿校服尺码为“XXL”的人数个.13.已知一个40个数据的样本,把它分成6组,第一组到第四组的频数分别是10、5、7、13,第五组的频率是0.1,那么第六组的频数是.14.在一个样本容量为80的样本所绘制的频数分布直方图中,第一、二、三、四小组所对应的各个长方形高的比为2:3:4:1,那么第四组的频数是.15.某校对600名男生的身高进行了测量,身高在1.68米~1.73米,这一小组的频率为0.2,则该组共有人.16.在一次体育测试中,10名女生完成仰卧起坐的个数如下:38、52、47、46、50、53、61、72、45、58,则10名女生仰卧起坐个数不少于50个的频率为.17.一组数据共50个,分为6组,第1﹣4组的频数分别是5,7,8,10,第5组的频率是0.20,那么第6组的频数是.18.如图,直方图从左至右各长方形的高的比为2:3:4:6:1,第二组的频数为9,作品总件数为件.19.秋季新学期开学,某中学对初一新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格.现随机抽取了部分学生的成绩制作成如下表格,则b=,c =.分数段频数频率60≤x<706a70≤x<80200.480≤x<9015b90≤x<100c0.1820.在一次生活垃圾分类知识竞赛中,某校七、八年级各有100名学生参加,已知七年级男生成绩的优秀率为40%,女生成绩的优秀率为60%;八年级男生成绩的优秀率为50%,女生成绩的优秀率为70%.对于此次竞赛的成绩,下面有三个推断:①七年级成绩优秀的男生人数小于八年级成绩优秀的男生人数;②七年级学生成绩的优秀率一定小于八年级学生成绩的优秀率;③七、八年级所有男生成绩的优秀率不一定小于七、八年级所有女生成绩的优秀率.所有合理推断的个数是个.21.某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分,请根据图表信息回答下列问题:(1)本次调查的样本容量为.(2)在频数分布表中,a=,b=,并将频数分布直方图补充完整;(3)若视力在4.6以上(含4.6)均属正常,根据上述信息估计全区初中毕业生中视力正常的学生有多少人?视力频数(人)频率4.0≤x<4.3200.14.3≤x<4.6400.24.6≤x<4.9700.354.9≤x<5.2a0.35.2≤x<5.510b22.某公司共有400名销售人员,为了解该公司销售人员某季度商品销售情况,随机抽取部分销售人员该季度的销售数量,并把所得数据整理后绘制成统计图表进行分析.频数分布表组别销售数量(件)频数频率A20≤x<4030.06B40≤x<6070.14C60≤x<8012aD80≤x<100m0.48E100≤x<12040.08合计b1请根据以上信息,解决下列问题:(1)频数分布表中,a=、b=;(2)补全频数分布直方图;(3)如果该季度销量不低于100件的销售人员将被评为“优秀员工”,试估计该季度被评为“优秀员工”的人数.23.某中学的一个数学兴趣小组在本校学生中开展主题为“垃圾分类知多少”的专题调查活动,采取随机抽样的方式进行问卷调查.问卷调查的结果分为A.“非常了解”、B.“比较了解”、C.“基本了解”、D.“不太了解”四个等级,划分等级后的数据整理成如下表格和频数分布直方图.等级频数频率非常了解30b比较了解0.25基本了解1000.5不太了解20合计a1根据以上信息,请回答下列问题:(1)表中a=,b=;(2)请补全频数分布直方图;(3)若该校有学生1800人,请根据调查结果估计这些学生中“不太了解”垃圾分类知识的人数.24.语文教研组为了解我校学生每天课外阅读所用的时间情况,从我校学生中随机抽取了部分学生进行问卷调查,并将结果绘制成如图不完整的频数分布直方图.每天课外阅读时间/h频数频率0<t≤0.5240.5<t≤1360.31<t≤1.50.41.5<t≤212b合计a1根据以上信息,回答下列问题:(1)表中a=,b=;(2)请补全频数分布直方图;(3)我校有学生4800人,请估计我校学生每天课外阅读时间超过1小时的人数.25.某校学生会干部对全校师生倡导的“武汉加油”的自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计图(图中信息不完整).已知A、B两组捐款人数的比为1:5.组别捐款额x(元)人数A1≤x<10aB10≤x<20100C20≤x<30D30≤x<40E40≤x<50请结合以上信息解答下列问题.(1)a=,本次调查样本的容量是;(2)先求出C组的人数,再补全“捐款人数分组统计图1”;(3)根据统计情况,估计该校参加捐款的5000名学生有多少人捐款在20至50元之间.参考答案1.B2.A3.C4.C5.A6.A7.D8.D9.B10.A 11.15.12.15.13.1.14.8.15.120.16.0.6.17.10.18.0.3,9.19.48.20.0.21.解:(1)20÷0.1=200(人),所以本次调查的样本为200名初中毕业生的视力情况,样本容量为200;故答案为:200.(2)a=200×0.3=60,b=10÷200=0.05;补全图形如下:故答案为:60,0.05;(3)5000×(0.35+0.3+0.05)=3500(人),答:估计全区初中毕业生中视力正常的学生有3500人.22.解:(1)b=3÷0.06=50,a=12÷50=0.24,故答案为:0.24,50;(2)m=50×0.48=24,补全频数分布直方图如下:(3)400×0.08=32(人),答:该季度被评为“优秀员工”的人数为32人.23.解:(1)∵被调查的总人数a=100÷0.5=200(人),∴b=30÷200=0.15,故答案为:200,0.15;(2)补全频数分布直方图如下:(3)1800×(1﹣0.15﹣0.25﹣0.5)=180(人).答:估计这些学生中“不太了解”垃圾分类知识的人数为180人.24.解:(1)a=36÷0.3=120,b=12÷120=0.1,故答案为:120,0.1;(2)1<t≤1.5的频数为:120×0.4=48,补全的频数分布直方图如右图所示;(3)4800×(0.4+0.1)=2400(人),即我校学生每天课外阅读时间超过1小时的有2400人.25.解:(1)a=100×=20,本次调查样本的容量是:(100+20)÷(1﹣40%﹣28%﹣8%)=500,故答案为:20,500;(2)500×40%=200,即C组的人数为200,补全“捐款人数分组统计图1”如图所示;(3)5000×(40%+28%+8%)=3800(人),答:该校5000名学生中大约有3800人捐款在20至50元之间。
人教新版七年级下册《10.2直方图》2024年同步练习卷(7)+答案解析
人教新版七年级下册《10.2直方图》2024年同步练习卷(7)一、选择题:本题共5小题,每小题3分,共15分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.一个容量为80的样本,最大值为147,最小值为50,取组距为10,则可以分成()A.10组B.9组C.8组D.7组2.将数据83,85,87,89,84,85,86,88,87,90分组,则这一组的频数是()A.4B.3C.2D.3.如果一组数据共有100个,则通常分成()A.组B.组C.组D.组4.某班统计了该班全体学生60秒内高抬腿的次数,绘制出频数分布表:次数频1241417134数给出以下结论:①组数是6;②组距是20;③全班有55名学生;④高抬腿次数在范围内的学生占全班学生的其中正确结论的个数为()A.1B.2C.3D.45.某次数学测验,抽取部分同学的成绩得分为整数整理制成统计图如图所示,根据图中信息,下列描述不正确的是()A.共抽取了50人B.估计这次测验的及格率分及以上为及格为C.估计80分及以上的人数所占的百分比为D.分这一分数段的频数是12二、填空题:本题共2小题,每小题3分,共6分。
6.某次测验后,分这组人数占全班总人数的,若全班有45人,则该组的频数为______.7.某养猪场对200头生猪的质量进行统计,得到频数直方图每一组含前一个边界值,不含后一个边界值如图所示,其中质量在及以上的生猪有______头.三、解答题:本题共3小题,共24分。
解答应写出文字说明,证明过程或演算步骤。
8.本小题8分为了解某校某年级学生一分钟跳绳情况,对该年级全部360名学生进行一分钟跳绳次数的测试,并把测得数据分成四组,绘制成如图的频数表和未完成的频数分布直方图每一组不含前一个边界值,含后一个边界值某校某年级360名学生一分钟跳绳次数的频数表组别次频数4896a72求a的值;把频数分布直方图补充完整;求该年级一分钟跳绳次数在190次以上的学生数占该年级全部学生数的百分比.9.本小题8分某校七班共有52人,一次英语考试的成绩单位:分如下:938428785769973056998280791007767914289937585958781687059667995486774788139868379626849667981578989859080列出频数分布表,画出频数分布直方图;该班65分及以上和85分及以上的人数所占百分比各是多少?结果精确到10.本小题8分某校在一次历史考试中,随机抽取了九年级班部分学生的成绩单位:分并根据统计结果绘制成了如图所示的两幅不完整的统计图,其中成绩在分的学生人数与成绩在分的学生人数之比为6:请结合图中的信息回答下列问题:本次共抽取学生______人;补全条形统计图;该校九年级学生共有2400人,请你估计成绩在分的人数有多少人.答案和解析1.【答案】A【解析】解:,故可以分成10组.故选:根据组距,最大值、最小值、组数以及样本容量的关系进行计算即可.本题考查频数分布直方表的制作方法,理解组距、组数与样本容量之间的关系是正确解答的关键.2.【答案】B【解析】解:在范围内的有87,88,87,所以这一组的频数为3,故选:一般称落在不同小组中的数据个数为该组的频数,频数与数据总数的比值为频率.本题主要考查了频数与频率,频率是指每个对象出现的次数与总次数的比值或者百分比,即频率=频数总数3.【答案】B【解析】解:数据的分组时,每组的数目不能太多,若太多的组数较少,不能反映数据的分布情况;组数又不能太多,若太多不能反映哪个范围是数值较多,不能正确反映数据的分布.故交合适的是分成组.故选:数据的分组时,每组的数目不能太多,组数又不能太多,若太多不能反映哪个范围是数值较多,都不能正确反映数据的分布.本题考查了数据的分组,数据的分组要根据实际情况进行确定.4.【答案】C【解析】解:①②由频数分布表可知,组距为,组数为7组,故①错误,不符合题意;②正确,符合题意;③全班学生数为人,③正确,符合题意;④跳高抬腿次数在范围内的学生占全班学生的,④正确,符合题意;故选:①②由频率分布表即可知组数和组距;③将各组频数相加即可得;④将范围的两分组频数相加,再将其人数除以总人数即可得百分比.本题考查了频数分布表,频数分布表能够表示出具体数字,知道频率=频数总数和考查根据图表获取信息的能力.5.【答案】D【解析】解:一共调查了人,此选项不符合题意;B.估计这次测验的及格率分及以上为及格为,此选项不符合题意;C.估计80分及以上的人数所占的百分比为,此选项不符合题意;D.分这一分数段的频数无法确定,此选项符合题意;故选:根据频数分布直方图中所反映的数据,利用频率=频数总数进行判断即可.本题考查频数分布直方图,掌握频率=频数总数是正确判断的关键.6.【答案】9【解析】解:由题意得,频数故答案为:根据频率即可求解.本题考查了频数和频率,解答本题的关键是掌握频率7.【答案】140【解析】解:由直方图可得,质量在及以上的生猪:头,故答案为:根据题意和直方图中的数据可以求得质量在及以上的生猪数,本题得以解决.本题考查频数分布直方图,解答本题的关键是明确题意,利用数形结合的思想解答.8.【答案】解:人;补全频数分布直方图如下:,答:该年级一分钟跳绳次数在190次以上的学生数占该年级全部学生数的百分比为【解析】用360减去第1、2、4组的频数和即可;根据以上所求结果即可补全图形;用第4组的频数除以该年级的总人数即可得出答案.本题考查频数率分布直方图,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.9.【答案】解:答案不唯一,合理即可由题知,最大值与最小值的差为,取组距为10,则数据可分为8组,列频数分布表如下,画频数分布直方图如下:分及以上的人数所占百分比;85分及以上的人数所占百分比【解析】根据数据最大值和最小值确定组距及组数,然后列表画图即可;根据中数据分别计算即可.本题主要考查统计的知识,熟练掌握频数分布直方图的画法是解题的关键.10.【答案】解:由题意知,分:人,分:人,分:人补全条形统计图如下:人,答:估计成绩在分的人数有288人.【解析】解:人,故答案为:50;由题意知,分:人,分:人,分:人,补全条形统计图如下:见答案.本题主要考查条形统计图和扇形统计图的知识,结合两种统计图计算各分数段人数是解题的关键.。
统编版高中语文选择性必修下册课时练习题 《归去来兮辞(并序)》(含答案)
第10.2课《归去来兮辞(并序)》课时同步练习班级:姓名:第一部分:文言基础练习1、下列各句中,加点词的解释不正确的一项是()A.生生所资.资:凭借B.悟已往之不谏.谏:谏止,劝止C.策.扶老以流憩策:拐杖D.景.翳翳以将入景:日光2、下列各项中,加点词的意义与现代汉语相同的一项是()A.悦亲戚之情话..B.将有事..于西畴C.既窈窕..以寻壑D.亦崎岖..而经丘3、下列句中,加点词的意义和用法不相同的一项是()A.公田之.利,足以为酒悟已往之.不谏B.诸侯以.惠爱为德农人告余以.春及C.饥冻虽.切,违己交病门虽.设而常关D.于.时风波未静寻程氏妹丧于.武昌4、对下列句子中加点词的活用类型,归类全都正确的一项是()①园日.渉以成趣②携幼.入室③乐琴书..之易安..以消忧④生生.所资⑤审容膝⑥时.矫首而遐观⑦眄庭柯以怡.颜⑧或棹.孤舟⑨倚南窗以寄傲.A.①⑥/②/③④/⑤⑦⑧/⑨B.①⑥/②⑨/③⑧/④⑤/⑦C.①④⑧/②⑤⑥/③⑦/⑨D.①⑦/②④⑤/③⑥/⑧⑨5、下列各项中,与例句句式特点相同的一项是()例句:乐夫天命复奚疑A.既自以心为形役B.问征夫以前路C.胡为乎遑遑欲何之D.遂见用于小邑6、下列各项中,对文化常识理解正确的一项是()A.辞,是介乎诗歌和散文之间的一种文体。
因为起源于战国时的楚国,也叫楚辞、楚辞体。
到了汉代,人们一般将辞、赋并称。
这种文体,富有抒情的浪漫色彩,很像诗,但是押韵和句式比较自由。
B.毛泽东有诗云“陶令不知何处去,桃花源里可耕田”,这里的“陶令”就是陶渊明,因为他做过八十余天的彭泽县令,故以陶令相称。
C.三径,指古代归隐者的家园或是院子里的小路,是古代隐士住处的代称。
“三径就荒”中的“三径”即为此意。
D.古人纪月日,除了用序数,还用一些特殊的称谓。
如把四季中每个季节的月份冠以“孟”“仲““季”,以示区分。
“仲秋至冬,在官八十余日”中的“仲秋”即指阳历八月。
7、补写出下列句子中的空缺部分。
课时提升作业(三十) 10.2
圆学子梦想 铸金字品牌 - 1 - 温馨提示: 此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。关闭Word文档返回原板块。 课时提升作业(三十)
直 方 图 (30分钟 50分) 一、选择题(每小题4分,共12分) 1.某校为了了解学生在校午餐所需的时间,抽取了20名同学在校午餐所需的时间,获得如下的数据(单位:min):10,12,15,10,16,18,19,18,20,28,22,25,20, 18,18,20,15,16,21,16.若将这些数据以4min为组距进行分组,则组数是( ) A.4 B.5 C.6 D.7 【解析】选B.(28-10)÷4=4.5,所以组数为5. 【易错提醒】根据组数=(最大值-最小值)÷组距计算,注意小数部分要进位. 2.在频数分布直方图中,有11个小长方形,若中间一个小长方形的高等于其他10个小长方形高的和的,且数据有160个,则中间一组的频数为( ) A.32 B.35 C.40 D.45 【解析】选A.由题意得中间一组的频数为总数据的,即160×=32. 3.(2014·武汉模拟)七年级有2000名学生参加“趣味数学竞赛”活动,从中抽取了若干名学生的得分进行统计,整理出下列不完整的表格和扇形图. 圆学子梦想 铸金字品牌
- 2 - 成绩x(分) 频数(人) 50≤x<60 10 60≤x<70 70≤x<80 80≤x<90 90≤x<100 50 若90分以上(含90分)的学生可获得一等奖;70分以上(含70分),90以下的学生可获得二等奖;其余学生可获得鼓励奖.根据统计图表中的数据,估计本次活动中,七年级学生获得二等奖的人数大约有( ) A.1 200人 B.120人 C.60人 D.600人 【解题指南】1.根据图表和扇形图先求出抽取的学生数. 2.再根据频数、频率之间的关系求出80≤x<90被抽查的人数、90≤x<100所占的百分比和70≤x<80的频数,然后用七年级参加“趣味数学竞赛”活动的总人数乘以二等奖的人数所占的百分比,即可得出答案. 【解析】选A.根据图表和扇形图得: 抽取的学生数是:=200(人), 80≤x<90被抽查的人数是:200×30%=60(人), 90≤x<100所占的百分比是:×100%=25%, 70≤x<80的频数是:200×(1-5%-10%-30%-25%)=60(人), 则七年级学生获得二等奖的人数大约有×2000=1200(人). 二、填空题(每小题4分,共12分) 4.八年级(1)班全体学生参加了学校举办的安全知识竞赛,如图是该班学生竞赛圆学子梦想 铸金字品牌 - 3 - 成绩的频数分布直方图(满分为100分,成绩均为整数),若将成绩不低于90分的评为优秀,则该班这次成绩达到优秀的人数占全班人数的百分比是 .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
温馨提示:此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。
关闭Word文档返回原板块。
45分钟课时检测练100分第2课时中和反应和pH一、选择题(本题包括10小题,每小题4分,共40分)1.生活中某些物质的pH近似为西瓜汁5.8、苹果汁3.1、泡菜3.4、鸡蛋清7.6,其中酸性最强的是( )A.苹果汁B.泡菜C.西瓜汁D.鸡蛋清【解析】选A。
pH<7的物质显酸性,数值越小,酸性越强,pH>7的物质显碱性,数值越大,碱性越强,由此确定苹果汁的酸性最强。
2.中和反应在日常生产和生活中有广泛的用途。
下列做法应用了中和反应的是( )A.用生石灰作食品干燥剂B.用熟石灰处理工厂污水中的硫酸C.用碳酸氢钠和柠檬酸等原料自制汽水D.用熟石灰与硫酸铜溶液来配制农药波尔多液【解析】选B。
A.生石灰作干燥剂是利用氧化钙与水的反应,不是酸与碱的反应,故此选项错误;B.用熟石灰处理工厂污水中的硫酸,是氢氧化钙与硫酸的反应,故此选项正确;C.用碳酸氢钠和柠檬酸等原料自制汽水,是利用盐与酸的反应,不是中和反应,故此选项错误;D.用熟石灰与硫酸铜溶液配制波尔多液是利用碱与盐的反应,不是中和反应,故此选项错误。
3.(2015·甘肃兰州模拟)“接叶连枝千万绿,一花两色浅深红”是对玫瑰花生动的写照。
我市苦水玫瑰远近闻名,某同学用“玫瑰花瓣”的汁液自制酸碱指示剂,有关记录如下表:向滴有少量该指示剂的NaOH溶液中逐渐滴加稀盐酸至过量,颜色变化是( )A.由浅红色变红色B.由棕黄色变浅红色C.由浅红色变棕黄色D.由红色变棕黄色【解析】选B。
该指示剂在碱性溶液中呈棕黄色,在酸性溶液中呈浅红色,所以向滴有少量该指示剂的NaOH溶液中逐渐滴加稀盐酸至过量,颜色变化是由棕黄色变浅红色。
4.常温下,下列说法错误的是( )A.pH=2的溶液显酸性B.pH=7的溶液显中性C.溶液的pH由5变成2,其酸性减弱D.pH>10的土壤不适于种植农作物,因为碱性太强【解析】选C。
常温下,pH=7时,溶液显中性;pH>7时,溶液显碱性,且pH数值越大,溶液碱性越强;pH<7时,溶液显酸性,pH数值越小,溶液酸性越大;植物一般生长在pH大约在6.5~7.5的土壤中,酸性太强或碱性太强均不适合植物生长。
5.下列各组物质的反应,需要加入酸碱指示剂才能判断反应是否发生的是( )A.Fe和硫酸铜溶液B.Zn和稀硫酸C.氢氧化钠溶液和稀盐酸D.澄清石灰水和二氧化碳【解析】选C。
A中铁的表面和溶液颜色均会发生变化;B中会产生气泡;C中两者虽然会发生化学反应,但由于生成物溶于水,故没有明显现象产生,可根据加入的指示剂颜色的变化,确定该反应是否发生;D中会出现浑浊现象。
6.下表是生活中一些物质的pH:有关它们的说法中正确的是( )A.牛奶的酸性比橘子汁强B.用湿润的pH试纸蘸取厕所清洁剂测其pHC.草木灰水显酸性D.橘子汁能使紫色石蕊溶液变色【解析】选D。
本题考查对酸碱度的认知应用能力。
pH小于7溶液显酸性,pH越小酸性越强,所以牛奶的酸性比橘子汁的酸性弱;测定溶液的pH时,pH试纸不能润湿,否则相当于将原溶液稀释,所测溶液的pH将改变;草木灰水的pH大于7,显碱性;橘子汁显酸性,能使紫色石蕊溶液变红色。
7.如图是稀HCl和NaOH溶液反应的pH变化曲线图,据图分析能得出的结论正确的是( )A.该反应是NaOH溶液滴入稀盐酸中B.a克是指加入NaOH溶液的质量C.A点时,溶液的溶质为NaOH、NaClD.B点表示稀盐酸和加入NaOH溶液质量一定相同【解析】选C。
开始时溶液的pH大于7,溶液呈碱性,故是将稀盐酸滴入氢氧化钠溶液中,A错误;横坐标表示加入盐酸的量,B错误;A点溶液呈碱性,溶液中的溶质有氯化钠和氢氧化钠两种物质,C正确;B点表示氢氧化钠与盐酸恰好完全反应,此时所加的盐酸与氢氧化钠的质量不一定相等,D错误。
8.(2015·辽宁营口模拟)某工厂排放的废水中含有硫酸,原来采用氢氧化钠溶液处理,使最终排出的溶液呈中性(如下图)。
现改用溶质质量分数与原来氢氧化钠溶液的溶质质量分数相同的氢氧化钾溶液处理,在废水流量不变的情况下,碱液的流量阀应做的调节为( )A.保持不变B.加大流量C.减小流量D.无法确定【解析】选B。
根据两个化学方程式中酸与碱的质量比来看:2NaOH+H2SO4Na2SO4+2H2O80 982KOH+H2SO4K2SO4+2H2O112 98中和等质量的H2SO4需要KOH的质量大于NaOH的质量,故改用KOH溶液后应调大碱液的流量。
9.如图所示,烧杯中有10 mL氢氧化钠溶液,滴入几滴酚酞,溶液瞬间变红。
某学生用滴管慢慢滴入稀盐酸,并不断搅拌至完全反应。
下列说法不正确的是( )A.反应后溶液红色褪去B.反应后溶液可导电C.反应后氢氧化钠溶液pH变小D.反应后溶液中Na+数目减小【解析】选D。
向滴有酚酞的氢氧化钠溶液中不断滴加盐酸,氢氧化钠溶液的碱性越来越弱,因此其pH逐渐变小,故C正确;向滴有酚酞的氢氧化钠溶液中不断滴加盐酸当恰好完全反应时,溶液呈中性,若继续滴加盐酸,溶液呈酸性,故溶液由红色变为无色,故A正确;反应后溶液中仍然存在自由移动的氯离子、钠离子,因此反应后溶液导电,故B正确;氢氧化钠与盐酸发生中和反应的实质是氢离子和氢氧根离子反应生成水,而对于氯离子、钠离子没有影响,因此钠离子反应后数目不变,故D错误。
【备选习题】(2015·重庆岩口复兴学校模拟)如图是酸与碱溶液反应的示意图,下列关于酸碱反应说法正确的是( )A.酸碱中和反应的实质是H++ OH-H2OB.生成盐和水的反应,都是中和反应C.当酸碱完全中和时,两者所用质量一定相等D.当酸碱完全中和时,所得盐溶液pH等于0【解析】选A。
酸碱中和反应的实质是酸中的H+与碱中OH-结合生成H2O,A说法正确;只有酸与碱生成盐和水的反应才属于中和反应,B说法不正确;当酸碱完全中和时,两者所用质量不一定相等,C说法不正确;当酸碱完全中和时,所得盐溶液pH等于7,D说法不正确。
10.(2015·北京朝阳区一模)向一定量的氢氧化钠溶液中逐滴加入pH=2的稀盐酸至过量。
下列图象中,能正确反映对应变化关系的是( )【解析】选D。
由于稀盐酸中含有一定量的水,所以随着不断滴加稀盐酸,溶液中水的量应不断增大,A不正确;由于加入pH=2的稀盐酸,最后溶液的pH应大于2,B不正确;完全反应后,生成的氯化钠的质量不变,但由于随着不断滴加稀盐酸,混合溶液的质量不断增加,氯化钠的质量分数也会不断减小,C 不正确;随着不断加酸,溶液中氢氧化钠的质量逐渐减小,质量分数也不断减小,完全反应后,氢氧化钠的质量分数为零,D 正确。
二、填空与简答题(本题包括4小题,共30分)11.(6分)某校同学开展了如下“溶液酸碱性的检验”的实验活动:(1)把自制的紫色紫薯汁按图1所示分别滴加到试管中,观察到的现象如下表所示:①图1中存放紫薯汁的仪器名称为 ;②据上表推测,紫薯汁能作酸碱指示剂,遇到稀硫酸溶液可能显示的颜色是 ;(2)用pH 试纸测定图1中部分溶液的酸碱度:草木灰水pH>7,属于(填“酸性”“中性”或“碱性”)溶液,白醋pH (填“>”“<”或“=”)7;(3)图2是三位同学分别测定土壤酸碱度的操作示意图,其中正确的是(填“A”“B”或“C”,下同),可能导致被测溶液pH数值发生改变的错误操作是。
【解析】(1)由图可知仪器的名称是滴瓶;由表格可知紫薯汁遇酸变红,故遇到稀硫酸显示的颜色也是红色。
(2)溶液pH<7为酸性,pH>7为碱性。
(3)根据pH测量方法可知B是正确的,C操作中溶液被稀释,所以pH数值会发生变化。
答案:(1)①滴瓶②红色(2)碱性<(3)B C12.(8分)(2015·河北模拟)如图所示的三个实验均可验证酸与碱能发生反应:(1)根据实验一回答:①加稀盐酸前,一定能观察到的实验现象是 ;②该实验通过稀盐酸与反应的现象,验证了酸与碱能发生反应。
(2)实验二通过对比两支试管中的现象,可以判断稀盐酸与Ca(OH)2能反应,该实验除需控制所加水和稀盐酸的温度、体积相同外,还需控制相同。
(3)实验三中,加入X可验证稀硫酸与碱能发生反应,符合此条件的X是下列物质中的。
A.酚酞B.CuOC.Na2CO3D.Ba(NO3)2【解析】(1)氢氧化钠与硫酸铜反应生成氢氧化铜蓝色沉淀,加入酸后氢氧化铜逐渐消失,溶液变为蓝色,推测酸与碱发生了化学反应;(2)由控制变量法分析,本实验中除了水和稀盐酸的种类不同外,其他各量必须保持相同,水和稀盐酸的温度、体积相同,还需控制氢氧化钙粉末的质量相同;(3)在碱中加入过量的酸后,溶液显酸性,再加入酚酞后溶液仍为无色,说明碱已经不存在了,进而证明了酸与碱确实发生了反应;如果H2SO4和NaOH没有反应,那么加入CuO后,CuO和H2SO4反应生成CuSO4,CuSO4会继续和NaOH反应生成Cu(OH)2蓝色沉淀,如果NaOH已反应掉,则不会有蓝色沉淀产生;由于硫酸是过量的,不管H2SO4和NaOH有没有发生反应,加入Na2CO3都会有气泡产生,加入Ba(NO3)2都会有白色沉淀产生。
答案:(1)①产生蓝色沉淀②氢氧化铜(2)氢氧化钙粉末的质量(3)A、B13.(8分)向盛有10 mL NaOH溶液(其中滴有少量无色酚酞溶液)的烧杯中逐滴加入稀盐酸,用pH计(用来精确测定溶液pH的仪器)测定溶液的pH,所得数据如下:(1)当加入稀盐酸的体积为mL时,NaOH溶液和稀盐酸恰好完全反应。
(2)当加入稀盐酸的体积为3 mL时,溶液显色;当加入稀盐酸的体积为14 mL时,溶液显色。
(3)当烧杯中溶液的pH=2.1时,溶液中的溶质有:。
【解析】本题考查学生对中和反应的认识和对表格数据的分析能力。
由表中数据可知:当加入10 mL稀盐酸时,溶液呈中性,酸碱恰好反应;当加入3 mL稀盐酸时,溶液显碱性,溶液显红色;当加入14 mL稀盐酸时,溶液显酸性,溶液为无色;当加入12 mL稀盐酸时,pH=2.1,盐酸过量,此时溶液中含有氯化钠和氯化氢。
答案:(1)10(2)红无(3)氯化钠和氯化氢14.(8分)(2015·上海松江区月考)将X溶液逐滴滴入Y溶液中,在滴加过程中,Y 溶液的pH变化情况如图所示。
(1)表格中符合这种变化情况的是(填写编号)组,理由是。
(2)处于图中m点时,溶液中的溶质为。
【解析】(1)结合函数图象可知开始溶液的pH小于7,最后溶液的pH大于7,应该是向酸中加碱,所以只有C符合;(2)m点时溶液呈酸性,溶液中的溶质为生成的CaCl2与剩余盐酸中的溶质HCl。
