2016第四章狭义相对论
大学物理学-狭义相对论教案

授课章节第4章 狭义相对论教学目的1. 理解爱因斯坦狭义相对论的两条基本原理及洛伦兹坐标、速度变换式;2. 掌握狭义相对论的时空观:即理解同时的相对性、长度的收缩和时间的膨胀,并能进行相关的计算;3. 了解狭义相对论动力学的几个结论及其具体应用。
教学重点、难点1. 正确地理解相对论的时空观;2. 掌握洛伦兹变换的物理意义;3. 理解长度收缩效应只发生在运动方向上;4. 理解“时间膨胀”效应是指运动着的钟比静止的钟慢;5. 在相对论动力学中,动能不能用221mv 进行计算,只能用202c m mc E K -=进行计算;6. 在经典物理中能量守恒律与质量守恒律彼此独立。
而在相对论中通过质能关系式把两个定律统一起来了。
即在相对论中能量守恒与质量守恒总是同时成立的。
教学内容 备注第四章 狭义相对论相对论研究的内容:研究物质的运动与空间、时间的联系。
狭义相对论:研究自然定律在所有惯性系中都表示为相同的形式(数学)问题。
广义相对论:研究自然定律在所有参照系中都表示为相同的形式(数学)问题。
§4.1 伽利略变换和经典力学时空观一、伽利略变换 经典力学时空观1、伽利略坐标变换方程:如图,两个参照系的坐标轴互相平行,参照系S '相对于参照系S 沿x 轴的正方向以速度u 运动,时间0='=t t 时、两坐标系的原点o 和o '重合。
则某一空—时点的坐标变换方程为tt zz y y utx x ='='='-=' 或 t t z z y y t u x x '='='='+'= (1)2、经典力学时空观伽利略坐标变换方程已经对时间、空间性质作了两条假设:(1)t t'=,t t '∆=∆,即时间间隔与参考系的运动状态无关;(2)L L '∆=∆,即空间长度与参考系的运动状态无关。
(同时测量棒两端点的坐标值),总之,时间和空间是彼此独立的,互不相关,并且不受物质和运动的影响,这就是经典力学的时空观,也称绝对时空观。
狭义相对论知识点总结

dP dt
d (mv) dt
d dt
(
m0 v)
1 2
5、相对论的动量与能量的关系
E2 m2c4 p2c2 E02
x x vt
1 (v)2
逆
c y y
变
z z
换
t
t
v c2
x
1 (v)2
c
ux
dx dt
ux
1
v c2
v ux
速 度 正 变
uy
dy dt
uy
1
v c2
ux
1 2
换
uz
dz dt
uz
1
v c2
ux
1 2
三、狭义相对论时空观
四、狭义相对论动力学基础
1、相对论质量:
m m0
1
v2 c2
m0—静止质量
2、相对论动量: P mv m0 v 1 v2 / c2
3、相对论能量:
静能: E 0 m 0 c 2 总能量:E m c 2 动能: Ek mc2 m0c2
4、狭义相对论力学的基本方程
F
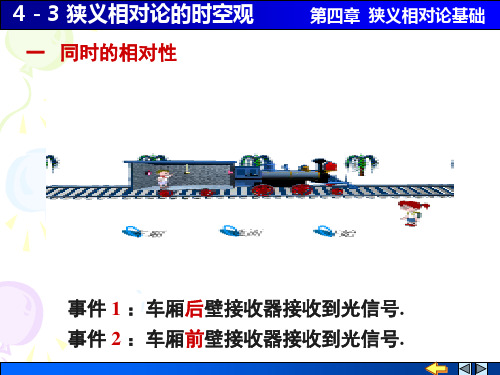
1、同时的相对性
只有在一个惯性系中同时同地发生的事件,在其它惯性 系中必同时发生.
2、长度的收缩
l l0
1
v2 c2
固有长度(原长): 相对物体静止的惯性系 测得长度.
注意:测量长度一定是同时读取两端坐标取差。
3、时间的延缓
t
tt发生的两事件 的时间间隔 .
狭义相对论知识点总结
一、狭义相对论的两个基本假设 1、爱因斯坦相对性原理
第4章 狭义相对论
第4章 狭义相对论一、基本要求1.掌握运动时间延缓和运动长度收缩原理; 2.理解质速关系和质能关系。
二、基本内容(一)本章重点和难点:重点:狭义相对论时空观中运动时间延缓和运动长度收缩。
难点:相对论动力学中质能关系。
(二)知识网络结构图:⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎩⎨⎧=⎩⎨⎧⎩⎨⎧)(2mc (E )质能关系运动质量变大质速关系相对论动力学运动长度收缩运动时间延缓相对论运动学光速不变原理爱因斯坦相对性原理基本原理(三)容易混淆的概念: 1.静止长度和运动长度静止长度0l ,也称固有长度,即观察者和被测物体在同一参照系所测长度;运动长度l ,即观察者和被测物体不在同一参照系所测长度。
2. 静止时间和运动时间静止时间0τ,也称固有时,即观察者和被测事件在同一参照系所测时间;运动时间τ,即观察者和被测事件不在同一参照系所测时间。
3.总能量、静能量和动能总能量E 由爱因斯坦质能关系式,等于动质量和光速的平方的乘积;静能量0E 等于静质量和光速的平方的乘积;动能k E 即总能量与静能量之差。
(四)主要内容:1.经典力学的相对性原理:一切彼此相对作匀速直线运动的诸惯性系中的力学规律是一样的。
即力学规律的数学形式都是相同的。
2.狭义相对论基本原理:(1)爱因斯坦相对性原理:物理定律在所有惯性参考系内都是等价的。
(2)光速不变原理:在所有惯性系中,光在真空中的速度恒等于c 。
3.洛伦兹变换:若S S 、'分别为两惯性系,S 系相对S '系以v 沿x 轴运动,在0='=t t 时两系重合,则一质点(或一事件)在S 系中的时空坐标(x 、y 、z 、t )与在S '系中的时空坐标(x '、y '、z '、t ')之间的关系为洛伦兹时空变换。
(1)洛伦兹时空变换同一事件在S 系中时空坐标(x 、y 、z 、t )与在S '系中的时空坐标(x '、y '、z '、t ')之间的关系为:⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧='='--='--='z z y y c v vt x x c v x c v t t 222)(1)(1逆变换为:⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧'='=-+'=-+=z z y y c v vtx x c v x c v t t 222)(1)(1(2)洛伦兹速度变换某质点相对于S 系速度u ,与相对S '系速度u '之间的关系为:PcE 021c vu v u u x x x--=';221)(1c v u c v u u x y y --=';221)(1c v u cvu u x z z --='逆变换为:21c vu v u u x xx '++'=;221)(1c v u c v u u x y y '+-'=;221)(1c v u c v u u x z z '+-'=4.狭义相对论时空观:(为简化公式,可令:22221,11c v cv -=-=βγ) (1)运动时间延缓公式:2201c v -=ττ其中:0τ为静止时间,也称固有时,即观察者和被测事件在同一参照系所测时间;τ为运动时间,即观察者和被测事件不在同一参照系所测时间。
大学物理第4章 狭义相对论时空观习题解答改

习 题4-1 一辆高速车以0.8c 的速率运动。
地上有一系列的同步钟,当经过地面上的一台钟时,驾驶员注意到它的指针在0=t ,她即刻把自己的钟拨到0'=t 。
行驶了一段距离后,她自己的钟指到6 us 时,驾驶员瞧地面上另一台钟。
问这个钟的读数就是多少? 【解】s)(10)/8.0(16/12220μ=-μ=-∆=∆c c s cu t t所以地面上第二个钟的读数为)(10's t t t μ=∆+=4-2 在某惯性参考系S 中,两事件发生在同一地点而时间间隔为4 s,另一惯性参考系S′ 以速度c u 6.0=相对于S 系运动,问在S′ 系中测得的两个事件的时间间隔与空间间隔各就是多少?【解】已知原时(s)4=∆t ,则测时(s)56.014/1'222=-=-∆=∆s cu t t由洛伦兹坐标变换22/1'c u ut x x --=,得:)(100.9/1/1/1'''8222220221012m c u t u c u ut x c u ut x x x x ⨯=-∆=-----=-=∆4-3 S 系中测得两个事件的时空坐标就是x 1=6×104 m,y 1=z 1=0,t 1=2×10-4 s 与x 2=12×104 m,y 2=z 2=0,t 2=1×10-4 s 。
如果S′ 系测得这两个事件同时发生,则S′ 系相对于S 系的速度u 就是多少?S′ 系测得这两个事件的空间间隔就是多少? 【解】(m)1064⨯=∆x ,0=∆=∆z y ,(s)1014-⨯-=∆t ,0'=∆t0)('2=∆-∆γ=∆cxu t t 2cxu t ∆=∆⇒ (m/s)105.182⨯-=∆∆=⇒x t c u (m )102.5)('4⨯=∆-∆γ=∆t u x x4-4 一列车与山底隧道静止时等长。
4-3 狭义相对论的时空观
6
2
12 x' x 9 3
6
S 系 ( 地面参考系 ) S' 系 (车厢参考系 )
事件 1 (x1, y1, z1,t1) (x'1 , y'1 , z'1 ,t'1 )
事件 2 (x2 , y2 , z2 ,t2 ) (x'2 , y'2 , z'2 ,t'2 )
同时 不同地
t' t'2 t'1 0
当 v c时 l l0 .
4 - 3 狭义相对论的时空观
第四章 狭义相对论基础
例2 设想有一光子火箭, 相对于地球以速率
v 0.95c 飞行,若以火箭为参考系测得火箭长度为
15 m,问以地球为参考系,此火箭有多长?
y y'
l0 15m
o o'
s'
v x' s
x
火箭参照系 地面参照系
解 :固有长度
S系(宇航员)观察,船身通过观测站的时间间隔为
t
x v
l0 v
3.75107 s
是否是原时?
S系(观测站): x1 x2 x
同一地点!
t t 1 (v)2 c
( t 为原时)
t t 1 ( v)2 2.25107 s c
4 - 3 狭义相对论的时空观
第四章 狭义相对论基础
方法三:洛仑兹变换
固有长度:物体相对静止时所测得的长度 .(最长)
4 - 3 狭义相对论的时空观
第四章 狭义相对论基础
注意
长度缩短纯粹是一种相对论效应,与物体内部结 构无关 . 长度测量值与被测物体相对于观测者的运动有关, 相对静止时最长 .
狭义相对论讲义课件

04
狭义相对论的时空观
同时性的相对性
01
同时性的相对性是狭义相对论 中的一个基本概念,指的是观 察者在不同参考系中观察到的 事件发生顺序可能会不同。
02
在相对论中,两个事件在不同 的参考系中同时发生,并不意 味着它们在所有参考系中都是 同时发生的。
狭义相对论的基本原理
相对性原理
物理规律在所有惯性参考系中形 式都保持不变。
光速不变原理
光在真空中的速度在所有惯性参 考系中都是相同的,约为每秒 299,792,458米。
02
洛伦兹变换
洛伦兹变换的定义
洛伦兹变换是用来描述不同惯性参考系之间坐 标和时间的变换。
在狭义相对论中,所有惯性参考系都是等价的 ,因此可以通过洛伦兹变换将一个惯性参考系 中的事件变换到另一个惯性参考系中。
3
通过洛伦兹变换,我们可以更好地理解狭义相对 论中的基本原理和概念,从而更深入地了解这个 理论。
03
光速不变原理
光速不变原理的表述
光速不变原理是狭义相对论的基本假设之一,它指出在任何惯性参考系中,真空 中光的传播速度都是恒定不变的,约为每秒299,792,458米。
光速不变原理可以表述为:无论观察者的运动状态如何,光的速度在真空中总是 相同的。
狭义相对论的质量和能量 质量与能量的关系
质量和能量是等价的:在狭义相对论中,质量和能量被视 为同一事物的两个方面,它们之间可以相互转换。
核能释放:核反应过程中,原子核中的质量会转化为能量 释放出来。
质能方程E=mc²:该方程表达了质量和能量之间的关系 ,其中E代表能量,m代表质量,c代表光速。
狭义相对论原文
狭义相对论原文
【实用版】
目录
1.狭义相对论的概述
2.狭义相对论的基本原理
3.狭义相对论的数学表达式
4.狭义相对论的实际应用
正文
【1.狭义相对论的概述】
狭义相对论,是爱因斯坦于 1905 年提出的一种物理学理论。
这一理论的基本思想是,物理定律的形式必须在所有惯性参考系中相同。
换句话说,如果我们在两个不同的运动状态下观察同一事件,那么我们得到的物理定律应该是一致的。
【2.狭义相对论的基本原理】
狭义相对论有两个基本原理,分别是相对性原理和光速不变原理。
相对性原理:所有惯性参考系中,物理定律的形式是相同的。
光速不变原理:在任何惯性参考系中,光在真空中的传播速度都是一个常数,约为每秒 3*10^8 米,通常用字母 c 表示。
【3.狭义相对论的数学表达式】
狭义相对论的数学表达式主要包括洛伦兹变换和时间膨胀公式。
洛伦兹变换:描述在两个不同运动状态下,空间和时间如何相互转换的公式。
时间膨胀公式:描述在高速运动状态下,时间如何变慢的公式。
【4.狭义相对论的实际应用】
狭义相对论虽然主要研究的是高速运动物体的性质,但是其影响已经深入到我们的日常生活中。
例如,GPS 定位系统就需要考虑狭义相对论的效应,因为卫星的运行速度非常快,而地面的观察者速度相对较慢。
如果不考虑狭义相对论,GPS 定位的误差会非常大。
此外,狭义相对论还揭示了质量和能量的等价性,为核能的研究和利用提供了理论基础。
第四章 狭义相对论
大学物理学
第四章 狭义相对论
4.1 伽利略变换和经典力学时空观 4.2 狭义相对论的基本原理 洛仑兹变换 4.3 狭义相对论的时空观 4.4 狭义相对论动力学
2
大学物理学
第四章 狭义相对论
4.1 伽利略变换和经典力学时空观
一、伽利略变换
u
1. 伽利略坐标变换
y y'
K' 系相对于 K 系沿 x 轴匀速 运动,当 t = t' = 0 时, O 与
在 S' 系中看来:
事件 1 发生的位置 x1' ( x1 u t1 ) 事件 2 发生的位置 x2' ( x2 u t2 )
所以有 x' (x ut)
由Δt = 0,则有
x'
u2
x
x' 1 c2
18
大学物理学
l l0
1
u2 c2
第四章 狭义相对论
物体在运动方向上的长度收缩 为固有长度的γ分之一。
——长度收缩效应
注意 ① l < l0 长度沿着运动方向收缩了。
② 若把尺子静止放置在 S 系,在 S' 系测量尺 子的长度,同样出现长度收缩效应。
③ 空间长度具有相对意义。
19
大学物理学
第四章 狭义相对论
例4.1 一火箭相对地球以速率 u = 0.6 c 做直线 运动,以火箭为参考系测得火箭长度为 15m, 则以地球为参考系测得的火箭长度是多少?若 火箭相对地球运动的速率为 u = 0.995 c,问在 地球上测得的火箭长度又是多少?
p
ud p
0
pu
u
u
d( pu) pdu pu
4.1狭义相对论基本原理
近代物理学的两朵乌云
19世纪的最后一天,欧洲著名的科学家欢 聚一堂。英国著名物理学家W.汤姆孙 William Thomson (即开尔文勋爵)发表 了新年祝词。他在回顾物理学所取得的伟 大成就时说,物理大厦已经落成,所剩只 是一些修饰工作。
一切力学现象原则上都能够从经典力学得到解释,对于电 磁现象,已形成麦克斯韦电磁场理论,这种理论还可用来 阐述波动光学的基本问题。热现象,有了唯象热力学和统 计力学的理论。以经典力学、经典电磁场理论和经典统计 力学为三大支柱的经典物理大厦已经建成,而且基础牢固, 宏伟壮观
Albert Einstein ( 1879 – 1955 )
20世纪最伟大的物理学家, 于 1905年和1915年先后创立了狭义相 对论和广义相对论, 他于1905年提 出了光量子假设, 为此他于1921年 获得诺贝尔物理学奖, 他还在量子 理论方面作出很多的重要的贡献 .
爱因斯坦的哲学观念:自然 界应当是和谐而简单的.
在日常生活中时间延缓和长度收缩是完全可以忽
略的, 但运动速度接近光速时, 这两种效应就变得非
常重要, 在高能物理的领域里得到大量的实验证实.
例1 设想有一光子火箭以 v 0.95c 速率相
对地球作直线运动 ,若火箭上宇航员的计时器记录 他观测星云用去 10 min , 则地球上的观察者测得此 事用去多少时间 ?
“设以地太球”(光速源度和:干涉u仪)相对于
光相对于“以太”的速度: c
光相对 于地 球的 速度:v vc u
大小随 c 的方向而变化
M1 u 以太风
S
M
M2
T
实验原理图
c u
v
v cu
c u vcu
2 - 第四章狭义相对论简介
今天来时空观及时空与物质关系的理论。 (所谓经典力学遇到障碍就是经典力学的 时空观出现了问题,相对论从根本上改变 了经典的时空观。) 相对论有狭义相对论广义相对论之分:
狭义相对论(special relativity) 关于惯性系时空观的理论;
广义相对论(General relativity) 关于一般参照系及引力的理论;
因为这意味着经典物理学出了问题,意味着什 么绝对时间、绝对空间、伽利略变换等等都是胡 言乱语。就像一朵乌云一样遮住了物理学晴朗的 天空。
一部分人感到沮丧,我们顶礼模拜的牛顿 定律尽然不灵了,这…岂不是科学的毁灭吗!
有一部分人不相信实验的真实性,继续改进实验 设备作实验。而且春天作了夏天作,秋天作了冬 天作;平地作了高山作…实验精度越来越高,能 作实验的人越来越多,乃至几乎每个大学都能作, 但结果仍然一样,地球上的光速与地球速度无关。
媒质密度决定。
u
B
如声波在空气中传播
传
播。C
G
C很大,故“以太”
应比钢还硬且星体在
其中运动时要畅行无
2阻)。C是相对“以太”
2)波速是相对于和 参照系的速度
静止媒质保持相对静 “以太”是宇宙间的 止的参照系的波速。 绝对静止参照 系。
按照以上分析,Maxwell方程只对绝对静止 的“以太”参照系成立,并且依照“GT”,在 不同的参照系中应测出不同的光速。这意味着 宇宙间存在一特殊的参照系---以太参照系,在 这个参照系中光速是C,其它惯性系中将测出不 同的光速。
§17-2 爱因斯坦假设 洛仑兹坐标变换
一、狭义相对论的两条基本原理
1)相对性原理:一切物理学定律对一切惯性系 参照系都是等价的。
2)光速不变原理----真空中的光速相对任何 惯性系,沿任意方向恒为C,且与光源的运 动状态无关。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
论 过渡到经典力学.经典力学是相对论力学的一种特
例或近似.
3
§4.1 伽利略变换 经典力学的时空观
普
通
物 狭义相对论和广义相对论
理
教 程
狭义相对论是关于高速情况下的时空观理论;
广义相对论是关于引力和时空结构的理论.
狭义相对论适用于一切惯性参考系,而广义
第 四
相对论适用于一切参考系.
章
相对论和时空观
伽利略坐标变换
当u c 变换无意义 速度有极限
12
普
通
物
理 教
作业: 普通物理教程(上):
程
习题4 P97
第 四
三、计算题
章
狭
2 、3 、6
义
相
对
论
13
普 §4.3 狭义相对论的时空观
通 物
理 4.3.1 同时性的相对性
教
程 在牛顿力学中,时间是绝对的。如两事
件在S系中被同时观察到,那么在S′中也是
普 通 物 理 教 程
第四章 狭义相对论
北京建筑工程学院 理学院 应用物理系
1
第四章 狭义相对论
普
通
物
理
教 程
§4.1
伽利略变换
经典力学的时空观
§4.2 狭义相对论的基本原理 洛伦兹变换
第
四 §4.3 狭义相对论的时空观
章
狭 §4.4 狭义相对论动力学基础
义 相 对 论
2
§4.1 伽利略变换 经典力学的时空观
15
普 §4.3 狭义相对论的时空观
通
物 理
设 S系中x1、x2两处发生两事件,时间
教 程
间隔为Δt t2 t1 .问 S′系中这两事件
发生的时间间隔是多少?
第 S 系 ( 地面参考系 )
四
章 狭
y'
v
义
1
事件 1
2 事件 2
(x1, y1, z1,t1) (x2 , y2 , z2 ,t2 )
第
变 换
z z
四 章
t t
逆 y y
变 换
z z
t t
狭 伽利略速度变换
义
相x vy
u
换 vz vz
逆 变
v v
x y
vx u vy
换 vz vz
6
§4.1 伽利略变换 经典力学的时空观
普
通
物 理
经典的时空观
教 程
① 时间和空间是独立存在;
② 同时是绝对的;
第 同时观察到的。但在狭义相对论中,一般来
四 章
说就不再是同时的了。这是光速不变原理的
直接结果
狭
义
相
以爱因斯坦火车为例
对
论
Einstein train
14
普 §4.3 狭义相对论的时空观
通 物 理 教 程
第 四 章
狭
义
相
对 论
事件 1 :车厢后壁接收器接收到光信号.
事件 2 :车厢前壁接收器接收到光信号.
相
对 论
o' 12
9
3
6
12 x'
9
3
6
Δt t2 t1
16
普 §4.3 狭义相对论的时空观
通 物 理
S' 系 (车厢参考系 ) y y'
v
教
程 第
(x'1 , y'1 , z'1 ,t'1 )
1
(x'2 , y'2 , z'2 ,t'2 ) o
o' 12
93
6
12 93
6
2
12 x' x 9 3
x ( x ut)
y
y
z z
t
(t
u c2
x)
11
§4.2 狭义相对论基本原理 洛伦兹变换
普
通
物 理
当u c时, 0, 1
教
程 x x ut
x x ut 伽利略
y y
第 四
z z
章
y y
变换
z z
发展
狭 t t x
义 相
c
t t
对 论
洛伦兹时空坐标变换
普
通
物 理
4.1.1 经典力学和相对论力学
教 程
经典十力九学世: 纪末二十世纪初以前的力学称
之.它的应用范围为低速;认为质量是不随速率变
化的常量.
第 四
相对论二力十学世: 纪以后的力学称之.它的应用范
章 围为高速(接近光速);认为质量随速率而变化.
狭
义 相
经典力学和相对论力学的关系:
对 当物体的运动速度远远低于光速时,相对论力学
z z
相 对 论
t
t
u c2
x
1
u
2
c
t
t
u c2
x
1
u
2
c
10
§4.2 狭义相对论基本原理 洛伦兹变换
普
通
物 理 教
令: u ,
c
1
1 u2 c2
程
时空坐标的
第
洛伦兹变换
四 章
x ( x ut)
狭 义 相
y
y
z z
对 论
t
(t
u c2
x)
时空坐标的洛 伦兹逆变换
第
③ 时间间隔是绝对不变量;
四 章
④ 空间间隔是绝对不变量.
狭
用牛顿的话来说:“绝对的真正的数学的时间
义 相
,就其本质而言,是永远均匀地流逝着,与任何外
对 论
界事物无关。”
“绝对空间就其本质而言是与任何外界事物无
关的,它从不运动,并且永远不变。”
7
§4.2 狭义相对论基本原理 洛伦兹变换
普
通
物 理
6
四
章
在一个惯性系同
狭 义 相 对
时发生的两个事件, 在另一个惯性系是
Δt
Δt
v c2
狭
义
经典力学是建立在绝对时空观的基之上;
相
对 论
狭义相对论是建立在相对时空观的基础之上;
广义相对论是建立在时空弯曲观的基础之上.
4
§4.1 伽利略变换 经典力学的时空观
普
通
物 理 教 程
4.1.2 伽利略变换 经典力学的时空观 y y u
K K p x, y,z,t
x, y, z,t
第 四
o o
章
合的时刻作为两坐标系共同的计时起点,y轴
和 轴y、 轴和z 轴互z相平行.
9
§4.2 狭义相对论基本原理 洛伦兹变换
普
通
物
从爱因斯坦狭义相对论的两个基本假设出发,
理 教
可导出洛伦兹变换式.
程
洛伦兹正变换
洛伦兹逆变换
第 四 章
x
x ut
1
u
2
c
狭
y y
义
z z
x
x ut
1
u
2
c
y y
c 2.99792458108m s1
8
§4.2 狭义相对论基本原理 洛伦兹变换
普
通
物 理
4.2.2 洛伦兹变换
教 程
y y u
K K p x, y,z,t
第 四
o o
x, y, z,t
章
x x
狭
z z
义
相
设K坐标系静止, 坐K标系相对于K坐标系
对 论
以速度 u沿x轴正向运动,并以 和o 两o原点重
4.2.1. 狭义相对论的基本原理
教 程
(1). 相对性原理
物理定律在所有惯性系中都是同形的,因此
各个惯性系中都是等价的,不存在特殊的绝对惯
第 四
性系.
章
或:物理定律在所有惯性系中具有数学形式
狭 不变性,即协变性.
义 相
(2). 光速不变原理
对 论
所有的惯性系中,光在真空中的传播速率具有相
同的值c .
x x
狭
z z
义
相
设K坐标系静止, 坐K标系相对于K坐标系
对 论
以速度 u沿x轴正向运动,并以 和o 两o原点重
合的时刻作为两坐标系共同的计时起点,y轴
和 轴y、 轴和z 轴互z相平行.
5
§4.1 伽利略变换 经典力学的时空观
普
通
物 理
伽利略坐标变换
教
程
x x ut
x x ut
正 y y
