中考数学复习第六章圆第一节圆的有关概念和性质随堂演练
中考数学复习 第六章 圆 第一节 圆的有关概念和性质练习

亲爱的同学:这份试卷将再次记录你的自信、沉着、智慧和收获,我们一直投给你信任的目光……学习资料专题第六章圆第一节圆的有关概念和性质姓名:________ 班级:________ 用时:______分钟1.(2018·淮安中考)如图,点A,B,C都在⊙O上,若∠AOC=140°,则∠B的度数是( )A.70° B.80° C.110° D.140°2.(2018·杭州中考)如图,⊙O的半径OA=6,以A为圆心,OA为半径的弧交⊙O于点B,C,则BC=( )A.6 3 B.6 2 C.3 3 D.3 23.(2019·易错题)已知⊙O的半径为10,圆心O到弦A B的距离为5,则弦AB所对的圆周角的度数是( )A.30° B.60°C.30°或150° D.60°或120°4.(2018·凉山州中考)如图,⊙O是△ABC的外接圆,已知∠ABO=50°,则∠ACB的大小为( )A.40° B.30° C.45° D.50°5.(2018·随州中考)如图,点A,B,C在⊙O上,∠A=40度,∠C=20度,则∠B=________度.6.(2019·原创题)如图,Rt△ABC是⊙O的内接直角三角形,其中∠BCA=90°,若BC=3,AB=5,OD⊥BC于点D,则OD的长为________.7.(2018·黑龙江中考)如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=6,EB=1,则⊙O的半径为________.8.(2019·易错题)等腰三角形ABC中,顶角A为40°,点P在以A为圆心,BC长为半径的圆上,且BP =BA,则∠PBC的度数为____________________.9.如图,⊙O是△ABC的外接圆,直径AD=4,∠ABC=∠DAC,则AC的长为______.10.(2019·原创题)如图,在△AB C的外接圆⊙O中,∠A=60°,AB为直径,点D是AC的中点,作DE⊥AB交AB于点E,若DE=3,求BC的长.11.(2018·河口一模)如图,直径为10的⊙A 经过点C 和点O ,点B 是y 轴右侧⊙A 优弧上一点,∠OBC =30°,则点C 的坐标为( )A .(0,5)B .(0,53)C .(0,523)D .(0,533)12.(2018·咸宁中考)如图,已知⊙O 的半径为5,弦AB ,CD 所对的圆心角分别是∠AOB,∠COD,若∠AOB 与∠COD 互补,弦CD =6,则弦AB 的长为( )A .6B .8C .5 2D .5 313.(2018·玉林中考)小华为了求出一个圆盘的半径,他用所学的知识,将一宽度为2 cm 的刻度尺的一边与圆盘相切,另一边与圆盘边缘两个交点处的读数分别是“4”和“16”(单位:cm ),请你帮小华算出圆盘的半径是________cm .14.(2019·易错题)已知⊙O 的半径为10 cm ,AB ,CD 是⊙O 的两条弦,AB∥CD,AB =16 cm ,CD =12 cm ,则弦AB 和CD 之间的距离是____________cm .15.(2018·宜宾中考)如图,AB 是半圆的直径,AC 是一条弦,D 是AC ︵的中点,DE⊥AB 于点E ,且DE 交AC 于点F ,DB 交AC 于点G ,若EF AE =34,则CGGB=________.16.(2018·无锡中考)如图,四边形ABCD 内接于⊙O,AB =17,CD =10,∠A=90°,cos B =35,求AD 的长.17.如图,在半径为5的⊙O 中,直径AB 的不同侧有定点C 和动点P ,已知BC∶CA =4∶3,点P 在AB ︵上运动.(1)当点P 与点C 关于AB 对称时,求CP 的长; (2)当点P 运动到AB ︵的中点时,求CP 的长; (3)点P 在AB ︵上运动时,求CP 的长的取值范围.18.(2018·乐山中考)《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸),问这块圆柱形木材的直径是多少?”如图所示,请根据所学知识计算:圆柱形木材的直径AC是( )A.13寸B.20寸C.26寸D.28寸参考答案【基础训练】1.C 2.A 3.D 4.A5.60 6.2 7.5 8.30°或110°9.2 210.解:如图,连接OD.∵在Rt△ADE 中,∠A=60°, ∴∠ADE=30°.∵点D 是AC 的中点,则OD⊥AC, ∴∠ODE=60°.又∵DE=3,∴OD=2 3. 又∵点O 是AB 的中点,根据中位线定理得BC =2OD =4 3. 【拔高训练】 11.A 12.B13.10 14.2或14 15.5516.解:∵四边形ABCD 内接于⊙O,∠A=90°, ∴∠C=180°-∠A=90°,∠ABC+∠ADC=180°. 如图,连接BD ,作AE⊥BC 于点E ,DF⊥AE 于点F ,则四边形CDFE 是矩形,EF =CD =10. 在Rt△AEB 中,∵∠AEB=90°,AB =17, cos∠ABC=35,∴BE=AB·cos∠ABE=515,∴AE=AB 2-BE 2=685,∴AF=AE -EF =685-10=185.∵∠ABC+∠ADC=180°,∠CDF=90°,∴∠ABC+∠ADF=90°. ∵cos∠ABC=35,∴sin∠ADF=cos∠ABC=35.在Rt△ADF 中,∵∠AFD=90°,sin∠ADF=35,∴A D =AFsin∠ADF =18535=6.17.解:(1)∵点P 与点C 关于AB 对称,∴CP⊥AB. 如图,设垂足为点D.∵AB 为⊙O 的直径, ∴∠ACB=90°.∵AB=10,BC∶CA=4∶3, ∴BC=8,AC =6. 又∵△ACD∽△ABC, ∴AC AB =CDBC,∴CD =4.8, ∴CP=2CD =9.6.(2)如图,连接AP ,PB ,过点B 作BE⊥PC 于点E.∵点P 是AB ︵的中点, ∴AP=BP =52, ∠ACP=∠BCP=45°. ∵BC=8, ∴CE=BE =4 2. 又∵PB=52,∴PE=PB 2-BE 2=32, ∴CP=CE +PE =7 2.(3)点P 在AB ︵上运动时,恒有CP≥CA,即CP≥6. 当CP 过圆心O 时,CP 取得最大值10, ∴CP 的取值范围是6≤CP≤10. 【培优训练】 18.C。
安徽省2019年中考数学总复习第六章圆第一节圆的基本性质好题随堂演练
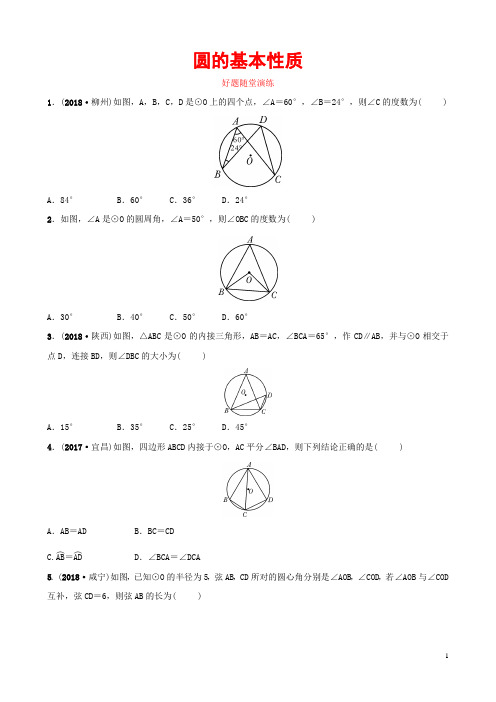
圆的基本性质好题随堂演练1.(2018·柳州)如图,A ,B ,C ,D 是⊙O 上的四个点,∠A=60°,∠B=24°,则∠C 的度数为( )A .84°B .60°C .36°D .24°2.如图,∠A 是⊙O 的圆周角,∠A=50°,则∠OBC 的度数为( )A .30°B .40°C .50°D .60°3.(2018·陕西)如图,△ABC 是⊙O 的内接三角形,AB =AC ,∠BCA=65°,作CD∥AB,并与⊙O 相交于点D ,连接BD ,则∠DBC 的大小为( )A .15°B .35°C .25°D .45°4.(2017·宜昌)如图,四边形ABCD 内接于⊙O,AC 平分∠BAD,则下列结论正确的是( )A .AB =ADB .BC =CD C.AB ︵=AD ︵ D .∠BCA=∠DCA5.(2018·咸宁)如图,已知⊙O 的半径为5,弦AB ,CD 所对的圆心角分别是∠AOB,∠COD,若∠AOB 与∠COD 互补,弦CD =6,则弦AB 的长为( )A.6 B.8 C.5 2 D.5 36.如图,四边形ABCD为⊙O的内接四边形,已知∠C=∠D,则AB与CD的位置关系是______________.7.(2018·宜昌)如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.(1)求证:四边形ABFC是菱形;(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.参考答案1.D 2.B 3.A 4.B 5.B 6.AB∥CD7.(1)证明:∵AB是直径,∴∠AEB=90°,即AE⊥BC,∵AB=AC,∴BE=CE,∵AE=EF,∴四边形ABFC是平行四边形,∵AC=AB ,∴四边形ABFC 是菱形.(2)解:设CD =x.如解图,连接BD.∵AB 是直径,∴∠ADB=∠BDC=90°, ∴AB 2-AD 2=CB 2-CD 2,∴(7+x)2-72=42-x 2,解得x =1或-8(舍去), ∴AC=8,BD =82-72=15,∴S 菱形ABFC =AC·BD=815.S 半圆=12·π·42=8π.。
河北省2019年中考数学一轮复习 第六章 圆 第一节 圆的基本性质好题随堂演练

第六章 圆好题随堂演练1.(2018·衢州)如图,点A ,B ,C 在⊙O 上,∠ACB=35°,则∠AOB 的度数 是( )A .75°B .70°C .65°D .35°2.(2018·盐城)如图,AB 为⊙O 的直径,CD 是⊙O 的弦,∠ADC=35°,则∠CAB 的度数为( ) A .35° B .45° C .55° D .65°3.(2017·宜昌改编)如图,已知点A ,B ,C ,D 在⊙O 上,AC 平分∠BAD,则下列结论正确的是( ) A .AB =AD B .BC =CD C.AB ︵=AD ︵D .∠BCA=∠DCA4. 如图,⊙O 的半径为13,弦AB 的长度是24,ON⊥AB,垂足为点N , 则ON = .5.如图,四边形ABCD 为⊙O 的内接四边形,已知∠C=∠D,则AB 与CD 的位置关系是 .6.(2017·牡丹江)如图,在⊙O 中,AC ︵=CB ︵,CD⊥OA 于D ,CE⊥OB 于E ,求证:AD =BE.7.(2017·安徽)如图,在四边形ABCD 中,AD =BC ,∠B=∠D,AD 不平行于BC ,过点C 作CE∥AD 交△ABC 的外接圆⊙O 于点E ,连接AE. (1)求证:四边形AECD 为平行四边形; (2)连接CO ,求证:CO 平分∠BCE.8.(2018·宜昌)如图,在△ABC 中,AB =AC ,以AB 为直径的圆交AC 于点D ,交BC 于点E ,延长AE 至点F ,使EF =AE ,连接FB ,FC. (1)求证:四边形ABFC 是菱形;(2)若AD =7,BE =2,求半圆和菱形ABFC 的面积.参考答案1.B 2.C 3.B 4.5 5.AB∥CD3 / 5第6题解图6.证明:如解图,连接OC. ∵AC ︵=CB ︵, ∴∠AOC=∠BOC.∵CD⊥OA 于点D ,CE⊥OB 于点E , ∴∠CDO=∠CEO=90°.在△COD 和△COE 中,⎩⎪⎨⎪⎧∠DOC=∠EOC,∠CDO=∠CEO,CO =CO ,∴△COD≌△COE(AA S ),∴OD=OE. ∵AO=BO ,∴AD=BE.7.证明:(1)∵∠B=∠D,∠B=∠E, ∴∠D=∠E.∵CE∥AD,∴∠E+∠DAE=180°, ∴∠D+∠DAE=180°,∴AE∥DC.又∵CE∥AD,∴四边形AECD 为平行四边形;(2)如解图,过点O 作OM⊥EC,ON⊥BC,垂足分别为M 、N.∴EM=MC ,BN =NC.∵四边形AECD 是平行四边形, ∴AD=EC ,又∵AD=BC ,∴EC=BC , ∴MC=NC ,∴OM=ON ,∴CO 平分∠BCE. 8.(1)证明:∵AB 是直径,5 / 5∴∠AEB=90°,即AE⊥BC, ∵AB=AC ,∴BE=CE ,∵AE=EF ,∴四边形ABFC 是平行四边形, ∵AC=AB ,∴四边形ABFC 是菱形;(2)解:设CD =x.如解图,连接BD. ∵AB 是直径,∴∠ADB=∠BDC=90°, ∴AB 2-AD 2=CB 2-CD 2,∴(7+x)2-72=42-x 2,解得x =1或-8(舍去), ∴AC=8,BD =82-72=15, ∴S 菱形ABFC =AC·BD=815. S 半圆=12·π·42=8π.。
安徽省2019年中考数学总复习第六章圆第一节圆的基本性质好题随堂演练

安徽省2019年中考数学总复习第六章圆第一节圆的基本性质好题随堂演练好题随堂演练1.(2018·柳州)如图,A,B,C,D是⊙O上的四个点,∠A=60°,∠B=24°,则∠C的度数为( )A.84° B.60° C.36° D.24°2.如图,∠A是⊙O的圆周角,∠A=50°,则∠OBC的度数为( ) A.30° B.40° C.50° D.60°3.(2018·陕西)如图,△ABC是⊙O的内接三角形,AB=AC,∠BCA=65°,作CD∥AB,并与⊙O相交于点D,连接BD,则∠DBC的大小为( ) A.15° B.35° C.25° D.45°4.(2017·宜昌)如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是( )A.AB=AD B.BC=CDC.=D.∠BCA=∠DCA5.(2018·咸宁)如图,已知⊙O的半径为5,弦AB,CD所对的圆心角分别是∠AOB,∠COD,若∠AOB与∠COD互补,弦CD=6,则弦AB的长为( ) A.6 B.8C.5D.5 36.如图,四边形ABCD为⊙O的内接四边形,已知∠C=∠D,则AB与CD的位置关系是______________.7.(2018·宜昌)如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.(1)求证:四边形ABFC是菱形;(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.参考答案1.D2.B3.A4.B5.B6.AB∥CD7.(1)证明:∵AB是直径,∴∠AEB=90°,即AE⊥BC,∵AB=AC,∴BE=CE,∵AE=EF,∴四边形ABFC是平行四边形,∵AC=AB,∴四边形ABFC是菱形.(2)解:设CD=x.如解图,连接BD.∵AB是直径,∴∠ADB=∠BDC=90°,∴AB2-AD2=CB2-CD2,∴(7+x)2-72=42-x2,解得x=1或-8(舍去),∴AC=8,BD==,∴S菱形ABFC=AC·BD=8.S半圆=·π·42=8π.。
河北省2021年中考数学一轮复习第六章圆第一节圆的基本性质好题随堂演练

第六章 圆好题随堂演练1.(2021·衢州)如图,点A ,B ,C 在⊙O 上,∠ACB=35°,那么∠AOB 的度数 是( )A .75°B .70°C .65°D .35°2.(2021·盐城)如图,AB 为⊙O 的直径,CD 是⊙O 的弦,∠ADC=35°,那么∠CAB 的度数为( ) A .35° B .45° C .55° D .65°3.(2021·宜昌改编)如图,点A ,B ,C ,D 在⊙O 上,AC 平分∠BAD,那么以下结论正确的选项是( ) A .AB =AD B .BC =CD C.AB ︵=AD ︵D .∠BCA=∠DCA4. 如图,⊙O 的半径为13,弦AB 的长度是24,ON⊥AB,垂足为点N , 那么ON = .5.如图,四边形ABCD 为⊙O 的内接四边形,∠C=∠D,那么AB 与CD 的位置关系是 .6.(2021·牡丹江)如图,在⊙O 中,AC ︵=CB ︵,CD⊥OA 于D ,CE⊥OB 于E ,求证:AD =BE.7.(2021·安徽)如图,在四边形ABCD 中,AD =BC ,∠B=∠D,AD 不平行于BC ,过点C 作CE∥AD 交△ABC 的外接圆⊙O 于点E ,连接AE. (1)求证:四边形AECD 为平行四边形; (2)连接CO ,求证:CO 平分∠BCE.8.(2021·宜昌)如图,在△ABC 中,AB =AC ,以AB 为直径的圆交AC 于点D ,交BC 于点E ,延长AE 至点F ,使EF =AE ,连接FB ,FC. (1)求证:四边形ABFC 是菱形;(2)假设AD =7,BE =2,求半圆和菱形ABFC 的面积.参考答案1.B 2.C 3.B 4.5 5.AB∥CD第6题解图6.证明:如解图,连接OC. ∵AC ︵=CB ︵, ∴∠AOC=∠BOC.∵CD⊥OA 于点D ,CE⊥OB 于点E , ∴∠CDO=∠CEO=90°.在△COD 和△COE 中,⎩⎪⎨⎪⎧∠DOC=∠EOC,∠CDO=∠CEO,CO =CO ,∴△COD≌△COE(AA S ),∴OD=OE. ∵AO=BO ,∴AD=BE.7.证明:(1)∵∠B=∠D,∠B=∠E, ∴∠D=∠E.∵CE∥AD,∴∠E+∠DAE=180°, ∴∠D+∠DAE=180°,∴AE∥DC.又∵CE∥AD,∴四边形AECD 为平行四边形;(2)如解图,过点O 作OM⊥EC,ON⊥BC,垂足分别为M 、N.∴EM=MC ,BN =NC.∵四边形AECD 是平行四边形, ∴AD=EC ,又∵AD=BC ,∴EC=BC , ∴MC=NC ,∴OM=ON ,∴CO 平分∠BCE.8.(1)证明:∵AB 是直径, ∴∠AEB=90°,即AE⊥BC, ∵AB=AC ,∴BE=CE ,∵AE=EF ,∴四边形ABFC 是平行四边形, ∵AC=AB ,∴四边形ABFC 是菱形;(2)解:设CD =x.如解图,连接BD. ∵AB 是直径,∴∠ADB=∠BDC=90°, ∴AB 2-AD 2=CB 2-CD 2,∴(7+x)2-72=42-x 2,解得x =1或-8(舍去), ∴AC=8,BD =82-72=15, ∴S 菱形ABFC =AC·BD=815. S 半圆=12·π·42=8π.。
河南省2019年中考数学总复习第六章圆第一节圆的基本性质好题随堂演练word格式

圆的基本性质好题随堂演练1.如图,在⊙O 中,AB ︵=BC ︵,点D 在⊙O 上,∠CDB =25°,则∠AOB =( )A .45°B .50°C .55°D .60°2.(2018·南充)如图,BC 是⊙O 的直径,A 是⊙O 上的一点,∠OAC =32°,则∠B 的度数是( )A .58°B .60°C .64°D .68°3.(2018·菏泽)如图,在⊙O 中,OC ⊥AB ,∠ADC =32°,则∠OBA 的度数是( )A .64°B .58°C .32°D .26°4.(2018·威海)如图,⊙O 的半径为5,AB 为弦,点C 为AB ︵的中点,若∠ABC =30°,则弦AB 的长为( )A.12B .5C.532D .5 35.(2018·邵阳)如图所示,四边形ABCD 为⊙O 的内接四边形,∠BCD =120°,则∠BOD 的大小是( )A .80°B .120°C .100°D .90°6.(2018·广东省卷)已知AB ︵所对的圆心角是100°,则AB ︵所对的圆周角是____________°.7. 如图,⊙O 的半径为13,弦AB 的长度是24,ON ⊥AB ,垂足为点N ,则ON =__________.8.(2019·原创)已知圆内接四边形ABCD ,两组对边的延长线分别相交于点E 、F ,且∠E =40°,∠F =45°,则∠A =________________°.9.(2018·黄冈)如图,△ABC 内接于⊙O ,AB 为⊙O 的直径,∠CAB =60°,弦AD 平分∠CAB ,若AD =6,则AC =__________.10. (2017·牡丹江)如图,在⊙O 中,AC ︵=CB ︵,CD ⊥OA 于点D ,CE ⊥OB 于点E ,求证:AD =BE.参考答案1.B 2.A 3.D 4.D 5.B 6.50 7.5 8.47.5 9.2310.证明:如解图,连接OC ,∵ AC ︵=CB ︵,∴∠AOC =∠BOC ,∵CD ⊥OA ,CE ⊥OB ,∴∠CDO =∠CEO =90°, 在△CDO 和△CEO 中,⎩⎪⎨⎪⎧∠DOC=∠EOC ∠CDO=∠CEO,CO =CO∴△CDO ≌△CEO ,∴OD =OE. 又∵ AO =BO ,∴AD =BE.。
安徽省2019年中考数学总复习第六章圆第一节圆的基本性质好题随堂演练
圆的基本性质好题随堂演练1.(2018·柳州)如图,A ,B ,C ,D 是⊙O 上的四个点,∠A=60°,∠B=24°,则∠C 的度数为( )A .84°B .60°C .36°D .24°2.如图,∠A 是⊙O 的圆周角,∠A=50°,则∠OBC 的度数为( )A .30°B .40°C .50°D .60°3.(2018·陕西)如图,△ABC 是⊙O 的内接三角形,AB =AC ,∠BCA=65°,作CD∥AB,并与⊙O 相交于点D ,连接BD ,则∠DBC 的大小为( )A .15°B .35°C .25°D .45°4.(2017·宜昌)如图,四边形ABCD 内接于⊙O,AC 平分∠BAD,则下列结论正确的是( )A .AB =ADB .BC =CD C.AB ︵=AD ︵ D .∠BCA=∠DCA5.(2018·咸宁)如图,已知⊙O 的半径为5,弦AB ,CD 所对的圆心角分别是∠AOB,∠COD,若∠AOB 与∠COD 互补,弦CD =6,则弦AB 的长为( )A.6 B.8 C.5 2 D.5 36.如图,四边形ABCD为⊙O的内接四边形,已知∠C=∠D,则AB与CD的位置关系是______________.7.(2018·宜昌)如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.(1)求证:四边形ABFC是菱形;(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.参考答案1.D 2.B 3.A 4.B 5.B 6.AB∥CD7.(1)证明:∵AB是直径,∴∠AEB=90°,即AE⊥BC,∵AB=AC,∴BE=CE,∵AE=EF,∴四边形ABFC是平行四边形,∵AC=AB ,∴四边形ABFC 是菱形.(2)解:设CD =x.如解图,连接BD.∵AB 是直径,∴∠ADB=∠BDC=90°,∴AB 2-AD 2=CB 2-CD 2,∴(7+x)2-72=42-x 2,解得x =1或-8(舍去), ∴AC=8,BD =82-72=15,∴S 菱形ABFC =AC·BD=815.S 半圆=12·π·42=8π.。
2019年中考数学一轮复习第六章圆第一节圆的基本性质好题随堂演练
第六章圆好题随堂演练1.(2018·衢州)如图,点A ,B ,C 在⊙O 上,∠ACB =35°,则∠AOB 的度数 是( )A .75°B .70°C .65°D .35°2.(2018·盐城)如图,AB 为⊙O 的直径,CD 是⊙O 的弦,∠ADC =35°,则∠CAB 的度数为( ) A .35° B .45°C .55° D .65°3.(2017·宜昌改编)如图,已知点A ,B ,C ,D 在⊙O 上,AC 平分∠BAD ,则下列结论正确的是() A .AB =AD B .BC =CD C.AB ︵=AD ︵D .∠BCA =∠DCA4.如图,⊙O 的半径为13,弦AB 的长度是24,ON ⊥AB ,垂足为点N , 则ON =.5.如图,四边形ABCD 为⊙O 的内接四边形,已知∠C =∠D ,则AB 与CD 的位置关系是.6.(2017·牡丹江)如图,在⊙O 中,AC ︵=CB ︵,CD ⊥OA 于D ,CE ⊥OB 于E ,求证:AD =BE.7.(2017·安徽)如图,在四边形ABCD 中,AD =BC ,∠B =∠D ,AD 不平行于BC ,过点C 作CE ∥AD 交△ABC 的外接圆⊙O 于点E ,连接AE. (1)求证:四边形AECD 为平行四边形; (2)连接CO ,求证:CO 平分∠BCE.8.(2018·宜昌)如图,在△ABC 中,AB =AC ,以AB 为直径的圆交AC 于点D ,交BC 于点E ,延长AE 至点F ,使EF =AE ,连接FB ,FC. (1)求证:四边形ABFC 是菱形;(2)若AD =7,BE =2,求半圆和菱形ABFC 的面积.参考答案1.B2.C3.B4.55.AB∥CD第6题解图6.证明:如解图,连接OC. ∵AC ︵=CB ︵, ∴∠AOC =∠BOC.∵CD ⊥OA 于点D ,CE ⊥OB 于点E , ∴∠CDO =∠CEO =90°.在△COD 和△COE 中,⎩⎪⎨⎪⎧∠DOC=∠EOC,∠CDO=∠CEO,CO =CO ,∴△COD ≌△COE(AA S ),∴OD =OE. ∵AO =BO ,∴AD =BE.7.证明:(1)∵∠B =∠D ,∠B =∠E , ∴∠D =∠E.∵CE ∥AD ,∴∠E +∠DAE =180°, ∴∠D +∠DAE =180°,∴AE ∥DC.又∵CE ∥AD ,∴四边形AECD 为平行四边形;(2)如解图,过点O 作OM ⊥EC ,ON ⊥BC ,垂足分别为M 、N.∴EM =MC ,BN =NC.∵四边形AECD 是平行四边形, ∴AD =EC ,又∵AD =BC ,∴EC =BC , ∴MC =NC ,∴OM =ON ,∴CO 平分∠BCE.8.(1)证明:∵AB 是直径, ∴∠AEB =90°,即AE ⊥BC , ∵AB =AC ,∴BE =CE ,∵AE =EF ,∴四边形ABFC 是平行四边形, ∵AC =AB ,∴四边形ABFC 是菱形;(2)解:设CD =x.如解图,连接BD. ∵AB 是直径,∴∠ADB =∠BDC =90°, ∴AB 2-AD 2=CB 2-CD 2,∴(7+x)2-72=42-x 2,解得x =1或-8(舍去), ∴AC =8,BD =82-72=15, ∴S 菱形ABFC =AC·B D =815. S 半圆=12·π·42=8π.。
2019年中考数学总复习第六章圆第一节圆的基本性质好题随堂演练word版本
圆的基本性质好题随堂演练1.(2018·柳州)如图,A,B,C,D是⊙O上的四个点,∠A=60°,∠B=24°,则∠C 的度数为( )A.84° B.60° C.36° D.24°2.如图,∠A是⊙O的圆周角,∠A=50°,则∠OBC的度数为( )A.30° B.40° C.50° D.60°3.(2018·陕西)如图,△ABC是⊙O的内接三角形,AB=AC,∠BCA=65°,作CD∥AB,并与⊙O相交于点D,连接BD,则∠DBC的大小为( )A.15° B.35° C.25° D.45°4.(2017·宜昌)如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是( )A.AB=AD B.BC=CDC.AB ︵=AD ︵ D .∠BCA =∠DCA5.(2018·咸宁)如图,已知⊙O 的半径为5,弦AB ,CD 所对的圆心角分别是∠AOB ,∠COD ,若∠AOB 与∠COD 互补,弦CD =6,则弦AB 的长为( )A .6B .8C .5 2D .5 36.如图,四边形ABCD 为⊙O 的内接四边形,已知∠C =∠D ,则AB 与CD 的位置关系是______________.7.(2018·宜昌)如图,在△ABC 中,AB =AC ,以AB 为直径的圆交AC 于点D ,交BC 于点E ,延长AE 至点F ,使EF =AE ,连接FB ,FC.(1)求证:四边形ABFC 是菱形;(2)若AD =7,BE =2,求半圆和菱形ABFC 的面积.参考答案1.D 2.B 3.A 4.B 5.B 6.AB ∥CD7.(1)证明:∵AB 是直径,∴∠AEB =90°,即AE ⊥BC ,∵AB =AC ,∴BE =CE ,∵AE =EF ,∴四边形ABFC 是平行四边形, ∵AC =AB ,∴四边形ABFC 是菱形.(2)解:设CD =x.如解图,连接BD.∵AB 是直径,∴∠ADB =∠BDC =90°, ∴AB 2-AD 2=CB 2-CD 2,∴(7+x)2-72=42-x 2,解得x =1或-8(舍去), ∴AC =8,BD =82-72=15,∴S 菱形ABFC =AC·B D =815.S 半圆=12·π·42=8π.。
河北省中考数学一轮复习第六章圆第一节圆的基本性质好题随堂演练
第六章圆好题随堂演练1.(2021·衢州)如图,点 A,B,C在⊙O上,∠ACB=35°,那么∠AOB的度数是()A.75° B .70° C .65° D .35°2.(2021·盐城)如图,AB为⊙O的直径,CD是⊙O的弦,∠ADC=35°,那么∠CAB的度数为( ) A.35° B .45° C .55° D .65°3.(2021·宜昌改编)如图,点A,B,C,D在⊙O上,AC平分∠BAD,那么以下结论正确的选项是()A.AB=AD B.BC=CD︵︵D.∠BCA=∠DCA=AD如图,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为点N,那么ON=.1/55.如图,四边形ABCD为⊙O的内接四边形,∠C=∠D,那么AB与CD的位置关系是.︵︵6.(2021·牡丹江)如图,在⊙O中,AC=CB,CD⊥OA于D,CE⊥OB于E,求证:AD=BE.(1)7.(2021·安徽)如图,在四边形ABCD中,AD=BC,∠B=∠D,AD不平行于BC,过点C作CE∥AD交△ABC的外接圆⊙O于点E,连接AE.(2)求证:四边形AECD为平行四边形;(3)连接CO,求证:CO平分∠BCE.(4)(5)(6)(7)(8)(9)(10)(11)(12)(13)8.(2021·宜昌)如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点(14)F,使EF=AE,连接FB,FC.(15)求证:四边形ABFC是菱形;假设AD=7,BE=2,求半圆和菱形ABFC的面积.2/5参考答案1.∥CD3/5第6题解图6.证明:如解图,连接OC.︵︵AC=CB,∴∠AOC=∠BOC.∵CD⊥OA于点D,CE⊥OB于点E,∴∠CDO=∠CEO=90°.∠DOC=∠EOC,在△COD和△COE中,∠CDO=∠CEO,CO=CO,∴△COD≌△COE(AA S),∴OD=OE.∵AO=BO,∴AD=BE.7.证明:(1)∵∠B=∠D,∠B=∠E,∴∠D=∠E.∵CE∥AD,∴∠E+∠DAE=180°,∴∠D+∠DAE=180°,∴AE∥DC.又∵CE∥AD,∴四边形AECD为平行四边形;如解图,过点O作OM⊥EC,ON⊥BC,垂足分别为M、N.∴EM=MC,BN=NC.∵四边形AECD是平行四边形,∴AD=EC,又∵AD=BC,∴EC=BC,∴MC=NC,∴OM=ON,∴CO平分∠BCE.4/58.(1)证明:∵AB是直径,∴∠AEB=90°,即AE⊥BC,∵AB=AC,∴BE=CE,∵AE=EF,∴四边形ABFC是平行四边形,∵AC=AB,∴四边形ABFC是菱形;解:设CD=x.如解图,连接BD.∵AB是直径,∴∠ADB=∠BDC=90°,2222∴AB-AD=CB-CD,2222或-8(舍去),∴(7+x)-7=4-x,解得x=1∴AC=8,BD=82-72=15,∴S菱形=AC·BD=815. ABFCS=12半圆2·π·4=8π.5/5。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 / 4
教学资料参考范本
中考数学复习第六章圆第一节圆的有关概念和性质随堂演练
撰写人:__________________
时 间:__________________
2 / 4
1.如图,线段AB是⊙O的直径,弦CD⊥AB,∠CAB=20°,则∠AOD
等于( )
A.160° B.150° C.140° D.120°
2.(20xx·青岛)如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠AED=20°,则∠BCD的度数为
( )
A.100° B.110° C.115° D.120°
3.(20xx·泰安)如图,△ABC内接于⊙O,若∠A=α,则∠OBC等于( )
A.180°-2α B.2α
C.90°+α D.90°-α
4.(20xx·潍坊)如图,四边形ABCD为⊙O的内接四边形.延长AB与DC相交于点G,AO⊥CD,垂足为
E,连接BD,∠GBC=50°,则∠DBC的度数为( )
A.50° B.60° C.80° D.85°
5.如图,⊙C过原点,与x轴,y轴分别交于A,D两点.已知∠OBA=30°,点D的坐标为(0,2),则
⊙C的半径是( )
A. B. C.4 D.2
6.如图,圆内接四边形ABCD中两组对边的延长线分别相交于点E,F,且∠A=55°,∠E=30°,则
∠F= .
7.(20xx·济南)如图,AB是⊙O的直径,∠ACD=25°,求∠BAD的度数.
3 / 4
8.(20xx·临沂)如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E.
(1)求证:DE=DB;
(2)若∠BAC=90°,BD=4.求△ABC外接圆的半径.
4 / 4
参考答案
1.C 2.B 3.D 4.C 5.B 6.40°
7.解:∵∠ACD=25°,∴∠ABD=25°.
∵AB是⊙O的直径,∴∠ADB=90°.
在△ABD中,∠BAD=180°-∠ABD-∠ADB=180°-25°-90°=65°.
8.(1)证明:∵AD平分∠BAC,BE平分∠ABC,
∴∠BAD=∠CAD,∠ABE=∠CBE,
又∠BED=∠ABE+∠BAD,
∠DBE=∠DBC+∠CBE,
∠DBC=∠DAC,
∴∠BED=∠DBE,
∴DE=DB.
(2)解:如图,连接CD.
∵∠BAC=90°,
∴BC是圆的直径,
∴∠BDC=90°.
∵∠BAD=∠CAD,∴=,
∴BD=CD,
∴△BCD是等腰直角三角形.
∵BD=4,∴BC=4,
∴△ABC的外接圆的半径为2.
