小学五年级数学《组合图形的面积》知识点+试题(带答案)
《组合图形的面积》练习题(含答案)

助学堂组合图形的面积测试题1、下面的图形是由两个三角形组成的,请画出这两个三角形。
AB DC2、已知平行四边形的面积是48平方分米,求阴影部分的面积。
3dm8dm3、求下面个图形的面积、(单位:分米)(1)(2)1486 6123 612(3)(4)82.55.4 4 1.54.2 634、如图所示,梯形的周长是52厘米,求阴影部分的面积。
1014165、校园里有一块花圃,(如图所示),算出它的面积。
(单位:米)6 2256、大小正方形如图放置,阴影部分为重叠部分,求空白部分面积。
(单位:厘米)1577助学堂227、有一块土地如图所示,你能用几种方法求出它的面积?(单位:米)12158227、如图所示,一个平行四边形背分成A、B两被封,A的面积比B的面积打40平方米,A的上底是多少?BA8米【参考答案】1 解:AB DC2 解:48÷8×3÷2=9(平方分米)3(1)解:8×6+(8+12)×3÷2=78(平方分米)3(2)解:(14+12)×6÷2+12×6÷2=114(平方分米)3(3)解:5.4×4.2+5.4×6÷2=38.88(平方分米)3(4)解:2.5×1.5+(2.5+4)×(8-3-1.5)÷2+4×3=27.125(平方分米)4 解:10×(52-10-14-16)÷2=60(平方厘米)5 解:2×2+(5-2)×6=22(平方米)6 解:大正方形面积为:22×22=484(平方厘米)小正方形面积为:15×15=225(平方厘米)阴影部分面积为:7×7=49(平方厘米)空白部分的面积为:484+225-2×49=611(平方厘米)7 解:方法一:12 15助学堂82212×8+(15+8)×(22-12)÷2=211(平方米)方法二:1215822(15-8)×(22-2)÷2+22×8=211(平方米)8 解:40÷8=5(平方米)。
北师大版五年级数学上册《组合图形的面积》专项测试卷及答案

北师大版五年级数学上册《组合图形的面积》专项测试卷及答案学校:___________班级:___________姓名:___________考号:___________一、填空题1.在括号里填上合适的面积单位(平方米,公顷,平方千米)。
“世界水晶之都”东海县占地面积约是2000( );中国“天眼”大型射电望远镜的反射面积达25万( );2022年为冬奥会建造的国家速滑馆占地面积约17( )。
2.在括号里填上合适的数。
1.6平方千米=()公顷0.38公顷=( )平方米4500000平方米=( )公顷=( )平方千米8.025公顷=( )公顷( ) 平方米3.新丰实验田有一块菜地(如图),这块菜地的面积是( )平方米。
4.下图是一段木料的横截面,每个小方格的边长是1分米,它的面积大约是( )平方分米。
(提示:不满一格的算半格)5.游泳馆指示牌的面积是( )cm2。
二、选择题6.北京故宫占地面积大约是72()。
A.平方分米B.公顷C.平方米D.平方千米7.顶天寺(朝阳山)在陕西省礼泉县东北烟霞镇和叱干镇交界处,距离县城30千米。
西北至东南走向,长1.8千米,宽1.6千米,面积3.5平方千米。
3.5平方千米=()公顷。
A.0.35B.3.5C.35D.3508.图中每个小方格的边长表示1cm,小鸟的面积最接近()。
A.60cm2B.120cm2C.80cm2D.40cm29.一块平行四边形绿地,因为盖房子被占掉了一部分,剩下部分如图中阴影部分所示。
剩下部分的面积是()。
A.120m2B.96m2C.72m210.笑笑在计算少先队中队旗的面积时,列出了算式“806060202⨯-⨯÷”,请你判断图()可以表示笑笑的思路。
A.B.C.D.三、判断题11.如图是两个完全相同的大长方形,估计心形的面积时将不满整格的按半格计算,再加上整格的,等分成的方格越小,估计的结果就越接近实际面积。
( )12.测量和计算土地面积时,通常用公顷、平方千米作单位。
北师大版小学五年级数学上册《组合图形的面积》试题及答案-6页文档资料

五年级数学(上册):《组合图形的面积》试题1、求图形的面积(单位:厘米)梯形面积:三角形面积:(8+12)×8.5÷2 12×3÷2= 20×8.5÷2 = 36÷2= 170÷2 = 18(cm2)= 85(cm2)图形面积= 梯形面积–三角形面积: 85-18=67(cm2)2、校园里有两块花圃(如图),你能计算出它们的面积吗?(单位:m)图形面积=长方形面积6×(5-2)+ 正方形面积(2×2)图形面积=长方形面积 - 梯形面积6×(5-2)+ 2×2 10×6 –[(3+6)×2÷2 ]= 6×3 + 4 = 60 -[ 9×2÷2 ]= 18 + 4 = 60 - 9= 22(m2) = 51(m2)3、下图直角梯形的面积是49平方分米,求阴影部分的面积。
直角梯形的高=直角三角形的高(阴影部分面积)直角梯形的高= 49÷(6+8)×2 直角三角形面积= 6×7÷2= 49÷14× 2 = 42÷2= 3.5× 2 = 21(dm²)= 7(dm²)4、图中梯形中空白部分是直角三角形,它的面积是45平方厘米,求阴影部分面积。
直角梯形的高=直角三角形的高梯形面积=(5+12)×7.5÷2= 45÷12×2 = 17×7.5÷2= 3.75×2 = 127.5÷2= 7.5(cm2) = 63.75(cm2)阴影部分面积=梯形面积–空白部分面积:63.75 - 45 = 18.75(cm2)5、阴影部分面积是40平方米,求空白部分面积。
(单位:米)梯形的高=三角形的高(阴影部分三角形)梯形面积=(6+10)×8÷2= 40÷10× 2 = 16×8÷2= 4× 2 = 128÷2= 8(m2) = 64(m2)空白部分面积=梯形面积–阴影部分面积:64–40 = 24(m2)6、如图,平行四边形面积240平方厘米,求阴影部分面积。
《组合图形的面积》练习题(含答案)

3(4)
解:2.5×1.5+(2.5+4)×(8-3-1.5)÷2+4×3=27.125(平方分米)
4
解:10×(52-10-14-16)÷2=60(平方厘米)
5
解:2×2+(5-2)×6=22(平方米)
6பைடு நூலகம்
解:大正方形面积为:22×22=484(平方厘米)
7.如图所示,一个平行四边形背分成A.B两被封,A的面积比B的面积打40平方米,A的上底是若干?
B
A
8米
【参考答案】
1
解:
A
B D
C
2
解:48÷8×3÷2=9(平方分米)
3(1)
解:8×6+(8+12)×3÷2=78(平方分米)
3(2)
解:(14+12)×6÷2+12×6÷2=114(平方分米)
3(3)
4.如图所示,梯形的周长是52厘米,求暗影部分的面积.
10
14
16
5.校园里有一块花园,(如图所示),算出它的面积.(单位:米)
6 2
2
5
6.大小正方形如图放置,暗影部分为重叠部分,求空白部分面积.(单位:厘米)
15
7
7
22
7.有一块地盘如图所示,你能用几种办法求出它的面积?(单位:米)
12
15
8
22
小正方形面积为:15×15=225(平方厘米)
暗影部分面积为:7×7=49(平方厘米)
空白部分的面积为:484+225-2×49=611(平方厘米)
7
解:办法一:
五年级数学组合图形的面积试题
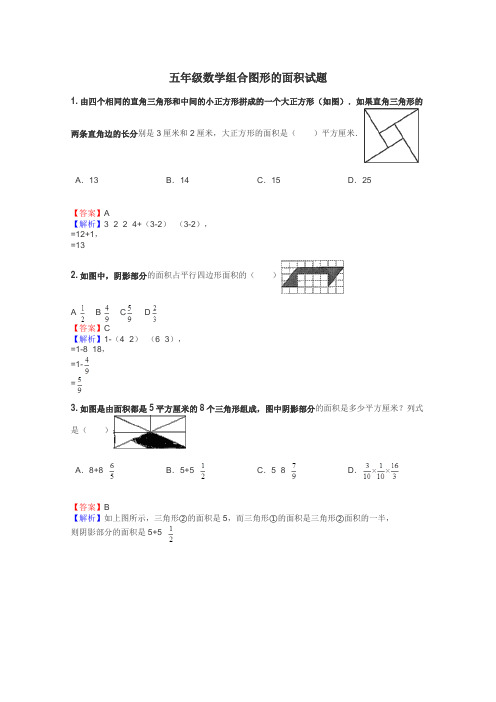
五年级数学组合图形的面积试题1.由四个相同的直角三角形和中间的小正方形拼成的一个大正方形(如图).如果直角三角形的两条直角边的长分别是3厘米和2厘米,大正方形的面积是()平方厘米.A.13B.14C.15D.25【答案】A【解析】3×2÷2×4+(3-2)×(3-2),=12+1,=132.如图中,阴影部分的面积占平行四边形面积的()A B C D【答案】C【解析】1-(4×2)÷(6×3),=1-8÷18,=1-=3.如图是由面积都是5平方厘米的8个三角形组成,图中阴影部分的面积是多少平方厘米?列式是()A.8+8×B.5+5×C.5×8×D.【答案】B【解析】如上图所示,三角形②的面积是5,而三角形①的面积是三角形②面积的一半,则阴影部分的面积是5+5×4.下列图形的面积是()A.800B.700C.750D.600【答案】A【解析】观察图形可知,这个图形的面积等于上面的三角形的面积与下面的平行四边形的面积之和,据此利用三角形和平行四边形的面积公式计算即可解答问题。
32×10÷2+32×20=160+640=8005.图中图形的面积最大的是()A.A B.B C.C【答案】B【解析】设三个图形的高都是h,则:三角形的面积=12h÷2=6h;平行四边形的面积=7h;梯形的面积=(8+3)h÷2=5.5h;7h>6h>5.5h,所以平行四边形的面积最大。
6.用同一条铁丝围成下列图形,围成的图形()的面积最大。
A.圆 B.长方形 C.正方形【答案】A【解析】假设铁丝的长度为12.56分米,则围成的正方形的边长是:12.56÷4=3.14(分米),正方形的面积是:3.14×3.14=9.8596(平方分米);长方形的长和宽的和是:12.56÷2=6.28(分米),长和宽越接近面积越大,若长可为3.15分米,宽为3.13分米,长方形的面积是:3.15×3.13=9.8595(平方分米);圆的半径是:12.56÷2÷3.14=2(分米),圆的面积是:3.14×22=12.56(平方分米);9.8595<9.8596<12.56;所以围成的圆的面积最大。
【人教新课标】五年级上册数学试题-六、4.组合图形的面积(含答案)

六、4.组合图形的面积一、填空乐园1.在一个上底是6厘米、下底是9厘米、高是4厘米的梯形中剪去一个最大的三角形,剩下的部分面积是( )平方厘米。
2.一个平行四边形,面积是54平方分米,如果高缩小到原来的21,要使面积不变,底应该( )。
3.三角形的底扩大a 倍,高扩大b 倍,面积扩大( )倍。
4.如图,要使三角形ABE 的面积是梯形AECD 面积的一半.BE 的长应是( )。
5.下面平行四边形的面积是15平方厘米,阴影部分的面积是( )平方厘米。
6.如图,现有6x6的方格,每个小方格的边长都是1,那么图中阴影部分的面积的总和等于( )。
7.如图,每两个相邻点之间的距离都是1厘米,三角形ABG 的面积是( ),梯形CDEF 的面积是( ),这个图形的面积是( )。
8.如图,每两个相邻的点之间的距离都是1厘米,平行四边形ABCE 的面积为( ),梯形ABDE 的面积为( )。
9.如图,若每个小正方形的面积都是1平方厘米,那么图中阴影部分的面积是( )平方厘米。
10.如图.每相邻三个点所形成的三角形都是面积为1的正三角形,则三角形ABC的面积为( )。
11.如图,平行四边形ABCD的底边DC长5 cm,直角三角形DCE的直角边EC长4厘米。
已知两块阴影部分的面积和比三角形EFG的面积大5平方厘米,则CF=( )厘米。
12.将一个正方形的一组对边各延长4厘米后,就成了一个长方形,这个长方形的面积比原来正方形的面积多32平方厘米,这个长方形的面积是原来正方形面积的( )倍。
二、判断快车1.两个等底等高的三角形都能拼成一个平行四边形。
( )2.在平行四边形内画一个三角形,三角形的面积一定等于平行四边形面积的一半。
( ) 3.两个面积相等的梯形,形状也一定相同。
( )4.梯形只有一条高,三角形有三条高。
( )5.两个完全一样的直角梯形可以拼成一个等腰梯形。
( )6.周长相等的两个平行四边形的面积不一定相等。
( )7.把一个长方形木框拉成平行四边形后,它的面积一定与原来长方形的面积相等。
数学五年级上册《组合图形的面积》同步练习题(含答案)
6.4 组合图形的面积(同步练习)一、填空题(共6题;共14分)1.一个正方形的边长增加2厘米,面积增加了20平方厘米,扩大后正方形的面积是________平方厘米.2.求不规则图形的面积,一般利用________和________的方法,将不规则图形转化成________3.把2个边长4厘米的正方形拼成一个长方形,这个长方形的周长是________厘米,面积是________平方厘米。
4.比较下面各图中阴影部分面积的大小。
_____________________5.如图是用边长1厘米的小正方形拼成的,它的周长是________厘米,面积是________平方厘米.6.图中阴影部分是_______形,它的底是小正方形的_______,它的高是_______。
二、单选题(共6题;共12分)7.如下图,图中阴影部分的面积是()cm²。
A. 12B. 16C. 18D. 368.右图是刘大伯家的一面墙。
若砌这面墙每平方米用砖185块,一共需要用()块砖。
A. 7400B. 6350C. 59209.计算左下图组合图形的面积,下面四幅图中,可以列式为“30×12+(9+ 30)×(20-12)÷2”的是()。
A. B. C. D.10.两个完全一样的直角三角形重叠成右图形状,形成两个梯形,这两个梯形的面积大小关系是( )。
A. A大B. B大C. 相等D. 无法确定11.下面组合图形的面积是()平方米。
A. 216B. 380C. 596D. 16412.如图所示,甲、乙是两个完全相同的长方形,两幅图的阴影面积相比,下列说法正确的是( )。
A. 甲>乙B. 甲=乙C. 甲<乙D. 无法判断三、判断题(共6题;共12分)13.面积相等的图形,形状一定相同.()14.在梯形中,阴影①的面积与阴影②的面积相等。
()15.不规则图形用单位方格纸测面积,单位越小测得结果越准确()16.任何一个梯形都可以分成两个等高的三角形。
【小学】北师大版五年级数学上册《第六章 组合图形的面积》单元测试题有答案
北师大版小学五年级数学上册《第六章组合图形的面积》单元测试题一.选择题(共8小题)1.如图中,每个方格的面积是1平方厘米,估计这片树叶的面积大约是()平方厘米.A.2021.25C.352.深圳土地总面积约1953平方千米,合()公顷.A.B.19530C.195300D.19530003.如图中的阴影部分是一片湿地,估一估,这片湿地的面积最接近()公顷.(每个小方格代表一公顷)A.25B.65C.12021.1504.如图,两条虚线相互平行,两条虚线间的距离为hm.从左往右,各图形中的涂色部分的总面积分别标记为①、②、③、④,则()A.①=②=③B.②=③=④C.①=②=④D.①=②=③=④=2hm25.求组合图形A的面积.不正确的方法是()A.组合图形A的面积=长方形的面积﹣梯形的面积B.组合图形A的面积=三角形的面积梯形的面积C.组合图形A的面积=长方形的面积梯形的面积D.组合图形A的面积=正方形的面积三角形的面积6.以下表达正确的是()A.1平方千米=1000平方米B.100公顷=1平方千米C.1公顷=100平方米7.如图,平行四边形底边的中点是A,它的面积是48m2.涂色三角形的面积是()m2.A.4B.8C.128.如图,长方形的长为12厘米,宽为5厘米,阴影部分甲的面积比乙的面积大15平方厘米,那么,ED的长是()A.厘米B.厘米C.厘米D.厘米二.填空题(共10小题)9.如图组合图形的面积是平方厘米.10.如图方格中图形的面积为cm2(每个小方格的边长表示1cm).11.2平方千米=平方米8公顷=平方米96000000平方米=公顷=平方千米.12.钓鱼岛自古以来就是的领土,钓鱼岛列岛总面积约为630公顷,是平方千米.13.如图所示每个小方格的面积表示1cm2,估计圣诞树的面积是平方厘米.14.估计如图各图形的面积大约是多少平方厘米.(每个小方格的面积均为1cm2)图①:cm2图②:cm2图③:cm215.估计下面两片树叶的面积.(假设每个小方格的面积是1cm2)①面积约是,②面积约是.16.如果1平方米能站9人,那么1公顷能站人,1平方千米能站人.17.如图,三角形ABC的面积是50cm2,是平行四边形EFCD面积的2倍,图中阴影部分的面积是cm2.18.如图是一个平行四边形被分成了三个三角形,涂色图形的面积是40cm2,没涂色的三角形的面积是cm2.三.判断题(共5小题)19.60公顷>6平方千米.(判断对错)2021间教室的面积约为50平方米,那么2021这样的教室总面积约为1公顷.(判断对错)21.一亿个小学生手拉手可以绕地球赤道大约3圈半.(判断对错)22.我国古代数学家刘徽利用出入相补原理来计算平面图形的面积.(判断对错)23.计算组合图形的面积时,可以把组合图形分成几个简单的图形,然后再进行计算..(判断对错)四.计算题(共1小题)24.计算下面各图的面积.五.应用题(共5小题)25.上海路小学校园里有一块草地(如图).这块草地的面积是多少平方米?26.如图中每个小方格的面积为1m2.(1)请你估一估,这个池塘的面积大约是m2.(不满一格的按半格计算)(2)如果这个池塘每平方米可种莲藕3株,且每株可产莲藕,每千克莲藕可卖元,这个池塘产的莲藕能卖多少元?27.实验小学有一块地,近似平行四边形,底是172米,高为80米,现在要在这块地种上草坪,平均每平方米草坪15元;(1)这块草坪的面积大约是多少平方米?(2)种这块草坪一共需要多少元?28.一块麦田(如图),去年共收小麦90吨,平均每公顷收小麦多少吨?29.如图是公园的草坪,中间是人行道.(1)绿化的面积是多少平方米?(2)如果用边长是2分米的正方形地砖,在两块绿地之间铺人行道,要用多少块地砖?参考答案与试题解析一.选择题(共8小题)1.解:5×5=25(平方厘米)答:这片树叶的面积大约是25平方厘米故选:B。
五年级数学上册 第六单元—组合图形的面积 (含答案)
组合图形的面积【知识点拨】解决图形面积:(1)观察图形,分析图形,找出图形中所包含的基本图形。
(2)把某些图形进行在面积相等条件下的形状或位置改动(叫做等积变形)。
(3)做出适当的辅助线,铺路搭桥,沟通联系。
算组合图形面积的方法通常用分割法、割补法、添补法、平移法、旋转法、剪拼法,加辅助线法等方法,对图形进行恰当合理的变形,找出解题的途径,正确计算。
【随堂练习】1、求下列图形的面积。
(单位:分米)2、求下面阴影部分的面积。
(单位:厘米)3、图中平行四边形面积是280 平方厘米,求阴影部分的面积。
4、用“割补”或“扩展”法求下图中各图形的面积。
(每一方格为1cm²)5、如图,大正方形和小正方形的边长分别是4 厘米和3 厘米,求阴影部分的面积。
6、如下图是两个正方形组成的,已知大正方形边长10 分米,小正方形的边长7 分米,求阴影部分的面积。
参考答案1、求下列图形的面积。
(单位:分米)2、求下面阴影部分的面积。
(单位:厘米)3、图中平行四边形面积是280 平方厘米,求阴影部分的面积。
解:280÷14=20cm(20-12)×14÷2=56cm²4、用“割补”或“扩展”法求下图中各图形的面积。
(每一方格为1cm²)S①=8.5cm²S②=5.5cm²S③=10cm²5、如图,大正方形和小正方形的边长分别是4 厘米和3 厘米,求阴影部分的面积。
解:4×4+3×3=25cm²4×(4+3)÷2=14cm²3×3÷2=4.5cm²25-14-4.5=6.5cm²答:阴影部分的面积6.5cm²6、如下图是两个正方形组成的,已知大正方形边长10 分米,小正方形的边长7 分米,求阴影部分的面积。
解:10×10+7×7=149dm²7×(10+7)÷2=59.5dm²10×10÷2=50dm²149-59.5-50=39.5dm²答:阴影部分的面积39.5dm²7、如图,ABCD 是长8 厘米,宽为6 厘米的长方形,AF 是4 厘米,求△AEF。
【重难点突破】北师大版五年级上册数学第六单元 组合图形的面积(含答案)
【重难点突破】北师大版五年级上册-第六单元组合图形的面积(含答案)一、选择题1.图中每个小方格的面积表示1平方厘米,估计这个米老鼠图片的面积是()平方厘米。
A.10B.20C.35D.502.在一个长10cm,宽7cm的长方形中剪一个最大的正方形,剩下部分的面积是()cm2。
A.12B.21C.49D.703.如图,平行四边形的面积是484平方厘米,梯形(阴影)的面积是()平方厘米。
A.185B.370C.740D.4074.一张边长4cm的正方形纸(如图),从相邻两边的中点连一条线段,沿这条线段剪去一个角,剩下的面积是()cm2。
A.14B.12C.10D.85.下图是由一个大正方形与一个小正方形拼成的,已知小正方形的边长为4cm,阴影部分的面积为28cm2。
那么空白部分的面积为()cm2。
A.20B.24C.28D.326.如图是一块长方形ABCD的场地,长AB=102m,宽AD=51m,从A、B两处入口的中路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪面积为.A.5050m2B.4900m2C.5000m2D.4998m27.下图,这个梯形的面积是()cm2.A.10B.25C.50D.1008.比较下面阴影部分的面积,()是错误的.A.①和②的面积相等B.④的面积最小C.③和④面积相等D.②比③的面积小9.一块正方形木板,一边截去15厘米,另一边截去10厘米,剩下的木板比原来面积减少1750平方厘米,那么原来正方形木板边长是()厘米.A.75B.74C.76D.7710.已知如图阴影部分的面积是3平方厘米,则两个正方形中较小的正方形的面积为.()A.3平方厘米B.6平方厘米C.12平方厘米D.无法确定二、图形计算11.求阴影部分面积。
(单位:cm)12.如图,组合图形的面积是多少平方厘米?13.如图,ABCD是一个直角梯形,求图中阴影部分的面积.14.计算下列图形的面积.(1)(2)三、填空题15.在括号里填上合适的单位。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学五年级数学《组合图形的面积》知识
点+试题(带答案)
本文介绍了组合图形的面积计算方法,包括分割法和添补法。
同时,也提到了通过数格子的方法来计算不规则图形的面积,并举了几个例子来说明如何应用这些方法。
第一段:介绍了组合图形的概念和计算面积的方法。
可以将其改写为:“组合图形由几个简单的图形组合而成,计算它的面积有多种方法,其中常用的是分割法和添补法。
分割法将图形分割成基本的图形,越简单的分割方法解题越简单,同时要考虑与给定条件的关系。
添补法则是通过补上一个简单的图形,使整个图形变成一个大的规则图形。
”
第二段:介绍了如何估计和计算不规则图形的面积。
可以将其改写为:“估计和计算不规则图形的面积,通常使用方格图来进行估计和计算。
因此,借助方格图能够帮助建立估计和计算不规则图形面积的方法。
”
第三至五段:分别举了几个例子来说明如何应用组合图形的面积计算方法。
这些例子已经没有格式错误或明显问题,因此不需要进行修改或删除。
6、给定平行四边形面积为240平方厘米,求阴影部分面积。
首先,计算梯形的下底,即平行四边形的底,得到20厘米。
然后,计算梯形面积为210平方厘米。
最后,用平行四边形面积减去梯形面积,得到阴影部分面积为30平方厘米。
7、已知梯形ABCD的面积为140平方厘米,AB=15厘米,DC=5厘米,求阴影部分的面积。
首先,计算梯形的高为14
厘米。
然后,计算阴影部分三角形的面积为105平方厘米。
8、给定图形中阴影部分,求阴影部分面积。
阴影部分可
以分成一个大三角形和一个小三角形,分别计算它们的面积,再将两个面积相加即可得到阴影部分面积为27平方厘米。
9、求梯形的面积。
首先,计算直角三角形的面积为6平
方厘米,然后计算梯形的高为2.4厘米。
最后,用梯形公式计
算面积为18平方厘米。
10、已知梯形ABCD的面积为37.8平方厘米,BE长7厘米,EC长4厘米,求平行四边形ABED的面积。
首先,计算梯形的高为4.2厘米。
然后,用平行四边形的高等于梯形的高的性质,计算平行四边形的面积为37.8平方厘米。
