数据结构第五章数组和广义表
数据结构第五章 数组与广义表

压缩存储方法:只需要存储下三角 (含对角线)上的元素。可节省一 半空间。
可以使用一维数组Sa[n(n+1)/2]作为n阶对称矩阵A的存 储结构,且约定以行序为主序存储各个元素,则在Sa[k]和矩
阵元素aij之间存在一一对应关系: (下标变换公式)
i(i+1)/2 + j 当i≥j k = j(j+1)/2 + i 当i<j
q = cpot[col];
T.data[q].i = M.data[p].j; T.data[q].j = M.data[p].i; T.data[q].e = M.data[p].e; ++cpot[col]; }
分析算法FastTransposeSMatrix的时间 复杂度:
for (col=1; col<=M.nu; ++col) … … for (t=1; t<=M.tu; ++t) … … for (col=2; col<=M.nu; ++col) … … for (p=1; p<=M.tu; ++p) … …
//对当前行中每一个非零元
处
brow=M.data[p].j;
理
if (brow < N.nu ) t = N.rpos[brow+1];
M
else { t = N.tu+1 }
的
for (q=N.rpos[brow]; q< t; ++q) { ccol = N.data[q].j; // 乘积元素在Q中列号
一、三元组顺序表
对于稀疏矩阵,非零元可以用三元组表示, 整个稀疏矩阵可以表示为所有非零元的三元组所 构成的线性表。例如:
《数据结构与算法》第五章-数组和广义表学习指导材料

《数据结构与算法》第五章数组和广义表本章介绍的数组与广义表可视为线性表的推广,其特点是数据元素仍然是一个表。
本章讨论多维数组的逻辑结构和存储结构、特殊矩阵、矩阵的压缩存储、广义表的逻辑结构和存储结构等。
5.1 多维数组5.1.1 数组的逻辑结构数组是我们很熟悉的一种数据结构,它可以看作线性表的推广。
数组作为一种数据结构其特点是结构中的元素本身可以是具有某种结构的数据,但属于同一数据类型,比如:一维数组可以看作一个线性表,二维数组可以看作“数据元素是一维数组”的一维数组,三维数组可以看作“数据元素是二维数组”的一维数组,依此类推。
图5.1是一个m行n列的二维数组。
5.1.2 数组的内存映象现在来讨论数组在计算机中的存储表示。
通常,数组在内存被映象为向量,即用向量作为数组的一种存储结构,这是因为内存的地址空间是一维的,数组的行列固定后,通过一个映象函数,则可根据数组元素的下标得到它的存储地址。
对于一维数组按下标顺序分配即可。
对多维数组分配时,要把它的元素映象存储在一维存储器中,一般有两种存储方式:一是以行为主序(或先行后列)的顺序存放,如BASIC、PASCAL、COBOL、C等程序设计语言中用的是以行为主的顺序分配,即一行分配完了接着分配下一行。
另一种是以列为主序(先列后行)的顺序存放,如FORTRAN语言中,用的是以列为主序的分配顺序,即一列一列地分配。
以行为主序的分配规律是:最右边的下标先变化,即最右下标从小到大,循环一遍后,右边第二个下标再变,…,从右向左,最后是左下标。
以列为主序分配的规律恰好相反:最左边的下标先变化,即最左下标从小到大,循环一遍后,左边第二个下标再变,…,从左向右,最后是右下标。
例如一个2×3二维数组,逻辑结构可以用图5.2表示。
以行为主序的内存映象如图5.3(a)所示。
分配顺序为:a11 ,a12 ,a13 ,a21 ,a22,a23 ; 以列为主序的分配顺序为:a11 ,a21 ,a12 ,a22,a13 ,a23 ; 它的内存映象如图5.3(b)所示。
数据结构课件-DS05-数组与广义表.ppt

的 i, 此即为该元素的行号。 j = k - i * (i + 1) / 2
此即为该元素的列号。 例,当 k = 8, 3*4 / 2 = 6 k < 4*5 / 2 =10,
取 i = 3。则 j = 8 - 3*4 / 2 = 2。
第 章 数组和广义表
a00 a01 a02 a03 上
n=4
第 章 数组和广义表
第五章 数组
数组的类型定义和表示方法 特殊矩阵和稀疏矩阵存储方法
及运算的实现 广义表的结构特点
第 章 数组和广义表
数组可以看成是一种特殊的线性表,即线性表 中数据元素本身也是一个线性表
5.1.1 二维数组的定义
定义
)
)
)
(a11 a12 ... ... a1n)
)
)
Amn
(a21
n1
n
aj1ij kj1mk in*l
第 章 数组和广义表
5.2.1 特殊矩阵
为节约存储,只存对角线及对角线以上的元素, 或者只存对角线及对角线以下的元素。前者称为 上三角矩阵,后者称为下三角矩阵。
a00 a01 a02 a0n1
aaan121000
a11
a21 an11
a12
a22 an12
数据元素同构
数组运算
给定一组下标,存取相应的数据元素
给定一组下标,修改数据元素的值
第 章 数组和广义表
矩阵Am×n看成n个列向量的线性表
第 章 数组和广义表
矩阵Am×n看成m个行向量的线性表
第 章 数组和广义表
中南大学数据结构与算法第5章数组和广义表课后作业答案

第5章数组与广义表习题练习答案5.1请按行及按列优先顺序列出四维数组A2*3*2*3的所有元素在内存中的存储次序,开始结点为a0000。
解:按行优先的顺序排列时,先变化右边的下标,也就是右到左依次变化,这个四维数组的排列是这样的:(将这个排列分行写出以便与阅读,只要按从左到右的顺序存放就是在内存中的排列位置) a0000a0001a0002a0010a0011a0012a0100a0101a0102a0110a0111a0112a0200a0201a0202a0210a0211a0212a1000a1001a1002a1010a1011a1012a1100a1101a1102a1110a1111a1112a1200a1201a1202a1210a1211a1212按列优先的顺序排列恰恰相反,变化最快的是左边的下标,然后向右变化,所以这个四维数组的排列将是这样的,(这里为了便于阅读,也将其书写为分行形式):a0000a1000a0100a1100a0200a1200a0010a1010a0110a1110a0210a1210a0001a1001a0101a1101a0201a1201a0011a1011a0111a1111a0211a1211a0002a1002a0102a1102a0202a1202a0012a1012a0112a1112a0212a02125.2 给出C语言的三维数组地址计算公式。
解:因为C语言的数组下标下界是0,所以Loc(A mnp)=Loc(A000)+((i*n*p)+k)*d其中Amnp表示三维数组。
Loc(A000)表示数组起始位置。
i、j、k表示当前元素的下标,d表示每个元素所占单元数。
5.3设有三对角矩阵A n*n,将其三条对角线上的元素逐行地存储到向量B[0...3n-3]中,使得B[k]=a ij,求:(1)用i , j 表示k的下标变换公式。
(2)用k 表示i,j 的下标变换公式。
数据结构第五章
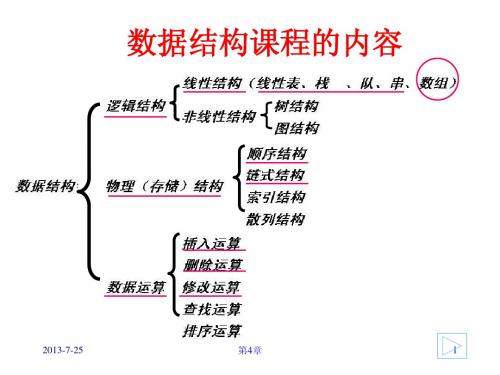
5.3.1 特殊矩阵
是指非零元素或零元素的分布有一定规律的矩阵。
1、对称矩阵 在一个n阶方阵A中,若元素满足下述性质: aij = aji 0≦i,j≦n-1 则称A为对称矩阵。
对称矩阵中的元素关于主对角线对称,故只 要存储矩阵中上三角或下三角中的元素,这样, 能节约近一半的存储空间。
2013-7-25 第4章 18
5.3 矩阵的压缩存储
在科学与工程计算问题中,矩阵是一种常用 的数学对象,在高级语言编制程序时,常将 一个矩阵描述为一个二维数组。 当矩阵中的非零元素呈某种规律分布或者矩 阵中出现大量的零元素的情况下,会占用许 多单元去存储重复的非零元素或零元素,这 对高阶矩阵会造成极大的浪费。 为了节省存储空间,我们可以对这类矩阵进 行压缩存储:
5.2 数组的顺序表示和实现 由于计算机的内存结构是一维的, 因此用一维内存来表示多维数组,就必 须按某种次序将数组元素排成一列序列 ,然后将这个线性序列存放在存储器中 。 又由于对数组一般不做插入和删除 操作,也就是说,数组一旦建立,结构 中的元素个数和元素间的关系就不再发 生变化。因此,一般都是采用顺序存储 的方法来表示数组。
即为多个相同的非零元素只分配一个存储空间; 对零元素不分配空间。
课堂讨论: 1. 什么是压缩存储? 若多个数据元素的值都相同,则只分配一个元素值的 存储空间,且零元素不占存储空间。 2. 所有二维数组(矩阵)都能压缩吗? 未必,要看矩阵是否具备以上压缩条件。 3. 什么样的矩阵具备以上压缩条件? 一些特殊矩阵,如:对称矩阵,对角矩阵,三角矩阵, 稀疏矩阵等。 4. 什么叫稀疏矩阵? 矩阵中非零元素的个数较少(一般小于5%)
通常有两种顺序存储方式:
⑴行优先顺序——将数组元素按行排列,第i+1个行 向量紧接在第i个行向量后面。以二维数组为例,按 行优先顺序存储的线性序列为: a11,a12,…,a1n,a21,a22,…a2n,……,am1,am2,…,amn 在PASCAL、C语言中,数组就是按行优先顺序存 储的。 ⑵列优先顺序——将数组元素按列向量排列,第j+1 个列向量紧接在第j个列向量之后,A的m*n个元素按 列优先顺序存储的线性序列为: a11,a21,…,am1,a12,a22,…am2,……,an1,an2,…,anm 在FORTRAN语言中,数组就是按列优先顺序存储的。
第5章 数据结构 多维数组和广义表

按列优先存储的寻址方法与此类似。
数据结构(C版)
广义线性表——多维数组
数组的存储结构与寻址——多维数组
n(n>2)维 数组一般也采用 按行优先和按列 优先两种存储方 法。请自行推导 任一元素存储地 址的计算方法。 Loc(aijk ) = Loc(a000) +( i×m2×m3 + j×m3 + k )×c
如何压缩存储?
只存储上三角(或下三角)部分的元素。
数据结构(C版)
a00 a10 a 20 a30
a01 a11 a21 a31
a02 a12 a22 a32
a03 a13 a23 a33
上 三 角 矩 阵
a00 a01 a02 a10 a11 a12 a a a 20 21 22
(a) 三对角矩阵
按行 存储
元素aij在一维数组中的序号 =2 + 3(i-1)+( j-i + 1)+1 =2i+ j+1 ∵一维数组下标从0开始 ∴元素aij在一维数组中的下标 =2i+ j (b) 寻址的计算方法
0
1
2
3
4
5
6
7
8
9 10
11 12
a00 a01 a10 a11 a12 a21 a22 a23 a32 a33 a34 a43 a44
数组——线性表的推广
a11 a21 … am1 a12 a22 … am2 … … … … a1n a2n … amn
A=(A1,A2,……,An)
其中: Ai=(a1i,a2i,……,ami) (1≤i≤n)
A=
二维数组是数据元素为线性表的线性表。
数据结构课件PPT数组和广义表
{ q=1; for (col=1;col<=T.mu;++col) for(p=1;p<=M.tu;++p) if ( M.data[p].j==col ) { T.data[q].i=M.data[p].j; T.data[q].j=M.data[p].i; T.data[q].e=M.data[p].e; ++q; } }
(row) (col) (value)
[0] 1 4 22
[0] 1 5 91
[1] 1 7 15
[1] 2 2 11
[2] 2 2 11
[2] 3 6 28
[3] 2 [4] 3来自6 17 4 -6[3] 4 [4] 4
1 22 3 -6
[5] 4 6 39
[5] 6 2 17
[6] 5 1 91
[6] 6 4 39
cpot[1]=1 cpot[col]=cpot[col-1]+num[col-1]
稀疏矩阵的快速转置(算法5.2)
Status FastTransposeSMatrix(TSMatrix M,TSMatrix &T) { T.mu=M.nu; T.nu=M.mu; T.tu=M.tu;
if (T.tu) { for (col=1;col<=M.nu;++col) num[col]=0; for (t=1;t<=M.tu;++t) ++num[M.data[t].j]; cpot[1]=1; for ( col=2;col<=M.nu;++col) cpot[col]=cpot[col-1]+num[col-1]; for (p=1;p<=M.Tu;++p) { col=M.data[p].j; q=cpot[col]; T.data[q].i=M.data[p].j; T.data[q].j=M.data[p].i; T.data[q].e=M.data[p].e; ++cpot[col]; } }
大学数据结构课件--第5章 数组和广义表
a 32 a 33 a 34 0 0
a 43 a 44 a 45 0
a 54 a 55 a 56 a 65 a 66
5.3.2 稀疏矩阵
稀疏矩阵的存储:如何表示非零元素的位置信息 1. 三元组表:每个元素用一个三元组(i,j,v)来表示。 i j v
0 1 6 1 1 6 2 3 8 12 9
2
3 4 5 6 7 8
2
5.2 数组的顺序表示和实现
a00 a00 a10 a01 存储单元是一维结构,而数组是个多维结构 , …… …… 则用一组连续存储单元存放数组的数据元素就有 am-1,0 a0,n-1 个次序约定问题。 a01 a10
a11
……
a11
……
二维数组可有两种存储方式: am-1,1 a1,n-1
……
K=
i*n-i(i-1)/2+j-i n(n+1)/2
当 i≤j 当i>j
0 a11 ... a1n-1 ... ... ... ... 0 0 0 an-1n-1
当i ≤ j时,a[i][j]是非零元素, a[i][j]前面有i行,共有n+(n-1)+(n-2)+…(n-(i-1))
=i(n+[n-(i-1)])/2=i*n-i(i-1)/2个元素,a[i][j]前面有j列,共j-i个非零元素,
A m× n
( a10 a11 … a1,n-1 )
=
注:
( … … …… ) ( am-1,0 am-1,2 … am-1,n-1 ) ( ( ( (
① 数组中的元素都具有统一的类型; ② 数组元素的下标一般都具有固定的上界和下界,即数组一旦 被定义,它的维数和维界就不再发生改变; ③ 数组的基本操作简单:初始化、销毁、存取元素和修改元素值
数据结构(C)严蔚敏(数组与广义表)PPT课件
a00
Am×n
=
a10 ...
am-1,0
a01 a11 ...
am-1,1
a02 a12 ...
am-1,2
... a0,n-1
...
a1,n-1
... ...
... am-1,n-1
Data Structure
03.12.2020
Page 5
按行序为主序存放
0
1
n-1
Am×n
=
a00 a10 ...
a00
Am×n
=
a10 ...
am-1,0
a01 a11 ...
am-1,1
a02 a12 ...
am-1,2
... a0,n-1
...
a1,n-1
... ...
... am-1,n-1
列向量
a00
Am×n
=
a10 ...
am-1,0
a01 a11 ...
am-1,1
a02 a12 ...
初始条件:A 是 n 维数组,e 为元素变量,随后是 n 个下标值。 操作结果:若各下标不超界,则e赋值为所指定的A的元素值,并返回OK。
Assign(&A, e, index1, ..., indexn)
初始条件:A 是 n 维数组,e 为元素变量,随后是 n 个下标值。 操作结果:若下标不超界,则将 e 的值赋给A中指定下标的元素。
a00 a10 ……. am-1,1 a01 a11 …….. am-1,1 ………. a0,n-1 a1,n-1 …….. am-1 ,n-1
Page 7
按行序为主序存放
0
Am×n
数据结构数组和广义表
数据结构05数组与广义表数组与广义表可以看做是线性表地扩展,即数组与广义表地数据元素本身也是一种数据结构。
5.1 数组地基本概念5.2 数组地存储结构5.3 矩阵地压缩存储5.4 广义表地基本概念数组是由相同类型地一组数据元素组成地一个有限序列。
其数据元素通常也称为数组元素。
数组地每个数据元素都有一个序号,称为下标。
可以通过数组下标访问数据元素。
数据元素受n(n≥1)个线性关系地约束,每个数据元素在n个线性关系地序号 i1,i2,…,in称为该数据元素地下标,并称该数组为n维数组。
如下图是一个m行,n列地二维数组A矩阵任何一个元素都有两个下标,一个为行号,另一个为列号。
如aij表示第i行j列地数据元素。
数组也是一种线性数据结构,它可以看成是线性表地一种扩充。
一维数组可以看作是一个线性表,二维数组可以看作数据元素是一维数组(或线性表)地线性表,其一行或一列就是一个一维数组地数据元素。
如上例地二维数组既可表示成一个行向量地线性表: A1=(a11,a12,···,a1n)A2=(a21,a22, ···,a2n)A=(A1,A2, ···,Am) ············Am=(am1,am2, ···,amn)也可表示成一个列向量地线性表:B1=(a11,a21,···,am1)B2=(a12,a22, ···,am2)A=(B1,B2, ···,Bm) ············Bn=(a1n,a2n, ···,amn)数组地每个数据元素都与一组唯一地下标值对应。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数据结构第五章数组和广义表(总6页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第五章数组和广义表:习题习题一、选择题1.假设以行序为主序存储二维数组A[1..100,1..100],设每个数据元素占两个存储单元,基地址为10,则LOC(A[5,5])=( )。
A. 808B. 818C. 1010D. 10202.同一数组中的元素( )。
A. 长度可以不同 B.不限 C.类型相同 D. 长度不限3.二维数组A的元素都是6个字符组成的串,行下标i的范围从0到8,列下标j的范圈从1到10。
从供选择的答案中选出应填入下列关于数组存储叙述中( )内的正确答案。
(1)存放A至少需要( )个字节。
(2)A的第8列和第5行共占( )个字节。
(3)若A按行存放,元素A[8]【5]的起始地址与A按列存放时的元素( )的起始地址一致。
供选择的答案:(1)A. 90 B. 180 C. 240 D. 270(2) A. 108 B. 114 C. 54 D. 60(3)[8][5] B. A[3][10] [5][8] [O][9]4.数组与一般线性表的区别主要是( )。
A.存储方面B.元素类型方面C.逻辑结构方面D.不能进行插入和删除运算5.设二维数组A[1..m,1..n]按行存储在数组B[1..m×n]中,则二维数组元素A[i,j]在一维数组B中的下标为( )。
A. (i-l)×n+jB. (i-l)×n+j-lC.i×(j-l) D. j×m+i-l6.所谓稀疏矩阵指的是( )。
A.零元素个数较多的矩阵B.零元素个数占矩阵元素中总个数一半的矩阵C.零元素个数远远多于非零元素个数且分布没有规律的矩阵D.包含有零元素的矩阵7.对稀疏矩阵进行压缩存储的目的是( )。
A.便于进行矩阵运算B.便于输入和输出C.节省存储空间D. 降低运算的时间复杂度8.稀疏矩阵一般的压缩存储方法有两种,即( )。
A.二维数组和三维数组B.三元组和散列C.三元组和十字链表D.散列和十字链表9.有一个100×90的稀疏矩阵,非0元素有10个,设每个整型数占两字节,则用三元组表示该矩阵时,所需的字节数是( )。
A. 60B. 66 C.18000 D.3310. A[N,N]是对称矩阵,将下面三角(包括对角线)以行序存储到一维数组T[N(N+I)/2]中,则对任一上三角元素a[i][j]对应T[k]的下标k是( )。
A. i(i-l)/2+jB. j(j-l)/2+iC. i(j-i)/2+1D. j(i-l)/2+111.已知广义表L=((x,y,z),a,(u,t,w)),从L表中取出原子项t的运算是( )A. head(tail(tail(L)))B. tail(head(head(taiI (L))))C. head(tail(head(taiI(L))))D. head(tail(head(tail(tail (L)))))12.广义表A=(a,b,(c,d),(e,(f,g))),则下面式子的值为( )。
Head(TaiI(Head(TaiI(Tail(A)))))A.(g) B.(d)13.广义表((a,b,c,d))的表头是( ),表尾是( )。
B.( )C.(a,b,c,d)D.(b,c,d)14.设广义表L=((a,b,c)),则L的长度和深度分别为( )。
和1 和3 和2 和315.下面说法不正确的是( )。
A. 广义表的表头总是一个广义表B.广义表的表尾总是一个广义表C.广义表难以用顺序存储结构D.广义表可以是一个多层次的结构二、填空题1.数组的存储结构采用____存储方式。
2.二维数组A[10][20]每个元素占一个存储单元,并且A[0][O]的存储地址是200,若采用行序为主方式存储,则A[6][12]的地址是____ ,若采用列序为主方式存储,则A[6][12]的地址是____。
3.三维数组a[4][5][6](下标从0开始计,a有4×5×6个元素),每个元素的长度是2,则a[2][3][4]的地址是____。
(设a[0][0][0]的地址是100 0,数据以行为主方式存储)4. n阶对称矩阵a满足a[i][j]=a[j][i],i,j=1..n,,用一维数组t存储时,t的长度为____, glist p;{ glist q,h,t,s;if (p==NULL) q=NULL;else{ if____{q= (glist)malloc( sizeof (gnode));q->tag=0;q->=p->; }elsef____;if______{ t=reverse (p->val. ptr. tp);s=t;while( s->val. ! =NULL)s=s->val .;s->val .ptr. tp=( glist) malloc( sizeof (gnode));s=s->val .; s->tag=l;s->val.=NULL;s-> }else{ q=( glist) malloc( sizeof( gnode));q->tag=l;q-> }}}return (q);}三、判断题1.数组不适合作为任何二叉树的存储结构。
( )2.稀疏矩阵压缩存储后,必会失去随机存取功能。
( )3.数组是同类型值的集合。
( )4.数组可看成线性结构的一种推广,因此与线性表一样,可以对它进行插入,删除等操作。
( )5.一个稀疏矩阵Am*n采用三元组形式表示,若把三元组中有关行下标与列下标的值互换,并把m和n的值互换,则就完成了Am*n的转置运算。
( )6.广义表的取表尾运算,其结果通常是个表,但有时也可是个单元素值。
( )7.若一个广义表的表头为空表,则此广义表亦为空表。
( )8.广义表中的元素或者是一个不可分割的原子,或者是一个非空的广义表。
( )9.所谓取广义表的表尾就是返回广义表中最后一个元素。
( )10.广义表的同级元素(直属于同一个表中的各元素)具有线性关系。
( )11. 一个广义表可以为其他广义表所共享。
( )四、简答题1.在以行序为主序的存储结构中,给出三维数组A2*3*4的地址计算公式(下标从0开始计数)。
2.数组A中,每个元素A嘶]的长度均为32个二进位,行下标从-1到9,列下标从1到11,从首地址s开始连续存放主存储器中,主存储器字长为16位。
求:(1)存放该数组所需多少单元(2)存放数组第4列所有元素至少需多少单元(3)数组按行存放时,元素A[7,4]的起始地址是多少(4)数组按列存放时,元素A[4,7]的起始地址是多少3.将数列1,2,3,…,n*n,依次按下列方式存放在二维数组A[1..n,1一n]中。
例如:n=5时,二维数组为4.画出下列广义表的链接存储结构,并求其深度。
((((),a,((b,c),(),d),(((e))))5.已知题图5-1为广义表的链接存储结构,写出该图表示的广义表。
题图5-16.设有广义表K1(K2(K5(a,K3(c,d,e)),K6(b,k)),K3,K4(K3,f)),要求:(1)指出K1的各个元素及元素的构成。
(2)计算表K1,K2,K3,K4,Ks,K6的长度和深度。
(3)画出K1的链表存储结构。
五、算法设计题1.对于二维整型数组A[m,n],分别编写相应函数实现如下功能:(1)求数组A4边元素之和。
(2)当m=n时分别求两条对角线上的元素之和,否则显示m≠n的信息。
2.编写子程序,将一维数组A[n*n](n<=10)中的元素按蛇形方阵存放在二维数组B[n][n]中,即:B[0][0]=A[0];B[0][1]=A[1];B[1][0]= A[2];B[2][0]=A[3];B[1][1]=A[4];B[0][3]=A[6];依此类推,如图题5-2所示:3.编写一个函数将两个广义表合并成一个广义表。
合并是指元素的合并,如两个广义表((a,b),(c))与(a,(e,f))合并后的结果是((a,b),(c),a,(e,f第五章数组与广义表第5章数组与广义表一、选择题, A,B,B二、填空题1.顺序存储方式。
2. 313, 327。
3. 1166。
*(n+1)/2,i*(i+l)/2。
5.线性表。
6.由其余元素构成的子表。
7.深度。
8.(),(()),2,2。
9. head (head (tail(L))). 10. (i= =k) break, i+l, i-l, i!=k。
11. p->tag==0, h=p-> p->next!=NULL, q=t, reverse(h)。
三、判断题1.× 2.× 3.√4.×5.×6.×7.× 8.× 9.×10. √ 11. √四、简答题1. LOC(A[i][j][k]=LOC(A[0][0][0]+i*12+j*4+k.2.(1) 12l*32/16=242。
(2) 11*32/16=22(3) LOC(A[0][0])+(8*11+3)*32/16=LOC(A[0][0])+182.(4) LOC(A[0][0])+182。
3.程序如下所示:#define NMAX 10#include <stdio.h>main(){int i,j,n,k,m;int a [NMAX] [NMAX];scanf( "%d", &n);m=l;for (i=O; i<n; i++){ for (j=i*n,k=O; j<(i+1)*n; j++,k++)a[i][k]=m++;}for(i=O; i<n; i++){for(j=O;j<n;j++)printf ("%4d",a [i][j]);printf(¨\n");}}4.深度为4广义表的链接存储结构为:5.((x,(y)),((()),(),(z)))6.ki由k2, k3, k4构成k1 k2k3k4k5k6长度: 3 2 3 2 2 2深度: 4 3 1 2 2 l五、算法设计题1. (1)#define M 5#define N 7long sum side (int a[M] [N]) int equal(GListNod e *ha, GListNode *hb);sublist;while(p!=NULL) data= =hb->val. data)return l;elsereturn O;else sublist;q=hb->val.sublist; sublist;r=h; //r指向前驱while (p!=NULL){r-p;p=p->link;}r->link=s;s->link=NULL;}。
