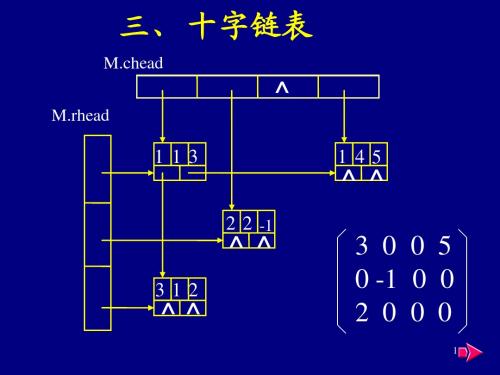
广义表的存储结构
《数据结构》习题集:第5章

第5章数组与广义表一、选择题1.在以下讲述中,正确的是(B )。
A、线性表的线性存储结构优于链表存储结构B、二维数组是其数据元素为线性表的线性表C、栈的操作方式是先进先出D、队列的操作方式是先进后出2.若采用三元组压缩技术存储稀疏矩阵,只要把每个元素的行下标和列下标互换,就完成了对该矩阵的转置运算,这种观点(A )。
A、正确B、错误3.二维数组SA 中,每个元素的长度为3 个字节,行下标I 从0 到7,列下标J 从0 到9,从首地址SA 开始连续存放在存储器内,该数组按列存放时,元素A[4][7]的起始地址为(B)。
A、SA+141B、SA+180C、SA+222D、SA+2254.数组SA 中,每个元素的长度为3 个字节,行下标I 从0 到7,列下标J 从0 到9,从首地址SA 开始连续存放在存储器内,存放该数组至少需要的字节数是( C )。
A、80B、100C、240D、2705.常对数组进行的两种基本操作是(B )。
A、建立与删除B、索引和修改C、查找和修改D、查找和索引6.将一个A[15][15]的下三角矩阵(第一个元素为A[0][0]),按行优先存入一维数组B[120]中,A 中元素A[6][5]在B 数组中的位置K 为( B )。
A、19B、26C、21D、157.若广义表A 满足Head(A)=Tail(A),则A 为(B )。
A、()B、(())C、((),())D、((),(),())8.广义表((a),a)的表头是( C ),表尾是(C )。
A、aB、bC、(a)D、((a))9.广义表((a,b),c,d)的表头是( C ),表尾是(D )。
A、aB、bC、(a,b)D、(c,d)10.广义表((a))的表头是( B ),表尾是(C )。
A、aB、(a)C、()D、((a))11.广义表(a,b,c,d)的表头是(A ),表尾是(D )。
A、aB、(a)C、(a,b)D、(b,c,d)12.广义表((a,b,c,d))的表头是(C ),表尾是(B )。
第5章 广义表
12
例:求下列广义表操作的结果(严题集5.10②) (k, p, h) ; 1. GetTail【(b, k, p, h)】=
2. GetHead【( (a,b), (c,d) )】= 3. GetTail【( (a,b), (c,d) )】=
(c,d)
((c,d)) ;
;
4. GetTail【 GetHead【((a,b),(c,d))】】=(b) ; 5. GetTail【(e)】= 6. GetHead 【 ( ( ) )】= 7. GetTail【 ( ( ) ) 】= () ; . .
讨论:广义表与线性表的区别和联系? 广义表中元素既可以是原子类型,也可以是列表; 当每个元素都为原子且类型相同时,就是线性表。
3
广义表是递归定义的线性结构,
LS = ( 1, 2, , n ) 其中:i 或为原子 或为广义表
例如: A = ( ) F = (d, (e)) D = ((a,(b,c)), F) C = (A, D, F) B = (a, B) = (a, (a, (a, , ) ) )
13
(a,b)
()
()
5.5 广义表的存储结构
由于广义表的元素可以是不同结构(原子或列表),难以用 顺序存储结构表示 ,通常用链式结构,每个元素用一个结 点表示。 注意:列表的“元素”还可以是列表,所以结点可能有两种形 式 1.原子结点:表示原子,可设2个域或3个域,依习惯而选。 法1:标志域,数值域 tag=0 标志域 value 数值域 法2:标志域、值域、表尾指针 tag=0 atom
} ADT Glist
10
基 结构的创建和销毁 InitGList(&L); DestroyGList(&L); 本 CreateGList(&L, S); CopyGList(&T, L); 操 作 状态函数
数据结构之第8章 广义表

3. 建立广义表的链式存储结构
假定广义表中的元素类型ElemType为char类型,
每个原子的值被限定为英文字母。
并假定广义表是一个表达式,其格式为:元素之
间用一个逗号分隔,表元素的起止符号分别为左、右
圆括号,空表在其圆括号内不包含任何字符。例如
“(a,(b,c,d))”就是一个符合上述规定的广义表格式。
/*广义表结点类型定义*/
广义表的两种基本情况 :
g2 1
∧
g1
1
∧
∧*Βιβλιοθήκη * 第 1 个元素**
…
*
*
∧
第 2 个元素
第 n 个元素
(a)空表
(b)非空表
为原子的情况 :
g3 0 a
∧
8.3 广义表的运算
1. 求广义表的长度 在广义表中,同一层次的每个结点是通过link域
链接起来的,所以可把它看做是由link域链接起来的
{ h->tag=1;
/*新结点作为表头结点*/
h->val.sublist=CreatGL(s); /*递归构造子表并链到表头结点*/ }
else if (ch==')') h=NULL; /*遇到')'字符,子表为空*/ else { h->tag=0; /*新结点作为原子结点*/ h->val.data=ch; } } else h=NULL; ch=*s; s++; if (h!=NULL) if (ch==',') h->link=CreatGL(s); else h->link=NULL; return h; }
单链表。这样,求广义表的长度就是求单链表的长度,
《算法与数据结构》-期中试卷

《算法与数据结构》课程期中试卷一、判断题(本大题共10小题。
每小题1分,共10分。
) (注意:将判断结果填入以下表格中。
对的打√,错的打×。
)1. 算法分析的目的是研究算法中输入和输出的关系。
( 错 )2. 可以随机访问任一元素是链表具有的特点。
( 错)3. 用一维数组存储一棵完全二叉树是有效的存储方法。
(对 )4. 在队列第i 个元素之后插入一个元素不是队列的基本运算。
( 错 )5. Tail (Tail (Head (((a,b),(c,d)))))= (b)。
( )6. 如果一个叶子是某二叉树的中序遍历的最后一个结点,则它必是该二叉树的前序遍历下的最后一个结点。
( 错)比如只有根节点和左子树的特殊情况。
7. 由权值分别为3, 8, 6, 2的叶子生成一棵哈夫曼树,它的带权路径长度为35。
(对 ) 带权路径长度=1*8+2*6+3*3+3*2=35(书P146)8. Head (Tail (Head (((a,b),(c,d)))))= (b)。
( )9. 数据结构包括数据间的逻辑结构、数据的存储方式和数据的运算三个方面。
(对 )逻辑结构、存储结构和数据的操作(运算)三个方面10. 线性的数据结构可以顺序存储,也可以链接存储;非线性的数据结构只能链接存储。
(错 ) 比如完全二叉树。
二、单项选择题(本大题共15小题。
每小题2分,共30分。
)(注意:以下各题只有一个正确答案,请将选择的结果填入以下表格中。
) 1. 下面程序段的时间复杂度为________。
s=0;for (i=1;i<n ;i++) for (j=1;j<i ;j++) s += i*j ;A. O(1)B. O(logn)C. O(n)D. O(n 2)[D] 就是s= s +i*j ;运算次数 ,T=(1+2+3…………n)=n(n+1)/2,为n^22. 以下数据结构中哪一个是线性结构_ ___。
A. 有向图B. 线索二叉树C. 队列D. 二叉排序树[C]堆栈,线性表(循序表,链表),队列都是线性结构。
广义表的应用课程设计

广义表的应用课程设计一、课程目标知识目标:1. 理解广义表的定义和基本概念;2. 学会使用广义表表示复杂的线性结构;3. 掌握广义表的基本操作,如创建、插入、删除、查找等;4. 能够运用广义表解决实际问题。
技能目标:1. 能够运用广义表的基本操作,实现线性结构的存储和运算;2. 能够分析实际问题,选择合适的广义表结构进行建模;3. 能够编写简单的程序,利用广义表解决具体问题;4. 培养学生的逻辑思维能力和编程实践能力。
情感态度价值观目标:1. 培养学生对数据结构和算法的兴趣,激发学习热情;2. 培养学生的团队协作意识和解决问题的能力;3. 培养学生面对复杂问题,勇于尝试、积极探究的精神;4. 增强学生的自信心和成就感,鼓励他们发挥创新精神。
课程性质:本课程为计算机科学领域的数据结构与算法课程,旨在帮助学生掌握广义表这一数据结构,并运用其解决实际问题。
学生特点:学生具备一定的编程基础,对数据结构有一定了解,但可能对广义表的认识较为陌生。
教学要求:结合学生特点,注重理论与实践相结合,通过实例讲解、课堂互动、上机实践等环节,使学生掌握广义表的应用。
同时,关注学生的情感态度,激发学习兴趣,培养其解决问题的能力和团队协作精神。
在教学过程中,将课程目标分解为具体的学习成果,以便于教学设计和评估。
二、教学内容1. 广义表的定义与基本概念:- 线性表、广义表的概念与区别;- 广义表的元素、表头、表尾及表长等基本概念。
2. 广义表的存储结构:- 顺序存储结构;- 链式存储结构。
3. 广义表的基本操作:- 创建广义表;- 插入、删除、查找等操作;- 广义表的遍历。
4. 广义表的应用:- 利用广义表解决实际问题,如多项式的表示与运算;- 广义表在数据压缩中的应用;- 广义表在计算机图形学中的应用。
5. 教学案例与上机实践:- 结合实际案例,分析广义表的应用场景;- 上机实践,编写程序实现广义表的基本操作;- 团队协作,共同探讨广义表在解决复杂问题中的应用。
数据结构广义表

结点结构是无论什么结点都有三个域:
第一个域是结点类型标志tag; 第二个域是指向一个列表的指针(当tag=1时) 或一个原子(当tag=0时); 第三个域是指向下一个结点的指针tp。
3 广义表的存储结构
形式描述为:
typedef enum{ ATOM, LIST }ElemTag typedef struct GLNode { //定义广义表结点 ElemTage tag; //公共部分,用以区分 原子结点和表结点 Unin{ //原子结点和表结点的联合部分 AtomType atom;//原子类型结点域, // AtomType由用户定义 struct GLNode *hp,; //表结点的表头指针域 }; struct GLNode *tp; //指向下一个结点的指针 }*Glist; //广义表类型
5. E=(a,E)
这是一个递归列表,其元素中有自己。
广义表也可以用图形表示,例如前述的广义表D和E可表示为:
广义表D
D
广义表E
E
C
A
B
a
e
a b c d
2 广义表的基本运算
广义表的基本运算 ⑴ 取表头 HEAD(LS); ⑵ 取表尾 TAIL(LS)。
3 广义表的存储结构
广义表中的数据元素可以是单元素,或是广义表, •很难用顺序存储结构表示,常采用链式存储结构。 1.表头表尾链存储结构 有两类结点:表结点和单元素结点。
P 1 3 1 1
A=y((c,3),(D,2)) C=x((1,10),(2,6))
^
1 2
A
z y 1 1 1 3
C
x 0 0 15 ^
B
1 2
1 2
^
数据结构C语言版期末考试试题(有答案)

“数据结构”期末考试试题一、单选题(每小题2分,共12分)1.在一个单链表HL中,若要向表头插入一个由指针p指向的结点,则执行( B)。
A. HL=ps p一>next=HLB. p一>next=HL;HL=pC. p一>next=Hl;p=HL;D. p一>next=HL一>next;HL一>next=p;2.n个顶点的强连通图中至少含有(B)。
A.n—l条有向边B.n条有向边C.n(n—1)/2条有向边D.n(n一1)条有向边3.从一棵二叉搜索树中查找一个元素时,其时间复杂度大致为( C )。
A.O(1)B.O(n)C.O(1Ogzn)D.O(n2)4.由权值分别为3,8,6,2,5的叶子结点生成一棵哈夫曼树,它的带权路径长度为( D )。
A.24 B.48C. 72 D. 535.当一个作为实际传递的对象占用的存储空间较大并可能需要修改时,应最好把它说明为(B)参数,以节省参数值的传输时间和存储参数的空间。
A.整形B.引用型C.指针型D.常值引用型·6.向一个长度为n的顺序表中插人一个新元素的平均时间复杂度为( A )。
A.O(n) B.O(1)C.O(n2) D.O(10g2n)二、填空题(每空1分,共28分)1.数据的存储结构被分为顺序结构链接结构索引结构散列结构四种。
2.在广义表的存储结构中,单元素结点与表元素结点有一个域对应不同,各自分别为值域和子表指针域。
3.——中缀表达式 3十x*(2.4/5—6)所对应的后缀表达式为————。
4.在一棵高度为h的3叉树中,最多含有—(3h一1)/2—结点。
5.假定一棵二叉树的结点数为18,则它的最小深度为—5—,最大深度为—18—·6.在一棵二叉搜索树中,每个分支结点的左子树上所有结点的值一定—小于—该结点的值,右子树上所有结点的值一定—大于—该结点的值。
7.当向一个小根堆插入一个具有最小值的元素时,该元素需要逐层—向上—调整,直到被调整到—堆顶—位置为止。
数据结构第五章
5.3.1 特殊矩阵
是指非零元素或零元素的分布有一定规律的矩阵。
1、对称矩阵 在一个n阶方阵A中,若元素满足下述性质: aij = aji 0≦i,j≦n-1 则称A为对称矩阵。
对称矩阵中的元素关于主对角线对称,故只 要存储矩阵中上三角或下三角中的元素,这样, 能节约近一半的存储空间。
2013-7-25 第4章 18
5.3 矩阵的压缩存储
在科学与工程计算问题中,矩阵是一种常用 的数学对象,在高级语言编制程序时,常将 一个矩阵描述为一个二维数组。 当矩阵中的非零元素呈某种规律分布或者矩 阵中出现大量的零元素的情况下,会占用许 多单元去存储重复的非零元素或零元素,这 对高阶矩阵会造成极大的浪费。 为了节省存储空间,我们可以对这类矩阵进 行压缩存储:
5.2 数组的顺序表示和实现 由于计算机的内存结构是一维的, 因此用一维内存来表示多维数组,就必 须按某种次序将数组元素排成一列序列 ,然后将这个线性序列存放在存储器中 。 又由于对数组一般不做插入和删除 操作,也就是说,数组一旦建立,结构 中的元素个数和元素间的关系就不再发 生变化。因此,一般都是采用顺序存储 的方法来表示数组。
即为多个相同的非零元素只分配一个存储空间; 对零元素不分配空间。
课堂讨论: 1. 什么是压缩存储? 若多个数据元素的值都相同,则只分配一个元素值的 存储空间,且零元素不占存储空间。 2. 所有二维数组(矩阵)都能压缩吗? 未必,要看矩阵是否具备以上压缩条件。 3. 什么样的矩阵具备以上压缩条件? 一些特殊矩阵,如:对称矩阵,对角矩阵,三角矩阵, 稀疏矩阵等。 4. 什么叫稀疏矩阵? 矩阵中非零元素的个数较少(一般小于5%)
通常有两种顺序存储方式:
⑴行优先顺序——将数组元素按行排列,第i+1个行 向量紧接在第i个行向量后面。以二维数组为例,按 行优先顺序存储的线性序列为: a11,a12,…,a1n,a21,a22,…a2n,……,am1,am2,…,amn 在PASCAL、C语言中,数组就是按行优先顺序存 储的。 ⑵列优先顺序——将数组元素按列向量排列,第j+1 个列向量紧接在第j个列向量之后,A的m*n个元素按 列优先顺序存储的线性序列为: a11,a21,…,am1,a12,a22,…am2,……,an1,an2,…,anm 在FORTRAN语言中,数组就是按列优先顺序存储的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广义表的存储结构
广义表是一种表示数据结构的层次形式。
广义表的数据结构具有弹性,可以用来表示任意复杂度的对象,广泛应用于计算机科学中,在许多普通的程序设计语言中,这是一种重要的数据类型。
简而言之,它可以表示更复杂的结构,例如树形结构和图形结构。
广义表是一种递归结构,它由多个元素构成。
一个广义表的元素可以是一个基本的值,也可以是一个广义表,表示下一级的数据结构。
基本元素可以是任何数据类型,而广义表的元素可以是任意复杂度的数据结构。
因此,广义表用来表示任意复杂度的数据结构有着十分强大的表示能力,成为一种强大的数据结构表示方式。
当处理广义表的存储问题时,需要考虑到其数据的特点,只有当特点被有效考虑到时,储存和操作广义表才能更有效地实现。
为了实现更有效的存储,一般有三种方式可以考虑:链式储存、双亲表示法和结点表示法。
链式储存是一种比较简单的方式,把广义表的每个元素都以链表的形式存储下来,这种方式可以方便地查找元素,操作形式也比较简单,但是因为引入了指针,而且每个结点只有一个指针,所以存储空间利用率低,不够高效。
双亲表示法是利用普通表表示广义表的一种方式,它把广义表的每个元素都储存在一个有限的表格中,每个元素的表格包括元素的值、子节点的位置、双亲节点的位置等,以此来表示广义表的结构关系。
双亲表示法的优点是其存储效率高,把每个元素的值和其结构关系存储在一张表中,存储空间利用率比较高,但是它的查找和操作效率比
较低,需要大量的遍历操作。
结点表示法是另一种表示广义表的方式,它把广义表的每个元素都储存在一个节点中,每一个节点中包含元素的值,以及指向该元素的子节点和双亲节点的指针,因此可以表示出广义表的层次结构。
结点表示法既可以查找结点和操作结点,又能存储元素的值和结构关系,所以其存储空间利用率较高,查找和操作也比较快,比较灵活。
总之,当处理广义表的存储问题时,可以通过链式储存、双亲表示法和结点表示法来实现更有效的存储,其中结点表示法比较灵活,在存储空间利用率上要优于其他方法。
因此在实践中,一般采用结点表示法来存储广义表,从而使得广义表的储存和操作更加有效。
