诺顿等效电路
电路定理——戴维南,诺顿,等效

P 20V (4A) 80W
产生功率 80W
例3.2.1 图(a)所示电路,已知i=1A;试求电压u
解用电流为1A电流源替换网络N 列节点方程: 解得:
4 3 1 1 1 u 1 2 3 2 6 3
u 2V
例3.2.2 图(a)所示电路,电路中仅电阻R可变,已知 R=R1时,测得电流i1=5A、i2=4A;当R=R2时,测得电流 i1=3.5A,i2=2A;当R=R3时,测得i2=8A,问此时测得的电 流i1等于多少?
u u u Ro i u oc
' "
例1、求图(a)所示单口网络的戴维南等效电路。 i
解:在端口标明开路电压uoc参考方向,注意到i=0,
u oc 1V (2) 2A 3V
将单口网络内电压源短路,电流源开路,得图(b)
Ro 1 2 3 6
(1 ) R2 u2 us R1 (1 ) R2
1 i1 us R1 (1 ) R2
例3.1.2 求电流 i1 与激励 u s 的函数关系
齐次定理: i1 Gus 设: i1 1A 节点1、2电压记1V 3V
电压源的电压等于该网络的开路电压uoc,这个 电阻等于从此单口网络两端看进去,当网络内部所有 独立源均置零(No)时的等效电阻R0 i =0 N
+
R0 戴维南等效电阻
3.3 等效电源定理
u _ oc
No
也称为输出电阻
例3.3.1 图(a)所示电路,求当RL分别等于2Ω、4Ω及16Ω时, 该电阻上电流i.
将已知条件代入得:
6 K U N 4 4 R U N 0 3 K 2 R U 2 N
诺顿定理

这就是说:若线性含源单口网络的端口电压 u 和 i 电流 为非关联参考方向,则其VAR可表示为
i
= isc –
u Ro
(4-31)
电路分析基础——第一部分:4-7
2/4
ia
N
+
u –
M
=
b (a)
a
N
isc
b (b)
ai
+
isc
Ro
u –
M
b
a
N0
Rab = Ro
b
图4-59 诺顿定理
电路分析基础——第一部分:4-7
戴维南(Thevenin)定理:线性单口网络 N,就其端口来 看,可等效为一个电压源串联电阻支路(图4-42a)。电 压源的电压等于该网络 N 的开路电压uoc(图b);串联电 阻R o 等于该网络中所有独立源为零值时所得的网络N0 的等效电阻Rab(图c )。
这就是说:若线性含源单口网络的端口电压 u 和 i 电流 为非关联参考方向,则其VAR可表示为
u = uoc – Roi
(4-27)
电路分析基础——第一部分:4-7
1/4
诺顿(Norton)定理:线性含源单口网络 N,就其端口来
看,可等效为一个电流源并联电阻的结合(图4-59a)。
电流源的电流等于该网络 N 的短路电流isc;并联电阻 R o 等于该网络中所有独立源为零值时所得的网络N0的 等效电阻R(图b )。
求得诺顿等效电路后,再把4电阻接上得图(c),由此可得
I=
9.6 ×
1.67 4+1.67
= 2.78A
电路分析基础——第一部分:第四章 目录
第四章 分解方法及单口电路
戴维南定理和诺顿定理实验
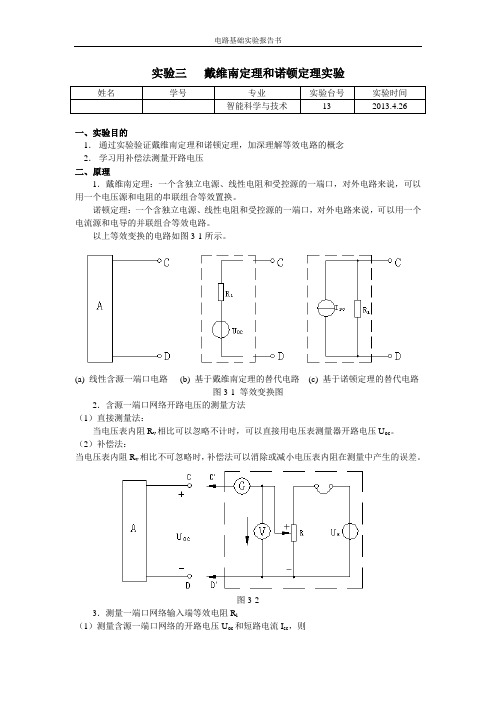
实验三戴维南定理和诺顿定理实验一、实验目的1.通过实验验证戴维南定理和诺顿定理,加深理解等效电路的概念2.学习用补偿法测量开路电压二、原理1.戴维南定理:一个含独立电源、线性电阻和受控源的一端口,对外电路来说,可以用一个电压源和电阻的串联组合等效置换。
诺顿定理:一个含独立电源、线性电阻和受控源的一端口,对外电路来说,可以用一个电流源和电导的并联组合等效电路。
以上等效变换的电路如图3-1所示。
(a) 线性含源一端口电路(b) 基于戴维南定理的替代电路(c) 基于诺顿定理的替代电路图3-1 等效变换图2.含源一端口网络开路电压的测量方法(1)直接测量法:当电压表内阻R v相比可以忽略不计时,可以直接用电压表测量器开路电压U oc。
(2)补偿法:当电压表内阻R v相比不可忽略时,补偿法可以消除或减小电压表内阻在测量中产生的误差。
图3-23.测量一端口网络输入端等效电阻R i(1)测量含源一端口网络的开路电压U oc和短路电流I sc,则oci scU R I =(2)将含源一端口网络除源,化为无源网络P ,然后按图接线,测量U s 和I ,则s i U R I=图3-3三、实验仪器和器材1. 0-30V 可调直流稳压电源 2. +15直流稳压电源 3. 0~200mA 可调恒流源 4. 电阻 5. 电阻箱6. 交直流电压电流表/电流表 7. 实验电路板 8. 短接桥 9. 导线四、实验内容及步骤1. 测量含源一端口网络的外部伏安特性测量含源一端口网络的外部伏安特性:用电阻箱作为一端口网络的外接电阻R L ,如图3-4所示,测量结果在表3-1中。
图3-42. 验证戴维南定理电压源用直流稳压电源代替,调节电源输出电压,使之等于U OC ,R i 用电阻箱代替,在CD 端接入负载电阻R L ,改变电阻值,侧去电流和电压。
结果如表3-2所示。
OC CD i SCUR R I ==图3-5表3-2 验证戴维南定理3. 验证诺顿定理按图3-6接线,构成诺顿等效电路,其中ISC 为可调电流源。
戴维南和诺顿等效电路

实验七戴维南和诺顿等效电路一、实验目的1.求出一个已知网络的戴维南等效电路。
2.求出一个已知网络的诺顿等效电路。
3.确定戴维南定理的正确性。
4.确定诺顿定理的正确性。
二、实验器材直流电压源 1个电压表1个电流表 1个电阻 3个三、实验原理及实验电路1.戴维南定理任何一个具有固定电阻和电源的线性二端网络,都可以用一个串联电阻的等效电压源来代替。
这个等效电压源的电压可称为戴维南电压U th,它等于原网络开路时的端电压U oc,如图13所示为测量二端网络开路端电压实验电路。
串联电阻可称为戴维南电阻R th,它等于原网络两端的开路电压U oc除以短路电流I sc。
所以 U th=U ocR th=U oc/I sc短路电流I s c可在原网络两端连接一个电流表来测量,如图14所示为测试二端网络短路电流实验电路。
短路电流I s c也可在原网络的输出端连接一条短路线来计算。
确定戴维南电阻R th的另一种方法是,将含源网络中所有的电压源用短路线代替,把所有的电流源断路,这时输出端的等效电阻就是R th。
在实验室里对一个未知网络确定其戴维南电阻R th的最好方法是,在未知网络两端连接一个可变电阻,然后调整阻值直至端电压等于开路电压U oc的一半,这时可变电阻的阻值就等于戴维南电阻R th。
2.诺顿定理任何具有固定电阻和电源的线性二端网络都可用一个并联电阻的等效电流源来代替。
这个等效电流源的电流称为诺顿电流I n,并等于原网络两端之间的短路电流I sc。
并联电阻称为诺顿电阻R n,并等于戴维南等效电路里的戴维南电阻R th。
这个并联电阻的求法也与戴维南电阻R th的求法一样。
在图15中,当电阻R L连接在网络两端时,端电压U a b与在戴维南等效电路两端连接R L时的电压是一样的。
R L连接在诺顿等效电路的两端情况也相同。
图13 测试二端网络开路端电压图14 测试二端网络短路电流实验电路四、实验步骤1.建立如图13所示测量二端网络开路端电压实验电路。
电路定理——戴维南,诺顿,等效

电路定理——戴维南,诺顿,等效
1.戴维南定理
戴维南定理是一种简化线性电路分析的方法,它的出发点是利用电压和电流之间的关系,把原来的电路转化为一个等效的电压源和电阻的串联电路,从而简化了电路的分析。
戴维南定理的基本思想是:在一个电路中,任何两个端点之间都可以看成是一个电压源和一个内部电阻的串联,其等效电路的电压源等于这两个端点之间的电压,内部电阻等于这两个端点看到的电阻。
式子表示为:
Vth=Voc
Rth = Voc/Isc
其中,Vth为等效电路的电压源,Rth为等效电路的内部电阻,Voc为开路电压,Isc 为短路电流。
2.诺顿定理
In = Isc
3.等效电路
等效电路是指具有相同电学特性的两个电路,它们在电性能上是等价的,可以相互替代。
在分析和设计电路时,我们可以将一个复杂的电路转化为一个简单的等效电路来替代原电路,从而使分析和设计电路变得更容易。
等效电路的基本特点是:
1)等效电路与原电路在端口参数方面具有相同的电学特性。
等效电路的应用主要有以下两个方面:
1)简化电路分析。
将一个复杂的电路转化为等效电路来代替原电路,从而使电路的分析变得更简单和方便。
2)设计和优化电路。
根据等效电路的特性和性能,我们可以对电路进行优化和设计,从而实现电路的更好性能和更高效的运行。
本文简要介绍了戴维南定理、诺顿定理和等效电路的概念和基本原理。
希望读者可以通过学习这些电路定理,更好地掌握电路分析和设计的技能。
戴维宁与诺顿等效电路之转换基本电学I

4-11
Chapter4
直流迴路
基本電學I
4-1 節點電壓法
節點電壓法應用於多節點電路
4-2
如下圖(a)所示,試求流過各電阻之電流大小及方向?
(a)
(b)
例4-2圖(1)
4-12
Chapter4
直流迴路
基本電學I
4-1 節點電壓法
Chapter4
直流迴路
基本電學I
4-1 節點電壓法
1.將本題中6V極性上下顛倒,重算各電阻之電流。
(1)以下方公共點為接地參考節點,如圖(b)。 (2)選定獨立節點,並設定其節點電壓為V1。 (3)假設流入或流出「獨立節點」的各支路電流方向,並標 示如I1、I2、I3等。 (4)以歐姆定律寫出各支路電流的算式。 V1 - (- 6) V1 - (- 12ቤተ መጻሕፍቲ ባይዱ V1
3.假設流入或流出「獨立節點」的電流方向,並以I1、I2、I3 及等標示之。 遇有已知電流(如電流源),則以其方向為該支路之電流方 向,如例題4-4。
4-4
Chapter4
直流迴路
基本電學I
4-1 節點電壓法
4-1.2 解題步驟
4.以歐姆定律寫出各支路電流的算式。 有N個節點的電路通常需列出N-1個算式,該支路如有電流 源者,直接以電流源電流為支路電流。
I1 = V - (- 12) V1 - 6 V ,I 2 = 1 ,I 3 = 1 3 2 6 V1 - 6 V1 - (- 12) V1 + + = 0 3 2 6
4-7
(a)
(5) 以KCL寫出電流方程式: I1+I2+I3=0
例4-1圖 (b)
Chapter4
电路中的诺顿定理介绍
电路中的诺顿定理介绍电路中的诺顿定理是电路分析中常用的一种方法,它可以将复杂的电路简化为等效电流源和等效电阻的串联电路。
诺顿定理的应用可以使电路分析更加简单和高效。
本文将介绍诺顿定理的原理和应用,并通过实例进行说明。
一、诺顿定理的原理诺顿定理是基于电路中的电流源和电阻之间的等效性原理提出的。
在电路中,我们经常需要分析某一部分电路的电流变化情况,但是当电路复杂时,电流的计算变得非常繁琐。
而诺顿定理通过将复杂电路简化为等效电流源和电阻的串联电路,大大简化了电路分析的过程。
诺顿定理的主要思想是将原电路中的各个支路电阻替换为等效电流源,其中等效电流等于原支路电阻上的电流。
通过这种替换,我们可以得到一个简化的电路,它与原电路在电流特性上是完全一致的。
二、诺顿定理的应用诺顿定理在电路分析中有着广泛的应用。
下面通过一个实例来说明诺顿定理的具体应用。
假设有一个复杂的电路,其中包含多个电阻和电流源,我们的目标是求解电阻R1上的电流。
首先,我们需要使用诺顿定理将电路进行等效替换。
1. 首先,根据原电路,我们将电阻R1拆解出来。
2. 然后,我们断开电阻R1的连接,将一个电流表连接在断开的地方,用于测量原电路中R1上的电流。
3. 接下来,将电流表所在的两端点连接起来,此时等效电路中只剩下电流表和电阻R1。
4. 在等效电路中,将电流表测量到的电流记为In,此时电流表相当于等效电阻R1上的电流源。
5. 最后,将测得的电流In除以等效电阻R1,得到R1上的实际电流。
通过上述步骤,我们成功将原电路中复杂的电路结构简化为等效电流源和电阻的串联电路,大大简化了电路的分析过程。
三、诺顿定理的优点诺顿定理作为一种电路分析方法,具有以下几个优点:1. 简化分析:诺顿定理能够将复杂电路简化为简单等效电流源和电阻的串联电路,大大简化了电路分析的过程。
2. 精确性:经过等效替换后的电路与原电路在电流特性上完全一致,因此分析结果是准确的。
3. 可视化:等效替换后的电路结构更加简单明了,易于理解和观察电路的特性。
电路中的诺顿定理应用举例
电路中的诺顿定理应用举例电路中的诺顿定理是电路分析中常用的一种方法,用于简化复杂电路的求解。
该定理通过将电路中的电源和电阻以一个等效电流源和等效电阻的方式代替,使得电路的分析更加简单和高效。
本文将通过几个具体的例子来展示诺顿定理在电路中的应用。
例一:串联电阻电路假设有一个由三个电阻串联而成的电路,电源电压为V,每个电阻的阻值分别为R1、R2和R3。
我们希望求解整个电路中的电流以及整个电路的等效电阻。
根据诺顿定理,我们首先将电源和电阻R1拆开,将电阻R2和R3合并成一个等效电阻Re。
这样,电路就变成了两个电阻串联的电路。
然后,我们在等效电阻Re处设置一个等效电流源In,其大小为V/Re。
最后,我们将电流源In与电阻R1串联,得到一个简化后的电路。
利用串联电阻的电流分配定理,我们可以得到电流源In流过电阻R1的电流为I1 = In * (R1 / (R1 + Re))。
然后,我们再利用电流分配定理求解电阻R2和R3上的电流。
计算得到每个电阻上的电流后,我们可以求解整个电路中的电流为I = I1 + I2 + I3。
同时,我们可以将电源电压V除以整个电路中的电流得到等效电阻Req = V / I。
至此,我们成功地利用诺顿定理简化了该串联电阻电路的求解过程。
例二:并联电阻电路假设有一个由三个电阻并联而成的电路,电源电压为V,每个电阻的阻值分别为R1、R2和R3。
我们希望求解整个电路中的电流以及整个电路的等效电阻。
根据诺顿定理,我们首先将电源和电阻R1拆开,将电阻R2和R3合并成一个等效电阻Re。
这样,电路就变成了两个电阻并联的电路。
然后,我们在等效电阻Re处设置一个等效电流源In,其大小为V/Re。
最后,我们将电流源In与电阻R1并联,得到一个简化后的电路。
利用并联电阻的电压分配定理,我们可以得到电流源In产生的电压与电阻R1之间的关系为V1 = In * (R1 / (R1 + Re))。
然后,我们再利用电压分配定理求解电阻R2和R3上的电压。
电阻电路的诺顿定理分析
电阻电路的诺顿定理分析电阻电路的诺顿定理是电路分析中的重要理论之一。
它通过将电路中的电压源与电阻网络分离,简化了电路分析的过程。
本文将介绍电阻电路的诺顿定理及其应用。
一、诺顿定理的定义诺顿定理是20世纪初美国工程师奥古斯特·诺顿提出的,它指出:在任意电阻电路中,可以用一个等效电流源与一个等效电阻串联来代替这个电阻网络。
根据诺顿定理,我们可以将电路中的电压源与电阻网络分离成两个部分:等效电流源与等效电阻。
等效电流源的大小等于电路中的总电流,而等效电阻等于电路中的总电阻。
二、诺顿等效电流源的计算为了计算诺顿等效电流源的大小,我们需要先计算电路中的总电流。
总电流可以通过欧姆定律得到:总电流等于电路中的总电压除以总电阻。
一般情况下,我们可以通过串并联电阻的计算将电路转化为一个简化的等效电阻。
然后,可以根据欧姆定律计算出总电流。
三、诺顿等效电阻的计算诺顿等效电阻是指将电路中的所有独立电压源置零,并将电阻网络看作是一个无源网络。
通过这种转换,我们可以得到等效电阻。
计算诺顿等效电阻的方法取决于电路的复杂程度。
对于简单的串并联电阻网络,我们可以直接应用串并联电阻的计算方法来计算等效电阻。
对于复杂的电路,我们可能需要使用更复杂的方法,如戴维南定理或梅肖尔定理。
四、诺顿定理的应用诺顿定理在电路分析中有广泛的应用。
它可以帮助我们简化复杂的电路,便于分析和计算。
一般情况下,如果我们只关心电路中的某个部分,而不关心电压源的情况下,可以使用诺顿定理来简化电路。
通过将电压源与电阻网络分离,我们可以用一个等效电流源和等效电阻来代替复杂的电路。
此外,诺顿定理还可以应用于电路的最大功率传输问题。
根据诺顿定理,电路的最大功率传输发生在负载电阻等于诺顿等效电阻的情况下。
总结:电阻电路的诺顿定理是分析电路中电压源与电阻网络之间关系的重要理论。
诺顿定理通过将电路转化为等效电流源与等效电阻,简化了电路分析与计算的过程。
通过诺顿定理,我们可以更方便地分析复杂的电路,并且可以应用于最大功率传输问题。
电阻网络中的戴维南诺顿等效变换解析实例
电阻网络中的戴维南诺顿等效变换解析实例在电路分析中,戴维南诺顿等效电路是一种常用的方法,用来简化复杂的电阻网络。
通过将电路中的所有电源替换为等效电流源和等效电阻,我们可以更方便地进行电路分析和计算。
本文将通过一个实例,详细介绍戴维南诺顿等效变换的具体步骤和解析方法。
假设我们有一个由多个电阻组成的电路,如下图所示:[图示电路]该电路中包含多个电阻,我们需要对其进行分析,计算出特定端口的电压和电流。
首先,我们要进行戴维南诺顿等效变换,将电源替换为等效电流源和等效电阻。
戴维南诺顿等效变换的步骤如下:步骤一:计算等效电流源的数值在原电路中,我们需要确定特定端口的电流。
为了计算等效电流源,我们需要断开该端口,并用电阻R连接。
然后,通过欧姆定律计算在该电阻上的电压V。
根据欧姆定律,V = I * R,其中I为等效电流源的大小。
步骤二:计算等效电阻的数值在步骤一中,我们已经得到了等效电流源的数值。
现在,我们需要计算等效电阻的大小。
为了计算等效电阻,我们需要在断开的端口处测量开路电压Voc。
然后,用欧姆定律计算在开路电压下的电流Isc。
最后,等效电阻的数值为R = Voc / Isc。
步骤三:确定等效电流源和等效电阻的位置和方向在步骤一和步骤二中,我们已经得到了等效电流源和等效电阻的数值。
现在,我们需要确定它们在电路中的位置和方向。
等效电流源与断开的端口相连,方向与实际电流的方向相反。
等效电阻与实际电阻位置相同。
通过以上步骤,我们成功地将原始电路转化为了戴维南诺顿等效电路。
接下来,我们可以利用等效电路来进行电路分析。
例如,我们希望计算特定端口的电压。
在等效电路中,我们只需要计算等效电源与该端口之间的电压。
通过应用基本的电路分析技巧,结合欧姆定律和基尔霍夫定律,我们可以轻松地计算出所需的电压。
除了计算特定端口的电压之外,戴维南诺顿等效电路还可以用于计算特定端口的电流以及其他电路参数。
通过将复杂的电路简化为等效电流源和等效电阻,我们能更加便捷地进行电路分析,并得到准确的结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
诺顿等效电路是和戴维南等效电路同时出现的,二者合称“发电机”等效电路,其解题原理又称为诺顿定理或者戴维南定理。
诺顿(戴维南)等效电路的本质,是将二端网络等效为一个含有内阻发电机,即任何二端网络经过等效变换后,可以用带内阻的发电机来表示,这对于二端网络外部的物理量的计算是等效的。
对于诺顿等效电路,就是将二端网络等效为电流源与内部电阻并联的形式;对于戴维南等效电路,就是将二端网络等效为电压源与内部电阻串联的形式。
这样对于外部电路的电压、电流的计算,完全是等效的。
需要说明的是:1、等效指的是针对网络外部,对网络内部并不等效;2、将外部的负载短路(诺顿等效)、或者外部负载断开(戴维南等效)后,电路的结构会变的较为简单,所以计算也会变得较为简单。
因此戴维南(诺顿)等效计算的方法,是电路分析很有效的计算方法。
1、Uoc的求法:R开路,求出的端口电压即Uoc;
2、Isc的求法:R短路,得到的短路电流即Isc。
3、Req的求法:①内部独立电源失效(置零),即独立电压源短路、独立电流源开路,受控源不不变。
②网络内部不含受控源,仅仅是电阻元件的串、并联,或者包含Y、△连接,通过串并联、Y-△变换,可求出端口的电阻,即Req;③内部含有受控源,采用加压求流法:在端口外加电压U,设流入的电流为I,根据电路变化找出变化规律,得到:Req=U/I。
④如果Uoc 和Isc都已经求出,可以利用:Req=Uoc/Isc。
