二次函数常用公式、结论及训练.doc
二次函数知识点汇总(全)
二次函数知识点(第一讲)一、二次函数概念:1.二次函数的概念:一般地,形如2y ax bx c =++(a b c ,,是常数,0a ≠)的函数,叫做二次函数。
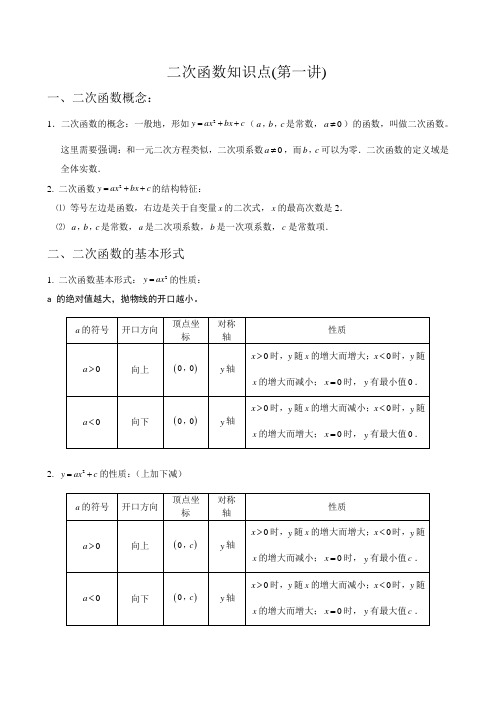
这里需要强调:和一元二次方程类似,二次项系数0a ≠,而b c ,可以为零.二次函数的定义域是全体实数.2. 二次函数2y ax bx c =++的结构特征:⑴ 等号左边是函数,右边是关于自变量x 的二次式,x 的最高次数是2. ⑵ a b c ,,是常数,a 是二次项系数,b 是一次项系数,c 是常数项.二、二次函数的基本形式1. 二次函数基本形式:2y ax =的性质: a 的绝对值越大,抛物线的开口越小。
2. 2y ax c =+的性质:(上加下减)3. ()2y a x h =-的性质:(左加右减)4. ()2y a x h k =-+的性质:三、二次函数图象的平移1. 平移步骤:方法一:⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+,确定其顶点坐标()h k ,; ⑵ 保持抛物线2y ax =的形状不变,将其顶点平移到()h k ,处,具体平移方法如下:【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位2. 平移规律在原有函数的基础上“h 值正右移,负左移;k 值正上移,负下移”.概括成八个字“左加右减,上加下减”.方法二:⑴c bx ax y ++=2沿y 轴平移:向上(下)平移m 个单位,c bx ax y ++=2变成m c bx ax y +++=2(或m c bx ax y -++=2)⑵c bx ax y ++=2沿轴平移:向左(右)平移m 个单位,c bx ax y ++=2变成c m x b m x a y ++++=)()(2(或c m x b m x a y +-+-=)()(2)四、二次函数()2y a x h k=-+与2y axbx c =++的比较从解析式上看,()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式,后者通过配方可以得到前者,即22424b ac b y a x a a -⎛⎫=++ ⎪⎝⎭,其中2424b ac b h k a a -=-=,. 五、二次函数2y ax bx c =++图象的画法五点绘图法:利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.一般我们选取的五点为:顶点、与y 轴的交点()0c ,、以及()0c ,关于对称轴对称的点()2h c ,、与x 轴的交点()10x ,,()20x ,(若与x 轴没有交点,则取两组关于对称轴对称的点).画草图时应抓住以下几点:开口方向,对称轴,顶点,与x 轴的交点,与y 轴的交点.六、二次函数2y ax bx c =++的性质1. 当0a >时,抛物线开口向上,对称轴为2bx a =-,顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭,.当2b x a <-时,y 随x 的增大而减小;当2b x a >-时,y 随x 的增大而增大;当2bx a=-时,y 有最小值244ac b a-.2. 当0a <时,抛物线开口向下,对称轴为2b x a =-,顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭,.当2bx a <-时,y 随x 的增大而增大;当2b x a >-时,y 随x 的增大而减小;当2bx a=-时,y 有最大值244ac b a -.七、二次函数解析式的表示方法1. 一般式:2y ax bx c =++(a ,b ,c 为常数,0a ≠);2. 顶点式:2()y a x h k =-+(a ,h ,k 为常数,0a ≠);3. 两根式:12()()y a x x x x =--(0a ≠,1x ,2x 是抛物线与x 轴两交点的横坐标).注意:任何二次函数的解析式都可以化成一般式或顶点式,但并非所有的二次函数都可以写成交点式,只有抛物线与x 轴有交点,即240b ac -≥时,抛物线的解析式才可以用交点式表示.二次函数解析式的这三种形式可以互化.八、二次函数的图象与各项系数之间的关系1. 二次项系数a二次函数2y ax bx c =++中,a 作为二次项系数,显然0a ≠.⑴ 当0a >时,抛物线开口向上,a 的值越大,开口越小,反之a 的值越小,开口越大; ⑵ 当0a <时,抛物线开口向下,a 的值越小,开口越小,反之a 的值越大,开口越大.总结起来,a 决定了抛物线开口的大小和方向,a 的正负决定开口方向,a 的大小决定开口的大小.2. 一次项系数b在二次项系数a 确定的前提下,b 决定了抛物线的对称轴. ⑴ 在0a >的前提下,当0b >时,02ba -<,即抛物线的对称轴在y 轴左侧;当0b =时,02ba -=,即抛物线的对称轴就是y 轴;当0b <时,02ba->,即抛物线对称轴在y 轴的右侧.⑵ 在0a <的前提下,结论刚好与上述相反,即当0b >时,02ba ->,即抛物线的对称轴在y 轴右侧;当0b =时,02ba -=,即抛物线的对称轴就是y 轴;当0b <时,02ba-<,即抛物线对称轴在y 轴的左侧.总结起来,在a 确定的前提下,b 决定了抛物线对称轴的位置.ab 的符号的判定:对称轴abx 2-=在y 轴左边则0>ab ,在y 轴的右侧则0<ab ,概括的说就是“左同右异” 总结:3. 常数项c⑴ 当0c >时,抛物线与y 轴的交点在x 轴上方,即抛物线与y 轴交点的纵坐标为正; ⑵ 当0c =时,抛物线与y 轴的交点为坐标原点,即抛物线与y 轴交点的纵坐标为0; ⑶ 当0c <时,抛物线与y 轴的交点在x 轴下方,即抛物线与y 轴交点的纵坐标为负. 总结起来,c 决定了抛物线与y 轴交点的位置.总之,只要a b c ,,都确定,那么这条抛物线就是唯一确定的.二次函数解析式的确定:根据已知条件确定二次函数解析式,通常利用待定系数法.用待定系数法求二次函数的解析式必须根据题目的特点,选择适当的形式,才能使解题简便.一般来说,有如下几种情况:1. 已知抛物线上三点的坐标,一般选用一般式;2. 已知抛物线顶点或对称轴或最大(小)值,一般选用顶点式;3. 已知抛物线与x 轴的两个交点的横坐标,一般选用两根式;4. 已知抛物线上纵坐标相同的两点,常选用顶点式.九、二次函数图象的对称二次函数图象的对称一般有五种情况,可以用一般式或顶点式表达 1. 关于x 轴对称2y ax bx c =++关于x 轴对称后,得到的解析式是2y ax bx c =---;()2y a x h k =-+关于x 轴对称后,得到的解析式是()2y a x h k =---;2. 关于y 轴对称2y ax bx c =++关于y 轴对称后,得到的解析式是2y ax bx c =-+;()2y a x h k =-+关于y 轴对称后,得到的解析式是()2y a x h k =++;3. 关于原点对称2y ax bx c =++关于原点对称后,得到的解析式是2y ax bx c =-+-; ()2y a x h k =-+关于原点对称后,得到的解析式是()2y a x h k =-+-; 4. 关于顶点对称(即:抛物线绕顶点旋转180°)2y ax bx c =++关于顶点对称后,得到的解析式是222b y ax bx c a=--+-;()2y a x h k =-+关于顶点对称后,得到的解析式是()2y a x h k =--+.5. 关于点()m n ,对称 ()2y a x h k =-+关于点()m n ,对称后,得到的解析式是()222y a x h m n k =-+-+-根据对称的性质,显然无论作何种对称变换,抛物线的形状一定不会发生变化,因此a 永远不变.求抛物线的对称抛物线的表达式时,可以依据题意或方便运算的原则,选择合适的形式,习惯上是先确定原抛物线(或表达式已知的抛物线)的顶点坐标及开口方向,再确定其对称抛物线的顶点坐标及开口方向,然后再写出其对称抛物线的表达式.十、二次函数与一元二次方程:1. 二次函数与一元二次方程的关系(二次函数与x 轴交点情况):一元二次方程20ax bx c ++=是二次函数2y ax bx c =++当函数值0y =时的特殊情况. 图象与x 轴的交点个数:① 当240b ac ∆=->时,图象与x 轴交于两点()()1200A x B x ,,,12()x x ≠,其中的12x x ,是一元二次方程()200ax bx c a ++=≠的两根.这两点间的距离21AB x x =-=.② 当0∆=时,图象与x 轴只有一个交点; ③ 当0∆<时,图象与x 轴没有交点.1' 当0a >时,图象落在x 轴的上方,无论x 为任何实数,都有0y >; 2' 当0a <时,图象落在x 轴的下方,无论x 为任何实数,都有0y <.2. 抛物线2y ax bx c =++的图象与y 轴一定相交,交点坐标为(0,)c ;3. 二次函数常用解题方法总结:⑴ 求二次函数的图象与x 轴的交点坐标,需转化为一元二次方程;⑵ 求二次函数的最大(小)值需要利用配方法将二次函数由一般式转化为顶点式;⑶ 根据图象的位置判断二次函数2y ax bx c =++中a ,b ,c 的符号,或由二次函数中a ,b ,c 的符号判断图象的位置,要数形结合;⑷ 二次函数的图象关于对称轴对称,可利用这一性质,求和已知一点对称的点坐标,或已知与x 轴的一个交点坐标,可由对称性求出另一个交点坐标. ⑸ 与二次函数有关的还有二次三项式,二次三项式2(0)ax bx c a ++≠本身就是所含字母x 的二次函数;下面以0a >时为例,揭示二次函数、二次三项式和一元二次方程之间的内在联系:二次函数考查重点与常见题型1. 考查二次函数的定义、性质,有关试题常出现在选择题中,如:已知以x 为自变量的二次函数2)2(22--+-=m m x m y 的图像经过原点, 则m 的值是2. 综合考查正比例、反比例、一次函数、二次函数的图像,习题的特点是在同一直角坐标系内考查两个函数的图像,试题类型为选择题,如: 如图,如果函数b kx y +=的图像在第一、二、三象限内,那么函数12-+=bx kx y 的图像大致是( )y y y y1 10 x o-1 x 0 x 0 -1 x A B C D3. 考查用待定系数法求二次函数的解析式,有关习题出现的频率很高,习题类型有中档解答题和选拔性的综合题,如: 已知一条抛物线经过(0,3),(4,6)两点,对称轴为35=x ,求这条抛物线的解析式。
(word完整版)二次函数知识点总结,推荐文档
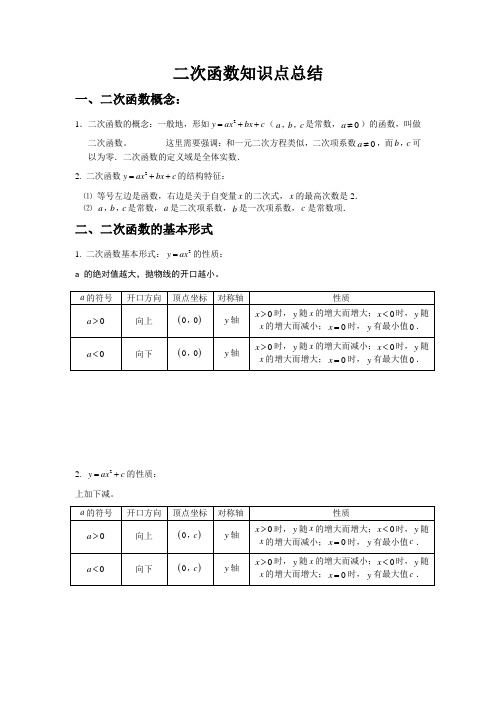
二次函数知识点总结一、二次函数概念:1.二次函数的概念:一般地,形如2=++(a b cy ax bx c,,是常数,0a≠)的函数,叫做二次函数。
这里需要强调:和一元二次方程类似,二次项系数0,可a≠,而b c 以为零.二次函数的定义域是全体实数.2. 二次函数2=++的结构特征:y ax bx c⑴等号左边是函数,右边是关于自变量x的二次式,x的最高次数是2.⑵a b c,,是常数,a是二次项系数,b是一次项系数,c是常数项.二、二次函数的基本形式1. 二次函数基本形式:2=的性质:y axa 的绝对值越大,抛物线的开口越小。
y ax c=+的性质:上加下减。
3. ()2y a x h =-的性质:左加右减。
4. ()2y a x h k =-+的性质:1. 平移步骤:⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+,确定其顶点坐标()h k ,; ⑵ 保持抛物线2y ax =的形状不变,将其顶点平移到()h k ,处,具体平移方法如下: 【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位2. 平移规律在原有函数的基础上“h 值正右移,负左移;k 值正上移,负下移”. 概括成八个字“左加右减,上加下减”. 四、二次函数()2y a x h k =-+与2y ax bx c =++的比较从解析式上看,()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式,后者通过配方可以得到前者,即22424b ac b y a x a a -⎛⎫=++ ⎪⎝⎭,其中2424b ac b h k a a -=-=,. 六、二次函数2y ax bx c =++的性质1. 当0a >时,抛物线开口向上,对称轴为2bx a =-,顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭,.当2bx a<-时,y 随x 的增大而减小; 当2bx a>-时,y 随x 的增大而增大; 当2bx a =-时,y 有最小值244ac b a -.2. 当0a <时,抛物线开口向下,对称轴为2bx a =-,顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭,.当2b x a <-时,y 随x 的增大而增大;当2b x a >-时,y 随x 的增大而减小;当2bx a=-时,y 有最大值244ac b a-.七、二次函数解析式的表示方法1. 一般式:2y ax bx c =++(a ,b ,c 为常数,0a ≠);2. 顶点式:2()y a x h k =-+(a ,h ,k 为常数,0a ≠);3. 两根式(交点式):12()()y a x x x x =--(0a ≠,1x ,2x 是抛物线与x 轴两交点的横坐标). 注意:任何二次函数的解析式都可以化成一般式或顶点式,但并非所有的二次函数都可以写成交点式,只有抛物线与x 轴有交点,即240b ac -≥时,抛物线的解析式才可以用交点式表示.二次函数解析式的这三种形式可以互化.八、二次函数的图象与各项系数之间的关系1. 二次项系数a⑴ 当0a >时,抛物线开口向上,a 的值越大,开口越小,反之a 的值越小,开口越大; ⑵ 当0a <时,抛物线开口向下,a 的值越小,开口越小,反之a 的值越大,开口越大. 2. 一次项系数b在二次项系数a 确定的前提下,b 决定了抛物线的对称轴.(同左异右 b 为0对称轴为y 轴)3. 常数项c⑴ 当0c >时,抛物线与y 轴的交点在x 轴上方,即抛物线与y 轴交点的纵坐标为正; ⑵ 当0c =时,抛物线与y 轴的交点为坐标原点,即抛物线与y 轴交点的纵坐标为0; ⑶ 当0c <时,抛物线与y 轴的交点在x 轴下方,即抛物线与y 轴交点的纵坐标为负. 总结起来,c 决定了抛物线与y 轴交点的位置.十、二次函数与一元二次方程:1. 二次函数与一元二次方程的关系(二次函数与x 轴交点情况):一元二次方程20ax bx c ++=是二次函数2y ax bx c =++当函数值0y =时的特殊情况. 图象与x 轴的交点个数:① 当240b ac ∆=->时,图象与x 轴交于两点()()1200A x B x ,,,12()x x ≠,其中的12x x ,是一元二次方程()200ax bx c a ++=≠的两根.. ② 当0∆=时,图象与x 轴只有一个交点;③ 当0∆<时,图象与x 轴没有交点.1' 当0a >时,图象落在x 轴的上方,无论x 为任何实数,都有0y >; 2' 当0a <时,图象落在x 轴的下方,无论x 为任何实数,都有0y <. 2. 抛物线2y ax bx c =++的图象与y 轴一定相交,交点坐标为(0,)c ;。
二次函数的相关公式

二次函数的相关公式二次函数可是中学数学里的一个重要角色呀!咱先来说说二次函数的一般式,那就是 y = ax² + bx + c (a ≠ 0)。
这里面的 a、b、c 都有着自己独特的作用。
a 决定了抛物线的开口方向和大小,要是 a 大于 0,抛物线开口向上,像个开心的笑脸;要是 a 小于 0,抛物线开口向下,就像个愁眉苦脸。
b 呢,它和 a 一起影响着抛物线的对称轴,对称轴的公式是 x = -b / (2a)。
c 就是抛物线和 y 轴的交点纵坐标啦,当 x = 0 时,y = c 。
顶点式 y = a(x - h)² + k 也很常用。
这个公式里,(h,k)就是抛物线的顶点坐标。
通过这个式子,咱们能一下子就找到抛物线的顶点,多方便!还有一个交点式 y = a(x - x₁)(x - x₂),这里的 x₁和 x₂是抛物线和 x 轴交点的横坐标。
记得我当年上学的时候,有一次数学考试,最后一道大题就是关于二次函数的。
题目给出了一个二次函数的一般式,让我们求出它的顶点坐标和对称轴,还问这个函数有没有最大值或者最小值。
当时我一看这题,心里有点小紧张,不过很快就冷静下来了。
我先把对称轴的公式写出来,算出对称轴,再把对称轴的值代入函数求出顶点的纵坐标,一步步稳稳地做下来。
最后得出答案的时候,心里那叫一个踏实。
咱们在学习二次函数的时候,一定要多做练习题,这样才能熟练掌握这些公式。
比如说,给定一个抛物线的顶点和另一个点的坐标,让我们写出它的顶点式。
这时候就得灵活运用顶点式的特点来解题。
还有啊,实际生活中二次函数也有很多用处呢。
比如说投篮的时候,篮球的运动轨迹就可以用二次函数来描述。
建筑师在设计桥梁的时候,也会用到二次函数的知识来确定桥梁的形状和受力情况。
总之,二次函数的这些公式就像是我们解决数学问题的法宝,只要我们用心去学,用心去用,就能在数学的世界里畅游无阻!所以,同学们,加油吧,把这些公式牢牢地装在我们的脑袋里,让它们为我们的学习和生活服务!。
初中数学二次函数公式大全

初中数学二次函数公式大全
初中数学二次函数公式大全
初中数学二次函数公式大全包括以下方面:
1. 一般式:y = ax^2 + bx + c,其中 a、b、c 为常数,称 y 为x 的二次函数。
顶点坐标为 (-b/2a,(4ac-b^2)/4a)。
2. 顶点式:y = a(x-h)^2 + k,其中 a、h、k 为常数,称 y 为x 的二次函数。
顶点坐标为 (h,k)。
3. 交点式 (和 x 轴):y = ax^2 + bx + c,其中 a、b、c 为常数,和 x 轴交点坐标为 x = -b/2a。
4. 两根式:y = a(x-x1)(x-x2),其中 a、x1、x2 为常数,称 y 为x 的二次函数。
和 x 轴交点坐标为 x1 = -b/2a,x2 = -b/2a。
5. 抛物线的特性:1) 抛物线是轴对称图型,对称轴为直线x = -b/2a。
2)抛物线有一个顶点P,坐标为P(-b/2a,(4ac-b^2)/4a)。
3)二次项系数a决定抛物线的开口方位与大小,a > 0 时,抛物线进取开口;a < 0 时,抛物线往下开口。
a 越大,则抛物线的开口越小。
4) 一次项系数 b 与二次项系数 a 一同决定对称轴的位置。
在 a 和
b 同号时,对称轴在 y 轴左;在 a 和 b 异号时,对称轴在 y 轴右。
5) 常数项 c 决定抛物线和 y 轴交点。
抛物线和 y 轴交于 (0,c)。
以上是初中数学二次函数公式大全的主要内容,这些内容是考生必做的课程之一,了解和记忆数学科目公式与定律,是考生备考的重要部分。
二次函数知识点总结及基础训练

二次函数复习资料第一部分 二次函数基础知识✧ 相关概念及定义二次函数的概念:一般地,形如2y ax bx c =++(a b c ,,是常数,0a ≠)的函数,叫做二次函数。
这里需要强调:和一元二次方程类似,二次项系数0a ≠,而b c ,可以为零.二次函数的定义域是全体实数. 二次函数2y ax bx c =++的结构特征:⑴ 等号左边是函数,右边是关于自变量x 的二次式,x 的最高次数是2.⑵ a b c ,,是常数,a 是二次项系数,b 是一次项系数,c 是常数项. ✧ 二次函数各种形式之间的变换二次函数c bx ax y ++=2用配方法可化成:()k h x a y +-=2的形式,其中ab ac k a b h 4422-=-=,. 二次函数由特殊到一般,可分为以下几种形式:①2ax y =; ②k ax y +=2; ③()2h x a y -=;④()k h x a y +-=2; ⑤c bx ax y ++=2.✧ 二次函数解析式的表示方法一般式:2y ax bx c =++(a ,b ,c 为常数,0a ≠); 顶点式:2()y a x h k =-+(a ,h ,k 为常数,0a ≠);两根式:12()()y a x x x x =--(0a ≠,1x ,2x 是抛物线与x 轴两交点的横坐标).注意:任何二次函数的解析式都可以化成一般式或顶点式,但并非所有的二次函数都可以写成交点式,只有抛物线与x 轴有交点,即240b ac -≥时,抛物线的解析式才可以用交点式表示.二次函数解析式的这三种形式可以互化. 二次函数2ax y =的性质二次函数2y ax c =+的性质✧ 二次函数y a x h =-的性质:✧ 二次函数()2y a x h k =-+的性质✧ 抛物线2y ax bx c =++的三要素:开口方向、对称轴、顶点.a 的符号决定抛物线的开口方向:当0>a 时,开口向上;当0<a 时,开口向下;a 相等,抛物线的开口大小、形状相同.对称轴:平行于y 轴(或重合)的直线记作2bx a=-.特别地,y 轴记作直线0=x . 顶点坐标坐标:),(ab ac a b 4422--顶点决定抛物线的位置.几个不同的二次函数,如果二次项系数a 相同,那么抛物线的开口方向、开口大小完全相同,只是顶点的位置不同.✧ 抛物线c bx ax y ++=2中,c b a ,,与函数图像的关系 二次项系数a二次函数2y ax bx c =++中,a 作为二次项系数,显然0a ≠.⑴ 当0a >时,抛物线开口向上,a 越大,开口越小,反之a 的值越小,开口越大; ⑵ 当0a <时,抛物线开口向下,a 越小,开口越小,反之a 的值越大,开口越大.总结起来,a 决定了抛物线开口的大小和方向,a 的正负决定开口方向,a 的大小决定开口的大小.一次项系数b在二次项系数a 确定的前提下,b 决定了抛物线的对称轴. ⑴ 在0a >的前提下,当0b >时,02ba-<,即抛物线的对称轴在y 轴左侧; 当0b =时,02ba-=,即抛物线的对称轴就是y 轴; 当0b <时,02ba->,即抛物线对称轴在y 轴的右侧. ⑵ 在0a <的前提下,结论刚好与上述相反,即 当0b >时,02ba->,即抛物线的对称轴在y 轴右侧; 当0b =时,02ba-=,即抛物线的对称轴就是y 轴; 当0b <时,02ba-<,即抛物线对称轴在y 轴的左侧. 总结起来,在a 确定的前提下,b 决定了抛物线对称轴的位置. 总结:常数项c⑴ 当0c >时,抛物线与y 轴的交点在x 轴上方,即抛物线与y 轴交点的纵坐标为正; ⑵ 当0c =时,抛物线与y 轴的交点为坐标原点,即抛物线与y 轴交点的纵坐标为0; ⑶ 当0c <时,抛物线与y 轴的交点在x 轴下方,即抛物线与y 轴交点的纵坐标为负. 总结起来,c 决定了抛物线与y 轴交点的位置.总之,只要a b c ,,都确定,那么这条抛物线就是唯一确定的. ✧ 求抛物线的顶点、对称轴的方法公式法:a b ac a b x a c bx ax y 442222-+⎪⎭⎫ ⎝⎛+=++=, ∴顶点是),(a b ac a b 4422--,对称轴是直线abx 2-=.配方法:运用配方的方法,将抛物线的解析式化为()k h x a y +-=2的形式,得到顶点为(h ,k ),对称轴是直线h x =.运用抛物线的对称性:由于抛物线是以对称轴为轴的轴对称图形,所以对称点的连线的垂直平分线是抛物线的对称轴,对称轴与抛物线的交点是顶点.用配方法求得的顶点,再用公式法或对称性进行验证,才能做到万无一失. ✧ 用待定系数法求二次函数的解析式一般式:c bx ax y ++=2.已知图像上三点或三对x 、y 的值,通常选择一般式. 顶点式:()k h x a y +-=2.已知图像的顶点或对称轴,通常选择顶点式.交点式:已知图像与x 轴的交点坐标1x 、2x ,通常选用交点式:()()21x x x x a y --=. ✧ 直线与抛物线的交点y 轴与抛物线c bx ax y ++=2得交点为(0, c ).与y 轴平行的直线h x =与抛物线c bx ax y ++=2有且只有一个交点(h ,c bh ah++2).抛物线与x 轴的交点:二次函数c bx ax y ++=2的图像与x 轴的两个交点的横坐标1x 、2x ,是对应一元二次方程02=++c bx ax 的两个实数根.抛物线与x 轴的交点情况可以由对应的一元二次方程的根的判别式判定:①有两个交点⇔0>∆⇔抛物线与x 轴相交;②有一个交点(顶点在x 轴上)⇔0=∆⇔抛物线与x 轴相切; ③没有交点⇔0<∆⇔抛物线与x 轴相离.平行于x 轴的直线与抛物线的交点可能有0个交点、1个交点、2个交点.当有2个交点时,两交点的纵坐标相等,设纵坐标为k ,则横坐标是k c bx ax =++2的两个实数根.一次函数()0≠+=k n kx y 的图像l 与二次函数()02≠++=a c bx ax y 的图像G 的交点,由方程组 2y kx ny ax bx c=+⎧⎨=++⎩的解的数目来确定:①方程组有两组不同的解时⇔l 与G 有两个交点; ②方程组只有一组解时⇔l 与G 只有一个交点;③方程组无解时⇔l 与G 没有交点.抛物线与x 轴两交点之间的距离:若抛物线c bx ax y ++=2与x 轴两交点为()()0021,,,x B x A ,由于1x 、2x 是方程02=++c bx ax 的两个根,故ac x x a b x x =⋅-=+2121,()()a a ac b a c a b x x x x x x x x AB ∆=-=-⎪⎭⎫⎝⎛-=--=-=-=444222122122121✧ 二次函数图象的对称:二次函数图象的对称一般有五种情况,可以用一般式或顶点式表达关于x 轴对称2y a x b x c =++关于x 轴对称后,得到的解析式是2y ax bx c =---; ()2y a x h k =-+关于x 轴对称后,得到的解析式是()2y a x h k =---;关于y 轴对称2y a x b x c =++关于y 轴对称后,得到的解析式是2y ax bx c =-+; ()2y a x h k =-+关于y 轴对称后,得到的解析式是()2y a x h k =++;关于原点对称2y a x b x c =++关于原点对称后,得到的解析式是2y ax bx c =-+-; ()2y a x h k =-+关于原点对称后,得到的解析式是()2y a x h k =-+-; 关于顶点对称2y a x b x c =++关于顶点对称后,得到的解析式是222b y ax bx c a=--+-;()2y a x h k =-+关于顶点对称后,得到的解析式是()2y a x h k =--+.关于点()m n ,对称 ()2y a x h k =-+关于点()m n ,对称后,得到的解析式是()222y a x h m n k =-+-+-总结:根据对称的性质,显然无论作何种对称变换,抛物线的形状一定不会发生变化,因此a 永远不变.求抛物线的对称抛物线的表达式时,可以依据题意或方便运算的原则,选择合适的形式,习惯上是先确定原抛物线(或表达式已知的抛物线)的顶点坐标及开口方向,再确定其对称抛物线的顶点坐标及开口方向,然后再写出其对称抛物线的表达式.✧ 二次函数图象的平移平移步骤:⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+,确定其顶点坐标()h k ,; ⑵ 保持抛物线2y ax =的形状不变,将其顶点平移到()h k ,处,具体平移方法如下:【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位平移规律在原有函数的基础上“h 值正右移,负左移;k 值正上移,负下移”.概括成八个字“左加右减,上加下减”.✧ 根据条件确定二次函数表达式的几种基本思路。
二次函数的性质与定理

二次函数的性质与定理一、引言二次函数是数学中一个重要的概念,也是数学中的一条经典曲线。
在本文中,我们将介绍二次函数的性质与定理,以帮助读者更好地理解和应用二次函数。
二、基本形式二次函数的一般形式为:y = ax^2 + bx + c其中,a、b、c为常数,且a ≠ 0。
三、顶点坐标二次函数的顶点坐标可通过以下公式计算得出:顶点横坐标为:x = -b / 2a顶点纵坐标为:y = c - b^2/4a四、对称轴二次函数的对称轴可通过以下公式计算得出:对称轴方程为:x = -b / 2a五、开口方向二次函数的开口方向由二次项系数a的正负确定:当a > 0时,二次函数开口向上;当a < 0时,二次函数开口向下。
六、零点二次函数的零点即为函数与x轴的交点,可以通过以下公式计算得出:首先,使用求根公式Δ = b^2 - 4ac 计算判别式。
若Δ > 0,则二次函数有两个不同的实数根;若Δ = 0,则二次函数有一个重根;若Δ < 0,则二次函数没有实数根。
七、抛物线二次函数的图像为一条抛物线,其凹凸性由二次项系数a的正负确定:当a > 0时,抛物线开口向上,为一条凹向上的抛物线;当a < 0时,抛物线开口向下,为一条凹向下的抛物线。
八、最值对于开口朝上的二次函数,最小值为函数的顶点纵坐标;对于开口朝下的二次函数,最大值为函数的顶点纵坐标。
九、图像平移对二次函数进行平移操作时,可以通过改变顶点坐标达到不同的平移效果:将二次函数沿x轴正方向平移h个单位,顶点坐标变为(x-h, y);将二次函数沿x轴负方向平移h个单位,顶点坐标变为(x+h, y);将二次函数沿y轴正方向平移k个单位,顶点坐标变为(x, y-k);将二次函数沿y轴负方向平移k个单位,顶点坐标变为(x, y+k)。
十、总结通过本文的介绍,我们了解了二次函数的性质与定理,包括顶点坐标、对称轴、开口方向、零点、抛物线、最值以及图像平移。
二次函数解法公式法
二次函数解法公式法二次函数是数学中的一种函数形式,其一般表达式为f(x)=ax^2+bx+c,其中a、b、c为常数,且a≠0。
二次函数在解决实际问题中有着广泛的应用,可以用来描述抛物线、开口方向等各种现象。
二次函数的解法有多种,其中一种常用的解法是使用二次函数的解法公式。
二次函数的解法公式可以帮助我们快速求解二次函数的解,并且可以通过解析解的方式得到准确的结果。
二次函数的解法公式主要包括两个公式,分别是求根公式和顶点公式。
下面我们来详细介绍这两个公式的求解方法。
1. 求根公式:求根公式是用来求解二次函数的x的解的公式,其表达式为:x=(-b±√(b^2-4ac))/2a其中,±表示两个解,√表示开方,b^2-4ac称为判别式。
求根公式的推导过程较为复杂,这里我们不再详细展开,只介绍如何使用求根公式求解二次函数的解。
我们需要确定二次函数的系数a、b、c的值,然后代入求根公式中即可求得解。
需要注意的是,判别式b^2-4ac必须大于等于0,否则二次函数没有实数解。
2. 顶点公式:顶点公式是用来求解二次函数的顶点坐标的公式,其表达式为:x=-b/2ay=f(x)=f(-b/2a)顶点公式的求解比较简单,只需要将二次函数的系数a、b代入公式中即可得到顶点坐标。
顶点公式可以帮助我们确定二次函数的最值,即抛物线的最高点或最低点。
通过求解顶点坐标,我们可以得到二次函数的凹凸性和开口方向。
除了使用求根公式和顶点公式,我们还可以通过图像法、配方法等方式来解二次函数的方程。
图像法是通过绘制二次函数的图像来寻找函数的零点、最值和凹凸性等特征。
通过观察抛物线的形状和位置,可以直观地得到二次函数的解。
配方法是一种通过将二次函数转化为完全平方式来求解的方法。
通过配方,我们可以将二次函数转化为一次函数相乘的形式,从而更容易求解。
总结起来,二次函数解法公式法是一种快速求解二次函数的解的方法。
通过求根公式和顶点公式,我们可以准确地求解二次函数方程的解和顶点坐标。
二次函数知识点总结及典型例题和练习
二次函数知识点总结及典型例题和练习(极好)知识点一:二次函数的概念和图像 1、二次函数的概念一般地,如果)0,,(2≠++=a c b a c bx ax y 是常数,,特别注意a 不为零,那么y 叫做x 的二次函数。
)0,,(2≠++=a c b a c bx ax y 是常数,叫做二次函数的一般式。
2、二次函数的图像二次函数的图像是一条关于abx 2-=对称的曲线,这条曲线叫抛物线。
抛物线的主要特征:①有开口方向;②有对称轴;③有顶点。
3、二次函数图像的画法--------五点作图法:(1)先根据函数解析式,求出顶点坐标,在平面直角坐标系中描出顶点M ,并用虚线画出对称轴(2)求抛物线c bx ax y ++=2与坐标轴的交点:当抛物线与x 轴有两个交点时,描出这两个交点A,B 及抛物线与y 轴的交点C ,再找到点C 的对称点D 。
将这五个点按从左到右的顺序连接起来,并向上或向下延伸,就得到二次函数的图像。
当抛物线与x 轴只有一个交点或无交点时,描出抛物线与y 轴的交点C 及对称点D 。
由C 、M 、D 三点可粗略地画出二次函数的草图。
如果需要画出比较精确的图像,可再描出一对对称点A 、B ,然后顺次连接五点,画出二次函数的图像。
【例1】 已知函数y=x 2-2x-3,(1)写出函数图象的顶点、图象与坐标轴的交点,以及图象与 y 轴的交点关于图象对称轴的对称点。
然后画出函数图象的草图;(2)求图象与坐标轴交点构成的三角形的面积:(3)根据第(1)题的图象草图,说 出 x 取哪些值时,① y=0;② y<0;③ y>0二次函数的解析式有三种形式:(1)一般式:)0,,(2≠++=a c b a c bx ax y 是常数,(2) 交点式:当抛物线c bx ax y ++=2与x 轴有交点时,即对应的一元二次方程02=++c bx ax 有实根1x 和2x 存在时,根据二次三项式的分解因式))((212x x x x a c bx ax --=++,二次函数c bx ax y ++=2可转化为两根式))((21x x x x a y --=。
二次函数知识归纳与总结
二次函数知识归纳与总结二次函数的概念和图像1、二次函数的概念一般地,如果特)0,,(2≠++=a c b a c bx ax y 是常数,,特别注意a 不为零那么y 叫做x 的二次函数。
)0,,(2≠++=a c b a c bx ax y 是常数,叫做二次函数的一般式。
2、二次函数的图像二次函数的图像是一条关于abx 2-=对称的曲线,这条曲线叫抛物线。
抛物线的主要特征:①有开口方向;②有对称轴;③有顶点。
3、二次函数图像的画法 五点法:(1)先根据函数解析式,求出顶点坐标,在平面直角坐标系中描出顶点M ,并用虚线画出对称轴(2)求抛物线c bx ax y ++=2与坐标轴的交点:当抛物线与x 轴有两个交点时,描出这两个交点A,B 及抛物线与y 轴的交点C ,再找到点C 的对称点D 。
将这五个点按从左到右的顺序连接起来,并向上或向下延伸,就得到二次函数的图像。
当抛物线与x 轴只有一个交点或无交点时,描出抛物线与y 轴的交点C 及对称点D 。
由C 、M 、D 三点可粗略地画出二次函数的草图。
如果需要画出比较精确的图像,可再描出一对对称点A 、B ,然后顺次连接五点,画出二次函数的图像。
二次函数的解析式二次函数的解析式有三种形式:口诀----- 一般 两根 三顶点 (1)一般 一般式:)0,,(2≠++=a c b a c bx ax y 是常数,(2)两根 当抛物线c bx ax y ++=2与x 轴有交点时,即对应二次好方程02=++c bx ax 有实根1x 和2x 存在时,根据二次三项式的分解因式))((212x x x x a c bx ax --=++,二次函数c bx ax y ++=2可转化为两根式))((21x x x x a y --=。
如果没有交点,则不能这样表示。
a 的绝对值越大,抛物线的开口越小。
(3)三顶点 顶点式:)0,,()(2≠+-=a k h a k h x a y 是常数,二次函数的最值如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当abx 2-=时,a b ac y 442-=最值。
二 次 函 数 规 律 总 结
二次函数规律总结解析式y=ax²a为常数,a≠0y=ax² +ca,c为常数,a≠0一般式:y=ax²+bx+ca,b,c为常数,a≠0顶点式:y=a(x-h)2a,h为常数,a≠0顶点式:y=a(x-h)2+ka,b,c为常数,a≠0交点式:y=a(x-x₁)(x-x2)a,b,c为常数,a≠0图像形状注:在3种形式的互相转化中,有如下关系: h=-b/2a k=(4ac-b2)/4a x₁,x₂=(-b±√b2-4ac)/2a开口方向及大小a>0时,开口方向向上,a<0时,开口方向向下。
IaI还可以决定开口大小,IaI越大开口就越小,IaI越小开口就越大。
顶点坐标-b/2a,(4ac-b2)/4a(0,0)-b/2a, (4ac-b2)/4a(0,c)-b/2a, (4ac-b2)/4a(h, k) (h,k)与x轴交点A(x₁,0).B(x₂,0)对称轴X=-b/2aX=0X=-b/2aX=0X=-b/2a X=h x=h 两焦点距离的一半:(/x2-x1/)/2这类问题一般是给出方程的两根,可以设二次函数“两点式”,再根据所得的条件一步一步推出结论a,b决定对称轴位置,a与b同号时(即ab>0),对称轴在y轴左a与b异号时(即ab<0),对称轴在y轴右。
c决定抛物线与y轴交点。
交于(0,c),c是纵截距。
增减性先找到对称轴X=-b/2a,再找开口方向a,画出简图就可以找到增减性。
最值a>0时,开口方向向上有最小值ymin=(4ac-b2)/4aa<0时,开口方向向下有最大值ymax=(4ac-b2)/4a平移规律以y=ax²为例,左加右减,(改变X),上加下减(改变C)变为顶点式。
有要求再化成一般式。
轴对称y=ax²+bx+cy=a(x-h)2+k 关于x轴对称的解析式为:y=-ax²-bx-c;关于y轴对称的解析式为:y=ax²-bx+c;关于x轴对称的解析式为:y= -a(x-h)2-k;关于y轴对称的解析式为:y= a(x+h)2+k;图像与轴交点y=ax²+bx+c与y轴的交点(0,c),与x轴交点的横坐标为方程ax²+bx+c=0的根函数小结正比例函数一次函数反比例函数解析式y = k x ( k≠0 )y=k x + b(k,b为常数,且k ≠0)y=k/x或y=kx-1 (K为常数,K不等于0)图像k>0 k<0 k>0,b>0 k>0,b<0 k<0, b>0 k<0 b<0 k>0 k<0 增减性X y X y平移规律对称规律以y=kx为例,左加右减,(改变X),上加下减(改变b),有要求再化成一般式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中函数问题涉及到的常用公式或结论及其训练一、 常用公式或结论(1)横线段的长 = x 大-x 小 =x 右-x 左 =横标之差的绝对值(用于情况不明)。
纵线段的长 = y 大-y 小=y 上-y 下 = 纵标之差的绝对值(用于情况不明)。
(2)点轴距离:点P (x 0 ,y 0)到X 轴的距离为0y ,到Y 轴的距离为o x 。
(3)两点间的距离公式:若A (x 1,y 1),B(x 2,y 2), 则 AB=221212()()x x y y -+- (4)点到直线的距离:点P (x 0 ,y 0)到直线Ax+By+C=0 (其中常数A,B,C 最好化为整系数,也方便计算)的距离为:0022Ax By Cd A B++=+(5)中点坐标公式:若A(x 1,y 1),B (x 2,y 2),则线段AB 的中点坐标为(1212,22x x y y ++)(6)直线的斜率公式:若A (x 1,y 1),B (x 2,y 2)(x 1≠x 2),则直线AB 的斜率为:1212=AB y y k x x --,(x 1≠x 2) (7)两直线平行的结论:已知直线l 1: y=k 1x+b 1 ; l 2: y=k 2x+b 2①若l 1//l 2,则k 1=k 2;②若k 1=k 2,且b 1 ≠b 2,则 l 1//l 2。
(8)两直线垂直的结论:已知直线l 1: y=k 1x+b 1 ; l 2: y=k 2x+b 2 ①若l 1┴l 2,则k 1•k 2 =-1;②若k 1•k 2 =-1,则l 1┴l 2(9)直线与抛物线(或双曲线)截得的弦长公式:【初高中数学重要衔接内容之一,设而不求的思想】直线y=kx+n 与抛物线y=ax 2+bx+c (或双曲线y=m/x )截得的弦长公式是:AB=2121x x k -•+=2122124)(1x x x x k -+•+证明如下:设直线y=kx+n 与抛物线y=ax 2+bx+c (或双曲线y=m/x )交于A (x 1, y 1), B (x 2, y 2)两点,由两点间的距离公式可得:AB=221221)()(y y x x -+-,因为A (x 1, y 1),B (x 2, y 2)两点是直线y=kx+n 与抛物线抛物线y=ax 2+bx+c (或双曲线y=m/x )的交点,所以 A (x 1, y 1),B (x 2, y 2)两点也在直线y=kx+n 上,∴y 1=kx 1+n, y 2=kx 2+n, ∴y 1-y 2=(kx 1+n )—(kx 2+n )=kx 1-kx 2=k (x 1-x 2), ∴AB=2212221)()(x x k x x -+-=2212))(1(x x k -+=2121x x k -•+=2122124)(1x x x x k -+•+而x 1, x 2显然是直线y=kx+n 与抛物线y=ax 2+bx+c (或双曲线y=m/x )组成方程组后,消去y (用代入法)所得到的那个一元二次方程的两根,从而运用韦达定理x 1+x 2 , x 1•x 2可轻松求出,进而直线与抛物线(或双曲线)截得的弦长就很容易计算或表示出来。
(10)由特殊数据得到或联想的结论:①已知点的坐标或线段的长度中若含有23、等敏感数字信息,那很可能有特殊角出现。
②在抛物线的解析式求出后,要高度关注交点三角形和顶点三角形的形状,若有特殊角出现,那很多问题就好解决了。
③还要高度关注已知或求出的直线解析式中的斜率K的值,若3K=±,则直线3与X轴的夹角为0±,则直线30;若K=1±;则直线与X轴的夹角为045;若K=3与X轴的夹角为060教学建议:在八年级下册讲一次函数与反比例函数时,就引入上述绝大多数公式,然后再强化练习,为后续学习打下基础。
二、基本公式或结论训练--------破解函数难题的基石(一)横线段的长度计算:【特点:两端点的y标相等,长度=-】。
x x大小(1)若A(2,0),B(10,0),则AB=————————。
(2)若A(-2,0),B(-4,0),则AB=——————————。
(3)若M(-3,0),N(10,0),则MN=——————————。
(4)若O(0,0),A(6,0),则OA=————————。
(5)若O(0,0),A(-4,0),则OA=——————————。
(6)若O(0,0),A(t,0),且A在O的右端,则OA=———。
(7)若O(0,0),A(t,0),且A在O的左端,则OA=———。
(8)若A(-2t,6),B(3t,6),且A在B的右端,则AB=————。
(9)若A(4t,m),B(1-2t,m),且B在A的左端,则AB=——————。
(10)若P(2m+3,a),M(1-m,a),且P在M的右端,则PM=————————。
注意:横线段上任意两点的y标是相等的,反之y标相等的任意两个点都在横线段上。
】。
(二)纵线段的长度计算:【特点:两端点的x标相等,长度=-y y大小(1)若A(0,5),B(0,7),则AB=——————————。
(2)若A(0,-4),B(0,-8),,则AB=——————。
(3)若A(0,2),B(0,-6),则AB=————————。
(4)若A(0,0),B(0,-9),则AB=————————。
(5)若A(0,0),B(0,-6),则AB=————————。
(6)若O(0,0),A(0,t),且A在O的上端,则OA=————————。
(7)若O(0,0),A(0,t),且A在O的下端,则OA=——————————。
(8)若A(6,-4t),B(6,3t),且A在B的上端,则AB=————————。
(9)若M (m,1-2t),N(m,3-4t),且M 在N 的下端,则MN=————————。
(10)若P (t,3n+2),M(t,1-2n),且P 在M 的上端,则PM=————————。
注意:纵线段上任意两点的x 标是相等的,反之x 标相等的任意两个点都在纵线段上。
(三)点轴距离:一个点(x y 标标,)到x 轴的的距离等于该点的y 标的绝对值(即y 标),到y 轴的距离等于该点的x 标的绝对值(即x 标)。
(1)点(-4,-3)到x 轴的距离为————————,到y 轴的距离为————————。
(2)若点A (1-2t,223t t +-)在第一象限,则点A 到x 轴的距离为————,到y 轴的距离为__________。
(3)若点M (t,243t t ++)在第二象限,则点M 到x 轴的距离为 ;到y 轴的距离为———。
(4)若点A (-t,2t-1)在第三象限,则点A 到x 轴的距离为—,到y 轴的距离为 。
(5)若点N (t ,-t 2+2t-3)点在第四象限,则点N 到x 轴的距离为——————,到y 轴的距离为_________。
(6)若点P (t ,t 2+2t-3)在x 轴上方,则点P 到x轴的距离为____________。
(7)若点Q(t,t2-2t-6)在x轴下方,则点Q到x轴的距离为_____________。
(8)若点D(t,t2+4t-5)在y轴左侧,则点D到y轴的距离为____________。
(9)若点E(n,2n+6)在y轴的右侧,则点E到y轴的距离为_______________。
(10)若动点P(t,t2-2t+3)在x轴上方,且在y轴的左侧,则点P到x轴的距离为_________________,到y轴的距离为——————————。
(11)若动点P(t,t2-2t+3)在x轴上方,且在y轴的右侧,则点P到x轴的距离为———————,到y轴的距离为————————————。
(12)若动点P(t,t2-2t+3)在x轴下方,且在y轴的左侧,则点Px轴的距离为———————,到y轴的距离为——————————。
(13)若动点P(t,t2-2t+3)在x轴下方,且在y轴的右侧,则点P到x轴的距离为———————,到y轴的距离为——————————。
注意:在涉及抛物线,直线,双曲线等上的动点问题中,在动点坐标“一母示”后,还要高度关注动点运动变化的区域(例如:动点P在抛物线y=x2-2x+3上位于x轴下方,y轴右侧的图象上运动),以便准确写出动点坐标中参数字母的取值范围,以及点轴距离是等于相应x(或y)的相反数,标标还是其本身。
(四)中点坐标的计算:若【A (x 1,y 1),B(x 2,y 2),,则线段AB 的中点坐标为(1212,22x xy y ++)】(1)若A (-4,3),B (6,7),则AB 中点为————————————。
(2)若M (0,-6),N (6,-4),则MN 的中点坐标为————————————。
(3)若P (1-32,),Q (1132,),则PQ 的中点坐标为————————。
(4)若A(1,2),B(-3,4),且B 为AM 的中点,则M 点的坐标为——————————。
(5)若A(-1,3),B(0,2),且A 为BP 中点,则P 点坐标为————————————。
(6)点P (-5,0)关于直线x=2的对称点的坐标为————————————。
(7)点P (6,0)关于直线x=1的对称点的坐标为————————————。
(8)点P (6,2)关于直线x=3的对称点的坐标为___________。
(9)点Q (-4,3)关于直线x=-3的对称点的坐标为——————————。
(10)点M (-4,-2)关于直线x=2的对称点的坐标为————————————。
(11)点P (4,-3)关于直线x=-1的对称点的坐标为————————————。
(12)点M (-4,2)关于直线y=-1的对称点的坐标为——————————。
(13)点T (4,-3)关于直线y=1的对称点的坐标为——————————。
(14)点Q (0,-3)关于x轴的对称点的坐标为————————————。
(15)点N (4,0)关于y轴的对称点的坐标为——————。
(五)由两直线平行或垂直,求直线解析式。
【两直线平行,则两个k 值相等;两直线垂直,则两个k 值之积为-1.】(1)某直线与直线y=2x+3平行,且过点(1,-1),求此直线的解析式。
(2)某直线与直线y=12-x+1平行,且过点(2,3),求此直线的解析式。
(3)某直线与直线y=253x --平行,且过点(-3,0),求此直线的解析式。
(4)某直线与y 轴交于点P (0,3),且与直线y=112x -平行,求此直线的解析式。
(5)某直线与x 轴交于点P (-2,0),且与直线y=142x -+平行,求此直线的解析式。
