湖南省大学生物理竞赛试卷及答案
大学生物理竞赛试题及答案

大学生物理竞赛试题及答案
一.填空题(每题两空,每空2分,共48分)
1.一火箭在环绕地球的椭圆轨道上运动,为使它进入逃逸轨道需要增加能量,为此发动机进行了短暂的点火,把火箭的速度改变了,只有当这次点火在轨道点,且沿
着方向时,所需为最小。
2.一个质量为的小球从一个半径为,质量为的光滑半圆柱顶点下滑,半圆柱底面和水平面光滑接触,写出小球在下滑过程中未离开圆柱面这段时间内相对地面的坐标系的运动轨迹方程。
如果半圆柱固定,小球离开半圆柱面时相对y轴的偏转角。
3.常温下,氧气可处理成理想气体,氧气分子可视为刚性双原子分子。
的氧气在温度下体积为.(1)若等温膨胀到,则吸收热量为
_______________________________;(2)若先绝热降温,再等压膨胀到(1)中所达到的终态,则吸收热量为___________________。
4.我们可以用热机和热泵(逆循环热机)构成一个供暖系统:燃烧燃料为锅炉供热,令热机工作于。
大学生物理竞赛试题及解答

其中 ^i 代表 x 轴正方向上的单位矢量. 你能否举出理由说明此结果并不正确. 31 ( 6 分) 用牛顿环测定透镜曲率半径实 验中, 为什么有时圆环条纹的中心并非暗斑, 甚至出现亮班 ( 理论上应是暗斑) ? 用什么数 据处理方法能消除它对曲率半径测量的影 响? 四、 在下面两题中任选一题作答. ( 10 分)
(D ) 此问题中谈 a 点、 b 点的电势无意
义 .
71 ( 3 分) 如图示, S 、 S 1、 S 2 为狭缝, P 1、 为线偏振片 (P 及 P ′ 可以撤去) , 其 P 2、 P、 P′
率, ∃ v 为一固定的速率间隔, 则速率在 v ± ∃ v 范围内的分子的百分率随着温度的增加 将 , 速率在 v p 到 v 之间的分子 的百分率随着温度的增加将 . 31 ( 2 分) 从单一热源吸取热量并将其完 全用来对外作功, 是不违反热力学第二定律 的, 例如 过程就是这种情况 . 41 ( 5 分) 如图示, 截面积为 A 、 单位长度 上匝数为 n 的螺绕环上套一边长为 l 的方形 线 圈, 今 在 方 形 线 圈 中 通 以 交 流 电 流 I = I 0 sin Ξt, 螺绕环两端为开端, 则其间电动势的 大小为
中 P 1 和 P 2 的偏振化方向互相垂直, P 和 P ′ 的偏振化方向互相平行, 且与 P 1、 P 2 的偏振 化方向皆成 45° 角. 在下列四种情况下, 屏上 有无干涉条纹. ( 四种情况全部填对才能得 分).
① 撤 掉 P 、P ′ , 保 留 P 1、P 2 , 屏 上 干涉条纹; ② 撤掉 P ′ 保留 P 、 P 1、 P 2 , 屏上 干涉条纹; ③ 撤 掉 P , 保 留 P 1、P 2、P ′ , 屏上 干涉条纹; ④ P 1、P 2、P 、P ′ 同 时 存 在, 屏 上 干涉条纹; ( 81 2 分) 卢瑟福 Α粒子散射实验证实了 , 斯 特 恩—盖 拉 赫 实 验 证 实 了
物理竞赛大学试题及答案

物理竞赛大学试题及答案一、选择题(每题4分,共40分)1. 光在真空中的传播速度是:A. 299,792,458 m/sB. 299,792,458 km/sC. 299,792,458 cm/sD. 299,792,458 mm/s答案:A2. 牛顿第二定律的表达式是:A. \( F = ma \)B. \( F = mv \)C. \( F = m \frac{v^2}{r} \)D. \( F = \frac{Gm_1m_2}{r^2} \)答案:A3. 根据热力学第一定律,系统内能的增加等于:A. 系统对外做的功B. 系统吸收的热量C. 系统对外做的功和系统吸收的热量之和D. 系统对外做的功和系统放出的热量之和答案:C4. 电磁波的波长、频率和速度之间的关系是:A. \( \lambda = \frac{c}{f} \)B. \( \lambda = cf \)C. \( \lambda = \frac{f}{c} \)D. \( \lambda = \frac{1}{cf} \)答案:A5. 以下哪项是描述电流的物理量:A. 电压B. 电阻C. 电荷D. 电流答案:D6. 根据库仑定律,两个点电荷之间的力与它们电荷量的乘积成正比,与它们之间距离的平方成反比。
这个定律的数学表达式是:A. \( F = k \frac{q_1q_2}{r^2} \)B. \( F = \frac{q_1q_2}{kr^2} \)C. \( F = k \frac{r^2}{q_1q_2} \)D. \( F = \frac{k}{q_1q_2r^2} \)答案:A7. 在理想气体状态方程中,P、V、T分别代表:A. 压力、体积、温度B. 功率、体积、时间C. 功率、速度、温度D. 压力、速度、时间答案:A8. 光的折射定律,即斯涅尔定律,描述的是:A. 入射角和折射角的关系B. 入射角和反射角的关系C. 折射角和反射角的关系D. 入射角和折射角以及反射角的关系答案:A9. 根据欧姆定律,电阻R、电流I和电压V之间的关系是:A. \( R = \frac{V}{I} \)B. \( R = IV \)C. \( I = \frac{V}{R} \)D. \( V = IR \)答案:D10. 以下哪个公式描述了动能和势能的关系:A. \( KE = \frac{1}{2}mv^2 \)B. \( PE = mgh \)C. \( KE + PE = constant \)D. \( KE = PE \)答案:C二、填空题(每题4分,共20分)1. 根据能量守恒定律,一个封闭系统的总能量在没有外力作用的情况下保持______。
湖南省第五届大学生物理竞赛试卷
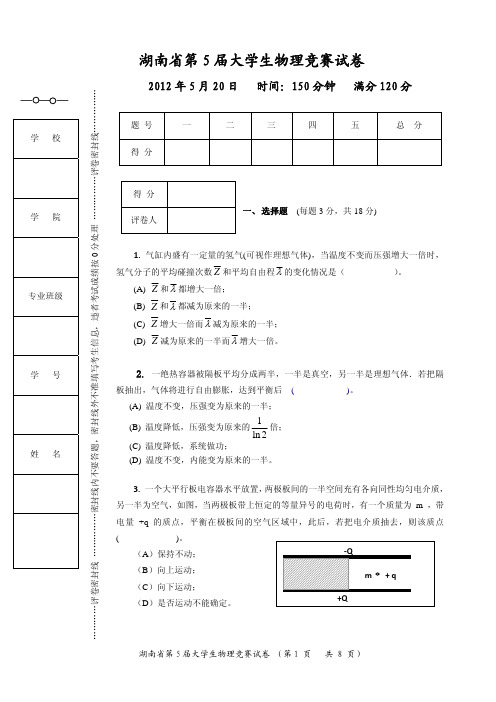
(
)。
(A)保持不动;
‐Q
(B)向上运动; (C)向下运动; (D)是否运动不能确定。
m +q +Q
湖南省第 5 届大学生物理竞赛试卷 (第 1 页 共 8 页)
4. 一个在磁场 B 中的金属窄条(宽度为 h,厚度为 b),
B
通以电流 I,如图,若金属中是电子导电,则 (
)。
I
(A) 导体顶部电势高于底部电势;
(B) 导体顶部电势低于底部电势;
(C) 导体顶部电势与底部电势一样高; (D) 无法确定。
5. 一束自然光自空气射向一块平板玻璃(如图),设入射角等于布儒斯特角 i0 ,则在界面 2 的反
射光是 (
)。
(A) 是自然光;
(B) 是完全偏振光且光矢量的振动方向垂直于入射面;
(C) 是完全偏振光且光矢量的振动方向平行于入射面;
,
(3) 多次观察某一分子的速率,发现其速率大于 v0 的几率=
。
4. 一平面简谐波在弹性媒质中传播时,某一时刻在传播方向上媒质中某质元在负的最大位移处,
则它的动能为
,势能为
(填最大、最小、零)。
5. 设空气中声速为 330 m ⋅ s−1 ,一列火车以 30 m ⋅ s−1 的速度行驶,机车上汽笛的频率为 600Hz 。
有
条,其中属于巴耳末系的谱线有
条。
8. 某一宇宙射线中的介子的动能 Ek = 7M 0c 2 ,其中 M 0 是介子的静止质量。则在实验室中观察
到它的寿命是它的固有寿命的
倍。
湖南省第 5 届大学生物理竞赛试卷 (第 3 页 共 8 页)
………………………………密 ……………………………………………封 ……………………………………………………线………………………………………
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
湖南省第4届大学生物理竞赛试卷2011年5月14日 时间:150分钟 满分120分一、 选择题 (每题3分,共18分)1.设某种气体的分子速率分布函数为)(v f ,则速率在1v ~2v 内的分子的平均速率为( )。
(A) ⎰21)(v v v d v vf ; (B) ⎰21)(v v v d v f v ;(C) ⎰⎰2121)()(v v v v v d v f vd v vf ; (D) ⎰⎰∞)()(21v d v f vd v f v v 。
2. 如图所示带负电的粒子束垂直地射入两磁铁之间的水平磁场,则( )。
(A) 粒子向N 极移动; (B) 粒子向S 极移动; (C) 粒子向下偏转; (D) 粒子向上偏转。
3.如图所示,一个带电量为 q 的点电荷位于立方体的 A 角上,则通过侧面 abcd 的电场强度通量等于( )。
A 、 06εq ;B 、012εq; C 、024εq ; D 、048εq。
4. 如图a 所示, 一光学平板玻璃 A 与待测元件 B 之间形成空气劈尖,用波长 nm 500=λ 的单色光垂直照射,看到的反射光的干涉条纹如图b 所示,有些条纹弯曲部分的顶点恰好于其右边条纹的直线部分的切线相切,则工件的上表面缺陷是 ( ) 。
(A ) 不平处为凸起纹,最大高度为nm 500; (B ) 不平处为凸起纹,最大高度为nm 250;Aqcb da(C ) 不平处为凹槽,最大高度为nm 500; (D ) 不平处为凹槽,最大高度为nm 250。
5. 在图示三种透明材料构成的牛顿环装置中,用单色光垂直照射,在反射光中看到干涉条纹,则在接触点P 处形成的圆斑为( ) 。
(A) 全明; (B) 全暗;(C) 右半部明,左半部暗; (D) 右半部暗,左半部明。
6. 已知粒子在一维矩形无限深势阱中运动,其波函数为: axax 23cos1)(πψ⋅=)(a x a ≤≤-那么粒子在6/5a x =处出现的几率密度为( )。
(A) )2/(1a ; (B) a /1 ; (C) a 2/1 ; (D) a /1 。
二、填空题(每题3分,共21分)1. 一匀质细杆长为l ,质量为m ,杆两端用线吊起,保持水平,现有一条线突然断开,则断开瞬间另一条线的张力为 。
2. 图示两条曲线分别表示氦、氧两种气体在相同温度T 时分子按速率的分布,其中曲线 1 表示 _ _气分子的速率分布曲线,曲线 2 表示 __ _ 气分子的速率分布曲线。
3. 一氧气瓶的容积为V ,充入氧气的压强为1P ,用了一段时间后压强降为2P ,则瓶中剩下的氧气的内能与未用前氧气的内能之比为 。
4. 长直导线中通有电流 I ,长L 的金属棒AB 以速度V平行于vf(v)12I alVA B长直导线作匀速运动。
棒近导线一端与导线的距离为a ,则金属棒中的感应电动势i ε的大小为 ,i ε的方向为 。
5. 电荷线密度为 1λ 的无限长均匀带电直线,其旁垂直放置电荷线密度为 2λ 的有限长均匀带电直线AB ,两者位于同一平面内,则AB 所受静电作用力的大小F= 。
6. 三个偏振片1P 、2P 与3P 堆叠在一起,1P 与3P 的偏振化方向相互垂直,2P 与1P 的偏振化方向间的夹角为 30,强度为0I 的自然光垂直入射于偏振片1P ,并依次透过偏振片1P 、2P 与3P ,若不考虑偏振片的吸收和反射,则通过三个偏振片后的光强为 。
7. 如果一个光子的能量和一个德布罗意波长为λ 的电子的总能量相等,设电子静止质量为e m ,则光子的波长为 。
三、简答题(共14分)1. 红外线是否适宜于用来观察康普顿效应,为什么? (红外线波长的数量级为510A ,电子静止质量311011.9-⨯=e m kg ,普朗克常量s J 1063.634⋅⨯=-h ) (本题5分)2. 假定在实验室中测得静止在实验室中的+μ子(不稳定的粒子)的寿命为6102.2-⨯s ,而当它相对于实验室运动时实验室中测得它的寿命为51063.1-⨯s .试问:这两个测量结果符合相对论的什么结论? +μ子相对于实验室的速度是真空中光速c 的多少倍?(本题5分)3. 为什么窗玻璃在日光照射下我们观察不到干涉条纹?(本题4分) 四、计算题(1至5小题每题10分,第6小题7分,共57分)1. 在高处自由下落一个物体,质量为m ,空气阻力为2kv -,落地时速度为m v ,问物体从多高处落下?2. 一半径为R ,质量为m 的匀质圆盘,平放在粗糙的水平桌面上。
设盘与桌面间的摩擦系数为μ,令圆盘最初以角速度0ω绕通过中心且垂直盘面的轴旋转,问它将经过多少时间才停止转动?3. 在半径为R 的圆柱形区域中有沿轴向的均匀磁场,磁感应强度满足kte B B -=0 ,有一根长度也是R 的金属杆放在圆柱内,其两端与柱面的壁相接,并处在与磁感线垂直的方向上,试求出:(1)在柱形区域内,涡旋电场强度E ; (2)在金属杆上,感应电动势ε。
4. 轴在同一水平面上的两个相同的圆柱体, 两轴相距L 2,它们以相同的角速度ω相向转动。
一质量为 m 的木板搁在两圆柱体上 , 木板与圆柱体之间的滑动摩擦系数为μ。
问木板偏离对称位置后将如何运动?周期为多少?5. 实验表明,在靠近地面处有相当强的电场,电场强度E垂直于地面向下,大小约为C /N 100;在离地面km .51高的地方,E也是垂直于地面向下的,大小约为C /N 25。
(1) 试计算从地面到此高度大气中电荷的平均体密度;(2) 假设地球表面处的电场强度完全是由均匀分布在地表面的电荷产生,求地面上的电荷面密度。
(已知:212120m N C 10858---⋅⋅⨯=.ε)6. 设粒子在宽度为a的一维无限深势阱运动时,其德布罗意波在阱内形成驻波,ωωL2试利用这一关系导出粒子在阱中的能量计算式。
(本题7分) 五、证明题(10分)定体摩尔热容量V C 为常量的某理想气体,经历如图所示的pV 平面上的两个循环过程1111A C B A 和2222A C B A ,相应的效率分别为1η和2η,试证1η与2η相等。
湖南省第3届大学生物理竞赛试卷O1A p1B 1C 2C 2B 2A 1V 2V V2.(本题15分)是给出5种测量温度的方法,并简述每种方法的实验原理。
2010年湖南大学物理竞赛卷答案 一、填空题(每题4分共40分) 1. h 1v /(h 1h 2)2. mgl μ21 参考解: M =⎰M d =()mgl r r l gm l μμ21d /0=⎰3. (1) AM , (2) AM 、BM4. 半径为R 的无限长均匀带电圆柱面5. ωλB R 3π 在图面中向上 6.)2/cos(/d d π+==t A NbB t x NbB ωωt NBbA ωωsin =7. t E R d /d 20πε8. 291 Hz 或309 Hz9. }]/)1([cos{φω+++=u x t A y (SI) 10. 平行或接近平行二、计算题(每题10分共80分)1. 解:分别取m 1和链条m 为研究对象,坐标如图. 设链条在桌边悬挂部分为x , a m T g m 11=-, ma l xgm T =-/,解出)/1(21l x g a -= 2分当链条刚刚全部滑到桌面时x = 0,a ==g 21 4.9 m/s 21分xt x x t a d d d d d d d d vvv v -=⋅==1分 x l x g x a d )/1(21d d --=-=v v 2分两边积分 ⎰⎰--=002d )1(d 2l x l xg v v v 2分22222)4/3(/21gl l gl gl =-=v==2321gl v 1.21 m/s 2分(也可用机械能守恒解v )2. 解:(1) 选细棒、泥团为系统.泥团击中后其转动惯量为 ()()224/331l m Ml J +=2分 在泥团与细棒碰撞过程中对轴O 的角动量守恒()ωαJ l m =⋅cos 4/30v 2分∴ ()()l m M m ml Ml l m 2716cos 36169314/3cos 0220+=⎪⎭⎫ ⎝⎛+⋅=ααωv v 2分 (2) 选泥团、细棒和地球为系统,在摆起过程中,机械能守恒.()()()θθωcos 14/3cos 121212-+-=mgl Mgl J 2分 ()mgl Mgl ml Ml 4321)16931(21cos 1222++=-ωθ∴ ()()⎥⎦⎤⎢⎣⎡++-=-g m M l m M 724827161cos 21ωθ()()⎥⎦⎤⎢⎣⎡++-=-gl m M m M m 271632cos 541cos 22021αv 2分3. 解:(1) 系统开始处于标准状态a ,活塞从Ⅰ→Ⅲ为绝热压缩过程,终态为b ; 活塞从Ⅲ→Ⅱ为等压膨胀过程,终态为c ;活塞从Ⅱ→Ⅰ为绝热膨胀过程,终态为d ;除去绝热材料系统恢复至原态a ,该过程为等体过程。
该循环过程在p -V 图上对应的曲线如图所示。
图3分(2) 由题意可知 p a =1.013×105 Pa ,V a =3×10-3m 3, T a = 273K ,V b =1×10-3m 3, V c =2×10-3m 3. ab 为绝热过程,据绝热过程方程 )5/7(,11==--γγγb b a a V T V T ,得K 424)(1==-a ba b T V V T γ 1分 bc 为等压过程,据等压过程方程 T b / V b = T c / V c848==bbc c V T V T K 1分 cd 为绝热过程,据绝热过程方程 )(,11a d d d c c V V V T V T ==--γγ,得K 721)(1==-c dc d T V V T γ 1分(3) 在本题循环过程中ab 和cd 为绝热过程,不与外界交换热量; bc 为等压膨胀过程,吸收热量为 Q bc =νC p (T c -T b )式中R C p 27=.又据理想气体状态方程有p a V a = νRT a ,可得J 1065.1)(273⨯=-⋅=b c aa a bc T T T V p Q 2分 da 为等体降温过程,放出热量为)(a d V da T T C Q -=νJ 1024.1)(252⨯=-⋅=a d aa a T T T V p 2分 4. 解:(1) 设两球壳上分别带电荷+Q 和-Q ,则其间电位移的大小为 D =Q / (4r 2) 两层介质中的场强大小分别为E 1 = Q / (40 r 1r 2) 1分E 2 = Q / (40 r 2r 2) 1分 在两层介质中场强最大处在各自内表面处,即E 1M = Q / (4r 121R ), E 2M = Q / (4r 2R 2)两者比较可得 ()()21221122212///R R R R E E r r M M ==εεVp Oadc b V b V c V a已知R 2<2R 1,可得E 1M <E 2M ,可见外层介质先击穿. 3分(2) 当外层介质中最大场强达击穿电场强度E M 时,球壳上有最大电荷.Q M= 40r 2R 2E M 2分此时,两球壳间电压(即最高电压)为 ⎰⎰⋅+⋅=21d d 2112R R RR r E r E U⎰⎰π+π=21220210d 4d 4R Rr M RR r M rrQ r r Q εεεε ⎪⎪⎭⎫⎝⎛-+-=2221112R R R R R R RE r r M r εεε 3分5. 解:当线框的一部分进入磁场后,线框内产生动生电动势和感应电流I .因为有自感且线框电阻忽略,所以线框内感应电流I 的微分方程是:v a B t IL0d d = ① 2分 线框的运动方程为: I va B t m 0d d -= ② 2分 联立方程得: 0d d 222=+v vωt1分 其中 mLaB 0=ω 1分∴ t c t c ωωcos sin 21+=v 1分当 t = 0时,v = v 0 ∴ c 2 = v0 且因t = 0时,I =0 ∴ c 1 =0∴ t ωcos 0v v = 1分 线框沿x 方向移动的距离为: t x ωωsin 0v =2分如用能量方法解,则对应于① ②两式评分如下:2220212121LI m m +=v v 2分 把上式两边对时间求导,得 0d d d d =+tI LI t m v ∵ v a B t IL 0d d = 2分 代入上式得 0d d 0=+a IB tm v1分6. 解:设入射波的表达式为 )22cos(1φλν+π-π=xt A y 1分则反射波的表达式为 ])872(22cos[2φλλν+-⨯π-π=x t A y )2322cos(φλν+π-π+π=x t A 3分驻波的表达式为 21y y y +=)432cos()432cos(2φνλ+π-ππ-π=t x A 1分在t = 0时,x = 0处,有y = 0和 ( d y / d t ) < 0,故得:0)4/3cos()4/3cos(2=π-π-φA0)4/3sin()4/3cos(22<π-π-⋅π-φνA由上两式求得 = /4 2分B 点(λ21=x )的振动方程为 )π41π43π2cos()π4321π2cos(2+--=t A y B νλλ)212cos(2π-π=t A νt A νπ=2sin 2 3分7. 解:(1) 斜入射时的光栅方程λθk i d d =-sin sin , k = 0,±1,±2,… 3分 规定i 从光栅G 的法线n -n 起,逆时针方向为正;从光栅G 的法线n -n 起,逆时针方向为正. (2) 对应于i = 30°,设 = 90°,k = k max1,则有λ1max 30sin 90sin k d d =︒-︒)30sin 90)(sin /(1max ︒-︒=d d k λ= 2.10取整 k max1 = 2. 2分(3) 对应于i = 30°,设 = -90°, k = k max2, 则有 λ2max 30sin )90sin(k d d =︒-︒-]30sin )90)[sin(/(2max ︒-︒-=d d k λ = - 6.30取整 k max1 = -6. 2分 (4) 但因 d / a = 3,所以,第-6,-3,… 级谱线缺级. 2分 (5) 综上所述,能看到以下各级光谱线:-5,-4,-2,-1,0,1,2,共7条光谱线. 1分8. 解:设粒子A的速度为A v,粒子B的速度为B v ,合成粒子的运动速度为V.由动量守恒得220220220/1/1/1cV VM cm cm BBAA-=-+- v v v v 2分因1v v v ==B A ,且B A v v-=,所以 0=V . 2分即合成粒子是静止的.由能量守恒得2022202220/1/1c M c c m c c m =-+-v v 3分解出 2200/12cm M v -= 3分θ G L 2 Cnn i d sin θd sin i屏第k 级谱线光栅 透镜4m BA x湖南省第一届大学生物理竞赛试题2008年4月26日 时间:150分钟 满分120分一、填空题(每空3分,共36分)1.一质点作直线运动,加速度为t A a ωωsin 2=,已知0=t 时,质点的初始状态为00=x ,A v ω-=0,则该质点的运动方程为 。
